Abstract
Research on hollow nanoshells has, for years, claimed to involve free, pre-existing nanobubbles as soft templates. It is a challenge to demonstrate this due to the difficulty of in situ observation during solution-based reactions. We show that no available free-bubble theory can describe the mysterious behavior of the bubble number density n. A new mechanism of collision coalescence of bubble–particle systems is suggested to form hollow nanoshells. By approximating relative velocity as ∼R−z (R is bubble radius), numerical simulations can reproduce the counterintuitive observations in the regime 1 < z < 2. We discuss the mechanism based on successful synthesis of grain-monolayer thin, fractal-like incomplete, multi-metallic nanoshells with superior catalytic activity. The behaviors of n, R, and shell thickness h are closely reproduced by z = 1.6.
Export citation and abstract BibTeX RIS
1. Introduction
Nanobubbles help in synthesizing hollow nanoshells. Such shells are spherical and have narrowly distributed radii R (figure 1). It seems as if bubbles never change their radius or ever collide. This suggests pre-existing, free nanobubbles. The collision coalescence of bubble–particle systems (BPSs) seems obviously mistaken. It is a great challenge to observe the formation of the shells. The high pressures and temperatures during hydrothermal synthesis make the reaction system a black box. In this work, we will demonstrate that the collision coalescence of BPSs can explain the formation of nanoshells, while no simpler theory is compatible with the empirical observations.
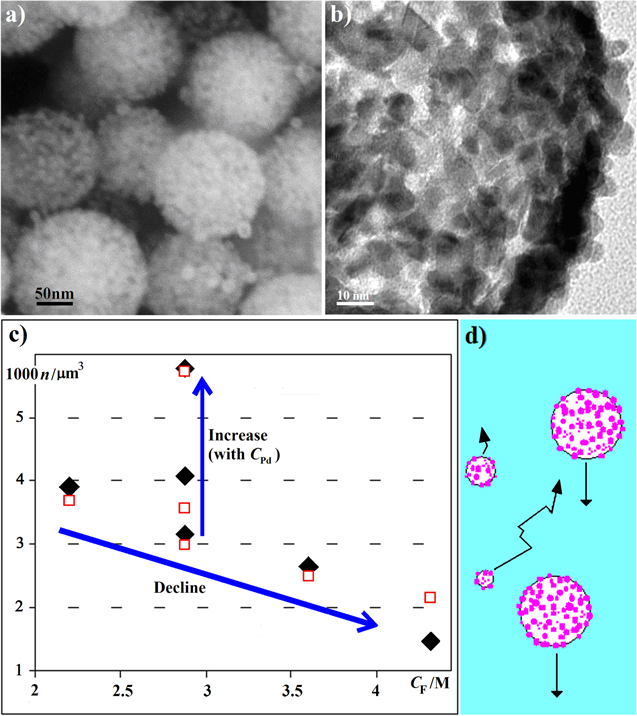
Figure 1. (a) SEM of Pd shells from a typical synthesis (from [3]) and (b) a TEM image revealing the hollow interior and the shell thickness h. Regular appearance and uniform radius R speak against collisions. (c) Bubble number density n versus concentration CF of the gas supplying acid: the black diamonds are from our Pd shell experiments. Usually, predicted n increases with CF and fail by several orders of magnitude. Collision coalescence simulation (hollow squares) fits, also at different CPd. (d) Similarly sized larger bubble–particle systems (BPSs) have similar speeds and seldom meet. Small BPSs have high relative speeds and Brownian motion. They likely meet large BPSs but add little volume.
Download figure:
Standard image High-resolution image2. The oddly behaving bubble number density n
The number density n of shells (and thus of bubbles during growth) is proportional to the mass density of the available shell material. For example, palladium concentration CPd is multiplied by atomic weight mPd and divided by a shell's mass. The latter equals shell volume  times density ρPd = 12.02 g cm−3 divided by a porosity parameter p. In general:
times density ρPd = 12.02 g cm−3 divided by a porosity parameter p. In general: ![$n={C}_{{x}}{m}_{{x}}/[{V}_{{\rm{s}}}({\rho }_{{x}}/p)].$](https://content.cld.iop.org/journals/0957-4484/27/24/245602/revision1/nanoaa22d5ieqn2.gif) The specific surface of smooth shells is 4πR2/[Vs(ρx/p)], being for example only 6 m2 g−1 for dense (p = 1) Pd shells. A typical product (figure 1(a)) has instead a five times larger BET surface area of 30 m2 g−1. A rough surface is defined to be one where the depressions are still wider than they are deep; such that they can triple surface areas. Our fivefold value proves true porosity (holes deeper than wide), and indicates a porosity factor of p = 1.5 to 2. However, the porosity p cannot be far above unity (consider the shells' structural integrity), and a log-normal distributed R gives only a 5% relative error to n. One can therefore estimate n for many reports that claim the involvement of free, pre-existing bubbles. SiO shells [1] imply up to 10 bubbles per μm3, which is similar to the number of bubbles derived from observations of ice fractures with about 20 bubbles per μm3 [2]. Pd shells [3], with similar radii, imply between 10−2 and 10−3 (figure 1(c)). ZnSe microshells [4] imply only 3 × 10−4 down to 5 × 10−5, almost a million times less than 20/μm3 [2]. Where are the missing bubbles if they pre-existed? Worse, shell thickness h can stay constant when R doubles [1], although the shell material spreads over the bubble surface (∼R2), implying that n decreased to only 25%. If diffusive gas exchange removes 75% of bubbles before shell growth starts, the size distribution would Ostwald ripen [5] into a sub-population of bubbles that shrink away completely and a second sub-population of bubbles that grow to about 10 μm, at which point they reach the surface within one minute. This speaks against pre-existing bubbles, and indeed, shell-synthesis usually involves gas production during the assembly of the shells. Even the SiO shells blamed entirely on already present gases [1] involve a gas producing decomposition (SiO → Si + O). While n varies by over six orders of magnitude among reports, the bubbles' gas molecules are usually on the order of the number of atoms in the shell. There are about 20 times more Pd atoms in the Pd shells [3] (5 to 60 million) than gas particles in the bubbles. The report on hydroxyapatite microspheres [6] similarly calculates 30 to 90 million CO2 molecules in its average bubbles. Thus, the hypothesis that bubbles and shells come into existence together and that their numbers are closely correlated may yet arise, but the issue is not this trivial. With the Pd shells, n increases with the concentration of the Pd that turns formic acid into gas (figure 1(c)), as intuitively expected. However, a greater gas supply at constant CPd decreases n. If the grains which build the shells immediately generate and maintain bubbles, collision coalescence (figure 1(d)) of such BPSs is inevitable. Every single grain is likely immediately the particle of a small BPS. Details of the collision statistics explain the otherwise counterintuitive relations.
The specific surface of smooth shells is 4πR2/[Vs(ρx/p)], being for example only 6 m2 g−1 for dense (p = 1) Pd shells. A typical product (figure 1(a)) has instead a five times larger BET surface area of 30 m2 g−1. A rough surface is defined to be one where the depressions are still wider than they are deep; such that they can triple surface areas. Our fivefold value proves true porosity (holes deeper than wide), and indicates a porosity factor of p = 1.5 to 2. However, the porosity p cannot be far above unity (consider the shells' structural integrity), and a log-normal distributed R gives only a 5% relative error to n. One can therefore estimate n for many reports that claim the involvement of free, pre-existing bubbles. SiO shells [1] imply up to 10 bubbles per μm3, which is similar to the number of bubbles derived from observations of ice fractures with about 20 bubbles per μm3 [2]. Pd shells [3], with similar radii, imply between 10−2 and 10−3 (figure 1(c)). ZnSe microshells [4] imply only 3 × 10−4 down to 5 × 10−5, almost a million times less than 20/μm3 [2]. Where are the missing bubbles if they pre-existed? Worse, shell thickness h can stay constant when R doubles [1], although the shell material spreads over the bubble surface (∼R2), implying that n decreased to only 25%. If diffusive gas exchange removes 75% of bubbles before shell growth starts, the size distribution would Ostwald ripen [5] into a sub-population of bubbles that shrink away completely and a second sub-population of bubbles that grow to about 10 μm, at which point they reach the surface within one minute. This speaks against pre-existing bubbles, and indeed, shell-synthesis usually involves gas production during the assembly of the shells. Even the SiO shells blamed entirely on already present gases [1] involve a gas producing decomposition (SiO → Si + O). While n varies by over six orders of magnitude among reports, the bubbles' gas molecules are usually on the order of the number of atoms in the shell. There are about 20 times more Pd atoms in the Pd shells [3] (5 to 60 million) than gas particles in the bubbles. The report on hydroxyapatite microspheres [6] similarly calculates 30 to 90 million CO2 molecules in its average bubbles. Thus, the hypothesis that bubbles and shells come into existence together and that their numbers are closely correlated may yet arise, but the issue is not this trivial. With the Pd shells, n increases with the concentration of the Pd that turns formic acid into gas (figure 1(c)), as intuitively expected. However, a greater gas supply at constant CPd decreases n. If the grains which build the shells immediately generate and maintain bubbles, collision coalescence (figure 1(d)) of such BPSs is inevitable. Every single grain is likely immediately the particle of a small BPS. Details of the collision statistics explain the otherwise counterintuitive relations.
3. No free-bubble theory fits shell syntheses
We discuss mostly hollow Pd shells, but the counterintuitive behaviors have been observed in many other experiments. Hollow Pd shells were obtained in a synthesis [3] where formic acid at initial concentration CF reduces  ions and supplies gases. A 'typical' synthesis is defined by the vector (r, CF, CPd, T) being (0.64, 2.88 M, 0.15 mM, 100 °C). The autoclave filling ratio r describes the initial height of the fluid column, but r = 0.8 becomes r100°C = 0.9, halving the space above the expanded fluid and increasing gas pressures. Vapor pressures depend only on T and Antoine equations predict [7] that, even at 190 °C and r only 0.2 (r190°C = 0.223), 98% of water is still in the liquid phase. Nevertheless, below r = 0.53, mostly irregular aggregates result, and networks result at r = 0.8. The strong r-dependence implies gas release, which makes many parameters time-dependent.
ions and supplies gases. A 'typical' synthesis is defined by the vector (r, CF, CPd, T) being (0.64, 2.88 M, 0.15 mM, 100 °C). The autoclave filling ratio r describes the initial height of the fluid column, but r = 0.8 becomes r100°C = 0.9, halving the space above the expanded fluid and increasing gas pressures. Vapor pressures depend only on T and Antoine equations predict [7] that, even at 190 °C and r only 0.2 (r190°C = 0.223), 98% of water is still in the liquid phase. Nevertheless, below r = 0.53, mostly irregular aggregates result, and networks result at r = 0.8. The strong r-dependence implies gas release, which makes many parameters time-dependent.
With CF at 0.72 M, only nanoparticle aggregates are obtained. From CF = 1.44 M to 5 M one observes R = 43 to 180 nm, all ±15% (figure 2). R increases with CF. However, a larger CF should provide more gas pressure and smaller radii, a common experimental observation [6] with nanobubbles. The Laplace pressure ΔP = 2γ/R dominates the bubble pressure and is upheld by the oversaturation ΔCgas according to Henry's law (ΔP = ΔCgas KH). Hence,  and a straightforward
and a straightforward  has indeed been reported [1]. An increase of R with gas concentration is predicted for non-interacting bubbles in a closed volume [8] (similar to shielding [9]). However, those are meta-stable states [5]. Neither the models' numbers nor slopes fit the data, and n would need to adjust before the shell growth, as if anticipating a future equilibrium.
has indeed been reported [1]. An increase of R with gas concentration is predicted for non-interacting bubbles in a closed volume [8] (similar to shielding [9]). However, those are meta-stable states [5]. Neither the models' numbers nor slopes fit the data, and n would need to adjust before the shell growth, as if anticipating a future equilibrium.
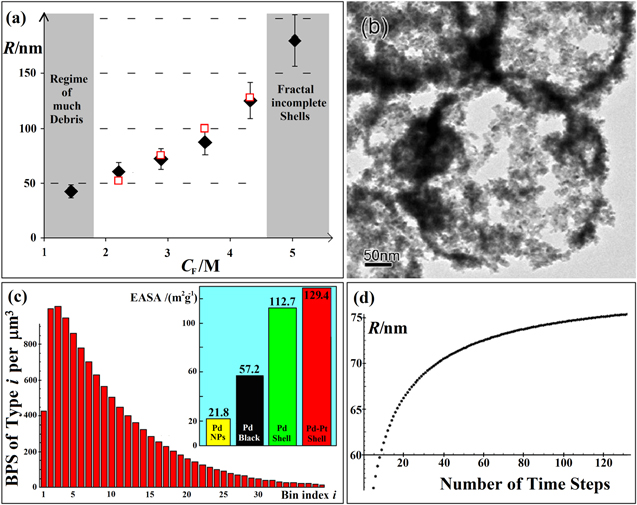
Figure 2. (a) Radius R of Pd shells versus CF, experimental (diamonds) and simulated (hollow squares). Approaching 5 M, incomplete shells occur. (b) Fractal incomplete shells with 88 m2 g−1 BET area (from [3]). (c) The number (per μm3) of BPSs with up to 100i Pd grains versus i after 50 min simulated time; the inset compares the electroactive surface area (EASA) of Pd nanoparticles, Pd black, incomplete Pd shells and a similar Pd–Pt bimetallic product. (d) Example for the evolution of the average radius of the BPS over time for a typical simulation.
Download figure:
Standard image High-resolution imageLarge shells' surfaces are incomplete (figure 2(b)), hence, yet higher CF cannot produce stable shapes. The respective shell thicknesses h are 13, 21, 16, 12, 10, and 7 nm (±20%). One may expect  because the Pd is distributed over the shell surface, but R triples while h decreases by a factor of three from 21 to 7 nm. Therefore, although CF increases the gas supply, this counterintuitively decreases n (figure 1(c)). This suggests collision growth: size R depends on the amount of Pd the BPSs carry; and larger capture cross sections deplete smaller BPSs due to differing relative mobility. CF increases R, and the collision cross section is then larger early on, thus fewer shells result. Early on, n may be proportional to CPd, but the final R is stabilized dynamically by the number of grains on the BPS and local gas concentrations, so R becomes independent of CPd. In the cited, meta-stable [5] many-bubble scenarios [8], R would depend crucially on CPd. The experimental data however could not be clearer: R stays constant when varying CPd. Keeping CF at 2.88 M, CPd = 0.15, 0.25, and 0.4 mM results in h = 16, 23, and 28 ± 5 nm, when irregular grain aggregates start to appear. R does not change. This is confirmed impressively with CF = 5 M and CPd = 0.4 mM: R is 180 nm again, but h adjusted to a thick 18 nm. Also n is thus almost as before, because the two effects compensated each other. CF decreases n. CPd increases it, because the number of grains, which is the initial n, increases proportionally. CPd does not, but CF does tune R. This suggests dynamic stability from ongoing acid conversion at a rate that increases with CF. More Pd increases the total rate, but at the BPS, the local concentration is important. Diffusion calculations show that global flow equilibrium is reached and can therefore determine the final R. More Pd can increase gas production only very early on. CPd is irrelevant for the later growth stages because the initial collision rates are proportional to the initial density squared, which removes more grains faster.
because the Pd is distributed over the shell surface, but R triples while h decreases by a factor of three from 21 to 7 nm. Therefore, although CF increases the gas supply, this counterintuitively decreases n (figure 1(c)). This suggests collision growth: size R depends on the amount of Pd the BPSs carry; and larger capture cross sections deplete smaller BPSs due to differing relative mobility. CF increases R, and the collision cross section is then larger early on, thus fewer shells result. Early on, n may be proportional to CPd, but the final R is stabilized dynamically by the number of grains on the BPS and local gas concentrations, so R becomes independent of CPd. In the cited, meta-stable [5] many-bubble scenarios [8], R would depend crucially on CPd. The experimental data however could not be clearer: R stays constant when varying CPd. Keeping CF at 2.88 M, CPd = 0.15, 0.25, and 0.4 mM results in h = 16, 23, and 28 ± 5 nm, when irregular grain aggregates start to appear. R does not change. This is confirmed impressively with CF = 5 M and CPd = 0.4 mM: R is 180 nm again, but h adjusted to a thick 18 nm. Also n is thus almost as before, because the two effects compensated each other. CF decreases n. CPd increases it, because the number of grains, which is the initial n, increases proportionally. CPd does not, but CF does tune R. This suggests dynamic stability from ongoing acid conversion at a rate that increases with CF. More Pd increases the total rate, but at the BPS, the local concentration is important. Diffusion calculations show that global flow equilibrium is reached and can therefore determine the final R. More Pd can increase gas production only very early on. CPd is irrelevant for the later growth stages because the initial collision rates are proportional to the initial density squared, which removes more grains faster.
4. The complete growth mechanism of the shells
4.1. Out-bubbling
When heating, the liquid outgases and bubbles rise to the surface. The pressure under the lid, Plid, rises and squeezes later bubbles, which stay too small to reach the surface in time. Out-bubbling thus stops itself, similar to when closing a bottle with a carbonated beverage. The terminal drift velocity is proportional to R2 (see supplementary material stacks.iop.org/NANO/27/245602/mmedia) [10], and the rising-speed of R = 25 μm bubbles in water is 1 mm s−1 [11]. Indeed, R = 5 to 25 μm bubbles rise 8 cm min−1 [12]. 500 nm bubbles need 20 h to rise through the 3 cm fluid column.
4.2. Reduction
Formic acid reduces Pd(II) into Pd(0): (H2PdCl4 + HCOOH → Pd + 4 HCl + CO2). Higher T favors reduction of Pd-ions at Pd grains and therefore increases the grain diameter d (figure S1) as usually observed [4]. Growing Pd grains decarbonylate/dehydrate HCOOH into H2O and CO, but more importantly decarboxylate it into H2 and CO2. CO2 dissolves in water, but H2 is quickly oversaturated. H2 production slows after Pd(II) is exhausted and the Pd grains' surfaces are no longer renewed [13]. Heated, open autoclaves produce about 4 ml of H2 in the first hour, after which visible production stops. That corresponds to only 10 mM of acid and adds only a few atm in the closed system. Most HCOOH reacts to ethyl formate, the most readily forming ester [14], which boils at 54 °C if pure. Its concentration and vapor pressures etc are unknown.
4.3. Diffusion
Gas is steadily produced at the Pd and fed via the Pd surface into an attached bubble. Assume that gas concentrations are homogeneous:  for all present gases and vapors i. Index 'A' denotes the considered surface, either of a bubble or of the liquid's meniscus under the lid. Henry's law states that the partial pressures under the lid equal those upheld by diffusion into the bubble (
for all present gases and vapors i. Index 'A' denotes the considered surface, either of a bubble or of the liquid's meniscus under the lid. Henry's law states that the partial pressures under the lid equal those upheld by diffusion into the bubble (
 is the Henry constant). These pressures also balance each other mechanically by pushing on the liquid between bubble and meniscus. The Laplace pressure 2γ/R (0.6 to 2.8 MPa) is added to Plid, resulting in the total bubble pressure Pb. Fick's diffusion flux is proportional to the gradient
is the Henry constant). These pressures also balance each other mechanically by pushing on the liquid between bubble and meniscus. The Laplace pressure 2γ/R (0.6 to 2.8 MPa) is added to Plid, resulting in the total bubble pressure Pb. Fick's diffusion flux is proportional to the gradient  (Recall that index 'A' denotes the considered surface; Ci is therefore the concentration at a general point away from the considered surface.) Estimating the bubble's local diffusion loss for H2 (see supplementary material), C increases until it is on the order of 2γ/(KH R), only 5 to 20 mM. The global diffusion time constant is on the order of an hour and consistent with the 4 ml H2 flowing from open autoclaves. The final R and n are also roughly consistent with the assumption that a bubble interacts mostly with its close environment rather than via diffusive gas exchange with other bubbles [7].
(Recall that index 'A' denotes the considered surface; Ci is therefore the concentration at a general point away from the considered surface.) Estimating the bubble's local diffusion loss for H2 (see supplementary material), C increases until it is on the order of 2γ/(KH R), only 5 to 20 mM. The global diffusion time constant is on the order of an hour and consistent with the 4 ml H2 flowing from open autoclaves. The final R and n are also roughly consistent with the assumption that a bubble interacts mostly with its close environment rather than via diffusive gas exchange with other bubbles [7].
4.4. BPS
Many stabilization mechanisms for free bubbles have been proposed. Hydrogen bonds may reduce gas diffusion [2], which is similar to the suggestion of hydrophobic particles creating an ice-like hydration shell [15, 16], or ions [17] such as hydroxide ions [18]. These scenarios are however all in doubt [19, 20]. Pinning of the fluid/gas contact line on surfaces increases curvature radii [21] but is not directly applicable, because the surfaces are initially those of Pd grains with d only 5 nm. Capillary interaction between the grains embedded in the BPS surface lowers the mean curvature of the interface between them, thus removing the Laplace pressure [22]. Ostwald ripening is arrested when small BPSs evolve faceted polyhedral shapes, which has been observed experimentally [23]. Homogeneous bubble nucleation needs extreme over-saturations. Heterogeneous nucleation starts on the Pd grains, where the gas concentration is largest. Grains never separate from the bubbles they produce because they favor the interfacial location.
A dynamic BPS equilibrium radius is possible because the gas production at the Pd particles decreases during shell growth. One reason is the depletion of HCOOH in the local environment around a larger number of Pd grains. Moreover, BPSs with q grains produce less than q-times the gas that a q = 1 system produces: grains joining an established shell on the outside shield grains further inside. Moreover, grains compete for HCOOH in the local environment. The environment is now half shielded from influx by the large bubble, which completely engulfs most grains. These are several almost independent effects, and all decrease gas production while balancing the lower outflow as less gas escapes due to decreased Laplace pressure and grains shielding the bubble. R's growth slows to a halt. Large BPSs rarely mutually collide. Adding small BPSs does not change a large R because volume is proportional to R3. Grains can slowly fuse firmly together in spite of the fact that a more complete or thicker shell may still develop.
5. Simulation of collision coalescence
Collision growth of clusters explains many phenomena such as sizes of raindrops under warm clouds [24], stable homogenization of emulsions [25], and particle size distributions in spray dryers [26]. Our calculations involve tests of algorithm stability, time optimizations, and many physical assumptions (see supplementary material). We use bins i. Their BPSs have on average  grains. The number densities
grains. The number densities  are initially zero, except for the initial grain number density
are initially zero, except for the initial grain number density  in the first bin. We derive a typical population balance equation:
in the first bin. We derive a typical population balance equation:
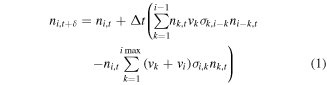
Ri may stay zero until some minimum  and then linearly grow with i. Most importantly, it rises ever more slowly with i. This is modeled by
and then linearly grow with i. Most importantly, it rises ever more slowly with i. This is modeled by  a time-independent effective radius (as if the global gas concentration does not change). It reproduces R's observed dependence on CF if
a time-independent effective radius (as if the global gas concentration does not change). It reproduces R's observed dependence on CF if  and x ≈ 1.3. We can reproduce the observations, including reaction times. The fits do depend on certain assumptions; however, recall that available theories of free bubbles cannot model the parameters' behavior. Collision coalescence can describe it. Two further results depend on the effective relative velocity between any two BPSs indexed by i and k, which depends on Ri of the 'projectile' (not the target), namely via
and x ≈ 1.3. We can reproduce the observations, including reaction times. The fits do depend on certain assumptions; however, recall that available theories of free bubbles cannot model the parameters' behavior. Collision coalescence can describe it. Two further results depend on the effective relative velocity between any two BPSs indexed by i and k, which depends on Ri of the 'projectile' (not the target), namely via  Values of z smaller or equal to unity lead to
Values of z smaller or equal to unity lead to  and cannot produce a peaked distribution. Size selection improves with higher z. However, another result is that n increases with CF at
and cannot produce a peaked distribution. Size selection improves with higher z. However, another result is that n increases with CF at  At z = 1.6, CF = 2.2 M, CPd = 0.15 mM, and after t = 50 min (25 time steps), the distribution of BPSs has already peaked (figure 2(c)). The distribution over the n-bins is much broader (the long tail misleads) than the distribution of radii, which peaks at a lower bin. Thus, the average is only
At z = 1.6, CF = 2.2 M, CPd = 0.15 mM, and after t = 50 min (25 time steps), the distribution of BPSs has already peaked (figure 2(c)). The distribution over the n-bins is much broader (the long tail misleads) than the distribution of radii, which peaks at a lower bin. Thus, the average is only  The process size-selects effectively, because R's standard deviation decreases with t. R stabilizes about 25% below
The process size-selects effectively, because R's standard deviation decreases with t. R stabilizes about 25% below  (figure 2(d)).
(figure 2(d)).
6. Conclusion
The counterintuitive behavior of important parameters in nano-shell syntheses led to a novel analysis that focuses on the number density n of the involved bubbles. The analysis was applied to several published reports, and it was found that free-bubble theories fail to account for the observed behaviors. The suggested collision coalescence between bubble–particle systems (BPSs) is consistent with all observations. The stability of the radius is partially a dynamic stability at all radii, but the collision process statistics also runs into a certain average radius R. The evolving size distributions reproduce bubble number densities n that are otherwise usually several orders of magnitude wrong. The simulations use an effective relative collision velocity that depends on a power z. Only  allows size selection as well as the counterintuitive decrease of n when increasing shell material. Also, grain-monolayer thin, incomplete and multi-metallic shells with superior catalytic activity were synthesized via a new hydrothermal route. The power z = 1.6 reproduces these experiments very well.
allows size selection as well as the counterintuitive decrease of n when increasing shell material. Also, grain-monolayer thin, incomplete and multi-metallic shells with superior catalytic activity were synthesized via a new hydrothermal route. The power z = 1.6 reproduces these experiments very well.