Abstract
The influence of external magnetic and electric fields on the properties of a multiferroic with a helical magnetic structure is described. Thermodynamics of the phase transition from the antiferromagnetic ferroelectric to the new magnetic state is described for a multiferroic with a perovskite-type structure. In this magnetic state a spiral spin structure and weak ferromagnetism can exist simultaneously. Such a state is a result of the first-order phase transition at a certain temperature below TN when, due to the Dzyaloshinskii–Moriya effect, a helical magnetic structure occurs. In this state the vectors of electrical polarization and the helicoid of magnetic moments in perovskites are mutually perpendicular and lie in the basic (ab) plane perpendicular to the main c axis. In this case an additional electrical polarization proportional to the square of magnetization appears in the (ab) plane which reduces the common polarization of the ferroelectric. It is shown that a weak ferromagnetic moment m occurs along the c axis in an applied magnetic field in addition to a modulated magnetic structure appearing in the (ab) plane. The dependence of these phenomena on the applied electric field is considered. It is shown that a sign-alternating electric field causes a linear-in-the-field variation of the magnetic moment opposite in sign to the electric field variation (i.e., the greater is the electric field, the smaller is the magnetic moment m). The observed hysteresis phenomena determining the temperature ranges of overheating and overcooling of each phase under applied magnetic and electrical fields are explained.
Export citation and abstract BibTeX RIS
1. Introduction
Multiferroic (MF) crystals are of interest due to the coexistence of magnetism and ferroelectricity [1, 2], different phase states and phase transitions, including the known first-order transition of an antiferromagnet–insulator into a ferromagnetic 'metal glass' [3, 4]. The transition into a 'magnetic glass' depends strongly on external effects such as mechanical tension and magnetic fields [3, 5]. In several perovskite-type multiferroics, such as BiFeO3 and BiMnO3, electrical polarization (EP) occurs due to a symmetry change inherent in these crystals which takes place well above the Neel point TN. However, EP in new (Eu,Y)MnO3 multiferroics is induced by a helical spin ordering which takes place only below TN. A rather large external magnetic field changes the spin configuration in such MFs, which radically affects their ferroelectric properties [6–8].
The perovskite type Eu1−xYxMnO3 crystals have an orthorhombic structure and exhibit different magnetic and dielectric properties. They become nearly collinear antiferromagnets (AFM) and paraelectrics at T < TN ≈ 50 K, ferroelectrics (FE) at T < TFE ≈ 30 K (the polarization P is along the x axis), and weak ferromagnets (WFM) (m is along the c (z) axis) with a simultaneous appearance of a spiral structure (along the y axis) at T < TWF ≈ 20 K [9]. An increase of yttrium concentration x leads to the evolution of a low-temperature magnetic state from a WFM to a spiral one and is accompanied by a sharp change of the volume ferroelectric polarization [10, 11].
Previously it was phenomenologically shown [12] that in an applied magnetic field a decrease of spontaneous EP with a simultaneous increase of the magnetic moment of the WFM was obligatory in Eu1−xYxMnO3 perovskites, due to the existence of the Dzyaloshinskii–Moriya (DM) effect [13, 14].
For the lanthanide Eu0.75Y0.25MnO3 it was experimentally shown [15] that the magnetoelectric effect occurs under an applied magnetic field of a specific (threshold) value. In this case, the spiral magnetic structure (SMS) and WFM are formed simultaneously as a result of first-order phase transition at a critical temperature below the point TFE of the ferroelectric transition. The temperature range of this transition is broadened with increasing magnetic field. Within this temperature range the magnetic moment rapidly rises and the correction to EP is negative, also rapidly increasing in absolute value with increasing magnetic field above its threshold [15]. Such a behavior is explained in [12] on the basis of the phenomenological expansion of free energy in small corrections to the spontaneous polarization p (the px component) and in a small wavevector q (the qy component) of the spiral structure (cycloid).
The aim of this study is the phenomenological explanation of the thermodynamic state of perovskites as multiferroics (in applied magnetic and electric fields) with due regard for the temperature dependence of sublattice magnetizations of the antiferromagnet. The role of spin–orbital interaction in the occurrence of WFM and its influence on the spontaneous polarization is clarified. The magnetoelectric effect in the absence of spontaneous polarization below TN is also discussed. The influence of an applied electric field in different directions on the described effects is considered.
2. Enhancement of weak ferromagnetism in external magnetic field due to modulations of spin structure
Let us give an elementary discussion of the reasons for the above phenomena. According to the Moriya microscopic approach [13], the energy of spin interaction of i and i + 1 ions, bilinear in the spin–orbital interaction and exchange interaction, in the second-order of perturbation theory is written as
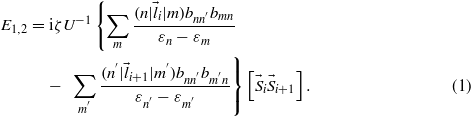
Here we consider the localized electron orbital states of magnetic ions and spin–orbital interaction as a disturbance, and the orbital states are supposed to be nondegenerate in the crystal field. The superexchange integral bnn'bm'n/U is a matrix in the quantum number space of i and i + 1 ions (n and n' are the basic orbital states of i and i + 1 ions, m and m' are the excited states of these ions), bnm is the transfer integral, and U is the energy required for the electron transfer from an ion to its nearest neighbor to create a polar state. The expression in the curly brackets in equation (1) before ![$[{\vec{S}}_{i}{\vec{S}}_{i+1}]$](https://content.cld.iop.org/journals/0953-8984/25/23/236001/revision1/cm467466ieqn79.gif) is the DM vector D [15], which depends on the quantum states of the
is the DM vector D [15], which depends on the quantum states of the 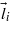 and
and 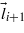 orbital moments.
orbital moments.
In the perovskite-type structure the D vector depends on the displacement  of oxygen atom, for example, along the x axis, and on the distance
of oxygen atom, for example, along the x axis, and on the distance 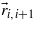 between the adjacent magnetic ions, for example, along the y axis. The D vector may be written as
between the adjacent magnetic ions, for example, along the y axis. The D vector may be written as ![$\vec{D}={\lambda }^{\prime}[\vec{u}{\vec{r}}_{i,i+1}]$](https://content.cld.iop.org/journals/0953-8984/25/23/236001/revision1/cm467466ieqn89.gif) , or phenomenologically
, or phenomenologically ![$\vec{D}=\lambda [\vec{p}\vec{\nabla }]$](https://content.cld.iop.org/journals/0953-8984/25/23/236001/revision1/cm467466ieqn90.gif) , where the electric polarization p is proportional to the displacement u (p ∝ u). Here and below
, where the electric polarization p is proportional to the displacement u (p ∝ u). Here and below  and u are identical
and u are identical 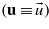 . The dimensionalities of the pseudo-scalar constants λ' and λ are different, λ = (e1[e2 e3])ζ, (ei are the unit orts, ζ is a scalar). In a nonuniform spin structure D is constant due to invariability of
. The dimensionalities of the pseudo-scalar constants λ' and λ are different, λ = (e1[e2 e3])ζ, (ei are the unit orts, ζ is a scalar). In a nonuniform spin structure D is constant due to invariability of 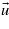 and
and 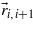 values.
values.
In the crystal unit cell the lengths and directions of interatomic bonds can vary with temperature T and applied magnetic field H. Accordingly, the quantum states and the transfer integrals in equation (1) are varied with an external action, which leads to rotations of the spins 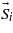 and
and 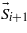 .
.
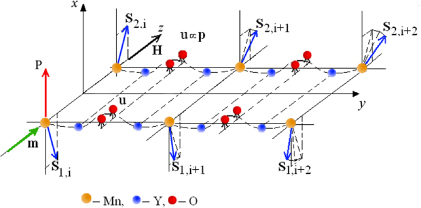
There are several positions of oxygen, europium, and yttrium ions in the Eu1−xYxMnO3 crystal, and the geometry of their bonds with Mn atoms is different. The change of these bonds in the (yz) plane and along the x axis may be different with temperature variation. As was suggested in [16, 17], bending of the rare earth–oxygen planes probably occurs with a temperature change in the presence of nonmagnetic Y ions (differing in size from Eu ions) located between the MnO6 octahedra (figure 1). In this case, the O atoms are 'ejected' from the (yz) plane at the expense of a corresponding reorientation of the atomic orbitals and magnetic moments [4]. This changes the energy of the exchange interaction between the magnetic ions.
Figure 1. The magnetoelectric effect in the YMnO3 multiferroic as a result of spin–orbital interaction. The spins S of Mn ions (solid blue arrows) in the i,i + 1 and i + 2 unit cells of two sublattices (i = 1,2) are shown. The spin canting in adjacent ions is responsible for the formation of a spiral magnetic structure along the y axis, while maintaining the same the DM vector Di,i+1 = λ' (u × ri,i+1). Multidirectional spins canting in sublattices determine the average magnetization m along the z axis caused by the magnetic field H applied along the z axis. The 'ejection' of oxygen ions O from the (zy) plane with the displacement u along the x axis is shown. In this case the electric polarization p is formed as a correction to the spontaneous polarization. Dotted lines conditionally show bending of the rare earth–oxygen planes. This (bending) is possible due to the small size of the Y ion, because the smaller the size of these ions, the greater the frustration (i.e., modulations) of the magnetic structure [4].
Download figure:
Standard image High-resolution imageAs shown in [18], the ferroelectric moment in perovskite-type manganites (in particular, in LuMnO3) is not associated with atomic displacements in the (yz) planes, but mainly depends on the lanthanide–oxygen bond lengths along the x axis. Because of atomic displacements the magnetic properties and polar state of the crystal proved to be mutually dependent. The more strongly these planes are bent, the more this ejection, i.e., the greater the displacement u of the O atoms and the related electric polarization p occurring due to the DM effect (px component). In this case, the wavenumber qy of the SMS increases as a result of atomic displacements and orbital transformation.
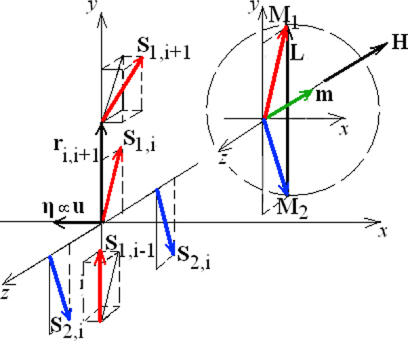
Let us consider the AFM spin ordering of Mn ions in 1 and 2 sublattices along the z axis (figure 2). Small canting of spins S in the (xz) and (yz) planes in adjacent sites can be in the same direction along the z axis. The triangle formed by the moments of two sublattices M1,M2 and the AFM moment 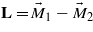 rotates around the z axis in the (xy) plane at large angles. The values of M1 and M2 are the thermodynamic averages of individual moments
rotates around the z axis in the (xy) plane at large angles. The values of M1 and M2 are the thermodynamic averages of individual moments 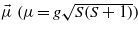 over the 1 and 2 sublattices. As the moment L rotates, the spin cycloid along the y axis retains an equal direction of spin canting in the chains along the z axis (as shown in figure 2). In this case, the magnetization
over the 1 and 2 sublattices. As the moment L rotates, the spin cycloid along the y axis retains an equal direction of spin canting in the chains along the z axis (as shown in figure 2). In this case, the magnetization 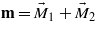 (WFM) appears along the z axis, which increases with applying magnetic field along the same axis. Thus, the uniform canting of magnetic moments M1 and M2 from the (xy) plane to the z axis leads to the uniform displacement
(WFM) appears along the z axis, which increases with applying magnetic field along the same axis. Thus, the uniform canting of magnetic moments M1 and M2 from the (xy) plane to the z axis leads to the uniform displacement  of oxygen atoms along the x axis. Due to the spin–orbital interaction, this spin canting results in the deformations and deviations of electronic orbitals which move oxygen atoms. The greater the magnetization m, the greater the displacements
of oxygen atoms along the x axis. Due to the spin–orbital interaction, this spin canting results in the deformations and deviations of electronic orbitals which move oxygen atoms. The greater the magnetization m, the greater the displacements  . As noted above, the cycloid of magnetic moments is characterized by the wavevector q along the y axis.
. As noted above, the cycloid of magnetic moments is characterized by the wavevector q along the y axis.
Figure 2. A perovskite as a weak ferromagnet–multiferroic. The M1 and M2 magnetic moments of the sublattices 1 and 2 are conditionally shown in the inset. The moment difference L and the sum m are indicated by black and green arrows, respectively. The vector η appears due to spin–orbit interactions. The vector 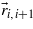 is the same in each sublattice. The dotted lines show rotations of spins S in the cells i − 1,i and i + 1 of the sublattices. Moment m remains constant on the appearance of a spiral twist of M and L in the (xy) plane (indicated by the dashed circle in the inset).
is the same in each sublattice. The dotted lines show rotations of spins S in the cells i − 1,i and i + 1 of the sublattices. Moment m remains constant on the appearance of a spiral twist of M and L in the (xy) plane (indicated by the dashed circle in the inset).
Download figure:
Standard image High-resolution imageSuch a synchronous atomic rearrangement is, actually, the magnetoelectric effect, since the displacements u (associated with m) modify the existing spontaneous polarization P by a small value p. As shown below, in this case, P and p have opposite signs (px ∝ ζqyM2). A decrease of the total polarization due to spin–orbital interaction, resulting in a correction p, is associated with the modulation of the spin structure q. An increase of the wavenumber q increases the polarization p, and, hence, the displacement u, i.e., the canting of magnetic moments. This means that an increase of the wavenumber qy increases the spontaneous magnetization m, i.e., the weak magnetism is enhanced.
3. Correction to magnetic susceptibility induced by the cycloid spin structure in an antiferromagnet
When the applied magnetic field H increases, the augmentation of magnetization 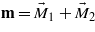 is caused by the magnetic susceptibility χm, which increases by a value δχm due to the spin modulation. As shown below, this augmentation is associated with the wavevector q. If the magnetoelectric effect was not caused by the SMS, the spontaneous magnetization of a weak ferromagnetic m along the z axis would be caused by the Dzyaloshinskii field HD:
is caused by the magnetic susceptibility χm, which increases by a value δχm due to the spin modulation. As shown below, this augmentation is associated with the wavevector q. If the magnetoelectric effect was not caused by the SMS, the spontaneous magnetization of a weak ferromagnetic m along the z axis would be caused by the Dzyaloshinskii field HD:
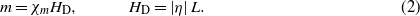
Here η is a small value of relativistic nature, caused by the spin–orbital interaction1, the vector η (η ∝ u ∝ p) is parallel to the x axis, and the AFM vector 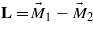 is along the y axis (figure 2).
is along the y axis (figure 2).
This is associated with the presence in the free energy of a constant correction in the form

which is a scalar because L changes sign under inversion of all coordinates, including the coordinates of neighboring spins [19]. When applying an external magnetic field H along the z axis, the effective field is Heff = HD + H. Weak ferromagnetism occurs in the field Heff, and the corresponding magnetic moment is m = χmHeff, if L remains constant in the absence of spin modulation.
The properties of such systems near the transition to the paramagnetic phase (in an external magnetic field) can be described in terms of the Landau theory [19]. Thermodynamic averages m,L and M are found by minimizing the free energy and, in general, should be considered along with the macroscopic parameters q and p. However, in perovskite Eu1−xYxMnO3, the transition temperature in the cycloid MF state with q ≠ 0 and p ≠ 0 is significantly less than the temperature of transition to the AFM state. Then, describing MF, we assume that the M values in all the phenomenological expressions are averaged parameters almost independent of temperature.
The WFM moment m remains constant when a spiral twist of M1,2 and L moments appears in the plane (xy). In the presence of the SMS, the Ly component is a sign-alternating value, and the above correction of equation (3) is absent, since the averaging over the coordinate y at constant 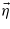 and
and 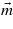 values gives
values gives ![$\langle \vec{\eta }[\vec{m}\vec{L}]\rangle =0$](https://content.cld.iop.org/journals/0953-8984/25/23/236001/revision1/cm467466ieqn200.gif) , where
, where 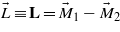 is a function periodically varying with y. Thus the existence of the cycloid of the magnetic moments is not contrary to the presence of WFM in the effective magnetic field.
is a function periodically varying with y. Thus the existence of the cycloid of the magnetic moments is not contrary to the presence of WFM in the effective magnetic field.
As shown in [15], both these states—WFM and cycloid with WFM moment—can transform into each other by a first-order phase transition due to the peculiarities of the crystal structure, in particular, the vitreous. We do not consider this phase transformation in this paper.
The correction δχm related to the wavevector q is nonzero only with due regard for quadratic terms ![$\langle (\vec{\nabla }[\vec{m}\vec{L}])^{2}\rangle \not = 0$](https://content.cld.iop.org/journals/0953-8984/25/23/236001/revision1/cm467466ieqn205.gif) in the free energy. Taking into account that a rise of qy ∝ px increases m, a corresponding correction in energy should be negative and proportional to the value
in the free energy. Taking into account that a rise of qy ∝ px increases m, a corresponding correction in energy should be negative and proportional to the value  . With the contribution
. With the contribution 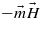 in the applied magnetic field H, it takes the form
in the applied magnetic field H, it takes the form 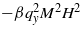 , where the parameter β is positive and the positive value δχm is
, where the parameter β is positive and the positive value δχm is 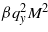 [20–22]2 (see comment in footnote 2).
[20–22]2 (see comment in footnote 2).
Thus, the space modulation of the sublattice magnetic moments in AFM increases the magnetic susceptibility proportional to the square of the wavenumber qy of the cycloid arising in a MF along with an electric moment.
4. Temperature behavior of a multiferroic in the presence of spontaneous polarization
Let us write the free energy F by considering a temperature change of the sublattice moment M ≈ L/2 in the absence of an external magnetic field
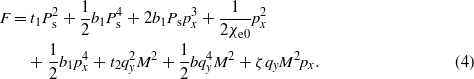
Equation (4) is written on the assumption of the spontaneous polarization Ps existing below TN. Here Px = Ps + px is the total perovskite polarization,  is the spontaneous polarization, px is the correction to Ps,χe0 is the electric susceptibility, ζ is a scalar, |λ| = |ζ|,t1 = a1(T − T1), t2 = a(T − T2),T1 ≡ TFE, T2 is the temperature of transition to a modulated state, a,a1,b,b1 are the positive phenomenological constants. From (4) we approximately obtain
is the spontaneous polarization, px is the correction to Ps,χe0 is the electric susceptibility, ζ is a scalar, |λ| = |ζ|,t1 = a1(T − T1), t2 = a(T − T2),T1 ≡ TFE, T2 is the temperature of transition to a modulated state, a,a1,b,b1 are the positive phenomenological constants. From (4) we approximately obtain

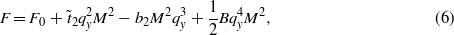
where  , B = [b + b1(χe0ζM2)4], and the parameter F0 does not depend on the wavenumber qy or the sublattice magnetization M. Note that this approach makes sense for negative
, B = [b + b1(χe0ζM2)4], and the parameter F0 does not depend on the wavenumber qy or the sublattice magnetization M. Note that this approach makes sense for negative 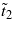 values, allowing a phase transition from the AFM state to the SMS state with a finite wavenumber qy. It is possible only for rather large M values: M2 > 2t2/(χe0ζ2).
values, allowing a phase transition from the AFM state to the SMS state with a finite wavenumber qy. It is possible only for rather large M values: M2 > 2t2/(χe0ζ2).
Hence we find the value of the wavenumbers 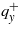 of the appearing helical structure. Below the transition point to the SMS state the temperature behavior of
of the appearing helical structure. Below the transition point to the SMS state the temperature behavior of 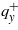 is determined by
is determined by  :
:
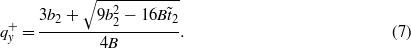
The sign of px depends on the sign of the wavenumber qy of the spiral. Sign (+) for qy in equation (7) corresponds to the sign (+) before the square root in this expression and to the minimum free energy (6), if the DM parameter ζ is positive. Sign (−) corresponds to the sign (−) before the square root in the expression for 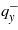 (see equation (9)) and to the free energy minimum (6), if the parameter ζ is negative. Values
(see equation (9)) and to the free energy minimum (6), if the parameter ζ is negative. Values 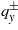 describe the branches F+ and F− as the results of those solutions for qy (see equation (8) and figure 3).
describe the branches F+ and F− as the results of those solutions for qy (see equation (8) and figure 3).
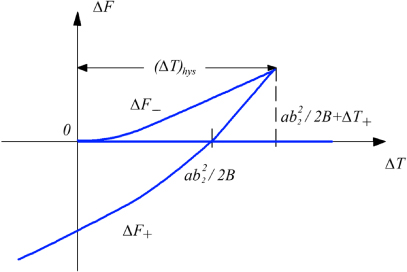
Figure 3. Thermal hysteresis in a multiferroic. The overheating ΔT+ of a cycloid-spiral magnetic state, coexistent in the magnetic field simultaneously with a weak ferromagnetic phase, is shown. The branches of solutions for F with the values qy equal to zero and 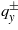 are depicted.
are depicted.
Download figure:
Standard image High-resolution imageAccording to equation (5), under coordinate inversion the sign of vector p is reversed, i.e., the signs of vectors Ps and p remain opposite.
In the applied magnetic field the coefficient 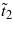 in equations (4) and (7) effectively changes from
in equations (4) and (7) effectively changes from  to
to  , and the first-order phase transition takes place at the reduced temperature
, and the first-order phase transition takes place at the reduced temperature  , at which the number qy undergoes a jump from zero to
, at which the number qy undergoes a jump from zero to 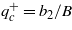 . In this point the polarization also changes by a jump:
. In this point the polarization also changes by a jump: 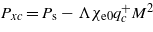 .
.
The system is able to overheat due to hysteresis effects in which this modulated (MF with WFM) and FE phases coexist. Here 'overheating' means a non-equilibrium coexistence of the SMS with WFM phase above the point 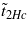 of phase transition in a magnetic field.
of phase transition in a magnetic field.
The value of thermal hysteresis (ΔT)hys can be estimated from the dependence F(T), on the basis of equation (6). The branches ΔF+ ≡ F+ − F0 and ΔF− ≡ F− − F0 are shown in figure 3 (the signs ± correspond to signs for 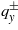 ). Here
). Here  , and the region of MF overheating is
, and the region of MF overheating is
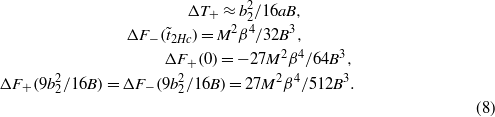
The overheating of the SMS existing simultaneously with WFM phase in a magnetic field was observed in Eu0.75Y0.25MnO3 [15].
The coexistence regions and changes in the relative volume fraction of the MF phase (below TFE) and the WFM phase in different T ranges are shown in the phase diagram of figure 3 in relation to the history of the action of magnetic and electric fields. It was established [15] that the WFM phase without the SMS coexisted with the FE phase also below the temperature Tf of spin freezing (vitrification), which corresponds to the first-order phase transition into a so-called 'magnetoelectric glass' [15]. In the absence of magnetic field the WFM phase was not observed below Tf, and only the FE phase was presented.
It follows from equations (6) and (7) that, if the point 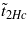 is close to aTf in the presence of the magnetic field, then the spontaneous EP on cooling in the region
is close to aTf in the presence of the magnetic field, then the spontaneous EP on cooling in the region  can increase by the simple law
can increase by the simple law  , which seems to be observed in the experiment for Eu0.75Y0.25MnO3 [15].
, which seems to be observed in the experiment for Eu0.75Y0.25MnO3 [15].
Above, it was implicitly assumed that the parameter ζ is positive. If it is negative ζ < 0, the coefficient b2 in equation (6) changes sign and, instead of equation (7), the solution is the wavenumber
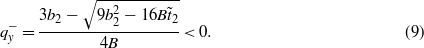
Thus, according to (9), the sign of the spiral is actually reversed. However, it follows from equation (5) that the sign of the polarization p is unchanged for ζ < 0. The jump 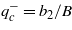 becomes negative in the transition point to the spiral-cycloid magnetic state, and the polarization px undergoes a similar negative jump of
becomes negative in the transition point to the spiral-cycloid magnetic state, and the polarization px undergoes a similar negative jump of  .
.
Using equations (6) and (7) we define the correction pxH to EP and the correction δm = (δχm)H to the magnetic moment at the expense of the applied magnetic field
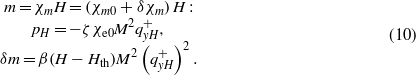
Here Hth is the threshold field associated with the magnetic anisotropy, and qyH is the wavenumber taking account of an external magnetic field.
Taking into account the data [12, 15], the 'magnetic' correction to the spontaneous EP in the intermediate temperature range between the temperature of 'vitrification' Tf and the point of ferroelectric transition TFE is shown in figure 4. In this region the first-order phase transition from an AFM ferroelectric into a spiral MF takes place in the magnetic field at a temperature 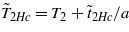 .
.
Figure 4. The influence of weak ferromagnetism on a spiral multiferroic. The temperature behavior of the spontaneous polarization in the absence of a magnetic field (blue curve 1) and in the presence of a magnetic field (red curve 2) is shown. A negative correction p (curve 2) to the spontaneous polarization Ps appears in the intermediate temperature range between the Tf and TFE points. In this range, a transition to the spiral multiferroic takes place at a temperature 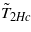 . The correction p appears in the presence of a sufficiently strong magnetic field.
. The correction p appears in the presence of a sufficiently strong magnetic field.
Download figure:
Standard image High-resolution imageOur reasoning for a positive coefficient β was given above. The magnetic field is assumed to be sufficiently large to overcome the threshold Hth value associated, for example, with the 'freezing' of the system or/and with the magnetic anisotropy. We suppose that qy = 0 and the field η is very weak (if at all), since a finite qy was not observed in the experiment in the absence of an external magnetic field. Here η is the magnetic field occurring due to spin–orbital interaction (see equation (2)).
Equation (10) shows that at low temperature the polarization pH should increase rather rapidly with the magnetic moment M, proportionally to  , if the parameter b2 ∝ ζ3 is small and B ≈ b. In this case, the wavenumber
, if the parameter b2 ∝ ζ3 is small and B ≈ b. In this case, the wavenumber 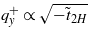 rises more slowly. These nuances of behavior of Eu1−xYxMnO3 type perovskites require experimental verification.
rises more slowly. These nuances of behavior of Eu1−xYxMnO3 type perovskites require experimental verification.
5. Modulations of spin structure in the absence of spontaneous electric polarization
Now we write by analogy with equation (4) the expression for the thermodynamic potential in the absence of spontaneous polarization Ps below TN and in the presence of an external magnetic field H

Here A,B,C and D are the phenomenological parameters. A changes sign at the point of phase transition to the AFM state, and thus the difference of sublattice magnetizations L depends on the temperature. B,C and D are positive, the sum of magnetizations m and field H are directed along the z axis. The vector L cyclically changes its direction in the (xy) plane (see figure 2), so that L is its root-mean-square value.
Assuming that the px,qy,ζ, and H values are small, we obtain after minimization of Φ for m that
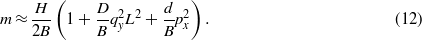
Whereas the minimization of Φ for px gives a value
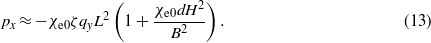
Then, according to (11)–(13), the thermodynamic potential approximately takes the form
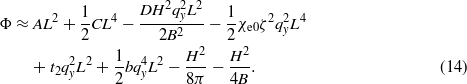
It follows from (14) that the temperature at which the spin modulation occurs due to the spin–orbital interaction ζ, can be found from the equation

and the square of the wavenumber of occurred spin modulation is

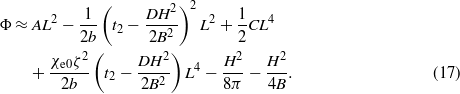
From (17) the square of the parameter of transition L2 from the paramagnetic to the AFM state with modulated spin structure is defined. Thus, according to (15)–(17), the function L(T), which describes the phase transition with temperature to the AFM state in the presence of a magnetic field, experiences a disturbance due to the influence of the magnetic field and spin modulations. In particular, TN shifts to higher temperatures in an external magnetic field according to the equation for TN:
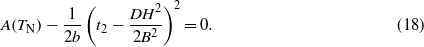
According to (15) and (18) TN coincides with the temperature of occurrence of modulated spin structure at A = 0 and  , that is at
, that is at
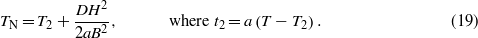
Equation (16) shows that the wavenumber qy has two equivalent values, differing in sign. Accordingly, the electric polarization px also has two values opposite in sign. Therefore, in the absence of an external electric field, such a crystal, on average, has no polarization in the presence of the DM effect. It is possible that a similar situation arises in the langasite crystals in the absence of spontaneous polarization above TN [23–25]. Application of an electric field permits one to choose the specific qy and px values for such a multiferroic.
6. Role of an external electric field
Now suppose that an electric field E is applied along the x axis in the presence of spontaneous polarization Ps which is parallel to the x axis (at T < TFE < TN). We consider two cases: when the field E coincides with the direction of vector p (that is E↑↑p and Ex < 0), and when it is opposite to p (E↑↓p and Ex > 0). Then equation (4) for the free energy can be written as
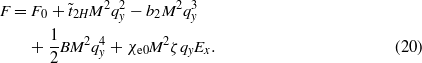
In deriving (20) we used equation (5) and the phenomenological parameters from equation (6). Here px ≈ χe0Ex − χe0ζM2qy,ζ > 0, and qy > 0, and the sign (+) is omitted. The first-order transition from AFM into the modulated spin structure takes place, if at the transition point F(qy > 0) = F(qy = 0) and ∂F(qy ≠ 0)/∂qy = 0. In this case, to find the wavenumber qy and the transition temperature point  , we obtain two equations. The first one is
, we obtain two equations. The first one is
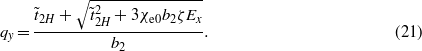
The second equation, in general, is
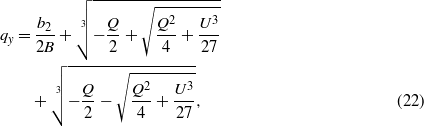
where  ,
, 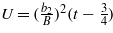 , and
, and 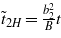 ,
, 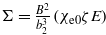 , where t and Σ are dimensionless variables. At E = 0, it follows from (22) that
, where t and Σ are dimensionless variables. At E = 0, it follows from (22) that 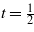 and
and 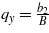 , with
, with  , and the sum of the roots of the third degree in (22) is the sum of complex-conjugate numbers
, and the sum of the roots of the third degree in (22) is the sum of complex-conjugate numbers 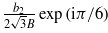 and
and 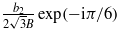 , which is equal to
, which is equal to 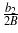 .
.
From (21) and (22) at small E values we can obtain that the point of first-order phase transition into a spiral MF is described by the values
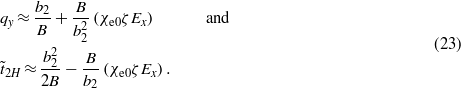
We recall that here  is the reduced critical temperature of the transition, which is equal to
is the reduced critical temperature of the transition, which is equal to  at Ex = 0.
at Ex = 0.
It is evident from (23) that at the transition point, the wavenumber qy increases when the applied electric field Ex is positive (that is, E↑↓p) and decreases for negative Ex (E↑↑p). In such a case, at positive Ex, the polarization px ≈ χe0Ex − χe0ζM2qy decreases in its modulus due to the increase of the term χe0Ex, if the field correction to the wavenumber  is small and
is small and  , i.e. the parameter of spin–orbital interaction ζ is small. The essential decrease in the polarization px was observed in the Eu0.75Y0.25MnO3 crystal [15] on the application of a positive Ea (i.e., Ea = Ex > 0).
, i.e. the parameter of spin–orbital interaction ζ is small. The essential decrease in the polarization px was observed in the Eu0.75Y0.25MnO3 crystal [15] on the application of a positive Ea (i.e., Ea = Ex > 0).
According to (23), the temperature of the transition to the spiral MF decreases for a positive Ex, and increases for a negative Ex. As follows from equations (20) and (21), the transition point 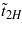 becomes zero at
becomes zero at

If the electric field exceeds the threshold E* value the transition temperature 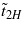 formally becomes negative:
formally becomes negative:

This means that the correction p is formed at a lower temperature if E↑↓p. In this case the electric field suppresses the polarization p at large positive values of Ex, since E↑↓p. Equations (24) and (25) for the transition point to a spiral MF in the electric field are valid for certain intermediate values of the applied field.
Experimental data for Eu0.75Y0.25MnO3 [15] show that small changes of Ex and δm are opposite in sign, and δm changes linearly with Ex. Taking into account of the fact that the magnetic spiral is destroyed when Ex increases, the correction to the magnetic susceptibility δχm in the presence of the electric field can contain a negative term −ζ'qyEx, where the positive parameter ζ' is related to the spin–orbital interaction. In this case the magnetic moment δm ∝− ζ'qyExH, which corresponds to the experiment [15].
Since by equation (23), the transition temperature increases for negative values of Ex, i.e. E↑↑p, then the system 'unfreezes' and is in the temperature range where the phase transition occurs over the wavenumber qy (i.e., over the correction to the polarization px). In this case, the magnetization m increases sharply due to the DM effect (proportional to 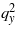 ) [12]. At the same time the number qy increases dramatically, and the modulus of the negative correction px increases when the temperature drops below the transition point (see figure 4).
) [12]. At the same time the number qy increases dramatically, and the modulus of the negative correction px increases when the temperature drops below the transition point (see figure 4).
7. Summary
Summarizing the results, we can conclude that the orthorhombically distorted perovskites, which are ferroelectrics below TN, can claim to be effective multiferroics with mutually perpendicular vectors of the electric polarization and the spiral of magnetic moments (both) perpendicular to the main c axis. In the perovskite-type crystals in the absence of a center of symmetry, the DM effect works in the plane perpendicular to the c axis. Because of this, an additional polarization and spiral modulation of the magnetic moments with mutually perpendicular directions appear in the ab(xy) plane. This additional EP is proportional to the square of the magnetization (as an inherent parameter of transition to the AFM state at TN).
In the applied magnetic field the appearance of electric polarization p at T < T2Nc (due to DM) must be accompanied by the appearance of a WFM moment m along the c axis. In this case, the cycloid of magnetic moments is preserved. In an applied field H, the enhancement of the wavenumber qy in WFM with decreasing temperature leads to an increase in the spontaneous magnetization m. At the same time, a positive correction to magnetic susceptibility appears which is quadratic in the wavevector qy and sublattice magnetization M.
On this basis, the thermodynamics of the first-order phase transition of an AFM ferroelectric into a spin-cycloid MF with WFM and jumps of electrical polarization and magnetization is described. Analysis of the thermodynamic potential in an external magnetic field indicates the possibility of the appearance of the SMS below TN in the absence of spontaneous EP. The function of the difference in the sublattice magnetizations L(T) is found, which describes the phase transition from the paramagnetic to the AFM state. The function L(T), dependent on the magnetic field and spin modulation, shows that the point TN shifts to higher temperatures in an external magnetic field.
Of particular interest is the dependence of the phenomena on the an applied electric field E. In the absence of an electric field, the crystal with the spin-modulated structure, on average, does not have EP. However, an applied electric field significantly affects the polarization and magnetic structure. For example, if the electric field is applied along the x axis, the polarization px appears and the wavevector qy changes in such a multiferroic.
We have shown that in the field E the correction p to the spontaneous polarization (which appears due to the DM effect) increases if p coincides with the direction of E. Simultaneously decreases the wavenumber q of the magnetic spiral. In the field E, the temperature of the p onset increases. Otherwise (i.e., when E↑↓p) with increasing Ex, the modulus |px| of the negative correction px is reduced, thus increasing the overall polarization Px. Then the temperature of appearance of the correction px decreases. Simultaneously, when Ex increases, a WFM moment m (in the presence of a constant magnetic field) gradually increases if p and E are parallel and decreases if p and E are antiparallel.
The application of a sign-alternating electric field causes a linear-in-field change of the magnetic moment, opposite in sign to the change of the electric field, it is also possible due to the DM effect. This effect has been observed experimentally in the crystal Eu0.75Y0.25MnO3 [15].
Hysteresis phenomena greatly complicate the described effects. In this paper we define the temperature ranges of overheating and overcooling of MF under the application of magnetic and electric fields. In this case we take into account the proximity of the transition points in the ferroelectric, multiferroic and weak ferromagnetic states, as well as to the magnetoelectric glassy state. It is shown that overheating of the MF occurs in a much narrower temperature range than its overcooling. This corresponds to the experimental data [15].
Acknowledgments
We thank Dr K O Funtov for his help in the design of the figures. This study is supported by the Russian Foundation for Basic Research project Nos 11-02-12089 and 11-02-00636a and by the Program of the Russian Academy of Sciences 'Strongly correlated electronic systems'.
Footnotes
- 1
All the phenomenological parameters λ,λ',η and ζ, (here |λ| = |ζ|) are proportional to the same spin–orbital interaction, but they have different dimensionalities because they enter into different phenomenological equations. For convenience, we use a certain parameter in the corresponding equation.
- 2
This correction related to the DM effect is true only at sufficiently weak magnetic fields, which still practically do not untwist the cycloid. In strong magnetic fields, the untwisting of cycloid takes place, for example according to mechanism of the phase transition into a homogeneous AFM state, which is induced by a magnetic field [20–22]. In such a case, the period of cycloid sharply increases near the critical value of the field.