Abstract
We present a general approach for calculating the magic-angle condition for time-resolved spectroscopy of isotropic samples. Allowing for arbitrary static polarizations and propagation directions of each pulse enables us to retrieve not only the known magic-angle conditions for linear and circular polarization, but also analogous conditions for anisotropy-free spectroscopy using elliptically polarized laser pulses. The results are exemplified on transient absorption and transferred to coherent two-dimensional spectroscopy. Furthermore we derive for transient absorption spectroscopy the relation between the measurable anisotropy and the molecular structure, i.e., the angle between the pumped and probed transition dipole moments (TDMs). The impact of multiple spectrally overlapping signals is considered and discussed on the example of a molecule with a two-fold degenerate TDM.
Export citation and abstract BibTeX RIS
1. Introduction
Third-order nonlinear spectroscopy techniques are versatile tools for the investigation of the properties and dynamics of various materials. Transient absorption spectroscopy is the most common method in which a pump laser is used to excite the system under study and detection is subsequently performed optically. A probe pulse monitors the change in absorbance ΔA caused by the pump pulse. In such an experiment, an anisotropic distribution of transition dipole moments (TDMs) is created by the pump pulse depending on its polarization [1]. Hence, the differential absorbance signal depends on the polarizations and the propagation directions of the pump and the probe pulse.
Employing ultrahigh time resolution, the anisotropic distribution of TDMs that is generated by the pump pulse evolves because of population and orientation changes [2–6]. Both processes influence the anisotropy of the distribution. On the one hand, states with a molecular structure different from the initial state may be populated. Thus, anisotropy measurements can be used to determine the relative orientation of TDMs with respect to the molecular structure [7–9] and to reveal time constants and reaction paths of, e.g., energy transfer in reaction centres [10, 11], exciton delocalization in dendrimers [12, 13], ligand docking [14–16], or electron hopping in proteins [17, 18]. On the other hand, the molecules may rotate. In solution, rotational diffusion makes the excited subensemble isotropic with time [9, 19]. If only population changes are of interest, all these anisotropy-changing effects and their associated decays complicate the measured signal. Therefore, experimental conditions have been derived under which a spectroscopic signal contains contributions neither from molecular structural changes nor from rotational diffusion but reflects the pure population dynamics. The most prominent condition is the 'magic-angle' configuration for linearly polarized pump and probe pulses in which the two polarization directions subtend a relative angle of  [1]. The case of circularly polarized pump pulses and linearly polarized probe pulses was treated by Cho [20] who showed that by choosing an angle of 90° − χMA ≈ 35.3° between the propagation directions of pump and probe one can suppress contributions from electric quadrupole transition moments allowing for a selective measurement of the combined electric-dipole–magnetic-dipole nonlinear response terms contributing to the circularly polarized two-dimensional (2D) pump–probe signal.
[1]. The case of circularly polarized pump pulses and linearly polarized probe pulses was treated by Cho [20] who showed that by choosing an angle of 90° − χMA ≈ 35.3° between the propagation directions of pump and probe one can suppress contributions from electric quadrupole transition moments allowing for a selective measurement of the combined electric-dipole–magnetic-dipole nonlinear response terms contributing to the circularly polarized two-dimensional (2D) pump–probe signal.
In this publication, we generalize the conditions known from the literature and analyse the geometry of arbitrary propagation directions and polarizations with arbitrary ellipticity. We find that anisotropic contributions in transient absorption signals can also be suppressed for elliptical polarization. Our calculations focus on the most commonly used isotropic samples, e.g., randomly oriented molecules in solution.
Fundamental quantities are introduced in section 2. We then present two theoretical models, a transition-probability approach (section 3) and a response-function approach (section 4), to investigate the most general case of polarization effects. In section 5, the magic angle is calculated for transient absorption with elliptically polarized laser pulses and in section 6 for coherent 2D spectroscopy. Finally, the transition-probability approach is applied to calculate the anisotropy which contains information about the molecular structure and the rotational dynamics, and we consider the impact of overlapping signal contributions (section 7) before concluding in section 8.
2. Fundamental quantities
2.1. Beam configuration and signal
Transient absorption data are often analysed for any given probe wavelength λ via the absorbance change
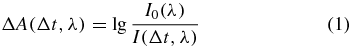
from the probe intensity I0(λ) measured when no pump pulse is present and the probe intensity I(Δt, λ) obtained when the sample was excited by the pump pulse at a time delay Δt earlier and employing the decadic logarithm,  . The pump and probe pulses are spatially overlapped in the sample, as shown exemplarily in figure 1. In general these pulses do not propagate collinearly, but their wave vectors enclose an angle β. The linear polarization vectors of the pulses in figure 1 also enclose an arbitrary angle χ. To measure only population changes, the magic angle [1] of
. The pump and probe pulses are spatially overlapped in the sample, as shown exemplarily in figure 1. In general these pulses do not propagate collinearly, but their wave vectors enclose an angle β. The linear polarization vectors of the pulses in figure 1 also enclose an arbitrary angle χ. To measure only population changes, the magic angle [1] of  is applied. As any polarization vector lies in a plane perpendicular to the propagation direction, the angle β affects the polarization vector in the laboratory coordinate system. To maintain the magic-angle configuration for any β it is necessary to choose either the pump or the probe polarization parallel to the rotation axis of β, which is chosen as the X axis in figure 1.
is applied. As any polarization vector lies in a plane perpendicular to the propagation direction, the angle β affects the polarization vector in the laboratory coordinate system. To maintain the magic-angle configuration for any β it is necessary to choose either the pump or the probe polarization parallel to the rotation axis of β, which is chosen as the X axis in figure 1.
Figure 1. Pump–probe transient absorption geometry. Pump and probe beam are spatially overlapped in the sample and their wave vectors enclose the angle β. Adjusting the angle χ between the linear polarization vectors of the pump and probe pulses to the magic angle of  suppresses structural information and orientation dynamics in the measured signal. The coordinate system used throughout this paper is shown on the left. The pump wave vector is always assumed to be parallel to the Z direction.
suppresses structural information and orientation dynamics in the measured signal. The coordinate system used throughout this paper is shown on the left. The pump wave vector is always assumed to be parallel to the Z direction.
Download figure:
Standard image High-resolution imageWhen the anisotropy is of interest, two measurements are performed, one with mutually parallel pump and probe polarizations (ΔA∥), i.e., χ = 0°, and one with mutually perpendicular polarizations (ΔA⊥), i.e. χ = 90°. Again it is necessary to choose one of the polarizations parallel to the X axis to maintain the parallel configuration for any angle β. The anisotropy defined as
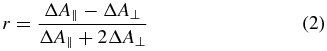
allows determining the angle between the participating pump and probe TDMs if their degeneracy is known. For example, if the pumped and probed TDMs  and
and  , respectively, are non-degenerate, one can determine from r the angle
, respectively, are non-degenerate, one can determine from r the angle

that they enclose [9]. However, overlapping and/or degenerate bands might impede such a straightforward analysis; only for special cases of degenerate TDMs an equivalent relation can be given [6, 15, 21].
2.2. Light–matter interaction
In general the measured transient absorption signal
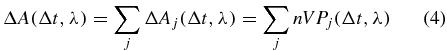
of (1) consists, at each wavelength, of several spectrally overlapping contributions ΔAj(Δt, λ), like ground-state bleach, stimulated emission, excited-state absorption or product absorption. We consider isotropic samples, e.g., randomly oriented molecules in solution. The intermolecular interaction is assumed to be negligibly small which is valid for sufficiently low concentrations [22]. Furthermore we assume that the molecules interact only with the incoming laser pulses and not with the signal emitted from other particles. Then the macroscopic signal results from multiplying the probability Pj(Δt, λ) that a single molecule contributes to the signal, ΔAj, with the particle density n in the volume V that is illuminated by both the pump and the probe beam. We describe the system with the single-particle Hamiltonian

consisting of an unperturbed part, H0, and an interaction part, H'(t), given in dipole approximation as
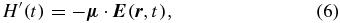
where the  dependence on the left-hand side has been dropped in the single-particle picture at a given position r. Thus the probability Pj(Δt, λ) depends on the vector property of the electric dipole operator μ and the electric field
dependence on the left-hand side has been dropped in the single-particle picture at a given position r. Thus the probability Pj(Δt, λ) depends on the vector property of the electric dipole operator μ and the electric field  in (6). To consider orientation effects, we focus on this vector dependence.
in (6). To consider orientation effects, we focus on this vector dependence.
2.3. Electric field polarization
The electric field interacting with the sample consists of two laser pulses in the case of transient absorption. Each laser pulse is described as a plane polychromatic wave

consisting of an oscillating term with centre frequency ω and propagation direction  , a complex-valued envelope E(r, t) and like in the Jones formalism [23] a complex-valued polarization vector
, a complex-valued envelope E(r, t) and like in the Jones formalism [23] a complex-valued polarization vector  . In the most general case, both the envelope and the polarization vector depend on time t [24] and space
. In the most general case, both the envelope and the polarization vector depend on time t [24] and space  . Such pulses can be generated by a polarization pulse shaper [25, 26]. In this paper, we concentrate on laser pulses with static polarization but variable ellipticity, as e.g. generated with a broadband wave-plate.
. Such pulses can be generated by a polarization pulse shaper [25, 26]. In this paper, we concentrate on laser pulses with static polarization but variable ellipticity, as e.g. generated with a broadband wave-plate.
Without loss of generality we choose the laboratory Z axis as propagation direction of one of the beams, say the pump, and therefore the polarization vector
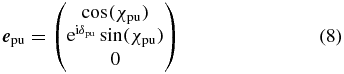
lies in the XY plane perpendicular to the propagation direction as depicted in figure 1. The ratio of the polarization amplitudes in X and Y direction is described by the angle
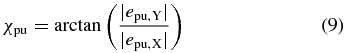
and the phase difference between the X and Y polarization components by the angle δpu. The probe polarization in the laboratory frame
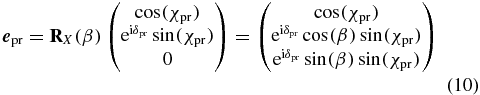
is described analogously, but in addition the rotation matrix RX(β) performs a rotation about the laboratory X axis with the angle β to take into account the different propagation direction.
3. Transition-probability approach
In order to determine Pj in (4) we start by using time-dependent perturbation theory to calculate the transition probability (superscript 'T')
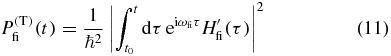
for a transition from an initial state |i〉 to a final state |f〉 of a molecular system due to the perturbative electric field of the laser pulses [27, 28]. After applying the interaction Hamiltonian from (6)
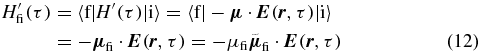
with the electric field of a single laser pulse from (7), the amplitude and the orientation of the TDM μfi and  , respectively, the resulting transition probability
, respectively, the resulting transition probability
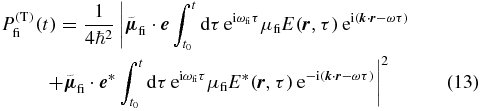
can be simplified in the rotating-wave approximation in which the first of the two terms in (13) dominates near the resonance ω → ωfi. The transition probability for times t after the end of the laser–pulse interaction is then the product of an orientation factor and an amplitude factor. While the amplitude describes in fact the population evolution that we ultimately want to measure, we here want to find anisotropy-free conditions irrespective of those dynamics. Thus we consider here specifically the orientation factor

that depends explicitly on vectorial properties. We find that  is proportional to the squared projection of the complex electric field polarization vector
is proportional to the squared projection of the complex electric field polarization vector  onto the normalized TDM direction
onto the normalized TDM direction  .
.
In a transient absorption experiment the system under study may behave as depicted in figure 2. The pump pulse excites a system from the initial (ground) state |0〉 to an excited state |1〉; during time Δt the system evolves from |1〉 to |2〉; finally, the probe pulse triggers the transition from |2〉 to |3〉. Without loss of generality, we can use this representative signal path to derive the orientation dependence of a single signal contribution Pj (4). Based on (14), we first calculate the transition probabilities,


for both the pump and the probe interaction. From here on we label the TDM directions ( ,
,  ) and the transition probabilities (
) and the transition probabilities ( ,
,  ) with the corresponding pulse rather than the involved states. For deriving anisotropy-free conditions, it is relevant that the pump and the probe pulses can interact with different TDM directions
) with the corresponding pulse rather than the involved states. For deriving anisotropy-free conditions, it is relevant that the pump and the probe pulses can interact with different TDM directions  and
and  , respectively, which enclose in general an arbitrary angle α.
, respectively, which enclose in general an arbitrary angle α.
Figure 2. Pump–probe dynamics. One possibility of how the system may evolve and interact with the light pulses in transient absorption: the pump pulse induces the first transition |0〉 → |1〉 and after the evolution of the system |1〉 → |2〉 during time Δt, the subsequent probe pulse causes the transition |2〉 → |3〉. The pump and probe transitions have their TDMs,  and
and  , oriented in a certain direction, enclosing the angle α.
, oriented in a certain direction, enclosing the angle α.
Download figure:
Standard image High-resolution imageThe derivation of Pj in (4) can be divided into three steps. In contrast to the chronological order in figure 2, we first consider a probe TDM pointing in direction (θ, ϕ) and calculate the probability Ppu that a corresponding pump TDM was excited by the pump pulse. In the second step the probability  of probing an excited molecule with such a probe TDM will be determined. Finally we will combine the results for Ppu and
of probing an excited molecule with such a probe TDM will be determined. Finally we will combine the results for Ppu and  to derive the probability Pj for a single signal contribution.
to derive the probability Pj for a single signal contribution.
To calculate Ppu we have to define the normalized pump and probe TDM directions  and
and  , respectively. We assume arbitrary but real-valued TDMs which enclose an angle α. The orientation of the TDMs is described in spherical coordinates with the polar angle θ and the azimuthal angle ϕ. In the Cartesian coordinate system of figure 1 the Z direction corresponds to θ = 0°, the X direction to (θ = 90°, ϕ = 0°), and the Y direction to (θ = 90°, ϕ = 90°). First we define a probe TDM
, respectively. We assume arbitrary but real-valued TDMs which enclose an angle α. The orientation of the TDMs is described in spherical coordinates with the polar angle θ and the azimuthal angle ϕ. In the Cartesian coordinate system of figure 1 the Z direction corresponds to θ = 0°, the X direction to (θ = 90°, ϕ = 0°), and the Y direction to (θ = 90°, ϕ = 90°). First we define a probe TDM
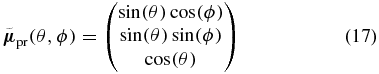
pointing in the direction (θ, ϕ), which is depicted as red arrow in figure 3. The corresponding pump TDM then has to point to somewhere on the blue circle around  because of the assumption that the pump and probe TDMs enclose the angle α. To describe all possible pump TDM directions we choose an initial element
because of the assumption that the pump and probe TDMs enclose the angle α. To describe all possible pump TDM directions we choose an initial element
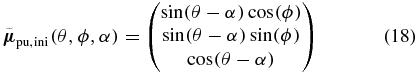
and rotate it around  by using the three-dimensional rotation matrix
by using the three-dimensional rotation matrix  which rotates counter-clock-wise around the unit vector
which rotates counter-clock-wise around the unit vector  by the angle γ resulting in the pump TDM direction
by the angle γ resulting in the pump TDM direction
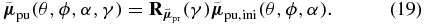
Figure 3. Pump–probe TDM relation. If the probe TDM of an excited molecule is oriented in direction  (red arrow), a pump TDM
(red arrow), a pump TDM  pointing onto the blue circle was excited, because all these pump TDMs enclose the angle α with the probe TDM.
pointing onto the blue circle was excited, because all these pump TDMs enclose the angle α with the probe TDM.
Download figure:
Standard image High-resolution imageIn an isotropic sample each of the pump TDMs on the blue circle in figure 3 contributes to the signal for a given  with the same probability. Therefore, the pump TDMs point on each infinitesimal line element
with the same probability. Therefore, the pump TDMs point on each infinitesimal line element

of the circle with the same orientation probability density (superscript 'O')  given by
given by
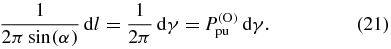
If any anisotropy were present before excitation, for example due to an orientation or alignment process [29–33] not considered here, the probability distribution for  would depend on direction.
would depend on direction.
Now we multiply the orientation probability  of (21) with the transition probability
of (21) with the transition probability  of (15), insert the pump TDM direction of (19) and the pump polarization vector of (8) and integrate over all possible pump TDMs pointing on the blue circle. As a result derived with Mathematica [34] we get the pump probability
of (15), insert the pump TDM direction of (19) and the pump polarization vector of (8) and integrate over all possible pump TDMs pointing on the blue circle. As a result derived with Mathematica [34] we get the pump probability
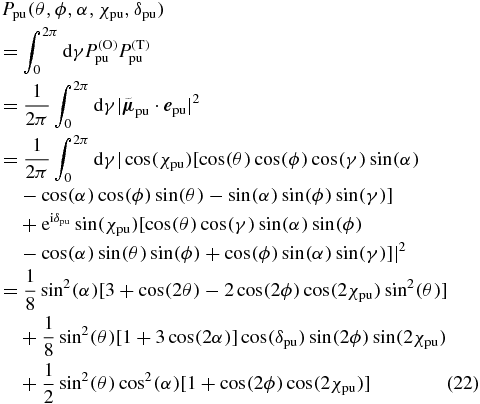
depending on the chosen direction (θ, ϕ) for the probe TDM, the angle α between the pump and probe TDMs and the electric field polarization (χpu, δpu) of the pump pulse.
For an illustration, let us draw a vector for every probe TDM orientation (θ, ϕ), choosing the corresponding pump probability Ppu as its length. All these vectors (figure 4, left, green) point on a three-dimensional surface. This surface illustrates the angular (θ, ϕ) distribution of the pump probability Ppu. Such a distribution is exemplarily depicted for a pump pulse propagating in the Z direction with linear (figure 4), circular (figure 5) and elliptical (figure 6) polarization. In each figure the left image refers to an angle of α = 0° and the right image to an angle of α = 90° between the pump and probe TDMs.
Figure 4. Pump distribution Ppu(θ, ϕ) for a linearly polarized pump pulse. For each direction (θ, ϕ) a vector is drawn with length Ppu(θ, ϕ) as illustrated by the green arrows in the left image. All these vectors point on a three-dimensional surface. This pump distribution Ppu(θ, ϕ) is depicted here for a linearly polarized pump pulse (χpu = 0°, δpu = 0°). The case α = 0° is shown on the left, while the right-hand side depicts the case for α = 90°.
Download figure:
Standard image High-resolution imageFigure 5. Pump distribution Ppu(θ, ϕ) for a circularly polarized pump pulse (χpu = 45°, δpu = 90°) with α = 0° (left) and α = 90° (right).
Download figure:
Standard image High-resolution imageFigure 6. Pump distribution Ppu(θ, ϕ) for an elliptically polarized pump pulse (χpu = −45°, δpu = −70°) with α = 0° (left) and α = 90° (right).
Download figure:
Standard image High-resolution imageIn figure 4 the linearly polarized (χpu = 0°, δpu = 0°) pump pulse leads to the commonly known cos 2 distribution for parallel (α = 0°) and a torus-shaped distribution for perpendicular (α = 90°) TDMs. Both distributions inherit the symmetry of the three-dimensional polarization vector  . In the case of linear polarization in X direction the distribution is rotationally symmetric around the X axis and has mirror-plane symmetry with respect to the YZ plane.
. In the case of linear polarization in X direction the distribution is rotationally symmetric around the X axis and has mirror-plane symmetry with respect to the YZ plane.
Circular polarization (χpu = 45°, δpu = 90°) as indicated by the blue circle in figure 5 leads to rotation symmetry around the propagation direction (Z axis) instead of the polarization direction and to mirror-plane symmetry with respect to the XY plane [35, 36].
In the case of elliptically polarized light (χpu = 45°, δpu = 70°) in figure 6 only the XY mirror-plane symmetry is maintained independent of α, but no rotation symmetry remains.
Now we proceed with the second step and insert the probe TDM direction (17) and the probe polarization (10) into (16) to calculate the probability
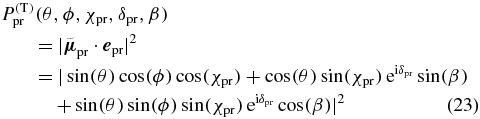
to probe an excited molecule with its probe TDM pointing into the chosen direction (θ, ϕ). Again we use each direction vector (θ, ϕ) with length  to construct a surface that illustrates the probe distribution as depicted in figure 7 (left, red) for a linearly polarized probe pulse.
to construct a surface that illustrates the probe distribution as depicted in figure 7 (left, red) for a linearly polarized probe pulse.
Figure 7. Pump and probe distributions. The left side depicts the pump distribution Ppu (blue, χpu = 0°, δpu = 0°, α = 0°) and the probe distribution  (red, χpr = −54.7°, δpr = 0°) separately, whereas the right side illustrates the overlap distribution
(red, χpr = −54.7°, δpr = 0°) separately, whereas the right side illustrates the overlap distribution  .
.
Download figure:
Standard image High-resolution imageIn the last step we have to consider the probability that the probe TDM of a molecule points into the chosen direction (θ, ϕ). In an isotropic sample this probability is independent of direction. Therefore, the probe TDM points on each infinitesimal small area

of the unit sphere with the same orientation probability density  given by
given by
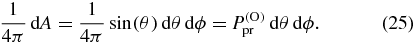
Finally we multiply the pump probability Ppu (22) with the probe orientation probability  (25) and the probe transition probability
(25) and the probe transition probability  (23) and integrate over all possible orientations (θ, ϕ). As a result we get the probability
(23) and integrate over all possible orientations (θ, ϕ). As a result we get the probability
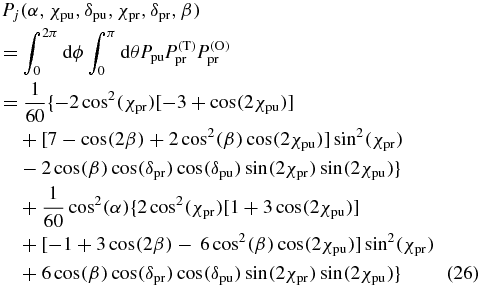
that a single molecule contributes to the pump–probe signal ΔAj depending on the angle α between the pump and probe TDMs and the electric field polarization of the pump (χpu, δpu) and the probe pulse (χpr, δpr, β). The same result is derived in the appendix by an alternative approach using Euler rotations. For multiple spectrally overlapping signals it is necessary to repeat the calculation above for all pump and probe TDMs combinations of the involved signal paths and to sum the signals according to (4).
A graphical interpretation of (26) is shown in figure 7. The pump pulse generates an excited distribution shaped by the pump polarization and the angle α (figure 7, left, blue). The probe pulse queries a distribution shaped by the probe polarization (figure 7, left, red). Therefore, the probability Pj depends on the product of both distributions (figure 7, right, green) over which one has to integrate, i.e., their overlap.
The α dependence of the pump-induced distribution Ppu connects the probability Pj to the molecular structure. On the one hand, one can exploit this property to extract structural information from anisotropy measurements; on the other hand, one can suppress the structure dependence of the signal to extract information on population dynamics. Removing the structure dependence is possible if the α-related deformation of the pump-induced distribution does not affect the intersection volume between the pump and probe distribution.
To find magic-angle configurations for arbitrarily polarized pump and probe pulses, thus, the α dependence of the probability Pj has to vanish. According to (26), this is the case for each configuration that fulfils
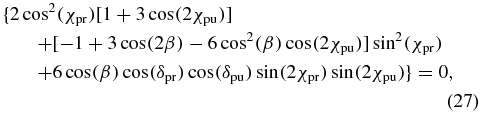
because α occurs in (26) only in the second term. Equation (27) is a central result of the present work as it provides the most general magic-angle condition for arbitrary excitation geometry and static pulse polarizations. We will discuss examples for particular realizations of (27) and their relation to the known magic-angle limiting cases in section 5.
4. Response-theory approach
Compared to the transition-probability approach, the response-theory approach is less illustrative but more general. It fits into the general framework of nonlinear response functions [22, 28, 37, 38] and therefore allows us to discuss magic-angle conditions not only for transient absorption, but also for 2D spectroscopy and third-order spectroscopy in general. These techniques are based on the third-order polarization [22, 28]
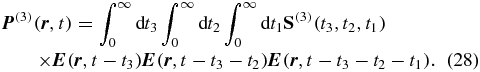
Because we are interested in orientation effects, we focus on the tensor properties of the response function S(3) and the vector properties of the electric field  . The third-order response function S(3) is a tensor T(4) of rank-4 that interacts three times with the complex polarization vector of the electric field
. The third-order response function S(3) is a tensor T(4) of rank-4 that interacts three times with the complex polarization vector of the electric field

The three polarization vectors  ,
,  and
and  are assigned to individual laser pulses with different but constant polarization. This approximation is possible if the electric field
are assigned to individual laser pulses with different but constant polarization. This approximation is possible if the electric field  consists of temporally separated laser pulses. In third-order spectroscopy, the information contained in the measured signal is filtered by the phase matching, phase cycling and time ordering applied in the specific experiment. These filter conditions also affect the orientation effects in the signal, e.g., the time ordering defines the order of the polarization vectors in (29) and therefore the outcome of this equation. For transient absorption no phase cycling is applied. According to the phase matching conditions
consists of temporally separated laser pulses. In third-order spectroscopy, the information contained in the measured signal is filtered by the phase matching, phase cycling and time ordering applied in the specific experiment. These filter conditions also affect the orientation effects in the signal, e.g., the time ordering defines the order of the polarization vectors in (29) and therefore the outcome of this equation. For transient absorption no phase cycling is applied. According to the phase matching conditions
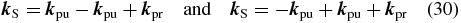
for a pump–probe signal detected along direction  the sample interacts twice with the pump and once with the probe pulse. These experimental conditions result in the two combinations
the sample interacts twice with the pump and once with the probe pulse. These experimental conditions result in the two combinations
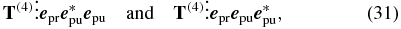
respectively, we have to consider [28]. Like the filter conditions, mentioned above, the polarization sequence is an additional filter parameter, which allows to measure specific elements of the tensor T(4).
In this paper we discuss the orientation effects of isotropic samples, like randomly oriented noninteracting molecules in solution. To perform rotational averaging (denoted below by an arc) on the tensor T(4) in the laboratory-fixed frame A, B, C, D  {X, Y, Z}, we have to average each tensor element via
{X, Y, Z}, we have to average each tensor element via
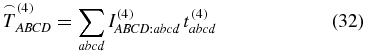
where the tensor t(4) describes a single oriented molecule in the molecule-fixed frame a, b, c, d  {x, y, z}, and the weighting factor
{x, y, z}, and the weighting factor
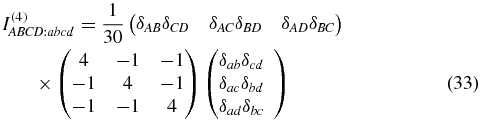
is known from the literature [28, 39] with δij being the Kronecker symbol. The 81 elements of an arbitrary rank-4 tensor decrease down to 21 nonzero elements
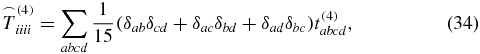
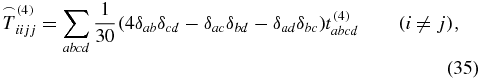
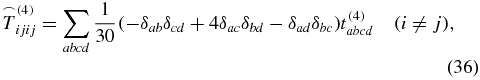
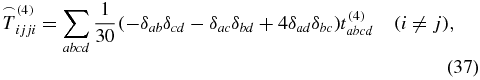
for a rotationally averaged tensor. But because of
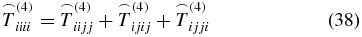
only three of these elements are independent [37, 40]. As in (29), the rotationally averaged tensor interacts three times with the electric field of the laser pulses,
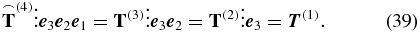
The vanishing arc denotes that the contracted tensors are not isotropic since the electric field polarization introduces a preferred direction. Each interaction such as in
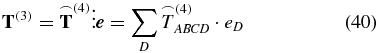
results in a tensor contraction and finally the remaining tensor of rank one,  , carries the vector property of the third-order polarization
, carries the vector property of the third-order polarization  .
.
A different interpretation of the interactions in (39) is as follows. The polarization of the electric field is used to select the combination of the tensor elements being measured. Therefore, the question arises which tensor elements are relevant for a magic-angle condition. Because the magic angle is applied to suppress orientation effects and retain only isotropic signals, we have to search for the isotropic part of  , i.e., after two pump–pulse interactions. Again rotational averaging
, i.e., after two pump–pulse interactions. Again rotational averaging
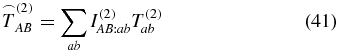
provides the answer. The tensor  contains the isotropic part of T(2). Using the weighting factor
contains the isotropic part of T(2). Using the weighting factor

known from the literature [28, 39], rotational averaging results in a tensor
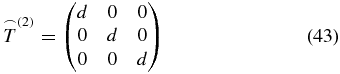
described by a diagonal matrix consisting of nine elements

that belong to the tensor t(4) in the molecule-fixed frame. Therefore, to perform a third-order response experiment under magic-angle condition, we have to select electric field polarization vectors for which the measured signal contains only the mentioned nine tensor elements of t(4).
Under ideal phase matching, the third-order polarization emits a signal field

with the centre frequency ωS that is in a transient absorption experiment self-heterodyne detected [22, 28],
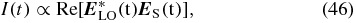
using the probe pulse as the local oscillator  . Therefore the projections
. Therefore the projections
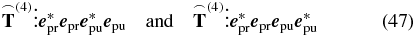
of the emitted signal field onto the polarization  reach the detector.
reach the detector.
In the final step, we apply our definitions of the electric field polarizations (8) and (10) to solve the equation
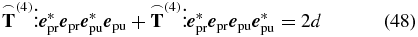
with d given by (44) to find an experimental configuration fulfilling the magic-angle condition, i.e., a configuration for measuring only the isotropic signal d (44). This procedure is simplified by the following approach. First, we remove the isotropic contribution from the general tensor  by setting each individual tensor element in (44) equal to zero. Then, with the remaining tensor
by setting each individual tensor element in (44) equal to zero. Then, with the remaining tensor  , the anisotropy signal results in
, the anisotropy signal results in
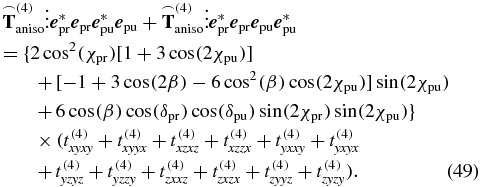
To measure under magic-angle conditions, the anisotropic signal contribution (49) has to vanish. This is achieved for each configuration that fulfils (27), i.e., the same condition is retrieved here as in the transition-probability approach. Apart from this confirmation of the transition-probability approach (section 3), the response-theory approach can also be used to derive magic-angle conditions for geometries other than pump–probe spectroscopy (see, e.g., section 6 for 2D spectroscopy).
5. Generalized magic-angle condition for transient absorption
As concluded in sections 3 and 4, an anisotropy-free pump–probe measurement requires an experimental configuration in which the pump polarization (χpu, δpu), the probe polarization (χpr, δpr) and the probe direction angle β fulfil the magic-angle condition (27). Interestingly, the phase differences δpu and δpr occur only in the last of the three terms of (27). Thus if we demand for this term
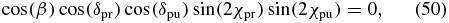
the remaining magic-angle condition
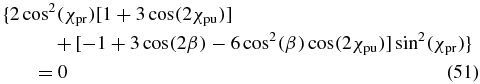
is valid for any phase difference δpu and δpr, i.e., it is valid for any ellipticity that can be achieved for a given angle χpu and χpr. However, these angles still have to fulfil (51). Equation (50) offers five possibilities for how any dependence of (27) onto the phase differences δpu and δpr can be eliminated.
Case 1. The amplitude ratio of the pump pulse χpu could be set to 0° such that sin (2χpu) = 0. This corresponds to selecting a linear pump polarization along the X axis and it is intuitively clear that the phase difference δpu is not relevant if the pump polarization consists only of an X component. The resulting rotation symmetry with respect to the X axis (see figure 4) cancels the β dependence and simplifies (51) to
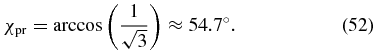
For a linearly polarized probe pulse (δpr = 0°) this is the well-known magic-angle condition [1], but the condition is also valid for an elliptical polarized probe pulse with any phase difference δpr, because the δpr dependence vanishes from our general magic-angle condition (27) due to fulfilment of (50).
Case 2. To fulfil (50), we choose the probe polarization to be parallel to the X axis, χpr = 0°, such that sin (2χpr) = 0. The β dependence vanishes due to rotation symmetry with respect to the X axis. Then the phase difference δpr is not relevant because the probe polarization consists only of an X component. Equation (51) then simplifies to
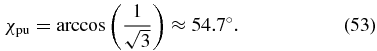
Similar to the first case, for linearly polarized pump pulses, δpu = 0°, this is the well-known magic-angle condition and our general approach extends this condition to elliptically polarized pump pulses with any phase difference δpu.
Case 3. Now we choose the pump polarization to be parallel to the Y axis, χpu = 90°, such that sin (2χpu) = 0. With only the Y polarization component, the phase difference δpu is again not relevant. In contrast to cases 1 and 2, the configuration shows no rotation symmetry around the X axis and β does not vanish, but is connected to χpr via the magic-angle condition

that remains from (51). This condition is again valid for elliptically polarized probe pulses with any phase difference δpr.
Case 4. We choose a horizontal probe polarization located in the YZ plane, χpr = 90°, such that sin (2χpr) = 0. Without the vertical X part, the polarization does again not depend on the phase difference δpr. Similar to case 3, the rotation symmetry with respect to the X axis vanishes. Now the angle β is connected to χpu via the magic-angle condition

remaining from (51), which is valid for an elliptically polarized pump pulse with any phase difference δpu.
Case 5. The last possibility to fulfil (50) for any δpu and δpr dependence is to set β = 90°, such that cos (β) = 0. Such a perpendicular configuration is not very practical for the thin-film cuvettes used in most time-resolved liquid-phase measurements although it may be an option in the gas phase. The magic-angle condition (51) then simplifies to
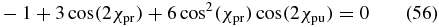
and is valid for elliptically polarized pump and probe pulses with any phase difference δpu and δpr, respectively.
In cases 1 and 2 discussed above, the polarizations of the pump and the probe pulses are given by the magic-angle conditions (52) and (53), respectively. It is possible to choose any phase difference δpr or δpu, respectively, but the amplitude-ratio angle is determined by the magic angle of  . To find a magic-angle configuration for an arbitrary pump or probe polarization, one of the options from cases 3–5 has to be applied. If one, e.g., wants to excite the system under study with an arbitrarily polarized pump pulse in the common nonperpendicular geometry, case 4 would lead to an anisotropy-free configuration. Solving (55) for β results in
. To find a magic-angle configuration for an arbitrary pump or probe polarization, one of the options from cases 3–5 has to be applied. If one, e.g., wants to excite the system under study with an arbitrarily polarized pump pulse in the common nonperpendicular geometry, case 4 would lead to an anisotropy-free configuration. Solving (55) for β results in
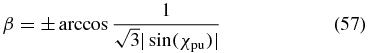
and connects the amplitude ratio χpu of the pump pulse to the propagation angle β of the probe pulse. This relationship is depicted by the black curve in figure 8 and three special cases of (57) are shown as coloured plot markers.
Figure 8. Generalized magic-angle condition. The black curve represents the relationship (57) between the propagation angle β of the probe beam and the amplitude ratio χpu of the pump polarization vector for an arbitrarily polarized pump pulse and a probe pulse with a linear polarization vector in the YZ plane (χpr = 90°). Below χpu = 35.3° no solution exists and therefore no magic-angle configuration can be found. The coloured plot markers highlight three special cases. Circular (red ○) pump polarization and linear pump polarization for collinear (green ◊) and noncollinear (blue □) propagation direction.
Download figure:
Standard image High-resolution imageCase 4(a). For collinear pump and probe pulses propagating along the Z direction (β = 0°) the amplitude ratio becomes χpu = 35.3° (figure 8, green ◊). Subtracting both amplitude-ratio angles,
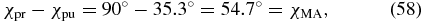
reveals that the angle of 35.3° is the known magic angle, just measured with respect to the X axis instead of the Y axis. This is only valid for a collinear geometry (β = 0°). For the commonly used noncollinear geometry (β > 0°), it is necessary to adjust the angles β and χpu according to (57). If we choose, for example, β = 10° as often employed in pump–probe experiments a corrected angle of χpu ≈ 35.9° is required. Thus, in contrast to (52) and (53) it is not sufficient to rotate the polarization of one of the pulses about 54.7° to achieve the magic-angle configuration if we start with horizontally polarized pump and probe pulses (χpu = 90° and χpr = 90°), because of the lacking rotation symmetry around the X axis.
Case 4(b). In the second special limit of case 4, a linearly polarized pump pulse (δpu = 0) whose polarization is contained in the YZ plane (χpu = 90°) results in an angle β = 54.7° (figure 8, blue □).
Case 4(c). Finally for a circularly polarized pump pulse (χpu = 45°, δpu = π/2) we derive an angle of β = 35.3° = 90° − χMA (figure 8, red ○) also found by Cho [20] for a transient circular dichroism experiment.
Below an amplitude ratio of χpu = 35.3° = 90° − χMA no solution exists for our limitation of a probe pulse with a linear polarization vector (δpr = 0°) located in the YZ plane (χpr = 90°) and therefore no magic-angle configuration.
Our result generalizes the known anisotropy-free condition of linearly and circularly polarized pulses (coloured plot markers in figure 8) to elliptically polarized pulses (black line in figure 8).
By design, the signal fulfilling (50) does not depend on the phase difference δpu as resulting from the third-order interaction within the electric dipole approximation. This means that any remaining experimentally detected presence of a δpu-dependent signal indicates either higher-order interactions or violation of the electric dipole approximation. Thus, such an arrangement allows access exclusively to signals of fifth- or higher-order interaction or it can be used as a sensitive probe for nondipolar transitions like chiral signals that stem from the combined electric dipole, magnetic dipole and electric quadrupole interaction [28]. Applications of phase-cycling methods should be compatible with the generalized magic angle as well.
6. Magic-angle condition for 2D spectroscopy
Concerning the electric field polarization, one advantage of 2D spectroscopy compared to transient absorption spectroscopy is the possibility to control the polarization state of up to four instead of two laser pulses. Therefore more polarization combinations are accessible to filter out the desired information from the measured signal as Hochstrasser [37] and Zanni and coworkers [38] demonstrated. They found polarization sequences that enhance weak cross peaks that would ordinarily be covered by dominating diagonal peaks. Several sample applications are available in the literature [41–49].
In the literature on 2D spectroscopy specific polarization sequences are often recorded and combined linearly to obtain derived quantities. However, for anisotropy-free dynamics, the magic-angle condition could also be employed [50], because the response-theory approach in section 4 is not restricted to transient absorption spectroscopy. If we consider linear polarization and choose for 2D spectroscopy in pump–probe geometry the first two pulses to be in parallel polarization, then the known angle of  between the first two and the third pulse fulfils the magic-angle condition. The same angle
between the first two and the third pulse fulfils the magic-angle condition. The same angle  is valid for 2D spectroscopy in phase-matched box geometry if the polarization vectors of the four pulses are selected to be pairwise parallel.
is valid for 2D spectroscopy in phase-matched box geometry if the polarization vectors of the four pulses are selected to be pairwise parallel.
At least two ways exist to implement such a configuration. On the one hand, the  vectors of the four laser beams may enclose small angles with respect to each other and enter the sample approximately collinearly. Thus, the influence of the propagation vectors onto the polarization vectors may be neglected and in this near-collinear geometry, the polarization vectors
vectors of the four laser beams may enclose small angles with respect to each other and enter the sample approximately collinearly. Thus, the influence of the propagation vectors onto the polarization vectors may be neglected and in this near-collinear geometry, the polarization vectors  are rotated by 54.7° with respect to
are rotated by 54.7° with respect to  . On the other hand, when the four beams enclose a larger mutual angle and the near-collinear approximation is not valid, the propagation vectors of the first two pulses
. On the other hand, when the four beams enclose a larger mutual angle and the near-collinear approximation is not valid, the propagation vectors of the first two pulses  and
and  can be considered to define a plane, and the corresponding polarization vectors
can be considered to define a plane, and the corresponding polarization vectors  and
and  can be chosen to be perpendicular with respect to that plane. Likewise, the last two pulses
can be chosen to be perpendicular with respect to that plane. Likewise, the last two pulses  and
and  can be considered to define a plane with
can be considered to define a plane with  and
and  being perpendicular to that plane. To fulfil the magic-angle condition, it is then necessary to choose propagation vectors for which both planes enclose the magic angle of 54.7°. This geometry thus works for larger inter-beam angles.
being perpendicular to that plane. To fulfil the magic-angle condition, it is then necessary to choose propagation vectors for which both planes enclose the magic angle of 54.7°. This geometry thus works for larger inter-beam angles.
7. Anisotropy spectroscopy
7.1. Single signal contribution
The magic-angle conditions discussed so far allow to exclusively measure population changes, because the anisotropy signal is suppressed. In contrast to that, one can also use a particular polarization configuration of the experimental setup to measure specifically the anisotropy signal. Again we can apply our general model from section 3 to connect the measured anisotropy to informations about the molecular structure, i.e., the angle α between the pump and probe TDMs. Using the anisotropy definition (2) for measured absorbance changes (4) and the probability Pj (26) we can calculate the anisotropy with our approach according to
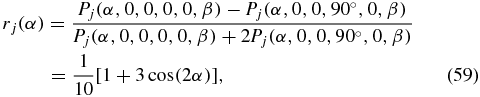
which is in agreement with the literature result for linearly polarized pulses [51]. According to (59), the valid range for the anisotropy is −0.2 ⩽ rj ⩽ 0.4. As the system evolves with the time delay Δt, the structural information α and its dynamic behaviour is masked by rotational diffusion, which results finally in randomly oriented molecules. Therefore, the anisotropy decays to zero.
7.2. Overlapping signal contributions
If the signals of multiple combinations of pump and probe TDMs overlap, the measurable anisotropy
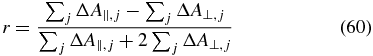
depends on all signal contributions. With the relation [1]
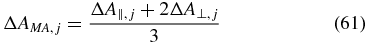
for absorbance changes detected in magic-angle configuration, it is possible to rewrite (60) to obtain
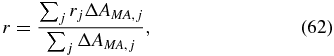
and thus the anisotropy is the average over the anisotropies rj of each single signal contribution with the corresponding magic-angle signal ΔAMA, j as a weighting factor. Therefore, the averaged anisotropy −∞ < r < ∞ clearly deviates from the range −0.2 ⩽ rj ⩽ 0.4 of a single signal contribution, e.g., if the magic-angle signals ΔAMA, j have differing signs. In figure 9 this behaviour of the anisotropy
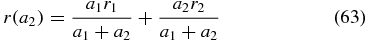
is visualized for two overlapping signals a1 = 1 and a2 with anisotropies of r1 = 0.4 and r2. Both, changes in the signal amplitude a2 and changes in the anisotropy r2 influence the measured anisotropy r. At a2 = −a1, (63) has a pole and the anisotropy r diverges. Experimental anisotropy data which actually diverge because of overlapping signal contributions can be found in the literature [52–54].
Figure 9. Diverging anisotropy. The plotted curves  of the overlapping signals a1 and a2 exemplify the effect of overlapping anisotropy signals. The amplitude a1 = 1 and the anisotropy r1 = 0.4 of one signal are fixed, whereas a2 and r2 of the other signal vary.
of the overlapping signals a1 and a2 exemplify the effect of overlapping anisotropy signals. The amplitude a1 = 1 and the anisotropy r1 = 0.4 of one signal are fixed, whereas a2 and r2 of the other signal vary.
Download figure:
Standard image High-resolution image7.3. Degenerate transition dipole moments
An example for overlapping anisotropy contributions are molecules with degenerate TDMs. In such a system [6, 15, 21], the orientation of the TDM is not defined by a single vector. Instead it is possible to draw a three-dimensional surface shaped depending on the degeneracy and every vector pointing to any point of this surface represents a valid orientation of the degenerate TDM. A set of suitable basis vectors can be used to describe all these directions. Such degenerate TDMs occur typically in highly symmetric molecules such as porphyrin or benzene. These molecules have a two-fold degeneracy composed of two perpendicular basis vectors, which form a disc as depicted in figure 10. Assuming that the pump TDM is degenerate, we can always choose one of the two basis vectors to enclose an angle of 90° with the probe TDM. The other basis vector encloses in general an arbitrary angle α with the probe TDM. According to (59) and (62) we can calculate the anisotropy
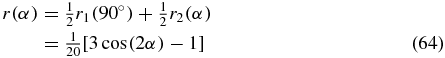
as the average over both signal contributions [21]. The weighting factor of 1/2 is the same for both pump TDMs because both are pumped with the same probability and both signals have the same sign. It is also possible to express the anisotropy
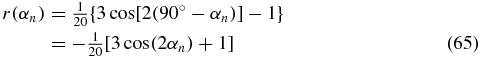
dependent on the angle αn = 90° − α between the normal of the disc-shaped surface in figure 10 and the probe TDM. The result (65), derived with our general approach, is in agreement with the literature [6, 15, 21].
Figure 10. Degenerate TDM. In a molecule with a two-fold degenerate pump TDM  , each orientation (green arrows in the disc) contributes to the measured signal. We can describe all possibilities with two basis vectors
, each orientation (green arrows in the disc) contributes to the measured signal. We can describe all possibilities with two basis vectors  and one basis vector can always include an angle of 90° with the corresponding probe TDM
and one basis vector can always include an angle of 90° with the corresponding probe TDM  . The other basis vector encloses the angle α and the surface normal
. The other basis vector encloses the angle α and the surface normal  the angle
the angle  with the probe TDM.
with the probe TDM.
Download figure:
Standard image High-resolution image8. Conclusion
In this paper we discussed two approaches for calculating magic-angle conditions in third-order spectroscopy of isotropic molecular samples. Allowing for elliptical polarization and arbitrary propagation directions of each laser pulse we obtained a generalized magic-angle condition for elliptically polarized pulses of which the linear and circular polarizations known from the literature are limiting cases. The generality of the approach enabled us to investigate the influence of the pump and probe propagation directions onto the magic-angle configuration and allowed us to calculate a corrected magic angle for a noncollinear geometry.
In addition, we found magic-angle configurations under which the measured third-order signal does not depend on the phase differences between the polarization components of the pump δpu and/or the probe pulse δpr. Thus, if in such a configuration e.g. a δpu-dependent signal occurs, it results either from a higher-order interaction or the electric dipole approximation is violated. Such a signal could be isolated by polarization phase cycling of the phase difference δpu.
Furthermore, the results were also transferred to 2D spectroscopy and third-order spectroscopy in general utilizing the universality of the response-theory approach. A configuration for magic-angle 2D spectroscopy in box geometry was suggested that avoids the often used approximation of nearly collinear beams.
Finally, we calculated, in agreement with the literature, the anisotropy and its relation to the angle α between the corresponding TDMs not only for a single signal but also for multiple overlapping signal contributions on the example of a two-fold degenerate TDM.
Acknowledgments
We thank Ulrike Selig-Parthey for fruitful discussions and her contribution to section 7.2. This work was supported by the DFG within the Research Unit 'Light-induced dynamics in molecular aggregates' (FOR 1809). AS thanks the German National Academic Foundation (Studienstiftung des deutschen Volkes) for a scholarship. PN further acknowledges the DFG for support within the Emmy-Noether program.
Appendix.: Euler-rotation approach
To validate the correctness of the rotational averaging procedure in the transition-probability approach (see section 3), we here use an alternative approach using Euler rotations. Again we assume arbitrary but real-valued TDMs
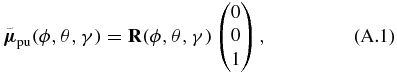
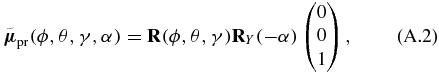
enclosing an angle α, here achieved by a rotation matrix RY rotating the initial vector around the Y axis. The Euler rotation matrix [55]
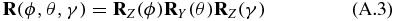
allows to choose an arbitrary orientation. Now we apply our definition of the pump (A.1) and probe (A.2) TDM directions and the definition of the pump (8) and probe (10) electric field polarization vectors to the corresponding equations of the transition probability (15) and (16) and perform rotational averaging [39, 56–60],
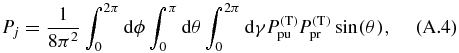
over the product of the pump and probe transition probabilities to calculate the probability Pj. The result is the same as in (26).










