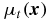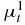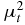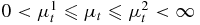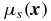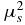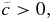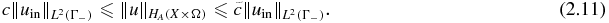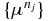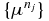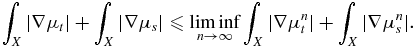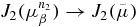Abstract
This paper provides a theoretical study of reconstructing absorption and scattering coefficients based on the radiative transport equation (RTE) by using the total variation regularization method. The function space for solutions of the RTE is a natural one from the form of the boundary value problem of the RTE. We analyze the continuity and differentiability of the forward operator. We then show that the total variation regularization method can be applied for a stable solution. Convergence of the total variation-minimizing solution in the sense of the Bregman distance is also obtained.
Export citation and abstract BibTeX RIS
1. Introduction
The radiative transport equation (RTE) as a forward model to describe the propagation or radiation of particles inside a medium arises in a wide variety of applications in sciences and engineering, including neutron transport, optical molecular imaging, infrared and visible light photography in space and atmosphere, heat transfer, astrophysics, atmospheric science (which is also known as remote sensing) and so on. In these areas, based on suitably chosen function spaces, solvability of the RTE, properties of the solutions and numerical analysis of the RTE are intensively studied. We refer the reader to [1, 11–13, 31, 34, 36, 37] and the references therein for details on this subject.
As RTE-based inverse problems are difficult to study theoretically and to solve numerically, so far, many studies of the RTE-based inverse problems are limited to employing an approximation of the RTE as the forward model. One of the most popular approximation models is based on the diffusion approximation of the RTE. Theoretical and numerical analysis of diffusion-based biomedical molecular imaging problems can be found in numerous papers; for example, in [16], following the procedure of the standard regularization method with a quadratic penalty term, rigorous theoretical analysis of diffusion-based coefficients reconstruction optical tomography is investigated; in [24], mathematical theory and numerical analysis of diffusion-based bioluminescence tomography (BLT) are provided; in [25], solution existence and convergence of numerical methods are for a BLT approach which optimizes optical coefficients when an underlying bioluminescent source distribution is reconstructed to match the measured data. In addition to diffusion-based biomedical molecular imaging, in [22], a theoretical framework of x-ray dark tomography based on the modified Leakeas–Larsen approximation is investigated.
Recently, there has been much research interest in inverse problems based on the RTE in biomedical imaging applications. For linear light source inverse problems, in [23], a comprehensive mathematical framework on the solution existence, uniqueness, continuous dependence on the data and convergence of numerical methods for the BLT problem via standard Tikhonov regularization is established, and in [21, 30], numerical implementations in the two-dimensional case are described. For nonlinear coefficient identification problems, in [7, 33], by analyzing the singular decomposition of the albedo operator in different regimes, stability estimate is derived and uniqueness of the coefficient identification is proved, and in [2, 3, 14, 15], numerical techniques are proposed based on the L1 space, considered to be the 'physically relevant' function space. For general references on the mathematical background and imaging techniques, we refer the reader to [32] and references therein.
In this paper, we provide a theoretical study of reconstructing the absorption and scattering coefficients based on the RTE by using the total variation regularization method.
In the study of the forward model, we use L∞-norm for the parameters and choose a function space HA(X × Ω) for the solution of the RTE problem. The function space HA(X × Ω) is a natural one from the form of the RTE and the inflow boundary condition, i.e., it is the space of all functions that are square integrable together with the spatial directional derivative along the angular direction and are such that their values on the incoming boundary are square integrable. We show the continuity and differentiability of the forward operator with respect to the chosen norms.
The inverse problem of parameter identifications is ill-posed and regularization is needed in solving the inverse problem. Since the parameters are piecewise smooth functions or even piecewise constants in applications, it is beneficial to use total variation regularization. Regularization methods for parameter identifications have attracted much attention and many papers are devoted to study the solution existence, uniqueness and, most importantly, the stability, convergence and convergence rate of regularization methods. A general reference on the regularization methods is [17]. For total variation regularization methods on nonlinear inverse problems, theoretical analysis on the convergence and convergence rate can be found in [6, 8–10, 18, 20, 28, 29, 35]. From these papers, under some source conditions, if the forward operator satisfies the nonlinearity conditions in the sense of metric or Bregman distance, the convergence rate can be obtained. But in many practical parameter identification problems, the nonlinearity conditions for the forward problem are difficult to check, especially when the selected parameter space is a non-reflexive Banach space, e.g. a BV space. In [26], with the use of the compactness properties of the forward solution spaces, convergence rate for the total variation regularization of coefficient identification problems in elliptic problems is obtained. In this paper, we demonstrate that the total variation regularization method can be applied for a stable solution and show the convergence of the solutions of the regularized problem as the regularization parameter approaches zero. The convergence is in the sense of the Bregman distance.
The rest of the paper is organized as follows. In section 2, we introduce the notation and function spaces used in this paper and then review the solvability result of the RTE problem based on a naturally chosen function space HA(X × Ω). In section 3, we analyze the continuity and differentiability of the forward operator and then identify the adjoint problem. In section 4, we study the solution existence, stability estimate and convergence of the total variation-minimizing solutions in the sense of Bregman distance.
2. Notation and physical model
The propagation of light within biological media is described by the RTE. In this section, we discuss the RTE problem.
2.1. Notation and the radiative transport equation
We assume that the spatial domain  is bounded with a C1 boundary ∂X. The outward normal vector is denoted by
is bounded with a C1 boundary ∂X. The outward normal vector is denoted by  for
for  . By
. By  , we denote the unit sphere. We will need the following incoming and outgoing boundaries as subsets of Γ = ∂X × Ω:
, we denote the unit sphere. We will need the following incoming and outgoing boundaries as subsets of Γ = ∂X × Ω:

Denote by  the infinitesimal area element on the unit sphere Ω. In the spherical coordinate system,
the infinitesimal area element on the unit sphere Ω. In the spherical coordinate system,  , for 0 ⩽ θ ⩽ π and 0 ⩽ ψ < 2π, we have
, for 0 ⩽ θ ⩽ π and 0 ⩽ ψ < 2π, we have  . We need an integral operator S defined by
. We need an integral operator S defined by
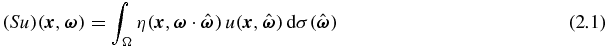
with η a nonnegative normalized phase function:
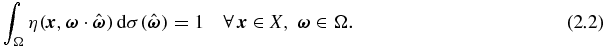
In many applications, the function η is independent of  . However, in our general study, we allow η to depend on
. However, in our general study, we allow η to depend on  . Moreover, we can allow η to be a general function of
. Moreover, we can allow η to be a general function of  ,
,  and
and  , i.e., in the form
, i.e., in the form  . One well-known example is the Henyey–Greenstein phase function (cf [27]):
. One well-known example is the Henyey–Greenstein phase function (cf [27]):
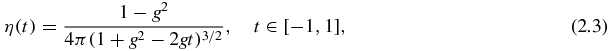
where the parameter g ∈ ( − 1, 1) is the anisotropy factor of the scattering medium. Note that g = 0 for isotropic scattering, g > 0 for forward scattering and g < 0 for backward scattering.
With the above notation, we can write the boundary value problem (BVP) of the RTE:
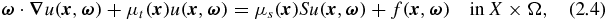

Here μt = μa + μs, μa is the macroscopic absorption cross section, μs is the macroscopic scattering cross section, uin is the incoming flow on the incoming boundary and  is the internal source function. The expression
is the internal source function. The expression  is a directional derivative,
is a directional derivative,
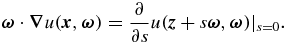
In this paper, we consider the inverse problem of parameter identification through knowledge of the incoming flow and corresponding measurement data um on the outgoing boundary. There is no internal source so that the forward problem is
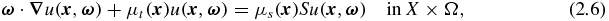

We impose the following assumptions on the coefficients.
Assumptions
- (A1) The function
 is uniformly positive and bounded; i.e., there exist two positive constants
is uniformly positive and bounded; i.e., there exist two positive constants  and
and  , such that
, such that  a.e. in X.
a.e. in X. - (A2) The function
 is uniformly positive and bounded; i.e., there exist two positive constants
is uniformly positive and bounded; i.e., there exist two positive constants  and
and  , such that
, such that  a.e. in X.
a.e. in X. - (A3) There is a constant c0 > 0 such that μt − μs ⩾ c0 > 0 a.e. in X.
Next, we will introduce a function space for  , and show the regularity of solution of the above BVP under this space frame.
, and show the regularity of solution of the above BVP under this space frame.
2.2. Function spaces
We introduce some function spaces that will be needed later in the paper:
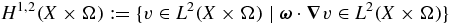
is a Hilbert space with the inner product
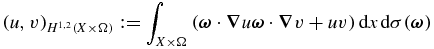
and the corresponding norm  . We also need the function space L2(Γ±) on Γ±, which are Hilbert spaces of functions v on Γ± with the inner products
. We also need the function space L2(Γ±) on Γ±, which are Hilbert spaces of functions v on Γ± with the inner products
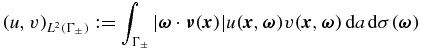
and corresponding norms  .
.
From a result on the trace of an H1, 2(X × Ω) function ([1]), we know that if v ∈ H1, 2(X × Ω) and  , then
, then  , and for some constant c depending only on X, the following inequality holds:
, and for some constant c depending only on X, the following inequality holds:
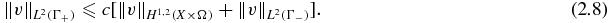
It is known that for each uin ∈ L2(Γ−), the problem (2.6)–(2.7) has a unique solution u ∈ H1, 2(X × Ω). The solution of the BVP (2.6)–(2.7) will be sought from the function space
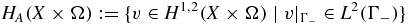
with the norm
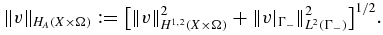
Proposition 2.1. If v ∈ HA(X × Ω), then  , and for some constant c depending only on X,
, and for some constant c depending only on X,
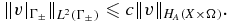
Obviously, we can take c = 1 in the above inequality in bounding  .
.
Corresponding to equation (2.6), we introduce the linear integro-differential operator L by the formula
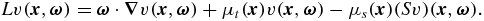
Then we have the following result (cf [1, theorem 3.1]).
Proposition 2.2. Under the assumption on coefficients, in the space HA(X × Ω), the norm  is equivalent to the following norm:
is equivalent to the following norm:
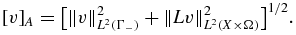
2.3. Solvability of the RTE problem
Consider the BVP (2.6)–(2.7), assuming that uin ∈ L2(Γ−). Introduce the following variational problem.
Variational problem. Find a function u ∈ HA(X × Ω), such that

where
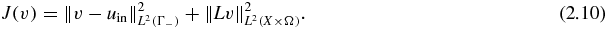
The following result is standard (cf [1]).
Theorem 2.1. Assume (A1)–(A3). Let uin ∈ L2(Γ−). Then
- (1)there exists a unique solution u ∈ HA(X × Ω) to the variational problem (2.9);
- (2)
- (3)for some constants c and
 independent of u and uin, the following bounds hold:
independent of u and uin, the following bounds hold:

Based on (2.9), we introduce the weak formulation of the BVP (2.6)–(2.7):
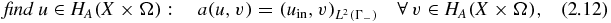
where
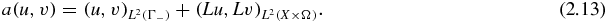
Recall the assumptions (A1)–(A3). With the norm equivalence result, proposition 2.2, we can show the boundedness and  -ellipticity of the bilinear form a( ·, ·):
-ellipticity of the bilinear form a( ·, ·):
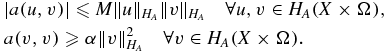
Applying the Lax–Milgram lemma, we conclude that the weak formulation (2.12) has a unique solution u ∈ HA(X × Ω). We will use the weak formulation to analyze the properties of the forward operator.
2.4. Measurements
The measured light intensity in the optical tomography experiments is generally taken on the boundaries of the regions of interest. There are mainly two types of imaging systems for measurements frequently used in optical tomography, namely, optical fiber-based imaging systems and CCD camera-based imaging systems ([2, 33]). We can treat the measurement data from the imaging system as angularly averaged data or angularly resolved data. Let B be the measurement operator acting in the space HA(X × Ω). For angularly averaged data, the measurement operator can be defined as
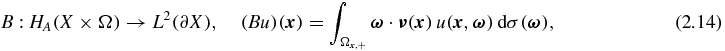
where
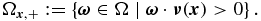
This is, the outgoing current of photons on the boundary. For the angularly resolved data, the measurement operator can be defined as ([33])
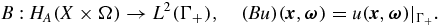
This is simply the outgoing boundary value of the solution of the transport equation. Obviously, the angularly resolved data are richer than the angularly averaged data because angular dependence is allowed. However, in practice, collecting angularly resolved data is too expensive and angularly averaged data are more popularly in use. In this paper, we will focus on angularly averaged measurement data (2.14).
Proposition 2.3. The angularly averaged measurement data-based measurement operator B: HA(X × Ω) → L2(∂X) is well defined, linear and bounded, and for some constant c > 0 depending only on X, we have
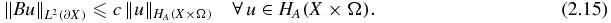
Proof. From proposition 2.1,
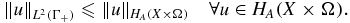
Let us bound  in terms of
in terms of  :
:

Thus, (2.15) holds. □
3. Forward operator
In an optical tomography problem, the object is illuminated by an incident light source on the boundary and the resulting light intensity u is measured on the boundary, denoted as Bu; as is mentioned previously, we use the angularly averaged measurement. This establishes a nonlinear relation between the optical coefficients μt and μs, characterizing the medium and the corresponding measurements Bu on the boundary ∂X. The mathematical model is the following.
Forward operator. For a given light source uin ∈ L2(Γ−), define
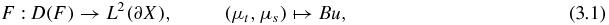
where u denotes the solution of the BVP (2.6)–(2.7), whereas the admissible set is

From theorem 2.3 and proposition 2.4, we see that the forward operator is well defined on D(F).
In the following, we analyze properties of the forward operator.
3.1. Continuity and differentiability
To prove the continuity and differentiability of the forward operator F, we first recall the solvability of the governing BVP
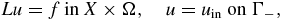
where f ∈ L2(X × Ω). Similar to theorem 2.3, the following result holds.
Theorem 3.1. Assume (A1)–(A3) and f ∈ L2(X × Ω), uin ∈ L2(Γ−). Then there is a unique solution u ∈ HA(X × Ω) to the variational problem:
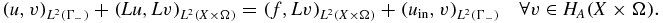
Moreover,
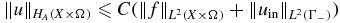
with a constant C depending only on the domain and the bounds of the coefficients.
Theorem 3.2. Assume (A1)–(A3) on (μt, μs) and  , and let u and
, and let u and  denote the solutions of (2.6)–(2.7) with uin ∈ L2(Γ−) corresponding to coefficients (μt, μs) and
denote the solutions of (2.6)–(2.7) with uin ∈ L2(Γ−) corresponding to coefficients (μt, μs) and  , respectively. Then
, respectively. Then
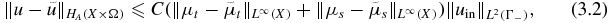
with a constant C depending only on the domain and the bounds of the coefficients.
Proof. We use the weak formulation (2.12) for the solution  with the parameters
with the parameters  and the solution u with the parameters (μt, μs). Then the difference
and the solution u with the parameters (μt, μs). Then the difference  satisfies
satisfies
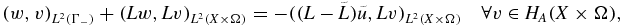
where  denotes the linear operator in (2.6) corresponding to
denotes the linear operator in (2.6) corresponding to  and we used the fact that
and we used the fact that  a.e. in X × Ω.
a.e. in X × Ω.
Applying theorem 3.1,
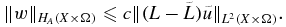
Observe that
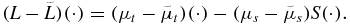
We can then obtain the inequality (3.2). □
As a corollary of theorem 3.2 and proposition 2.4, we can obtain the Lipsichitz continuity property of the forward operator.
Theorem 3.3 (Lipsichitz continuity). Let the assumptions (A1)–(A3) hold. Then the forward operator F: D(F) → L2(∂X) is Lipschitz continuous with respect to the topologies of L∞(X) × L∞(X) and L2(∂X).
The Lipschitz continuity of the forward operator F indicates a certain differentiability. Differentiability is very important in analyzing convergence properties of the regularization method.
Theorem 3.4 (Differentiability). Let uin ∈ L2(Γ−) be given, and let (μt, μs) ∈ D(F), (δμt, δμs) ∈ D(F) such that (μt + αδμt, μs + αδμs) ∈ D(F) for all  with |α| sufficiently small. Then the Fr
with |α| sufficiently small. Then the Fr chet derivative of the forward operator F at (μt, μs) in the direction (δμt, δμs) is given by
chet derivative of the forward operator F at (μt, μs) in the direction (δμt, δμs) is given by
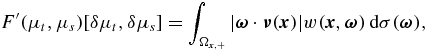
where w is the solution of the following problem:
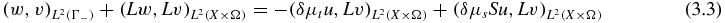
for all v ∈ HA(X × Ω), and u is the solution of BVP (2.6)–(2.7). Moreover,
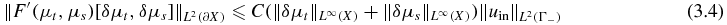
with a constant C depending only on the domain and the bounds of the coefficients.
The proof of theorem 3.4 is similar to that of theorem 3.2 and that of theorem 3.5 below, and is hence omitted. Thus, F'(μt, μs) defines a bounded linear operator mapping from L∞(X) × L∞(X) to L2(∂X) and the estimate (3.4) holds.
Theorem 3.5. The linear Taylor expansion of the forward operator F around (μt, μs) ∈ D(F) is second-order accurate, i.e., for  the following bound holds:
the following bound holds:
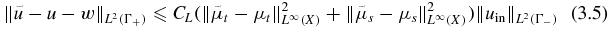
with a constant CL > 0 depending only on the domain and the bounds of the coefficients, where  and u are the solutions of the BVP (2.6)–(2.7) corresponding to
and u are the solutions of the BVP (2.6)–(2.7) corresponding to  and (μt, μs), respectively, and w is the solution to the problem (3.3).
and (μt, μs), respectively, and w is the solution to the problem (3.3).
Proof. Let  . Using (2.12) and (3.3), we can obtain
. Using (2.12) and (3.3), we can obtain

for all v ∈ HA(X × Ω). Applying theorems 3.1 and 3.2, we obtain from the previous equality that
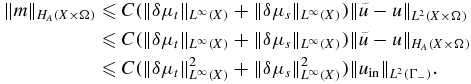
The result (3.5) then follows. □
3.2. Adjoint problem
A formula for the derivative operator F'(μt, μs) was derived in theorem 3.4. Here, we derive an adjoint equation for the calculation of the adjoint of the derivative operator F'(μt, μs). The adjoint equation is important in numerical calculations as well as in analyzing the back transport effect in application. Recall that the  derivative of the forward operator F can be computed by solving the following BVP (cf (3.3)):
derivative of the forward operator F can be computed by solving the following BVP (cf (3.3)):
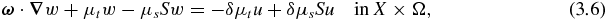

Theorem 3.6 (Adjoint problem). Let (μt, μs) ∈ D(F). Assume uin ∈ L∞(Γ−). Then the adjoint of the derivative operator F'(μt, μs) is given by
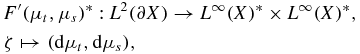
where
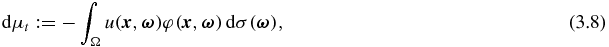
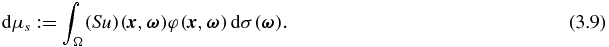
Here, u denotes the solution to the forward problem (2.6)–(2.7) and  is the solution of the following adjoint problem:
is the solution of the following adjoint problem:
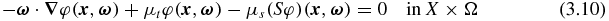

Proof. We multiply both sides of the equation (3.6) by φ and integrate
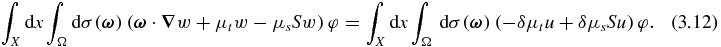
The left side of (3.12) is equal to
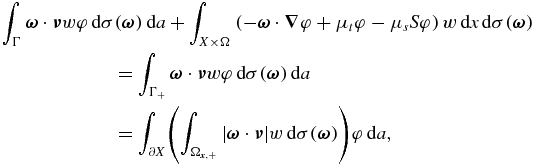
whereas the right side of (3.12) is

So
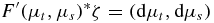
with dμt defined by (3.8) and dμs defined by (3.9).
Since uin ∈ L∞(Γ−), by [1, lemma 3.2], u ∈ L∞(X × Ω). By a variant of theorem 2.3, φ ∈ L2(X × Ω). Then it is easy to see dμt ∈ L2(X). Similarly, dμs ∈ L2(X). □
4. Inverse problem
The goal of the inverse problem is to reconstruct the optical properties of tissues, i.e., the functions  and
and  , from knowledge of the map Λ: uin↦Bu. In practice, only a finite source–detector pair can be used in the measurement process, i.e., we have only partial information on the map Λ. This makes the problem undetermined, causing the parameter identification problem to be severely ill-posed. To overcome the ill-posedness, multiple excitation and finite observations are used in the numerical analysis, where the finite observations are the discretized measurements at some locations on ∂X ([16]). Here, for convenience in presenting the theory, we consider the observation corresponding to every excitation in the continuous form. We do the experiment a few times and determine (μt, μs) by matching the predictions calculated from the forward problem with the measured data on ∂X. More precisely, let k0 be the number of experiments. For k = 1, ..., k0, let us denote by
, from knowledge of the map Λ: uin↦Bu. In practice, only a finite source–detector pair can be used in the measurement process, i.e., we have only partial information on the map Λ. This makes the problem undetermined, causing the parameter identification problem to be severely ill-posed. To overcome the ill-posedness, multiple excitation and finite observations are used in the numerical analysis, where the finite observations are the discretized measurements at some locations on ∂X ([16]). Here, for convenience in presenting the theory, we consider the observation corresponding to every excitation in the continuous form. We do the experiment a few times and determine (μt, μs) by matching the predictions calculated from the forward problem with the measured data on ∂X. More precisely, let k0 be the number of experiments. For k = 1, ..., k0, let us denote by  the inflow value function for the kth experiment and by mk the corresponding angularly averaged measurement. Then our inverse problem is to determine (μt, μs) such that for k = 1, ..., k0, the solution uk := uk(μt, μs) of the BVP (2.6)–(2.7) with uin replaced by
the inflow value function for the kth experiment and by mk the corresponding angularly averaged measurement. Then our inverse problem is to determine (μt, μs) such that for k = 1, ..., k0, the solution uk := uk(μt, μs) of the BVP (2.6)–(2.7) with uin replaced by  satisfies
satisfies
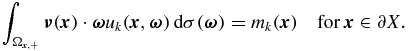
Mathematically, it means to solve a system of nonlinear equations:
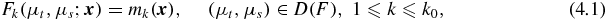
where  is the forward operator corresponding to the inflow boundary value
is the forward operator corresponding to the inflow boundary value  . Because of the effects of the experimental environment and the accuracy of laboratory equipment, the measurement mk is not accurate. For k = 1, ..., k0, let δk ⩾ 0 be the noise level, i.e.
. Because of the effects of the experimental environment and the accuracy of laboratory equipment, the measurement mk is not accurate. For k = 1, ..., k0, let δk ⩾ 0 be the noise level, i.e.  , where mt, k denotes the true value of mk on ∂X. Then define a noise level vector
, where mt, k denotes the true value of mk on ∂X. Then define a noise level vector  . The inverse problem (4.1) is ill-posed; hence some regularization methods are used in order to obtain a stable solution. To treat well the possibly discontinuous or highly oscillating coefficients, we use the output least-squares method with total variation regularization. That is, we minimize the following functional:
. The inverse problem (4.1) is ill-posed; hence some regularization methods are used in order to obtain a stable solution. To treat well the possibly discontinuous or highly oscillating coefficients, we use the output least-squares method with total variation regularization. That is, we minimize the following functional:
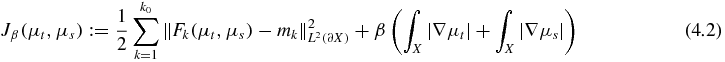
over the admissible set
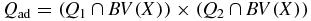
for the coefficient pair μ = (μt, μs). Here β > 0 is a regularization parameter,
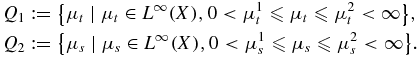
The symbol ∫X|∇μt| denotes the total variation semi-norm ([19]) of μt ∈ L1(X):
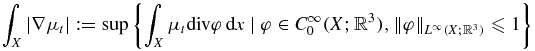
and ∫X|∇μs| is defined similarly. BV(X) denotes the bounded variation space
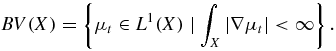
It is a Banach space under the norm
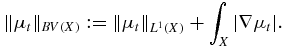
For k = 1, ..., k0, let  be the exact measurement data on ∂X. To simplify the notation, we denote (μt, μs) as μ, and denote the first item on the right hand of (4.2) as J1(μ), the second item as βJ2(μ). Then our purpose is to analyze the minimization problem:
be the exact measurement data on ∂X. To simplify the notation, we denote (μt, μs) as μ, and denote the first item on the right hand of (4.2) as J1(μ), the second item as βJ2(μ). Then our purpose is to analyze the minimization problem:
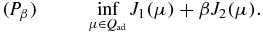
In the following, we will prove that the problem (Pβ) has a solution μβ. Furthermore, the problem
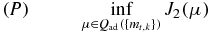
also has a solution μ† which is called the total variation-minimizing solution of the system of equations Fk(μ) = mt, k, 1 ⩽ k ⩽ k0, where

4.1. The regularized problems
The main result here is on the solution existence to both problems (Pβ) and (P). First, we recall some properties of the BV(X) space ([5, 19]).
- (i)Let {μn} be a bounded sequence in BV(X). Then there are a subsequence
 and an element μ ∈ BV(X) such that
and an element μ ∈ BV(X) such that  converges to μ in L1(X).
converges to μ in L1(X). - (ii)Let {μn} be a sequence in BV(X) which converges to μ in L1(X). Then μ ∈ BV(X) and

Note that if {μn}⊂BV(X) converges to μ ∈ BV(X), then
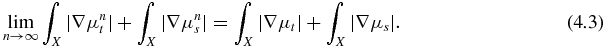
- (i)A solution μβ of the problem (Pβ) exists.
- (ii)A solution μ† of the problem (P) exists.
Proof. (i) It is clear that Jβ(μ) ⩾ 0 on the admissible set Qad. There exists a minimizing sequence {μn} ∈ Qad such that

Hence {Jβ(μn)} is bounded, Jβ(μn) ⩽ J0 for some constant J0. By the definition of Jβ(μ) with μ replaced by μn,
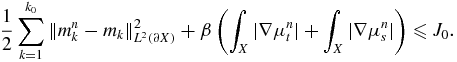
Here, we denote by  the solution of the BVP (2.6)–(2.7) with μ replaced by μn, and
the solution of the BVP (2.6)–(2.7) with μ replaced by μn, and
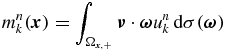
is the corresponding measurement on the boundary. From the last inequality,  is bounded in L2(∂X),
is bounded in L2(∂X),  and
and  are bounded in BV(X). On the other hand, from theorem 2.3,
are bounded in BV(X). On the other hand, from theorem 2.3,

So  is uniformly bounded in HA(X × Ω). By possibly extracting a subsequence, there exist
is uniformly bounded in HA(X × Ω). By possibly extracting a subsequence, there exist  ,
,  and
and  satisfying
satisfying
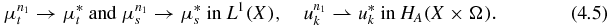
Then, there exist further subsequences  and
and  such that
such that  and
and  a.e. on X. Note that
a.e. on X. Note that

Since  for all n2, we have
for all n2, we have  , and hence
, and hence  . Similarly,
. Similarly,  . From proposition 4.1,
. From proposition 4.1,
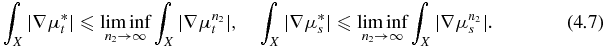
Now let us show that for k = 1, ..., k0,  on ∂X. We first note that
on ∂X. We first note that
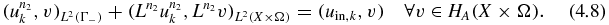
Here,  denotes the linear integro-differential operator corresponding to the coefficients
denotes the linear integro-differential operator corresponding to the coefficients  . Next, let us denote by L* the linear integro-differential operator with the coefficients μ*. Let v ∈ HA(X × Ω) be arbitrary but fixed. We will show that
. Next, let us denote by L* the linear integro-differential operator with the coefficients μ*. Let v ∈ HA(X × Ω) be arbitrary but fixed. We will show that
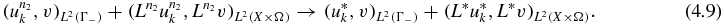
Since  in HA(X × Ω), by the definition of space HA(X × Ω),
in HA(X × Ω), by the definition of space HA(X × Ω),  also in L2(Γ−), which implies that
also in L2(Γ−), which implies that
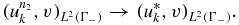
Moreover,
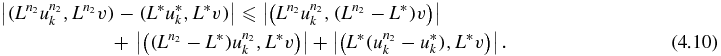
For the first item on the right,
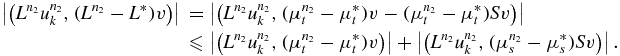
Now,

The values  are uniformly bounded. Since
are uniformly bounded. Since  and
and  converge to
converge to  almost everywhere, an application of the Lebesgue dominant convergence theorem on the term
almost everywhere, an application of the Lebesgue dominant convergence theorem on the term  shows that
shows that
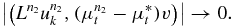
Similarly,
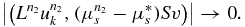
Thus, we obtain
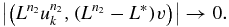
For the second term on the right of (4.10), write
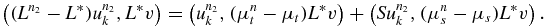
By the same argument, we then conclude that
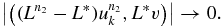
For the last term on the right of (4.10), we have
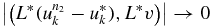
due to the condition that  in HA(X × Ω).
in HA(X × Ω).
Combining the above results, we see that (4.9) is valid, implying that for 1 ⩽ k ⩽ k0,  is the solution of the BVP (2.6)–(2.7) with the coefficients
is the solution of the BVP (2.6)–(2.7) with the coefficients  and
and  corresponding to the inflow value
corresponding to the inflow value  . Furthermore,
. Furthermore,  on ∂X.
on ∂X.
Now, let us check that  is a minimizer of problem (Pβ). Note that
is a minimizer of problem (Pβ). Note that  in HA(X × Ω), so by the definition of space HA(X × Ω) and [1, lemma 2.2], we can conclude that
in HA(X × Ω), so by the definition of space HA(X × Ω) and [1, lemma 2.2], we can conclude that  in L2(∂X). Then, by [4, exercise 2.7.2], for 1 ⩽ k ⩽ k0,
in L2(∂X). Then, by [4, exercise 2.7.2], for 1 ⩽ k ⩽ k0,
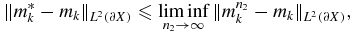
so
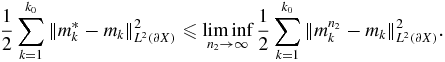
Together with (4.7), we have
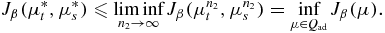
This completes the proof of (i).
(ii) Let {μn} be a sequence in Qad({mt, k}) such that

From the assumption on the absorption and scattering coefficients, it is obvious that {μn} is bounded in L1(X). Following from (4.11), we know that {μn} is bounded in BV(X). Hence, there exist a subsequence  of {μn} and an element μ† such that
of {μn} and an element μ† such that  converges to μ† in L1(X) and
converges to μ† in L1(X) and

A subsequence  of
of  exists, converging to μ† a.e. on X. Since
exists, converging to μ† a.e. on X. Since  , μ† ∈ Qad. On the other hand, for k = 1, ..., k0, we have
, μ† ∈ Qad. On the other hand, for k = 1, ..., k0, we have
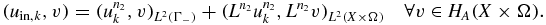
As in the proof of (i), we have  in HA(X × Ω),
in HA(X × Ω),  is the solution of the BVP:
is the solution of the BVP:
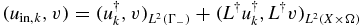
and satisfies the measurement boundary condition. Thus, μ† ∈ Qad({mt, k}). Furthermore, from inequalities (4.11) and (4.12), we have
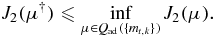
This means μ† is a solution of the problem (P). Thus, the proof is completed. □
Theorem 4.2 (Stability). Let the regularization parameter β > 0 be fixed. For 1 ⩽ k ⩽ k0, let  be a sequence which converges to mk in L2(∂X), and let
be a sequence which converges to mk in L2(∂X), and let  be the minimizers of the problems:
be the minimizers of the problems:
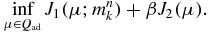
Here, to show explicitly the dependence of J1 on the measurement data, we use  instead of J1(μ). Then, a subsequence
instead of J1(μ). Then, a subsequence  of
of  and
and  exist, such that
exist, such that  converges to
converges to  in L1(X) and
in L1(X) and

Furthermore,  is a solution to (Pβ).
is a solution to (Pβ).
Proof. For all n and μ ∈ Qad, we have
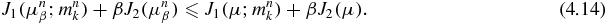
Since  is a bounded sequence in L2(∂X), from the above inequality, it follows that the sequence
is a bounded sequence in L2(∂X), from the above inequality, it follows that the sequence  is bounded in BV(X). By proposition 4.1, a subsequence
is bounded in BV(X). By proposition 4.1, a subsequence  of
of  and
and  exist such that
exist such that  converges to
converges to  in L1(X) and
in L1(X) and

Since  for all n1, it follows that
for all n1, it follows that  . Hence,
. Hence,  . By the argument used in the proof of theorem 4.2, a subsequence
. By the argument used in the proof of theorem 4.2, a subsequence  of
of  exists such that
exists such that  weakly converges to
weakly converges to  in HA(X × Ω), and
in HA(X × Ω), and  weakly converges to
weakly converges to  in L2(∂X). Thus, we have
in L2(∂X). Thus, we have
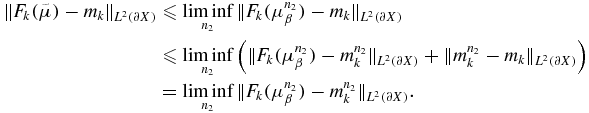
So
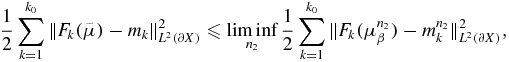
which means that

Together with (4.14) and (4.15), we obtain that for any μ ∈ Qad,
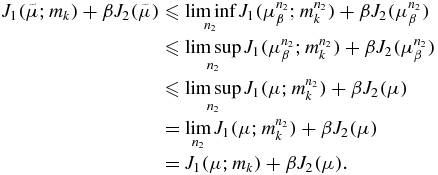
This implies that  is a solution of the problem (Pβ) and
is a solution of the problem (Pβ) and
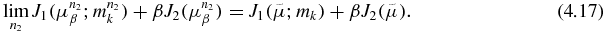
Finally, let us show (4.13) holds, that is,  as n2 → ∞. Assume
as n2 → ∞. Assume  . Then from (4.15), we have
. Then from (4.15), we have

From the definition of limit superior, there exists a subsequence  of
of  such that
such that  converges to
converges to  almost everywhere,
almost everywhere,  and
and  . Since (4.17) holds, we obtain that
. Since (4.17) holds, we obtain that

4.2. Convergence
We will show that the solutions of the problem (Pβ) with the noisy measurement data  converge toward a solution of the problem (P) as β → 0 and the noise level
converge toward a solution of the problem (P) as β → 0 and the noise level  , 1 ⩽ k ⩽ k0. For the noise level vector
, 1 ⩽ k ⩽ k0. For the noise level vector  , the arithmetic mean of the square of k0 noise levels is
, the arithmetic mean of the square of k0 noise levels is ![$m(\delta ^{n})=\big[\big(\delta _1^n\big)^2+\cdots +\big(\delta _{k_0}^n\big)^2\big]/k_{0}$](https://content.cld.iop.org/journals/0266-5611/29/9/095002/revision1/ip473169ieqn144.gif) .
.
We measure the convergence with respect to the Bregman distance, which is briefly recalled here. Let B be a Banach space with B* being the dual space of it; R: B → ( − ∞, ∞] is a proper convex functional and ∂R(q) stands for the subdifferential of R at q ∈ Dom R := {q ∈ B∣R(q) < ∞} ≠ ∅ defined by
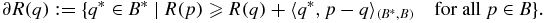
The set ∂R(q) may be empty; however, if R is continuous at q, then it is nonempty. Furthermore, ∂R(q) is convex and weak* compact. In the case ∂R(q) ≠ ∅, for any fixed p ∈ B, we denote
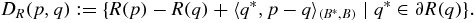
Then for a fixed element q* ∈ ∂R(q),

is called the Bregman distance with respect to R and q* of two elements p, q ∈ B.
The Bregman distance is not a metric on B. However, for each q* ∈ ∂R(q), the  for any p ∈ B and
for any p ∈ B and  . Furthermore, in the case R is the strictly convex function,
. Furthermore, in the case R is the strictly convex function,  if and only if p = q.
if and only if p = q.
Theorem 4.3. (Convergence) For any positive vector sequence δn → 0 such that for βn := β(δn) → 0, m(δn)/βn → 0 as n → ∞, let  be a sequence in L2(∂X) such that for every k,
be a sequence in L2(∂X) such that for every k,  , and let
, and let  be the minimizers of the problems
be the minimizers of the problems

Then, a subsequence  of
of  and an element
and an element  exist such that
exist such that

and

Furthermore,  is a solution to the problem (P) and for all
is a solution to the problem (P) and for all  ,
,

Proof. For all n, by the definition of  , for any μ ∈ Qad, we have
, for any μ ∈ Qad, we have
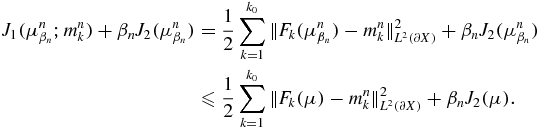
In particular, for any μ ∈ Qad({mt, k}),
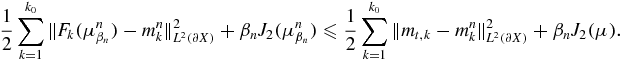
From the above inequality, we have
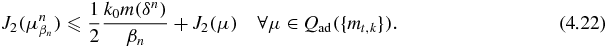
Since m(δn)/βn → 0,  is bounded in BV(X). By proposition 4.1, we conclude that there exist a subsequence
is bounded in BV(X). By proposition 4.1, we conclude that there exist a subsequence  of
of  and
and  , such that
, such that


By the same reasoning as in the proof of theorem 4.3, a subsequence  of
of  exists, such that, for 1 ⩽ k ⩽ k0,
exists, such that, for 1 ⩽ k ⩽ k0,
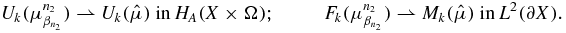
On the other hand,
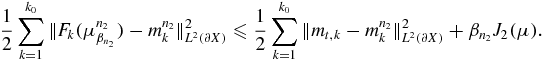
When  and
and  , the first item on the right of the above inequality approaches zero, and so
, the first item on the right of the above inequality approaches zero, and so
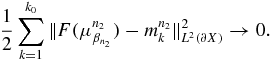
Moreover, from
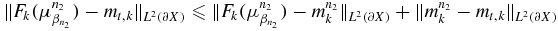
and  , we conclude that
, we conclude that
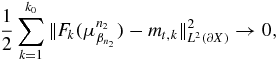
i.e.,  as n → ∞ in L2(∂X). Recall that
as n → ∞ in L2(∂X). Recall that  in L2(∂X). By the uniqueness of the weak limit,
in L2(∂X). By the uniqueness of the weak limit,  , i.e.,
, i.e.,  .
.
It remains to prove (4.21). For any μ ∈ Qad({mt, k}), by (4.22) and (4.24), we have
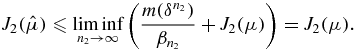
This means that  is a solution to the problem (P). Again using (4.22) and (4.24), we have
is a solution to the problem (P). Again using (4.22) and (4.24), we have
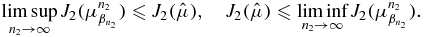
So

From (4.23) and (4.25), by [5, proposition 10.1.2], the sequence  weakly converges to
weakly converges to  in BV(X) . Thus, for all
in BV(X) . Thus, for all  ,
,

which is (4.21). □
5. Summary
In this paper, we present a theoretical analysis of the parameter identification problem for the radiative transport equation (RTE) with angularly averaged measurement data. The parameters are sought in subspaces of L∞(X), whereas the solution of the RTE BVP is from the space of square integrable functions that have square integrable directional derivatives along the angular direction and that have square integrable traces on the incoming boundary. We analyze properties of the forward operator in this function space setting, including the continuity and differentiability with respect to the parameters. The total variation regularization method is considered for the parameter identification problem where the parameters may have discontinuity or high oscillation and we show that the method leads to a stable solution. We also show the convergence of the total variation-minimizing solution in the sense of the Bregman distance. Lack of compactness property of the function spaces presents a major challenge for the theoretical analysis of the problem and this challenge is overcome with careful arguments.
Acknowledgments
The authors thanks the anonymous referees for valuable comments. This work is supported by the National Natural Science Foundation of China under grant no. 91230119.