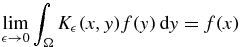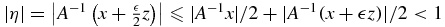Abstract
The reconstruction of images from data modeled by circular or spherical mean Radon transforms plays an important role in thermoacoustic and photoacoustic tomography. We consider a modification of a summability-type approximate reconstruction method described in earlier work and show that in the limit it leads to exact reconstruction. Among the consequences of this development are certain two- and three-dimensional inversion-type formulas in which the detectors lie on ellipses or ellipsoids respectively.
Export citation and abstract BibTeX RIS
1. Introduction
Given a sufficiently regular scalar valued function f on 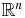 , n ⩾ 2, its spherical mean Radon transform at ξ and r,
, n ⩾ 2, its spherical mean Radon transform at ξ and r, 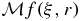 where
where 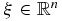 and r > 0, is the average of f over the sphere of radius r centered at ξ. It can be expressed as the following integral over the unit sphere in
and r > 0, is the average of f over the sphere of radius r centered at ξ. It can be expressed as the following integral over the unit sphere in 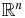 :
:

where dσ(u) denotes the usual rotation invariant surface measure on the unit sphere 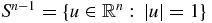 . In particular,
. In particular,
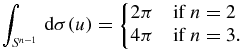
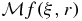 is used to model the data in various models of thermoacoustic and photoacoustic tomography, where f represents the phantom and ξ the position of a detector. More specifically, in such models the phantom f is taken to have compact support, usually in a ball, and the data
is used to model the data in various models of thermoacoustic and photoacoustic tomography, where f represents the phantom and ξ the position of a detector. More specifically, in such models the phantom f is taken to have compact support, usually in a ball, and the data 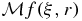 are known for all relevant r and for ξ on the boundary of a set containing the support of f.
are known for all relevant r and for ξ on the boundary of a set containing the support of f.
A basic problem is the following: suppose 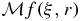 is known for all relevant r and for ξ in a given subset of Rn. Find an algorithm to reconstruct f.
is known for all relevant r and for ξ in a given subset of Rn. Find an algorithm to reconstruct f.
In certain instances, such as the case when the set of detectors is a sphere, this and related questions have been successfully addressed by several investigators, for example [3–5] and [7]. Indeed, thermoacoustic and photoacoustic tomography and the spherical mean Radon transform have been the main subject matter of many studies. A comprehensive background, including many of the known results concerning the spherical mean Radon transform and an extensive list of references, can be found in [11]. However, many questions still remain, such as those concerned with reconstruction procedures involving more general sets of detector geometries. See [11, section 19.5 on pages 860–861] for related and further examples of open questions.
In [2], certain summability-type approximate reconstruction algorithms valid for a wide class of detector geometries were introduced using heuristic arguments motivated by the methods in [12]. Numerical evidence was provided to demonstrate the high quality of the resulting reconstructions. However, no mathematically rigorous results showing exact reconstruction in the limit, with improving resolution, were offered. The point of this paper is to prove, using certain technical modifications, that in the cases n = 2 and n = 3 the method does indeed lead to exact reconstruction in the limit. The cases n = 2 and n = 3 are, of course, the most prominent in practical applications. Among the consequences of our development are certain inversion-type formulas where the detectors need not be restricted to a circle but can lie on more general ellipses.
The usual so-called filtered backprojection-type algorithms are based on regularizations of exact and explicit, but somewhat ill-conditioned, inversion formulas. Examples of such algorithms applied to circular mean Radon transform data can be found in [3, section 4], see also [6] and [8]. While the method treated here may be considered to be a filtered backprojection-type algorithm, it does not rely on any explicit inversion formulas but on the contrary, as shown in subsection 3.3 below, it gives rise to such formulas as limiting cases.
We use standard mathematical notation and only mention the fact that we use the symbol c, with or without a subscript, to denote generic constants whose exact value depends on the context.
2. The setup
In what follows, Ω is a bounded open convex subset of Euclidean space, 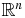 , whose boundary Λ is an ellipsoid centered at the origin. More specifically, there is an invertible real positive definite symmetric matrix A such that
, whose boundary Λ is an ellipsoid centered at the origin. More specifically, there is an invertible real positive definite symmetric matrix A such that
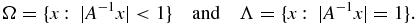
The phantom f is a bounded measurable function that vanishes outside a compact subset of Ω and the set of detectors consists of all points ξ on the boundary, Λ, of Ω. Thus  is known for all ξ in Λ and all positive r. Note that
is known for all ξ in Λ and all positive r. Note that 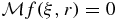 for all r > r1 where r1 is the length of the major axis of Ω which is twice the largest eigenvalue of A.
for all r > r1 where r1 is the length of the major axis of Ω which is twice the largest eigenvalue of A.
To approximately reconstruct f(x) from the data 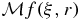 , with (ξ, r) in Λ × ]0, r1[, we consider kernels K(x, y) of the form
, with (ξ, r) in Λ × ]0, r1[, we consider kernels K(x, y) of the form

where λ is a measure on Λ and k(x, ξ, r) is a sufficiently regular function on Ω × Λ × ]0, r1[ so that as a function of y the kernel K(x, y) is an integrable function on Ω for each x in Ω. Thus, we may write
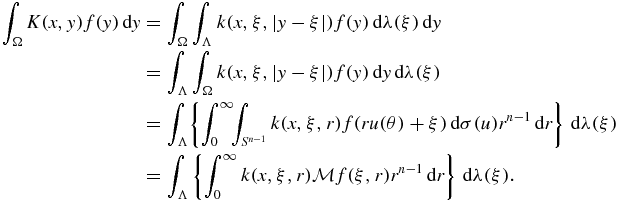
In other words, if the kernel K(x, y) is of the form (2) then ∫ΩK(x, y)f(y) dy can be computed in terms of the circular mean data  with (ξ, r) in Λ × ]0, r1[, namely
with (ξ, r) in Λ × ]0, r1[, namely
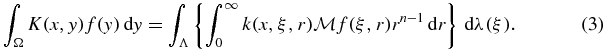
Definition. We say that K (x, y), a function of the variables
(x, y), a function of the variables  > 0 and (x, y) ∈ Ω × Ω, is a summability kernel on Ω if for each x in Ω
> 0 and (x, y) ∈ Ω × Ω, is a summability kernel on Ω if for each x in Ω
- (s1) as a function of y the kernel K
 (x, y) is an integrable function on Ω for all positive
(x, y) is an integrable function on Ω for all positive  , and
, and - (s2)
 for any bounded measurable function f that vanishes outside a compact subset of Ω and is continuous at x.
for any bounded measurable function f that vanishes outside a compact subset of Ω and is continuous at x.
The above notion of summability kernel is analogous to the corresponding notion found in Fourier analysis, for example see [10, item 2.2, page 9], adapted to our application.
In [2], kernels K (x, y) of the form (2) were considered with
(x, y) of the form (2) were considered with
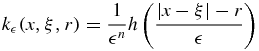
where h(t) satisfies the following properties:
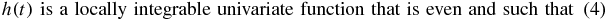
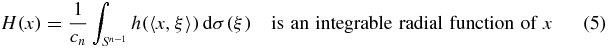
with total integral one, i.e.
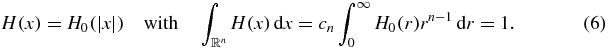
The constant cn in both (5) and (6) is the surface area of Sn − 1.
In [2], heuristic rationale was used to justify the above choice and the results of numerical experiments where provided showing that ∫ΩK (x, y)f(y) dy, computed in terms of spherical mean data of f via (3), is a good approximation of f for several representative examples. However, no mathematically rigorous proof was provided showing that this choice results in a summability kernel.
(x, y)f(y) dy, computed in terms of spherical mean data of f via (3), is a good approximation of f for several representative examples. However, no mathematically rigorous proof was provided showing that this choice results in a summability kernel.
Here we restrict ourselves to the cases n = 2 and 3, use the modification
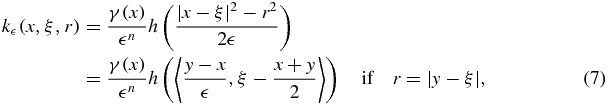
and show that the corresponding kernel

is a summability kernel. The function γ(x) and the measure dλ(ξ) are defined below.
The argument of h in the modification (7) is analytic in all the variables and in view of (8) seems easier to deal with algebraically than the original form. In spite of this, for reasons that are given after the statement of the lemma below, in the case n = 2 we restrict our considerations to the special case

considered in [2, section 4.1].
Here γ(x) is chosen so that 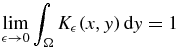 . In what follows we will show that it is a constant multiple of 1 − |A−1x|2. (See the discussion immediately preceding the statement of the lemma below.)
. In what follows we will show that it is a constant multiple of 1 − |A−1x|2. (See the discussion immediately preceding the statement of the lemma below.)
If Λ is a circle or sphere, then the measure dλ(ξ) is simply the usual arc length measure or surface measure, respectively. In the general case, the measure dλ(ξ) is defined so that
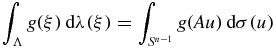
for every continuous function g(ξ) on Λ where A is the matrix such that Λ = {x: |A−1x| = 1}. For example, in the case n = 2 the measure dλ(ξ) can be defined in terms a smooth parametrization ξ(t) as |A−1ξ'(t)| dt. Thus, if ξ(t), a ⩽ t ⩽ b, is a smooth parametrization of Λ and g(ξ) is a continuous function on Λ, then x(t) = A−1ξ(t) is a parametrization of S1 and the desired measure may be described by
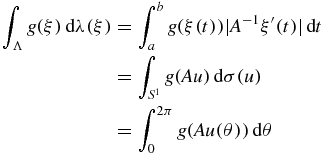
where u(θ) = (cos θ, sin θ). Note that if Λ is an ellipse or an ellipsoid that is not a circle or a sphere, then dλ(ξ) is not the arc length measure or surface measure on Λ.
It is evident from (8) that the resulting kernel K (x, y) satisfies property (s1) of a summability kernel on Ω. Thus, to conclude that it is indeed a summability kernel on Ω it suffices to verify property (s2).
(x, y) satisfies property (s1) of a summability kernel on Ω. Thus, to conclude that it is indeed a summability kernel on Ω it suffices to verify property (s2).
To this end, suppose K (x, y) is of form (8) and f is a bounded measurable function on Ω. Then
(x, y) is of form (8) and f is a bounded measurable function on Ω. Then
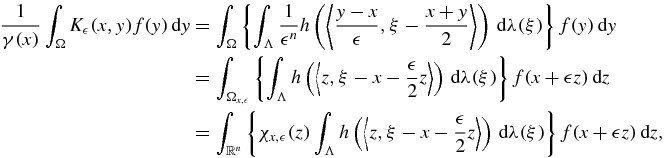
where χx,  (z) is the indicator function of the set Ωx,
(z) is the indicator function of the set Ωx,  = {z: z + x/
= {z: z + x/ ∈ Ω/
∈ Ω/ }, that is
}, that is
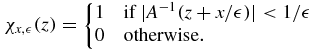
Now, if the last expression in braces is bounded by an integrable function, namely if
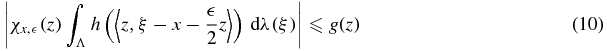
where g(z) is independent of  and is integrable over
and is integrable over 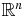 , and f is continuous at x then the dominated convergence theorem implies that
, and f is continuous at x then the dominated convergence theorem implies that
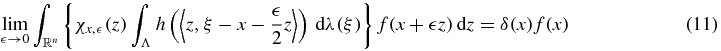
where
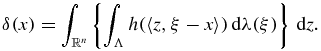
If δ(x) is finite and does not vanish on Ω, then taking  shows that K
shows that K (x, y) is a summability kernel.
(x, y) is a summability kernel.
We summarize these observations as follows.
Lemma 1. Suppose h satisfies (4)–(6). If for each x ∈ Ω the function h also enjoys property (10), then K (x, y) defined by (7) and (8) is a summability kernel for Ω.
(x, y) defined by (7) and (8) is a summability kernel for Ω.
To establish (10) the special cases of the Funk–Hecke formula

play a significant role in our considerations. The presence of the factor (1 − t2)−1/2 makes the case n = 2 more difficult than the case n = 3. In fact, to avoid dealing with this factor, in the case n = 2 we restrict our attention to the particular example of h given by (9).
In the case n = 3, property (10) is not difficult to establish. However, to avoid irrelevant technical difficulties, we will assume that in addition to (4)–(6) there are positive constants C and p with p > 3 such that the function H(x) defined by (5) satisfies

3. Circular mean data
In this section, we restrict our attention to the case n = 2 and the function h(t) described by (9). The function H(x) of (5) corresponding to this particular h(t) is
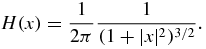
The details can be found in [12, sections 2.2 and 2.3].
3.1. The basic result
The following lemma shows that relation (10) is indeed fulfilled in the special case when h is the function defined by (9).
Lemma 2. If x ∈ Ω and h(t) is the function defined by (9), then
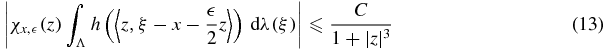
where C is finite and depends on x but is independent of z and  .
.
Proof. Suppose Ω = {x: |x| < 1} and Λ = ∂Ω = S1 so if 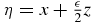 with z ∈ Ωx,
with z ∈ Ωx,  then
then
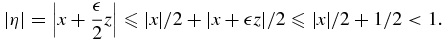
Our first objective is to obtain an expression for
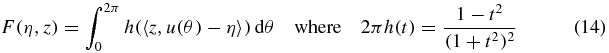
that is explicit enough to allow us to determine whether F(η, z) is integrable on 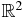 as a function of z for |η| < 1.
as a function of z for |η| < 1.
We begin by observing that
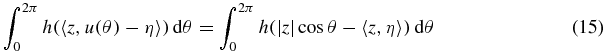
and that
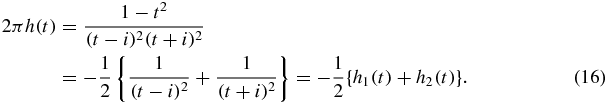
Since  , it follows that
, it follows that

Let a = |z| and b = 〈z, η〉. To evaluate

use the substitution, [1, p 154],
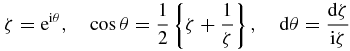
to express I1 as a contour integral over the unit circle in the complex plane
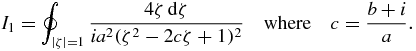
The roots of ζ2 − 2cζ + 1 are  and since (ζ+)(ζ−) = 1 it follows that one is inside and the other is outside the unit disc. (Both roots have modulus 1 if and only if c is real and −1 ⩽ c ⩽ 1. In our case, Im c = 1/a > 0.) The residues are
and since (ζ+)(ζ−) = 1 it follows that one is inside and the other is outside the unit disc. (Both roots have modulus 1 if and only if c is real and −1 ⩽ c ⩽ 1. In our case, Im c = 1/a > 0.) The residues are
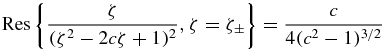
and the residue theorem implies
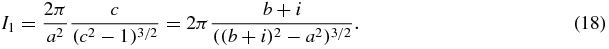
The branch of the square root in (18) corresponds to the root of ζ2 − 2cζ + 1 that is inside the unit disc. This particular choice of branch plays no role in determining the bound for |Re I1|.
To express the last expression for I1 in terms of its real and imaginary parts, use 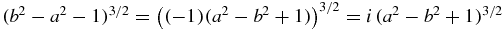 , let
, let 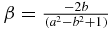 and write
and write
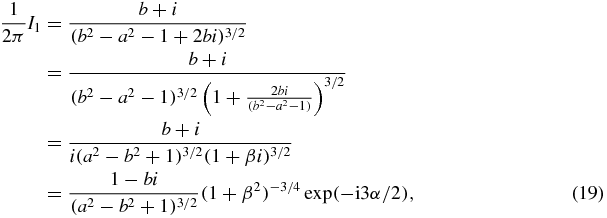
where 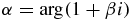 .
.
From (19), it follows that
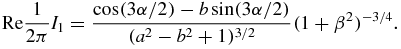
Now observe that
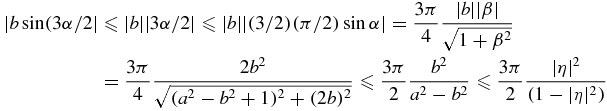
where the last inequality follows from the fact that b2 ⩽ |η|2a2 and a2 − b2 ⩾ (1 − |η|2)a2 because b = 〈z/|z|, η〉|z| and a = |z|. Use
- |cos (3α/2| ⩽ 1,
- (1 + β2)−3/4 ⩽ 1, and

to conclude that
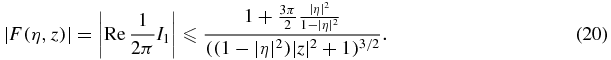
Recalling that |η| < 1 we may simplify (20) to
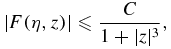
where the constant C depends x but is independent of z and  .
.
This proves (13) in the case when Λ is a circle.
In the general case, write
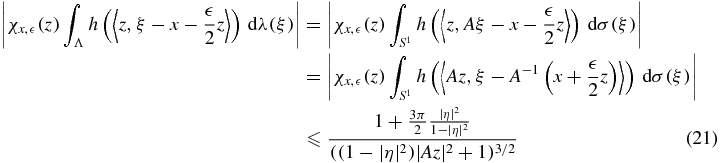
where the inequality follows from (20) with 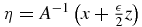 . The facts that
. The facts that
- if c1 and c2, with c1 ⩽ c2, are the eigenvalues of A then c1|z| ⩽ |Az| ⩽ c2|z| and

allow us to conclude that (21) can be reduced to (13). □
The proof of lemma 2 is now complete.
3.2. Immediate consequences
The result of lemma 2 allows us to compute the value of the factor δ(x) in (11).
Corollary 1. If h(t) is the function defined by (9) and x is in Ω, then

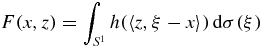
is integrable over 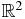 as a function of z, we may use polar coordinates
as a function of z, we may use polar coordinates
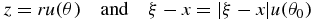
where u(θ) = (cos θ, sin θ) and write
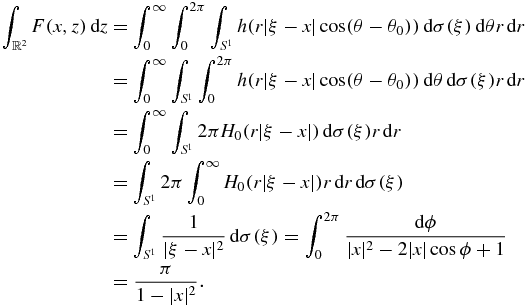
This verifies (22) in the case Λ = S1.
In the case when Λ is a more general ellipse, (22) can be verified by writing
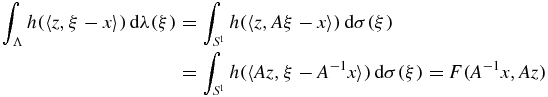
and
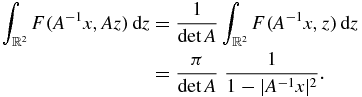
□
This completes the proof of corollary 1.
In view of the remarks preceding these results we may conclude the following.
Corollary 2. If h(t) is the function defined by (9), then
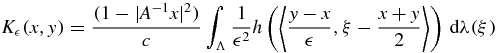
is a summability kernel on Ω.
3.3. Inversion formulas
In view of (2), (3) and (8), corollary 2 implies various inversion formulas for f(x) in terms of 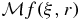 . Recall that the phantom f is a bounded measurable function that vanishes outside a compact subset of Ω. A direct application of these observations leads to the following.
. Recall that the phantom f is a bounded measurable function that vanishes outside a compact subset of Ω. A direct application of these observations leads to the following.
Theorem 1. If h(t) is the function defined by (9), x is in Ω and f is a bounded measurable function that is continuous at x and vanishes outside a compact subset of Ω, then

Additional manipulation of the left-hand side of (23) leads to other formulation. Two examples are given below.
Since the function f and the variables x and ξ are fixed in these manipulations, for convenience, we use the following abbreviated notation:

Thus, the inner integral on the left-hand side of (23) may expressed as
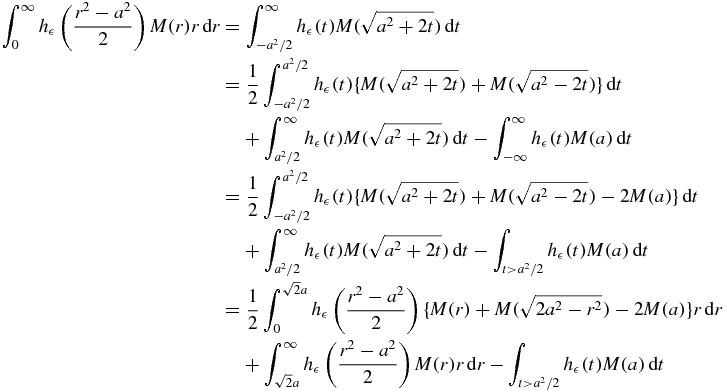
where we have used the change of variable 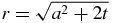 and the facts that h
and the facts that h ( − t) = h
( − t) = h (t) and ∫∞− ∞h
(t) and ∫∞− ∞h (t) dt = 0. Note that lim
(t) dt = 0. Note that lim → 02πh
→ 02πh (t) = −1/t2 and if M(r) is twice continuously differentiable then
(t) = −1/t2 and if M(r) is twice continuously differentiable then 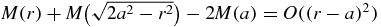 as r → a so that limit as
as r → a so that limit as  → 0, of the expression following the last equality in the above displayed string of equalities, exists and equals
→ 0, of the expression following the last equality in the above displayed string of equalities, exists and equals
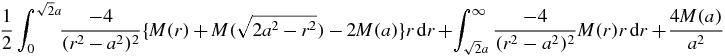
times the constant factor 1/2π. Since f in C20(Ω) is a sufficient condition for M(r) to be twice continuously differentiable, we may summarize the above manipulation as follows.
Theorem 2. If x is in Ω and f is in C20(Ω), then
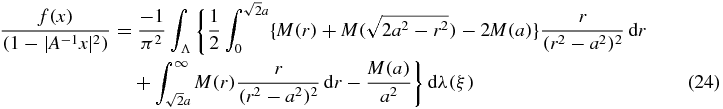
where 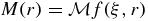 and a = |x − ξ|.
and a = |x − ξ|.
The next variant of our inversion formula for f(x) in terms of 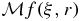 relies on the fact that if h(t) is the function defined by (9), then
relies on the fact that if h(t) is the function defined by (9), then
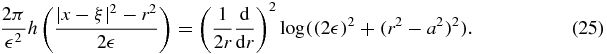
Substituting the right-hand side of identity (25) into the appropriate place on left-hand side of (23), assuming that 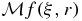 is twice continuously differentiable, and integrating by parts twice in the r variable, leads to
is twice continuously differentiable, and integrating by parts twice in the r variable, leads to
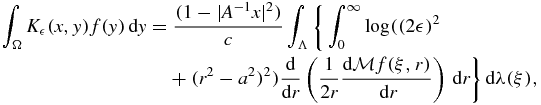
where K (x, y) is the kernel of corollary 2. If we let
(x, y) is the kernel of corollary 2. If we let  → 0 corollary 2 allows us to conclude the following.
→ 0 corollary 2 allows us to conclude the following.
Theorem 3. If x is in Ω and f is in C20(Ω), then
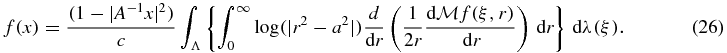
Identity (26) is similar but not identical to [3, formula (4)].
4. Spherical mean data
In this section, we consider the case n = 3 where we can prove a somewhat more general result.
4.1. The basic result
The following lemma shows that the relation (10) is valid for fairly general functions h that satisfy (4) and (5).
Lemma 3. If h(t) is a function that enjoys properties (4)–(6) and (12), then h(t) also satisfies (10) for every x in Ω.
Proof. First, note that for any z in 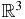 we have
we have

Formula (27) will be useful in what follows and can be seen from
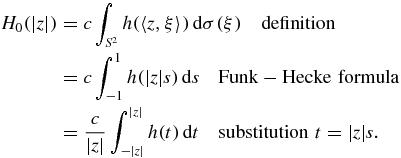
Next, assume Ω = {x: |x| < 1} and for x in Ω write
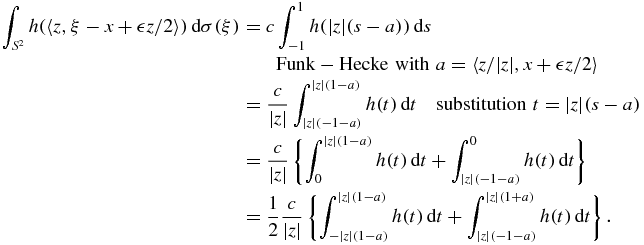
The next to last equality follows from the fact that
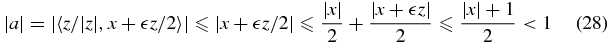
so that 1 − a > 0 and −1 − a < 0, while the last equality follows from the fact that h( − t) = h(t).
In view of (27), the last equality implies that
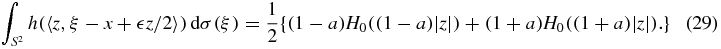
Since H0(|z|) satisfies (12), inequality (28) allows us to conclude that
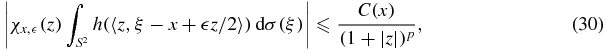
where p is a constant, p > 3 and C(x) is independent of z and  . Inequality (30) of course implies the desired conclusion when Ω = {x: |x| < 1}. The case when Ω is a solid ellipsoid, namely Ω = {x: |A−1x| < 1}, follows by the same reasoning as used in lemma 2 so the proof of lemma 3 is complete. □
. Inequality (30) of course implies the desired conclusion when Ω = {x: |x| < 1}. The case when Ω is a solid ellipsoid, namely Ω = {x: |A−1x| < 1}, follows by the same reasoning as used in lemma 2 so the proof of lemma 3 is complete. □
4.2. Consequences
Corollary 3. If x ∈ Ω and h(t) is a function that enjoys properties (4)–(6) and (12), then
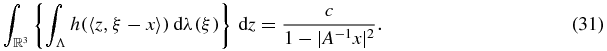
Proof. Because the expression in braces found in formula (31) is integrable over  as a function of z, we may start the computation as is corollary 1 and, instead of the contour integration to evaluate the integral over S2, the use of the Funk–Hecke formula leads to an elementary integration. Namely, we may write
as a function of z, we may start the computation as is corollary 1 and, instead of the contour integration to evaluate the integral over S2, the use of the Funk–Hecke formula leads to an elementary integration. Namely, we may write

which verifies (31) in the case Λ = S2. The case when Λ is a more general ellipsoid follows by the same reasoning as used in the proof of corollary 1. □
Corollary 4. If x ∈ Ω and h(t) is a function that enjoys properties (4)–(6) and (12), then
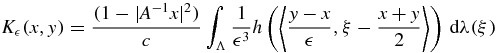
is a summability kernel on Ω.
Theorem 4. Suppose x ∈ Ω and h(t) is a function that enjoys properties (4)–(6) and (12). If f is a bounded measurable function that is continuous at x and vanishes outside a compact subset of Ω, then
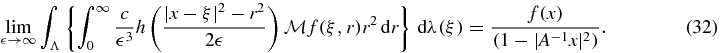
The use of specific function h(t) in (32) and additional manipulation leads, as in subsection 3.3, to various additional inversion-type formulas. An example of such an h(t) is
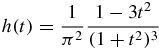
and the function H(x) associated with it via (5) is
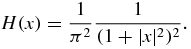
For more examples, see [12, sections 2.2 and 2.3].
Acknowledgments
We wish to thank two reviewers who brought the related articles [9, 13, 14] to our attention. These important articles treat some of the same material we do, namely the spherical mean Radon transform. Their authors use differing but apropos cacluli that lead to exact inversion formulas valid for functions defined on elliptical domains. The focus of our work is an appropriately adapted summability procedure that gives rise to effective inversion algorithms and, as an added feature, in the limiting case leads to exact inversion-type formulas. Our methods and techniques are significantly different from those found in [9, 13, 14] and so are our results.