Abstract
We recently improved the famous result of Parikh and Wilczek, who found a probability of emission of Hawking radiation that is compatible with a non-strictly thermal spectrum, showing that such a probability of emission is really associated with two non-strictly thermal distributions for bosons and fermions. Here, we finalize the model by finding the correct value of the pre-factor of the Parikh and Wilczek probability of emission. In fact, that expression has a ∼ sign instead of the equality. In general, in this kind of leading order tunneling calculation, the exponent indeed arises from the classical action, and the pre-factor is an order of Planck constant correction. But in the case of emissions of Hawking quanta, the variation of the Bekenstein–Hawking entropy is of the order of 1 for an emitted particle with energy of the order of the Hawking temperature. As a consequence, the exponent in the Parikh and Wilczek probability of emission is of the order of unity and one asks, what is the real significance of that scaling if the pre-factor is unknown? Here we solve the problem assuming the unitarity of the black hole (BH) quantum evaporation and considering the natural correspondence between Hawking radiation and quasi-normal modes (QNMs) of excited BHs, in a 'Bohr-like model' that we recently discussed in a series of papers. In those papers, QNMs are interpreted as natural BH quantum levels (the 'electron states' in the 'Bohr-like model'). Here we find the intriguing result that, although in general it is well approximated by 1, the pre-factor of the Parikh and Wilczek probability of emission depends on the BH quantum level 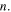 We also write down an elegant expression of the probability of emission in terms of the BH quantum levels.
We also write down an elegant expression of the probability of emission in terms of the BH quantum levels.
Export citation and abstract BibTeX RIS
Hawking radiation [1] is today studied in an elegant and largely used way through the tunneling mechanism; see [2–8, 41, 46–48] and references within. Let us see how that mechanism works. One considers an object that is classically stable. If it becomes unstable from a quantum-mechanical point of view, one naturally suspects tunneling. Hawking's famous mechanism of particle creation by BHs [1] is, in turn, described in terms of tunneling arising from vacuum fluctuations near the BH horizon [2–8, 41, 46–48]. When a virtual particle pair is created just inside the BH horizon, the virtual particle with positive energy can tunnel out. Thus, it materializes outside the BH as a real particle. In an analogous way, when a virtual particle pair is created just outside the horizon, the particle with negative energy can tunnel inward. In both cases, the particle with negative energy is absorbed by the BH. The result is that the BH mass decreases and the particle with positive energy propagates toward infinity. Thus, subsequent emissions of Hawking quanta appear.
Working with  (Planck units), in a strictly thermal approximation the probability of emission of Hawking quanta is [1–3, 9]
(Planck units), in a strictly thermal approximation the probability of emission of Hawking quanta is [1–3, 9]

where ω is the energy frequency of the emitted particle and 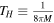 is the Hawking temperature. Taking into account the energy conservation, i.e. the BH contraction enabling a varying BH geometry, one gets the remarkable correction of Parikh and Wilczek [2, 3]
is the Hawking temperature. Taking into account the energy conservation, i.e. the BH contraction enabling a varying BH geometry, one gets the remarkable correction of Parikh and Wilczek [2, 3]
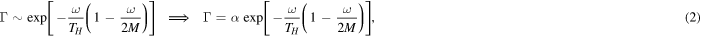
where 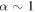 and the additional term
and the additional term 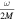 is present. We have recently improved the Parikh and Wilczek tunneling picture, showing that the probability of emission (2) is, indeed, associated with the two distributions [8]
is present. We have recently improved the Parikh and Wilczek tunneling picture, showing that the probability of emission (2) is, indeed, associated with the two distributions [8]

for bosons and fermions respectively, which are not strictly thermal.
We note that equation (2) has a ∼ sign instead of the equality. In fact, in this kind of leading order tunneling calculation, the exponent arises from the classical action and the pre-factor is an order of Planck constant correction. But in the case of emissions of Hawking quanta the variation of the Bekenstein–Hawking entropy [2, 3]

is of the order of 1 for an emitted particle with energy of the order of the Hawking temperature. As a consequence, the exponent in the right side of equations (2) and (4) is of the order of unity and we ask, what is the real significance of that scaling if the pre-factor is unknown? Here we solve the problem considering the natural correspondence between Hawking radiation and BH QNMs in a 'Bohr-like model' that we recently discussed in a series of papers [9–12], and together with collaborators [13, 14].
We consider Dirac delta perturbations [9–12], which represent subsequent absorptions of particles with negative energies. Such perturbations are associated with emissions of Hawking quanta in the above discussed mechanism of particle pair creation. The BH response to perturbations are QNMs [9–16], which are frequencies of radial spin-j perturbations obeying a time independent Schröedinger-like equation [9–12, 16]. They are the BH modes of energy dissipation whose frequencies are allowed to be complex [9–12, 16]. The intriguing idea to model the quantum BH in terms of BH QNMs arises from a remarkable paper by York [17]. For large values of the quantum 'overtone' number n, where 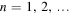 , QNMs become independent of both the spin and the angular momentum quantum numbers [9–12, 15, 16], in perfect agreement with Bohr's Correspondence Principle [18], which states that 'transition frequencies at large quantum numbers should equal classical oscillation frequencies'. Thus, Bohr's Correspondence Principle enables an accurate semi-classical analysis for large values of the principal quantum number
, QNMs become independent of both the spin and the angular momentum quantum numbers [9–12, 15, 16], in perfect agreement with Bohr's Correspondence Principle [18], which states that 'transition frequencies at large quantum numbers should equal classical oscillation frequencies'. Thus, Bohr's Correspondence Principle enables an accurate semi-classical analysis for large values of the principal quantum number 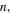 i.e, for excited BHs. Using that principle, Hod has shown that QNMs release information about the area quantization, as QNMs are associated with the absorption of particles [19, 20]. Hod's work was refined by Maggiore [15] who solved some important problems. On the other hand, as QNMs are countable frequencies, ideas on the continuous character of Hawking radiation did not agree with attempts to interpret QNMs in terms of emitted quanta, preventing the association of QNMs with Hawking radiation [16]. Recently, the authors of [21–24] and ourselves and collaborators [10–14] observed that the non-thermal spectrum of Parikh and Wilczek [2, 3] also implies the countable character of subsequent emissions of Hawking quanta. This issue enables a natural correspondence between QNMs and Hawking radiation, permitting us to interpret QNMs also in terms of emitted energies [10–14]. Dirac delta perturbations due to discrete subsequent absorptions of particles with negative energies, which are associated with emissions of Hawking quanta in the mechanism of particle pair creation by quantum fluctuations, indeed generate BH QNMs [10–14]. In other words, the BH contraction due to the energy conservation is not a 'one shot process'. It generates oscillations of the horizon instead, which are the QNMs. We also stress that the correspondence between emitted radiation and proper oscillation of the emitting body is a fundamental behavior of every radiation process in science. Based on such a natural correspondence between Hawking radiation and BH QNMs, one can also consider QNMs in terms of quantum levels for emitted energies [10–14].
i.e, for excited BHs. Using that principle, Hod has shown that QNMs release information about the area quantization, as QNMs are associated with the absorption of particles [19, 20]. Hod's work was refined by Maggiore [15] who solved some important problems. On the other hand, as QNMs are countable frequencies, ideas on the continuous character of Hawking radiation did not agree with attempts to interpret QNMs in terms of emitted quanta, preventing the association of QNMs with Hawking radiation [16]. Recently, the authors of [21–24] and ourselves and collaborators [10–14] observed that the non-thermal spectrum of Parikh and Wilczek [2, 3] also implies the countable character of subsequent emissions of Hawking quanta. This issue enables a natural correspondence between QNMs and Hawking radiation, permitting us to interpret QNMs also in terms of emitted energies [10–14]. Dirac delta perturbations due to discrete subsequent absorptions of particles with negative energies, which are associated with emissions of Hawking quanta in the mechanism of particle pair creation by quantum fluctuations, indeed generate BH QNMs [10–14]. In other words, the BH contraction due to the energy conservation is not a 'one shot process'. It generates oscillations of the horizon instead, which are the QNMs. We also stress that the correspondence between emitted radiation and proper oscillation of the emitting body is a fundamental behavior of every radiation process in science. Based on such a natural correspondence between Hawking radiation and BH QNMs, one can also consider QNMs in terms of quantum levels for emitted energies [10–14].
Let us see how the model works. By introducing the effective temperature [8, 10–12]

one rewrites equation (5) in a Boltzmann-like form similar to equation (1)

where ![$\mathrm{exp}[-{\beta }_{E}(\omega )\omega ]$](https://content.cld.iop.org/journals/0264-9381/32/19/195007/revision1/cqg518925ieqn8.gif) is the effective Boltzmann factor, with
is the effective Boltzmann factor, with 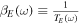 . Thus, the effective temperature replaces the Hawking temperature in the equation of the probability of emission [8, 10–12]. We emphasize that there are various fields of science where one takes into account the deviation from the thermal spectrum of an emitting body by introducing an effective temperature that represents the temperature of a blackbody that would emit the same total amount of radiation. We introduced the concept of effective temperature in BH physics in [10, 11] and used it in [8, 10–12] and, together with collaborators, in [13, 14]. The effective temperature depends on the energy frequency of the emitted radiation and the ratio
. Thus, the effective temperature replaces the Hawking temperature in the equation of the probability of emission [8, 10–12]. We emphasize that there are various fields of science where one takes into account the deviation from the thermal spectrum of an emitting body by introducing an effective temperature that represents the temperature of a blackbody that would emit the same total amount of radiation. We introduced the concept of effective temperature in BH physics in [10, 11] and used it in [8, 10–12] and, together with collaborators, in [13, 14]. The effective temperature depends on the energy frequency of the emitted radiation and the ratio 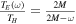 represents the deviation of the BH radiation spectrum from the strictly thermal feature [8, 10–12]. The introduction of the effective temperature permits the introduction of other effective quantities. Considering the initial BH mass before the emission, M, and the final BH mass after the emission,
represents the deviation of the BH radiation spectrum from the strictly thermal feature [8, 10–12]. The introduction of the effective temperature permits the introduction of other effective quantities. Considering the initial BH mass before the emission, M, and the final BH mass after the emission,  , one introduces the BH effective mass and the BH effective horizon [8, 10–12] as
, one introduces the BH effective mass and the BH effective horizon [8, 10–12] as

during the BH contraction, i.e. during the emission of the particle [10–12]. Such effective quantities are average quantities [8, 10–12]. In fact,  is the average of the initial and final horizons while
is the average of the initial and final horizons while 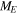 is the average of the initial and final masses [8, 10–12]. The effective temperature
is the average of the initial and final masses [8, 10–12]. The effective temperature 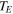 is the inverse of the average value of the inverses of the initial and final Hawking temperatures (before the emission
is the inverse of the average value of the inverses of the initial and final Hawking temperatures (before the emission  , after the emission
, after the emission 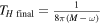 ) [8, 10–12].
) [8, 10–12].
For large values of the principal quantum number 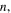 i.e, for excited BHs, and independently of the angular momentum quantum number, the QNM expression of the Schwarzschild BH that takes into account the non-strictly thermal behavior of the radiation spectrum is obtained, replacing the Hawking temperature with the effective temperature in the standard strictly thermal equation for the quasi-normal frequencies as [8, 10–12]
i.e, for excited BHs, and independently of the angular momentum quantum number, the QNM expression of the Schwarzschild BH that takes into account the non-strictly thermal behavior of the radiation spectrum is obtained, replacing the Hawking temperature with the effective temperature in the standard strictly thermal equation for the quasi-normal frequencies as [8, 10–12]

where a and b are real numbers with 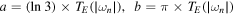 for
for  (scalar and gravitational perturbations),
(scalar and gravitational perturbations), 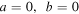 for j = 1 (vector perturbations) and
for j = 1 (vector perturbations) and 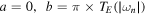 for half-integer values of j. On the other hand, as
for half-integer values of j. On the other hand, as 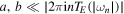 , a fundamental consequence is that the quantum of the area obtained from the asymptotics of
, a fundamental consequence is that the quantum of the area obtained from the asymptotics of 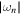 is an intrinsic property of Schwarzschild BHs because for large n the leading asymptotic behavior of
is an intrinsic property of Schwarzschild BHs because for large n the leading asymptotic behavior of 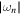 is given by the leading term in the imaginary part of the complex frequencies, and it does not depend on the spin content of the perturbation [10–12, 15]. An intuitive derivation of equation (8) can be found in [10, 11]. We rigorously derived such an equation in the appendix of [12]. Further important clarifications on the derivation of equation (8) have been highlighted in a recent review paper [37] through Hawking's periodicity arguments [38].
is given by the leading term in the imaginary part of the complex frequencies, and it does not depend on the spin content of the perturbation [10–12, 15]. An intuitive derivation of equation (8) can be found in [10, 11]. We rigorously derived such an equation in the appendix of [12]. Further important clarifications on the derivation of equation (8) have been highlighted in a recent review paper [37] through Hawking's periodicity arguments [38].
Equation (8) has the following elegant interpretation [10, 11]. The quasi-normal frequencies determine the position of the poles of a Green's function on the given background, and the Euclidean BH solution converges to a non-strictly thermal circle at infinity with the inverse temperature 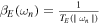 [10, 11]. Thus, the spacing of the poles in equation (8) coincides with the spacing
[10, 11]. Thus, the spacing of the poles in equation (8) coincides with the spacing 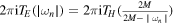 expected for a non-strictly thermal Green's function [10, 11]. We found the physical solution for the absolute values of the frequencies (8) in [10–12]. Considering the leading asymptotic behavior, one gets [10–12]
expected for a non-strictly thermal Green's function [10, 11]. We found the physical solution for the absolute values of the frequencies (8) in [10–12]. Considering the leading asymptotic behavior, one gets [10–12]

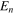 is interpreted as the total energy emitted by the BH at that time, i.e. when the BH is excited at a level n [10–12]. Considering emission from the ground state (i.e. a BH that is not excited) to a state with large
is interpreted as the total energy emitted by the BH at that time, i.e. when the BH is excited at a level n [10–12]. Considering emission from the ground state (i.e. a BH that is not excited) to a state with large 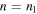 and using equation (9), the BH mass changes from
and using equation (9), the BH mass changes from 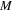 to [10–12]
to [10–12]

In the transition from the state with  to a state with
to a state with 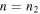 where
where 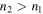 the BH mass changes again from
the BH mass changes again from 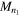 to
to

where
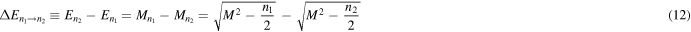
is the jump between the two levels due to the emission of a particle with a frequency 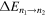 . Thus, in our BH model [12], during a quantum jump a discrete amount of energy is radiated and, for large values of the principal quantum number
. Thus, in our BH model [12], during a quantum jump a discrete amount of energy is radiated and, for large values of the principal quantum number 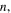 the analysis becomes independent of the other quantum numbers. In a certain sense, QNMs represent the 'electron' that jumps from one level to another one and the absolute values of the QNM frequencies represent the energy 'shells' [2]. In the Bohr model of the hydrogen atom [25, 26] electrons can only gain and lose energy by jumping from one allowed energy shell to another, absorbing or emitting radiation with an energy difference in the levels according to the Planck relation (in standard units)
the analysis becomes independent of the other quantum numbers. In a certain sense, QNMs represent the 'electron' that jumps from one level to another one and the absolute values of the QNM frequencies represent the energy 'shells' [2]. In the Bohr model of the hydrogen atom [25, 26] electrons can only gain and lose energy by jumping from one allowed energy shell to another, absorbing or emitting radiation with an energy difference in the levels according to the Planck relation (in standard units) 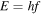 , where
, where 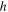 is the Planck constant and
is the Planck constant and 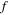 the transition frequency. In our Bohr-like BH model [10–12], QNMs can only gain and lose energy by jumping from one allowed energy shell to another, absorbing or emitting radiation (emitted radiation is given by Hawking quanta) with an energy difference of the levels according to equation (12). The similarity is completed if one notes that the interpretation of equation (9) is of a particle, the 'electron', quantized on a circle of length [10, 11]
the transition frequency. In our Bohr-like BH model [10–12], QNMs can only gain and lose energy by jumping from one allowed energy shell to another, absorbing or emitting radiation (emitted radiation is given by Hawking quanta) with an energy difference of the levels according to equation (12). The similarity is completed if one notes that the interpretation of equation (9) is of a particle, the 'electron', quantized on a circle of length [10, 11]

which is analogous to the electron traveling in circular orbits around the hydrogen nucleus, similar in structure to the solar system, of the Bohr model [25, 26]. On the other hand, the Bohr model is an approximated model of the hydrogen atom with respect to the valence shell atom model of full quantum mechanics. In the same way, our Bohr-like BH model [12] should be an approximated model with respect to the definitive, but at the present time unknown, BH model arising from a full quantum gravity theory.
As En is interpreted as the total energy emitted at level n [12], considering the expressions (10) and (11) for the residual BH mass one also needs [12]

In fact, BHs cannot emit more energy than their total mass and the total energy emitted by the BH cannot be imaginary. The expression (14) gives a maximum value for the overtone number n

which corresponds to 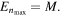 On the other hand, we recall that by using the Generalized Uncertainty Principle, Adler, Chen and Santiago [27] have shown that the total BH evaporation is prevented in exactly the same way that the Uncertainty Principle prevents the hydrogen atom from total collapse. In fact, the collapse is prevented not by symmetry, but by dynamics, as the Planck distance and the Planck mass are approached [27]. That important result implies that equation (14) has to be slightly modified, becoming (the Planck mass is equal to 1 in Planck units) [12]
On the other hand, we recall that by using the Generalized Uncertainty Principle, Adler, Chen and Santiago [27] have shown that the total BH evaporation is prevented in exactly the same way that the Uncertainty Principle prevents the hydrogen atom from total collapse. In fact, the collapse is prevented not by symmetry, but by dynamics, as the Planck distance and the Planck mass are approached [27]. That important result implies that equation (14) has to be slightly modified, becoming (the Planck mass is equal to 1 in Planck units) [12]

Thus, one gets a slightly different value of the maximum value of the overtone number n

Then, the countable sequence of QNMs for emitted energies cannot be infinity although n can be extremely large [12]. In fact, restoring ordinary units and considering a BH mass of the order of 10 solar masses, one easily gets 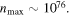 On the other hand, we expect further corrections to our semi-classical analysis when the Planck scale is approached, as we need a full theory of quantum gravity to obtain a correct description of the Planck scale's physics.
On the other hand, we expect further corrections to our semi-classical analysis when the Planck scale is approached, as we need a full theory of quantum gravity to obtain a correct description of the Planck scale's physics.
Our Bohr-like BH model in [10–12] is in full agreement with the previous literature of BH thermodynamics, as in references [15, 28, 29]. Moreover, it is also in full agreement with the famous result of Bekenstein on the area quantization [30]. In fact, we found an area quantum arising from a jump among two neighboring quantum levels  and n with a value
and n with a value 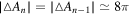 (see equation (37) in [12]), which is totally consistent with Bekenstein's result [30]. Clearly, all these similarities with the Bohr semi-classical model of the hydrogen atom and all these consistences with well known results in the literature of BHs, starting with the universal Bekenstein result, cannot be coincidences, but are confirmations of the correctness of the analysis in [10–12] instead.
(see equation (37) in [12]), which is totally consistent with Bekenstein's result [30]. Clearly, all these similarities with the Bohr semi-classical model of the hydrogen atom and all these consistences with well known results in the literature of BHs, starting with the universal Bekenstein result, cannot be coincidences, but are confirmations of the correctness of the analysis in [10–12] instead.
Concerning the important issue of the BH entropy, we recall the recent interesting result in which the entropy is connected with the tunneling mechanism [40, 42]. Jiang and Han [40] have indeed quantized the BH entropy by combining the proposal about the BH adiabatic invariance and the proposal about the oscillating velocity of the BH horizon, where the velocity is obtained in the tunneling framework.
Now, let us proceed in calculating the correct value of the pre-factor of equations (2) and (4). We recall that, today, the majority of researchers thinks that BH quantum evaporation is a unitary process and that Hawking's original claim on the information loss in BH evaporation [9] was wrong. Various approaches are indeed proposed by various researchers in order to solve the BH information paradox and to recover unitarity in BH evaporation. Here we recall: (i) the approach of [21–24] where the authors found the existence of correlations among Hawking radiation that are elegantly described as hidden messengers in BH evaporation permitting us to restore unitarity in gravitational collapse; (ii) the famous ADS/CFT correspondence [31], which was endorsed by both Susskind [32] and Hawking [33], who reversed his opinion in 2004 and recently claimed that BH evaporation is unitary [34]; (iii) the approach of the so called 'fuzzballs' [35]; and (iv) our recent approach based on the time evolution of our Bohr-like BH model [39]. We have indeed shown in [39] that the time evolution of our Bohr-like BH model is governed by a time dependent Schrödinger equation for the system composed of Hawking radiation and BH QNMs. The physical state and the correspondent wave function are written in terms of a unitary evolution matrix instead of a density matrix [39]. In that way, the final state results in being a pure quantum state instead of a mixed one [39]. The approach in [39] permits us also to solve the entanglement problem connected with the information paradox because emitted Hawking quanta results in being entangled with BH QNMs. Thus, hereafter we will assume the unitarity of BH quantum evaporation. Following [39], now we show that, fixing two quantum levels m and n, the energy emitted in an arbitrary transition  , with
, with 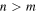 proportional to the effective temperature associated with the transition and that the constant of proportionality depends only on the difference
proportional to the effective temperature associated with the transition and that the constant of proportionality depends only on the difference  . Setting [39]
. Setting [39]

where Mm and Mn are given by equations (10) and (11), let us see if there are values of the constant K for which equation (18) is satisfied. We recall that [39]

because the effective temperature is the inverse of the average value of the inverses of the initial and final Hawking temperatures; see the above discussion. Thus, equation (18) can be rewritten as [39]

Using equations (10) and (11), equation (20) becomes [39]

which implies that equation (18) is satisfied for 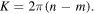 Hence, one finds [39]
Hence, one finds [39]

Using equation (6), the probability of emission between the two levels n and m can be written in the intriguing form [39]

Thus, the probability of emission between two arbitrary levels characterized by the two 'overtone' quantum numbers m and n scales like ![$\mathrm{exp}[-2\pi (n-m)].$](https://content.cld.iop.org/journals/0264-9381/32/19/195007/revision1/cqg518925ieqn47.gif) In particular, for
In particular, for 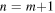 the probability of emission has its maximum value
the probability of emission has its maximum value 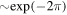 , i.e. the probability is maximum for two adjacent levels, as one can intuitively expect [39]. If one fixes m, the assumption of unitarity in BH evaporation permits the probabilities (23) to be normalized to unity as
, i.e. the probability is maximum for two adjacent levels, as one can intuitively expect [39]. If one fixes m, the assumption of unitarity in BH evaporation permits the probabilities (23) to be normalized to unity as

where nmax is the maximum value for the 'overtone' number n given by equation (17) and n = m corresponds to the probability that the BH does not emit. Putting 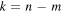 and
and ![$\mathrm{exp}[-2\pi ]=X\ $](https://content.cld.iop.org/journals/0264-9381/32/19/195007/revision1/cqg518925ieqn51.gif) equation (24) becomes
equation (24) becomes

The sum in equation (25) is the kth partial sum of the geometric series and can be solved as [36]

Thus, one gets

which permits us to solve for α
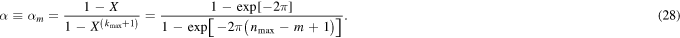
Hence, we find that the pre-factor α depends on the BH quantum level 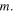 Inserting the result (28) in equation (23) we fix the probability of emission between the two levels m and n as
Inserting the result (28) in equation (23) we fix the probability of emission between the two levels m and n as
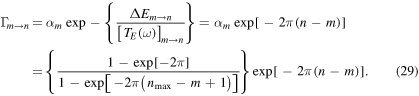
From the quantum mechanical point of view, one can physically interpret Hawking radiation like energies of quantum jumps among the unperturbed levels (9) [8, 10–13].
It might be a benefit for the reader to rewrite equation (30) in terms of ω and M using  and
and 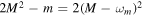 . One gets:
. One gets:
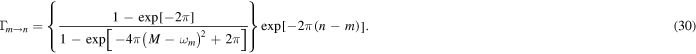
Equation (31) can be useful when exploring 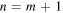 expressions throughout the spectrum as a function of
expressions throughout the spectrum as a function of 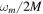 .
.
In any case, we note from equation (28) that

and, for increasing m

with

In other words, the dependence of the pre-factor α on the BH quantum level m is in general well approximated by 1 in all the process of BH evaporation for which our analysis works, including late times in the evaporation process. Clearly, as we are using a semi-classical approximation, deviations could be present at the Planck scale. On the other hand, we need a full theory of quantum gravity in order to achieve the Planck scale physics.
The analysis in this work is strictly correct only for 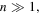 i.e. only for excited BHs. This is because we assumed an emission from the ground state to a state with large
i.e. only for excited BHs. This is because we assumed an emission from the ground state to a state with large  in the discussion. On the other hand, a state with large
in the discussion. On the other hand, a state with large  is always reached at late times, maybe not through sole emission from the ground state, but, indeed, through various subsequent emissions of Hawking quanta. For the sake of completeness, it is better to explicitly describe in which part of this process needed to reach a large n the description in this paper would start to be valid [42]. Let us consider again an astrophysics BH with an original mass M of the order of 10 solar masses. By inserting
is always reached at late times, maybe not through sole emission from the ground state, but, indeed, through various subsequent emissions of Hawking quanta. For the sake of completeness, it is better to explicitly describe in which part of this process needed to reach a large n the description in this paper would start to be valid [42]. Let us consider again an astrophysics BH with an original mass M of the order of 10 solar masses. By inserting 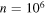 in equation (9) one gets
in equation (9) one gets 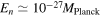 . In other words, the BH lost a negligible part of its mass. Thus, we understand that our description is valid for almost all the process of BH evaporation.
. In other words, the BH lost a negligible part of its mass. Thus, we understand that our description is valid for almost all the process of BH evaporation.
It is also interesting to include a comparison between the importance of the deviation from thermality described in this paper and that due to other phenomena, such as the backscattering of Hawking radiation on the Schwarzschild metric (which is already present at early times in the evaporation) [42]. This is a different physical phenomenon due to the existence of a BH potential barrier [43, 44]. Let us consider a scalar field Φ in the Schwarzschild spacetime [43]. As this spacetime is spherically symmetric, one can separate the Klein–Gordon equation governing the scalar field, i.e. [43]

into spherical harmonics [43]

Introducing the Regge-Wheeler tortoise coordinate x, defined through the relation [37]

one gets the resulting radial wave equation of [43]

where the potential is [43]

and m is the mass of the scalar field [43]. Near the BH horizon we get 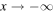 . As a consequence, the potential falls off exponentially [43]
. As a consequence, the potential falls off exponentially [43]

On the other hand, for 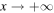 one gets [43]
one gets [43]
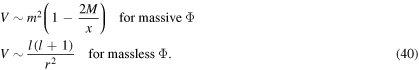
The gravitational field will be partially scattered off on the potential (38) by the incoming waves. Thus, we obtain a superposition of incoming and outgoing waves [43]. As a consequence, the spectrum is not precisely thermal [43].
Although the two phenomena generating deviation from the strict thermal behavior of the Hawking radiation spectrum are different, we recall an interesting recent work where both of them are taken into account [45].
Conclusion remarks
Assuming the unitarity of BH quantum evaporation [21–24, 31–35] and considering the natural correspondence between Hawking radiation and BH QNMs, in a 'Bohr-like model' for excited BHs that we recently discussed in a series of papers [10–13], we have found the intriguing result that the pre-factor of the Parikh and Wilczek probability of emission, although if in general well approximated by 1, depends on the BH quantum level  Then, one gets that the emission of Hawking radiation, in the tunneling framework, is completely determined by equations (3) and (29).
Then, one gets that the emission of Hawking radiation, in the tunneling framework, is completely determined by equations (3) and (29).
Acknowledgments
The author thanks the referees for useful comments that permitted us to improve this paper.

