UWB pulse propagation into human tissues

Simple models of the human anatomy are useful to evidence the main mechanisms underlying electromagnetic field interaction with the human tissues. With reference to UWB signal propagation, a multilayer planar model of the human thorax, derived from the VH data set, was used by Staderini (2002) to predict signal reflection and attenuation into the different layers. However, the so-called 'Virtual population' has been recently developed, comprising a man (Duke, 34 years old), a woman (Ella 26 years old), and several children (Christ et al 2010). While the VH model represents a relatively 'big man' (1.80 m tall, 103.0 kg weight), Duke, being 1.77 m tall, and weighting 72.4 kg, is closer to the 'standard man' dimensions (ICRP 1975, Ellis 1990). To build the multilayer planar model, a section of the Duke's anatomy passing through the heart has been considered. Figure 1 shows the considered section as well as the line used to obtain the layers' sequence for the planar model. The multilayer planar model is depicted in figure 2.

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

Simulations have been performed considering the absorption and reflection of a plane wave, with a UWB frequency spectrum, impinging orthogonally (y-axis in figure 2) on the surface of the planar multilayer model. The reflection coefficient at the air–skin interface, the transmission into the layers, the reflections at the interfaces between the different layers, and the time behaviour of the pulse propagating into the different tissues can be evaluated by using the transmission line formalism, which substitutes to each tissue layer a transmission line of the same length. Each transmission line is characterized by its propagation constant and characteristic impedance both dependent on the frequency and on the dielectric properties of the corresponding tissue. Since the considered signals have a UWB frequency occupation, the dispersive behaviour of human tissues has been taken into account through the Cole–Cole model (Cole and Cole 1941) using the parameters computed in Gabriel et al (1996b).

The time and frequency behaviours of the incident and reflected signals reported in the following sections have been computed with the circuital CAD MWO™ (AWR El Segundo, CA) by using the harmonic balance solver.

To validate the results obtained with MWO, the full-wave electromagnetic solver Microwave Studio™ (MWS–CST Darmstadt Germany) has been used. In MWS, the plane wave propagating into the multilayer planar model has been simulated through a parallel plate transmission line, filled with the dielectric layers of figure 2. However, since in MWS the dielectric dispersion is represented according to the Debye's model (Debye 1929), the comparison between MWS and MWO has been conducted considering a first order Debye dispersion mechanism for the dielectric properties of tissues. Moreover, a plane wave propagating into a vertical section (7 cm high) of the Duke's thorax has been also studied to put into evidence the representativeness of the multilayer model. When an anatomical model of the human body is studied, as in this case, MWS does not allow us to introduce the dielectric properties' dependence on the frequency; so, the values at 2 GHz have been used (Gabriel et al 1996b, accessible online at http://niremf.ifac.cnr.it/tissprop/htmlclie/htmlclie.htm).

Finally, to deepen the validity of the obtained results, Monte Carlo simulations have been performed in MWO randomly changing both the dielectric properties of the considered tissues and the thicknesses of the tissues' layers. A maximum deviation of ±10% from the nominal values has been allowed, according to the spread on the measured values reported in Gabriel et al (1996a).

In order to evaluate the feasibility of breath and heartbeat activity monitoring through UWB radar, it is fundamental to correctly define the amplitude of the signal impinging on the human body. Since UWB radar emissions should be compliant with compatibility emission masks issued by regulatory bodies, these masks have been used to evaluate the maximum amplitude allowed for the UWB pulses.

In USA, the Federal Communications Commission (FCC) issued regulations for UWB medical imaging systems allocating a frequency band between 3.1 and 10.6 GHz and defining the EIRP measured on a specified bandwidth (FCC 02-48 2002). In Europe, the European Technical Standard Institute (ETSI) in close cooperation with the Electronic Communications Committee (ECC) developed a regulation, approved by the European Commission in 2009, with limits for the maximum EIRP allowed for UWB indoor communications (EC 2009).

Since in this work a medical application is considered, the shape and amplitude of the UWB pulses have been made compliant with the FCC emission mask. Being this mask defined in terms of EIRP, which includes both the radiated power and the directivity of the antenna, to evaluate the maximum amplitude of the source signal the pulse radiated by a half-heart shaped antenna (Pittella et al 2011), fed by a sequence of UWB pulses with a repetition rate of 1 MHz and various time behaviours, has been considered. In particular, the Gaussian pulse with standard deviation (σ) of 100 ps and its first four derivatives have been studied (Cavagnaro et al 2013). For each pulse, the maximum source amplitude that gives rise to an EIRP in compliance with the FCC emission mask has been computed as reported in figure 3.

Zoom In Zoom Out Reset image size

Figure 3 shows that the peak in the spectrum of the pulses with time behaviour given by higher derivatives of the Gaussian pulse shifts toward higher frequencies. Accordingly, being their frequency spectrum better centred with respect to the FCC emission mask, higher amplitude values can be considered for the source voltage. To translate the obtained source's amplitudes into electric field values, two different approaches have been used for the fixed and the wearable radar systems, respectively.

In the case of fixed radar system, where a distance between the radar and the subject of about 1 m is considered, the same MWO model employed to evaluate the EIRP has been used to evaluate the corresponding electric field, by way of an electric field probe in the time domain. Starting from the first derivative of the Gaussian pulse with a source amplitude of 0.2 V, a maximum electric field value of 0.111 V m⁻¹ has been thus obtained. The amplitudes of 0.149, 0.308, 0.578 V m⁻¹ have been obtained for the second, third and fourth derivatives of the Gaussian pulse, respectively.

In the case of wearable radar system, where a distance between the radar and the subject of about 1 cm is considered, the body model is in the near field of the radiating antenna. In this case, to obtain the maximum electric field value which corresponds to the source amplitudes compliant with the FCC mask, an electromagnetic simulation has been performed with MWS. In particular, the previously cited half-heart shaped antenna (Pittella et al 2011) has been considered in front of an indefinite homogeneous slab with the properties of 2/3 muscle, and it has been excited with a monocycle pulse with a maximum amplitude of 0.2 V. Then, the time behaviour of the electric field inside the box has been recorded, obtaining a maximum amplitude equal to 10.5 V m⁻¹.

In the following, the obtained values will be used as the maximum amplitudes of the incident plane wave to study the propagation of the different pulses in the multilayer planar model.

Figure 4(a) shows the reflection coefficient of a plane wave impinging orthogonally on the multilayer model as a function of the frequency, while figure 4(b) shows the attenuation undergone by a plane wave travelling into the multilayer model (y axis of figure 2), from the skin layer to the lung and the way back, as a function of the frequency.

Zoom In Zoom Out Reset image size

From figure 4(a) it can be noted that the reflection coefficient is approximately equal to −3 dB in the whole considered frequency band, that means that about half of the electromagnetic power incident on the multilayer model is reflected back and half is transmitted into the body. From figure 4(b) it can be noted that the attenuation of the signal is close to −100 dB at 3 GHz and that it increases dramatically with the frequency. These data are in agreement with those obtained in Varotto and Staderini (2011) where a signal attenuation of −93 dB has been evaluated at 3.1 GHz for a different body model.

The UWB incident pulses as well as the pulses reflected back from the multilayer body model are shown in figure 5 considering a distance between the UWB source and the body model equal to 1 m. In figures 5(a)–(d) the incident signals have a time behaviour equal to the first four derivatives of the Gaussian pulse, and the maximum amplitude allowed by the FCC mask, as obtained in section 2.3. From figure 5 it can be noted that the first reflected signal, due to the interface between air and skin, arrives at the location of the UWB antenna after about 7 ns from the onset of the incident signal, corresponding to a round trip 2 m long. Moreover, the reflected pulses show an inversion with respect to the incident ones caused by a negative value of the reflection coefficient, which in turn is due to the lower value of the impedance of the human body with respect to the free space impedance.

Zoom In Zoom Out Reset image size

To look at the reflected signals with higher detail, figure 6 shows a zoom of the four reflected signals between 5 and 20 ns. From figure 6 it can be noted the presence of a small reflected pulse coming later in time after the initial reflections. In particular, it is interesting to note that this small signal appears at exactly the same time for all the considered cases, i.e. after about 9 ns from the onset of the first reflected signal.

Zoom In Zoom Out Reset image size

Considering an average dielectric constant of 50 for the different tissues comprising the thorax model at the different frequencies considered, the speed of the electromagnetic field into the biological tissue is

$$\begin{equation*} \frac{{3 \cdot 10^8 }}{{\sqrt {50} }}\quad {\rm m\ s}^{ - 1} \approx 0.42 \cdot 10^8\ {\rm m\ s}^{ - 1} , \end{equation*}$$

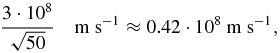
and the distance covered in 9 ns is

$$\begin{equation*} d = 0.42 \cdot 10^8 \times 9 \cdot 10^{ - 9} = 37.8\;{\rm cm}{\rm .} \end{equation*}$$

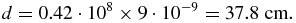
Accordingly, it could be argued that the reflection comes from a layer located about 19 cm deep into the model. At this distance the interface between the lung and bone is found (figure 2). To explain why the interface between lung and bone should be different from the other interfaces, it can be noted here that the lung dielectric properties used in the simulations are those of deflated lung, which show a high discontinuity with the bone characteristics, as shown in figure 7 where the permittivity of the different tissues comprising the multilayer model are reported at 3.0 and 10.0 GHz. Figure 7 evidences that, at 3 GHz, the relative dielectric constant of deflated lung is equal to 48, while that of bone is 12; similarly, at 10 GHz, deflated lung shows a relative dielectric property of 40, while bone presents a value of 9. From figure 7 a great discontinuity can be observed between fat and heart also, and at the interface between bone and muscle. However, the interface between fat and heart is located at 3.2 cm from the surface of the model (see figure 2), so that the signal reflected by this interface covers the round trip from the skin to the heart and back in about 1.5 ns, and arrives nearly superimposed to the air–skin reflection.

Zoom In Zoom Out Reset image size

To discriminate among the other possible reflections, and to verify that the small reflected signal found at about 16 ns effectively comes from the lung–bone interface, further simulations have been carried out. To this end, the geometry of the multilayer model has been changed considering the lung with an indefinite length, or considering the bone with an indefinite length. In the first case, lung with an indefinite length, the pulse reflection at 16 ns was not present any more in the reflected signal; in the latter case, bone with an indefinite length, the reflection was still there, even if with a slightly different time behaviour with respect to that depicted in figure 6. Moreover, a model with the layer of muscle behind the bone with an indefinite length was studied also, finding that the reflection was still evident with very small changes in its time behaviour. Since the indefinite length of a layer gives a matching condition, i.e. no reflections are obtained at the end of the layer, the obtained results show that the pulse reflection at 16 ns is obtained from the lung–bone interface.

Concerning the amplitude of the reflected pulses, figure 5 shows that the pulses reflected by the air–skin interface have more or less a −3 dB reduction with respect to the incident pulses (the maximum amplitude of the reflected signal is about 0.707 of that of the incident one), in agreement with figure 4(a).

On the contrary, figure 6 shows that even if the incident pulses have amplitudes higher for higher derivatives of the Gaussian pulse, the pulses reflected by the lung–bone interface have lower amplitudes for higher derivatives. This result can be understood considering that, according to figure 3 and thanks to the frequency behaviour of the FCC mask, higher amplitudes can be used for the source signal when higher derivatives of the Gaussian pulse are used; on the other side, these signals, having a higher frequency content, undergo a higher attenuation while travelling into the different tissues, as obtainable from figure 4(b). In this respect, it is interesting to note from figures 5(a) and 6(a) that the signal reflected by the lung–bone interface shows an attenuation of approximately −60 dB from the incident signal. If the attenuation undergone by a plane wave travelling from the skin layer to the bone and the way back is evaluated as a function of the frequency, the value of −60 dB is obtained at about 2 GHz. Accordingly, it can be argued that the pulse reflected back from the innermost layers is composed by the lower frequencies, which are those that undergo a lower attenuation while travelling into the different body tissues. To confirm this hypothesis, figure 8 shows the spectrum of the signal travelling into the different body layers compared with the spectrum of the incident signal, for the four time behaviours considered (figures 8(a)–(d)).

Zoom In Zoom Out Reset image size

From the figure it can be noted the different frequency occupation of the incident pulses, with the maximum value moving toward higher frequencies for higher derivatives of the Gaussian pulse (from figures 8(a)–(d)), as well as the frequency occupation of the pulses arriving at the lung–bone interface. In particular, it is interesting to note from figure 8(a), where the spectra of the signal are reported at the different interfaces present into the multilayer model, how the spectrum of the signal changes while travelling into the body, losing the higher frequencies. At the lung–bone interface the frequency occupation of the four signals is very close to each other.

As a validation of the results obtained with the circuital solver MWO, a simulation has been performed with the full electromagnetic solver MWS. As stated in section 2.2, since in MWS the frequency dependence of the dielectric properties is defined according to the Debye's model, the same dispersion model has been used in MWO in this test case. Figure 9 shows the reflected pulses evaluated by the two software packages when the monocycle impinges on the multilayer planar model.

Zoom In Zoom Out Reset image size

From the figure good agreement between the two results can be obtained both with reference to the amplitude of the reflected signal and to its time of arrival. From figure 9 it is interesting to note that the model used to represent the dispersion of tissues' dielectric properties influences the obtained results. In particular, the Debye's model leads to higher signal amplitudes than those obtained with the Cole–Cole model.

To simulate the breath activity increasing lengths for the layer representing the lung have been considered, according to the inspiration and expiration of the air; a corresponding reduction of the distance between the radar antenna and the body has been then introduced. In particular, the lung length was 70 mm in the initial thorax model (figure 2), corresponding to a resting state with a deflated lung. This length has been increased up to 80 mm (extended lung), corresponding to a tidal breath.

The resting state is close to the situation studied in the previous section. Accordingly, the reflection coming from the skin layer will arrive after about 7 ns from the centre of the incident pulse, while the signal reflected by the lung–bone interface will arrive about 9 ns after the pulse coming from the skin. Since the source is centred in time at 1 ns, the first reflection will arrive at about 8 ns, and the reflection from the bone at about 17 ns. Figure 10(a) shows the reflected signals arriving at the receiver location obtained from the two planar models with deflated lung and extended lung in the time window from 7 to 10 ns, while figure 10(b) shows the same signals from 15 to 20 ns.

Zoom In Zoom Out Reset image size

As it can be noted from figure 10, the two cases of deflated lung (resting phase) and extended lung are clearly discernible in time. Indeed, the peak of the reflected pulse coming from the skin is at 7.72 ns in the case of resting state and at 7.66 ns in the case of extended lung (figure 10(a)), corresponding to a movement of 9 mm. A similar time shift can be obtained from the later reflected pulses. Looking at the vertical scales of figure 10, it is evident that, when the radar system is placed far from the body, the respiratory activity can be monitored looking at the signal reflected by the air–skin interface.

As stated before, the dielectric properties of deflated lung are different from those of bone. However, during the inspiration phase, the lung extends due to air inhalation. Accordingly, the dielectric properties of lung change together with lung dimensions, lowering with respect to the values of deflated lung. As an example, the relative permittivity of inflated lung is 20.13 at 3 GHz, and 16.15 at 10 GHz (Gabriel 1996b, accessible online at http://niremf.ifac.cnr.it/tissprop/htmlclie/htmlclie.htm).

To investigate if the different dielectric properties influence the signal reflection, figure 11 shows the time behaviours of the reflected signals arriving at the receiver location in the case of resting state (deflated lung) and in the case of tidal breath, modelled with a lung extension of 80 mm and using the dielectric properties of inflated lung (inflated lung).

Zoom In Zoom Out Reset image size

Comparing figures 10 and 11, it can be noted that while no difference is obtained in the signal reflected by the air–skin interface when extended or inflated lung is considered (figures 10(a) and 11(a)), a different behaviour between the signals reflected in the two lung models is evident in the late-in-time reflection (figures 10(b) and 11(b)). In particular, the reflection from the inflated lung comes earlier and with greater amplitude than the reflection from the extended lung. Accordingly it can be derived that in this case the late reflection does not come from the lung–bone interface anymore, but from the heart–lung interface that, when the lung is inflated, represents an interface between two tissues with significant differences in the dielectric properties, more than the interface between inflated lung and bone.

If the radar is placed on the thorax (skin–radar distance of about 1 cm), the signal reflected back from the skin will not be discernible from the incident signal due to the very short time needed to cover the distance between the transmitting antenna and the thorax and the way back. Moreover, since the skin layer will move together with the radar device, the first reflection from the thorax will have no differences between resting and tidal phases. However, as described in section 3.2, the reflection coming from the lung–bone interface could allow detecting the breath activity.

Figure 12(a) shows the reflected signals in the two cases of deflated lung (resting state) and extended lung, while figure 12(b) shows the reflected signals in the case of deflated lung and tidal breath, this latter case simulated with the dielectric properties of inflated lung together with a higher dimension of the lung. From figure 12 it can be noted that the different lung length changes the time of arrival of the pulse reflected from the lung–bone interface, and that modifying both the lung length and lung dielectric properties a change both in the amplitude and in the time of arrival of the reflected signal is obtained (figure 12(b)). This last result is the same obtained in the case of a fixed radar system, and it can be explained accordingly, i.e. the reflection of the UWB pulse is obtained in this case at the interface between the heart and the inflated lung.

Zoom In Zoom Out Reset image size

To find out differences between the obtained results and those achievable using an anatomical model, a full-wave electromagnetic simulation has been performed with MWS considering a plane wave incident on part of the Duke's thorax, at the height of the section depicted in figure 1. As detailed in the methods section, in this case the dielectric properties of the tissues have been taken equal to the values at 2.0 GHz.

Figure 13 shows the reflected pulse obtained by MWS. The late-in-time reflected pulse is clearly evident, even if more oscillations can be noted with respect to the pulse reflected by the multilayer planar model.

Zoom In Zoom Out Reset image size

Finally, to deepen the validity of the obtained results, a Monte Carlo simulation has been conducted changing both the dielectric properties and the thicknesses of the considered tissues. In particular a maximum deviation of ±10% from the initial values has been allowed. Moreover, to put into evidence the influence of the skin layer, a Monte Carlo simulation has been performed changing only the skin properties. Figure 14 shows examples of the obtained results considering the reflected pulse in the case of inflated lung.

Zoom In Zoom Out Reset image size

In particular, figure 14(a) reports 20 Monte Carlo iterations allowing a ±10% change in both thickness and dielectric properties of all the tissues making the multilayer model, while figure 14(b) shows the outputs obtained allowing a ±10% change of the dielectric properties of the skin only. From the figure it can be noted that small differences both in the amplitude and in the time of arrival are obtained in the reflected pulse, thus confirming the validity of the obtained results.

To model the cardiac activity, the lung has been considered in a resting state while the heart length has been changed from 74 to 94 mm with a 5 mm step.

Figure 15 shows the reflected signals in the time window from 6 to 12 ns for the five considered heart dimensions. The figure evidences that the different dimensions are clearly discernible from the time of arrival of the peak of the received UWB waveform.

Zoom In Zoom Out Reset image size