ABSTRACT
We study the application of Lyot coronagraphy to future Extremely Large Telescopes (ELTs), showing that Apodized Pupil Lyot Coronagraphs enable high-contrast imaging for exoplanet detection and characterization with ELTs. We discuss the properties of the optimal pupil apodizers for this application (generalized prolate spheroidal functions). The case of a circular aperture telescope with a central obstruction is considered in detail, and we discuss the effects of primary mirror segmentation and secondary mirror support structures as a function of the occulting mask size. In most cases where inner working distance is critical, e.g., for exoplanet detection, these additional features do not alter the solutions derived with just the central obstruction, although certain applications such as quasar-host galaxy coronagraphic observations could benefit from designs that explicitly accomodate ELT spider geometries. We illustrate coronagraphic designs for several ELT geometries including ESO/OWL, the Thirty Mirror Telescope, the Giant Magellan Telescope, and describe numerical methods for generating these designs.
Export citation and abstract BibTeX RIS
1. INTRODUCTION
Direct imaging of faint companions around nearby stars is an exciting and ambitious goal. This requires contrast ratios of the order of 10−8 at angular separations of only tenths of a second of arc. Detection of a faint source near the star is hampered by the presence of background noise due to diffracted stellar light. Coronagraphy is one of the main elements used for the suppression of this starlight. Several ground-based instruments are being built to achieve the goal of detecting and characterizing extrasolar planets—the Gemini Planet Imager (GPI; Macintosh et al. 2006a; Macintosh et al. 2008), SPHERE (Beuzit et al. 2006), or HiCIAO (Tamura et al. 2006). These projects typically aim at the detection and spectroscopic characterization of relatively young objects (giant planets and brown dwarfs) a few 100 Myr old around nearby stars. According to theoretical models, contrast ratios of about 10−7 are expected for 100 Myr old, Jupiter-mass objects in the near infrared J, H, K bandpasses (Baraffe et al. 2003; Burrows et al. 2004). This goal seems achievable with ground-based extreme adaptive optics on 8 m class telescopes. According to these models, objects older than a few Gyr would be even fainter (by 1 or 2 orders of magnitude) and hardly detectable with these instruments. Very young objects with more favorable contrast ratios might be discovered in star-forming regions and very young associations (such as Taurus or Ophiucus), but this requires higher angular resolution because of the distance to the potential targets in recently formed systems (>150 pc). High contrast imaging instruments on the next generation of Extremely Large Telescopes (ELTs; Macintosh et al. 2006b) will be necessary to search these regions for faint companions.
Classical methods like the Lyot Coronagraph are not efficient enough to provide the contrast necessary to detect extrasolar planets by imaging. More advanced techniques have been studied intensively in the past few years (Roddier & Roddier 1997; Rouan et al. 2000; Baudoz et al. 2000; Aime et al. 2002; Kuchner & Traub 2002; Soummer et al. 2003b; Kasdin et al. 2003; Guyon et al. 2005; Mawet et al. 2005; Foo et al. 2005), some of which have already been developed in the lab and tested on the sky. Early studies have been done on Lyot coronagraphy on ELT geometries (Sivaramakrishnan & Yaitskova 2005), and on the effects of spiders on Apodized Pupil Lyot Coronagraph (APLC) designs that do not explicitly account for the presence of spiders (Sivaramakrishnan & Lloyd 2005). In this paper we study the APLCs invented by Aime et al. (2002) and Soummer et al. (2003a) for rectangular and circular aperture geometries. Soummer (2005) generalized these solutions to telescopes with arbitrarily shaped apertures. Here we apply the methods of Soummer (2005) to ELT currently under development and discuss the interesting possibility of multiple-stage APLC.
The effect of coronagraphs on speckle and photon noise has been studied by Aime & Soummer (2004b) and Soummer et al. (2007): the detection limits set by the signal-to-noise ratio (S/N) can be obtained by combining the coronagraphic response to a perfect wave, with the residual intensity halo created by the aberrations. Coronagraph design and optimization can be first tackled without considering aberrations, in order to produce the highest coronagraphic efficiency.
In Section 2, we discuss the principle and theory of APLCs and give a method to generate these solutions on arbitrary apertures numerically, using an iterative algorithm. We prove the convergence of the algorithm, and draw general conclusions on the sensitivity of APLCs to the geometrical parameters, based on the theoretical properties of generalized prolate spheroidal functions. In Section 3, we analyze the performance (throughput, residual energy, contrast) as a function of pupil geometry and occulting mask size, in the case of circular apertures with central obstruction. We show that for relatively small masks, the effects of smaller features (segmentation secondary mirror support structures) are overshadowed by the effects of the central obstruction. We consider the possibility of noncircular occulting masks and show some examples of optimal apodizers solutions for various ELT geometries, where the pupil features are large enough to influence the apodizer. Wide field AO systems being designed now (e.g., Keck Next Generation AO) is an application where the APLC design can open up new scientific search spaces in extragalactic astronomy. An advantage of the APLC design is that it produces a simple point-spread function (PSF), which helps extended object characterization.
2. APODIZED PUPIL LYOT CORONAGRAPHY WITH ARBITRARY APERTURE SHAPES
2.1. Coronagraphy with Entrance Pupil Apodization
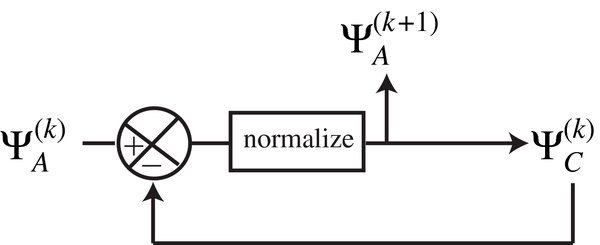
In this section, we follow the notations of Aime et al. (2002) and Soummer et al. (2003a) to recall the general formalism of coronagraphy with apodized pupils. The general layout of an APLC, given in Figure 1, is similar to a classical Lyot coronagraph with an additional upstream pupil apodization. The setup consists of an ensemble of apodizers, masks, and stops in four successive planes A, B, C, D, where A is the entrance aperture, B is the focal plane with the occulting mask, C is an image of the entrance aperture where a pupil mask called Lyot stop is placed, and D is the final image plane. We will consider the usual approximations of paraxial optics, and that the optical layout is properly designed to cancel the quadratic phase terms associated with the propagation, so that a Fourier transform exists between each plane.
Figure 1. Basic layout of an APLC is similar to a classical Lyot coronagraph, with an upstream apodized pupil in plane A. Hard-edged focal masks are placed in the focal plane B, and a Lyot stop identical to the entrance pupil in plane C. A remarkable difference between APLC and classical Lyot is that APLCs do not require to undersize the Lyot stop.
Download figure:
Standard image High-resolution imageThe telescope aperture function with the position vector  is denoted by
is denoted by  (index function equal to 1 inside the aperture
(index function equal to 1 inside the aperture  ), and
), and  is the apodizer transmission (1 without apodization). A hard-edged mask of transmission
is the apodizer transmission (1 without apodization). A hard-edged mask of transmission  is placed in the focal plane. M is the index function that describes the mask shape
is placed in the focal plane. M is the index function that describes the mask shape  , equal to 1 inside the coronagraphic mask and 0 outside (Ferrari et al. 2007). In plane C, the Lyot stop consists of a pupil mask, which can be eventually slightly undersized for optimization, but we will not consider this possibility in this paper. The field amplitude in the four successive planes are as follows:
, equal to 1 inside the coronagraphic mask and 0 outside (Ferrari et al. 2007). In plane C, the Lyot stop consists of a pupil mask, which can be eventually slightly undersized for optimization, but we will not consider this possibility in this paper. The field amplitude in the four successive planes are as follows:
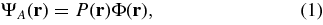
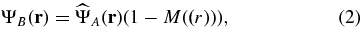
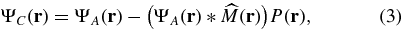

In these equations, 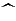 denotes the Fourier transform, and we assume that the focal lengths of the successive optical systems are identical (if not, an appropriate change of variables leads to the same result). Also, we re-orientate the axis in the opposite direction and omit the −1 proportionality factor for better readability. We consider the monochromatic case in this paper to analyze the properties of the solutions for arbitrary apertures. The chromatic formalism was given in previous papers and achromatization was studied by Soummer et al. (2003b) and Aime (2005b).
denotes the Fourier transform, and we assume that the focal lengths of the successive optical systems are identical (if not, an appropriate change of variables leads to the same result). Also, we re-orientate the axis in the opposite direction and omit the −1 proportionality factor for better readability. We consider the monochromatic case in this paper to analyze the properties of the solutions for arbitrary apertures. The chromatic formalism was given in previous papers and achromatization was studied by Soummer et al. (2003b) and Aime (2005b).
Lyot (or Roddier coronagaphs) can be well understood by the analysis of the Lyot plane amplitude (Equation (3)), which can be interpreted as a two-wave interference between the pupil amplitude and the wave diffracted by the mask. In the case of a classical Lyot coronagraph, the subtraction of these two terms is not efficient (Figure 2, left panel). One can deduce two complementary coronagraphic approaches from the analysis of this figure.
- 1.A perfect subtraction of the two terms is obtained if the wave diffracted by the mask is equal to the pupil amplitude, at least in a reduced area of the pupil. This case corresponds to the band-limited mask coronagraph (Kuchner & Traub 2002).
- 2.The APLC approach is to apodize the pupil transmission so that the amplitude profile of the wave diffracted by the mask corresponds to the shape of the pupil transmission shape. Optimal apodization functions exist for this problem and are given by the prolate spheroidal functions.
Figure 2. Two complementary approaches to improve the Lyot coronagraph where the pupil amplitude and the wave diffracted by the mask (Equation (3)) do not match one another (left). The subtraction can be improved by producing a flat diffraction term using a band-limited mask (Kuchner & Traub 2002; top right), or by using an optimal pupil apodization of the pupil (bottom left).
Download figure:
Standard image High-resolution imageThe intensity in the final focal plane is not invariant by translation, but we will use the terminology of coronagraphic PSF according to the general usage in the community.
2.2. Generalized Prolate Spheroidal Functions
According to Equation (3) and Figure 2, the condition for a total extinction of the starlight is obtained if the wave diffracted by the mask (the convolution integral) is equal to the entrance pupil amplitude (the apodization function):
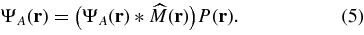
Solutions to Equation (5) can be found if  is the eigenfunction of the convolution integral. This problem is well known in signal processing and is equivalent to a generalization of the uncertainty principle (Papoulis 1968), or to the search of band-limited functions having the maximum encircled energy within a given spatial domain. A total extinction solution exists for a Roddier coronagraph with a prolate apodization (Ferrari et al. 2007). Unfortunately, a total extinction is not achievable with an APLC, but thank to the properties of prolate functions discussed below, it is possible to approach this perfect solution with optimal properties.
is the eigenfunction of the convolution integral. This problem is well known in signal processing and is equivalent to a generalization of the uncertainty principle (Papoulis 1968), or to the search of band-limited functions having the maximum encircled energy within a given spatial domain. A total extinction solution exists for a Roddier coronagraph with a prolate apodization (Ferrari et al. 2007). Unfortunately, a total extinction is not achievable with an APLC, but thank to the properties of prolate functions discussed below, it is possible to approach this perfect solution with optimal properties.
In coronagraphic terms, the solution of this problem corresponds to the pupil apodization that produces the most concentrated starlight behind a given focal plane mask (and thus blocked). This formal problem has been solved analytically for rectangular and circular unobstructed apertures (Aime et al. 2001, 2002; Soummer et al. 2003a), using linear and circular prolate functions (Slepian & Pollak 1961; Frieden 1971; Papoulis 1981). Formal solutions exist in the generalized case for any shape of aperture (Slepian 1964, 1965; Papoulis 1968), and such solutions find a direct application in coronagraphy. In Appendix  , and writing as Λ0 the associated eigenvalue, we obtain a new set of equations for the four planes:
, and writing as Λ0 the associated eigenvalue, we obtain a new set of equations for the four planes:

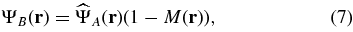
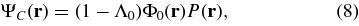
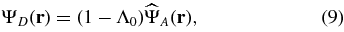
If the focal plane mask  is symmetric, the Fourier transform of its index function,
is symmetric, the Fourier transform of its index function,  , is real and symmetric and the eigenfunctions are real. If the mask is not symmetric, its Fourier transform is Hermitian and the eigenvalues Λn are real, but the eigenfunctions are complex. In the following, we will only consider symmetric focal plane masks (e.g., circular), since there is no particular reason to choose an asymmetric mask in most common cases, and the symmetry of the mask guarantees a real apodizer.
, is real and symmetric and the eigenfunctions are real. If the mask is not symmetric, its Fourier transform is Hermitian and the eigenvalues Λn are real, but the eigenfunctions are complex. In the following, we will only consider symmetric focal plane masks (e.g., circular), since there is no particular reason to choose an asymmetric mask in most common cases, and the symmetry of the mask guarantees a real apodizer.
One of the possible criteria to evaluate the performance of a coronagraph is the residual energy inside the Lyot stop (here identical to the pupil), normalized to the apodizer throughput. This criterion finds a very simple expression as a function of the eigenvalue:

As discussed by Ferrari et al. (2007), important analytical simplifications are obtained if the mask domain  is a scaled version of the pupil domain
is a scaled version of the pupil domain  . More generally, prolate solutions exist in any case, and we will study in Section 3.2 the impact of the choice of the mask geometry on the overall performance.
. More generally, prolate solutions exist in any case, and we will study in Section 3.2 the impact of the choice of the mask geometry on the overall performance.
2.3. Multistage APLC
It is remarkable that the Lyot stop amplitude is proportional to the entrance pupil amplitude, inside the aperture area  , even in the presence of secondary mirror support structures: all the discontinuities in the pupil appear in negative, with no light bleeding into the pupil as illustrated in the Lyot plane in Figure 3. This property derives straightforwardly from the eigenvalue problem and we can recognize the prolate apodization, identical inside the aperture in both planes to a scaling factor. The apodization function can be exactly recovered to the eigenvalue attenuation factor by multiplying the Lyot stop amplitude by the pupil function. In the case illustrated in Figure 3, the apodizer has been calculated for the exact geometry and although the apodizer looks rotationally symmetric to the eye, it is slightly different from the apodizer that would have been calculated with the same mask and no spider vanes in the pupil. In the case where the support structures are not included in the definition of the apodizer, residual light is diffracted in the Lyot plane and has to be mitigated by the Lyot stop optimization (Sivaramakrishnan & Lloyd 2005). This might be preferable for practical reasons to use a rotationally symmetric apodizer in the case of pupil rotation. Small features like segmentation behave in a similar way. However, in the cases of small gaps between segments, it is not beneficial to include the segmentation in the calculation of the apodizer and the diffracted light can be optimized in the Lyot plane with a reticulated Lyot stop (Sivaramakrishnan & Yaitskova 2005).
, even in the presence of secondary mirror support structures: all the discontinuities in the pupil appear in negative, with no light bleeding into the pupil as illustrated in the Lyot plane in Figure 3. This property derives straightforwardly from the eigenvalue problem and we can recognize the prolate apodization, identical inside the aperture in both planes to a scaling factor. The apodization function can be exactly recovered to the eigenvalue attenuation factor by multiplying the Lyot stop amplitude by the pupil function. In the case illustrated in Figure 3, the apodizer has been calculated for the exact geometry and although the apodizer looks rotationally symmetric to the eye, it is slightly different from the apodizer that would have been calculated with the same mask and no spider vanes in the pupil. In the case where the support structures are not included in the definition of the apodizer, residual light is diffracted in the Lyot plane and has to be mitigated by the Lyot stop optimization (Sivaramakrishnan & Lloyd 2005). This might be preferable for practical reasons to use a rotationally symmetric apodizer in the case of pupil rotation. Small features like segmentation behave in a similar way. However, in the cases of small gaps between segments, it is not beneficial to include the segmentation in the calculation of the apodizer and the diffracted light can be optimized in the Lyot plane with a reticulated Lyot stop (Sivaramakrishnan & Yaitskova 2005).
Figure 3. APLC with generalized prolate spheroidal apodization. As expected, the secondary support structures appear bright in the Lyot plane. However, it is remarkable that these structures do not influence the field in the aperture domain, for example classical Lyot coronagraphs. The field amplitude inside the aperture domain in the Lyot plane (right) is proportional to the initial entrance pupil apodization (left), since the apodizer is the eigenfunction of the system. Both figures are displayed with appropriate scalings so that the apodizer inside the aperture appears identical in both panels.
Download figure:
Standard image High-resolution imageThis proportionality property between the entrance aperture and the Lyot plane enables the possibility of multiple-stage APLCs (Aime & Soummer 2004a). After the Lyot stop, the field amplitude is proportional to the entrance pupil apodization, and can be used as the entrance pupil of a second APLC. For the second coronagraphic stage, the apodization is therefore produced by the output of the first stage, and no additional apodizing element is needed. In principle, several successive stages can be used. Each coronagraphic stage provides the same rejection factor of the starlight. An interesting aspect of this approach is that there is only one physical apodizer involved, at the entrance of the system. Therefore, the throughput is not reduced by successive stages, and the total residual energy after k coronagraphic stages is simply:

Multiple-stage APLCs require that the Lyot stop field amplitude be proportional to a prolate function. In broadband, with a gray apodizer and a hard-edge mask, this is only verified at a single wavelength and multistage APLCs produce a limited improvement compared to the ideal case, even using a numerical optimization of the mask size. A perfect achromatic solution can be obtained with an apodizer producing the requisite chromatic apodization and the result is close to that of an achromatic APLC (Aime 2005a). Interferometric methods can be used to produce such an apodizer (El Azhari et al. 2006; Carlotti et al. 2007). A simple method for partial achromatization is to manufacture an absorbing apodizer where the material is itself chromatic, and approximates the required wavelength variation (Soummer et al. 2006).
2.4. Effect of Mask Size on the Optimal Apodization
As shown in Section 2.2, the geometry of  and
and  defines an eigenvalue problem, with the optimum solution (Λ0, φ0) for coronagraphy. Once the geometry of the mask has been chosen, a scale parameter for its size remains as a free parameter. This parameter corresponds to the so-called prolateness parameter c (Frieden 1971). For rectangular and circular geometries, the eigenvalue Λ0 can be controlled by the size of the focal plane mask (Aime et al. 2002; Soummer et al. 2003a), and is a strictly increasing function of the mask size that approaches one asymptotically. APLCs take advantage of the particular shape of this function, which saturates quickly, and thus enables very high rejections with values of Λ0 very close to 1, for relatively small masks (typically a few resolution elements). This monotonic behavior of the eigenvalue with the mask size is less obvious in the case of arbitrary geometries. However, it is still true and we detail the mathematical demonstration of this property in Appendix
defines an eigenvalue problem, with the optimum solution (Λ0, φ0) for coronagraphy. Once the geometry of the mask has been chosen, a scale parameter for its size remains as a free parameter. This parameter corresponds to the so-called prolateness parameter c (Frieden 1971). For rectangular and circular geometries, the eigenvalue Λ0 can be controlled by the size of the focal plane mask (Aime et al. 2002; Soummer et al. 2003a), and is a strictly increasing function of the mask size that approaches one asymptotically. APLCs take advantage of the particular shape of this function, which saturates quickly, and thus enables very high rejections with values of Λ0 very close to 1, for relatively small masks (typically a few resolution elements). This monotonic behavior of the eigenvalue with the mask size is less obvious in the case of arbitrary geometries. However, it is still true and we detail the mathematical demonstration of this property in Appendix
2.5. Computation of Generalized Prolate Apodizers
Prolate spheroidal function exists for any geometry, and we calculate the eigenfunctions using a numerical algorithm presented in Figure 4. This algorithm was initially proposed by Guyon & Roddier (2000) to calculate optimal apodizations for the Roddier phase mask. We recently discovered that this method is also known in the field of signal processing and laser optics (Papoulis 1968; Schulz 2004) and based on classical tools of functional analysis (Riesz & Sz.-Nagy 1990, p. 491).
Figure 4. Schematic representation of the iterative algorithm to generate prolate apodizers. Starting with an initial estimate, we propagate to the Lyot plane, and subtract the result from the pupil amplitude. The pupil mask is then applied and the result is normalized to one. This algorithm converges to the prolate function of zeroth order corresponding to the geometry of the system.
Download figure:
Standard image High-resolution imageThe convergence of the algorithm can be demonstrated using the fact that eigenfunctions φn form a complete orthogonal basis over the aperture  . We start the algorithm with an initial estimate of the entrance pupil apodization, Ψ(0)A, which can be decomposed over the prolate basis:
. We start the algorithm with an initial estimate of the entrance pupil apodization, Ψ(0)A, which can be decomposed over the prolate basis:
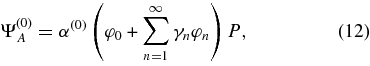
where α(0) is a coefficient that corresponds to the projection of Ψ(0)A onto φ0. Superscripts denote the iteration number. We consider the pupil itself P for our initial estimate, as it insures to have a nonzero projection onto the first eigenfunction φ0. This pupil complex amplitude is propagated to the Lyot plane, and we obtain
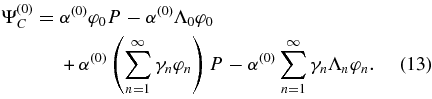
This Lyot plane amplitude is then subtracted from the pupil amplitude and limited to the pupil:
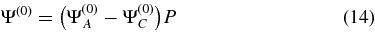
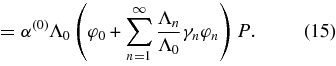
We obtain the next iterate after renormalization:

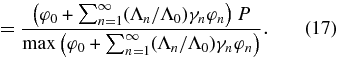
This expression can be generalized to the kth iterate after some algebra:
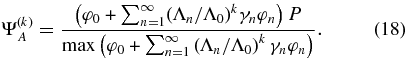
Because eigenvalues are ordered as Λ0 > Λ1 > Λ2 > ⋅ ⋅ ⋅ >0 (Slepian 1964), the convergence of the algorithm to the first eigenvalue Φ0 is always guaranteed. In the perfect case, the ratio  is constant over
is constant over  and equal to 1 − Λ0. We use the uniformity of this ratio as a stopping criterion for the algorithm, as it gives a proxy for the precision on the eigenvalue. We find satisfactory results when we stop the iterations when the precision on the eigenvalue is 0.1%.
and equal to 1 − Λ0. We use the uniformity of this ratio as a stopping criterion for the algorithm, as it gives a proxy for the precision on the eigenvalue. We find satisfactory results when we stop the iterations when the precision on the eigenvalue is 0.1%.
3. PERFORMANCE AND SENSITIVITY TO GEOMETRY
3.1. Effect of Central Obstruction
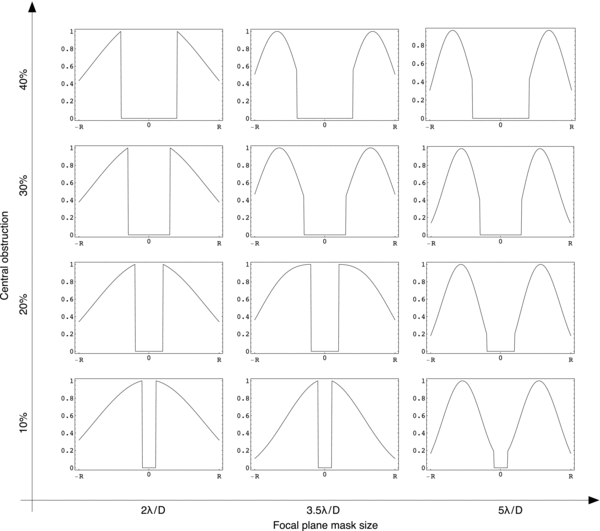
In this section we study the performance and sensitivity of an APLC to central obstruction in a circular aperture, with circular focal plane mask. We first generate a large number of apodizers to sample finely the obstruction and mask size parameter space. Depending on the obstruction and mask size, we identify two morphologies of apodizers: bell shaped or bagel shaped. In Figures 5 and 6, we show the prolate apodizers for a range of obstruction and mask sizes.
Figure 5. Given telescope geometry defines an integral eigenvalue problem in which for any mask size (eigenvalue), an apodization can be computed (eigenfunction). This figure illustrates the apodization that can be obtained for a few telescope geometries varying the size of the central obstruction (y-axis), and as a function of the mask's size (x-axis).
Download figure:
Standard image High-resolution imageFigure 6. Line plots corresponding to Figure 5.
Download figure:
Standard image High-resolution imageSmall obstruction and small masks produce bell-shaped apodizers (bottom left in Figure 5), whereas large obstructions and/or large mask (top right in Figure 5) produce bagel-shaped apodizers. Denoting by D1 the diameter of the primary aperture and by D2 the diameter of the obstruction, the existence of these two regimes can be understood by comparing the scales of D1/α and D2, where α denotes the mask diameter in resolution elements (Soummer 2005). Indeed, in the convolution product of Equation (3), the extent of the term  is proportional to D1/α. For example, if D1/α ≪ D2, the convolution product
is proportional to D1/α. For example, if D1/α ≪ D2, the convolution product  will go to zero at the center of the aperture and the apodizer will be bagel shaped. Conversely, if D1/α ≫ D2, the convolution product at the center of the aperture will only have a negligible dip, and the resulting apodizer is bell shaped. Empirically, we consider that the bell/bagel transition is obtained for α ≈ D1/(2D2). For example, for a 20%, the transition region between bell-shaped and bagel-shaped apodizer is for a mask size greater than 2.5Λ/D.
will go to zero at the center of the aperture and the apodizer will be bagel shaped. Conversely, if D1/α ≫ D2, the convolution product at the center of the aperture will only have a negligible dip, and the resulting apodizer is bell shaped. Empirically, we consider that the bell/bagel transition is obtained for α ≈ D1/(2D2). For example, for a 20%, the transition region between bell-shaped and bagel-shaped apodizer is for a mask size greater than 2.5Λ/D.
This discussion can be generalized for any features in the pupil, and in particular for secondary mirror support structures and segments. For a given feature of characteristic size d, we observe a similar effect where the apodization function is modified around the structure, when the mask size is larger than D/(2d) (in resolution element units). This is illustrated in Figure 14 where we can see that the secondary mirror support structures start to influence the optimal apodization shape for masks sizes greater than 5λ/D (in this figure, the vanes are approximately of width D/10).
In the case of telescope geometries where the secondary mirror support structures are very thin (as for example on Gemini where d ≈ 1 cm), their effect is negligible in the calculation of the optimal apodizer. Sivaramakrishnan & Lloyd (2005) estimated the effects of such spiders on APLC coronagraphic contrast. These very thin support structures only affect the theoretical prolate apodizer for very large focal plane masks (a few ten λ/D). The apodizer would present similar features to that observed in Figure 14. Because of the scientific goals on a 8 m class telescope, such large mask are not considered and spiders are ignored for the calculation of the apodizer. Also, a nonrotationally symmetric apodizer would be much more difficult to manufacture and align, especially if pupil rotation is involved for an Alt-Az telescope.
The first consequence of these two regimes (bell/bagel), already discussed in Soummer (2005), is the impact on the throughput. By throughput we mean here the ratio of the number of companion's photons reaching the final science detector over the total number of companion photons that enter the coronagraph. This definition corresponds to the total throughput and does not take into account the final shape of the image of an off-axis source, whose spatial distribution can affect the instrument S/N. However, as seen in Equation (9) the off-axis response field after an APLC is still a prolate function of order zero, whose eigenvalue is very close to unit; as a consequence, most of the light is concentrated in the core of the PSF and making most of the photons readily available for the detection or characterization of the companion. Thus for the remainder of this paper we will use this definition of throughput. bell-shaped apodizers have a much lower throughput than bagel-shaped apodizers. A representation of the throughput for the parameter space we studied is shown in Figure 7. For line plots as a function of central obstruction, see Figure 2 of Soummer (2005). The transition region between low-throughput bell-shaped and high-throughput bagel-shaped apodizers is visible along the diagonal in the figure where the contour lines increase sharply, and is indicated by an arrow. It is interesting to note that for a given geometry, the throughput is not a monotonic function: after a steep increase in throughput, which corresponds to the bell–bagel transition, the throughput decreases again. This throughput decrease with mask size in the bagel regime is analog to that observed for rectangular and circular apertures where the apodizer strength increases with mask size.
Figure 7. Throughput of the prolate spheroidal optimal apodizer for a variety of telescope geometries with different central obstruction, and for a range of mask sizes. The transition region between the two regimes of apodizer (low-throughput bell-shaped and high-throughput bagel-shaped) is visible along the diagonal and indicated by the black arrow.
Download figure:
Standard image High-resolution imageSeveral criteria can be considered to study the sensitivity and to optimize APLCs. A first obvious criterion is the integrated residual energy, normalized to the apodizer throughput (Equation (10)). Because the apodizer throughput is not a monotonic function of mask size (e.g., due to the bell–bagel transition), it is not intuitive that the normalized residual energy e monotonicly decreases with mask size. Note that when the mask radius increases, the apodization function changes (possibly significantly, e.g., bell/bagel transition), and so does the PSF. We illustrate the residual energy criterion in Figure 8 for the circular geometry with central obstruction.
Figure 8. Residual energy normalized to the throughput, as defined in Equation (10), for circular telescopes with central obstruction and for a range of mask sizes. For any given geometry, this criterion is a monotonic decreasing function of the mask size. This result is also true for more complex telescope geometries.
Download figure:
Standard image High-resolution imageAnother interesting criterion is to consider the residual energy outside the mask area in the final focal plane, normalized to the throughput. Because the final focal plane amplitude 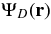 is proportional to the prolate function itself (Equation (9)), we can find a simple expression for this term (Soummer et al. 2003a):
is proportional to the prolate function itself (Equation (9)), we can find a simple expression for this term (Soummer et al. 2003a):
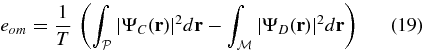
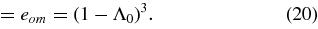
This last expression shows that the residual energy outside the mask has a similar behavior to the residual energy criterion, with no specific optimum mask size for a given geometry.
A slightly better criterion is the residual starlight energy in the region of the final focal plane where an off-axis companion can be detected, normalized to the apodizer throughput. For that, we define the inner working angle (IWA), as the minimum distance at which the transmission of an off-axis companion is significantly high. Although the off-axis transmission of a coronagraph is a smooth function of the angular position, a good rule of thumb is to consider the IWA equal to the mask radius augmented by one resolution element (see also, Lloyd & Sivaramakrishnan 2005). Intuitively, if a source is located just outside the mask, it is almost fully transmitted by the coronagraph. This criterion does not produce a significant difference compared to eom in the perfect monochromatic case and we did not represent the result. However, this is a better criterion for broadband optimization and it was used by Soummer (2005).
Another common criterion is based on the contrast at a given angular separation r0, between an average intensity level at a given radial distance in the final focal plane and the maximum of the PSF p for an off-axis source:
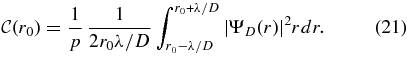
In Equation (21), we consider an arbitrary average of the contrast over an annulus of width 2λ/D, in order to remove the effects of ringing in the coronagraphic PSF. Note that both the apodizer and the Lyot stop impact the maximum intensity of an off-axis source p and that the actual off-axis transmission of the coronagraph can be included readily as a weighting function in p. We show a few of these contrast curves at an angular separation of r0 = 6 resolution elements in Figure 9. A contrast criterion is very useful for the optimization of a coronagraph over a particular region of interest, since the width of the annulus can be changed to suit science requirements. We also considered a definition of the contrast based on a one-dimensional average over a radial profile:
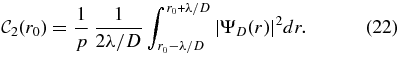
This definition produces similar results, which are not shown here. The criterion of the residual energy outside the mask area was used in Soummer (2005), and a discussion of contrast criteria for APLCs was also done by Martinez et al. (2008). A criterion based on the Airy throughput (Vanderbei et al. 2003) would be interesting to include the consideration of the useful flux of the planet, i.e., which fraction of the total planet flux can be used for detection. With an APLC, the off-axis PSF (planet) is simply the PSF produced by the apodized aperture, assuming that the source is sufficiently outside the focal plane mask area (outside the IWA). By definition, this PSF has maximum encircled energy within a circle equal to the focal plane mask area. The fractional energy of the PSF within this circle is Λ0, which is very close to 1 for an APLC (typicallyΛ0 > 0.99). This ensures that most of the planet flux is usable for detection with an APLC. Significant effect on the Airy throughput is observed in the case of shaped pupil apodization, and this criterion should be considered if this method is used to produce the apodizer of an APLC.
Figure 9. Evolution of the average contrast levels with the mask size, at an angular separation of r0 = 6λ/D and for a few obstruction ratios. The contrast is normalized according to Equation (21). Larger obstruction ratios lead to a decreased contrast, but at this location in the field, the contrast is little affected between 10% and 20% of obstruction. In some regions, the contrast is independent of the mask size, which has very important consequences for broadband optimization.
Download figure:
Standard image High-resolution imageIn the simple monochromatic case we presented here, these criteria provide consistent results and illustrate that there is no particular optimum for the mask size of an APLC for a given circular geometry with central obstruction. However, in large band, an optimum can be found in some cases, and these criteria are useful for the optimization and designs for a specific geometry. In particular, it is possible to optimize the mask size according to the chromatic properties of the apodizer (gray or chromatic apodizer; Soummer et al. 2006).
It is interesting to note that in some regions of the parameter space shown in Figures 8 and 9, the contrast (or other criterion) can be somewhat independent of the mask size. This has important consequences in the case of broadband optimization with the existence of quasi-achromatic solutions, which are used in the GPI coronagraph design (Macintosh et al. 2008), and which will be detailed in a future paper.
3.2. Case of Noncircular Focal Plane Masks
In the previous section, we only considered the case of a circular mask. As explained in Section 2.2, focal plane masks do not have to be circular, and as long as they are symmetric, the prolate apodizer is real. We study in this section the comparison between circular and noncircular masks for two examples.
For a hexagonal aperture, with similarities to the Keck telescope for example, or more generally for future segmented telescopes, the PSF corresponding to the hexagonal aperture shows some hexagonal symmetry. We study if a coronagraph would benefit from having a hexagonal focal plane mask that may match the PSF better. For that, we calculate the optimal generalized prolate apodization in two cases, with a circular mask and with a hexagonal mask (Figure 10). In this calculation, the hexagonal mask and the circular mask have the same surface. We find that the two prolate apodizers are very similar and the residual energy is slightly better for a circular mask. Corresponding contrast curves normalized to the off-axis PSF maximum are shown in Figure 11. Although we have not studied the entire parameter space for the hexagonal geometry, we conclude that there is no interest to use hexagonal masks in this case. A possible explanation for this behavior is that the apodizer circularizes the PSF. This is illustrated in Figure 12 where we show the PSFs corresponding to the same geometry as shown in Figure 10. The apodized PSF has been partially circularized by the apodizer.
Figure 10. Hexagonal pupil geometry (left) and generalized prolate solutions using a circular mask (top) and a hexagonal mask (bottom). The mask size is 5λ/D and both masks have the same surface. The central obstruction is 20%. Both apodizations are very close, and the residual energy with a circular mask is slightly better than with a hexagonal mask.
Download figure:
Standard image High-resolution imageFigure 11. Coronagraphic PSFs for the APLC with the hexagonal aperture and with a circular mask (solid line) and hexagonal mask (dashed line). The performance is slightly better with the circular mask. The coronagraphic PSF is normalized to the maximum of the off-axis source.
Download figure:
Standard image High-resolution imageFigure 12. PSF for the hexagonal clear aperture (left) and apodized aperture (right). The apodization tends to circularize the geometry of the PSF, which may explain why the APLC performance remains slightly better for a circular mask.
Download figure:
Standard image High-resolution imageAs mentioned previously and detailed by Ferrari et al. (2007), analytical derivations are possible if the mask  is a scaled version of the pupil shape
is a scaled version of the pupil shape  . We analyze the performance of a pierced mask, compared with the usual circular mask. We calculated the generalized prolate solution in both cases. In Figure 13, we show that the performance of the pierced mask is degraded for a Gemini/VLT-like aperture geometry. Intuitively, this can be explained because the hole at the center of the mask creates a leakage of light where the PSF is the brightest. Also, its diffraction is a uniform background in the Lyot stop since the pinhole at the center of the mask is much smaller than the resolution element.
. We analyze the performance of a pierced mask, compared with the usual circular mask. We calculated the generalized prolate solution in both cases. In Figure 13, we show that the performance of the pierced mask is degraded for a Gemini/VLT-like aperture geometry. Intuitively, this can be explained because the hole at the center of the mask creates a leakage of light where the PSF is the brightest. Also, its diffraction is a uniform background in the Lyot stop since the pinhole at the center of the mask is much smaller than the resolution element.
Figure 13. Comparison between APLC solutions obtained with a pierced focal plane mask and a classical circular occulting mask. The pierced mask is a scaled version of the pupil geometry, here comparable to Gemini/VLT. The contrast performance is degraded by the pierced mask. Same normalization as in Figure 11.
Download figure:
Standard image High-resolution image3.3. Application to ELT
The generalized prolate spheroidal solutions are highly relevant for APLCs on future ELT projects. Indeed, these telescopes will not be monolithic but will include necessarily segmentation, with relatively large central obstruction, and large secondary mirror support structures. All these characteristics are challenging for coronagraphy and typically reduce the delivered contrast. We have shown above that the generalized prolate functions enable APLCs to mitigate these adversities. Moreover, because of the ELTs' very high angular resolution, IWA is not a crucial parameter, and they can accommodate coronagraphs that work at a few resolution elements of IWA, as the APLC does.
In this section, we give a few examples of generalized prolate solutions for three possible ELT geometries. The aperture geometries we consider might not reflect the current status of these projects. Our point here is not to make a detailed technical study, but to illustrate the type of theoretical solutions we can consider for arbitrary aperture shapes. We will consider the following.
- 1.The ESO 100 m Overwhelmingly Large Telescope (OWL) (this geometry has been abandoned and now reduced to 42 m). This geometry has a large obstruction, thick support structures, and a large number of segments.
- 2.The Thirty Mirror Telescope (TMT). This geometry has segments, a triangular obstruction, and a complex system of support structures.
- 3.The Giant Magellan Telescope (GMT). This geometry consists of a daisy-type arrangement of seven circular telescopes. There are large gaps between the circular telescopes.
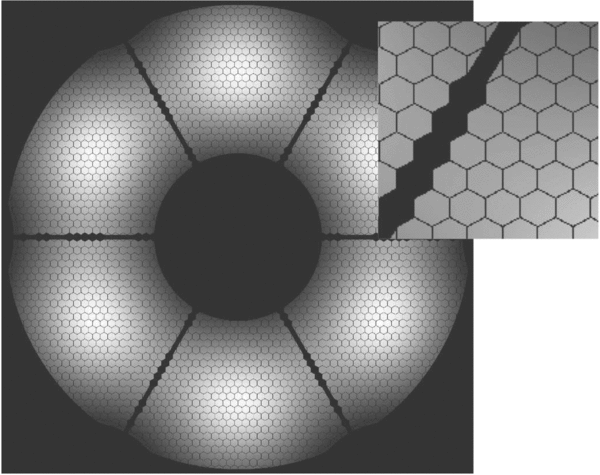
In Figure 14 we show three optimal apodizers for OWL with increasing mask sizes. The smallest mask size leads to a simple bagel-shaped apodizer, where smaller features (spider vanes, and support structures) do not visibly affect the shape of the apodizer. This geometry was also used in Figure 3 for the illustration of the Lyot plane before the application of the Lyot stop. In this case, it would be preferable to consider a rotationally symmetric apodizer and ignore the support structures, as Sivaramakrishnan & Lloyd (2005) do. For mask sizes about 5λ/D, the secondary mirror support structures start to alter the shape of the apodizer in a similar transition to the bell–bagel regimes. This transition makes the apodizer shape more complex and its throughput is also affected by this transition.
Figure 14. Generalized prolate apodizers for the OWL geometry, and for mask sizes of 5, 7, and 10 λ/D. The smallest mask shows a simple bagel-shaped function where the apodizer is little affected by the secondary mirror support structures. For larger masks, a transition analog to the transition bell–bagel occurs and the apodizer is affected by the geometry of the pupil. Segments are not included in this simulation.
Download figure:
Standard image High-resolution imageIn Figure 15, we show a calculation for the OWL geometry where the segments were included during the computation of the apodizer. Segment gaps are too small compared to the mask size to alter the shape of the optimal apodizer, and they should be ignored in this case. However, they will appear bright in the Lyot plane, and the Lyot stop should be reticulated to remove these bright segment gaps (Sivaramakrishnan & Yaitskova 2005).
Figure 15. Example of an apodizer for the OWL geometry where segments have been included in the computation of the optimal apodization. Gaps between segments are too small compared to the other features of the telescope and do not modify the optimal shape of the apodizer.
Download figure:
Standard image High-resolution imageIn Figure 16, we show three apodizers for the geometry of GMT. It is interesting to see that solutions exist even for this complex, nonconvex aperture. In some cases the result is somewhat surprising. For example in the right panel, the prolate apodizer almost completely obscures the central aperture.
Figure 16. Generalized prolate apodizers for the GMT aperture and mask sizes of 5, 10, and 15 λ/D.
Download figure:
Standard image High-resolution imageIn Figure 17, we show three examples for the geometry of TMT. Even in the smallest mask case, it is possible to see that the support structures modify the apodizer, which is not perfectly rotationally symmetric.
Figure 17. Generalized prolate apodizers for the TMT aperture and mask sizes of 5, 7, and 10 λ/D.
Download figure:
Standard image High-resolution imageThe features of ELT geometry include large secondary obstructions and support structures much larger than for 8–10 m class telescopes, for compactness and mechanical reasons. For example, in the case of TMT, the secondary supports can be as large as 30–50 cm in some designs (Ellerbroek et al. 2006). Compared to the 1 cm Gemini secondary supports, this is an order of magnitude larger (relative to the telescope diameter). This means that secondary supports start to matter more for prolate apodizations when applied to ELT geometries, especially for masks diameters between five and ten resolution elements. A detailed study is needed to determine whether it is better to consider smaller mask sizes with a multiple-stage APLC or larger masks with more complex apodization profiles.
4. CONCLUSION
Hitherto APLCs design have been developed for circular geometries. With the emergence of several ELT projects in the last few years, the increased resolution of the telescopes enables coronagraph design to explore areas that current designs for 8–10 m telescopes do not explore. In particular, for the same angular diameter on the sky, the occulting mask on an ELT is wider in resolution element units. This enables apodizer design to reflect telescope geometries better, either using a comparable mask ∼200 mas (equivalent to a 10–20 λ/D occulting mask) for better contrast, or a much smaller mask size (equivalent to a few λ/D) for more aggressive science goals with improved IWA.
We showed that APLCs can be calculated for any geometry of aperture, using generalized prolate spheroidal apodizations. For a given geometry, an ensemble of apodization functions can be calculated for a range of focal plane mask sizes. We showed that there is no particular optimum solution as a function of the mask size, in light of a few common criteria (the residual energy in the focal plan outside the mask area, or the local final contrast).
We presented some examples of apodizer solutions for a few ELT geometries. ELT will typically have larger central obstruction and secondary support structures relative to their diameter, compared to current 8–10 m class telescopes. The consequence is that these features start to matter more for coronagraphy and in particular for APLCs, which can be designed to mitigate their effects. The trade-off for ELT APLC coronagraphy is to consider either small mask sizes (typically <4 − 5 resolution elements) in order to neglect the support structures and use a rotationally symmetric apodizer, or to consider more complicated structures in the apodizer. In addition, multiple-stage APLCs are a promising concept for ELTs, provided that coronagraphic achromatization is achieved. Multiple-stage APLC would in particular enable the use of smaller mask sizes, rotationally symmetric apodizers, where the high rejection would be provided by the multiplicative effect of this system. Based on current studies for the GPI, it is possible to manufacture apodizers with complex features as those illustrated in this paper. For example, high-energy beam sensitive glass (Canyon Materials Inc.) enables any apodizer function to be written by a focused e-beam machine, with features as small as 0.1μm.
If ELT AO performs at the 80%–95% Strehl ratio level in the H-band, APLC designs open the possibility of direct detection and characterization of older, cooler extrasolar jovian planets than current ExAO projects on 8–10 m class telescopes target. Taking advantage of the increased angular resolution, high contrast imaging on ELTs will also enable the study of more distant targets, like very young systems in star-forming clouds.
In addition, the development of wide field AO utilizing multiple laser guide stars, delivering 60%–80% Strehl ratios in K on existing 8–10 m class telescopes brings to mind the possibility of coronagraphically increased contrast to enable for instance detection and characterization of quasar host galaxy structure and spectral features, where a typical on-axis quasar luminosity is H > 18, and the angular extent of the quasar's host galaxy is about a second of arc or more, with a total brightness of H > 18–20 (Kukula et al. 2001). This application can tolerate much larger focal plane mask sizes than those required by ExAO systems dedicated to extrasolar planet discovery, and with an APLC, the off-axis PSF is not affected, which helps for extended objects imaging.
The work presented in this paper demonstrates new possibilities enabling coronagraphy on future ELTs, and provides tools to understand and tackle their coronagraphic design specificities.
R.S. is supported by a Michelson Postdoctoral Fellowship, under contract to the Jet Propulsion Laboratory (JPL) funded by NASA. JPL is managed for NASA by the California Institute of Technology and partially supported by an AMNH Kalbfleisch Fellowship. This work is based upon work partially supported by the National Science Fundation: AST-0215793 and AST-0334916 and has also been partially supported by the National Science Foundation Science and Technology Center for Adaptive Optics, managed by the University of California at Santa Cruz under cooperative agreement AST 98-76783.
APPENDIX A: DEFINITION OF GENERALIZED PROLATE SPHEROIDAL FUNCTIONS
We consider an arbitrary pupil aperture  and a finite mask shape
and a finite mask shape  , where the coordinates are given by the vectors
, where the coordinates are given by the vectors  in the pupil plane, and by
in the pupil plane, and by  in the image plane. The real-valued, square integrable function
in the image plane. The real-valued, square integrable function  with a bound support corresponds to the pupil domain
with a bound support corresponds to the pupil domain  .
.
The fractional energy in a finite domain  of the image plane
of the image plane
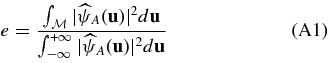
is maximum if  is the eigenfunction of the eigenvalue problem:
is the eigenfunction of the eigenvalue problem:
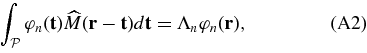
corresponding to the largest eigenvalue Λ = Λ0, and the maximum fractional energy is simply

For any given domains  and
and  , a whole family of these functions
, a whole family of these functions  exit, and they are called generalized prolate spheroidal functions. They form a complete orthogonal basis over
exit, and they are called generalized prolate spheroidal functions. They form a complete orthogonal basis over  , and thus the eigenvalues Λn associated with the functions φn are all distinct. Moreover, they follow the property:
, and thus the eigenvalues Λn associated with the functions φn are all distinct. Moreover, they follow the property:
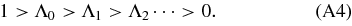
In the application to coronagraphy, we are only interested in the prolate function of order 0,  , since it has the largest eigenvalue (with value close to 1) and thus is the one that will enable the highest rejection (lowest residual energy e). Moreover, as shown for linear and circular geometries (Frieden 1971), zero-order prolates
, since it has the largest eigenvalue (with value close to 1) and thus is the one that will enable the highest rejection (lowest residual energy e). Moreover, as shown for linear and circular geometries (Frieden 1971), zero-order prolates  have the highest throughput, since they are nonzero at the origin. The proof of this result is based on classical manipulation of functional analysis and an elegant presentation can be found in Papoulis (1968).
have the highest throughput, since they are nonzero at the origin. The proof of this result is based on classical manipulation of functional analysis and an elegant presentation can be found in Papoulis (1968).
APPENDIX B: RESIDUAL ENERGY WITH APLCs
We consider a coronagraph with an arbitrary geometry, where the focal plane mask is  and the pupil
and the pupil  , and we consider the zeroth-order prolate apodization
, and we consider the zeroth-order prolate apodization  , corresponding to the eigenvalue Λ0. We define a new mask
, corresponding to the eigenvalue Λ0. We define a new mask 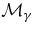 that is a scaled version of
that is a scaled version of  with scaling factor γ. A new eigenvalue problem is therefore defined for
with scaling factor γ. A new eigenvalue problem is therefore defined for  and
and  with optimal solution
with optimal solution  , and Λ0(γ) is a strictly increasing function of γ. In coronagraphic terms, this means that the residual energy e decreases monotonicly with the mask size and that there is therefore no optimum with regard to this criterion. In order to prove this result, we need to prove that for any γ ≠ 1, Λ0(γ) ≠ Λ0. The index function representing the dilated mask can be written as
, and Λ0(γ) is a strictly increasing function of γ. In coronagraphic terms, this means that the residual energy e decreases monotonicly with the mask size and that there is therefore no optimum with regard to this criterion. In order to prove this result, we need to prove that for any γ ≠ 1, Λ0(γ) ≠ Λ0. The index function representing the dilated mask can be written as  . Its Fourier transform is
. Its Fourier transform is  . Without loss of generality, we can consider γ ⩾ 1. The two eigenvalue equations for the domain
. Without loss of generality, we can consider γ ⩾ 1. The two eigenvalue equations for the domain  and both domains
and both domains  and
and  are
are
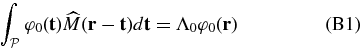
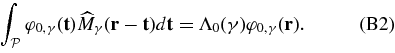
Using an adequate change of variables, Equation (B2) can be rewritten as
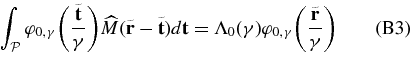
thus  and
and  are eigenfunctions of the same eigenvalue problem, associated with same eigenvalue Λ0. Therefore
are eigenfunctions of the same eigenvalue problem, associated with same eigenvalue Λ0. Therefore  , which is only true if γ = 1.
, which is only true if γ = 1.