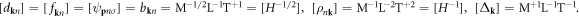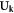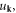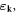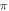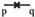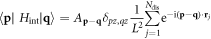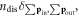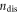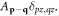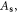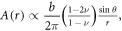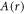Abstract
We provide a comprehensive theoretical framework to study how crystal dislocations influence the functional properties of materials, based on the idea of a quantized dislocation, namely a 'dislon'. In contrast to previous work on dislons which focused on exotic phenomenology, here we focus on their theoretical structure and computational power. We first provide a pedagogical introduction that explains the necessity and benefits of taking the dislon approach and why the dislon Hamiltonian takes its current form. Then, we study the electron–dislocation and phonon–dislocation scattering problems using the dislon formalism. Both the effective electron and phonon theories are derived, from which the role of dislocations on electronic and phononic transport properties is computed. Compared with traditional dislocation scattering studies, which are intrinsically single-particle, low-order perturbation and classical quenched defect in nature, the dislon theory not only allows easy incorporation of quantum many-body effects such as electron correlation, electron–phonon interaction, and higher-order scattering events, but also allows proper consideration of the dislocation's long-range strain field and dynamic aspects on equal footing for arbitrary types of straight-line dislocations. This means that instead of developing individual models for specific dislocation scattering problems, the dislon theory allows for the calculation of electronic structure and electrical transport, thermal transport, optical and superconducting properties, etc, under one unified theory. Furthermore, the dislon theory has another advantage over empirical models in that it requires no fitting parameters. The dislon theory could serve as a major computational tool to understand the role of dislocations on multiple materials' functional properties at an unprecedented level of clarity, and may have wide applications in dislocated energy materials.
Export citation and abstract BibTeX RIS
List of symbols in alphabetical order
| As | Classical electron–dislon scattering amplitude |
| A(k1, k2, k3) | Anharmonic coupling constant |
| bk | Phonon annihilation operator |
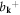
|
Phonon creation operator |
b, 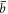
|
Phonon fields in coherent state form |
| b | Burgers vector |
| cijkl | Stiffness tensor |
| ckσ | Electron annihilation operator |
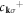
|
Electron creation operator |
| Ck | Lattice specific heat |
| Cs | κ-independent constant for dislon's constraint |
| Cqk | Correlation function of phonon displacement field |
| dk | Annihilation operator of dislon d-field |
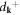
|
Creation operator of dislon d-field |
d, 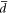
|
Dislon d-fields in coherent state form |
| D | Arbitrary loop enclosing the dislocation line |
| D[] | Functional measure |
| D0nk | Free phonon propagator |
| Dkq | Time-ordered phonon propagator |
| e | Electron charge |
| Ep | Electron single-particle energy |
| En | Eigenenergy of a generic Hamiltonian |
| fk | Annihilation operator of dislon f-field |
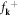
|
Creation operator of dislon f-field |
f, 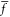
|
Dislon f-field in coherent state form |
| Fk | Generic fermionic operator |
| gk | Electron–dislon coupling constant |
| G | Electron Green's function |
| H | Hamiltonian |
| Ja | ath component of electrical current operator |
| Jnk | Phonon–dislon fluttering coupling constant |
| kTF | Thomas–Fermi screening wavevector |
| k | Crystal momentum |
| K | Thermal conductivity |
| L | Crystal size |
| m | Electron mass |
| mk | Momentum-dependent mass term in dislon Hamiltonian |
| Mk | Coefficient appearing |
| ndis | Dislocation number density |
| nk | Electron number operator |
| nB(F) | Bose (Fermi–Dirac) distribution function |
| n | Normal vector to slip plane |
| N | Number of total atoms in perfectly periodic crystal |
| Ndis | Number of dislocations |
| pk | Canonical momentum of dislon |
| pn | Fermionic Matsubara frequency |
| pph | Canonical momentum of phonon |
| r | Position vector in 2D Cartesian coordinate |
| r0 | Position vector of the dislocation core |
| R | Position vector in 3D Cartesian coordinate |
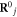
|
Atomic coordinate of jth atom in a perfect crystal |
| S | Action |
| S | Energy flow operator |
| T | Dislocation kinetic energy |
| Tk | Coefficient of dislocation's kinetic energy |
| u | Lattice displacement vector of a dislocation |
| uk | Scalar Fourier component of lattice displacement of a dislocation |
| Uph | lattice displacement of a phonon |
| U | Dislocation potential energy |
| vk | Group velocity |
| Vei | Electron–ion Coulomb potential |
| Veff | Effective electron–dislocation coupling constant |
| Vk | Fourier component of electron–ion potential |

|
Anharmonic coefficient in momentum space |
| Wk | Coefficient of dislocation's potential energy |
| Xk | Operator used to define phonon correlation function |
| Yk | Operator used to define phonon correlation function |
| Z | Partition function |
| Zk | Normalization constant for dislon quantization |
| β | Inverse temperature |
| γ | Linewidth of phonon propagator |
| Γ0 | Free electron current vertex function |
| Γb | Full electron current vertex function, bth component |
| Δk | anharmonicity coefficient |
| ε | Dielectric function |
| εk | Electron single particle energy |
| εk | Polarization vector of phonon (which distinguish the electron energy by context) |
| Θqk | Phonon spectral density function |
| κ | Z-component of momentum |
| λ | Lamé 1st parameter |
| Λk | Phonon–dislon anharmonic coupling constant |
| μ | Lamé 2nd parameter |
| μ | Chemical potential (same symbol with Lamé 2nd parameter but distinguishable by context) |
| ν | Poisson ratio |
| Ξk | Dislon field amplitude coefficient prefactor |
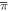 π π |
Momentum component of phonon field |
| ΠR | Retarded current–current correlation function |
| ρ | Mass density |
| ρe | Charge density operator |
| σ | Electrical conductivity |
| Σ | Self-energy |
| τ | Imaginary time |
| τk | Relaxation time |
ϕ 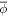
|
Phonon displacement field in coherent state form |
| Φ | Composite operator for phonon anharmonicity study |
ψ 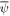
|
Electron fields in coherent state form |
| ωD | Debye frequency |
| ωk | Phonon dispersion relation |
| ωn | Bosonic Matsubara frequency |
| Ωk | dislon dispersion relation |
 |
Lagrangian |
1. Introduction
Dislocations are a common type of line defect in crystalline solids [1]. Since the first theoretical predictions of dislocations in 1934 [2–4] and experimental observations in 1956 [5–7], most dislocation studies have focused on their impacts on materials' mechanical properties, where a pure classical description of dislocations has been proven highly successful [1, 8, 9]. In addition to their influence on mechanical properties, dislocations are also known to affect a number of materials' functional properties such as electronic structure and electrical transport [10–25], thermal transport [26–36], optical properties [37–51], magnetic properties [52–63], and even superconductivity [64–76]. However, in contrast to the well-studied mechanical properties based on the classical dislocation framework, the theoretical studies of functional properties have long been restricted to numerous but scattered empirical dislocation models. In each specific case, a dislocation is modeled as a certain object and often accompanied by empirical parameters in order to fit experimental data. On the other hand, given the rapid development of novel functional materials and exotic condensed matter phases, alongside the advancement of nanoscience and device miniaturization, the interplay between dislocations and the various novel functional properties is simply beyond the grasp of those case-by-case, oversimplified empirical models. For instance, conventional dislocation theory becomes completely helpless if we ask simple questions like 'should dislocations increase or decrease the critical temperature of a dislocated superconductor', 'how do dislocations change magnetic order or optical spectra' or 'can dislocations drive a band insulator into a topological insulator', etc. In this sense, it is unimaginable to develop a separate model for each scenario.
Recently, some of us started to develop a theory based on the quantization of a dislocation and introduced the 'dislon' as the basic quanta of a quantized dislocation for arbitrary types of dislocation lines, including both edge and screw dislocations. Starting from a one-dimensional quantization approach [25, 36, 77], we treated electron [25] and phonon [36] scattering with an individual dislocation, and single electron-interacting dislocation pair scattering [77]. Later, we generalized the one-dimensional approach to a full three-dimensional quantization [76], but focused on the electron–dislocation superconductivity.
In this study, we generalize the dislon theory in 3D to include electron and phonon interactions with multiple dislocations. To demonstrate the possible utility of the dislon theory, we derive expressions for transport properties such as the electron relaxation time of electron–dislon scattering, the electrical conductivity caused by electron–dislocation scattering, and the thermal conductivity caused by phonon–dislocation interaction. The structure of this paper is as follows. In section 2, we provide a heuristic argument for dislons. Sections 3–5 are the full quantization procedure and free dislon theory. Sections 6–8 are the Hamiltonian theories for electron-dislon and phonon–dislon interactions, from which the effective electron and phonon theories after eliminating the dislon degrees of freedom are derived in sections 9–12. A significant portion of sections 6 and 12 has been reported in [76] and is rewritten here in greater detail to keep the study self-contained. In sections 11–15, the electronic and phononic transport properties are derived, followed by discussions, future perspective, and conclusions in sections 16, 17.
2. Heuristic argument
First, we would like to briefly introduce the motivation behind the theory: We plan to develop a unified, microscopic, and quantitative theory of dislocations which can be applied to calculate materials' functional properties. However, one question remains: why does a quantized dislocation approach have to be adopted to fulfill this goal? To see this, we should be aware that all the functional properties—no matter electrical, magnetic, optical, thermoelectric or superconducting properties—are intrinsically quantum properties, and can be well described by quantum many-body theories microscopically. Therefore, a quantum description of dislocations can easily be integrated into the modern many-body formalism, thereby taking full advantage of all theoretical field techniques. This motivates development of the 'dislon'—the quantized dislocation theory.
Despite strong motivation for introducing the idea of a quantized dislocation, what is the justification of the approach? In other words, why is a classical, quenched dislocation approach insufficient? To see this, we need to bear in mind that a dislocation is actually NOT a simple quenched defect. Taking phonons as an example, when a phonon scatters with a dislocation, it is widely accepted that the dominant interaction mechanism is scattering from a vibrating dislocation, called 'fluttering' [29, 31, 32, 78]. In fact, both theories [36, 79] and simulation [80] have shown the existence of resonance of the dislocation–phonon interaction, indicating a similar dynamic energy scale between a phonon and a dislocation which cannot be captured by any static, quenched disorder model. The electron–phonon scattering mechanism [81], together with the dislocation–phonon resonance, indicates the possible role that a dynamic dislocation may also play in electron–dislocation scattering problems.
On the other hand, a quantized dislocation, aka 'dislon', can incorporate both quenched dislocation effects and all the dynamic features on equal footing. Just as phonons are quantized fluctuations around a perfect periodic crystal structure, dislons are also quantized fluctuations around classical quenched dislocations. More rigorously, defining u as the lattice displacement vector (deviation from the equilibrium position), phonons are then cast as quantized propagating vibrational modes by rewriting u in terms of phonon creation and annihilation operators, while dislons are cast as quantized localized modes by writing u in terms of dislon creation and annihilation operators, but further satisfying a dislocation's rigorous definition 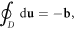 in which b is the Burgers vector and D is an arbitrary loop enclosing the dislocation line. By taking this rigorous definition as the classical limit, all classical effects of dislocations are automatically incorporated, but most importantly, a whole new territory to study the quantum effects of dislocations on materials also unfolds (imagine the huge difference between a classical elastic wave and a quantized phonon).
in which b is the Burgers vector and D is an arbitrary loop enclosing the dislocation line. By taking this rigorous definition as the classical limit, all classical effects of dislocations are automatically incorporated, but most importantly, a whole new territory to study the quantum effects of dislocations on materials also unfolds (imagine the huge difference between a classical elastic wave and a quantized phonon).
Prior to the formal derivation, we briefly argue the existence of a certain form of excitation beyond phonon excitation in a dislocated crystal from the perspective of eigenmode conservation. Assuming a perfect periodic solid containing N atoms, which has 3N eigenmodes labeled by 3N good quantum numbers called crystal momentum k. Assume the Debye frequency in this solid is 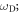 then, for a solid with 1 atom per unit cell in which only acoustic phonons exist, the Debye model tells us that [82]
then, for a solid with 1 atom per unit cell in which only acoustic phonons exist, the Debye model tells us that [82]
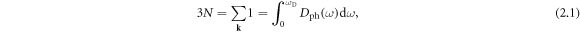
where 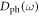 is the phonon density of states, which can be written as
is the phonon density of states, which can be written as
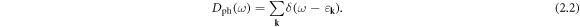
For a simple acoustic phonon,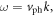 where
where 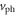 is speed of the acoustic phonon, and it can be shown directly that
is speed of the acoustic phonon, and it can be shown directly that 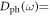
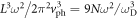 is valid, where L is the sample size.
is valid, where L is the sample size.
Now with dislocations present, crystal momenta k are no longer rigorously good quantum numbers, indicating a reduction in the phonon density of states 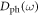 which represents the portion of extended, propagating eigenmodes which in general preserve translational symmetry. However, the total number of modes should still be conserved, giving
which represents the portion of extended, propagating eigenmodes which in general preserve translational symmetry. However, the total number of modes should still be conserved, giving
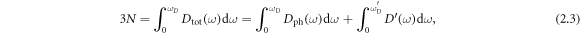
where an excess density of states 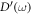 emerges to compensate the reduction of
emerges to compensate the reduction of 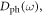 and can be intuitively treated as some localized modes. Despite the lack of a simple way to directly separate the
and can be intuitively treated as some localized modes. Despite the lack of a simple way to directly separate the 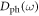 from
from  in the case of a dislocated crystal, the appearance of
in the case of a dislocated crystal, the appearance of 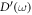 can be regarded as a result of translational symmetry breaking and the formation of local modes, which gives a qualitative, heuristic rationale for the possible existence of a 'dislon' excitation.
can be regarded as a result of translational symmetry breaking and the formation of local modes, which gives a qualitative, heuristic rationale for the possible existence of a 'dislon' excitation.
With this intuitive understanding in hand, we now formally introduce the dislon theory.
3. The theoretical foundation
First, we define the 3D Cartesian coordinate  Assuming a dislocation line is extending along the z-direction, we also define the 2D coordinate
Assuming a dislocation line is extending along the z-direction, we also define the 2D coordinate 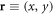 and assume the dislocation core is located at
and assume the dislocation core is located at 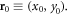
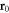 is a 2D vector since a dislocation is a line defect. For a single dislocation line, we define
is a 2D vector since a dislocation is a line defect. For a single dislocation line, we define 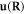 as the lattice displacement field at the spatial position
as the lattice displacement field at the spatial position 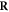 caused by the dislocation with dislocation core location
caused by the dislocation with dislocation core location 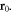 We further define the 3D momentum coordinate k =
We further define the 3D momentum coordinate k = 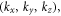 2D momentum
2D momentum 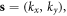 and crystal size as L. We separate x and y from the z direction by defining
and crystal size as L. We separate x and y from the z direction by defining  to emphasize the special direction along the dislocation line direction (hence
to emphasize the special direction along the dislocation line direction (hence 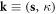 ). The displacement field
). The displacement field 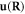 can be written as a generic form of mode expansion by a generic mode
can be written as a generic form of mode expansion by a generic mode 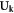 (the
(the 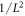 prefactor is for later convenience)
prefactor is for later convenience)
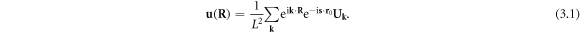
Under the static, or equivalently the long-wavelength limit, equation (3.1) should reduce to the displacement field of a classical quenched dislocation.
To see how a quenched dislocation satisfying the definition 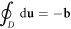 can be recovered from equation (3.1), we compare the displacement of a dislocation with that of a phonon. The phonon displacement field
can be recovered from equation (3.1), we compare the displacement of a dislocation with that of a phonon. The phonon displacement field 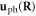 can be written as a mode expansion using a plane wave basis as [83]
can be written as a mode expansion using a plane wave basis as [83]
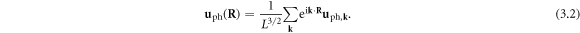
Under the static limit, there is no displacement for an acoustic phonon, i.e. 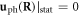 (perfect periodic lattice), where '
(perfect periodic lattice), where '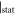 ' means taking a static, long-wavelength limit. In the momentum space representation, this static condition can be denoted as
' means taking a static, long-wavelength limit. In the momentum space representation, this static condition can be denoted as 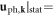
 Since the right-hand side is 0 and is independent of k, we can consider the static limit as a long-wavelength
Since the right-hand side is 0 and is independent of k, we can consider the static limit as a long-wavelength 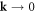 limit. This gives a mathematical expression for the static limit of an acoustic phonon:
limit. This gives a mathematical expression for the static limit of an acoustic phonon: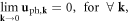 which can be regarded as a boundary condition. Since this boundary condition is trivial, it is usually overlooked in phonon studies.
which can be regarded as a boundary condition. Since this boundary condition is trivial, it is usually overlooked in phonon studies.
When a dislocation is present, the displacement field still exists under the static limit, since even a classical dislocation without any fluctuations can still create lattice displacement. Thus, this quenched classical static dislocation 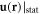 can also be mode-expanded using a 2D wavevector s as
can also be mode-expanded using a 2D wavevector s as
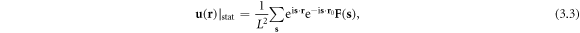
where 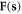 can be interpreted as a non-plane-wave expansion coefficient to be discussed shortly. In this situation, the constraint of a dislocation's expansion mode
can be interpreted as a non-plane-wave expansion coefficient to be discussed shortly. In this situation, the constraint of a dislocation's expansion mode 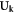 under the static limit in equation (3.1) is clear. As in the phonon case,
under the static limit in equation (3.1) is clear. As in the phonon case, 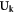 can be defined in a similar way using the inverse Fourier transform as a constraint, whereby
can be defined in a similar way using the inverse Fourier transform as a constraint, whereby
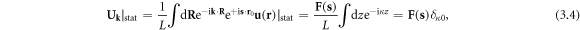
where the right-hand side is now independent of the z-component momentum  but still a function of s (keep in mind
but still a function of s (keep in mind 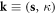 ). This shows that in the displacement field with a dislocation, the static limit is not
). This shows that in the displacement field with a dislocation, the static limit is not 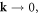 but involves only the z-component of momentum, i.e. the
but involves only the z-component of momentum, i.e. the  limit. Thus, the constraint which allows the reduction to a classical quenched dislocation can be written as
limit. Thus, the constraint which allows the reduction to a classical quenched dislocation can be written as
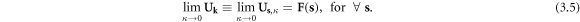
At this moment, we should bear in mind that 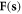 is still a function of s and it should satisfy the dislocation's definition
is still a function of s and it should satisfy the dislocation's definition 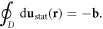 A valid form of
A valid form of 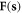 satisfying the definition is provided later in this section.
satisfying the definition is provided later in this section.
Up to this point, the entire derivation is valid for a generic vector displacement 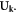 To further simplify, we define a generic scalar displacement component
To further simplify, we define a generic scalar displacement component 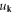 as
as
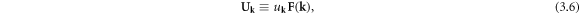
where 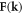 is an undetermined 3D function generalized from
is an undetermined 3D function generalized from 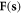 by satisfying
by satisfying 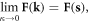 aka
aka 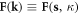 and
and 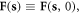 then we have
then we have
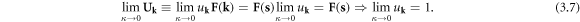
The procedure to introduce the scalar displacement  can also be understood from a comparison with phonons. For phonons, there is no need to separately quantize the three components of the displacement vector
can also be understood from a comparison with phonons. For phonons, there is no need to separately quantize the three components of the displacement vector  since the phonon displacement field satisfies
since the phonon displacement field satisfies  where
where 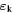 is the polarization vector obtained by solving a purely classical lattice wave equation. Here, the fact that
is the polarization vector obtained by solving a purely classical lattice wave equation. Here, the fact that 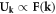 indicates that the three vector components of a dislocation are also linked through the function
indicates that the three vector components of a dislocation are also linked through the function 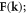 the
the 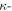 dependence of displacement indicates the existence of wave propagation along the dislocation line direction, from which the dynamic vibration can be taken into account. Therefore, to quantize a dislocation while considering the dynamic aspects, there are two generic approaches:
dependence of displacement indicates the existence of wave propagation along the dislocation line direction, from which the dynamic vibration can be taken into account. Therefore, to quantize a dislocation while considering the dynamic aspects, there are two generic approaches:
- (1)Quantize the vector Fourier component of lattice displacement
 directly, which is an approach of vector-field quantization. A quantization of a vector field has an analog with photon quantization, which is a gauge theory [84], and the quantization procedure may be related to the classical affine gauge field of dislocations [85].
directly, which is an approach of vector-field quantization. A quantization of a vector field has an analog with photon quantization, which is a gauge theory [84], and the quantization procedure may be related to the classical affine gauge field of dislocations [85]. - (2)Quantize the scalar Fourier component of lattice displacement
 defined through
defined through  which is much simpler. This is also similar to the phonon quantization, where the quantum fluctuation (dynamic effect) along each direction is assumed to be proportional to
which is much simpler. This is also similar to the phonon quantization, where the quantum fluctuation (dynamic effect) along each direction is assumed to be proportional to  the classical eigenvectors of the dynamic matrix. If we see approach (1) as a full gauge theory like quantum electrodynamics (QED), then the approach (2) is like a scalar QED [84], with much simpler structure but still retaining most of the quantum properties.
the classical eigenvectors of the dynamic matrix. If we see approach (1) as a full gauge theory like quantum electrodynamics (QED), then the approach (2) is like a scalar QED [84], with much simpler structure but still retaining most of the quantum properties.
Therefore, as long as we admit the way in which a phonon is quantized, we could consider equation (3.7) a valid and reasonable assumption. The lattice displacement field caused by a generic dislocation 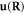 can be written as
can be written as
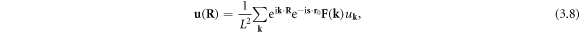
where 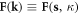 indicates a non-plane-wave mode expansion coefficient, which satisfies
indicates a non-plane-wave mode expansion coefficient, which satisfies
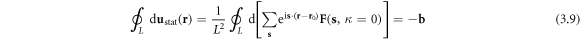
while the scalar mode 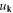 satisfies
satisfies
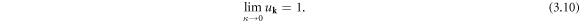
Equations (3.8)–(3.10) are the basis for a general dislocation theory from mode expansion perspective, prior to any quantization.
At this step, the distinctions between an acoustic phonon expanded from plane waves and a dislocation expanded from localized modes become clear, as summarized in table 1.
Table 1. Comparison between a phonon and a dislocation.
| Phonon | Dislocation | |
|---|---|---|
| Modes | Plane wave | Localized wave |
| Mode expansion | Equation (3.2) | Equation (3.3) |
| Static limit: expression |
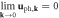
|
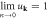
|
| Static limit: interpretation | Perfect periodic solids | Quenched dislocation |
Before proceeding to a specific type of dislocation, one may be wondering the underlying difference between vector quantization (1) and scalar quantization (2), and whether quantization of a dislocation loop is possible. Briefly speaking, approach (1) will maintain the gauge symmetry of a dislocation [85], i.e. it is a genuine topological defect which cannot be canceled by local operations. For approach (2), the gauge symmetry is broken (just as a scalar QED breaks photon gauge symmetry [84]), but the displacement field remains finite with dynamic effects retained. Since we are mostly interested in short time scale (∼ps) quantum emergent phenomena driven by electron–dislocation and phonon–dislocation interactions, the fate of a dislocation (much longer ∼s time scale) is not of concern, validating the approach (2). On the other hand, the quantization of a dislocation loop is possible in theory, which might resemble a quantized closed string in string theory [86]. Yet in practice, this will inevitably cause great mathematical complexity. Therefore, in this study, we only focus on scalar quantization of a straight dislocation line, which retains the mathematical elegancy and can be used to study a wide range of quantum effects associated with dislocations.
Up to now, all the steps are quite generic, without assuming any particular form of 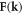 except for the dislocation's definition in equation (3.9). For a particular dislocation with Burgers vector b and slip plane normal n within the xz plane (figure 1), one choice of expansion coefficient
except for the dislocation's definition in equation (3.9). For a particular dislocation with Burgers vector b and slip plane normal n within the xz plane (figure 1), one choice of expansion coefficient 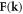 can be written as [29, 76, 87]
can be written as [29, 76, 87]
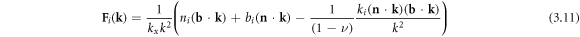
in which i = x, y, z are the indices of Cartesian direction, ν is the Poisson ratio. With this choice, it can be directly verified that the corresponding 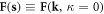 satisfies equation (3.9) [76]. For instance, for a screw dislocation line, we have
satisfies equation (3.9) [76]. For instance, for a screw dislocation line, we have 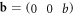 and
and  giving
giving 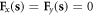 and
and 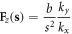 in the static limit, and resulting in
in the static limit, and resulting in 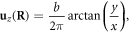 which is exactly the classical textbook result of the displacement field of a screw dislocation [1].
which is exactly the classical textbook result of the displacement field of a screw dislocation [1].
Figure 1. The coordinate system used for this study. The golden line along the z-direction is the dislocation line direction, and the slip plane is the xz plane. Since a dislocation is a line defect, the momentum component along the dislocation line is highlighted with a different label 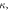 which shows later convenience.
which shows later convenience.
Download figure:
Standard image High-resolution imageThe equations (3.8)–(3.10) serve as the basis for the generality of the theory: by assuming different forms of 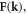 the theory can be used to describe dislocations in anisotropic materials; by assuming different boundary conditions of the expansion coefficient, it can even be used to describe different types of localized defects. To proceed, in section 4, by rewriting
the theory can be used to describe dislocations in anisotropic materials; by assuming different boundary conditions of the expansion coefficient, it can even be used to describe different types of localized defects. To proceed, in section 4, by rewriting 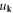 in terms of quantized operators, a quantized displacement of dislocation can be obtained.
in terms of quantized operators, a quantized displacement of dislocation can be obtained.
4. The quantization procedure of dislocations
To proceed toward a quantized theory, we need to define a canonical coordinate and its conjugate momentum [81]. Apparently, 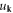 appearing in equation (3.8) seems to be a natural choice of the canonical coordinate. Here, we provide a more general proof of the uniqueness of quantization: putting any prefactor
appearing in equation (3.8) seems to be a natural choice of the canonical coordinate. Here, we provide a more general proof of the uniqueness of quantization: putting any prefactor 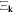 in front of
in front of 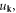 and defining the canonical coordinate as
and defining the canonical coordinate as 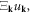 in the end, it still leads to the same way of quantization.
in the end, it still leads to the same way of quantization.
To see this, we first notice that the classical dislocation's Hamiltonian 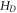 containing both kinetic energy
containing both kinetic energy 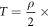
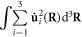 and potential energy
and potential energy 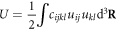 can be written as
can be written as
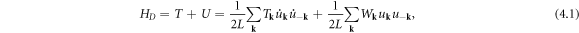
where 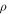 is the mass density and
is the mass density and 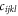 is the stiffness tensor. In an isotropic material,
is the stiffness tensor. In an isotropic material, 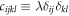 +
+ 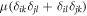 with
with 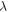 and
and 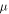 called Lamé parameters. Furthermore
called Lamé parameters. Furthermore 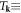
 and Wk ≡
and Wk ≡ ![$(\lambda +\mu ){[{\bf{k}}\cdot {\bf{F}}({\bf{k}})]}^{2}+\mu {k}^{2}{| F({\bf{k}})| }^{2},$](https://content.cld.iop.org/journals/1367-2630/20/2/023010/revision2/njpaaa383ieqn109.gif) which can be seen by substituting the
which can be seen by substituting the 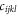 into the classical Hamiltonian.
into the classical Hamiltonian.
The canonical momentum conjugate to the canonical coordinate 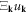 can be defined as
can be defined as 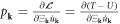 =
=  where
where  = T−U is the Lagrangian, then equation (4.1) can be rewritten in terms of the canonical coordinate
= T−U is the Lagrangian, then equation (4.1) can be rewritten in terms of the canonical coordinate 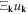 and its conjugate momentum
and its conjugate momentum 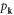 as
as
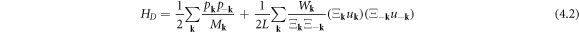
in which 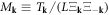 plays the role of 'mass' in the dislocation's Hamiltonian. As in the case of phonon quantization, now the canonical creation and annihilation operators are defined as
plays the role of 'mass' in the dislocation's Hamiltonian. As in the case of phonon quantization, now the canonical creation and annihilation operators are defined as
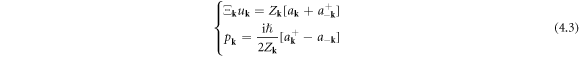
with 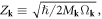
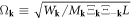
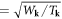
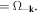 Then we have
Then we have 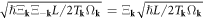
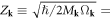
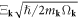 (where we have assumed
(where we have assumed 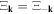 and further defined
and further defined 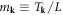 ), and have
), and have 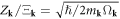 valid in all circumstances. Now we can see that no matter what
valid in all circumstances. Now we can see that no matter what 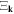 we choose, we obtain a unique quantization, since a consistent quantization is only a function of the ratio
we choose, we obtain a unique quantization, since a consistent quantization is only a function of the ratio 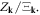 In this situation, for simplicity we can choose
In this situation, for simplicity we can choose  Therefore, the displacement field caused by a dislocation equation (3.8) can finally be written as in quantized form as
Therefore, the displacement field caused by a dislocation equation (3.8) can finally be written as in quantized form as
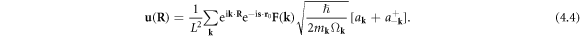
To proceed, we may need to understand the algebraic relation of operators 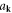 and
and 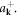 A natural choice would be the usual Bosonic commutation
A natural choice would be the usual Bosonic commutation ![$[{a}_{{\bf{k}}},{a}_{{\bf{k}}^{\prime} }^{+}]={\delta }_{{\bf{k}}{\bf{k}}^{\prime} };$](https://content.cld.iop.org/journals/1367-2630/20/2/023010/revision2/njpaaa383ieqn132.gif) however, we need to bear in mind that any algebraic relation needs to meet the constraint in equation (3.10), which indicates that
however, we need to bear in mind that any algebraic relation needs to meet the constraint in equation (3.10), which indicates that ![$\mathop{\mathrm{lim}}\limits_{\kappa \to 0}{u}_{{\bf{k}}}=\mathop{\mathrm{lim}}\limits_{\kappa \to 0}{Z}_{{\bf{k}}}[{a}_{{\bf{k}}}+{a}_{-{\bf{k}}}^{+}]=1\Rightarrow \mathop{\mathrm{lim}}\limits_{\kappa \to 0}[{a}_{{\bf{k}}}+{a}_{-{\bf{k}}}^{+}]=\tfrac{1}{{Z}_{{\bf{k}}}}.$](https://content.cld.iop.org/journals/1367-2630/20/2/023010/revision2/njpaaa383ieqn133.gif) Therefore, if Bosonic commutation relation
Therefore, if Bosonic commutation relation ![$[{a}_{{\bf{k}}},{a}_{{\bf{k}}^{\prime} }^{+}]={\delta }_{{\bf{k}}{\bf{k}}^{\prime} }$](https://content.cld.iop.org/journals/1367-2630/20/2/023010/revision2/njpaaa383ieqn134.gif) is valid, then we have
is valid, then we have
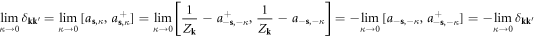
which leads to immediate inconsistency. Therefore, the dislocation's constraint (3.10) leads to a breakdown of the canonical quantization condition.
The breakdown of the canonical commutation relation is not a catastrophe, but can occur in a system with constraints [88]. As a simple example discussed in [89], usual canonical quantization gives ![$[x,{p}_{x}]={\rm{i}}\hslash $](https://content.cld.iop.org/journals/1367-2630/20/2/023010/revision2/njpaaa383ieqn135.gif) and
and ![$[y,{p}_{x}]=0,$](https://content.cld.iop.org/journals/1367-2630/20/2/023010/revision2/njpaaa383ieqn136.gif) which leads to immediate inconsistency if a particle's motion is restricted to a line
which leads to immediate inconsistency if a particle's motion is restricted to a line 
5. The dislon Hamiltonian
To proceed further, instead of using a canonical quantization condition, we define an alternative quantization condition as
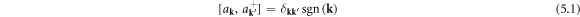
in which 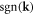 is a vector sign function satisfying
is a vector sign function satisfying 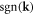
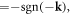 which is elaborated in appendix A.
which is elaborated in appendix A.
Now we can show directly that the operators 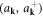 are consistent with constraint equation (3.10):
are consistent with constraint equation (3.10):
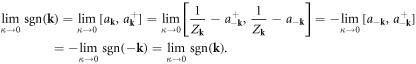
It is worth mentioning that the commutation relation equation (5.1) is not the only way leading to quantization—any odd function 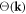 satisfying
satisfying 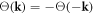 on the right hand side of equation (5.1) will be consistent with the constraint equation (3.10). However, we can also always absorb
on the right hand side of equation (5.1) will be consistent with the constraint equation (3.10). However, we can also always absorb  into the normalization factor to rescale operators
into the normalization factor to rescale operators 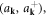 since the final Hamiltonian should not depend on the choice of
since the final Hamiltonian should not depend on the choice of 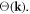 The choice of equation (5.1) can then be considered as the simplest choice with a clear physical interpretation as two conventional Bosonic fields, as discussed shortly in equation (5.6).
The choice of equation (5.1) can then be considered as the simplest choice with a clear physical interpretation as two conventional Bosonic fields, as discussed shortly in equation (5.6).
Now substituting equation (5.1) back into the classical dislocation's Hamiltonian equation (4.1), the dislon Hamiltonian in 3D can be written as
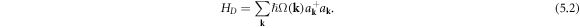
To further simplify the quantized dislocation's Hamiltonian equation (5.2), we adopt the concept of a supersymmetric Boson sea to reduce it to a more familiar form [90, 91]. Defining 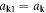 when
when 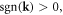
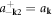 when
when 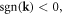 we have
we have 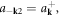 thus the operators
thus the operators 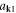 and
and 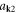 satisfy normal Boson canonical commutation relation
satisfy normal Boson canonical commutation relation ![$[{a}_{{\bf{k}}2},{a}_{{\bf{k}}^{\prime} 2}^{+}]={\delta }_{{\bf{k}}{\bf{k}}^{\prime} }.$](https://content.cld.iop.org/journals/1367-2630/20/2/023010/revision2/njpaaa383ieqn154.gif) The dislon Hamiltonian equation (5.2) can be rewritten as
The dislon Hamiltonian equation (5.2) can be rewritten as
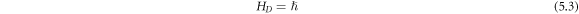
in which the  is the shorthand notation of
is the shorthand notation of 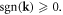
In addition, the boundary condition of  in equation (3.10) is greatly simplified as
in equation (3.10) is greatly simplified as
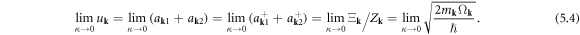
Now performing Keldysh rotation by defining a new set of operators as
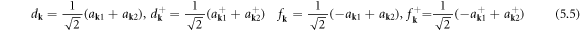
the dislon Hamiltonian equation (5.3) can then be rewritten as
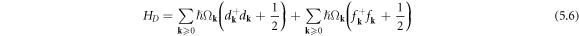
while the dislon's boundary condition equation (5.4) can be rewritten as
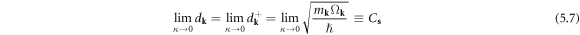
where  is a
is a 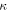 -independent constant.
-independent constant.
With this dislon Hamiltonian equation (5.6) and boundary condition equation (5.7) in hand, the non-interacting dislon theory in an isotropic medium is complete. In other words: a dislon is composed of two independent Bosonic fields, d-field and f-field, with only the d-field constrained by equation (5.7), which can be traced to the topological definition of a dislocation.
6. The Hamiltonian for electron-dislon interaction
For the electron–dislon interaction, we note that electron density will scatter with the charge imbalance caused by lattice displacement. A generic electron–ion interaction can be written in terms of deformation potential scattering as [81]
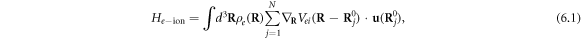
where the summation over j is over N atoms in the solids, 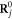 is the atomic coordinate for the jth atom in a perfect crystal, and the electron–ion Coulomb potential can be expanded as
is the atomic coordinate for the jth atom in a perfect crystal, and the electron–ion Coulomb potential can be expanded as 
 with Fourier component
with Fourier component  (
(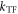 is Thomas–Fermi screening), and the charge density operator gives
is Thomas–Fermi screening), and the charge density operator gives 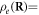
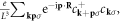 where
where 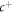 and c are the electron creation and annihilation operators, respectively.
and c are the electron creation and annihilation operators, respectively.
For the specific case of the displacement field caused by the dislocation, we could substitute equation (4.4) and the Coulomb potential expansion into equation (6.1), where we first obtain
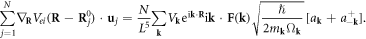
Then, using equation (5.5), the classical Hamiltonian equation (6.1) for an electron scattering from a single dislocation with core located at  can then be rewritten in a quantized way as
can then be rewritten in a quantized way as
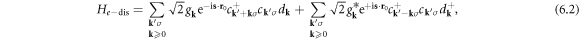
where the electron–dislon coupling constant gives 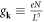
![$\times \,{V}_{{\bf{k}}}[{\rm{i}}{\bf{k}}\cdot {\bf{F}}({\bf{k}})]\sqrt{\tfrac{\hslash }{2{m}_{{\bf{k}}}{{\rm{\Omega }}}_{{\bf{k}}}}}={g}_{-{\bf{k}}}^{* }.$](https://content.cld.iop.org/journals/1367-2630/20/2/023010/revision2/njpaaa383ieqn170.gif) Here we see that the deformation potential scattering only couples with the displacement-like d-field of a dislon, but not momentum-like f-field.
Here we see that the deformation potential scattering only couples with the displacement-like d-field of a dislon, but not momentum-like f-field.
Up to this step, we have only treated one single dislocation line. To generalize to multiple dislocations, we can assume a set of dislocation core locations 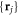 and sum over all dislocations,; however, later it can be shown that it would be much more convenient if we add multiple dislocations in effective theories, instead of adding into the interaction at this moment.
and sum over all dislocations,; however, later it can be shown that it would be much more convenient if we add multiple dislocations in effective theories, instead of adding into the interaction at this moment.
7. The phonon–dislon fluttering
Other than the case for electron-dislon scattering, which is intrinsically deformation potential scattering as shown in equation (6.2), the dominant interaction for phonon–dislon interaction is the so-called fluttering mechanism, which is a drag-like scattering coupling the first-order time-derivative of the phonon and the dislocation displacement field [29, 32, 87]. Previously we derived the phonon–dislocation fluttering mechanism using 1D dislocation quantization [36]; here we present a full 3D quantization approach. As a brief review of phonon quantization, the lattice displacement of a phonon 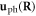 with a single phonon mode can be written as [83]
with a single phonon mode can be written as [83]
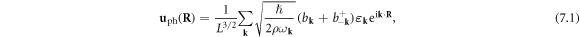
where 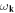 is the phonon dispersion, L3 is the system volume, and
is the phonon dispersion, L3 is the system volume, and 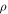 is the mass density. The hermiticity of
is the mass density. The hermiticity of 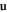 requires that the polarization vector satisfies
requires that the polarization vector satisfies 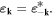
Now defining the canonical conjugate momentum density as 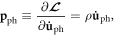 we have
we have
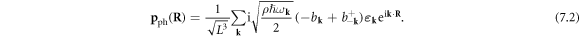
Now if we further define the displacement and momentum operators in Fourier transformed space
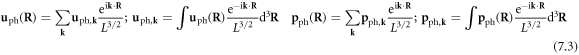
then we have
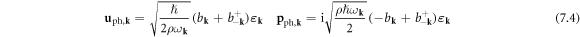
which satisfy  and
and 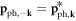 .
.
The phonon Hamiltonian can be written as
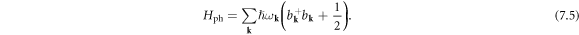
The phonon–dislocation interaction Hamiltonian is given by the following expression, called a fluttering mechanism, which is the cross term between the phonon 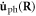 and dislon
and dislon 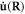 appearing in the kinetic energy T. Since
appearing in the kinetic energy T. Since  and
and 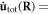
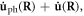 we have [29, 87]
we have [29, 87]
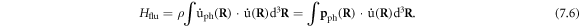
Now substituting equation (7.1) and equation (4.3) back into equation (7.6), using the fact that ![${p}_{{\bf{k}}}=\tfrac{{\rm{i}}}{{{\rm{\Xi }}}_{{\bf{k}}}}\sqrt{\tfrac{\hslash {m}_{{\bf{k}}}{{\rm{\Omega }}}_{{\bf{k}}}}{2}}[{a}_{{\bf{k}}}^{+}-{a}_{-{\bf{k}}}]$](https://content.cld.iop.org/journals/1367-2630/20/2/023010/revision2/njpaaa383ieqn185.gif)
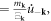 and recalling equation (5.5), we finally obtain the quantized phonon–dislon fluttering Hamiltonian as
and recalling equation (5.5), we finally obtain the quantized phonon–dislon fluttering Hamiltonian as
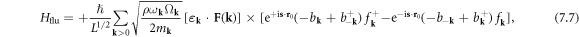
where we have used the facts that 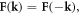
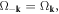
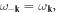 and
and 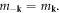
In other words, we have reached a nontrivial conclusion about the dislon: the non-interacting dislon theory equation (5.6) is composed of two independent fields d and f, where the coupling with an electron is through the displacement-like d-field with constraint equation (5.7), while the coupling with a phonon through fluttering is through the momentum-like f-field without constraint. Such decoupling shows great advantage when constructing an effective theory.
8. Phonon–dislon anharmonicity
Given the importance of anharmonic interactions to thermal transport, in this section, we derive a framework to study how the phonon–dislon anharmonic interaction may change the phonon properties. We notice that the integral of the cross term of strain energy 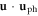 is zero according to classical theory [29, 87, 92]. Therefore, we only need to consider the 3rd order anharmonic term. The generic third order anharmonic interaction of the displacement field can be written as [93]
is zero according to classical theory [29, 87, 92]. Therefore, we only need to consider the 3rd order anharmonic term. The generic third order anharmonic interaction of the displacement field can be written as [93]
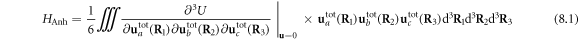
in which 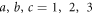 are the Cartesian coordinate components, and Einstein's summation convention has been adopted.
are the Cartesian coordinate components, and Einstein's summation convention has been adopted.
Now we note that the total displacement 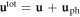 is a sum over both the phonon contribution
is a sum over both the phonon contribution 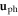 and dislocation contribution
and dislocation contribution 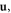 enabling us to re-arrange equation (8.1) according to the order of the dislocation's displacement
enabling us to re-arrange equation (8.1) according to the order of the dislocation's displacement 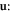
0th order in 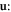
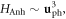 which gives the usual 3rd order three-phonon anharmonicity but does not involve any interaction with the dislon, hence will not be considered.
which gives the usual 3rd order three-phonon anharmonicity but does not involve any interaction with the dislon, hence will not be considered.
1st order in 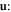
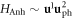 which gives the scenario that one incoming phonon interacts with one dislon and the phonon gets scattered. This is the most commonly encountered scenario given the high phonon density of states.
which gives the scenario that one incoming phonon interacts with one dislon and the phonon gets scattered. This is the most commonly encountered scenario given the high phonon density of states.
2nd order in 
 which gives the scenario that one dislon interacts with a phonon and gets scattered, which happens much less frequently since the dislon density of states is much lower. For this reason, we will not consider this scenario either.
which gives the scenario that one dislon interacts with a phonon and gets scattered, which happens much less frequently since the dislon density of states is much lower. For this reason, we will not consider this scenario either.
3rd order in 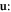
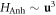 which is not only very rare (one dislon is split into two or vice versa) but also does not involve any interaction with phonons. We will not consider this scenario either.
which is not only very rare (one dislon is split into two or vice versa) but also does not involve any interaction with phonons. We will not consider this scenario either.
In this sense, the only interaction term of interest is thus the 1st order in 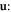
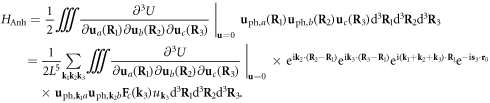
Since we are considering a translationally invariant system (large size of solid), the choice of origin does not matter (i.e. independent of 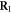 ), but only the relative distance between two spatial points matters (i.e.
), but only the relative distance between two spatial points matters (i.e.  and
and  ), hence we could define the coefficient
), hence we could define the coefficient 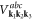 as
as
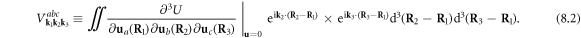
This enables the integration over R1 independently. Therefore, the anharmonic phonon–dislon interaction Hamiltonian can further be rewritten as
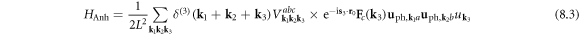
in which 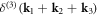 is a discrete Kronecker-delta function.
is a discrete Kronecker-delta function.
Substituting equations (7.4) and (4.3) into (8.3), we obtain the quantized phonon–dislon anharmonic interaction Hamiltonian
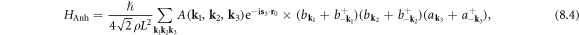
where 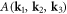 is the anharmonic phonon–dislon coupling strength, which is defined as
is the anharmonic phonon–dislon coupling strength, which is defined as
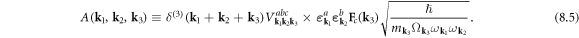
Now using equation (5.5), we rewrite equation (8.4) as
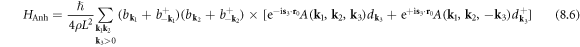
which concludes the anharmonic phonon–dislon interaction Hamiltonian.
9. Action forms of the electron–phonon–dislon interacting system
The constraint on the dislon's d-field equation (5.7) causes great technical difficulties in using a canonical operator approach. To solve a system with constrained dynamics and highlight the influence of a dislon on purely electronic or phononic degrees of freedom, a functional integral approach is adopted [88]. The first step is to rewrite all the Hamiltonians above into action form.
The transformation of Fermion (F) and Boson (B) operators between imaginary time and Matsubara frequency can be written as [81]
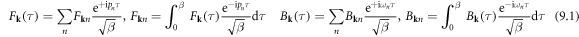
in which 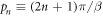 and
and 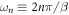 are the Fermionic and Bosonic Matsubara frequency, respectively, and
are the Fermionic and Bosonic Matsubara frequency, respectively, and 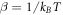 is the inverse temperature.
is the inverse temperature.
The non-interacting dislon Hamiltonian equation (5.6) can be rewritten in terms of action form in the Matsubara frequency domain as
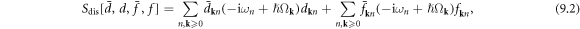
where 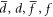 are the dislon fields written in coherent state form and n = 0, ±1, ±2.... are the Matsubara indices.
are the dislon fields written in coherent state form and n = 0, ±1, ±2.... are the Matsubara indices.
The electron action written in the functional integral form can be written as
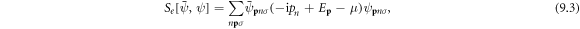
where 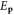 is the electron single-particle energy, μ is the chemical potential, and
is the electron single-particle energy, μ is the chemical potential, and 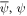 are the electron fields.
are the electron fields.
Now defining momentum-space charge density as 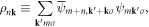 the electron–dislon interaction Hamiltonian equation (6.2) can be rewritten as an action form
the electron–dislon interaction Hamiltonian equation (6.2) can be rewritten as an action form
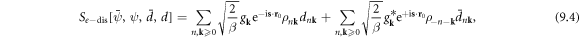
where ![${g}_{{\bf{k}}}\equiv \displaystyle \frac{eN}{{L}^{5}}{V}_{{\bf{k}}}[{\rm{i}}{\bf{k}}\cdot {\bf{F}}({\bf{k}})]\sqrt{\displaystyle \frac{\hslash }{2{m}_{{\bf{k}}}{{\rm{\Omega }}}_{{\bf{k}}}}}={g}_{-{\bf{k}}}^{* },$](https://content.cld.iop.org/journals/1367-2630/20/2/023010/revision2/njpaaa383ieqn219.gif) and boundary condition equation (5.7) is now rewritten from a canonical operator to a coherent state in the Matsubara frequency domain as
and boundary condition equation (5.7) is now rewritten from a canonical operator to a coherent state in the Matsubara frequency domain as
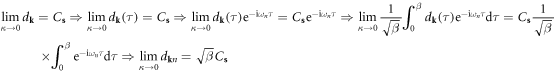
from which we have
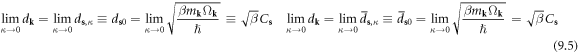
where 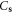 is an s-dependent constant defined in equation (5.7), and
is an s-dependent constant defined in equation (5.7), and 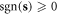 (appendix A).
(appendix A).
The phonon action can be written into action form as
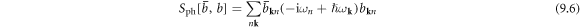
in which  is the phonon field written in Bosonic coherent state form, and
is the phonon field written in Bosonic coherent state form, and 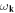 is the phonon dispersion relation. The phonon–dislon fluttering interaction Hamiltonian equation (7.7) can be rewritten in terms of action form as
is the phonon dispersion relation. The phonon–dislon fluttering interaction Hamiltonian equation (7.7) can be rewritten in terms of action form as
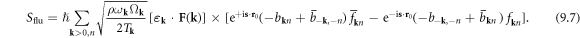
Now we rewrite the anharmonic Hamiltonian equation (8.6) into action form in imaginary time directly as
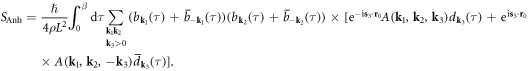
Now using the Keldysh rotated field defined in equation (11.3), i.e. 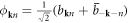 which has the physical meaning of a phonon displacement field, and using equation (9.1), we obtain the anharmonic phonon–dislon action in the Matsubara frequency domain as
which has the physical meaning of a phonon displacement field, and using equation (9.1), we obtain the anharmonic phonon–dislon action in the Matsubara frequency domain as
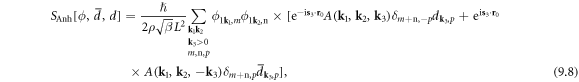
where the summation m, n, p is over the Bosonic Matsubara frequency.
With equations (9.2)–(9.8) in hand, we are ready to derive the electron and phonon effective theories when they start to interact with a dislon.
10. Effective electron theory
Taking into account the constraint equation (9.5), we define an effective action of the electron ![${{\rm{S}}}_{{\rm{e}}{\rm{f}}{\rm{f}}}[\bar{\psi },\psi ]$](https://content.cld.iop.org/journals/1367-2630/20/2/023010/revision2/njpaaa383ieqn225.gif) by integrating over the dislon degrees of freedom as
by integrating over the dislon degrees of freedom as
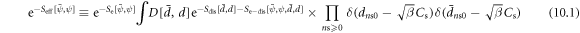
in which ![${S}_{D}[\bar{d},d]=\displaystyle \sum _{n,{\bf{k}}\geqslant 0}{\bar{d}}_{{\bf{k}}n}(-{\rm{i}}{\omega }_{n}+\hslash {{\rm{\Omega }}}_{{\bf{k}}}){d}_{{\bf{k}}n}$](https://content.cld.iop.org/journals/1367-2630/20/2/023010/revision2/njpaaa383ieqn226.gif) is the d-field portion of the dislon field, since only the d-field of the dislon couples with electrons.
is the d-field portion of the dislon field, since only the d-field of the dislon couples with electrons.
The method of imposing the constraint of equation (9.5) onto equation (10.1) is to introduce a Dirac δ-function, which is similar to the gauge-fixing method used in the Faddeev–Popov ghost [94], or to the length-fixing method in the nonlinear sigma model [95], while here it is fixing the dislon boundary condition instead of gauge fixing or length fixing.
Performing the Fourier transform so that 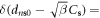
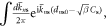 equation (10.1) can be rewritten as
equation (10.1) can be rewritten as
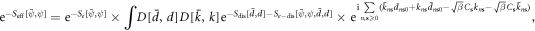
where we have defined a functional measure ![$D[\bar{k},k]\,\equiv $](https://content.cld.iop.org/journals/1367-2630/20/2/023010/revision2/njpaaa383ieqn229.gif)
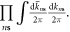
Now integrating over the dislon degrees of freedom and noticing 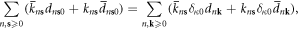 we obtain
we obtain
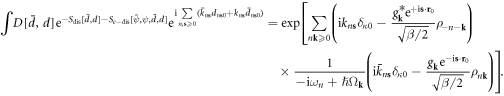
Now substituting the above equation back to equation (10.1) and integrating over the ![$[\bar{k},k]$](https://content.cld.iop.org/journals/1367-2630/20/2/023010/revision2/njpaaa383ieqn232.gif) field, after a few algebraic steps, we finally obtain the effective electron action as
field, after a few algebraic steps, we finally obtain the effective electron action as
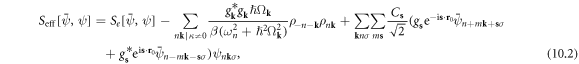
where we have used the identity 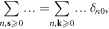 and neglected a constant
and neglected a constant 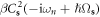 term since it does not interact with any field. Moreover, since there are only electronic degrees of freedom left, defined in both
term since it does not interact with any field. Moreover, since there are only electronic degrees of freedom left, defined in both 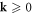 and
and 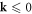 regions, after integrating over the dislon degrees of freedom, we do not need to restrict ourselves to the
regions, after integrating over the dislon degrees of freedom, we do not need to restrict ourselves to the 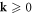 region but expect
region but expect  can be replaced by
can be replaced by 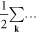 in all cases. Physically, for an electron with
in all cases. Physically, for an electron with 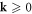 scattering with a dislocation, there is always a 'mirrored' electron with
scattering with a dislocation, there is always a 'mirrored' electron with 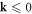 and scattering with the dislocation with the same amplitude. Mathematically, assuming that we quantize the system with the assumption
and scattering with the dislocation with the same amplitude. Mathematically, assuming that we quantize the system with the assumption 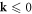 from the beginning, then, after eliminating the dislon degrees of freedom, we will obtain a system with identical physics but reside in the
from the beginning, then, after eliminating the dislon degrees of freedom, we will obtain a system with identical physics but reside in the 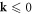 region. To simplify the effective Hamiltonian we have used
region. To simplify the effective Hamiltonian we have used 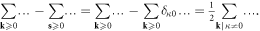
Rewriting electron action equation (10.2) back to Hamiltonian form by normal ordering, we have the effective electron Hamiltonian
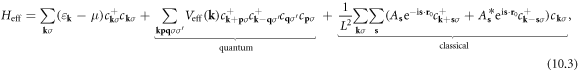
where the coupling coefficients are written as
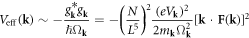
and ![${A}_{{\bf{s}}}\equiv \displaystyle \frac{{g}_{{\bf{s}}}{C}_{{\bf{s}}}}{\sqrt{2}}=\displaystyle \frac{eN}{2{L}^{3}}{V}_{{\bf{s}}}[{\rm{i}}{\bf{s}}\cdot {\bf{F}}({\bf{s}})].$](https://content.cld.iop.org/journals/1367-2630/20/2/023010/revision2/njpaaa383ieqn245.gif)
To recap a bit, in these expressions of 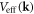 and
and 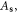 N is the total number of atoms, L is the system size,
N is the total number of atoms, L is the system size, 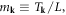
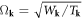 is the dislon dispersion, with
is the dislon dispersion, with 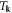 and
and 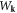 defined in equation (4.1),
defined in equation (4.1), 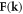 is defined in equation (3.11),
is defined in equation (3.11), 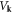 is the Coulomb interaction defined after equation (6.1), and s is the 2D version of k perpendicular to the dislocation line direction.
is the Coulomb interaction defined after equation (6.1), and s is the 2D version of k perpendicular to the dislocation line direction.
Equation (10.3) has clear physical meaning, indicating that the electron–dislocation interaction has two distinct effects: the classical effect is the quenched dislocation scattering, which can change the electron momentum perpendicular to the dislocation line direction (noticing s is the 2D wavevector perpendicular to the dislocation line direction), while the quantum effect can mediate a coupling between two electrons forming a Cooper pair, just as a phonon does. As one early application of the dislon theory, it has been shown that the competition between the classical and quantum effects can determine the shift of the transition temperature in a dislocated superconductor [76].
11. Effective phonon theory with fluttering interaction
We define the effective action of phonon as
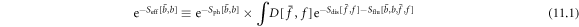
in which ![${S}_{{\rm{d}}{\rm{i}}{\rm{s}}}[\bar{f},f]=\displaystyle \sum _{n,{\bf{k}}\geqslant 0}{\bar{f}}_{{\bf{k}}n}(-{\rm{i}}{\omega }_{n}+\hslash {{\rm{\Omega }}}_{{\bf{k}}}){f}_{{\bf{k}}n}$](https://content.cld.iop.org/journals/1367-2630/20/2/023010/revision2/njpaaa383ieqn254.gif) is the f-field of the dislon, coupling with a phonon through the fluttering mechanism.
is the f-field of the dislon, coupling with a phonon through the fluttering mechanism.
Now integrating over the ![$[\bar{f},f]$](https://content.cld.iop.org/journals/1367-2630/20/2/023010/revision2/njpaaa383ieqn255.gif) field, we have
field, we have
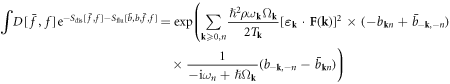
from which the effective phonon action equation (11.1) can be written directly as
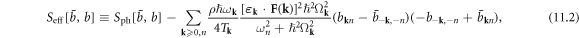
where we have used 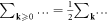 after eliminating the dislon degrees of freedom. Now performing Keldysh rotation, defining that
after eliminating the dislon degrees of freedom. Now performing Keldysh rotation, defining that
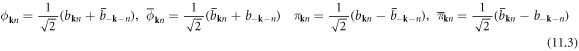
then using the equality 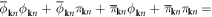
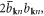 the free-phonon action equation (9.6) can be rewritten as
the free-phonon action equation (9.6) can be rewritten as
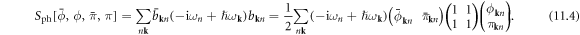
Now, noticing that  the fields ϕ and π are indeed real scalar fields, i.e. the complex scalar phonon fields
the fields ϕ and π are indeed real scalar fields, i.e. the complex scalar phonon fields  are decomposed into a displacement-like field ϕ and a momentum-like field π.
are decomposed into a displacement-like field ϕ and a momentum-like field π.
Now the effective phonon action can be written as
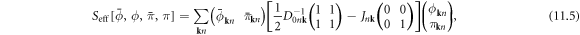
where the coupling constant of phonon–dislon fluttering is defined as ![${J}_{n{\bf{k}}}\equiv \displaystyle \frac{\rho \hslash {\omega }_{{\bf{k}}}}{2{T}_{{\bf{k}}}}\displaystyle \frac{{[{{\boldsymbol{\varepsilon }}}_{{\bf{k}}}\cdot {\bf{F}}({\bf{k}})]}^{2}{\hslash }^{2}{{\rm{\Omega }}}_{{\bf{k}}}^{2}}{{\omega }_{n}^{2}+{\hslash }^{2}{{\rm{\Omega }}}_{{\bf{k}}}^{2}},$](https://content.cld.iop.org/journals/1367-2630/20/2/023010/revision2/njpaaa383ieqn261.gif) and the free-phonon propagator
and the free-phonon propagator 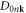 is defined as
is defined as 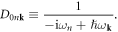 Diagonalizing the 2 × 2 matrix in equation (11.5), we have
Diagonalizing the 2 × 2 matrix in equation (11.5), we have
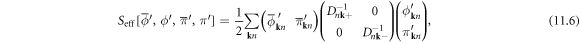
where we use the notation ![$[\bar{\phi }^{\prime} ,\phi ^{\prime} ,\bar{\pi }^{\prime} ,\pi ^{\prime} ]$](https://content.cld.iop.org/journals/1367-2630/20/2/023010/revision2/njpaaa383ieqn264.gif) to denote the diagonalized fields, and
to denote the diagonalized fields, and 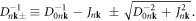 Without dislon–phonon coupling, i.e.
Without dislon–phonon coupling, i.e. 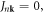 equation (11.6) should reduce back to the free phonon propagator
equation (11.6) should reduce back to the free phonon propagator 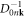 directly instead of giving a null result, which enables us to safely neglect the unphysical
directly instead of giving a null result, which enables us to safely neglect the unphysical 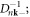 finally, we obtain the diagonalized effective phonon theory in 3D
finally, we obtain the diagonalized effective phonon theory in 3D
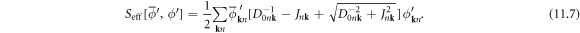
Notice that here, 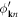 after rotation does not resemble a displacement operator, but is more like an annihilation operator.
after rotation does not resemble a displacement operator, but is more like an annihilation operator.
With this effective theory, a number of problems associated with dislocation–phonon interaction can be solved directly, including how dislocations may change phonon dispersion, and how the heat capacity in a dislocated crystal is changed, etc.
12. Effective phonon theory with anharmonicity
To obtain an effective phonon theory with anharmonicity, we first define a composite phonon displacement operator 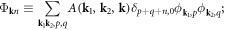 then equation (9.8) can be rewritten in terms of a simpler form as
then equation (9.8) can be rewritten in terms of a simpler form as
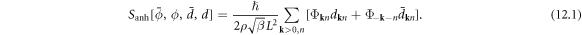
One thing worth mentioning is that
- (1)In the fluttering interaction, it is the dislon f-field which couples with the phonon
 field.
field. - (2)In the anharmonic interaction, it is the dislon d-field which couples with the phonon ϕ field.
This fact can be used to greatly simplify the phonon effective theory, as the fluttering and anharmonicity can be treated independently.
Assume that we only plan to study a complete phonon–dislon interaction system without considering electronic degrees of freedom, and define the effective action of phonon coupling with the d-field, ![${S}_{{\rm{e}}{\rm{f}}{\rm{f}}}[\bar{\phi },\phi ],$](https://content.cld.iop.org/journals/1367-2630/20/2/023010/revision2/njpaaa383ieqn272.gif) as
as
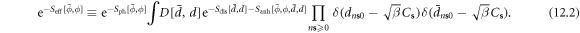
Using the same method implemented in section 10, performing a Fourier transform of the δ-function and integrating over the dislon degrees of freedom so that 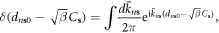 and defining the functional measure
and defining the functional measure ![$D[\bar{k},k]\equiv \displaystyle \prod _{n{\bf{s}}}\displaystyle \int \displaystyle \frac{d{\bar{k}}_{n{\bf{s}}}}{2\pi }\displaystyle \frac{d{k}_{n{\bf{s}}}}{2\pi },$](https://content.cld.iop.org/journals/1367-2630/20/2/023010/revision2/njpaaa383ieqn274.gif) we have
we have
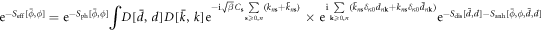
Now integrating over the dislon degrees of freedom, we have
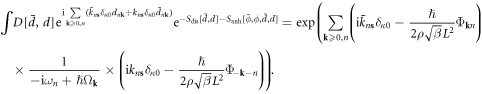
Now further defining the 2D version of the composite operator 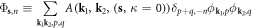 and integrating over the
and integrating over the ![$[\bar{k},k]$](https://content.cld.iop.org/journals/1367-2630/20/2/023010/revision2/njpaaa383ieqn276.gif) fields, after a few steps, we obtain
fields, after a few steps, we obtain
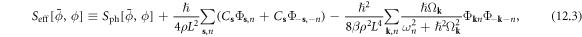
where we have seen that both the 2nd order quadratic term of displacement and 4th order quartic term exist.
At this step, equation (12.3) becomes a quadratic theory of the composite operator  To link back to phonon displacement properties, we first rewrite equation (12.3) in terms of phonon displacement fields as
To link back to phonon displacement properties, we first rewrite equation (12.3) in terms of phonon displacement fields as
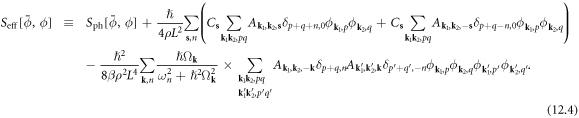
Now we examine the coefficients in the quadratic term. If we only look at 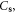 since
since 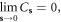 this makes the diagonal component
this makes the diagonal component 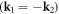 of the quadratic scattering term seemingly vanish. However, after a closer look, the combined coefficient
of the quadratic scattering term seemingly vanish. However, after a closer look, the combined coefficient 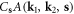 can be simplified using equations (5.7) and (8.5) as
can be simplified using equations (5.7) and (8.5) as
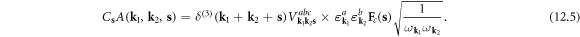
Which gives  since
since  Therefore, the quadratic scattering terms (2nd line in equation (12.4)) is maximized in the
Therefore, the quadratic scattering terms (2nd line in equation (12.4)) is maximized in the  limit, instead of approaching 0. Therefore, we can only keep the dominating diagonal term with
limit, instead of approaching 0. Therefore, we can only keep the dominating diagonal term with  and thus
and thus 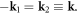 Since in reality,
Since in reality,  should not be divergent but contain a finite infrared long-wavelength physical cutoff, we further define a coefficient
should not be divergent but contain a finite infrared long-wavelength physical cutoff, we further define a coefficient 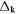 as
as 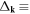
 where
where 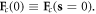
At this stage, the theoretical construction of dislon theory interacting with electrons and phonons is complete. With the new effective electron Hamiltonian equation (10.3), the influence of dislocations on materials' electronic and optical properties can be studied; with the effective phonon action equation (12.4), the influence of dislocations on materials' phononic and thermal properties can be studied. A new Hamiltonian or new actions means new opportunity. In this sense, we do not intend to exhaust all these opportunities; instead, we demonstrate the power of the dislon theory by providing a few case studies in the next few sections: computing the electron relaxation time for scattering with dislocations, the electrical conductivity caused by electron-dislocation scattering, and the thermal conductivity arising from phonon-dislocation interaction.
13. The relaxation time for electron–dislon scattering
Since the dislon d-field has a boundary condition equation (5.7), to compute transport properties, instead of directly applying the Feynman diagrams of electron–dislon interaction, which is done in the case of studying electron–phonon coupling, the effective electron theory equation (10.3) should be used in order to take into account the boundary condition properly. In this section, we focus on the classical scattering between an electron and dislon from equation (10.3), i.e.
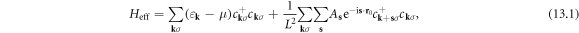
where we have used 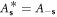 to simplify the quadratic part of equation (10.3), and written the scattering amplitude as
to simplify the quadratic part of equation (10.3), and written the scattering amplitude as ![${A}_{{\bf{s}}}=\displaystyle \frac{{g}_{{\bf{s}}}{C}_{{\bf{s}}}}{\sqrt{2}}=\displaystyle \frac{eN}{2{L}^{3}}{V}_{{\bf{s}}}[{\rm{i}}{\bf{s}}\cdot {\bf{F}}({\bf{s}})]$](https://content.cld.iop.org/journals/1367-2630/20/2/023010/revision2/njpaaa383ieqn293.gif) (distinguish this 1-index scattering amplitude from the anharmonic coupling coefficient
(distinguish this 1-index scattering amplitude from the anharmonic coupling coefficient 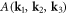 which has 3 indices). It is also worth mentioning that the Fourier transform of
which has 3 indices). It is also worth mentioning that the Fourier transform of  gives the scattering potential of classical deformation potential scattering, shown in an early study of dislon theory [76].
gives the scattering potential of classical deformation potential scattering, shown in an early study of dislon theory [76].
In the following part of this section, we generalize equation (13.1) to multiple dislocation lines, using a similar technique of studying impurity scattering [96], since both impurity scattering and electron–classical dislocation scattering are quenched, quadratic potential scattering.
For parallel dislocation arrays with dislocation core position 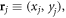
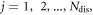 the electron effective Hamiltonian
the electron effective Hamiltonian  taking into account the parallel dislocations scattering can be written as
taking into account the parallel dislocations scattering can be written as
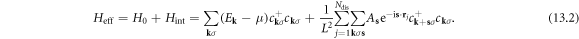
Written in this form, we can utilize the standard quantum many-body approach [81] to study the electron–dislocation array scattering problem. Define the imaginary time Green's function as 
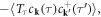 and non-interacting Green's function as
and non-interacting Green's function as 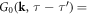
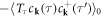 (diagonal) associated with the non-interacting Hamiltonian
(diagonal) associated with the non-interacting Hamiltonian 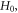 in which
in which 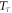 is the time-ordering operator. We further define the corresponding Fourier transformed Green's functions in the Matsubara frequency domain as
is the time-ordering operator. We further define the corresponding Fourier transformed Green's functions in the Matsubara frequency domain as
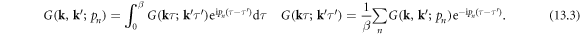
Then, we have the Dyson's equation (appendix B)
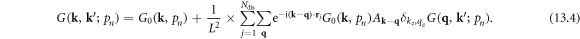
Here we need to bear in mind that the 's' is a 2D vector perpendicular to the dislocation direction, instead of a 3D vector, resulting in the  coefficient. In other words, classical electron–dislocation scattering will not change the electron momentum along the dislocation line direction, which is quite reasonable.
coefficient. In other words, classical electron–dislocation scattering will not change the electron momentum along the dislocation line direction, which is quite reasonable.
At this stage, we use diagrammatic tools to recap the problem:
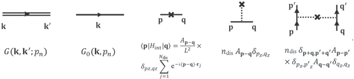
Then, equation (13.4) can be rewritten pictorially as:
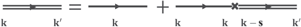
and a few low order Green's functions can be written in a diagrammatic way as
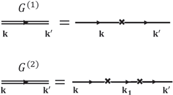
which correspond to following expressions
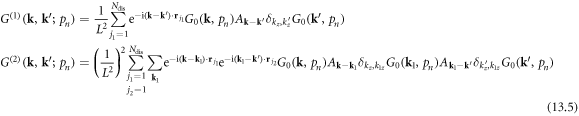
from which we could deduce the corresponding Feynman rules for electron–classical dislocation scattering, that
- (a)for each scattering vertex,
 is denoted by
is denoted by 
- (b)summation over all internal momenta is performed as usual.
Up to this step, no averaging process has taken place yet. However, when the dislocation core locations are purely random, in the regime that the sample size d is much greater than the electron phase coherence length 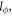 i.e.
i.e. 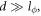 we can further consider the dislocation distribution as homogeneous and hence average over all possible configurations, i.e.
we can further consider the dislocation distribution as homogeneous and hence average over all possible configurations, i.e.
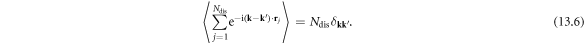
After this impurity averaging process, equation (13.5) can be rewritten as
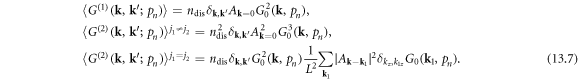
The corresponding Feynman rules taking into account the dislocation averaging, can be written as
- (a)for each vertex
 , we have
, we have  i.e. the dislocation density
i.e. the dislocation density  starts to appear.
starts to appear. - (b)for each interaction line
 , we have
, we have 
The expressions in equation (13.7) can be rewritten in a pictorial way as
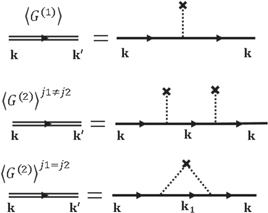
and we can build an arbitrarily complicated diagram, for example the following diagram
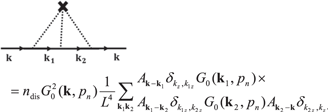
At this stage, the dislocation averaging scheme is complete, from which we can compute the self-energy and relaxation time for electron–classical dislocation scattering to arbitrarily high order.
Self-energy 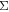 is composed of one-particle irreducible (1PI) diagrams with external legs amputated, and we have the following equation [81]
is composed of one-particle irreducible (1PI) diagrams with external legs amputated, and we have the following equation [81]
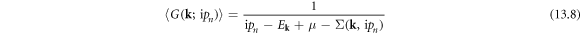
valid generally. With 1st-order Born approximation (FOBA), we write the following self-energy diagram
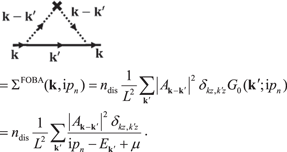
After analytical continuation (assuming infinitesimal 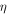 and
and 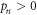 ) from Matsubara frequency to real frequency
) from Matsubara frequency to real frequency  we have
we have
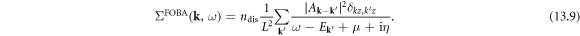
Hence the relaxation time 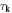 of electron—parallel dislocation array scattering can be written as
of electron—parallel dislocation array scattering can be written as
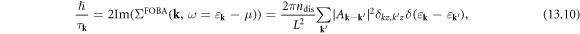
where we have recovered the normal Fermi's Golden rule. The benefit of taking this approach is to explore the scattering schemes to arbitrarily high order, or to take into account any electron–electron correlation effects. For instance, the possibility of weak localization arising from coherent superposition between scattering paths of impurities [83]—now for dislocation arrays—can be properly addressed using this approach. In any case, we may consider equation (13.10) as a good starting point to demonstrate the power of the dislon theory to compute electronic transport properties with parallel dislocation arrays.
14. Electrical conductivity with parallel dislocation arrays
In this section, we demonstrate another usage of dislon theory to compute the electrical conductivity for electron—parallel dislocation array scattering, at a full quantum level (beyond semi-classical approach). The electrical conductivity tensor 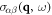 through the Kubo formula follows largely the standard many-body approach [81, 83, 96], and we apply the generic scheme of computing
through the Kubo formula follows largely the standard many-body approach [81, 83, 96], and we apply the generic scheme of computing  to the case of dislocation arrays:
to the case of dislocation arrays:
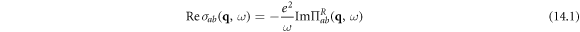
where  are the Cartesian coordinates, and
are the Cartesian coordinates, and 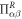 is the retarded current–current correlation function, which can be obtained by analytical continuation of the Matsubara current–current correlation function
is the retarded current–current correlation function, which can be obtained by analytical continuation of the Matsubara current–current correlation function 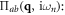
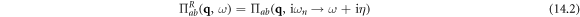
in which 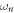 is the Bosonic Matsubara frequency. Hence, the central quantity of computing conductivity is to compute the Matsubara current–current correlation function
is the Bosonic Matsubara frequency. Hence, the central quantity of computing conductivity is to compute the Matsubara current–current correlation function
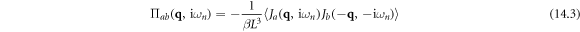
in which the current operator 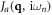 is written as
is written as
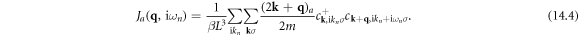
Diagrammatically, defining Fermionic 4-momentum 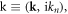 and Bosonic 4-momentum
and Bosonic 4-momentum 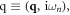 and further defining the bare two-terminal vertex function
and further defining the bare two-terminal vertex function 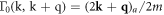 and the Full Green's function
and the Full Green's function 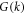 as
as
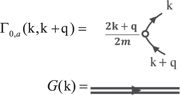
the current–current correlation function tensor can then be written as [83]
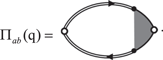
Written in equation form, we have
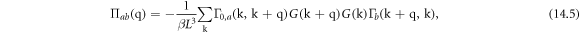
where  and
and  is the dressed current vertex function depending on the detailed interaction. When considering the dislocation array scattering, the dressed vertex function
is the dressed current vertex function depending on the detailed interaction. When considering the dislocation array scattering, the dressed vertex function  under full Born approximation can be written as
under full Born approximation can be written as
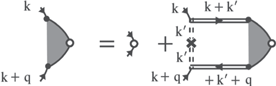
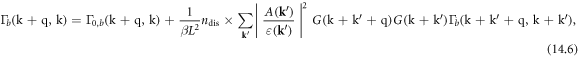
where 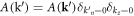 since it denotes the scattering strength with a quenched dislocation array, and
since it denotes the scattering strength with a quenched dislocation array, and 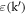 is the dielectric function screening the interaction. We should also keep in mind that the summation does not contain summation over Fermionic Matsubara frequency, since there is no dynamic inelastic scattering in this process.
is the dielectric function screening the interaction. We should also keep in mind that the summation does not contain summation over Fermionic Matsubara frequency, since there is no dynamic inelastic scattering in this process.
We now further compute the DC conductivity of electron–dislocation array scattering as a function of temperature. By taking the  limit, equation (14.5) can be further simplified as
limit, equation (14.5) can be further simplified as
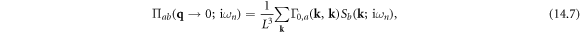
where we have defined that
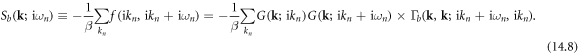
Now, using the residual theorem and Matsubara frequency summation technique, we have
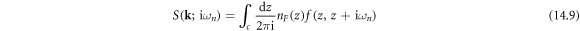
since the Fermionic Matsubara frequencies 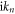 are the poles of the Fermi–Dirac distribution function
are the poles of the Fermi–Dirac distribution function 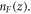 Further computing the contour integral, noticing the branch cuts caused by two Green's functions, we have
Further computing the contour integral, noticing the branch cuts caused by two Green's functions, we have
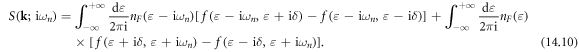
Now performing analytical continuation to real frequency 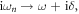 and noticing that
and noticing that 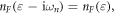 we have
we have
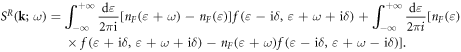
Noticing that 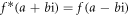 and
and 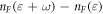
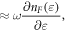 we have
we have
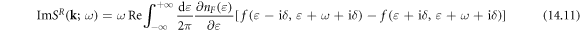
Finally, by substituting equations (14.11) and (14.7) back to equation (14.1), the DC electrical conductivity of electron–dislocation array scattering can be written as
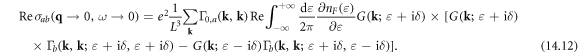
Now what remains is to compute the current vertex function 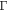 and electron Green's function
and electron Green's function 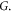 For vertex function, analytical continuing equation (14.6) back to real frequency, and shift variable
For vertex function, analytical continuing equation (14.6) back to real frequency, and shift variable 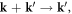 we have the following self-consistent equation of the vertex function as
we have the following self-consistent equation of the vertex function as
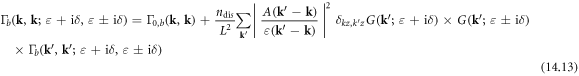
in which we have the non-interacting current vertex as  (
( are Cartesian coordinates). The Green's functions in equation (14.13) can be written as
are Cartesian coordinates). The Green's functions in equation (14.13) can be written as
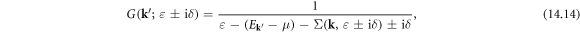
where the self-energy 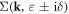 under the full Born approximation can be written as
under the full Born approximation can be written as
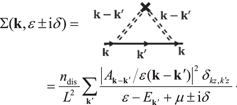
Now noticing the fact that 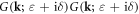
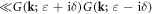 [96], and using the identity that
[96], and using the identity that 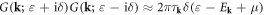 for weak interaction, in which the relaxation time is defined as
for weak interaction, in which the relaxation time is defined as 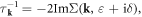 the DC conductivity of electron–dislocation array scattering equation (14.12) can be greatly simplified as
the DC conductivity of electron–dislocation array scattering equation (14.12) can be greatly simplified as
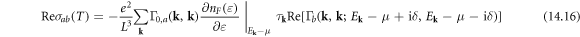
in which the relaxation rate under full Born approximation is given by
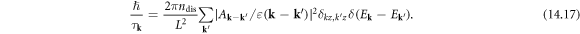
At this step, the temperature-dependent DC electrical conductivity tensor for electron–dislocation array scattering is complete: logically, to compute  using equation (14.16), one needs to first compute the current vertex function
using equation (14.16), one needs to first compute the current vertex function  which is computed from equation (14.13). To compute equation (14.13), one further needs the electron Green's function, which is computed through equations (14.14) and (14.15). The self-energy (14.15) contains the detailed information on electron–dislocation array interactions.
which is computed from equation (14.13). To compute equation (14.13), one further needs the electron Green's function, which is computed through equations (14.14) and (14.15). The self-energy (14.15) contains the detailed information on electron–dislocation array interactions.
15. Lattice thermal conductivity
It is well known that the dominant mechanism for phonon–dislocation scattering is the fluttering mechanism [29, 32] instead of the phonon–dislon anharmonicity, which seemingly allows one to merely focus on the fluttering mechanism. However, for the real thermal conductivity calculation, the three-phonon anharmonic interaction still matters on top of the fluttering mechanism. Given the non-perturbative nature of the fluttering mechanism [36] (equation (11.7)), it becomes impractical to adopt a perturbative approach to compute relaxation rate—the thermal conductivity should be computed directly using the phonon Green's function. In this section, we provide two equations to compute lattice thermal conductivity in a dislocated crystal: one is simpler, solely for fluttering mechanism, while the other is more involved but can take into account both the three-phonon and phonon–dislon anharmonic interactions together with the fluttering.
The generic thermal conductivity computed from the normal Green's function approach can be written as [97]
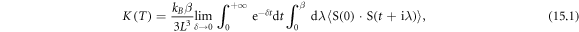
where the energy flow vector operator  can be written as
can be written as 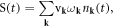 where
where 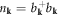 is the phonon number density operator,
is the phonon number density operator, 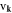 is the group velocity and
is the group velocity and 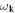 is the dispersion. Hence the central quantity to be computed is the 4-operator correlation
is the dispersion. Hence the central quantity to be computed is the 4-operator correlation 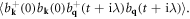 Using Wick's theorem, since the fluttering mechanism (11.7) is quadratic, the thermal average
Using Wick's theorem, since the fluttering mechanism (11.7) is quadratic, the thermal average  can be written as
can be written as
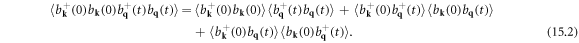
Now, neglecting the equal-time correlation 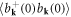 which does not contribute to transport, and neglecting
which does not contribute to transport, and neglecting 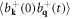 which does not conserve particle number hence has negligible probability [97–99], only the 3rd term in equation (15.2) is kept. The thermal conductivity in equation (15.1) can be simplified as
which does not conserve particle number hence has negligible probability [97–99], only the 3rd term in equation (15.2) is kept. The thermal conductivity in equation (15.1) can be simplified as
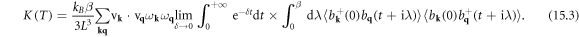
Now what remains is to compute the two-point correlation functions and link them to the fluttering action equation (11.7). Here, we show that the key is to link through the spectral density function  First, similar to the electron case in equation (8.3), we define the time-ordered phonon Green's function in imaginary time
First, similar to the electron case in equation (8.3), we define the time-ordered phonon Green's function in imaginary time 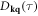
![$=\,-\langle {T}_{\tau }[{b}_{{\bf{k}}}(\tau ){b}_{{\bf{q}}}^{+}(0)]\rangle $](https://content.cld.iop.org/journals/1367-2630/20/2/023010/revision2/njpaaa383ieqn364.gif) and in the Matsubara frequency domain as
and in the Matsubara frequency domain as
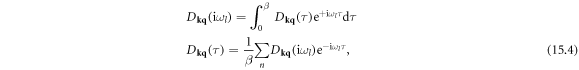
where 
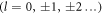 are the Bosonic Matsubara frequencies. With this definition, the Matsubara Green's function can be represented using Lehmann representation as
are the Bosonic Matsubara frequencies. With this definition, the Matsubara Green's function can be represented using Lehmann representation as
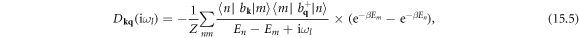
where 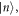
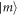 are the exact eigenstates of the full Hamiltonian with eigenvalues
are the exact eigenstates of the full Hamiltonian with eigenvalues 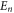 and
and  respectively. The retarded and advanced Green's functions can be written as analytical continuation of the Matsubara Green's function as
respectively. The retarded and advanced Green's functions can be written as analytical continuation of the Matsubara Green's function as 
Now if we define the spectral density function 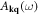
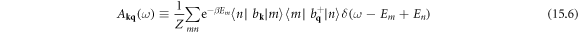
we then have 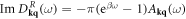 valid, where we used the identity that
valid, where we used the identity that 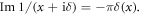
Using the same approach, we could also rewrite the correlation function 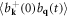 (t in real time at this step) in terms of Lehmann representation as
(t in real time at this step) in terms of Lehmann representation as
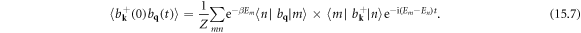
Then from equations (15.6) and (15.7), we have
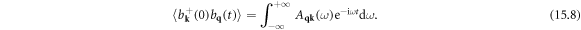
Similarly, we have
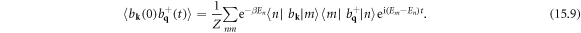
Then, using equation (15.6), we have
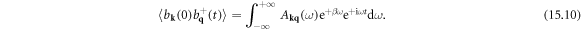
Now substituting equations (15.8) and (15.10) back to equation (15.3), the thermal conductivity 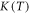 is written as
is written as
Using the fact that  we have
we have
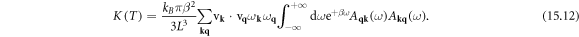
Finally, we obtain the thermal conductivity as
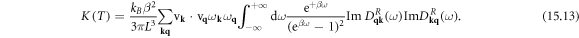
Equation (15.13) directly links the thermal conductivity 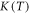 to the retarded phonon Green's function
to the retarded phonon Green's function 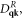 which can be obtained by analytical continuation of Matsubara Green's function as
which can be obtained by analytical continuation of Matsubara Green's function as 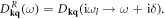 As a simple check, assuming that the phonon Green's function can be written in a simplified form as
As a simple check, assuming that the phonon Green's function can be written in a simplified form as
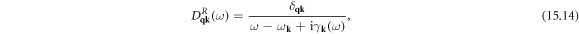
where  is the phonon dispersion and
is the phonon dispersion and  is the phonon spectral linewidth, we have
is the phonon spectral linewidth, we have
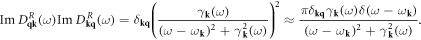
The second equality is valid since the function is peaked at  and we have assumed an infinitesimal linewidth limit. Written in this way, the thermal conductivity equation (15.13) can be further simplified as
and we have assumed an infinitesimal linewidth limit. Written in this way, the thermal conductivity equation (15.13) can be further simplified as
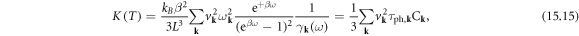
where 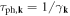 and
and ![${{\rm{C}}}_{{\bf{k}}}={\omega }_{{\bf{k}}}\partial /\partial T[{n}_{B}({\omega }_{{\bf{k}}})]/{L}^{3}$](https://content.cld.iop.org/journals/1367-2630/20/2/023010/revision2/njpaaa383ieqn385.gif) are phonon relaxation time and volumetric heat capacity, respectively, of a phonon with wavevector k, and
are phonon relaxation time and volumetric heat capacity, respectively, of a phonon with wavevector k, and  is the Bosonic occupation. Therefore, if the phonon relaxation rate
is the Bosonic occupation. Therefore, if the phonon relaxation rate 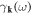 is known, equation (15.13) can be rewritten in a much simpler but well-known form, where the 2nd line of equation (15.15) is usually introduced in textbooks [100].
is known, equation (15.13) can be rewritten in a much simpler but well-known form, where the 2nd line of equation (15.15) is usually introduced in textbooks [100].
For fluttering mechanism action (9.7), the Matsubara Green's function can be directly written as follows using equation (11.7)
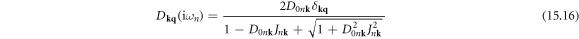
in which 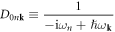 is the free phonon propagator. This form goes beyond any perturbative expansion and cannot be written in terms of equation (15.14), since the non-interacting phonon propagator
is the free phonon propagator. This form goes beyond any perturbative expansion and cannot be written in terms of equation (15.14), since the non-interacting phonon propagator  and interaction
and interaction  are highly entangled inside the '√ ' symbol.
are highly entangled inside the '√ ' symbol.
In real crystals, the contribution of thermal conductivity also contains three-phonon anharmonicity processes, where the coupling is the displacement field, which is proportional to  To facilitate the calculation with anharmonicity, we define another set of operators
To facilitate the calculation with anharmonicity, we define another set of operators 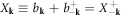 and
and  then we have
then we have
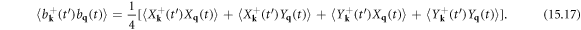
Then, if we define the correlation function for the displacement field in real time and frequency domain as
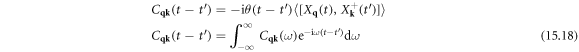
and following the same procedure of defining the spectral density function in equations (15.5)–(15.10), we have the spectral function written as
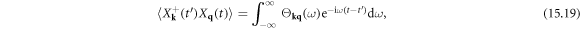
where the spectral function also satisfies 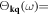
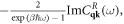 where
where  is the retarded correlation function
is the retarded correlation function 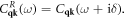 Now using the spectral function, following the same procedure of writing in terms of Lehmann representation, it can be proven that
Now using the spectral function, following the same procedure of writing in terms of Lehmann representation, it can be proven that
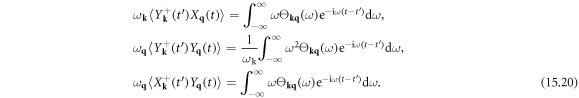
Substituting equations (15.19) and (15.20) back to equation (15.17), we have
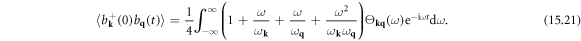
Similarly, we obtain
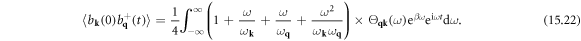
Now if we substitute equations (15.21) and (15.22) back to equation (15.3), we finally have an alternative expression of thermal conductivity using the displacement–displacement correlation function as
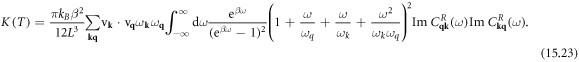
With equations (15.13) and (15.23) in hand, we conclude this section.
16. Perspective
In this section, we briefly list a few possible research topics which can directly benefit from dislon theory. Due to our own limitations, this list is by no means exhaustive nor guaranteed to show significant effect. However, the dislon theory provides a tool to make such exploration possible. The readers are certainly encouraged to explore more opportunities using dislon theory for a better understanding of a dislocated crystal.
- (1)How do dislocations change materials' electronic structure, such as bandgaps in a semiconductor? This may be possible since recent study [101] has shown that large strain is capable of tuning the bandgap, while dislocations can introduce long-range strain fields.
- (2)Can dislocations induce Anderson localization? This may be possible since an analog of light localization using dislocations has been reported [102], not to mention the randomness that random dislocation lines can create.
- (3)Can dislocations drive a normal band insulator into a topological insulator? This may be realizable since dislocations can carry special topological states [103], and the tunable bandgap may result in an inversion between conduction and valence bands, which is the basis of forming a topological insulator [104].
- (4)Should dislocations increase or decrease a materials' heat capacity? Early simulation shows a very complicated scenario [105] which might be explained by dislon theory.
- (5)What is the role of dislocations in phase transition processes, including both first order transitions and continuous phase transitions? Early studies show the possible role of dislocations in the crystal melting process [106], while dislon theory may provide a comprehensive picture by considering other degrees of freedom in the crystal.
- (6)How can dislocations improve the thermoelectric figure-of-merit? Dislon theory may help quantify a few recent experimental findings, where dislocations have shown to dramatically increase the figure-of-merit in thermoelectric materials [107].
- (7)What is the interplay between dislocations and magnetic ordering? Recent experiment has shown a unique ferromagnetic ordering of a single dislocation in an antiferromagnetic material [63], which may be explained by a direct generalization of dislon theory with a spin degree of freedom—the observed ordering can be understood if a lower energy configuration is formed when a 'spin dislon' starts to interact with the neighborhood magnetic environment.
- (8)If we do not restrict ourselves to dislocation-induced properties, since low-angle grain boundaries can be considered as an array of dislocations [108], the electronic properties of grain boundaries may be computed accordingly by constructing a dislon array. On the other hand, since infinitesimal dislocations have been applied to treat singularity of stress fields such as growth of fatigue cracks [109, 110], the generalization of the present dislon theory may allow the calculation of electronic properties near a crack tip which has long been considered challenging.
There may also be opportunities to study the role of dislocations in nonlinear and quantum optics, chemical reactivity, and superconductivity. For instance, one recent application using the dislon theory shows that there are intrinsically two different types of electron–dislocation interactions, whose competition determines the critical temperature in a dislocated crystal [76].
One problem worth mentioning is an inverse problem to study how phonons and electrons affect dislocation motion. It is well known that the electrons in a superconductor can have a drag-like effect on dislocations, called electronic damping [111–114], while phonons can also influence the dislocation motion [79, 115] which is examined in great detail in recent molecular dynamics simulations [116]. Since a dislocation's motion is slow compared to electronic and phononic processes, a pure classical and semi-classical theory is sufficient to describe dislocation motion without necessity to refer to a fully-quantized theory, although the mechanical properties can still be calculated from a Hamiltonian theory as done in density functional theoretical calculations [117].
17. Discussions and conclusions
In this study, we present a comprehensive theoretical framework of a quantized dislocation, namely a dislon, for arbitrary types of straight-line dislocations, and study its interplay with electronic and phononic degrees of freedom. Using this approach, one may be wondering how to check the validity of the dislon theory. In a few early studies of dislon theory, although the theoretical structure was simpler, we were able to perform a series of 'sanity checks' to examine the validity of dislon theory:
- (1)Reducibility to classical displacement: the lattice displacement field can always be reduced to the well-known results normally introduced in classical materials science textbooks. For instance, this can be seen from equation (3.11).
- (2)The consistent deformation potential scattering. In equation (10.3), the electron–dislocation classical scattering amplitude
 after a Fourier transform, gives
after a Fourier transform, gives  which is exactly the electron–dislocation deformation potential scattering form [118]. A detailed proof of this can be found in [76]. The benefit of the dislon approach is the elimination of any empirical parameters. In the classical deformation potential, there is an overall empirical prefactor in the expression of
which is exactly the electron–dislocation deformation potential scattering form [118]. A detailed proof of this can be found in [76]. The benefit of the dislon approach is the elimination of any empirical parameters. In the classical deformation potential, there is an overall empirical prefactor in the expression of  [118], while the dislon theory fixes the prefactor with microscopic details.
[118], while the dislon theory fixes the prefactor with microscopic details. - (3)
- (4)The phonon–dislocation interaction beyond any perturbative approach. This non-perturbative nature can be seen directly from equation (11.7), where the square root of the phonon Green's function prevents any perturbative analysis. In fact, this indicates the breakdown of all previously developed dislocation–phonon scattering theories, which are all based on perturbative theories. This conclusion, although seemingly drastic, has been confirmed by a recent and independent ab initio phonon–dislocation first-principles calculation of dislocation–phonon scattering, where the authors mentioned that 'Because of the breakdown of the Born approximation, earlier literature models fail, even qualitatively'[80]. This independent first-principles calculation provided great confidence in the validity of dislon theory.
- (5)There are also a number of related features resulting from the non-perturbative nature of phonon–dislocation interaction. First, in normal perturbative studies, when a phonon is scatted by a dislocation, the dispersion of the phonon is considered a constant without change. The non-perturbative analysis shows that strong phonon–dislon interaction can change the phonon dispersion in an anisotropic way [36], which has been confirmed by independent ab initio calculations as well [80]. Moreover, perturbation theories showed that the dislocation–phonon relaxation rate varies monotonically with phonon frequency, whether for static scattering [26, 27] or dynamic scattering [29, 32], while the dislon theory predicts a resonance peak of relaxation rate for dislocation–phonon scattering. The existence of such resonance has also been confirmed by the same ab initio dislocation–phonon calculation [80].
- (6)The prediction of superconducting transition temperature Tc in a dislocated superconductor. As seen in equation (10.3), there are two types of competing electron–dislocation interactions: classical and quantum. In one early study of dislon theory [76], we have shown that the Tc is determined by this competition effect: when the quantum effect is dominant, then Tc is increased, and vice versa. The computed Tc shows good agreement with a number of existing experimental data; particularly, it may provide a feasible explanation of the mysterious dislocation-induced superconductivity [75, 119].
- (7)A dislon is a quantized defect in crystalline solids. Recently, a quantized defect in liquid helium called 'angulon' has been developed by Lemeshko et al [120–122]. Despite the fact that the dislon and angulon are completely different quasiparticles appearing in different environments, they both demonstrated the feasibility of actually quantizing a defect, which facilitates an understanding of the role of this very defect in a certain system—solid or liquid—using the many-body approach. For instance, in one recent angulon study [122], the phonon–angulon scattering can be readily studied.
Although the dislon theory has shown some early triumphs by explaining the non-perturbative phonon–dislocation interaction or superconductivity, it is still in an infant stage. For instance, in dislocated semiconductors [22, 23] or ionic crystals [14], Coulomb scattering with charged dislocations becomes dominant due to the weak screening effect compared to metals. Such scattering has a pure classical nature and is related to the material-specific local atomic configuration near the dislocation core, but it has nothing to do with the dislocation's definition 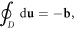 hence it has not been considered in this study. Even so, we feel that a direct generalization of section 3 can still be applied to charged dislocations, magnetic dislocations, or disclinations, or even be used to study more involved extended defects such as grain boundaries or nano-precipitates, which have both the 'extended' part and 'localized' part in space. Even so, we have no intention to treat an arbitrary dislocation such as a dislocation loop, where the expansion coefficient equation (3.11) becomes spatially dependent and an additional temporal variable is needed to track the position on the loop, which is the situation of string theory for a closed string and is mathematically formidable [123]. Moreover, as in dislon theory, where there are internal excitations as local vibrational modes, the internal excitation of other extended defects and their roles on materials' functional properties are worthwhile to explore. To facilitate future computation using this dislon theory, we provide a dimension analysis and a list of symbols (appendix C). To conclude, we hope and believe that the present dislon theory could serve as a computational tool to help clarify the role of crystal dislocations on a number of functional properties of materials, at a new level of clarity.
hence it has not been considered in this study. Even so, we feel that a direct generalization of section 3 can still be applied to charged dislocations, magnetic dislocations, or disclinations, or even be used to study more involved extended defects such as grain boundaries or nano-precipitates, which have both the 'extended' part and 'localized' part in space. Even so, we have no intention to treat an arbitrary dislocation such as a dislocation loop, where the expansion coefficient equation (3.11) becomes spatially dependent and an additional temporal variable is needed to track the position on the loop, which is the situation of string theory for a closed string and is mathematically formidable [123]. Moreover, as in dislon theory, where there are internal excitations as local vibrational modes, the internal excitation of other extended defects and their roles on materials' functional properties are worthwhile to explore. To facilitate future computation using this dislon theory, we provide a dimension analysis and a list of symbols (appendix C). To conclude, we hope and believe that the present dislon theory could serve as a computational tool to help clarify the role of crystal dislocations on a number of functional properties of materials, at a new level of clarity.
Acknowledgments
The authors dedicate this paper to Professor Mildred S Dresselhaus who had greatly supported and supervised this research. ML, YT and GC thank support by S3TEC, an Energy Frontier Research Center funded by the US Department of Energy (DOE), Office of Basic Energy Sciences (BES) under award No. DE-SC0001299/DE-FG02-09ER46577 (for fundamental research on electron–phonon interaction in thermoelectric materials) and by the Defense Advanced Research Projects Agency (DARPA) MATRIX program HR0011-16-2-0041 (for developing and applying the simulation codes). QM and YZ thank the support by the US DOE-BES Materials Science and Engineering Division, under Contract No. DE-AC02-98CH10886.
Appendix A.: A few useful identities for sgn(K) function
The vector sgn function is defined as
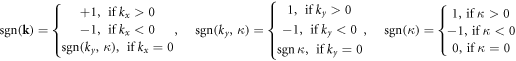
and a relevant 2D version
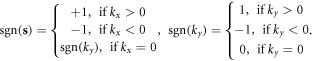
This particular way of defining the vector sgn function is one of many choices which will prove handy later based on the following Lemmas.
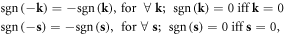
where 'iff' means 'if and only if'. The proof is straightforward.
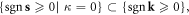
where ' ' is the notation for set. '
' is the notation for set. ' ' means set X satisfies condition C.
' means set X satisfies condition C.
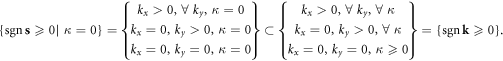
QED.
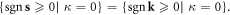
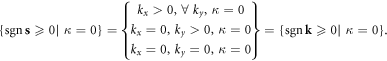
QED.
Appendix B.: The Derivation of Dyson's equation
Appendix. B.1. Heisenberg equation of motion (EoM)
For an arbitrary operator in imaginary time  we have
we have ![${\partial }_{\tau }O(\tau )={\partial }_{\tau }[{{\rm{e}}}^{\tau H}O{{\rm{e}}}^{-\tau H}]=[H,O](\tau )$](https://content.cld.iop.org/journals/1367-2630/20/2/023010/revision2/njpaaa383ieqn405.gif)
Appendix. B.2. EoM of Green's function in imaginary time
For Green's function 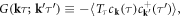 we have
we have
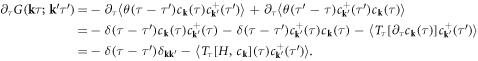
Up to this step, the expression is generic.
Now if we assume that the Hamiltonian H is quadratic, 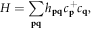 which is the case of external potential scattering, including dislocation scattering, and use the identity:
which is the case of external potential scattering, including dislocation scattering, and use the identity: ![$[AB,C]=A\{B,C\}-\{A,C\}B,$](https://content.cld.iop.org/journals/1367-2630/20/2/023010/revision2/njpaaa383ieqn408.gif) then we have
then we have
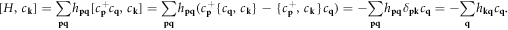
Then the EoM of Green's function can be written as
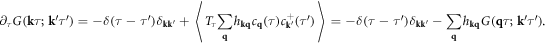
Appendix. B.3. Green's function in Matsubara frequency domain
Now we further define Green's function in the Matsubara frequency domain as
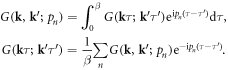
Then the EoM of Green's function in B.2 can be rewritten as
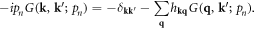
Appendix. B.4. Dyson's equation
Now, divide the Hamiltonian into a diagonal part  with eigenvalues
with eigenvalues  and off-diagonal part
and off-diagonal part  with matrix element
with matrix element 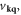 and define Green's function associated with Hamiltonian
and define Green's function associated with Hamiltonian  as
as  then, we have
then, we have
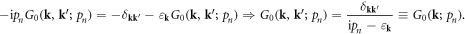
The EoM of Green's function in the Matsubara frequency can be written as
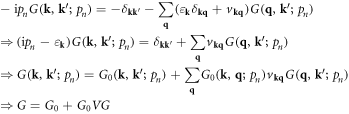
which is the Dyson's equation.
Appendix C.: Dimension analysis
Appendix. Fundamental constants
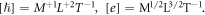
(static Coulomb)
Appendix. External parameters
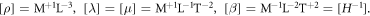
Appendix. Displacements
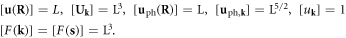
Appendix. Hamiltonians
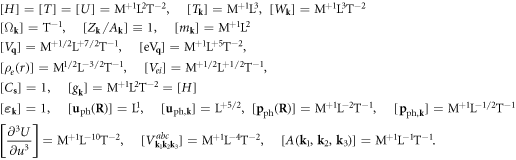
Appendix. Actions