Abstract
The Sun illuminates both the Moon and the Earth with practically the same luminous fluxes which are in turn reflected by them. The Moon provides a dim light to the Earth whereas the Earth illuminates the Moon with somewhat brighter light which can be seen from the Earth and is called earthshine. As the amount of light reflected from the Earth depends on part of the Earth and the cloud cover, the strength of earthshine varies throughout the year. The measure of the earthshine light is luminance, which is defined in photometry as the total luminous flux of light hitting or passing through a surface. The expression for the earthshine light in terms of the apparent magnitude has been derived for the first time and evaluated for two extreme cases; firstly, when the Sun's rays are reflected by the water of the oceans and secondly when the reflector is either thick clouds or snow. The corresponding values are 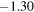 and
and 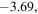 respectively. The earthshine value
respectively. The earthshine value 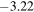 reported by Jackson lies within these apparent magnitudes. This paper will motivate the students and teachers of physics to look for the illuminated Moon by earthlight during the waning or waxing crescent phase of the Moon and to reproduce the expressions derived here by making use of the inverse-square law of radiation, Planck's expression for the power in electromagnetic radiation, photopic spectral luminous efficiency function and expression for the apparent magnitude of a body in terms of luminous fluxes.
reported by Jackson lies within these apparent magnitudes. This paper will motivate the students and teachers of physics to look for the illuminated Moon by earthlight during the waning or waxing crescent phase of the Moon and to reproduce the expressions derived here by making use of the inverse-square law of radiation, Planck's expression for the power in electromagnetic radiation, photopic spectral luminous efficiency function and expression for the apparent magnitude of a body in terms of luminous fluxes.
Export citation and abstract BibTeX RIS
Introduction
Heinrich Hertz [1] questioned whether the reflected part of the solar radiation should really be considered as part of the energy resources of the Earth. He answered by saying that the reflected solar radiation should be considered as the part of (energy) income utilized for illumination of the Earth, and this energy enables the Earth to circle the Sun not as a dark invisible mass, but to stand out as a bright star among the other planets; from them the Earth can be observed just as the other planets are visible from the Earth. He further said, 'It represents, so to speak, the astronomical upkeep allowance of the Earth' and it is not an insignificant portion of incoming energy that is thus reflected. As the Moon provides a dim light to the Earth during night by reflecting the Sun's rays, in the same way the Earth also reflects [2] the Sun's rays and illuminates the dark portion of the Moon; the illuminated Moon can be seen from the Earth known as earthshine [3, 4] (figure 1). Leonardo da Vinci [5] had explained the phenomenon in the early 16th century when he realized that both the Earth and the Moon reflect sunlight at the same time.
The measure of the earthshine light is luminance which is defined in photometry as the total luminous flux of light hitting or passing through a surface. To calculate the value of earthshine one requires the values of sunlight reaching the Earth, reflected part approaching towards the Moon, and the part once again reflected from the Moon which is visible from the Earth—called earthshine. The earthshine has so far not illuminated the pages of pedagogic journals in physics such as European Journal of Physics, Physics Education, The Physics Teacher, and American Journal of Physics and so on. The aim of this paper is to motivate the students and teachers of physics to observe earthshine during the waning or waxing crescent phase of the Moon and estimate its value in terms of the apparent magnitude in a simple way. This paper may remind a sizeable number of readers that they had, of course, observed earthshine in the past but they were unaware of it. The calculation of earthshine presented here for the first time can be reproduced even by undergraduate students who are supposed to have read the inverse-square law of radiation, Planck's expression for power in electromagnetic radiation and the phases of the Moon and its recurring cycle. They will also learn the photopic spectral luminous efficiency function and expression for the apparent magnitude of a body in terms of luminous fluxes.
It is worth devoting one paragraph to the basics of the phases of the Moon and the associated cycle so that students are comfortable with the topic of earthshine presented here and to remind teachers that they should cover these basics before discussing earthshine. Like Earth, half of the Moon is always lit by the Sun. As the Moon orbits the Earth, we see varying fractions of its illuminated sides but not the dark ones; the dark portions are visible during the occurrence of earthshine only. The appearances of the visible sides are the changing phases of the Moon. The Moon phase passes through eight major shapes during a cycle that repeats itself every 29.53 days. The phases always follow one another in same order—new moon, waxing crescent, first quarter, waxing gibbous, full moon, waning gibbous, last quarter, waning crescent and then new moon once again. The illuminated part of the Moon corresponding to these phases are respectively 0%, 25% on RHS, 50% on RHS, 75% on RHS, 100%, 75% on LHS, 50% on LHS, and 25% on LHS (figure 2). The phase corresponding to full moon could be possible because the plane of Moon revolution is inclined at an angle of 5.145° with plane of the rotation of the Earth around the Sun—the ecliptic plane; that is why solar and lunar eclipses do not happen more often because during most months the Moon is above or below the Earth.
Figure 1. Photograph of a crescent Moon showing earthshine.
Download figure:
Standard image High-resolution imageFigure 2. Half of the Moon is always lit by the Sun. As the Moon orbits the Earth, we see the different parts of the lighted area. The revolution of the Moon around the Earth makes the Moon look as if it is changing shape in the sky. These are called phases of the Moon. The Moon passes through eight major shapes during a cycle that repeats itself every 29.53 days. The phases always follow one another in same order—new moon, waxing crescent, first quarter, waxing gibbous, full moon, waning gibbous, third quarter, waning crescent and then new moon once again.
Download figure:
Standard image High-resolution imageEarthshine is most readily observable from shortly before until shortly after a new moon, during the waning or waxing crescent phase (figure 3). When the Moon is new as viewed from the Earth, the Earth is nearly fully lit up as viewed from the Moon. Despite being a rich source of information, earthshine is in fact very feeble, with brightness between a few thousand and a few tens of thousand times fainter than moonlight. Earthshine is used for astronomical scattering studies of the dark portion of a crescent Moon as well as for measuring the current albedo [6–9] of the Earth; albedo is the fraction of incoming solar energy reflected by the surface of the Earth and its atmosphere back into space, and is important in determining the amount of energy flowing into the climate system. At the simplest level, if the Earth's albedo increases, so that more sunlight is reflected, the climate will cool; conversely if the albedo decreases warmer climates will follow—in any case it affects the climate on the Earth. But climate change may in turn result in changes to the albedo; in other words they affect each other. Oceans reflect [10] the least amount of light, roughly 10%. Land reflects anywhere from 10%–25% of the Sun's light, and thick clouds or snow may reflect around 60%–90%. So, the part of the Earth where it is daytime and from which the Moon is visible determines how bright the Moon's earthshine appears at any given time.
Figure 3. Earthshine is most readily observable from shortly before until shortly after a new moon, during the waning or waxing crescent phase. The Sun's rays (A) light the surface of the Earth, get reflected (B) to illuminate the Moon and then reflected (C) light from the Moon appears as earthshine from the surface of the Earth.
Download figure:
Standard image High-resolution imageTheory
The solar energy which is electromagnetic [11, 12] in nature, follows Planck's radiation law [12–14]
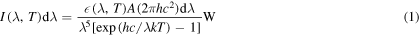
for the power  radiated between the wavelengths (in metres)
radiated between the wavelengths (in metres) 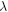 and
and 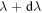 from the Sun's surface having uniform temperature
from the Sun's surface having uniform temperature 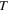 Kelvin, area
Kelvin, area 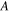 square metre and emissivity
square metre and emissivity 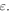 Here
Here 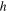 and
and 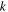 are Planck's constant and Boltzmann's constant, respectively. The wavelength
are Planck's constant and Boltzmann's constant, respectively. The wavelength 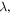 frequency
frequency 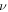 and velocity
and velocity 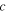 are joined by the relation
are joined by the relation

The wavelength 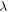 extends from below the radio frequencies at the long-wavelength end through gamma radiation at the short-wavelength end covering wavelengths from thousands of kilometres down to a fraction of the size of an atom; the limit for long wavelengths being the size of the Universe, while the short wavelength limit is in the vicinity of the Planck length [15]. However, in the present calculation it will be assumed that this electromagnetic spectrum is infinite and continuous. Considering the Sun to be an ideal blackbody (
extends from below the radio frequencies at the long-wavelength end through gamma radiation at the short-wavelength end covering wavelengths from thousands of kilometres down to a fraction of the size of an atom; the limit for long wavelengths being the size of the Universe, while the short wavelength limit is in the vicinity of the Planck length [15]. However, in the present calculation it will be assumed that this electromagnetic spectrum is infinite and continuous. Considering the Sun to be an ideal blackbody (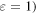 the solar flux
the solar flux 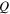 emitted over the entire wavelength from its unit area
emitted over the entire wavelength from its unit area 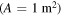 will be
will be

where  is the Stefan–Boltzmann constant. When this flux reaches the Earth this is diluted by the factor [13]
is the Stefan–Boltzmann constant. When this flux reaches the Earth this is diluted by the factor [13]

giving rise to the value of solar constant as

Here 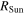 is the radius of the Sun and
is the radius of the Sun and  is the yearly mean distance between the Earth /Moon and the Sun.
is the yearly mean distance between the Earth /Moon and the Sun.
Solar luminous flux on the Earth (SLFOE)
It is well known that the wavelength region  to
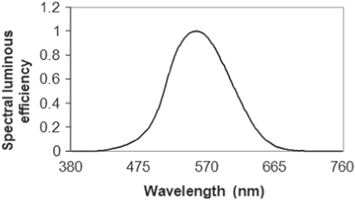
to 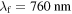 corresponds to visible light; however, the human eye is not equally sensitive to all wavelengths in this region. Rather, its spectral efficiency is highest at wavelength
corresponds to visible light; however, the human eye is not equally sensitive to all wavelengths in this region. Rather, its spectral efficiency is highest at wavelength 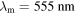 and becomes vanishingly small outside this interval. This behaviour is quantified by photopic spectral luminous efficiency
and becomes vanishingly small outside this interval. This behaviour is quantified by photopic spectral luminous efficiency  as a function [14, 16, 17] of
as a function [14, 16, 17] of 
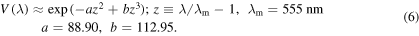
The curve corresponding to the above parameters overlaps with the experimental curve shown in figure 4 and therefore it has not been depicted. Also, at wavelength  the electromagnetic radiation of one watt provides a luminous flux of 683 lumens (lm). The number 683 was once referred to as the 'mechanical equivalent of light' in the literature [18]. Hence, according to (3) the luminous flux emitted at the surface of the Sun but with the power at each wavelength being weighted by multiplying it with
the electromagnetic radiation of one watt provides a luminous flux of 683 lumens (lm). The number 683 was once referred to as the 'mechanical equivalent of light' in the literature [18]. Hence, according to (3) the luminous flux emitted at the surface of the Sun but with the power at each wavelength being weighted by multiplying it with 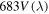 is given by
is given by
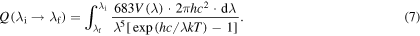
Figure 4. Plot of the spectral luminous efficiency values [17] V(λ) against the wavelength λ. It is well known that the wavelengths region 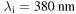 to λf = 760 nm correspond to the visible light; however the human eye is not equally sensitive to all wavelengths in this region. Rather its spectral efficiency is highest at wavelength λm = 555 nm and becomes vanishingly small outside this interval.
to λf = 760 nm correspond to the visible light; however the human eye is not equally sensitive to all wavelengths in this region. Rather its spectral efficiency is highest at wavelength λm = 555 nm and becomes vanishingly small outside this interval.
Download figure:
Standard image High-resolution imageThis is diluted by the factor [13] 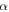 when it reaches the surface of the Earth giving the value of SLFOE [17] as
when it reaches the surface of the Earth giving the value of SLFOE [17] as

The above acronym variable SLFOE represents the amount of solar light arriving at a right angle on the Earth's surface covering an area of one square metre. Its unit is lux (lx).
Earthlight luminous flux on the Moon (ELFOM)
One can obtain the visual luminosity of the Earth 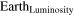 by multiplying the above flux (8) by Earth's albedo [18] in the visible range
by multiplying the above flux (8) by Earth's albedo [18] in the visible range 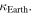 We get
We get

This is the amount of light reflected by the Earth in the direction normal to its surface area of one square metre under the assumption that the surface of the Earth is flat rather than a hemisphere keeping in view the pedagogic nature of the derivation. When this flux reaches the Moon it will be further diluted by the factor

Here 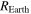 is the radius of the Earth and
is the radius of the Earth and 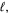 the distance between the Moon and the Earth. Multiplication of the expression (9) by the dilution factor
the distance between the Moon and the Earth. Multiplication of the expression (9) by the dilution factor 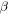 gives the expression for the ELFOM as
gives the expression for the ELFOM as

Here the acronym variable ELFOM represents the magnitude of earthy light the Moon intercepts in the direction normal to the incidence over an area of one square meter. Its unit is also lux. The condition that the Moon intercepts in the direction normal to the incidence is normally fulfilled during the full Earth illumination. Both the Earth and the Moon are, of course, spheres but in view of the pedagogic nature of the present calculation they are supposed to be flat plates as far as reflections are concerned.
Earthshine luminous flux on the Earth (ELFOE)
The illuminated dark portion of the crescent Moon will reflect the above mentioned flux as per its albedo [20]  in the visible range under the assumption that the surface of the Moon is flat. When this flux reaches the Earth it will be further diluted by the factor
in the visible range under the assumption that the surface of the Moon is flat. When this flux reaches the Earth it will be further diluted by the factor

Here 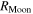 is the radius of the Moon and
is the radius of the Moon and 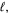 the distance between the Moon and the Earth. Multiplication of the expression (11) by Moon's albedo
the distance between the Moon and the Earth. Multiplication of the expression (11) by Moon's albedo 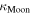 and the dilution factor
and the dilution factor 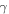 gives the expression for the ELFOE as
gives the expression for the ELFOE as
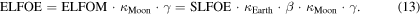
This is the desired expression of earthshine luminous flux. Here the acronym variable ELFOE represents the magnitude of earthshine light the Earth intercepts in the direction normal to the incidence over an area of one square metre under the assumption that the phase of the Moon is close to zero. This is consistent [4] with the fact that the earthshine is seen around the time of a new Moon when the Moon is hardly reflecting any sunlight in the Earth's direction; meanwhile, the Earth is facing the Sun and reflecting plenty of light back in the direction of the Moon. That reflected sunlight is in turn reflected back off the lunar surface to create earthshine.
It may be added here that the values of ELFOM and ELFOE will keep on changing around the year. The first reason being the distance between the Sun and the Earth which keeps on changing as it revolves in an elliptical orbit around the Sun—in the present paper the orbit is assumed to be circular. Secondly they are functions of  which has a minimum value
which has a minimum value 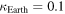 corresponding to the reflections of Sun's rays from the oceans of the Earth and a maximum value
corresponding to the reflections of Sun's rays from the oceans of the Earth and a maximum value 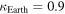 in case only thick clouds or snow are the reflectors; the corresponding extreme values of
in case only thick clouds or snow are the reflectors; the corresponding extreme values of 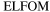 and
and 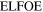 will be evaluated in the Numerical work section.
will be evaluated in the Numerical work section.
Apparent brightness of earthlight and earthshine
A nearby flashlight may appear to be brighter than a distant streetlight, but in absolute terms if they are compared side by side the flashlight is much dimmer. This statement contains the essence of the problem of determining stellar brightness in magnitude scale; optical astronomers almost always use something called the magnitude system [21, 22] to talk about the brightness of stars or any other astronomical object. Absolute magnitude, represented by the upper case letter M, is the hypothetical apparent magnitude of an object at a standard luminosity distance of exactly 10.0 parsecs or about 32.6 light years from the observer. The apparent magnitude, however, is represented by a lower case letter m, is a measure of its brightness as seen by an observer on the Earth and adjusted to the value it would have in the absence of the atmosphere. Generally the visible spectrum is used as the basis for the apparent magnitude. The brighter the object appears, the lower the value of its magnitude. The apparent magnitude [21] of a body in the visible band having flux F (in the unit lux) can be defined as

Here 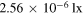 is the reference flux [23] in the same band such that of star Vega having apparent magnitude almost zero. The apparent magnitudes of the Sun with respect to the Earth, earthlight observed from the Moon and earthshine viewed from the Earth can be evaluated using the following expressions, respectively
is the reference flux [23] in the same band such that of star Vega having apparent magnitude almost zero. The apparent magnitudes of the Sun with respect to the Earth, earthlight observed from the Moon and earthshine viewed from the Earth can be evaluated using the following expressions, respectively

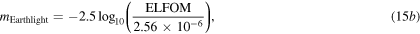
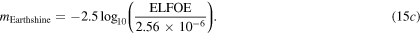
Students may verify that the apparent magnitude of the full Moon as observed from the Earth would be
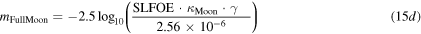
keeping in view that the value of solar luminous flux on the Moon would be equivalent to that on the Earth.
Numerical work
The solution of the integral of equation (7) is not possible analytically therefore this was evaluated numerically by Simpson's rule in the wavelength region 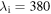 nm to
nm to 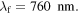 Substituting the values of data [11, 19, 20, 22, 24] corresponding to the Sun, Moon and the Earth from table 1 and the values of fundamental constants—Planck's constant
Substituting the values of data [11, 19, 20, 22, 24] corresponding to the Sun, Moon and the Earth from table 1 and the values of fundamental constants—Planck's constant 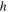
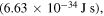 Boltzmann constant
Boltzmann constant 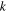
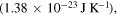 Stefan–Boltzmann constant
Stefan–Boltzmann constant 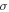
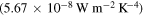 and the velocity of light
and the velocity of light 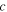
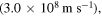 the dilution factors
the dilution factors  were estimated through expressions (4), (10) and (12), respectively
were estimated through expressions (4), (10) and (12), respectively
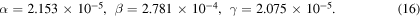
Table 1. Sun/Earth/Moon Data [11, 19, 20, 22, 24].
| Quantity | Symbol | Value |
|---|---|---|
| Radius of the Sun |
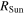
|
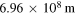
|
| Radius of the Moon |
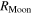
|
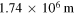
|
| Radius of the Earth |
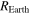
|
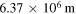
|
| Distance between Moon/Earth and Sun |
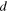
|
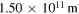
|
| Temperature of Sun's photosphere |
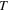
|
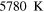
|
| Mean distance between Moon and the Earth |
|
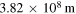
|
| Albedo of the Moon in the visible range |
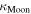
|
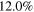
|
| Albedo of the Earth in the visible range |
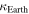
|
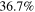
|
| Albedo of water of oceans on the Earth |
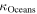
|
10% |
| Albedo of thick clouds/snow on the Earth |
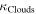
|
90% |
The quantities of interest SLFOE (8) and luminosity of the Earth (9) were evaluated
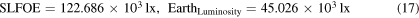
which, in turn, were used to find the values of ELFOM (11) and ELFOE (13) corresponding to the three cases—when the Sun's rays are reflected from the oceans, thick clouds or snow and the general surface of the Earth; it is reported in table 2. One can also calculate the apparent magnitudes of the Sun and the full Moon vide (15a) and (15d), respectively.

Table 2.
Earthlight luminous flux on the Moon 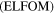 (vide (11)) and earthshine luminous flux on the Earth
(vide (11)) and earthshine luminous flux on the Earth 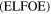 (vide (13)) values corresponding to three cases mentioned in column 2.
(vide (13)) values corresponding to three cases mentioned in column 2.
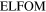
|

|
||||
|---|---|---|---|---|---|
| Albedo | Sun's rays are reflected from | Luminous flux 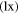
|
Apparent magnitude 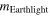
|
Luminous flux 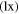
|
Apparent magnitude 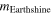
|
| 10% | Oceans | 3.412 | −15.31 | 8.496 · 10−6 | −1.30 |
| 90% | Thick clouds/snow | 30.707 | −17.70 | 7.646 · 10−5 | −3.69 |
| 36.7% | Average surface on the Earth | 12.522 | −16.72 | 3.118 · 10−5 | −2.71 |
The apparent magnitudes of earthlight as observed from the Moon and the earthshine observed from the Earth corresponding to the above-mentioned three cases were calculated (table 2). In fact the observer is supposed to be located on the Earth for quoting the value of apparent magnitude m but if one has to find the apparent magnitude of the Earth light itself then the Moon will be the suitable choice for location of the observer. The distance of the Vega star is practically same from both the Earth and the Moon.
Conclusions and discussion
The sunlight is reflected from the Earth and Moon both; the average albedo of the Moon and the Earth in the visible range are 0.12 and 0.367, respectively. The Moon provides a dim light to the Earth in the night whereas earthlight illuminates the dark portion of the crescent Moon with somewhat brighter light than the dim light from the Moon. Its observation from the Earth is called earthshine. Before satellite observations of the atmosphere were available, the observations related to earthshine were the only way to monitor the state of the Earth's atmosphere and the albedo of the Earth. As the amount of light reflected from the Earth depends on the part of the Earth facing the Moon or the cloud cover present, the strength of earthshine varies throughout the year. The apparent magnitude of earthshine light 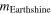 calculated here (15c) for the first time comes out to be in the range
calculated here (15c) for the first time comes out to be in the range 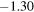 and
and 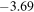 depending upon whether the Sun's rays are reflected from the oceans or thick clouds/snow, respectively. The experimental magnitude
depending upon whether the Sun's rays are reflected from the oceans or thick clouds/snow, respectively. The experimental magnitude 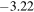 reported by Jackson [25] does lie within these extreme cases strengths; since a lower value of it represents a brighter earthshine the value reported by Jackson must have been measured while the Sun's rays were reflected from the thick clouds or snow on the Earth. It may be added here that the most probable value of
reported by Jackson [25] does lie within these extreme cases strengths; since a lower value of it represents a brighter earthshine the value reported by Jackson must have been measured while the Sun's rays were reflected from the thick clouds or snow on the Earth. It may be added here that the most probable value of 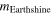 is
is  because this corresponds to the reflection of the Sun's rays from the average surface of the Earth.
because this corresponds to the reflection of the Sun's rays from the average surface of the Earth.
The apparent magnitudes of the Sun (15a) and full Moon (15d) are respectively, 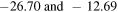 and these are also consistent with the reported values
and these are also consistent with the reported values 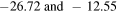 in the literature [21, 26]. The apparent magnitude of earthlight
in the literature [21, 26]. The apparent magnitude of earthlight 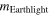 as observed from the Moon was also calculated for the first time and it lies between
as observed from the Moon was also calculated for the first time and it lies between 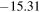 and
and 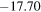 depending upon whether the Sun's rays are being reflected from oceans or thick clouds/snow. However, its most probable value being
depending upon whether the Sun's rays are being reflected from oceans or thick clouds/snow. However, its most probable value being 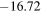 corresponding to the case the Sun's rays encounter the average surface of the Earth; this shows that the earthlight is
corresponding to the case the Sun's rays encounter the average surface of the Earth; this shows that the earthlight is  magnitude brighter than the full Moon as had been mentioned by Heinrich Hertz [1].
magnitude brighter than the full Moon as had been mentioned by Heinrich Hertz [1].
It may be added here that for the calculation of earthshine and its magnitude one requires the albedo in the visible range both for the Earth and the Moon whereas for actual effect of albedo on the climate of the Earth its value over the entire spectrum is needed. This value [19] is 0.306 which is lower than its counterpart in the visible range (0.367). This requires a thorough mapping of spectrum of earthshine through experiments by the experts. Regular photometric observations of the Moon's earthshine from the Big Bear Solar Observatory [27] since December 1998 have quantified the Earth's albedo. They have concluded an average terrestrial albedo of 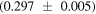 which agrees with that from simulations based upon both changing snow and ice cover and satellite derived cloud cover representing the site on the Earth
which agrees with that from simulations based upon both changing snow and ice cover and satellite derived cloud cover representing the site on the Earth 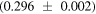 as well as the value 0.306 quoted by NASA [19].
as well as the value 0.306 quoted by NASA [19].
Earthshine is now being employed [28, 29] to search for extra-solar terrestrial planets for finding signs of life or habitability via spectroscopic bio-signatures. Spectroscopic bio-signatures are spectral features that are either indicative of a planetary environment that is hospitable to life (such as the presence of liquid water) or of strong indicators of life itself (such as abundant O2 in the presence of CH4). The much larger sharp rise (between 700 and 800 nm) is known as the red edge and is due to the contrast between the strong absorption of chlorophyll and the otherwise reflective leaf. Earth's deciduous plants have a sharp order-of-magnitude increase in leaf reflectance between 700 and 800 nm wavelengths.