Abstract
Exploration of macroscopic quantum entanglement is of great interest in both fundamental science and practical application. We investigate a hybrid quantum system that consists of two nitrogen-vacancy centers ensembles (NVE) coupled to a superconducting coplanar waveguide resonator (CPWR). The collective magnetic coupling between the NVE and the CPWR is employed to generate macroscopic entanglement between the NVEs, where the CPWR acts as the quantum bus. We find that, this NVE-CPWR hybrid system behaves as a system of three coupled harmonic oscillators and the excitation prepared initially in the CPWR can be distributed into these two NVEs. In the nondissipative case, the entanglement of NVEs oscillates periodically and the maximal entanglement always keeps unity if the CPWR is initially prepared in the odd coherent state. Considering the dissipative effect from the CPWR and NVEs, the amount of entanglement between these two NVEs strongly depends on the initial state of the CPWR and the maximal entanglement can be tuned by adjusting the initial states of the total system. The experimental feasibility and challenge with currently available technology are discussed.
Similar content being viewed by others
Introduction
Recently, significant progress has been made in the quantum hybrid system consisting of a variety of physical systems, which combines the merits of two or more physical systems and mitigates their individual weaknesses. Especially, the hybrid quantum model including solid-state spin systems and superconducting coplanar waveguide resonator (CPWR) systems1,2,3,4,5,6,7,8,9,10,11, provides a promising platform to study the intriguing quantum optic phenomena as well as the fundamental quantum information (QI) science. Especially, spin-qubit in the solid-state system attract considerable interest because they can be used to store and transfer the QI12. Additionally, the coherence times of isolated or peculiar spins are usually long due to their weak interaction with the environment. For instance, the diamond nitrogen-vacancy (NV) centers, which are formed by nitrogen atoms substituting for carbon atoms and adjacent vacancies in a diamond, feature long coherence times of electron (nuclear) spin with about one ms (one sec) in a wide temperature range13,14,15,16,17,18,19,20,21,22,23,24,25,26,27. More importantly, the NV centers have the ability to coherently couple to various external fields simultaneously, such as both optical and microwave fields28,29. However, induced by the vacuum fluctuations of the photons, individual NV center couples to the CPWR with a very weak strength far below the linewidth of CPWR with dozens of kHz30,31, which is unfavorable for the coherent exchange of QI. Whereas, the collective coupling strength between a NV centers spin ensemble (NVE) and the CPWR will be enhanced by the value of 
with 
the total number of NV centers in the spin ensembles2,3,32. More importantly, compared to the conventional electric-dipole couplings mechanism, the employment of collective magnetic coupling for manipulating spin ensembles brings vital advantages12,14,32,33,34. To date, series of experimental demonstrations of strong magnetic couplings between NVE and CPWR1,2,3,4,5 have attracted considerable interest in the potential applications35,36,37,38,39,40,41.
On the other hand, due to the fragile nature of single-particle suffering severely from decoherence, it is desired to explore various channels to effectively construct highly entangled states in larger quantum systems, which is one of the central ingredients for large-scale quantum computation42. Recently, much particular attention has been paid to quantum entanglement of macroscopic samples43,44,45,46 owing to their unique quantum characteristics47,48, such as robustness to single-particle decoherence and relatively simple experimental realization. Consequently, developing experiments and theories for the useful interfacing of disparate macroscopic quantum systems like NVEs is increasingly important and interesting. Lately, many efforts have been devoted to the achievement of entanglement between separate macroscopic atomic ensembles, polar molecule ensembles and electronic spin ensembles using different methods, including projective measurements45,49,50, quantum reservoir engineering51,52, spontanous/stimulated Raman scattering53,54, adiabatic quantum feedback55, intracavity electromagnetically induced transparency48 and so on.
In this work, we investigate a hybrid quantum system that consists of two separated NVEs coupled to a common CPWR, where each pair of NVE-CPWR interaction actually is a coherent coupling between two harmonic oscillators or bosonic fields with a collectively enhanced strength proportional to 
. In our case, the collective NVE-CPWR magnetic coupling is used to generate entanglement between the NVEs and decoherence effects from both the CPWR and the NVEs on the entanglement dynamics of NVEs have also been studied by employing the quantum trajectory method56,57,58,59. More importantly, we propose a practical scalable and tunable architecture in this model for investigating quantum dynamics of the NVEs and realizing entangled states between the NVEs. Furthermore, the present method provides us the potential feasibility of generating multi-NVE entanglement, which is a crucial element in the NVE-based quantum network. We find that, this NVE-CPWR hybrid system behaves as a system of three coupled harmonic oscillators and the excitation prepared initially in the CPWR can be transferred and distributed in these two NVEs. In the nondissipative case, the entanglement of NVEs oscillates periodically and the maximal entanglement always keeps unity if the CPWR is initially prepared in the odd coherent state and the situation becomes different in the case of even coherent state. Considering the dissipative effect from the CPWR and NVEs, the amount of entanglement between the two NVEs strongly depends on the initial state of the CPWR and the maximal entanglement can be tuned by adjusting the initial states of system. Our further study reveals that the maximal entanglement between the NVEs could be achieved through accurately adjusting the tunable parameters, such as the initial states of the resonator field as well as the coupling rates. Our detailed analysis could find a way to extract the optimal experimental parameters for maximal entanglement between the NVEs using the increasingly-developed nanoscale solid-state technology, even in the presence of dissipative effects of the spin ensemble and superconducting resonator.
Results
System and Model
The system under consideration is illustrated in Fig. 1, the device we study is a combined NVE-CPWR system governed by the Hamiltonian
Schematic setup of the hybrid system consisting of two NVEs and a CPWR, where the two separated NVEs are placed in the resonator’s surface and are coupled to the same CPWR through the collective magnetical coupling.
The inset shows the level structure of single NV center, where the electronic ground and first excited states are electron spin triplet states with S = 1 and 
GHz is the zero-field splitting between the 
sublevels and the lowest energy 
sublevel.
The microwave-driven CPWR (with the length L, the capacitance Cc and the inductance Fc) consists of a narrow center conductor and two nearby lateral ground planes, whose Hamiltonian has the following form (in units of 
where a 
is the annihilation (creation) operator of the full-wave mode and 
is the corresponding eigenfrequency. The distributions of current and voltage inside the CPWR have the expression 
and 
.
The Hamiltonian of a NVE containing 
NV centers reads 
where 
is the collective spin operator for the spin ensemble with 
, 
and 
. For clarity of our discussion, two symmetric Dicke excitation states 
with 
and 1 are introduced as 
and 
, which could be encoded as the qubit of NVE. Through the collective magnetic-dipole coupling, the NVE-CPWR interaction Hamiltonian can be described by 
with g being the single NV vacuum Rabi frequency. Due to the fact that the mode wavelength of CPWR is larger than the spatial dimension of the NVE when the spin ensemble is placed near the field antinode, all the NV spins in ensemble interact symmetrically with a single mode of electromagnetic field. Using the Holstein-Primakoff (HP) transformation60,61, the spin operators can be mapped into the boson operators as follows: 
and 
, where the operators 
and 
obey the standard boson commutator 
in the case of weak excitation.
So the total Hamiltonian of the NVE-CPWR coupling system is given by
where 
represents the collective coupling strength between the k-th NVE and CPWR with 
. Meeting the condition 
, we can obtain the following Hamiltonian 
. One can find that the interactions between the two NVEs and the CPWR could be reduced to the coupling of three bosonic fields or harmonic oscillators. Taking the dissipative effects from the NVEs and the CPWR into account, the dissipative dynamics of the total system can be effectively described by employing the quantum trajectory method56,57 with the conditional Hamiltonian58
where 
and 
are the decay rates of the k-th NVEs and the CPWR, respectively. This is a reasonable assumption for the region of interest, where the decay rates are not dominant and the CPWR has a very small probability to be detected with a photon. For simplicity, here we have assumed 
in our model.
Entanglement dynamics of Nitrogen-vacancy centers spin ensembles
In this section we will focus on the Entanglement dynamics of Nitrogen-vacancy centers spin ensembles. According to the Heisenberg motion equations, we can obtain the differential equations of the operators 
and 
as
Considering the initial conditions 
, we obtain the following analytical solution
where the expression of coefficients Xi, Yi and Zi (i = 1, 2, 3) are 
,
and 
with 
, 
, 
and 
. Here we set 
Suppose that the CPWR is initially prepared in an arbitrary normalized superposition of the coherent state 
62,63 and the NVEs are prepared in their vacuum states 
, where 
, 
and 
are the normalized coefficient with 
arbitrary complex numbers and * complex conjugation. Under these initial conditions, the time-dependent wave function of the total system 
can be expressed as 
with time evolution operator 
. A straightforward calculation yields
where we have used the relationships 
and 
. To investigate the entanglement dynamics between the NVEs, we need to trace over the degree of freedom of the CPWR as 
, which yields
where h.c. denotes Hermitian conjugate and 
is the inner product of the two coherent states 
and 
.
Through the calculation, the concurrence of two NVEs has the form
Here we have employed the relations 
, 
and 
.
Besides, the average phonon number 
of the CPWR can also be obtained as follows
where 
.
Firstly, we consider the simple case that the CPWR is initially prepared in the odd coherent state 
and the even coherent state 
with normalization constants 
and 
, respectively. So we can obtain 
and 
. As a result, the concurrence of NVEs and the average phonon number of CPWR can be expressed by
where 
.
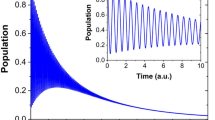
The entanglement dynamics of NVEs is plotted in Fig. 2 as functions of time and parameter 
in the nondissipative/dissipative case. In the present system, the collective magnetic coupling between the NVE and the CPWR is employed to generate macroscopic entanglement between the spin ensembles, where the CPWR acts as the common quantum bus. One can find that, in the nondissipative case, the concurrence oscillates periodically and the maximal value of the concurrence 
always keeps unity for any values of 
in the case of odd coherent state 
in Fig. 2(a). It implies that the excitation initially prepared in CPWR is reversibly transferred between the NVEs and the CPWR. The situation becomes different, as shown in the Fig. 2(c) for the even coherent state 
and the maximal values 
are gradually close to one with the growth of the 
. Considering the dissipative effect from the CPWR and NVEs in Fig. 2(b,d), it is worth noting that the amount of entanglement between the two NVEs strongly depends on the initial state of the CPWR and 
increases gradually. Another interesting feature is that the values of 
are enhanced with the growth of the values of 
. therefore, this NVE-CPWR hybrid system behaves as a composite system of three coupled harmonic oscillators and the excitation can be transferred and distributed in these two NVEs if we initially prepare the excitation in the common databus, namely, the CPWR.
The concurrence as a function of Gt and 
when the CPWR is initially prepared in (a,b) odd coherent state 
and (c,d) even coherent state 
, respectively. The left and right panels denote the nondissipative case 
and the dissipative case 
, 
, respectively.
In Fig. 3, we explicitly quantify the time-dependent concurrence and the average number of phonon 
of the CPWR by setting 
. One can find that the maximal values of concurrence appear if and only if 
is zero in the case of odd or even coherent state. However, the maximal values of concurrence can reach one in the case of the odd coherent state, rather than the even coherent state, which could be understood by the above expression in Eq. (10). We also show that the concurrence and 
oscillate with the same period and the period of the odd coherent state 
is longer than that of the even coherent state 
. To study the dynamics in more general cases, we assume that the CPWR is initially prepared in a coherent superposition state 
with 
the normalized coefficient. The dynamics of concurrence is plotted as functions of time and parameter 
in Fig. 4, where we set 
. It turns out that the of two NVEs in this case are entangled in an oscillating way and the decoherence effects degrade the entanglement between the spin ensembles, as shown in Fig. 4(b,d).
The concurrence (the grey line) and the average phonon number (the blue line) as functions of the dimensionless time, where we set 
and the CPWR is initially prepared in the odd coherent state (a) and even coherent state (b), respectively. The solid and dashed lines represent the nondissipative case 
, 
and the dissipative case 
, 
, respectively.
The concurrence as a function of Gt and 
when the CPWR is initially prepared in the coherent superposition state (a,b) 
and (c,d) 
, respectively, where 
. The left and right panels denote the nondissipative case 
and the dissipative case 
, 
, respectively.
Discussion
We now survey the relevant experimental parameters. First, a full wave frequency 
GHz of resonator mode could be obtained if the CPWR has the inductance 
nH and the capacitance 
pF. Second, to ensure that the NVE-CPWR coupling could obtain the maximal values, the NVEs should be located symmetrically in the position where the magnetic field of resonator is maximal. Thirdly, the feasibility of our scheme could be confirmed by series of experimental demonstration of NVE-CPWR strong magnetic coupling with the strength ~ dozens of MHz, as well as the experimental advances in excellent quantum control in the quantum hybrid system consisting of a superconducting flux qubit and NVE. Finally, the electron relaxation time 
of NV centers could reach 6 ms at room temperature64, even reach 
s if we place NV centers at lower temperature65. In addition, using a spin echo sequence, the dephasing time can be greatly enhanced by decoupling the electron spin from its local environment. Based this technique, the dephasing time of the NVE reaches 3.7 μs at room temperature35 and the dephasing time 
for NVE with natural abundance of 13C has been reported that it could reach 0.6 ms66, which has been prolonged to be T2 = 1.8 ms in the isotopically pure diamond sample67. Another major decoherence source is the dipole-interaction between the NV center spins and the redundant Nitrogen spins, which could be suppressed by enhancing the conversion rate from nitrogen to NV, while keeping the almost stable collective coupling constants35. Alternatively, by applying the external driving field to the electron spins of the Nitrogen atoms, the coherence time of the NVE could be It would increased if the flip-flop processes is much slower than the rate of flipping of these spins68.
In the above discussion, the the detrimental influence from the nuclear spin, such as 13C defects in the spin ensemble have been ignored, nevertheless, this problem could be alleviated by isotopically purified 12C diamond through the purification technique67,68. Note that the present method provides us the potential feasibility of generating multi-NVE entanglement, which is a crucial element in the NVE-based scalable quantum network. We emphasize that the multi-NVE dynamics itself is more complicated and could exhibit richer dynamical behavior than the two-qubit case69,70,71. Therefore, it is desirable to investigate the quantum dynamics of NVEs in a scalable way and to develop efficient methods for controlling the entanglement dynamics of many NVEs in a common resonator. However, this issue goes beyond the scope of the present paper. Noticeably, the multi-NVE dynamics in different model have been studied for large-scale arrays72.
In the following we provide the reason that we can use the quantum jump model (Eq. (3)) to study the dephasing effect. In this work we give a phenomenological model for deeply understanding the decay of NVE collective excitation induced by the dephasing effects, which is mainly from the inhomogeneous broadening. In other word the dephasing time of the NVE is around 1/κ. Because of the local environment difference, the frequencies of the electron spins in NVE are not identical and the mean frequency is denoted as 
. For single excitation of NVE, if the initial state is 
, we will lose the information of the collective excitation due to the inhomogeneous broadening. Therefore, after dephasing time 
, the NVE will reach the final state 
, which is completely mixed state with excitation number 1. We can easily to verify that the overlap between initial and the final state 
approaches to zero. Therefore, the initial and final state can be viewed as two orthogonal states. Besides, we find that the final mixed state 
is nearly decoupled with the reaonator mode, as there is no collective coupling enhancement for the mixed state. The single excitation decay equation can be written as 
. For the higher excitation states (Dicke states) with low excitation number 
, the similar results are held too. The initial collective state 
will decay to the final mixed state 
because of dephasing and the excitation number m is fixed during the processing. The initial and the final states for the m-th excitation states are also orthogonal. The evolution equation of it is 
. Therefore, we find that the pure dephasing induces the amplitude decay of the collective excitation of NVE. The decay rate is equal to the dephasing rate of the NVE.
In order to measure the macroscopic entanglement in realistic experimetns, we need to transfer the state from the NVEs to the states of two additional small flux qubits, each of which is attached on a NVE. So the task of entanglement dectection can be performed by the direct measurement on the states of additional flux qubits and implementation of transferring the state from NVEs to flux qubits could be realized by using the SWAP gate between the j-th NVE and the j-th flux qubits, like the method in40. We should note that, in order to guarantee the collective mode detected by the small qubit is the same mode prepared by the resonator, the coupling strength between the each NV center to the resonator mode should be proportional to that to the small qubit40.
In summary, we have presented a study on the dynamics of entanglement between spin ensembles via the collective coupling between the CPWR and NVEs in such a hybrid system composed by a CPWR and two NVEs. This NVE-CPWR hybrid system behaves as a system of coupled harmonic oscillators and the excitation prepared initially in the CPWR can be transferred and distributed in these two NVEs, where the CPWR plays the role of common databus. The decoherence effects from the CPWR and NVEs on the quantum dynamics of the entanglement between spin ensembles have also been studied. Therefore, the present system provides a platform to generate quantum entanglement between two or more NVEs embedded in the same resonator, which may be another route toward building a distributed QIP architecture and future NVE-based quantum network.
Method
Calculations of concurrence
Before using the concept of concurrence for bipartite entangled nonorthogonal states73,74 to measure entanglement between the NVEs, we transform the nonorthogonal form in Eq.(7) into an orthogonal form by rebuilding two orthogonal and normalized states as basis of the two-dimensional Hilbert space. Using the Gram–Schmidt orthogonalization process75, we can define
where 
and 
. In this new basis, the reduced density operator of NVEs (Eq.(7)) can be rewritten into
Therefore the elements of the orthogonal form ρ are
It is easy to obtain the square roots of eigenvalues of the matrix 
in Eq. (11) as 
, 
and 
. As a result, the concurrence of two NVEs has the form
Additional Information
How to cite this article: Liu, Y. et al. Entanglement dynamics of Nitrogen-vacancy centers spin ensembles coupled to a superconducting resonator. Sci. Rep. 6, 21775; doi: 10.1038/srep21775 (2016).
References
Kubo, Y. et al. Strong Coupling of a Spin Ensemble to a Superconducting Resonator. Phys. Rev. Lett. 105, 140502 (2010).
Amsüss, R. et al. Cavity QED with Magnetically Coupled Collective Spin States. Phys. Rev. Lett. 107, 060502 (2011).
Fink, J. M. et al. Dressed Collective Qubit States and the Tavis–Cummings Model in Circuit QED. Phys. Rev. Lett. 103, 083601 (2009).
Ranjan, V. et al. Probing Dynamics of an Electron–Spin Ensemble via a Superconducting Resonator. Phys. Rev. Lett. 110, 067004 (2013).
Grezes, C. et al. Multimode Storage and Retrieval of Microwave Fields in a Spin Ensemble. Phys. Rev. X 4, 021049 (2014)
Schuster, D. I. et al. High–Cooperativity Coupling of Electron–Spin Ensembles to Superconducting Cavities. Phys. Rev. Lett. 105, 140501 (2010).
Huebl, H. et al. High Cooperativity in Coupled Microwave Resonator Ferrimagnetic Insulator Hybrids. Phys. Rev. Lett. 111, 127003 (2013).
Eddins A. W., Beedle C. C., Hendrickson D. N. & Friedman J. R. Collective Coupling of a Macroscopic Number of Single-Molecule Magnets with a Microwave Cavity Mode. Phys. Rev. Lett. 112, 120501 (2014).
Probst. S., Rotzinger, H., Ustinov, A. V. & Bushev, P. A. Microwave multimode memory with an erbium spin ensemble. Phys. Rev. B 92, 014421 (2015).
Krimer. D. O., Hartl, B. & Rotter, S. Hybrid Quantum Systems with Collectively Coupled Spin States: Suppression of Decoherence through Spectral Hole Burning. Phys. Rev. Lett. 115, 033601 (2015).
Grezes, C. et al. Towards a spin-ensemble quantum memory for superconducting qubits. arxiv: 1510.06565 (2015)
Xiang, Z. L., Ashhab, S., You, J. Q. & Nori, F. Hybrid quantum circuits: Superconducting circuits interacting with other quantum system. Rev. Mod. Phys. 85, 623 (2013).
Jelezko, F., Gaebel, T., Popa, I. Gruber, A. & Wrachtrup, J. Observation of Coherent Oscillations in a Single Electron Spin. Phys. Rev. Lett. 92, 076401 (2004).
Zhu, X. et al. Coherent coupling of a superconducting flux qubit to an electron spin ensemble in diamond. Nature 478, 221–224 (2011).
Zhu, X. et al. Observation of dark states in asuperconductor diamond quantum hybrid system. Nature Commun. 5, 3424 (2014).
Jelezko, F. et al. Observation of Coherent Oscillation of a Single Nuclear Spin and Realization of a Two–Qubit Conditional Quantum Gate. Phys. Rev. Lett. 93, 130501 (2004).
Jiang, L. et al. Repective Readout of a single Electronic Spin via Quantum Logic with Nuclear Spin Ancillae. Science 326, 267–271 (2009).
Rabl, P. et al. A quantum spin transducer based on nanoelectromechanical. Nature Phys. 6, 602–608 (2010).
Togan, E. et al. Quantum entanglement between an optical photon and a solid–state spin qubit. Nature 466, 730–734 (2010).
Maurer, P. C. et al. Room–Temperature Quantum Bit Memory Exceeding One Second. Science 336, 1283–1286 (2012).
Neumman, P. et al. Quantum register based on coupled electron spins in a room–temperature solid. Nature Phys. 6, 249–253 (2010).
Liu, Y. C. et al. Coupling of a single diamond nanocrystal to a whispering–gallery microvavity: Photon transport benefitting from Rayleigh scattering. Phys. Rev. A 84, 011805 (2011).
Yu, X. C. et al. Coupling of diamond nanocrystals to a high–Q whispering–gallery microresonator. Phys. Rev. A 86, 043833 (2012).
Li, P. B. et al. Dissipative preparation of entangled states between two spatially separated nitrogen–vacancy centers. Phys. Rev. A 85, 042306 (2012).
Yang, W. L., Yin, Z. Q., Xu, Z. Y., Feng, M. & Du, J. F. One–step implementation of multiqubit conditional phase gating with nitrogen–vacancy center coupled to a high–Q silica microsphere cavity. Appl. Phys. Lett. 96, 241113 (2010).
Zhao, N. & Yin, Z. Q. Room-temperature ultrasensitive mass spectrometer via dynamical decoupling. Phys. Rev. A 90, 042118 (2014).
Yin, Z. Q., Li, T. C., Zhang, X. & Duan, L. M. Large quantum superpositions of a levitated nanodiamond through spin-optomechanical coupling. Phys. Rev. A 88, 033614 (2013).
Jacques, V., Dynamic Polarization of Single Nuclear Spins by Optical Pumping of Nitrogen–Vacancy Color Centers in Diamond at Room Temperature. Phys. Rev. Lett. 102, 057403 (2009).
Hanson, R., Mendoza, F. M., Epstein, R. J. & Awschalom, D. D. Polarization and Readout of Coupled Single Spins in Damond. Phys. Rev. Lett. 97, 087601 (2006).
Abdumalikov, A. A., Astafiev, O., Nakamura, Y., Pashkin, Y. A. & Tsai, J. Vacuum Rabi splitting due to strong coupling of a flux qubit and a coplanar–waveguide reasonator. Phys. Rev. B 78, 180502 (2008).
Twamley, J. & Barrett, S. D. Superconducting cavity bus for single nitrogen–vacancy defect center in diamond. Phys. Rev. B 81, 241202 (2010).
Imamoğlu, A. Cavity QED Based on Collective Magnetic Dipole Coupling: Spin Ensembles as Hybrid Two–Level–Systems. Phys. Rev. Lett. 102, 083602 (2009).
Wesenberg, J. H. et al. Quantum Computing with an Electron Spin Ensemble. Phys. Rev. Lett. 103, 070502 (2009).
Wallquist M., Hammerer K., Rabl P., Lukin M. & Zoller P. Hybrid quantum devices and quantum engineering. Phys. Scr. T137 014001 (2009).
Kubo, Y. et al. Hybrid Quantum Circuit with a Superconducting Qubit Coupled to a Spin Ensemble. Phys. Rev. Lett. 107, 220501 (2011).
Julsgaard, B., Grezes, C., Bertet, P. & Mømer, K. Quantum Memory for Microwave Photons in an Inhomogeneously Broadened Spin Ensemble. Phys. Rev. Lett. 110, 250503 (2013).
Putz, S. Protecting a spin ensemble against decoherence in the strong–coupling regime of cavity QED. Nature Phys. 10, 720–724 (2014).
Yang, W. L. et al. Quantum simulation of an artificial Abelian gauge field using nitrogen–vacancy–center ensembles coupled to superconducting. Phys. Rev. A 86, 012307 (2012).
Yang, W. L., Yin, Z. Q., Hu, Y., Feng, M. & Du, J. F. High–fidelity quantum memory using nitrogen–vacancy center ensemble for hybrid quantum computation. Phys. Rev. A 84, 010301 (2011).
Song, W. L. et al. One-step generation of multipartite entanglement among nitrogen–vacancy center ensembles. Sci. Rep. 5, 7755 (2015).
You, J. B., Yang, W. L., Xu, Z. Y., Chan, A. H. & Oh, C. H. Phase transition of light in circuit-QED lattices coupled to nitrogen-vacancy centers in diamond. Phys. Rev. B 90, 195112 (2014).
Stoneham, M. Trend: Is a room–temperature, solid–state quantum computer mere fantasy? Physics 2, 34 (2009).
Duan, L. M. Entangling Many Atomic Ensembles through Laser Manipulation. Phys. Rev. Lett. 88, 170402 (2002).
Li, L., Dudin, Y. O. & Kuzmich, A. Entanglement between light and an optical atomic excitation. Nature 498, 466–469 (2013).
Julsgaard, B., Kozhekin, A. & Polzik, E. S. Experimental long–lived entanglement of two macroscopic objects. Nature 413, 400–403 (2001).
Sørensen, A., Duan, L. M., Cirac, J. I. & Zoller, P. Many–particle entanglement with Bose–Einstein condensates. Nature 409, 63–66 (2001).
Reid, M. D. & Drummond, P. D. Quantum Correlations of Phase in Nondegenerate Parametric Oscillation. Phys. Rev. Lett. 60, 2731 (1988).
Lukin, M. D., Yelin, S. F. & Fleischhauer, M. Entangle of Atomic Ensembles by Trapping Correlated Photon States. Phys. Rev. Lett. 84, 4232 (2000).
Duan, L. M., Lukin, M. D., Cirac, J. I. & Zoller, P. Long–distance quantum communication with atomic ensembles and linear optics. Nature 414, 413–418 (2001).
Chou, C. W. et al. Measurement–induced entanglement for excitation stored in remote atomic ensembles. Nature 438, 828–832 (2005).
Krauter, H. et al. Entanglement Generated by Dissipation and Steady State Entanglement of two Macroscopic Objects. Phys. Rev. Lett. 107, 080503 (2011).
Muschik, C. A., Polzik, E. S. & Cirac, J. I. Dissipatively driven entanglement of two macroscopic atomic ensembles. Phys. Rev. A 83, 052312 (2011).
Matsukevich, D. N. et al. Entanglement of Remote Atomic Qubits. Phys. Rev. Lett. 96, 030405 (2006).
Ji, W., Wu, C., van Enk, S. J. & Raymer, M. G. Mesoscopic entanglement of atomic ensembles through nonreasonant stimulated Raman scattering. Phys. Rev. A 75, 052305 (2007).
Lisi, A. D., Siena, S. D., Illuminati, F. & Vitali, D. Quasideterministic generation of maximally entangled states of two mesoscopic atomic ensembles by adiabatic quantum feedback. Phys. Rev. A 72, 032328 (2005).
Plenio, M. B. & Knight, P. L. The quantum–jump approach to dissipative dynamics in quantum. Rev. Mod. Phys. 70, 101 (1998).
Beige, A., Braun, D., Tregenna, B. & Knight, P. L. Quantum Computing Using Dissipation to Remain in a Decoherence–Free Subspace. Phys. Rev. Lett. 85, 1762 (2000).
Browne, D. E., Plenio, M. B. & Huelga, S. F. Robust Creation of Entanglement between Ions in Spatially Separate Cavities. Phys. Rev. Lett. 91, 067901 (2003).
Zheng, S. B. Quantum logic gates for two atoms with a single reasonant interaction. Phys. Rev. A 71, 062335 (2005).
Hammerer, K., Søensen, A. S. & Polzik, E. S. Quantum interface between light and atomic ensemble. Rev. Mod. Phys. 82, 1041 (2010).
Chen, G. et al. Qubit–induced high–order nonliner interaction of the polar molecules in a stripline cavity. Phys. Rev. A 82, 013601 (2010).
Armour, A. D., Blencowe, M. P. & Schwab, K. C. Entangelement and Decoherence of a Micromechanical Resonator via Coupling to a Cooper–Pair Box. Phys. Rev. Lett. 88, 148301 (2002).
Garcia, L., Chhajlany, R. W., Li, Y. & Wu, L. A. Driving a mechanical reasonator into coherent states via random measurement. J. Phys. A: Math. Theor. 46, 852–859 (2013).
Neumann, P. Multipartite Entanglement Among Single Spins in Diamond. Science 320, 1326–1329 (2008).
Harrison, J., Sellars, M. J. & Manson, N. B. Measurement of the optically induced spin polarisation of N-V centres in diamond. Diam. Relat. Mater. 15, 586–588 (2006).
Stanwix, P. L. et al. Coherence of nitrogen–vacancy electronic spin ensembles in diamond. Phys. Rev. B 82, 201201 (2010).
Balasubramanian, G. et al. Ultralong spin coherence time in isotopically engineered diamond. Nat. Materials 8, 383–387 (2009).
Marcos, D. et al. Coupling Nitrogen–Vacancy Centers in Diamond to Superconducting Flux Qubits. Phys. Rev. Lett. 105, 210501 (2010).
de Vicente, J. I., Carle, T., Streitberger, C. & Kraus, B. Complete Set of Operational Measures for the Characterization of Three–Qubit Entanglement. Phys. Rev. Lett. 108, 060501 (2012).
Armstrong, S. et al. Multipartite Einstein–Podolsky–Rosen steering and genuine tripartite entanglement with optical networks. Nature Phys. 11, 167 (2015).
Song, W. L. et al. Entanglement dynamics for three nitrogen–vavancy centers coupled to a whispering–gallery–mode microcavity. Opt. Express 23, 13734–13751 (2015).
Badshah. F., Qamar, S. & Paternostro, M. Dynamics of interacting Dicke model in a coupled–cavity array. Phys. Rev. A 90, 033813 (2014).
Wang, X. Bipartite entangled non–orthogonal states. J. Phys. A: Math. Gen. 35, 165–173 (2002).
Jeong, H., Kim, M. S. & Lee, J. Quantum–information processing for a coherent superposition state via a mixedentangled coherent channel. Phys. Rev. A 64, 052308 (2001).
Mertins, F. & Schirmer, J. Algebraic propagator approaches and intermediate–state representations. I. The biorthogonal and unitary coupled–cluster methods. Phys. Rev. A 53, 2140 (1996).
Acknowledgements
This work was supported by the National Science Foundation of China (Grant Nos 11372122, 10874122 and 11074070) and the Program for Excellent Talents at the University of Guangdong province (Guangdong Teacher Letter [1010] No. 79).
Author information
Authors and Affiliations
Contributions
Y.M.L. conceive the idea. Y.M.L., Y.J.B. and H.Q.Z. carry out the research and write the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Liu, Y., You, J. & Hou, Q. Entanglement dynamics of Nitrogen-vacancy centers spin ensembles coupled to a superconducting resonator. Sci Rep 6, 21775 (2016). https://doi.org/10.1038/srep21775
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep21775
This article is cited by
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.
