INTRODUCTION

How can a system be flexible and adaptive, while maintaining a sufficient stability? There seems to be a trade-off between the two: a better stability is achieved at the expense of a worse flexibility (adaptability), and vice versa. Yet, it is essential that the system is stable to short-term fluctuations, or common insignificant events, while it should also be able to react to weak signals and rare important events, as well as adapting to long-term changes. This so-called stability–flexibility dilemma is of particular concern for the neural system, which presumably has evolved to give an efficient interaction with the environment. Such an evolutionary pressure is likely to be reflected in both structure and dynamics, which are results of processes at different time scales. A similar ‘dilemma’ of keeping a (dynamical) balance between stability and flexibility, or more generally, between order and disorder, is likely to apply also to mental processes and disorders.

For example, it has been hypothesized (Feinberg, 1982; Saugstad, 1994; Siekmeier and Hoffman, 2002) that mental disorders might be connected to the pruning of the neural networks of the developing brain. The idea is briefly the following: during initial development, a neural system generally overproduces many structural elements such as neurons, dendrites, axons, and synapses. This is known as the ‘overshoot phenomenon’, which enables the system to fine-tune itself subsequently to account for environmental factors, where competitive processes often govern the refinement of structure. For example, refinement can occur through the death of inappropriately connected neurons and through the reduction, pruning, of the number of synapses maintained by an individual neuron. This structural refinement is a necessary part of neural self-organization and provides further adaptability.

The pruning, which decreases the total number of synapses, is believed to result in an optimally efficient neural network, as the developing brain integrates and consolidates early experiences. In the last major step in brain development, some 40% of the neuronal synapses are eliminated (Saugstad, 1994). Although most of the pruning of synapses occurs in childhood, learning-associated brain plasticity including pruning seems to be a life-long process, although learning may take new forms while old forms are abandoned (Benefiel-Kunkel and Greenough, 1998; Ivanco and Greenough, 2000). Saugstad (1989a, 1989b, 1994) suggests that pruning is a crucial part of the development of the human brain, and that onset of puberty is linked to the last major step in brain development.

When the pruning is shut down too soon (early maturers), the synaptic density will be high and could be subject to mutual electrochemical influences. These tend to synchronize the neighboring neurons, which might be locked into a pattern of paroxysmal activity, which complicates the CNS function. In contrast, in late maturers the synaptic density will be below optimal, because of failure to shut down the pruning process. The reduced synaptic density and the associated tendency to desynchronization could lead to a general breakdown of circuitry. Saugstad's hypothesis says that both too early and too late shut down of the pruning process could lead to mental disorders. In early maturers, mano-depressive psychosis is more common, while late maturers more often get schizophrenia (Saugstad, 1994).

This kind of structural changes that normally occurs in the neural networks of the brain throughout life is also apparent at later stages in life, as the adaptability or learning capacity of the brain is gradually weakened. This is, of course, particularly apparent in dementia, such as Alzheimer's syndrome, where learning is severely impaired. Also strokes and lesions of various sorts can affect a natural and healthy balance between stability and flexibility, between order and disorder in our neural and mental processes.

In addition to the structural aspect of the dilemma, there is also a dynamical aspect. Most brain structures exhibit complex neurodynamics, including oscillations and chaotic-like behavior, as revealed by electroencephalography (EEG) and multiunit recordings (Bressler and Freeman, 1980; Freeman and Skarda, 1985; Skarda and Freeman, 1987), result of the nonlinear neurodynamics (‘chaos’), or of spontaneous neural activity (‘noise’). The functional significance of this behavior is, however, yet to be ascertained. Supposedly, the dynamics of certain cortical structures, and perhaps of the brain as a whole, reflect an evolutionary pressure to make the neural information processing as efficient as possible (Liljenström, 1995, 1997; Århem and Liljenström, 2001). The oscillations could amplify weak signals and sustain an input pattern for more accurate information processing, and the chaotic behavior could increase the sensitivity in initial, exploratory states.

The complex neurodynamics can be regulated by neuromodulators, and presumably also by intrinsic noise levels. All natural systems are inevitably exposed to external and/or internal fluctuations occurring at different temporal scales. For neural systems, such fluctuations can be problematic, but they may also be utilized for a more efficient information processing (see Århem et al, 2000). Thus, there should be a balance between stability and flexibility that ensures an efficient information processsing. Using mathematical modelling and computer simulations we address this stability–flexibility dilemma, assuming there is a close correspondence between the neural processes and the mental processes. A mathematical/theoretical approach should be an essential complement to experimental methods in understanding the complexity of biological systems and processes. Computational methods have since long been used in neuroscience, most successfully for the description of action potentials (Hodgkin and Huxley, 1952). Also, when investigating interactions between different neural levels, computational models can be useful, and sometimes the sole method of investigation. (For good overviews on this approach, see eg Arbib et al, 1997; Freeman, 2000.) In recent years, several works point at the importance of applying computational methods also to problems in clinical and experimental neuroscience, even with implications for psychology and psychiatry (Wright and Liley, 1996; Wright et al, 2000; Freeman, 1999; Gordon, 2000; Huber et al, 1999, 2000, 2001). In this work, we use a model of the three-layered paleocortex (olfactory cortex and hippocampus) which is comparatively well characterized with regard to structure, dynamics, and function. The relevance of this kind of approach to clinical and experimental neurobiology is discussed.

METHODS

In order to investigate relations between the neurodynamics of cortical structures and functions, such as perception and associative memory, we have developed a computational model of the olfactory cortex and the hippocampus. These cortical structures, which are similar in architecture and dynamics, constitute a suitable model system for many reasons, including a comparatively simple three-layered structure, a well-studied neurodynamics, and a relatively well-understood function. (For a good general overview of this kind of approach, see eg Arbib et al, 1997; Freeman, 2000.) In the current study, we use our model to address the problem of how neural systems can deal with the stability–flexibility dilemma, as will be discussed later.

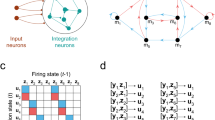
The model is of an intermediate complexity, with simple network units and realistic connections. Network units correspond to populations of neurons with a continuous input–output relation, corresponding to the average firing frequency or pulse density of neural populations. Three different types of network units (cell populations) are modelled, and the connectivity mimics the architecture of the olfactory cortex and the hippocampus. This implies a three-layered structure with two layers of inhibitory units and one layer of excitatory units. The top layer consists of inhibitory ‘feedforward interneurons’, which receive inputs from an external source or brain structure, and from the excitatory ‘pyramidal cells’ in the middle layer. They project only locally to the excitatory units. The bottom layer consists of inhibitory ‘feedback interneurons’, receiving inputs only from the excitatory units and projecting back to those. The two sets of inhibitory units are characterized by two different time constants and somewhat different connectivity to the excitatory units. In addition to the feedback from inhibitory units, the excitatory units receive extensive inputs from each other and from external structures. All connections are modelled with distance-dependent time delays for signal propagation, corresponding to the geometry and fiber characteristics of the real cortex. A mathematical description of the model is summarized below. (A more detailed description with parameter values, etc can be found in Liljenström, 1991; Liljenström and Hasselmo, 1995.)

The time evolution for a network of N neural units is given by a set of coupled nonlinear first-order differential delay equations for all the N internal states, u. With external input, I(t), characteristic time constant, τi, and connection weight wij between units i and j, separated with a time delay δij, we have for each unit activity, ui,

The input–output function, gi(ui), is a continuous sigmoid function, experimentally determined by Freeman (1979):

The gain parameter Qi determines the slope, threshold, and amplitude of the curve for unit i. This gain parameter is associated with the level of arousal, or alternatively, the level of any particular neuromodulator (Freeman, 1979; Servan-Schreiber et al, 1990; Cohen and Servan-Schreiber, 1993). C is generally a normalization constant. Neuronal adaptation is sometimes implemented as an exponential decay of the output, proportional to the time average of previous output (Liljenström and Hasselmo, 1995). In such cases, C is not a constant, but instead denotes the adaptation function, and the input–output relation becomes

where 〈〉T denotes the time average over the last T ms, and α is an adaptation parameter that is under neuromodulatory (cholinergic) control. Noise or spontaneous neural activity is represented by a Gaussian noise function, ξ(t), such that 〈ξ(t)〉=0 and 〈ξ(t)ξ(s)〉=2Aδ(t−s).

The connection weights wij are initially set and constrained by the general connectivity principles that have evolved for the three-layered cortex. To allow for learning and associative memory, the connection weights wij are incrementally changed, according to a learning rule of Hebbian type (Hebb, 1949), adapted for the system dynamics. It takes into account that there is a conduction delay, δij, between the output (presynaptic) activity of one network unit and its (postsynaptic) effect on the receiving unit. With learning rate η the change in connection weight between unit j and i is given by

where wmax is the maximum strength of an intrinsic synaptic connection.

Results with learning and memory can be further improved by using a modified learning rule, which is optimized for an oscillatory dynamics, and where weight modifications only occur for synchronized signals:

This new learning algorithm results in weight modifications that, in addition to the spatial aspects, include information of the exact signal timing. Thus, the mechanisms enable the storage of spatio-temporal patterns in contrast to solely spatial patterns. In addition, the induced learning performance is remarkably stable against noise and, because of the ability to decrease selectively weights, saturation effects as well as large shifts of the mean excitation–inhibition balance in the network are avoided. In short, the proposed learning rule has the essential prerequisites to provide an accurate and stable learning performance.

RESULTS

We use our cortical neural network for simulating dynamics and functions of real brain structures, and in particular to address the stability–flexibility dilemma of neural systems. Parameter values used for these simulations are, as far as possible, based on physiological and anatomical data, but some parameters, such as connection weights (synaptic strengths), levels of neuromodulation, etc were not possible to obtain from the experimental data, and had to be tuned.

We have previously shown that our cortical neural network model can reproduce essential characteristics of olfactory cortex and hippocampus neurodynamics (Liljenström, 1991, 1995, 1997; Liljenström and Hasselmo, 1995; Liljenström and Wu, 1995; Århem and Liljenström, 2001). It describes intrinsic oscillatory properties of these structures, and reproduces response patterns associated with a continuous random input signal and with a shock pulse given to the cortex. In the latter case, waves of activity move across the model cortex, consistent with corresponding global dynamic behavior of the functioning cortex. For a constant random input, the network is able to oscillate with two separate frequencies simultaneously, around 5 Hz (theta rhythm) and 40 Hz (gamma rhythm), purely as a result of its intrinsic network properties and time constants (obtained from membrane capacitances and resistances for the different types of cells). A balance between inhibition and excitation, in terms of connection strength and timing of events, is necessary for coherent frequency and phase of the oscillating neural units. Under certain conditions, the system can also display chaotic-like behavior, similar to what can be found in EEG traces, see Figure 1 (Bressler and Freeman, 1980; Freeman and Skarda, 1985; Skarda and Freeman, 1987, Freeman, 2000). All of these phenomena have been shown to depend critically upon the network structure, in particular feedforward and feedback inhibitory loops and long-range excitatory connections modelled with distance-dependent time delays. Details concerning neuron structure or spiking activity are not necessary for this type of dynamic behavior.

Figure 1
figure 1

Real (top) and simulated (bottom) EEG, showing the complex dynamics of cortical structures. The upper trace is from rat olfactory cortex (data courtesy of Leslie Kay), whereas the bottom trace is from a simulation with the current model of the olfactory cortex. The x-axis shows milliseconds, and the y-axis is in microvolts.

Full size image

In the following, we will focus on a few aspects related to the stability–flexibility dilemma, that is, how a neural system can be sensitive, flexible, and adaptive, while maintaining necessary stability. In particular, we show (1) how a complex neurodynamics can provide both flexibility and stability for the system and (2) how this neurodynamics can be regulated by means of neuromodulators (such as acetylcholine (ACh)) and noise, in order to change system sensitivity and response rapidness. We also investigate (3) how the network connectivity is linked to its dynamics and learning capacities, and what effects synaptic modification and pruning may have on the balance between stability and flexibility, relating to the pruning hypothesis (Feinberg, 1982; Saugstad, 1994; Siekmeier and Hoffman, 2002).

Complex Neurodynamics

What system properties are responsible for a flexible and adaptive response to external (and internal) changes? Flexibility, or adaptation, can be considered at several time scales. At an evolutionary scale, there is a slow adaptation that is genetically determined, resulting in the gross structure of the nervous system and the initial neural organization of the newborn brain. However, as discussed in the Introduction, already in the fetus, the genetically determined neural organization of the brain is modified by pruning, input from the developing sensory organs, various hormones and different kinds of fluctuations. Such influences give the brain a ‘final’ unique structure that is not possible to predict from the genes alone. The neural network structures of the brain are thus determined both by genetic order, and by more or less random effects, resulting in an undetermined and unpredictable final product. Learning that occurs throughout the life modifies the neural structures continuously, and provides adaptation at an intermediate time scale. At the shortest time scale, the neurodynamics of the brain provides rapid adaptation to fast changes in the (external and internal) environment.

How is it possible to be sensitive and flexible, adapting to environmental changes at different time scales, while maintaining necessary stability? In some cases, it may be important to be sensitive and react quickly to small changes in the (external or internal) environment. In other cases, it is important to be stable and nonreacting to insignificant fluctuations, perhaps of the same magnitude as the small ‘signals’ in the first case. How can the system change its sensitivity depending on circumstances? How much structural changes (primarily damages owing to ‘pruning’ of synapses and decay of neurons) can a neural network take before its function is impaired?

The evolutionary and genetically determined structure of the neural network is given in the model by the initial connectivity matrix, which mimics the three-layered structure of paleocortex. This overconnected structure, with one layer of excitatory network units (‘pyramidal cells’) and two layers of inhibitory network units (‘interneurons’) provides the basis for the oscillatory and chaotic-like dynamics observed in these structures. Figure 1 shows the oscillatory and chaotic-like dynamics of such structures as observed with EEG. The top trace shows the EEG of rat olfactory cortex, while the bottom trace shows simulated EEG using our cortical model. In Figure 2, the network dynamics is shown for two cases of external input, as a strong and a weak shock pulse, respectively, is applied to the input side of the network. The top traces are experimental data, and the bottom traces are computer simulations.

Figure 2
figure 2

Comparison of experimental data from rodent olfactory cortex (top; data courtesy WJ Freeman) with simulated data using our neural network model (bottom). The two top experimental traces are (left) field potential evoked by a large amplitude pulse to the lateral olfactory tract, and (right) field potentials evoked by a weak pulse.

Full size image

It is clear from the simulations that oscillatory or complex dynamics can provide a means for fast response to an external input, such as a sensory signal. If sensitivity to small changes in the input is desired, a partially chaotic-like dynamics could be optimal, but a too high sensitivity should be avoided. Oscillations can also be used for enhancing weak signals, and by ‘resonance’, large populations of neurons can be activated for any input. In addition, such ‘recruitment’ of neurons in oscillatory activity can eliminate the negative effects of noise in the input, by cancelling out the fluctuations of individual neurons. Noise can, however, also have a positive effect, which we will return to shortly. Finally, from an energy point of view, oscillations in the neuronal activity should be much more efficient than if a static neuronal output (from large populations of neurons) was required.

Neuromodulation and Internal Noise

In order for the system to make use of a rich variety of dynamical states, there has to be some kind of regulatory or control mechanisms. Many factors influence the dynamical state of brain structures, for example, the excitability of neurons and the synaptic strengths in the connections between them. A number of chemical agents act on these neural properties. Such agents, for example, ACh and serotonin (5-HT), can change the excitability of a large number of neurons simultaneously, or the synaptic transmission between them. ACh is also known to increase the excitability by suppressing neuronal adaptation, an effect similar to that of increasing the gain in general (see Liljenström and Hasselmo, 1995, and references therein).

The concentration of these ‘neuromodulators’ is directly related to the arousal or motivation (or mood) of the individual, and can have profound effects on the neural dynamics and on memory functions (Freeman, 2000). For example, ACh increases the oscillatory activity in the olfactory cortex and in brain slices of hippocampus. In addition, low levels of ACh have been found to accompany memory impairment in Alzheimer's syndrome (see Liljenström and Hasselmo, 1995, and references therein).

The frequencies of the network oscillations depend primarily upon intrinsic time constants and delays, as given by the experimental data, whereas the amplitudes depend predominantly upon connection weights and gains, which are under neuromodulatory control, and have to be tuned. Implementation of these neuromodulatory effects in the model caused changes analogous to those seen in physiological experiments. For example, a similar result as that of Figure 2 can be found for different levels of neuromodulation, and with a constant strength of the input pulse. A damped oscillatory response is the result of high neuronal excitability, corresponding to high levels of neuromodulation (ACh), and implemented as a high Q value in the input–output function, Equation (2), or a small α value in Equation (3).

In particular, ‘cholinergic’ increase in excitability and suppression of synaptic transmission could induce theta (and/or gamma) rhythm oscillations within the model, even when starting from an initially quiescent state with no oscillatory activity. Figure 3 shows how different oscillatory modes can be induced by neuromodulatory control, which involves increasing gain and decreasing connection weights. The activity evolution of one arbitrarily chosen excitatory network unit is shown for three different levels of ‘ACh’: (a) low, (b) intermediate, and (c) high.

Figure 3
figure 3

Different oscillatory modes can be induced by neuromodulatory control: increasing gain and decreasing connection weights. The activity evolution of one particular (arbitrarily chosen) excitatory network unit is shown for three different levels of ‘cholinergic’ action: (a) low levels, (b) intermediate levels, and (c) high levels.

Full size image

We have also used the model to simulate the neuromodulatory effects on learning and associative memory tasks. When storing and retrieving activity patterns, the model gives point attractors and limit cycle attractors intermittently as Q increases. When a particular pattern was learnt with Q<10.0 it was stored as a point attractor memory state. If learning instead was performed with 10.0⩽Q⩽13.0, the pattern was stored as a limit cycle. With 13.1⩽Q⩽15.4, we obtained point attractors, and with 15.5⩽Q⩽30.0 again limit cycles. Different, but overlapping, patterns were presented either as constant or as oscillatory inputs and stored as point attractor or limit cycle memory states. The simulation results showed that an oscillatory response typically gives a much shorter recall time than a constant activity. For example, the convergence time to a limit cycle memory state could be almost half as long as to a point attractor state, when the same degraded input pattern was used for recall. The recall time (convergence time) can be reduced further if larger Q values are used for learning and recall (Liljenström, 1995, 1997; Liljenström and Wu, 1995).

External or intrinsic fluctuations are usually damped and ‘ignored’ by the system, but, in some cases, they may be amplified and have an effect at a macroscopic scale. Simulation results show that noise, as well as neuromodulatory effects, can induce global network oscillations and reduce recall time. In fact, consonant with stochastic resonance theory (Bulsara et al, 1991; Mandell and Selz, 1993; Anishchenko et al, 1993), the rate of information processing, which in this case is the rate of convergence to a near limit cycle memory state, can be maximized for optimal noise levels (Liljenström and Wu, 1995).

Under certain circumstances, a small number of ‘noisy’ network units (with a high intrinsic random activity) is sufficient to induce global coherent oscillatory activity in a network with primarily ‘silent’ units (see Figure 4). The onset of global oscillatory activity depends on, for example, the noise level, the number and density of the noisy units, and the duration of the noise activity. The location and spatial distribution of these units in the network is also important for the onset of oscillations. If the noisy units are separated beyond a certain distance, or if the noise level is too low, no oscillations occur. Likewise, no transition to global oscillations occurs if the noise ‘frequency’ is too low.

Figure 4
figure 4

Noise-induced global network oscillations. The figure shows one noisy excitatory network unit (middle trace) and two nonactive units. The noise or ‘spontaneous activity’ of certain network units is here only appearing for a short period, 400 ms, which results in an onset of global oscillations about 500 ms after that period.

Full size image

Synaptic Modification and Network Pruning

As discussed above, the stability and flexibility of a neural network is largely determined by its connectivity. In general, an extensive connectivity with a certain degree of randomness ensures stability. Modifications of network connections provide flexibility. Learning and (associative) memory is presumably based on synaptic modifications, which include both growth and pruning of the neural networks of the brain. Such structural changes occur all the time during the lifetime of the individual. We simulate a continuous learning of our neural network model by a learning rule that modifies the connection weights continuously (in principle).

In Figure 5, we show how the model system learns and recalls input patterns continuously by means of near-limit cycle attractors. Here, 500 ms is allowed for the system to respond to (recognize) any particular input pattern, but if that pattern does not match any of the previously encoun-tered (stored) patterns, the system starts to store (learn) the new pattern as a new near-limit cycle attractor (memory) for another 500 ms. In the figure, the large, central system trajectory corresponds to the ‘attempt’ to converge to one of the stored memories, represented by a near-limit cycle attractor. The narrow system trajectory to the right in the figure corresponds to the learning of the current input pattern as a new near-limit cycle attractor when convergence to ang stores pattern failed. (The time series for one arbitrary excitatory unit is plotted against that of another.)

Figure 5
figure 5

‘Continuous’ learning and recall with the cortical neural network model. The two separate ‘attractors’ correspond to two separate memory states, the left one to a previously stored pattern, and the right one to a new memory state (see text for a detailed explanation).

Full size image

The effects of neuronal pruning are studied by removing certain connection weights in the neural network model. The rule for the adjustments can be described as: ‘prune the weights that are not changing, and are below a specific pruning limit’ (see Figure 6). The ‘pruning limit’ is calculated as the mean of the weight strengths plus a value that is determined from the input parameters.

Figure 6
figure 6

The pruning limit is calculated as the mean of the weight strengths plus a value determined from the input parameters. Connections that fall below the limit line are removed.

Full size image

In order to compare the results of different simulations, a convergence measure for the system was used. The convergence is a number between 0.0 and 1.0, telling how good the recognition of a distorted pattern is. It is obtained from the scalar product between the correct (learnt) pattern and the pattern that the system produces given a distorted version of the correct pattern. If these patterns match completely, the convergence would be 1.0.

In the convergence plot in Figure 7, there are four different graphs, each representing the convergence of a distorted pattern. The time course in the plots is from 1000 to 2000 ms. Before that, the system was taught the four original patterns, one at a time. Then, beginning at t=1000 ms, a distorted version of the first pattern was presented to the system for 200 ms. At every time step, the convergence of the distorted pattern was calculated for each learnt pattern. The uppermost of the four graphs is the convergence measure for the first distorted pattern, and the graphs below show how that pattern matches the three other learnt patterns.

Figure 7
figure 7

The convergence measure without pruning (a) and with pruning (b). The four graphs each represent the convergence of one of the four distorted patterns presented to the system for 200 ms at four successive times (see text for a detailed explanation).

Full size image

A comparison of the plots in Figure 7a (no pruning) and Figure 7b (pruning) shows that with pruning the peaks of the convergence graphs are slightly lower than in the case with no pruning. The amplitude of the oscillations is also varying less when pruning is turned on, while the frequency stays the same. When the mean of the convergence was calculated, then in general, the resulting value for the simulation with pruning turned out to be higher. Another result of pruning was that the recall of a memory was more distinct, that is, the overlap with other memories was reduced.

Most of the simulations were run with four patterns, but up to 20 patterns have been used. The pattern density was mostly about 20% (ie around 50 of 256 cells were turned ‘on’). Pattern densities of 10 and 50% were also tested, but the results of these simulations were about the same. The convergence was slightly poorer than with 20% but the relation between the pruning and nonpruning simulations stayed the same. Most of the simulations were run with a distortion level of 25% (ie 75% of the pattern was the same as the original). Distortion levels of 10 and 50% were also tested. As suspected, the convergence was best for the 10% distortion, poorer for 25%, and worst for 50%. The pruning result for the 10% distortion was better than for the nonpruning result (mean convergence). As discussed above, the result for pruning with 25% distortion was slightly better than without pruning. For the 50% distortion, the pruning and nonpruning results were about equal.

In order to measure some kind of an ‘energy effect’ of pruning, we introduced an energy measure based on the idea that the more neurons involved in learning and recognition, the more energy that would be consumed. Therefore, a simple energy term would be the sum of the entire weight matrix, since all elements wij⩾0. Thus, the system would consume less energy if there were fewer connections. This energy term was used to find the energy usage of the system both with pruning and without. In the graph in Figure 8, the values have been normalized (0.0 is the minimum energy and 1.0 is the maximum energy). There are clear differences between pruning and nonpruning. After the initiation period of about 25 ms, the energy of the pruning simulation dramatically decreases and stays low for the rest of the simulation, whereas in the nonpruning simulation the energy increases. At the end of the nonpruning simulation, the (relative) energy is about 58% while it in the pruning simulation is about 1%.

Figure 8
figure 8

The relative energy usage (number of synapses active, see text for explanation) was about 58% without pruning (dotted line) and about 1% with pruning (filled line).

Full size image

Figure 9 shows the network activity, with and without pruning, with activity levels coded as the height above a given plane. As can be seen from the figure, the peaks of the activity levels for the simulation with pruning were more equal in height. In other words, the synchronization was better in the pruning simulations than in the nonpruning ones.

Figure 9
figure 9

Snap shots of height-coded activity levels from a simulation without pruning (left) and with pruning (right).

Full size image

In summary, simulations with pruning showed that the system is extremely stable. It was possible to prune away more than 95% of the connection weights and still get good results. In addition, when pruning was applied, synchronization of network activity was increased, and the energy consumption (as defined above) was greatly reduced. This was because a great number of connection weights were removed, which in turn made the simulations some 10% faster. Further, the recall of memories was improved, in the sense that the recognition of the input patterns was more distinct and accurate. Although the peaks were higher without pruning, the mean of the convergence was better with pruning.

DISCUSSION

We have used a computational model of the three-layered paleocortex to investigate the relations between structure, dynamics, and functions of cortical neural networks. In particular, we have used this model to address the stability–flexibility dilemma of neural systems, assuming a close relation between neural processes and mental processes and disorders.

Apparently, a certain amount of disorder is beneficial to the system; too much order can be detrimental (eg getting stuck in a limit cycle attractor, corresponding to a repetitive cognitive or motor behavior). Our computer simulations support the view that, with an initial chaotic-like state, sensitive to the input, the system can rapidly converge to an attractor memory state. It should be important to avoid getting stuck in any stable limit cycle (or other) attractor state, and a chaotic dynamics could provide the necessary aperiodicity. At a higher level, it could be responsible for the brain's capacity to generate novel activity patterns, corresponding to its internal self-generated (‘creative’) thought processes (Skarda and Freeman, 1987). Several other roles for chaos in neural systems have been suggested (see eg Tsuda, 1991; Babloyantz and Lourenco, 1996; Arbib et al, 1997).

Further, the computer simulations show that noise can induce global synchronous oscillations and shift the system dynamics from one dynamical state to another. This in turn can change the efficiency of the information processing of the system. We also demonstrated that system performance can be maximized at an optimal noise level, analogous to the case of stochastic resonance. Thus, in addition to the (pseudo-)chaotic network dynamics, the noise produced by a few (or many) neurons could be used for making the system flexible, increasing the responsiveness of the system, and for avoiding the system to get stuck in any undesired oscillatory mode.

The dynamical state of a neural system determines its global properties and functions. For example, cortical oscillations (in particular the 40 Hz oscillations) seem to play a role in cognitive functions, including segmentation of sensory input, learning, attention, and consciousness (Eckhorn et al, 1988; Gray et al, 1989; Crick and Koch, 1990; Gray, 1994). The findings of zero phase stimulus-invoked synchrony between (visual) cortical neurons far apart has been suggested to solve the so-called binding problem: that an object is perceived as a whole, in spite of its different aspects being represented by different sets of neurons (Gray, 1994). Neurodynamical control should thus be crucial for the survival of the individual (or for an efficient functioning of an artificial autonomous system). It could result in a shift in the balance between sensitivity and stability of the system.

An efficient neural information processing supposedly requires an appropriate balance between flexibility and stability of the system. Ideally, the balance can shift depending on internal and external circumstances. Our computer simulations show that a regulated complex neurodynamics, which can shift its balance between sensitivity and stability, can result in an efficient information processing. A high interconnectivity, with extensive long-range excitatory connections, and more local inhibitory connections, can be extremely robust to network pruning and external or internal fluctuations. An oscillatory dynamics, resulting from a proper balance between excitation and inhibition, is another factor that provides both flexibility and stability to the system. In addition, such a dynamics is more energetically advantageous than a non-oscillatory dynamics. A pruned network is also more efficient in terms of energy usage (less synapses involved) and network activity levels, and it gives a more accurate learning/recall. However, pruning results in a less flexible network, where fewer patterns can be stored, as the number of modifiable connections is reduced.

Hence, all of the mechanisms discussed above result in a more efficient information processing, primarily expressed as a faster and/or more accurate response to an external input pattern. For example, neuromodulatory control that increases neuronal excitability and suppresses synaptic transmission can enhance system performance by reducing the recall time, or by increasing fidelity through the separation of input pattern activity. It seems that the most efficient information processing in this system is obtained when it initially has a chaotic-like dynamics, which converges to a near-limit cycle attractor in response to external stimuli. The rate of convergence to a memory attractor can be increased by various mechanisms, such as neuromodulatory, synchronizing, or pruning effects.

What is the significance and relevance of this kind of computational models and simulations for clinical and experimental neuroscience and psychiatry? To the extent that neural processes are closely linked to cognitive functions and mental processes, and that computational methods can successfully be used to model neural structures and processes, these methods should also be useful tools in understanding higher brain (mal-) functions. In particular, it is reasonable to believe that neural stability and flexibility is also reflected, at least to some extent, in the stability and flexibility at higher levels of brain function. Hence, an imbalance between stability and flexibility, or between order and disorder, at the neural level, is likely to have effects at the mental level, possibly linking to mental disorders.

For example, with reference to the pruning hypothesis (Feinberg, 1982; Saugstad, 1994; Siekmeier and Hoffman, 2002), the pruning effects that we found with our computer simulations could thus point at a shift in the balance between stability and flexibility of the neural networks of the brain, that possibly could be reflected in a similar shift at a cognitive/mental level. It is also conceivable that a suboptimal timing of the extensive pruning process that occurs during development could well have an effect on the stability–flexibility balance of the mental processes in later stages of life.

Even though it is difficult with the current model to make any conclusions about mental processes and disorders, computer models are likely to be used more extensively in the future, as a complement to experimental and clinical methods. Indeed, our modelling efforts have shown that problems such as the stability–flexibility dilemma for neural systems can be addressed and studied with computational methods. The kind of computational models we have used here, are far too simple to be directly applied in clinical neuroscience and psychiatry, but the results could possibly point at likely solutions and guide further experimental and clinical approaches. A greater understanding of the relation between neural and mental processes, as well as a further development and elaboration of computational models, is needed before we can make any successful use or prediction of such methods.