Identifying vital nodes based on reverse greedy method

Abstract

The identification of vital nodes that maintain the network connectivity is a long-standing challenge in network science. In this paper, we propose a so-called reverse greedy method where the least important nodes are preferentially chosen to make the size of the largest component in the corresponding induced subgraph as small as possible. Accordingly, the nodes being chosen later are more important in maintaining the connectivity. Empirical analyses on eighteen real networks show that the reverse greedy method performs remarkably better than well-known state-of-the-art methods.

Introduction

Network science is playing an increasingly significant role in many domains including physics, sociology, engineering, biology, management, and so on¹. Because of the heterogeneous nature of real networks², the overall connectivity of networks may depend on a small set of nodes, usually named as hub nodes. Taking the Internet as an example, several vital nodes attacked deliberately may lead to the collapse of the whole network³. Therefore, an efficient algorithm to identify vital nodes that have critical impacts on the network connectivity can help to better prevent catastrophic outages in power grids or the Internet^3,4,5,6, maintain the connectivity or design efficient attacking strategies for communication networks⁷, improve urban transportation capacity with low cost⁸, enhance robustness of financial networks⁹, and so on.

Till far, to identify vital nodes for network connectivity, the majority of known methods only make use of the structural information¹⁰. Typical representatives include degree centrality (DC)¹¹, H-index¹², k-shell index (KS)¹³, PageRank (PR)¹⁴, LeaderRank¹⁵, closeness centrality (CC)¹⁶, betweenness centrality (BC)¹⁷, and so on. Recently, Morone and Makse¹⁸ proposed a novel index called collective influence (CI), which is based on the site percolation theory and can find out the minimal set of nodes that are crucial for the global connectivity. CI performs remarkably better than some known methods in identifying the nodes’ importance for network connectivity^18,19. Furthermore, some sophisticated methods with even better performance have been reported, such as the belief propagation-guided decimation method^20,21 (BPD), the two-core based algorithm²² (CoreHD) and the explosive immunization method²³ (EI).

This paper proposes a novel method named reverse greedy (RG) method. The first word stands for the process that we add nodes one by one to an empty network, which is inverse to the usual process that removes nodes from the original network. The second word emphasizes that we choose the nodes added by minimizing the size of the largest component. Empirical analyses on eighteen real networks show that RG performs remarkably better than well-known state-of-the-art methods.

Algorithms

The core of the RG algorithm is the reverse process, which adds nodes one by one to an empty network while minimizes the cost function until all nodes in the considered network are added. Then, nodes are ranked inverse to the order of additions, that is to say, the later added nodes are more important in maintaining the network connectivity. Denote $G(V,E)$ the original network under consideration, where $V$ and $E$ are the sets of nodes and edges, respectively. This paper focuses on simple networks, where the weights and directions of edges are ignored, and the self loops are not allowed. The reverse process starts from an empty network ${G}_{0}({V}_{0},{E}_{0})$, where ${V}_{0}=\varnothing$ and ${E}_{0}=\varnothing$. At the $(n+1)$^th time step, one node from the remaining set $V-{V}_{n}$ is selected to add into the current network ${G}_{n}({V}_{n},{E}_{n})$ to form a new network of $(n+1)$ nodes, say ${G}_{n+1}({V}_{n+1},{E}_{n+1})$. Note that, all progressive networks ${G}_{n}$ ($n=0,1,2,\cdots \ ,N$, with $N$ being the size of the original network $G$) in the process are induced subgraphs of $G$. For example, ${G}_{n}$ is consisted of all edges in $G$ with both two ends belonging to ${V}_{n}$. According to the greedy strategy, the selected node $i$ should minimize the size of the largest component in ${G}_{n+1}$. If there are multiple nodes satisfying this condition, we will choose the one with the help of another structural feature of the node $i$ in $G$ (e.g., degree, betweenness, and so on). Therefore, the cost function can be defined as

$$cost(i,n+1)={G}_{n+1}^{\max }(i)+\varepsilon f(i),$$

(1)

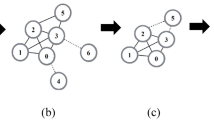
where ${G}_{n+1}^{\max }(i)$ is the size of the largest component after adding node $i$ into ${G}_{n}$, $f(i)$ is a certain structural feature of node $i$ in $G$, and $\epsilon$ is a very small positive parameter and has no effect on the results of RG as long as $\epsilon \ast maxf(i) < 1$ is guaranteed. The parameter $\epsilon$ works only when ${G}_{n+1}^{\max }(\bullet )$ are indistinguishable for multiple nodes. At each time step, we add the node minimizing the cost function into the network, and if there are still multiple nodes with the minimum cost, we will select one of them randomly. This process stops after $N$ time steps, namely all nodes are added with ${G}_{N}\equiv G$. An illustration of such process in a small network is shown in Fig. 1.

Figure 1

The process of RG in a network with six nodes. Here we use degree as the feature $f$ and for convenience in the later description we set $\epsilon =0.01$ (note that, $\epsilon$ should be positive yet small enough and it is set to be $1{0}^{-7}$ in the later experiments). Initially, the network is empty. At the first time step, ${G}_{1}^{\max }({v}_{1})={G}_{1}^{\max }({v}_{2})={G}_{1}^{\max }({v}_{3})={G}_{1}^{\max }({v}_{4})={G}_{1}^{\max }({v}_{5})={G}_{1}^{\max }({v}_{6})\ =\ 1$, and $cost({v}_{1},1)=1.04$, $cost({v}_{2},1)=1.03$, $cost({v}_{3},1)=1.03$, $cost({v}_{4},1)=1.03$, $cost({v}_{5},1)=1.03$, $cost({v}_{6},1)=1.02$. Therefore, we add node ${v}_{6}$ into the network because $cost({v}_{6},1)$ is the smallest. In the second time step, ${G}_{2}^{\max }({v}_{1})={G}_{2}^{\max }({v}_{2})={G}_{2}^{\max }({v}_{3})=1$, and ${G}_{2}^{\max }({v}_{4})={G}_{2}^{\max }({v}_{5})=2$, so we only compare three candidates ${v}_{1}$, ${v}_{2}$ and ${v}_{3}$. Since $cost({v}_{1},1)=1.04$, $cost({v}_{2},1)=1.03$ and $cost({v}_{3},1)=1.03$, we randomly select a node from $\{{v}_{2},{v}_{3}\}$. Here we choose ${v}_{2}$ for example. Repeat this process until all nodes are added into the network. Finally, we get the ranking of nodes as $\{{v}_{4},{v}_{5},{v}_{1},{v}_{3},{v}_{2},{v}_{6}\}$, in an inverse order of the additions. The symbol $n$ in the bottom of each plot stands for the corresponding time step.

Data

In this paper, eighteen real networks from disparate fields are used to test the performance of RG, including four collaboration networks (Jazz, NS, Ca-AstroPh and Ca-CondMat), two communication networks (Email-Univ and Email-EuAll), four social networks (PB, Sex, Facebook and Loc-Gowalla), one transportation network (USAir), one infrastructure network (Power), one citation network (Cit-HepPh), one road network (RoadNet-TX), one web graph (Web-Google) and three autonomous systems graphs (Router, AS-733 and AS-Skitter). Jazz²⁴ is a collaboration network of jazz musicians. NS²⁵ is a co-authorship network of scientists working on network science. Ca-AstroPh²⁶ is a collaboration network of Arxiv Astro Physics category. Ca-CondMat²⁶ is a collaboration network of Arxiv Condensed Matter category. Email-Univ²⁷ describes email interchanges between users including faculty, researchers, technicians, managers, administrators, and graduate students of the Rovira i Virgili University. Email-EuAll²⁶ is an email network of a large European Research Institution. PB²⁸ is a network of US political blogs. Sex²⁹ is a bipartite network in which nodes are females (sex sellers) and males (sex buyers) and edges between them are established when males write posts indicating sexual encounters with females. Facebook³⁰ is a sample of the friendship network of Facebook users. Loc-Gowalla³¹ describes the friendships of Gowalla users. USAir³² is the US air transportation network. Power³³ is a power grid of the western United States. Cit-HepPh³⁴ is a citation network of high energy physics phenomenology. RoadNet-TX³⁵ is a road network of Texas. Web-Google³⁵ is a web graph of the Google programming contest in 2002. Router³⁶ is a symmetrized snapshot of the structure of the Internet at the level of autonomous systems. AS-733³⁷ contains the daily instances of autonomous systems from November 8 1997 to January 2 2000. AS-Skitter³⁷ describes the autonomous systems from traceroutes run daily in 2005 by Skitter. These networks’ topological features (including the number of nodes, the number of edges, the average degree, the clustering coefficient³³, the assortative coefficient³⁸ and the degree heterogeneity³⁹) are shown in Table 1.

Table 1 The basic topological features of the eighteen real networks. $N$ and $M$ are the number of nodes and edges, $\langle k\rangle$ is the average degree, $C$ is the clustering coefficient, $r$ is the assortative coefficient and $H$ is the degree heterogeneity.

Besides real-world networks, we also work on ErdŐs-Rényi (ER) random networks⁴⁰ with different densities. We generate four ER random networks with $N=100000$ and $\langle k\rangle =6,9,12,15$, named as ER-6, ER-9, ER-12, ER-15, respectively.

Results

We apply two widely used metrics to evaluate algorithms’ performance. One is called robustness $R$⁴¹. Given a network, we remove one node at each time step and calculate the size of the largest component of the remaining network until the remaining network is empty. The robustness$R$ is defined as⁴¹

$$R=\frac{1}{N}\mathop{\sum }\limits_{Q=1}^{N}S(Q),$$

(2)

where $S(Q)$ is the number of nodes in the largest component divided by $N$ after removing $Q$ nodes. The normalization factor 1/$N$ ensures that the values of $R$ of networks with different sizes can be compared. Obviously, a smaller $R$ means a quicker collapse and thus a better performance. Another metric is the number of nodes to be removed to make the size of the largest component in the remaining network being no more than $0.01N$, denoted by, ${\rho }_{min}$. Obviously, a smaller ${\rho }_{min}$ means a better performance.

Here we use BC, CC, DC, H-index, KS, PR, CI, CI with reinsertion (short for CI+), BPD, CoreHD and EI as the benchmark algorithms (see details about these benchmark algorithms in Methods). Tables 2 and 3 compare $R$ and ${\rho }_{min}$ of RG and other benchmarks algorithms, respectively. Notice that, we use the random removal (Random) as the background benchmark in order to show the improvement by each method. Both BPD and CoreHD need a refinement process to insert back some removed nodes. In each step, it calculates the increase of the component size after the insertion of a node and select the node that gives the smallest increase. Such process stops when the largest component reaches $0.01N$. These two methods do not provide a ranking of all nodes, and thus we cannot obtain $R$ for them. For EI, according to²³, we set $K=6$ and the number of candidates being equal to 2000. So the networks with sizes smaller than 2000 fail to apply EI (those cases are marked by N/A in Tables 2–4). Each result of EI is obtained by averaging over 20 independent realizations. The radii of CI and CI+ are set to be 3 only except for AS-Skitter (its radius is set to be 2) because its size is too large and thus $radius=3$ will leads to too much computation.

Table 2 The Robustness $R$ for RG and other benchmarks. The best performed method for each network is emphasized in bold.

Table 3 The minimum number of nodes ${\rho }_{min}$ for RG and other benchmarks. The best performed method for each network is emphasized in bold.

Table 4 Running time of the twelve methods (seconds).

As shown in Table 2, subject to $R$, CI, CI+, EI and RG perform better than the classical centralities (e.g., BC, CC, DC, H-index, KS and PR) in almost all networks, and RG is overall the best method subject to $R$ for real networks. Figure 2 shows the collapsing processes of four representative networks, resulted from the node removal by RG and other benchmark algorithms. Obviously, RG can lead to faster collapse than all other algorithms, and CI+ is the second best algorithm. As shown in Table 3, subject to ${\rho }_{min}$, BPD, CoreHD, EI and RG perform better than the classical centralities and CI/CI+ in almost all networks. For real networks, RG and BPD perform remarkably better than other methods. For random networks, RG is among the best and much better than the classical centralities. However, RG is slightly worse than CI+ subject to $R$ and BPD subject to ${\rho }_{min}$. In random networks, the topological difference among different nodes is relatively small, and thus RG may mistakenly select some influential nodes as unimportant nodes at the early stage, leading to unsatisfactory results. Table 4 compares the CPU times of the 12 methods under consideration, from which one can see that RG is slower than DC, H-index, KS, PR and CoreHD, similar to CC and BPD and faster than BC, CI/CI+ and EI. Generally speaking, RG is an efficient method.

Figure 2

Comparing the performance of the background benchmark (random removal, denoted by blue circles), RG (red stars) and the other benchmark algorithms (black symbols). The $x$-axis is the fraction of nodes being removed (i.e., $Q$/$N$), and the $Y$-axis denotes the number of nodes in the largest component divided by $N$ (i.e., $S(Q)$). The four selected networks are (a) AS-733, (b) Sex, (c) Facebook, and (d) Cit-HepPh, respectively. Other networks exhibit similar results.

Discussion

To our knowledge, most previous methods directly identify the critical nodes by looking at the effects due to their removal¹⁰. In contrast, our method tries to firstly find out the least important nodes, so that the remaining ones are those critical nodes. To our surprise, such a simple idea eventually results in an efficient algorithm that outperforms many well-known benchmark algorithms. Beyond the percolation process considered in this paper, the reverse method provides a novel angle of view that may find successful applications in some other network-based optimization problems related to certain rankings of nodes or edges.

The performance of RG can be further improved by introducing some sophisticated skills. For example, instead of degree, $f(i)$ can be different for different networks or set in a more complicated way to improve the algorithm’s performance. In addition, the simple adoption of the greedy strategy may bring us to some local optimums. Such shortage can be to some extent overcame by applying the beam search⁴², which searches for the best set of $m$ nodes adding to the network that optimizes the cost function. The present algorithm is the special case for $m=1$. Although beam search is still a kind of greedy strategy, it usually performs much better when $m$ is larger. At the same time, the beam search with large $m$ costs a lot on time and space. Therefore, how to find a good tradeoff is also an open challenge in real practice.

Methods

Benchmark centralities

DC¹¹ of node $i$ is defined as

$$DC(i)=\sum _{j}{a}_{ij},$$

(3)

where $A=\{{a}_{ij}\}$ is the adjacency matrix, that is, ${a}_{ij}$ = 1 if $i$ and $j$ are directly connected and 0 otherwise.

H-index¹² of node $i$, denoted by $H(i)$, is defined as the maximal integer satisfying that there are at least $H(i)$ neighbors of node $i$ whose degrees are all no less than $H(i)$. Such index is an extension of the famous H-index in scientific evaluation⁴³ to network analysis.

KS¹³ is implemented by the following steps: Firstly, remove all nodes with degree one, and keep deleting the existing nodes until all nodes’ degrees are larger than one. All of these removed nodes are assigned 1-shell. Then recursively remove the nodes with degree no larger than two and set them to 2-shell. This procedure continues until all higher-layer shells have been identified and all network nodes have been removed.

PR¹⁴ of node $i$ is defined as the solution of the equations

$$P{R}_{i}(t)=s\mathop{\sum }\limits_{j=1}^{N}{a}_{ji}\frac{P{R}_{j}(t-1)}{{k}_{j}}+(1-s)\frac{1}{N},$$

(4)

where ${k}_{j}$ is the degree of node $j$ and $s$ is a free parameter controlling the probability of a random jump. In this paper, $s$ is set to $0.85$.

CC¹⁵ of node $i$ is defined as

$$CC(i)=\frac{N-1}{{\sum }_{j\ne i}{d}_{ij}},$$

(5)

where ${d}_{ij}$ is the shortest distance between nodes $i$ and $j$.

BC¹⁶ of node $i$ is defined as

$$BC(i)=\sum _{s\ne i,s\ne t,i\ne t}\frac{{g}_{st}(i)}{{g}_{st}},$$

(6)

where ${g}_{st}$ is the number of shortest paths between nodes $s$ and $t$, and ${g}_{st}(i)$ is the number of shortest paths between nodes $s$ and $t$ that pass through node $i$.

CI¹⁸ of node $i$ is defined as

$$CI(i)=({k}_{i}-1)\sum _{j\in \partial ball(i,\ell )}({k}_{j}-1),$$

(7)

where $ball(i,\ell )$ is the set of nodes inside a ball of radius $\ell$, consisted of all nodes with distances no more than $\ell$ from node $i$, and $\partial ball(i,\ell )$ is the frontier of this ball. CI+ is the version of CI with reinsertion.

BPD²¹ is rooted in the spin glass model for the feedback vertex set problem⁴⁴. At time $t$ of the iteration process, the algorithm estimates the probability ${q}_{i}^{0}(t)$ that every node $i$ of the remaining network $G(t)$ is suitable to be deleted. The explicit formula for this probability is

$${q}_{i}^{0}=\frac{1}{1+{e}^{x}\left[1+{\sum }_{k\in \partial i(t)}\frac{1-{q}_{k\to i}^{0}}{{q}_{k\to i}^{0}+{q}_{k\to i}^{k}}\right]{\prod }_{j\in \partial i(t)}[{q}_{j\to i}^{0}+{q}_{j\to i}^{j}]},$$

(8)

where $x$ is an adjustable reweighting parameter, and $\partial i(t)$ denotes node $i$’s set of neighbors at time $t$. The quantity ${q}_{i\to j}^{0}(t)$ is the probability that the neighboring node $j$ is suitable to be deleted if node $i$ is absent from the network $G(t)$, while ${q}_{i\to j}^{j}(t)$ is the probability that this node $j$ is suitable to be the root node of a tree component in the absence of node $i$. The node with the highest probability of being suitable for deletion is deleted from network $G(t)$ along with all its associated edges. This node deletion process stops after all the loops in the network have been destroyed. Then check the size of each tree component in the remaining network. If a tree component is too large (which occurs only rarely), an appropriately chosen node from this tree to achieve a maximal decrease in the tree size is deleted. Repeat this node deletion process until all the tree components are sufficiently small.

CoreHD²² simply removes highest-degrees nodes from the 2-core in an adaptive way (updating node degree as the 2-core shrinks), until the remaining network becomes a forest. Furthermore, CoreHD breaks the trees into small components. In case the original network has many small loops, a refined dismantling set is obtained after a reinsertion of nodes that do not increase (much) the size of the largest component.

EI²³ selects $m$ candidate nodes from the set of absent nodes at each step and calculate the score ${\sigma }_{i}$ of each of them using the following kernel

$${\sigma }_{i}=\sum _{j\in {N}_{i}}(\sqrt{| | {C}_{j}| | }-1)+{k}_{i}^{(eff)},$$

(9)

where ${N}_{i}$ represents the set of all connected components linked to node $i$, each of which has a size ${C}_{j}$, and ${k}_{i}^{(eff)}$ is an effective degree attributed to each node (please see²³ for the details). Then the nodes with the lowest scores are added to the network. This procedure is continued until the size of the giant connected component exceeds a predefined threshold. The minus one term in Eq. (9) is used to exclude any leaves connected to node $i$, since they do not contribute to the formation of the giant connected component and should be ignored.