Introduction

With the advent of high-throughput genotyping and sequencing technologies, genome-wide association studies (GWAS) have become the most popular methods for investigating the genetic architecture of quantitative traits in random populations. However, the ever-growing number of markers makes it difficult to automatically fit all markers simultaneously in a single model. The classical mixed model GWAS estimates and tests trait association one marker at a time (genome scanning approach) to avoid the high dimensionality problem, but this has turned the problem into a multiple test problem instead. The linear mixed model (LMM) association study (Yu et al. 2006) has demonstrated its effectiveness in correcting family structure and cryptic relatedness among samples (Kang et al. 2010). However, there are three caveats with the above one-dimensional scanning GWAS. The first caveat is the problem of multiple tests. Single-locus GWAS requires a very conservative Bonferroni correction to determine the critical value of the p value used to declare statistical significance. As a result, when the number of markers is extremely large, true biologically important markers may be missed due to the over stringent test criterion (decreased power) (Wang et al. 2016). Secondly, if a trait is controlled by more than one gene, the single locus GWAS model is never true and the estimated effects of markers will be seriously biased due to linkage disequilibrium between neighboring markers (Wen et al. 2018). Finally, the LMM implemented GWAS doubly fits candidate markers because the fitted markers are also included in the genetic relationship matrix. Such a double fitting leads to a competition between the fixed effect tested and the random effect in the polygene and thus causes reduced power as a consequence (Yang et al. 2014).

The three problems associated with the genome scanning GWAS can be avoided by using a multiple regression model where all markers are simultaneously included in the model. The polygenic nature of many quantitative traits makes such a multiple marker association study more appealing than the single marker scanning approach (Segura et al. 2012; Wang et al. 2016; Wen et al. 2018). However, the ordinary least squares regression cannot handle the situations where the number of predictors (p) is larger than the sample size (n), which is often the case in GWAS. If the number of variables is indeed larger than the sample size, there is no unique solution for the estimated marker effects and the estimation errors will be arbitrarily large (Kyung et al. 2010). In many GWAS populations, the number of markers can easily reach millions whereas the sample size is often in the order of thousands. It is commonly accepted that only a small subset of markers is truly associated with any traits. Therefore, some types of variable selection, penalized regression, or Bayesian shrinkage models must be adopted in multiple marker GWAS (de Los Campos et al. 2013). Bayesian methods require Markov chain Monte Carlo sampling, which can be very intensive in terms of computational time (Wang et al. 2005; Xu 2003; Yi 2004). Several typical penalized regression models have been proposed to address the high dimensionality problem, including ridge regression (RR) (Hoerl and Kennard 1970; Shen et al. 2013), least absolute shrinkage selection operator (LASSO) (Tibshirani 1996), and elastic net (Zou and Hastie 2005) that combines the L1 penalty of LASSO and the L2 penalty of RR.

LASSO is the most tested method for variable selection and prediction. It uses a penalized function to simultaneously reduce dimensionality of markers (variable selection) and to penalize large estimated effects of regression coefficients (shrinkage). The cyclic coordinate descent algorithm adopted in the GLMNET/R software package (Friedman et al. 2010) is surprisingly efficient for finding the LASSO estimates of regression coefficients. While demonstrating the promising performance of LASSO for many problems, the method does have some limitations or shortcomings. For example, when the number of sample size does not match the growth of the number of variables, the model often fails (Hu et al. 2012). Therefore, we must borrow some biological information to reduce the number of variables prior to calling the LASSO method for association studies.

One piece of the biological information is the physical position of each marker on the genome. If two markers are located side by side physically, they may co-segregate or segregate with a similar pattern. In statistics, this is called linkage disequilibrium (LD), but LD is primarily caused by physical linkage in most populations. Therefore, in most GWAS populations, LD is the biological information we can borrow for using it to reduce model dimension. We can combine multiple SNPs with high LD into a block. Markers of the entire genome may be divided into some manageable number of blocks, called bins (Hu et al. 2012; Xu 2013). Similar techniques by dividing markers into groups have been proposed by other research teams (Liu et al. 2008) with different names in different contexts, e.g., haplotypes (Xia et al. 2017), gene-based SNP groups, pathway-based SNP groups, and collapsing SNP groups and so on. These authors have shown that the group-based SNP association studies can be more powerful than the single SNP analysis. Motivated by the above studies, we proposed a bin model to reduce the data dimension by combining neighboring SNPs into bins. Once the number of bins is reduced to a manageable level, we then used LASSO to shrink and estimate the effects of bins on the phenotype of a trait under investigation. The number of bins is determined by the LD level of the genome. High LD requires a small number of bins to capture the whole genomic information while low LD needs a large number of bins to capture the same amount of information. The thumb rule is to convert SNPs into a desirable number of bins so that LASSO can comfortably handle all bins in the sample model.

It is commonly believed that multiple locus models (e.g., LASSO) are better than single marker scanning models (e.g., GEMMA). However, the multiple locus models can only handle a limited number of markers, say a few hundred thousand markers. When the number of markers reaches a million, all multiple locus models fail. When markers are binned and the bins are used in place of markers, the model dimension can be substantially reduced so that all bins can be fitted into a single model. This study is to develop an efficient method to construct bins and demonstrate that the bin model can be as efficient as multiple marker models in terms of power and Type 1 error, but the bin model can handle virtually unlimited number of markers.

Material and methods

Binning SNP genotypes

Bins defined here are different from the classical definitions of bins in a line crossing experiment involving two or a few parents (Wang et al. 2016; Xu 2013). In the classical definition, a bin is defined as a genomic segment that contains no recombination breakpoints across the entire population under study. That criterion of defining bins is too stringent for a random population that involves many (unknown number of) parents. In this study, we define a bin as a block of physically linked SNPs with high LD. There are a few steps in creating a bin, as described below.

The first step is to code the minor allele by 0 and the major allele by 1, or the other way around, for all markers consistently. This is a very important step because if the coding system is not consistent across markers, we will not be able to capture the genomic LD information. Let A1 be the minor allele and A2 be the major allele. The numerical codes for A1A1, A1A2, and A2A2 should be 0, 1, and 2, respectively. Again, A1 is the minor allele (not the reference allele) for all markers in the genome.

The second step is to standardize the genotype code variable. Let Zjk be the genotypic code for all n individuals (an n × 1 vector) at the jth marker within the kth bin, for j = 1,…,mk and k = 1,…,m, where mk is the number of markers within the kth bin and m is the number of bins. The total number of markers in the entire genome is \(M = \mathop{\sum}\nolimits_{k = 1}^m m_k\). Each Zjk variable must be standardized to have a mean 0 and a standard deviation 1.

The third step is to create bins by combining neighboring SNPs. Let Zk be an n × 1 vector of bin genotypes and it is the average value of all markers in the kth bin,

$$Z_k = \frac{1}{{m_k}}\mathop {\sum }\limits_{j = 1}^{m_k} Z_{jk}.$$
(1)

The number of markers in the bin (mk) is determined in such a way that var(Zk) > c but adding one more marker will make var(Zk) < c, where c is a constant number between 0 and 1 set by the investigator. One can choose the c criterion so that, with this c, the number of bins is a desired number that can be comfortably handled by LASSO.

Recall that each Zjk is a standardized variable with variance 1. If all the mk markers within this bin are independent, the variance would be var(Zk) = 1/mk. If all the mk markers within the bin are in perfect LD, the variance would be

$${\mathop{\rm{var}}} \left( {Z_k} \right) = \frac{1}{{m_k^2}}\left[ {m_k + 2m_k\left( {m_k - 1} \right)/2} \right] = 1.$$
(2)

Let dij be the LD parameter between markers i and j within the kth bin (correlation coefficient between Zjk and Zjk). The actual variance of bin k is

$${\mathop{\rm{var}}} \left( {Z_k} \right) = \frac{1}{{m_k^2}}\left[ {m_k + 2\mathop {\sum }\limits_{i = 1}^{m_k - 1} \mathop {\sum }\limits_{j = i + 1}^{m_k} d_{ij}} \right].$$
(3)

Therefore, the bin variance is a value between 1/mk and 1. If we set var(Zk) = 0.5, then mk will vary across bins depending on the LD of consecutive markers within bins.

Least absolute shrinkage selection operator

Assume that based on a certain c criterion we create m bins with the bin code denoted by Zk (an n × 1 vector) for the kth bin. We now use LASSO to estimate all bin effects. The LASSO method requires a centered response variable, i.e., the phenotypic values need to be adjusted by the fixed effects (including population structure effects if any) prior to the LASSO analysis. The centered y is described by the following multiple regression model:

$$y\prime = \mathop {\sum }\limits_{k = 1}^m Z_k\gamma _k + e,$$
(4)

where γk is the effect of bin k on the trait of interest. Let Z be an n × m matrix for all bin genotypes and γ be an m × 1 vector for all bin effects. The LASSO estimates of the bin effects are

$$\gamma ^{\rm{Lasso}} = \arg \mathop {{min}}\limits_{\gamma \in \Omega } \left\{ {\left( {y\prime - Z\gamma } \right)^T\left( {y\prime - Z\gamma } \right) + \lambda \left\| \gamma \right\|_1} \right\},$$
(5)

where λ is a LASSO shrinkage factor and \(\left\| \gamma \right\|_1 = \mathop {\sum }\nolimits_{k = 1}^m |\gamma _k|\). The GLMNET/R package (Friedman et al. 2010) can be used to estimate the LASSO regression coefficients. However, the package does not provide a way to perform significance tests for the regression coefficients. We adopted the method to calculate the variance of the LASSO estimated effect for a bin and used that variance to calculate the Wald test and the p value for each bin (Xu 2013). The Wald test for bin k is

$$W_k = \frac{{\hat \gamma _k^2}}{{{\it{var}}\left( {\hat \gamma _k} \right)}},$$

and the p value is

$$p_k = 1 - {\it{Pr}}\left( {\chi _1^2 \,<\, W_k} \right),$$

where \(\chi _1^2\) is a Chi-square variable with one degree of freedom (Kao et al. 1999). The beauty of the LASSO method is that no multiple test correction is needed because all markers are included in a single model. Therefore, the nominal critical value for the −log10 (pk) test statistic can be used, which is −log10 (0.05) = 1.30103.

LMM—the gold standard for comparison

Using LASSO to analyze the bin data is our new contribution. However, we need to compare the new method with alternative methods to demonstrate the advantages of our method over existing methods. The LMM is the routine method for GWAS and has been the gold standard for comparison. It automatically controls population structure effects (Q) and polygenic effect via a genomic relationship (kinship) matrix (K). Therefore, it is called the Q + K model (Yu et al. 2006). Let y be an n × 1 vector of phenotypic values for a trait of interest, the LMM describing y is

$$y = X\beta + W_j\mu _j + \xi + e,$$
(6)

where X is a design matrix capturing all non-genetic (fixed) effects, e.g., systematic environmental effects, population structural effects, and so on, β are the fixed effects, Wj is a vector of numerical codes for the jth marker for j = 1,…,M (M is the total number of markers, not the number of bins), μj is the effect of marker j on the trait (treated as a fixed effect), ξ is a vector of polygenic (random) effects with an assumed N(0, Kϕ2) distribution where ϕ2 is the polygenic variance and K is a marker inferred kinship matrix (defined later), e is a vector of residual errors with an assumed N(0, Iσ2) distribution, where σ2 is the residual error variance. The marker inferred kinship matrix is defined as

$$K = \frac{1}{d}\mathop {\sum }\limits_{j = 1}^M Z_jZ_j^T,$$
(7)

where d (a normalization factor) is the average value of the diagonal elements of the unnormalized matrix K. The restricted maximum likelihood (REML) method was used to estimate parameters {ϕ2, σ2} and the best linear unbiased estimates (BLUE) of the fixed effects, β and μj, were obtained via mixed model equations. The Wald test for H0:μj = 0 is

$$W_j = \frac{{\hat \mu _j^2}}{{{\it{var}}\left( {\hat \mu _j} \right)}}.$$
(8)

Under the null hypothesis, Wj follows approximately a Chi-square distribution with one degree of freedom. The corresponding p value was calculated using

$$p_j = 1 - \Pr \left( {\chi _1^2 \le W_j} \right).$$
(9)

Genome-wide association studies

The bin model analyzed with LASSO and further refined by the second stage of tuning is the new method, denoted by BIN-Ave-Lasso, where Ave in the middle means average. An intuitive method derived from it is to use one SNP marker per bin (the middle one in the bin) to form the independent variable matrix and use LASSO for multiple marker analysis. Once the middle marker in a bin is detected, a fine tuning second stage follows to evaluate all markers in the significant bins. This method is also new and is denoted by BIN-One-Lasso. The original SNPs analyzed by LASSO are an existing method, denoted by SNP-Lasso, which is used as an alternative method for comparison. The classical Q + K model implemented in LMM is another existing method for comparison and is denoted by Q + K-LMM. The four methods are summarized in Table 1. The Bin-Ave-Lasso and Bin-One-Lasso methods also include a series of bin methods using different c criteria.

Table 1 Annotation of methods used in this study
Full size table

Simulated data from beef genotypes

We used the genotypes of 608,696 SNPs of 1217 cattle of our own population to simulate a quantitative trait. We used the mean squared error (MSE) to measure the accuracy of an estimated quantitative trait nucleotides (QTN) effect. Of the 608,696 SNPs, we assigned 20 loci as QTN. We evaluated the accuracies for all the 20 simulated QTNs. The QTNs with positions, effects, and MSE’s are demonstrated in Table 2. We also assigned each of the 608,696 SNPs, a small effect randomly sampled from a normal distribution with mean 0 and a very small variance to mimic a polygenic effect. The 20 loci collectively contributed 50% of the phenotypic variance, and the polygenic effect contributed 25% of the phenotypic variance. The remaining 25% phenotypic variance was contributed by the residual errors. All the 608,696 SNPs were used to construct bins of the cattle genome under various thresholds. A series of threshold value c for constructing bins were examined, ranging from 0.1 to 1 incremented by 0.1, where c = 1 is equivalent to SNP-Lasso, i.e., using the original SNPs by LASSO.

Table 2 Information about the 20 simulated QTNs
Full size table

To evaluate the performance of the four methods, we generated 100 simulated samples from the above set up. The statistical power for a method was defined as the total number of QTNs detected per sample divided by 20 and then averaged over the 100 replicated samples. Type 1 error of a method was defined as the total number of SNPs above the significant thresholds in regions beyond the ±10 kb reserved interval of a simulated true effect divided by the total number of markers above the significant threshold, and then averaged across the 100 replicated samples. All four methods were used for analysis of this simulated data.

Actual beef data

The resource population consisted of 1225 Chinese Simmental cattle that were born in Ulagai, Inner Mongolia of China from 2008 to 2014. Each individual was observed and measured for growth and developmental traits until slaughtered at ages from 16 to 18 months old. All the 1225 cattle were genotyped by the Illumina Bovine HD BeadChip which contained 774,660 SNPs. Quality control procedures were carried out using the PLINK 1.9 (Purcell et al. 2007) to filter out SNPs with call rate <95%, minor allele frequency <0.05, and significant deviation from Hardy-Weinberg equilibrium (p < 10−5). Moreover, cattle with >10% missing genotypes were removed. After filtering with the above criteria, a total of 608,696 SNPs and 1217 individuals remained in the sample for analysis. Imputation for sporadic missing alleles were performed using the Beagle 3.3.2 (Browning and Browning 2009). The binning criterion c ranged from 0.1 to 1.0 incremented by 0.1, as done in the simulated data analysis.

In this real data analysis, bone weight was the trait of interest (response variables). Since the LASSO method cannot adjust for covariates, phenotypic values were adjusted prior to the GWAS, i.e., the response variables were centered prior to the analysis. The covariates subject to adjustment included the first three principal components (population structure) and the following fixed effects: (1) year effect, (2) fattening days effect, and (3) the effect of initial body weight (body weight when cattle entered the camp). The data centering process was conducted by fitting the original phenotypic values to the above three fixed effects and PCs using a general linear model. The residuals of the general linear model were the centered phenotypic values of the traits, which were eventually subject to the proposed GWAS analyses. All four methods listed in Table 1 were used for the real beef data.

Results

Analysis of simulated data

To attain an overall understanding of the bin model, we constructed bins for the 608,696 SNPs of the 1217 individuals using criterion c from 0.1 to 1.0 incremented by 0.1. Table 3 lists the total number of bins and the size per bin under different c values. Supplementary Tables S1–S9 show the number of bins per chromosome under different c values. There is a trend that the longer the chromosome, the more the number of bins. The numbers of bins also indicate the LD levels for chromosomes with similar length. For example, chromosomes 26 and 29 are similar in size, but when c < 0.8, the number of bins for chromosome 26 is smaller than the number of bins for chromosome 29. This phenomenon indicates that chromosome 29 has more markers within high LD blocks than chromosome 26.

Table 3 Bin information using different criteria
Full size table

Under each c criterion and using 0.05 as the p value criterion of significance test, we used the first 20 simulated samples to perform GWAS with BIN-Ave-Lasso and BIN-One-Lasso to evaluate the relationship between c and the power (Fig. 1a) and the relationship between c and the Type 1 error (Fig. 1b). Figure 1a shows that both methods have increased powers when c is increased, which is expected because binning neighboring SNPs will reduce the variance of a binned genotype compared with an individual SNP. In most cases, BIN-One-Lasso had a higher power than the BIN-Ave-Lasso except when c = 0.1 and c = 0.3 where the latter showed a higher power. Figure 1b shows that the two methods have decreased Type 1 errors when c is increased. Apparently, BIN-Ave-Lasso is superior over BIN-One-Lasso duo to its better control of the the Type 1 error. In subsequent analyses, we chose c = 0.9 as the binning criterion to compare the performances of the methods.

Fig. 1
figure 1

Statistical powers and Type 1 errors under various c criteria of binning. a Statistical powers averaged across 20 replicated samples. b Type 1 errors averaged across 20 replicated samples

Full size image

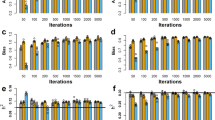
We now compare the powers and Type 1 errors of the new methods under c = 0.9 with existing methods from 100 replicated simulated samples. The results are given in Fig. S1, which show that BIN-One-Lasso has a much higher power than all existing methods and BIN-Ave-Lasso is much more efficient in controlling the Type 1 error than all other methods. We used the power to Type 1 error ratio to evaluate the overall performance of these four methods. As shown in Fig. 2, BIN-Ave-Lasso outperformed the other methods and the performance of BIN-One-Lasso was roughly equal to the SNP-Lasso method. The Q + K-LMM method, the most commonly used GWAS approach, was the worst one in terms of power to Type 1 error ratio. The computational speeds (AMD Opteron 6344 CPU2.59 GHz, Memory 272 G) of the four methods are compared in Fig. 3, showing that our new methods are most efficient in terms of computational time, only taking up to one-tenth of the computing time taken by the Q + K-LMM method.

Fig. 2
figure 2

Comparison of performance for BIN-Ave-Lasso, BIN-One-Lasso, Q + K-LMM, and SNP-Lasso averaged across 100 replicated samples

Full size image
Fig. 3
figure 3

Computing time (min) of BIN-Ave-Lasso, BIN-One-Lasso, Q + K-LMM, and SNP-Lasso across 100 replicated samples

Full size image

Since different methods used different threshold values for the test statistics to declare significance, we compared the ROC curves of the methods. An ROC curve is a plot of power against Type 1 error, the higher the curve, the better the method. We also compared the methods for a different type of ROC curve, where the power is plotted against the false discovery rate (FDR). The FDR is defined as the number of falsely detected markers or bins divided by the total number of detected markers or bins. The ROC curve plots are shown in Fig. 4, indicating that the new methods are always more powerful than the current methods compared. There is a slight difference between the two new methods: when the false positive rate is low, BIN-Ave-Lasso is more powerful than BIN-One-Lasso, and vice versa when the false positive rate is high. We also recorded the statistical powers for each QTN of the four different methods and ranked the 20 QTNs by their absolute values of effects in Table S10. The power of each QTN was defined as the fraction of the samples in which the QTN was detected. These QTN specific power comparisons are demonstrated in Fig. 5, showing that Q + K-LMM was too conservative to detect any QTN with absolute effect <0.23. When QTNs with absolute effects >0.35, all methods had 100% power except SNP-Lasso. In general, the power of BIN-One-Lasso is higher than other methods in detecting either large-effect QTNs or small-effect QTNs. Furthermore, because of the stringent significant threshold, Q + K-LMM has very low powers compared to other methods.

Fig. 4
figure 4

Statistical power plotted against Type 1 error and false discovery rate. a Statistical powers at different levels of Type 1 error. b Statistical powers at different levels of false discovery rate

Full size image
Fig. 5
figure 5

Statistical powers of all simulated QTNs for BIN-Ave-Lasso, BIN-One-Lasso, SNP-Lasso, and Q + K-LMM

Full size image

In summary, our new methods have similar performance compared to SNP-Lasso, but much model efficient to the Q + K-LMM method. In addition, the computational efficiency of the new methods is much higher than SNP-Lasso. Under the conventional significant threshold (p value = 0.05), BIN-One-Lasso is more powerful than BIN-Ave-Lasso while BIN-Ave-Lasso has a better control of Type 1 error.

Analysis of beef cattle data

We also used the four methods to analyze the real beef data for a trait called bone weight, which is defined as the total weight of all bones including the forequarter and hindquarter joints. Significant SNPs (bins) for all methods are listed in Table 4 for the two new methods and Table 5 for the two current methods. Manhattan plots for the new methods (BIN-Ave-Lasso and BIN-One-Lasso) are also shown in Fig. S2 along with the plots from Q + K-LMM and SNP-Lasso. In the analysis of bone weight, we found that BIN-Ave-Lasso is relatively conservative and BIN-One-Lasso is more powerful than all other methods, consistent to the observation from the simulation studies. Moreover, regions identified by BIN-One-Lasso has covered all SNPs identified by Q + K-LMM and SNP-Lasso.

Table 4 Description of significant SNPs (bins) associated with bone weight identified by BIN-Ave-Lasso and BIN-One-Lasso
Full size table
Table 5 Description of significant SNPs (bins) associated with bone weight identified by Q + K-LMM and SNP-Lasso
Full size table

Discussion

The next-generation sequencing technologies have produced large volumes of genomic data. Such big data face two major bottlenecks in GWAS: high dimensionality and heavy computational burden. Combining SNPs into bins is an efficient way to solve both problems simultaneously. The SNP block type of methods can effectively reduce the number of markers for analysis, e.g., only about 20,000 genes to fit a model when using a gene-based method to perform GWAS in cattle (Capomaccio et al. 2015). This is far less than the number of genome-wide markers (770K) in the Illumina Bovine HD BeadChip. Many previous studies also elucidated that SNP block-like methods are more powerful than the single- marker analysis counterpart.

In this study, the whole genome is divided into a manageable number of bins, and we can easily control the number of bins through controlling the c threshold of variance across individuals in the population. Our bin model is based on the LD level between consecutive markers within bins and thus takes advantage of the biological information (physical relationships of SNPs). This is quite different from dimension reduction statistics such as the principal component analysis. Our results showed that the bin model can effectively compress markers. We only compare the performance of the bin model with c = 0.9 to other methods based on the prior knowledge from Fig. 1. When we set c = 0.5, our bin model also has comparable performance to Q + K-LMM. However, if the c threshold is too small, the bin sizes will be relatively large and the LD levels within bins will become relatively low. In that case, the bin model cannot capture QTNs with small effects and the effects will be diluted by so many markers within bins. The bin model seems to contradict with the purpose of improving power in GWAS. With the bin model, we actually emphasize the ability of handling almost unlimited number of markers while still using a multiple marker model. The gain comes from the multiple marker model, not from the bins themselves. Without the bin model, we cannot use the multiple marker approach to performing GWAS when the number of markers is extremely large.

In practice, the LD level has a positive correlation with the marker density. For this reason, the efficiency of dimensionality reduction will increase when the density of markers is increased. Therefore, the proposed bin model will be more advantageous with high density sequence data than with low density marker data. However, the proposed bin model assumes that there is at most one true QTN in a bin. This means that the bin size cannot be too large. If the bin size is indeed too large, we need another assumption to compensate for it, that is all QTNs in the same bin must have effects in the same direction. An obvious consequence when the above assumptions are violated is the compromise of statistical power. Adding a weight to each marker is a feasible solution to this pitfall. In rare variant analysis, Han and Pan (2010) proposed to estimate the direction of effect for each marker in a marginal model and then assigned a weight to represent the direction of that marker effect. Lin and Tang (2011) used the estimated regression coefficient of each marker as the weight, where the regression was done one marker as a time. Moreover, the principal component analysis can also determine the weight. When the bin sizes are not too large, the chance of having more than one causal mutation within a single bin is minimum under the assumption that only a finite number of genes are causative for most quantitative traits.

LASSO is a penalized least-squares method with constraints on the absolute values of the regression coefficients. Due to this special penalty, LASSO leads to sparse selection of independent variables by shrinking most of the regression coefficients to zero. As a consequence, it is the ideal model to fit most quantitative traits, which are assumed to be controlled by a few genes with large effects and many genes with undetectably small effects (Hayes and Goddard 2001). Xu (2007) compared LASSO with several other methods (empirical Bayes, penalized likelihood (Zhang and Xu 2005), and stochastic search variable selection (Yi et al. 2003) for multiple QTL mapping (Xu 2007) and found that LASSO was as efficient as the empirical Bayes method but much more efficient in terms of computational speed. However, LASSO has an intrinsic limit in the ratio of model size to sample size—the sample size must be sufficiently large to match the growth of model size. Based on the above considerations, we proposed the new bin model to improve GWAS performance by taking advantage of the high efficiency of LASSO. We used the GlmNet/R package (Friedman et al. 2010) to perform the LASSO analysis and the program is extremely fast for a median sized data. In GlmNet/R, the optimal value of tuning parameter λ, which controls the degree of shrinkage, can be obtained through a k-fold cross-validation. The λ value from the cross-validation is used to calculate the MSE. In this study, the λ value producing the minimum MSE + 1 standard error is deemed the optimal tuning parameter in order to control the Type 1 error rate (Waldmann et al. 2013). The relaxed λ value producing the minimum MSE also can be used to obtain more significant markers. The procedure of cross-validation may result in unstable estimation of the tuning parameter partly because of refitting the model many times (Li et al. 2010). An alternative method is the Bayesian LASSO (Yi and Xu 2008), which treats the tuning parameter as an unknown parameter to be estimated from the data. This method provides an automatic way to determine the tuning parameter. However, the method involves time consuming MCMC samplings and cannot generate a sparse model for variable selection (Hans 2010).

The bin model cannot pinpoint causative variants when bin sizes are relative large. However, this issue can be solved by the two-stage approach proposed here, where we detected significant bins first and then fit a model included all markers within the significant bins. Many two-stage methods have been proposed for GWAS including, e.g., LMML (Shi et al. 2011), mrMLM (Wang et al. 2016), and ISIS EM-BLASSO (Tamba et al. 2017), which appear to be advantageous over a single stage genome scanning approach. In the first stage, these methods select a promising subset of markers through a correlation test between markers and traits of interest. The aim of this step is to reduce the number of markers. After this stage, the number of preliminarily associated markers is relatively small and can be easily handled by various penalized regression models in the second stage. The second stage model fitting can further reduce false positives, while a relaxed threshold in the first step can keep many potentially interested SNPs in the model. In our two-stage bin model, we used a second step of fine tuning to pick up specific markers within the associated bins. The model in the second stage LASSO analysis contains all markers in the significant bins. For example, if we identify 20 significant bins in the first stage and each significant bin contains 100 markers, then the total number of markers included in the second stage LASSO model would be just 20 × 100 = 2000, a small number easily handled by LASSO.

Conclusions

Multi-locus GWAS methods are more suitable for identifying causative variants than LMM that separates the connection between markers. However, the high dimensional problem has become a bottleneck for genome-wide multi-locus GWAS. In this study, we proposed a bin model to compress the scale of genome data by changing the c criterion of binning. The BIN-Ave-Lasso and BIN-One-Lasso methods can be used for genome-wide multi-locus GWAS. Our new approaches are faster and more powerful than Q + K-LMM and SNP-Lasso as demonstrated in the simulated studies. Moreover, the BIN-Ave-Lasso method has a much lower FPR while BIN-One-Lasso shows higher statistical power under the conventional threshold.