Avalanche outbreaks emerging in cooperative contagions

Abstract

The spreading of contagions can exhibit a percolation transition, which separates transitory prevalence from outbreaks that reach a finite fraction of the population^1,2. Such transitions are commonly believed to be continuous, but empirical studies have shown more violent spreading modes when the participating agents are not limited to one type. Striking examples include the co-epidemic of the Spanish flu and pneumonia that occurred in 1918 (refs 3, 4), and, more recently, the concurrent prevalence of HIV/AIDS and a host of diseases^5,6,7. It remains unclear to what extent an outbreak in the presence of interacting pathogens differs from that due to an ordinary single-agent process. Here we study a mechanistic model for understanding contagion processes involving inter-agent cooperation. Our stochastic simulations reveal the possible emergence of a massive avalanche-like outbreak right at the threshold, which is manifested as a discontinuous phase transition. Such an abrupt change arises only if the underlying network topology supports a bottleneck for cascaded mutual infections. Surprisingly, all these discontinuous transitions are accompanied by non-trivial critical behaviours, presenting a rare case of hybrid transition⁸. The findings may imply the origin of catastrophic occurrences in many realistic systems, from co-epidemics to financial contagions⁹.

Main

Percolation transition, depicting the formation of global connectivity on continual addition of links, occurs typically in contagion processes in social and biological systems¹. Spreading of activities can either terminate after a transitory prevalence or undergo an outbreak that reaches a finite fraction of the population, such as in the spread of epidemics^2,10, cybernetic viruses¹¹, opinions¹², and a wide range of failures, such as power blackouts^13,14 or road congestions¹⁵. Such phase transitions were long believed to be continuous, meaning that only a gradual onset of small-scale outbreak is present at the threshold of the controlling parameter, which measures the propensity of forming local connections¹.

Agents may, however, not spread in isolation. Empirical studies have shown more violent spreading modes when the participating agents are of multiple types, as most prominently exhibited in co-epidemics. The most striking example is the 1918 Spanish flu pandemic, which caused a prevalence in one third of the world population. Pathological evidence showed that a considerable proportion of the infecteds were co-infected by pneumonia^3,4. The spread of HIV/AIDS, as a more recent example, has been verified to be promoted by a host of other infectious diseases (including tuberculosis, herpes virus, syphilis, malaria and hepatitis) and vice versa^5,6. The boosted propagation of co-epidemics is rooted in the interaction of pathogens that mutually enhance the susceptibility for each other. Considerable attention has been received from epidemiologists in revealing their pathology. Their fundamental dynamics on the macroscopic scale is nevertheless much less understood. It thus remains a question: what is the typical scenario of outbreak that can emerge in the co-spreading of cooperative pathogens, or to what extent would such cooperation alter the classic spreading mode of a single agent?

On one hand, interaction of a positive-feedback nature tends to impose instability on a large system. The principle has been substantiated in interdependent networks^13,14 and in systems with reinforced contagion via neighbouring nodes¹⁶. On the other hand, a non-negligible influence will be exerted by the underlying networked medium, which strengthens or impairs the cooperation. The outbreak profile is thus shaped by both agent–agent and agent–network interactions, beyond the complication of single-agent processes.

Here we propose a mechanistic model for understanding cooperative contagions in the framework of percolation. We focus on identifying possible phase transitions that arise therein. Our results show a fundamentally different scenario from the classic ordinary percolation (OP; ref. 1). It reveals in particular that cooperation can lead to phase transitions of different orders, causing either a mild or an abrupt massive outbreak right at the threshold. The actual type of outbreak depends crucially on the underlying network topology, which regulates the efficacy of cooperation. An abrupt outbreak emerges only if the topology has a required global structure that supports a bottleneck for cascaded mutual infections. In this case, an avalanche-like outbreak may be imminent with no warning.

We formulate our model in terms of epidemic spreading. However, the implications can be valid for more general contagions. Suppose that two types of pathogens are to spread on the same network of contacts. Observations on realistic co-infection cases show that individuals that have been weakened by one disease would fall more easily prey to the other, owing to organic injury or a degraded immune system. The threshold for being infected is thus lowered at a secondary infection by the disease of the opposite type. Concisely, we assume here the following simple rules: a virgin node, referred to be at an uninfected state (‘S’) by either disease (namely disease A or B), has probability p to get infected by any infective neighbour; whereas a node that has been infected by one disease (being either active or recovered) has a raised probability q > p to get infected by the other (Fig. 1a).

Figure 1: Illustration of co-epidemic spreading process on a complex network.

a, Conditional infections on a given network. Whereas a virgin node is infected by a single disease with a normal probability p, a node that has already been infected by one disease falls prey to the other with a raised probability q. The figure demonstrates initial and secondary infections—that is, P(Ab|b) = P(aB|a) = q > P(A|S) = P(B|S) = p. b, Schematic of a bottleneck for strong cooperation. Suppose that two different diseases spread along separate pathways from node i on a network with a large ratio of long to short loops. In most cases, either of the diseases stops spreading in its subcritical regime and, consequently, the other on its own also cannot continue spreading. But if both diseases can survive until their merging at node j, disease B will intrude into the infected region of the opposite type a with probability q and initiate a large number of new infections in its vicinity. This is followed by cascaded mutual infections that contribute with a high probability to a giant doubly infected cluster.

To initiate an epidemic, we place a doubly infected node as a ‘seed’ on the network of study. After being infected, a node becomes infective itself (denoted by state ‘A’ or ‘B’ for the respective disease), and recovers (to state ‘a’ or ‘b’) after exactly one time step. The recovered nodes acquire immunity against the disease they had, but not to the other. We assume here, for simplicity, the same infection and recovery probabilities for both types of diseases. This symmetric case has, however, sufficed to generate a rich zoo of dynamics.

We performed extensive numerical simulations to identify the phase transition on both random and regular topologies. Erdős–Rényi (ER) networks represent a class of topologies of random connections found in nature. It can be constructed by connecting any two of N nodes with a given probability such that the node degrees are distributed around a fixed mean value 〈k〉 (ref. 2). On ER networks, we found a discontinuous transition (DT), but of a hybrid type. For percolation, two order parameters are used to characterize a phase transition—namely, the probability P of forming a giant affected cluster and the fraction ρ of node population that belongs to a giant cluster. For most contagion processes involving only one single agent, both P and ρ undergo a continuous transition (CT) on ER networks, exhibiting identical scalings P ∼ ρ ∼ (p − p_c)^β, around the critical point p_c = 1/〈k〉, with β ≍ 1 (ref. 1). It stands for a typical case within the universality class of OP. In contrast, for our co-epidemic model, we found giant infected clusters of a finite fraction already at the critical point. These giant clusters are well separated from premature clusters, which die out before having infected a non-infinitesimal fraction of the network. The former correspond to the separate sharp peaks in the logarithmized mass (infected population) distribution, whereas the latter correspond to the left power distribution, as shown in Fig. 2a. At criticality, a giant infected cluster is formed if and only if a giant doubly infected cluster is formed, and can hence be represented by this ensemble (see Supplementary Information). Figure 2b shows an apparent difference in the two order parameters that characterize the transition: whereas P_ab, denoting the probability that a seed develops into a giant doubly infected cluster, exhibits a CT, the fraction ρ_ab of doubly infected nodes shows clearly a DT, exhibited as a jump to a finite value at p_c (remains at 1/〈k〉).

Figure 2: Hybrid phase transition on Erdős–Rényi networks with mean degree 〈k〉 = 4.

a, Mass distribution of infected clusters at the threshold p_c ≍ 0.25 for 10⁸ realizations, with the secondary infection probability q = 1.0. The peaks on the right side, separated clearly from the left ramped distribution, correspond to giant clusters. b, Phase diagram for probability P_ab of forming giant clusters versus initial infection probability p showing a CT. Data are shown for system sizes N = 2¹⁴–2²⁵. Inset: DT shown by the fraction ρ_ab of doubly infected nodes versus p. Data for different N superpose exactly. The data points (dotted part) below p_c diminish as N approaches infinity. c, Plot of giant cluster size versus system size shows a linear scaling m_peak ∼ N at p_c, for N = 2¹⁴–2²⁵, thus supporting a strictly defined DT.

The DT shown by ρ_ab fulfils its strict definition, meaning that it holds valid all the way to the thermodynamic limit N → ∞. This is verified by the linear scaling of the giant cluster mass with the system size at p_c: m_peak ∼ N. Note that although self-supporting giant clusters can still be triggered for p < p_c in finite systems (dotted part of the curve in the inset of Fig. 2b), they would vanish when N → ∞. In fact, the data collapse for P_ab strongly suggests a standard finite size scaling (FSS; refs 1, 2)

with 1/ν = 0.20 and γ = β/ν = 0.12. ϕ is a scaling function which approaches a constant value for an infinite system. Here, the DT accompanied by non-trivial power laws of criticality actually presents a striking case of hybrid phase transition⁸.

Although ER networks are locally tree-like (they have mainly long loops for N → ∞), the behaviour on trees is distinctly different: only a CT is observed, as in the OP universality class. This thus implies that loops are crucial for the occurrence of a DT.

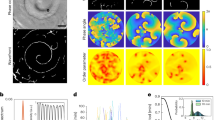
More insights are obtained by studying the process on regular topologies. A broad spectrum of phenomena are exhibited on regular lattices, which illuminate particularly the role of dimensionality. On 2D lattices, the system undergoes a typical CT in the OP universality class. This is indicated by the time course of the average number n(t) of newly infected nodes, at the critical point p_c(q = 0.99) ≍ 0.4503(1), which is fully consistent with the power law n(t) ∼ t^0.5843 expected for OP (ref. 1). The insets in Fig. 3a for P_ab and ρ_ab both show the typical scaling behaviour for OP on 2D lattices: P_ab ∼ ρ_ab ∼ (p − p_c)^β, with β ≍ 5/36 (ref. 1). Figure 3c shows accordingly a fractal cluster that forms at a slightly supercritical point.

Figure 3: Dependence of transition order on dimensionality.

a, Time courses of the average number n(t) of newly infected nodes around p_c on a 2D lattice, with q = 0.99. The central curve for p_c ≍ 0.4503(1) shows a scaling law, n ∼ t^0.5843, which is typical for CT in the universality class of OP. Insets: CTs shown by both order parameters P_ab andρ_ab. b, Time courses of n(t) for different values of p on a 4D lattice, with q = 0.99. The concavity of the curves typically indicates a bottleneck for forming a giant cluster. Upper inset: plot of ρ_ab versus p shows a DT. Lower inset: plot of P_ab versus p shows a CT of infinite order. c, Fractal infected cluster formed on a 2D lattice of size 1,024 × 1,024, obtained at p = 0.4504. The snapshot is captured at the end of the co-epidemic. d, Time course of the proportion of newly infected nodes of both diseases, simulated in the slightly supercritical regime on a 4D lattice.

We then examined the impact of higher dimensionality, which is claimed by the distinct behaviour shown on 4D lattices (Fig. 3b). For p ≤ p_c, n(t) decreases to zero faster than any power law, whereas for p > p_c, it stops midway and turns up, indicating that a small proportion of epidemics survive and keep spreading forever on an infinite lattice (p_c(q = 0.99) ≍ 0.111857(3)). This means that the surviving epidemics have passed through a bottleneck, analogous to the growth of a small droplet in a supercooled vapour, which exhibits a typical DT (ref. 17). Indeed, the density of surviving clusters ρ_ab jumps to a finite value at p_c—albeit with a continuous change in the probability P_ab. Thus, the transition is again hybrid, as shown from the drastic difference in the insets of Fig. 3b. (There we also found that P_ab decreases faster than any power law when p → p_c, that is, its transition is continuous, but of infinite order.)

Heuristically, the above dependence can be explained through the efficacy of cooperation. If cooperation takes effect already in the early stage, it would not effectively help the expansion of the cluster. This is the typical case on 2D lattices, where the spreading of each disease is constrained in at most only three outgoing directions from an infected node so that one frequently encounters the other. Consequently, most nodes are doubly infected (with q) shortly after being infected by either disease (see Fig. 3c). The pathogen at the propagating forefront has to infect the susceptible region on its own (with p), as it fails to acquire aid from the counterpart (except a narrow fringe). Cooperation hence plays little role in promoting the spreading forefront, permitting only OP.

In the opposite case, a bottleneck forms if there is little cooperativity in the early stage, but substantially more in the later stage. As seen on a 4D lattice, the merging probability of two pathways of different single diseases is greatly reduced, owing to a greater number of possible outgoing paths (seven directions). Neither disease can survive alone in the subcritical regime. But if both diseases can survive until their pathways merge, they can cause massive secondary infections by intruding into the accumulated infected regions of the opposite type, with the raised probability q (see illustration in Fig. 1b). Furthermore, the mutual intrusion will trigger more new infections in their vicinities and further the process in a cascaded way—an avalanche outbreak occurs. The concave time course for the proportion of newly infected nodes by both diseases in Fig. 3d is attributed exactly to this process, where a characteristic merging time of pathways appears. It breaks the scale invariance of criticality, which should be present in a CT (ref. 18). In this view, only network topologies that tend to postpone strong cooperation could support avalanche outbreaks. We hence conjecture that a necessary condition for DTs is a paucity of short loops and an abundance of long loops in the underlying network. This is true for ER networks and 4D lattices, but not for trees and 2D lattices.

Along this line, the behaviour on 3D lattices should fall between those demonstrated on 2D and 4D lattices. It shows, however, a sensitivity to minor factors (see Supplementary Information). This is a signature of the critical dimension. For example, the time courses n(t) in Fig. 4a, b for simple cubic lattices show different orders of transition for synchronous and asynchronous updating (SU/AU) schemes. A small updating latency intrinsic to the SU scheme is responsible for the disparity. We should, however, emphasize that a such small difference in the updating scheme would not change the universality class for most single-agent stochastic systems. The transition with SU is again hybrid (except that P_ab is of finite order). The infected giant cluster, as captured in Fig. 4c, is compact at p ≍ p_c, being consistent with a DT. There it exhibits cascaded mutual infections during the growth, where the active propagating fronts spread almost tangentially to the cluster surface.

Figure 4: Critical dimension for co-epidemics on lattices.

a, Continuous transition shown by the time courses of average number n(t) of newly infected nodes around p_c(q = 0.99) ≍ 0.1844 on a 3D lattice, with the asynchronous updating scheme. The scaling of the central curve n(t) ∼ t^0.494 indicates a typical transition in the universality class of OP for this dimension. b, Discontinuous transition indicated by the concavity of the time courses of n(t) at p_c(q = 0.99) ≍ 0.19205, with the synchronous updating scheme. These two plots together show the sensitivity to the updating latency for this dimension. c, Cascaded mutual infections on a compact cluster on a 3D lattice, with the synchronous updating scheme. The arrows indicate that the active forefronts intrude into the oppositely infected regions, almost tangentially to the cluster surface.

Connecting regular and fully random topologies, we further simulated the process on Newman–Watts small-world networks in 2D (refs 19, 20), where shortcuts are randomly added with probability φ on a 2D lattice (see Supplementary Information). As anticipated, a tricritical point in φ arises, which clearly sets apart DTs and CTs (ref. 21). But in Barabási–Albert networks, which also show the small-world property but have a power-law degree distribution²², only CTs with an almost-null threshold were observed.

Hence, the above study has shown that cooperation of multiple contagious agents may lead to different phase transitions, giving rise to either a mild or a massive outbreak at the threshold. A topology that tends to postpone strong cooperation to a later stage would most likely generate an avalanche outbreak by means of cascaded mutual infections. The studied process shares the principle of positive feedback with the damage spreading on interdependent networks^13,14—the latter, however, claiming that to be from the coupling of topologies. It hence provides a new mechanism for the category of discontinuous/abrupt percolation transitions of recent focus^{13,14,23,24,25,26,27,28}.

The discussed inter-agent cooperation is a natural ingredient that may underpin diverse complex phenomena, from co-epidemics to correlated failure spreading, to co-movement in financial contagions⁹. The potential abrupt change, as unveiled here, subjects those systems to greater fragility. The implication may a reason for crises, when it applies to the co-spreading of financial disturbances in correlated domains⁹. But we should point out that the studied cooperation merely belongs to a broad range of interactions of agents from game theory that could be susceptible to instability^29,30. Our work calls for further investigations in that respect.