Introduction

Since the first experimental realization of Bose-Einstein condensation (BEC) in 1995, there is a lot of experimental and theoretical work focusing on the dynamical properties of the ultracold system. The nonlinear phenomena, like soliton, vortex formation and evolution in the BEC system are the hot topics within the past decade in BEC related studies1,2,3,4,5,6,7. The particular nonlinear features, the categorization of bright/dark soliton for example, are dependent on the nonlinear inter-particle interaction constant in the theoretical model, for which the Gross-Pitaevskii equation (GPE) is chosen and proved to be pretty reliable. It is now known that the amplitude and sign of scattering length (as) determine the strength and the sign (attractive or repulsive) of the nonlinear inter-particle interaction. It is now possible to tune the amplitude and sign of the scattering length through magnetically controlled Feshbach resonance technique, so that the long pursued Bardeen-Cooper-Schrieffer to BEC crossover is realized experimentally8,9.

Given the flexible tunability, besides typical nonlinear features, ultracold system is the ideal choice for investigating many intriguing physics, among these is the ultracold physics analog of black hole event horizon in the exploration of cosmology and gravitational physics. This corresponds to the use of artificial black holes10,11. As indicated by Unruh in his seminal paper12, the supersonic flow excitations corresponds to a scalar field equation on a curved spacetime containing a horizon. The corresponding ultracold fluid analog is sonic horizon, when identifying the fluid flow with curved spacetime and excitation mode with curved spacetime fields. Due to their ultracold temperature and well isolation, trapped Bose-Einstein condensates were proposed as promising candidates for observing sonic black holes and Hawking radiation13. Experimental demonstration of sonic black holes14 and Hawking radiation15 had been realized by accelerating an elongated condensate in a step like potential. It is shown by numerical study16 that for a static ground state BEC system trapped in isotropic harmonic potential, when there is abrupt change of scattering length via Feshbach resonance technique, the system will expand/contract with time and under certain parametric setting there exists sonic horizon which is the spherical surface outside which the fluid flow speed surpass that of sound. Here in this paper we will perform an analytical study of the evolution of similar initial BEC system investigated in prior numerical study16. We utilized the Gross-Pitaevskii equation (GPE) model, through the modified variational approach, calculated the criterion for the formation and lifetime of the sonic horizon, and quantitatively corroborate the sonic horizon feature shown in prior work16. Also the damping effect arising from phonon excitation is analyzed numerically with pictorial demonstration.

This paper is arranged as follows, the next section makes the theoretical model analysis and gives the detailed calculation steps combined with pictorial demonstration regarding the key collective features of the system. The conclusive remarks are made in the last section.

Methods

The GPE model and modified variational ansatz

The study of the formation of sonic horizon could be carried out in expanding BEC in isotropic harmonic trap , in which an abrupt change in nonlinear interaction strength is the cause of the expansion. As in prior work, the Gross-Pitaevskii equation could be chosen as the theoretical model, but in order to give more precise description of the nonlinear interaction, tunable interaction strength parameter is incorporated in the model. The corresponding equation takes the following format,

The systems described by Eq. (1) start to evolve from the state ψ0 = ψ(r, 0) which solves the stationary equation of Eq. (1) with g(t ≤ 0) = g0. During the evolution, g(t) = g (t > 0). g(t) depends on the inter-particle scattering length which is adjusted through the Feshbach resonance technique. Assume initially (t < 0), the BEC system is in the ground state with distribution width σ0. The initial wave function (t = t0) takes the following form,

where φ(r) vs. r functional curve is very similar as that of exp (−r2/2) (zero nodes, decay from maximum value at r = 0 to minimum value 0 at +∞), its actual form is discussed in the ensuing steps. Different from regular variational treatment, here we choose the parameterized functional form φ instead of regular gaussian function to reach more precise description of the system. While it is generally true that φ may evolve into inexplicit form that is difficult to determine analytically, the evolution of the distribution width may bear significant physical meaning and can be solved analytically. Consider the following action of Eq. (1) with the Lagrangian density expressed as,

We use the following ansatz for ψ(r, t) (for d-dimensional case),

There are three real single-variable functions φ(x) (x = r/σ(t)), σ(t) and β(t) to be determined, C0(φ) is normalization constant determined by function φ(x) according to,

where Na is the total number of constituent particles.

Based on the formulation (3) and ansatz (4), we show in the subsection the principle calculation steps towards the typical collective mode of the system.

Oscillation mode

Substitute ansatz (4) into Eq. (1) and set the imaginary part to zero, we can directly obtain,

Combine with (6), the variation of action S with respect to σ and φ gives two coupled equations for φ(x) and σ(t) as follow,

where , k1(t) = ∫g1(t)σ2(t)dt, and V(σ) = V0(σ) + V1(σ), with

C1(φ), C2(φ) depend on φ, C3(φ) depends on φ as,

For weak nonlinear interaction (g(t) very small) which warrant neglecting V1(σ), Eq. (8) is integrable from (10) and we can solve for σ(t) as follow,

where

σ0 is the initial distribution width at t ≤ 0, with reflecting the system’s expansion/contraction speed for t > 0. We can see that σ(t) oscillates with period . We can also see that the distribution width σ(t) oscillates between the maximum value and minimum value and is just the breathing mode arising from the quantum pressure.

Results and extended analysis

Criterion and lifetime for the formation of the sonic horizon

Based on the analytical results regarding the oscillation mode derived in the previous section. We calculate the key physical quantities bearing significant physical meaning.

From formula (6), we can get the fluid velocity as,

The sound velocity17 in the weak interaction limit is

where φ(x) possesses the same qualitative feature as and is decreasing function of r for fixed time t, whereas v(r, t) is an increasing function of r. Suppose the BEC system is bounded as r ≤ R, the bounded function has maximum value βm at t = tm in the range 0 ≤ t ≤ T0, when βmR > cs(R, t) holds, there is timing range [t1, t2] with t1 ≤ tm ≤ t2 such that v0(r, t) = cs(r, t) or

has solution rc (0 < rc ≤ R) and rc is just the critical radius corresponding to the sonic horizon, below (above) which the fluid flow is subsonic (transonic).

It is not hard to see that the time tm for the appearance of is,

with

The lifetime of τ = t2 − t1 can be evaluated as follow. Around t = tm, both v(r, t) and cs(r, t) are decreasing function of t, so t1 = tm, but for significantly large R, cs decreases much faster than v(r, t) and coincides approximately at zero value which corresponds to in reference to v(r, t) ∝ cos(ωt)r. So the lifetime of the sonic horizon is

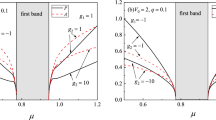
Figure 1 shows the variation of v0, cs with r for from Eqs (18) and (19), which cross at rc. We can see that the theoretically derived functional curves of v0 and cs match very well with the results (shown as Fig. 2 in prior work16) that are obtained from numerical simulation. Figure 2 shows the variation of rc (units of (ħ/mΩ)1/2) vs. t (units of Ω−1) with rc obtained from solving algebraic equation (20). We can see that our analytical results shown by these two figures agree very well with that reported by prior pure numerical analysis (shown in Fig 3 in ref. 16 with same timing range). We can see that although in the timing range under study, the system’s distribution width varies significantly, but in the intermediate region of r around rc, cs (∝|φ|2) varies in pace with v0 (∝r), so the crossing point rc between curves of cs and v0 is almost a constant in the timing range under study. Physically this means that the position of the sonic event horizon is relatively stable in most of the timing range under study. For the case of g1(t) ≠ 0, when the effect of V1(σ) has to be taken into account as the magnitude of g1(t) increase, σ(t) may not possess analytical solvable format as formula (14). But when the magnitude of g1(t) is not so big , the g1(t) term could be treated as perturbation, we anticipate the system showing the same qualitative feature as the case with g1(t) = 0. This can be seen when we plot the ‘potential’ curve of V(σ) (incorporating V1(σ)) to investigate its quasi-static mode. From Fig. (3), we can see for g(t) = g (constant) that is not too big , the quasi-static oscillation mode (around local minimum of V(σ)) exists and as shown by formula (23), the lifetime of sonic horizon is of order , if it appears when βmR > cs(R, t) holds.

Figure 1
figure 1

Sound velocity cs (solid line, based on formula (19)) and fluid velocity v0 (dashed line, based on formula (18)) in units of (Ω/m)1/2 vs. r (in units of (/mΩ)1/2) at , with ai = 200a0, af = 5ai.

Full size image
Figure 2
figure 2

Position of sonic horizon rc (based onEq. (20)) vs. in units of (/mΩ)1/2 for ai = 200a0, af = 5ai.

Full size image
Figure 3
figure 3

V(σ) vs. σ (in unit of> ) for three different nonlinear interaction constants: g1 = 0, 100, 1000 in unit of , a0 is the initial s-wave scattering length.

Full size image

Damped oscillation

The theoretical treatment made in the previous section does not consider the energy loss due to quantum fluctuation. Generally the energy loss due to the creation of Bogoliubov phonons will lead to the damping of the dynamical evolution. The Hamiltonian incorporating the Bogoliubov excitation reads18:

where ψ′ = ψ + δψ, ψ0 is the condensed part, , uq, vq solve the Bogoliubov-de Gennes equations, with are the phonon energies, are the free particle energies19. The formulation of Lagrangian from is as follows,

The spatial integral of change from that of as follows,

where

The expression for V(σ) (in Eq. (8)) will incorporate an additional term in addition to V1(σ) (Eq. (9)), which is equivalent to adding a damping term on the right hand side of Eq. (7b) whose detailed effects can be shown by numerical simulation. The damped oscillation is shown in Fig. 4. But the appearance of rc (sonic horizon) is still periodic although the oscillatory magnitude of the system’s distribution width gradually reduces due to the energy loss from phonon excitation.

Figure 4
figure 4

Damped oscillation of σ(t) with time t for ai = 200a0, af = 5ai.

Full size image

Conclusion

In this paper, based on the Gross-Pitaevskii equation and modified variational method, we calculate the evolution of Bose-Einstein condensates in isotropic harmonic potential when it suddenly experiences an abrupt change of s-wave scattering length via Feshbach resonance technique. We show through our analytical calculation that under certain condition, the fluid flow velocity can surpass that of sound beyond certain critical radius which signals the occurrence of sonic horizon. We derive the original analytical formula for the lifetime of the sonic horizon which agrees quantitatively with that reported in prior work with numerical simulation. The effect of quantum fluctuation is studied numerically and the damping phenomenon of the system distribution width σ(t) is identified. We also show pictorially the interaction strength dependence of the existence and stability trend of the quasi-static oscillation mode, demonstrating the applicability of the theoretical treatment presented in our work.

Additional Information

How to cite this article: Wang, Y. et al. Sonic horizon formation for oscillating Bose-Einstein condensates in isotropic harmonic potential. Sci. Rep. 6, 38512; doi: 10.1038/srep38512 (2016).

Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.