Introduction

Typically, the bigger the object, the more it interacts with its surroundings. Quantum interference between beams of molecules containing 60 to 430 atoms passing through diffraction gratings1,2,3,4 has been observed and such semi-macroscopic quantum behaviour has been given the moniker of a “Schrödinger-kitten”. The achievement of Bose-Einstein condensation in dilute atom gases (or in quantum-well microcavities5) has also pushed the boundaries of macroscopic quantum coherence6. In solid-state systems, quantum interference has been observed in certain macroscopic objects such as superconducting quantum interference devices (SQUIDs), which can be prepared and observed in a superposition state of a macroscopic electric current circulating in opposite directions7,8. Very recently, quantum superposition states involving the ground state and the first excited state of the quantized fundamental oscillation modes of macroscopic mechanical resonators have also been created9,10,11.

When an ensemble of atoms interacts with a common radiation field each atom can no longer be regarded as an individual radiation source, but the whole ensemble of atoms can be regarded as a macroscopic dipole moment12,13. This collective behaviour leads to cooperative radiation, i.e. the so-called superradiance, introduced by Dicke in 1954. Superradiance and its extended effects, has also been observed in solid state systems such as quantum dots14, quantum wells15 and coupled cavities16. This effect is generally characterized by an enhanced emission intensity that scales as the square of the number of atoms.

Recently, a particularly interesting consequence of this cooperative interaction was discussed by Svidzinsky et al17,18,19. In their work they showed that there could be cooperative delocalized effects even when just a single photon is injected into a large cloud of atoms. The state created via this mechanism is a highly-entangled Dicke state20. This state represents a coherent excitation distributed throughout a macroscopic ensemble. An interesting open question is if such a state can be realized and manipulated in a solid-state environment.

To answer this question we analyze what happens when a single-photon is injected into a large one-dimensional array of two-level-emitters (TLE). We find that because of the cooperative interaction between light and matter the structure acts like an effective optical cavity without mirrors19 and realizes a one-dimensional variation of the Dicke-state discussed by Svidzinsky et al17,18,19. We show that the delocalized state formed in this emitter-array can exhibit quantum behaviour through the coherent oscillatory dynamics of the state. We discuss how such a phenomenon might be realized in a multiple-quantum-well (MQW) array or a dc-SQUID array coupled to a transmission line and discuss physically-realistic parameters. To show how the quantum features of such an experiment might be verified, we apply the Markovian extension21 of the Leggett-Garg (LG) inequality22, to examine the quantum coherence of the delocalized state over the MQW structure and the dc-SQUID array. Finally, we discuss two other potential candidates for the experimental realization of our proposal.

Results

We consider an array containing N two-level emitters coupled to a photonic reservoir. A photon with wavevector k0 is incident on the array, as shown in Fig. 1(a). If the N-TLE array uniformly absorbs this incident photon (in practice, one can detune the incident photon from resonance, such that TLEs are equally likely to be excited23), the N-TLE can be in a collective excited state with one excitation delocalized over the whole system. Post-selecting this state (since in the vast majority of cases the photon will not be absorbed) results in the superposition state

of the exciton in this N-TLE structure, where zj is the position of the jth TLE. The state

describes the state with the jth TLE being in its excited state. Including the coupling between the TLE array and the 1D radiation fields, the state vector of the total system at time t can be written as:

where |0〉 denotes the zero-photon state, denotes one photon in the kz-mode and |g〉 is the TLE ground state. Note that the superposition state is a Dicke state19,24,25 and is a summation over all other Dicke states orthonormal to (the set of Dicke states are listed in Table I). The interaction between the TLE array and radiation fields can then be described by26,27

where is the frequency of the kz-mode photon, ω0 is the excitation energy of the TLE, is the lowering operator for the jth TLE, is the creation operator for one photon in the kz-mode and is the coupling strength between TLE and the kz-mode photon.

Table 1 The set of all Dick states19. Here, |j〉 = |g1, g2, …, gj–1, ej, gj+1, …, gN〉 describes the state with the jth two-level emitter in its excited state
Full size table
Figure 1
figure 1

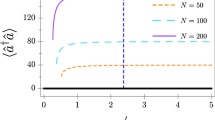
Dynamical evolution of the Dicke state and the density of states of the radiation field in the two-level-emitter array.

(a) Schematic diagram of the two-level-emitter array. The array contains N two-level emitters coupled to the one-dimensional photon reservoir. With proper excitation energy, the incident photon can excite one of the N two-level emitters and the Dicke state can be formed. The dynamical evolutions of the Dicke state for the TLE array containing (b) 20 (red dashed), 60 (blue dotted) and (c) 200 (black-solid) two-level emitters. These evolutions are obtained by solving the time-dependent Schrödinger equation [Eq. (5)~(9) ] in the limit of k0L ≫ 1. The period of the oscillations for the black solid curve in (c) is 0.054 time units. Here, the unit of time is normalized by the spontaneous decay rate ΓTLE of a single two-level emitter. The insets in (b) and (c) show that the normalized density of states of the radiation field in the TLE array containing 20 (red dashed), 60 (blue dotted) [the inset in (b)] and 300 (black solid) [the inset in (c)] two-level emitters. The green dashed-dotted curve of the inset in (c) is a Lorentzian fit for N = 200.

Full size image

In the limit of (L is the total length of the array), from the time-dependent Schrödinger equation

the probability amplitudes obey the equations28

where η = + and ⊥. Integrating Eq. (7) to obtain and inserting into Eq. (6), the dynamical evolution of the Dicke state can be written as19:

With the approximation and , Eq. (8) can be expressed as:

where Lph is the quantization length of the radiation field, v is the speed of light, h is the spacing between TLEs in the TLE array and ξ is a counting index, since the value of (zi − zj) can range between −Nh and Nh. The dynamical evolution of the Dicke state can thus be obtained by solving Eq. (9).

For the array containing N TLEs, the dynamical evolution of the state can be enhanced by the superradiant effect, Γarray = N ΓTLE, as shown in the red dashed and blue dotted curves shown in Fig. 1(b). For an extremely large array (L ≫ λ, where λ is the wavelength of the emitted photon), the probability to be absorbed across the whole sample is made uniform by sufficiently detuning the incident photon energy from that of the TLEs23. As mentioned earlier this means that the majority of photons pass through unabsorbed. Later we will discuss how the absorbtion event can be signalled by a two-photon correlation when this scheme is realized by arrays of quantum wells or superconducting qubits.

The solid curve in Fig. 1(c) represents Rabi-like oscillations together with an exponential decay. The enhanced decay rate proportional to N is a quantum effect, but may also be described in a semi-classical way by regarding the N TLEs as N classical harmonic oscillators17. For N ≫ 1, the summation in Eq. (8) can be replaced by the integration (N/L)2 ∫dz ∫dz′, showing that the effective coupling strength g between the state and the field is . The period of oscillations is therefore enhanced by a factor compared to the bare excitation-photon coupling.

The excitation dynamics of the other Dicke states can also be obtained by solving Eq. (6) and (7). For large N, the Dicke states with α ≪ N cannot reveal Rabi-like oscillations in their excitation dynamics because is the superposition state of only few TLE excited states |j〉. However, for states with α ~ N, the excitation dynamics can also show Rabi-like oscillations but the frequency of the oscillation is much smaller than that of the state . For example, from Eq. (6) and (7), the dynamical evolution of the Dicke state can be written as:

In the curly brackets of Eq. (10), the leading term resembles Eq. (8) and therefore leads to Rabi-like oscillations. However, the prefactor makes the Rabi frequency (N − 1) times smaller than that of b+(t). The origin of the frequency suppression by a prefactor comes from the fact that the coefficient of the state |N〉, which does not participate in Rabi-like oscillations, is (N − 1) times larger than those of the other states (see Methods for a detailed derivation). One could interpret this as a partial localization of the excitation in the array, suppressing the cooperative delocalized coherent oscillation effect. Since the rest of the terms in the curly brackets cannot result in oscillatory behaviour19, we can conclude that some of the Dicke states can have Rabi-like oscillations in their excitation dynamics, but the difference in the Rabi frequency makes the excitation dynamics of distinct from other Dicke states.

Effective two-level system

To illustrate that the Rabi-like oscillation is mathematically equivalent to an effective quantum coherent oscillations between two states (e.g., a spin or a single excitation cavity-QED system), we transform the Eq. (9) into the energy representation via and obtain29:

Equation (11) thus indicates that the density of states (DOS) D(q) of the radiation field in the TLE array,

where q ≡ kz − k0, ξ is a counting index and h denotes the separation between each period. The insets in Fig. 1(b) and 1(c) show the DOS for TLE array containing different number of emitters. As can be seen, when increasing the number of periods N, the line-shape of D(q) (black solid curve in the inset of Fig. 1(c)) becomes Lorentzian-like. Therefore, the TLE array coupled to radiation fields can be interpreted as a Dicke state coupled to a Lorentzian-like continuum, as shown in Fig. 2(a). Following the study by Elattari and Gurvitz29, for large N, our system can be mapped to the Dicke state coherently coupled to a resonant state |k0〉 with a Markovian dissipation as depicted in Fig. 2(b). The remaining part of the DOS which does not fit the Lorenzian distribution can be treated as an effective polarization decay.

Figure 2
figure 2

Correspondence of the two-level-emitter array to other systems.

(a) The two-level-emitter array coupled to the radiation field can be interpreted as the Dicke state coupled to a Lorentzian-like continuum spectrum if N is large enough. (b) The system can be further mapped to a Dicke state coherently coupled to a resonant state |k0〉 with a Markovian dissipation. The coupling strength g between and |k0〉 is .

Full size image

Extension of the Leggett-Garg Inequality

In order to verify the quantum coherence of the delocalized state rigorously one could apply a test like the Leggett-Garg (LG) inequality22. The LG inequality depends on the fact that at a macroscopic level several assumptions about our observations of classical reality can be made: realism, locality and the possibility of non-invasive measurement. However, a direct application of this inequality to our system seems extremely challenging because the measurement of a photon leaving the system and the measurements of the states30,31, are fundamentally invasive. To test the inequality unambiguously would require a fast projective (quantum non-demolition) measurement of the single photon state |k0〉, or the Dicke state . Such measurements are now in principle possible in optical32,33 and microwave34,35 cavities, but not in the effective cavity we describe here.

Some progress can be made by making further assumptions. It was shown by Huelga et al36,37,38 and others21,35 that the assumption of Markovian dynamics eliminates the need to assume non-invasive measurements if we can reliably prepare the system in a desired state (then the invasive nature of the second measurement, e.g., because of the destruction of the photon, does not affect the inequality). Under this Markovian assumption the inequality can be written in terms of population measurements of the state we wish to measure (which in general we describe as a single-state projective operator Q = |q〉〈q|, for some measurable state of the system |q〉),

where 〈PQ〉 is the expectation value of the zero-time population PQ ≡ PQ(t = 0) and 〈PQ(t)PQ〉 is the two-time correlation function.

To apply this to the system we have been discussing we must formalize further how, for large N, the system can be mapped to an effective two-level system [as shown in Fig. 2(c)]. The dynamics of this effective model can be described by a Markovian master equation:

where

Here, is the Liouvillian of the system, is the coherent interaction in this effective cavity-QED system, denotes the lowering (raising) operator for the Dicke state and . The state |vac〉 is the vacuum state which in the full basis is , i.e. no excitation in the Dicke state or in the resonant state k0. In the self-energy Σ[ρ], the s = |vac〉〈k0| operators describe the loss of the photon from the system with rate κ and the operators describe the loss of polarization with rate γ.

Note that if the zero-time state is the steady state then this is equivalent to the original22 LG inequality, but again demands non-invasive measurements. If the zero-time state is not the steady state, but some prepared state e.g. ρ(0) = Q, PQ(0) = 1, then a violation of this variant of the Leggett-Garg inequality indicates behaviour only beyond a classical Markovian regime, i.e. a strong indication of the quantumness of this delocalized state, though not irrefutable proof.

Experimental Realizations

In the experimental realizations discussed below, there are several experimentally-accessible systems that can mediate the one-dimensional coupling between two-level emitters and the photon fields. To show that this effect can be realized in a solid-state environment, we first consider in detail how to use a multiple-quantum-well (MQW) structure as the two-level-emitter array. In such a MQW structure, each single quantum well can be regarded as a two-level emitter. The quantum-well exciton will be confined in the growth direction (chosen to be the z-axis) and free to move in the x-y-plane. Due to the relaxation of momentum conservation in the z-axis, the coupling between the photon fields and the quantum wells is one-dimensional. Therefore, if we assume a incident photon with wavevector k0 on the MQW along the z-axis, the interacting Hamiltonian can be written exactly the same as the form in Eq. (4). Furthermore, quantum wells have the remarkable advantage that the phase factor ik0zj in can be fixed during the quantum-well growth process and since the photon fields travel in MQW only along the z-axis, a one-dimensional waveguide is not required.

To elaborate on the physical parameters necessary to realize the single-photon Dicke state we assume a MQW structure with a period of 400 nm, where each quantum well consists of one GaAs layer of thickness 5 nm (sandwiched between two AlGaAs slabs). The exciton energy ω0 of a single quantum well can take the value39 1.514 eV which results in the decay rate we utilized in Fig. 1, such that the resonant photon wavelength λ = 2πc/ω0≈ 820 nm. To identify when the state has been created, a pair of identical photons with wavevector k0 are produced by the two-photon down-conversion crystal, as shown in Fig. 3(a). One of the photons is directed to the detector-1 (D1) and the other along the growth direction of the MQW. The distance between the crystal and D1 is arranged to be the same as that between the crystal and the MQW. Once there is a click in D1, there should be one photon simultaneously sent into the MQW. The photon incident on the MQW generally passes through the MQW and registers a count in detector-2 (D2), but it could also excite one of the multiple quantum wells and form a delocalized exciton. The presence of a count in D1 and the absence of a count in D2 therefore tells us that the MQW has been prepared in the superposition state . Since the interaction between the photon fields and the MQW structure is identical to Eq. (4), the exciton dynamics of the and the density of states of the photon fields in MQW can show the same behaviours as those in Fig. 1(b) and (c) (here one unit of time is 10 picoseconds) when the MQW contains corresponding number N of the quantum wells.

Figure 3
figure 3

Multiple-quantum-well structure.

A schematic diagram of the GaAs/AlGaAs MQW structure. We assume that the MQW structure is grown along the z-axis, with a period of 400 nm and each quantum well consists of one GaAs layer of thickness 5 nm (sandwiched between two AlGaAs slabs). The exciton energy ω0 of a single quantum well is set to be39 1.514 eV, such that the resonant photon wavelength λ = 2πc/ω0≈ 820 nm. A pair of identical photons with wavevector k0 could be produced by a two-photon down-conversion crystal. One of the photons is directed to the detector-1 (D1) and the other along the growth direction of the MQW. (b) The inequality [Eq. (13)] as a function of time for the state |q〉 = |k0〉(red dashed curve) and (black solid curve) in a MQW system containing 200 periods. The region above the blue dashed line indicates the violation regime. In plotting this panel, the coupling constant g = 8.3 meV, between and |k0〉, is determined from the period of the Rabi-like oscillations in Fig. 1(c). The photon loss κ = 3.3 meV is obtained from the width of the Lorentzian fitting (the green dashed-dotted curve in the inset of Fig. 1(c). Here we have set the excitonic polarization decay rate γ as the spontaneous emission rate of the general GaAs/AlGaAs quantum well γ = ΓQW = 100 (1/ns).

Full size image

For a MQW structure containing a large number of quantum wells (i.e., N ≥ 200), the dynamical evolution of the superposition state shows Rabi-like oscillations. However, one should note that the Rabi-like oscillations here are different from the Rabi oscillations reported in secondary emission spectra40,41 of excitons in MQW structures. The secondary emission occurs when the MQW is illuminated by coherent light and emission occurs in a direction different from the excitation direction. However, in our system, the incident excitation is a single photon and the detector-2 [see Fig. 3(a)] receiving the emitted photon is positioned along the excitation direction. Furthermore, the MQW system we consider is Bragg-arranged (i.e., the inter-well spacing equals half the wavelength of light at the exciton frequency), for which the Rabi oscillations in secondary emission cannot appear41. Therefore, the Rabi-like oscillations in Fig. 1(c) are different from those in secondary emission but are a result of the coherent oscillations between the delocalized exciton state and the resonant photon state |k0〉.

If we can deterministically prepare the state |+〉 (dropping the k0 subscript for brevity) as described in Fig. 3(a), we can construct the inequality [Eq. (13)] with |q〉 = |+〉 by preparing that state so P+(0) = 1 and then (invasively) measuring the state of the quantum wells at a time t later (see below). This is then equivalent to the test to eliminate purely Markovian dynamics36,37,38.

The correlation function 〈P+(t)P+〉, where P+(0) = 1, can be calculated from

In Fig. 3(b), we plot as a function of time (solid black curve). The behaviour is oscillatory but damped due to the couplings to the Markovian photon dissipation and the excitonic polarization decay. A considerable violation (> 1) of the inequality of Eq. (13) appears in the region above the blue dashed line in Fig. 3(b). The violation there comes from the coherent oscillations between the states |+〉 and |k0〉 and is beyond the classical Markovian description.

The Dicke state |+〉 describes a particular coherent superposition of a single excitation across all N quantum wells. It has been shown that four-wave mixing and pump probe techniques30,31 can be used to measure the state of multiple excitations across multiple wells. Moreover, as we discussed before, only a few of the other Dicke states (|⊥〉) lead to Rabi-like oscillations with different oscillation frequencies. Thus it seems feasible that such an experiment can be used to determine the excitation density.

Similarly, if we could deterministically prepare the state |k0〉, we could construct the inequality (Eq. (13), with |q〉 = |k0〉) by preparing that state (so ) and then measuring when a single photon is detected at detector D2. The second measurement needed to construct the correlation functions in Eq. (13) is then simply given by the superoperator

where |vac〉 is the vacuum state. Again, we can assume the second measurement is just a normal projective measurement (after rescaling by κ), . Thus, while the photon measurement is much simpler than the quantum well one described earlier, in our scheme it is not clear if we can deterministically know when |k0〉 is created in the same way that |+〉 is, as |k0〉 is an effective state of the field modes. In Fig. 3(b), we plot as a function of time (dashed red curve). Again a considerable violation (> 1) of the inequality of Eq. (13) appears and indicates behaviour beyond the classical Markovian description.

Superconducting transmission line resonator coupled to N dc-SQUID-based charge qubits

The second realization provided here is to consider a superconducting transmission line resonator coupled to N dc-SQUID-based charge qubits16,42, as depicted in Fig. 4(a). With proper gate voltage, the Cooper-pair box formed by the dc-SQUID with two Josephson junctions can behave like a two-level system8 (charge qubit). The interacting Hamiltonian can adopt the form in Eq. (4). The incident photon with wavevector k0 propagating in the one-dimensional transmission line would excite one of the charge qubits and form the delocalized state over the N charge qubits. For the physical parameters we assume that the level separation of the charge qubit is 5 GHz, the relaxation rate of the excited state is 0.7 MHz and inter-SQUID spacing is half the wavelength of the light at the exciton frequency. Having an identical interaction between the dc-SQUID array and the photon fields as that in Eq. (4), the excitation dynamics can represent the same behaviours as shown in fig. 1(b) and (c) (where the one unit of time is microseconds).

Figure 4
figure 4

dc-SQUID array structure.

(a) N dc-SQUID-based charge qubits coupled to a one-dimensional transmission line.A Cooper-pair box formed by a dc-SQUID with two Josephson junctions can act like a two-level system by properly tuning the gate voltage. The incident photon in the transmission line can excite one of the charge qubits. A delocalized state spread over the charge-qubit array can therefore be formed. Here we assume that the level separation of the charge qubit is 5 GHz, the relaxation rate of the excited state is 1 MHz and the inter-SQUID spacing is half the wavelength of the light at the excitation frequency. (b) The inequality [Eq. (13)] is shown as a function of time for the state |q〉 = |k0〉, with the initial state being in the Dicke state in a dc-SQUID charge-qubit array containing 200 periods. In plotting this panel, the coupling constant g = 5.8 µeV, between and |k0〉, is determined from the period of the Rabi-like oscillations in Fig. 1(c). The photon loss κ = 2.3 µeV is obtained from the width of the Lorentzian fit [the green dashed-dotted curve in the inset of Fig. 1(c)]. Here we have set the excitonic polarization decay rate γ equal to the relaxation rate of the charge qubit γ = 0.7(1/µs).

Full size image

For a SQUID-array coupled to a transmission line, the measurement of the population of individual superconducting qubits has been achieved43. Recently, the progress in generating and measuring single microwave photons44,45,46,47,48 propagating in the transmission line42,49,50 make it easier to generate and detect single-photon Dicke states. Therefore, one can take this advantage to achieve the measurement of the qubit state through measuring the microwave photons. In this way, if we could prepare the state |+〉, the inequality Eq. (13) can thus be constructed with |q〉 = |k0〉 by preparing the Dicke state |+〉 (so ). Similarly, since we are not concerned with events after the second measurement, the second measurement is just a projective measurement, .

The correlation function , where , can be calculated from

In Fig. 4(b), we plot as a function of time. Since the initial state is prepared in the Dicke state |+〉, the curve starts at the origin instead of the unity. Due to the couplings to the Markovian photon dissipation and the polarization decay, the behaviour is oscillatory but damped. A considerable violation (> 1) of the inequality of Eq. (13) appears in the region above the blue dashed line in Fig. 4(b). The violation again comes from the coherent oscillations between the states |+〉 and |k0〉 and is beyond the classical Markovian description.

Of course, ultimately we cannot distinguish classical non-Markovian dynamics from quantum dynamics with this method, though certain complex Markovian systems can produce nonmonotonic and complex behaviour21 which is important to eliminate. To really show that either the large array of quantum wells or the dc-SQUID arrays is behave like a cavity without a mirror and exhibit quantum Rabi oscillations, more work needs to be done on full-state tomography techniques and precise measurements of excitonic states, so that either the full Leggett-Garg inequality, or some other test, can be investigated. One possibility to realize the full, non-invasive, LG inequality test for the circuit-QED case is to include an additional off-resonance cavity which dispersively measures the overall occupation of the qubits11 (i.e., 0 or 1 delocalized excitation). This could satisfy the criteria of the original LG inequality.

Discussion

In summary, we investigated the dynamical evolution of the delocalized state of a two-level-emitter array state. When the array contains a large number of emitters, the dynamical evolution shows Rabi-like oscillatory behaviour. By showing that the DOS of the radiation field in the TLE array is Lorentzian-like, the whole system can be mapped to an effective two-level system (e.g., like a single excitation cavity-QED system). For the physical implementation we suggested a multiplequantum- well structure and also a dc-SQUID array structure and discussed their relevant physical parameters. We also applied a Markovian variation of the original Leggett-Garg inequality, to examine the quantum coherence.

There are other experimentally-accessible systems that can mediate one-dimensional coupling between two-level emitters and the photon fields. Below we provide two potential candidates:

  1. I

    Consider N two-level quantum dots positioned near a metal nanowire, due to the quantum confinement, the surface plasmons propagate along the axis direction on the surface of the nanowire. The coupling between quantum dots and the surface plasmons enable51 the incident surface plasmons to excite one of the N quantum dots and the delocalized exciton over the N dots can then be formed.

  2. II

    The strong coupling between a microwave photon and electron spins could enable a long-lived quantum memory element for superconducting qubits. In a ensemble of spins, a coherent memory52 has been realized by using a pulsed magnetic field gradient. Though the quantum memory of the collective states in the electron spin ensemble is carried out in three-dimension, our theory can still be applied due to the similarity in the cooperative nature of the delocalized state. Therefore, it is possible to utilize the coherent quantum memory of a spin ensemble to examine some of the results we discuss in this work.

Methods

Details of the derivation of Eq. (8) and (10)

Integrating Eq. (7) to obtain and inserting into Eq. (6), we obtain28

where η = + and ⊥. Here b+ and b⊥ are coupled due to the fact that they decay to a common ground state. This coupling is referred as Fano coupling (or Agarwal-Fano coupling). However, as the number of periods N ≫ 1, this coupling is suppressed19. Eq. (19) therefore becomes

The dynamical evolution of the Dicke state |+〉 (dropping the k0 subscript for brevity) can be written as:

given that , in Eq. (21) thus gives . We can then exactly obtain Eq. (8).

Similarly, from Eq. (20), the dynamical evolution of the Dicke state |N − 1〉 (dropping the k0 subscript for brevity) can be written as:

given that (as listed in Table I), in Eq. (22) can be calculated as:

By inserting this into Eq. (22) we then obtain Eq. (10).

Details of the derivation of Eq. (13)

For clarity we present here a proof of Eq. (13), which originally appeared in21. We start the proof with the two-time state-state correlation 〈PQ(t)PQ(0)〉, which can be explicitly described by

where pn(0) is the probability of measuring the state n at the time origin t = 0 and is the result returned by the measurement apparatus (which we later assume to be one, but leave general here). If only a single state k contributes to the measurement observable, the above equation can be written as

The difference between the temporal correlations 2 〈PQ(t)PQ(0)〉 and 〈PQ(2t)PQ(0)〉 is then of the form

Let us proceed to consider the maximum value of 2Ωkk(t, 0) − Ωkk(2t, 0) for classical and Markovian dynamics. As stated by Chapman-Kolmogorov equation, the propagator Ωkk(2t, 0) can be represented by a decomposition over intermediate states

We then have

for the propagators which are dependent on the time difference. The maximum occurs when Ωkk(t) = 1 and the difference between temporal correlations becomes

Given that we have the upper bound in Eq. (3). Similarly, the lower bound of the temporal correlation difference is − 〈PQ〉.