A proposal for reconciling diverse experiments on the superconducting state in Sr₂RuO₄

Abstract

A variety of precise experiments have been carried out to establish the character of the superconducting state in Sr₂RuO₄. Many of these appear to imply contradictory conclusions concerning the symmetries of this state. Here we propose that these results can be reconciled if we assume that there is a near-degeneracy between a ${d}_{{x}^{2}-{y}^{2}}$ (B_1g in group theory nomenclature) and a ${g}_{xy({x}^{2}-{y}^{2})}$ (A_2g) superconducting state. From a weak-coupling perspective, such an accidental degeneracy can occur at a point at which a balance between the on-site and nearest-neighbor repulsions triggers a d-wave to g-wave transition.

Introduction

Sr₂RuO₄ (SRO) should be the poster child for the theory of “unconventional” superconductors: it is a clean, stoichiometric crystalline material, it settles into a Fermi liquid “normal state” in a range of temperatures, T, that extends roughly a factor of 20 above the superconducting (SC) T_c, the normal state fermiology is well established, the SC transition is sharp and of mean field type, and there is no doubt that the SC state is unconventional in the sense of a sign-changing order parameter with a mean equal to or near 0 along the Fermi surface^1,2,3,4. Of all the currently known unconventional superconductors, SRO is the one in which a Bardeen–Cooper–Schrieffer (BCS)-like weak coupling mean-field-theory treatment is most easily justified, meaning that the microscopic “mechanism” of superconductivity should be well defined. Instead, a large number of careful experiments have led to a set of observations that cannot be accounted for even at the scenario level by any current theory—25 years after the first phenomenological theories^5,6, we are still debating the symmetry of the SC order parameter⁴.

Indeed, some sets of observations almost appear to be mutually contradictory: the evidence^7,8,9 of time-reversal symmetry breaking (TRSB) in the SC state is difficult to reconcile with the existence of gapless nodal lines in the quasiparticle spectrum^{10,11,12,13,14,15}. The evidence of a two-component SC order parameter^16,17 is difficult to reconcile with the lack of singular T_c dependence on symmetry breaking strain¹⁸ or in-plane magnetic field¹⁹. The evidence of triplet (odd parity²⁰) pairing is difficult to reconcile with the evidence of singlet pairing from nuclear magnetic resonance (NMR)^21,22 and from the fact that the in-plane critical field appears to be Pauli-limited¹⁹.

It is always possible that some set of experimental observations are misleading—perhaps they reflect an extrinsic effect or have an alternative interpretation that has not been considered. Here we will take various observations at face value and attempt to construct a phenomenological scenario that can reconcile as many of them as possible. To do so, we have introduced a single “fine-tuned” assumption—that SRO happens to be close to a multi-critical point at which two symmetry-distinct pairing symmetries are degenerate—in particular, a ${d}_{{x}^{2}-{y}^{2}}$ (B_1g in group theory nomenclature) and a ${g}_{xy({x}^{2}-{y}^{2})}$ (A_2g) state. As we will discuss later in the paper, even with this assumption, there are some observations that either require a more complete theory to interpret (i.e., the interpretation does not follow simply from general symmetry considerations) or an alternative interpretation of the experiment.

The article is organized as follows: by way of introduction, we outline the primary experimental facts we have in mind. Those can be considered the axioms of our phenomenological theory. In the “Results” section, we first set forward the Landau–Ginzburg theory describing a near-degeneracy between a d-wave and a g-wave SC state and discuss some features of the resulting phase diagram. Next, we briefly address other features of the phases and phase transitions at a level that would be expected from a BCS-type treatment of the problem; while these considerations could straightforwardly be extended to include the effects of a realistic treatment of the multi-band character of the SRO fermiology, here we offer a stripped-down discussion that focuses on qualitative aspects of the problem. In particular, we explore the specific heat signatures of the various transitions expected in the theory. Finally, in the “Discussion” section, we discuss some of the experimental observations that are not immediately accounted for by our scenario. This particularly concerns reconciling our proposal with the observed Kerr signal, which requires including considerations of explicit breaking of spatial symmetries and effects of disorder. Moreover, in the “Results” section, we allude to proposed future work that could more seriously take account of specific microscopic aspects of SRO and thus could lead to further avenues for comparing theory with experiment. We conclude by discussing some possible experiments that could critically test the applicability of our proposed scenario.

Results

Experimental “facts” in SRO

There have been a remarkably large number of extremely careful experiments carried out to explore the character of the SC state in SRO. We will focus on a subset of these—that we will accept as experimental facts with clear implications.

• (1) There is a single SC transition with a well-defined T_c and the transition is largely mean-field like. This inference follows from the fact that the transition as seen in transport and in magnetization is sharp, and the specific heat shows a sharp mean-field-like anomaly at T_c. There is no indication of hysteresis (as could happen if the SC transition were first order), significant regimes of fluctuation SC above T_c, or any glassy feature of the SC transition⁴.

• (2) The SC phase is “unconventional”, that is, the SC order parameter changes sign in such a way that when averaged over the Fermi surface it is approximately zero. This inference follows ref. ³ from the extreme sensitivity of T_c to non-magnetic disorder, i.e., T_c → 0 when the elastic mean-free path, ℓ, approaches the clean limit SC coherence length, ξ₀ (The existence of nodal quasiparticles, discussed below, constitute additional evidence of unconventional pairing).

• (3) To a high level of precision, there are gapless nodal quasiparticles along line nodes that are more or less perpendicular to the Ru-O plane, i.e., they extend along the tetragonal c-axis. This follows from the low temperature behavior of the specific heat and from the low-temperature thermal conductivity¹³. Recent scanning tunneling microscopic (STM) studies further corroborate this conclusion¹⁵. While the location (in $\overrightarrow{k}$-space) of the nodes is not entirely clear, both the thermal conductivity experiments and the STM results are strongly suggestive that the line nodes lie along wave vectors that are at 45° to the Ru-O bond direction, that is along the tetragonal (1,1,0) and (1,−1,0) directions. If there is any gap at the putative nodal points, it has been estimated^12,13 that it must be <10 μeV, or <3% of the total gap.

• (4) The SC T_c(ϵ) is a smooth and non-singular function of symmetry breaking (shear) strain, ϵ, near ϵ = 0. In the case in which a stress is applied along (1,1,0), T_c is a weak linear function of the stress; since by symmetry T_c must be an even function of a purely shear strain, the linear stress dependence presumably reflects the fact that, in addition to a ϵ_xy (B_2g) component, the uniaxial stress produces a significant symmetric component of symmetric strain (with A_1g symmetry) ϵ₀. There is a nearly symmetric variation of T_c in response to uniaxial stress along (1,0,0). This suggests that, in this case, the induced symmetric strain is small and that what is being observed is primarily the response to a B_1g shear strain, ${\epsilon }_{{x}^{2}-{y}^{2}}$. Local measurements²³ (using scanning magnetometry) of T_c versus stress show a quadratic minimum at each location, ${T}_{{\rm{c}}}(\epsilon )={T}_{{\rm{c}}}(0)+\alpha {(\epsilon -\bar{\epsilon })}^{2}+\ldots$, where, however, T_c(0) and $\bar{\epsilon }$ vary from location to location in the crystal; the variation of $\bar{\epsilon }$ is, presumably, associated with a random quenched distribution of local strains. Indeed, an interpretation in terms of random strain is strongly indicated based on the fact that some regions of the crystal are seen to have local T_cs that are of order 10% higher than the zero-strain bulk T_c; given the sensitivity of the SC state to impurity scattering³, if what was being seen were regions with higher and lower than average impurity concentration, there would be a sharply defined maximum T_c (associated with all sufficiently clean portions of the crystal) and then a distribution of more disordered regions with reduced local T_cs. ¹

• (5a) Time reversal symmetry is spontaneously broken below a temperature T_trsb that is (in unstrained crystals) approximately equal to the SC T_c. This inference follows directly from the observation of an anomalous Kerr signal⁸, and from muon spin relaxation (μSr) experiments⁷; it is also consistent with experiments on the geometry dependence of the Josephson relation⁹, although beyond supporting the TRSB, this last set of experiments is still not fully digested.

• (5b) On symmetry grounds, equilibrium currents are possible in a TRSB SC state when not forbidden on the basis of purely spatial symmetries. This is particularly true for the case of chiral superconductors that break both time-reversal and inversion symmetry. Theoretical estimates of how large these expected currents should be vary greatly depending on details of the assumed microscopic structure of the state but initially suggested that they should be detectable by high-sensitivity magnetic scanning microscopy. However, careful searches²⁴ for the magnetic fields produced by such currents have failed to detect any such currents, despite sensitivity that is at least two orders of magnitude greater than what would be required to detect the currents implied by the most straightforward theoretical analysis (based on an assumed chiral p_x + ip_y state).

• (6) There is a sharp drop in the Knight-shift upon cooling through T_c, which continues to the lowest temperatures and fields that have been probed^21,22. While it is still necessary to pursue this experiment to lower fields (relative to H_c2) and lower T (relative to T_c), already the existing observations are strongly suggestive of a spin-singlet order parameter. The NMR spectrum shows no evidence of a phase transition (within the SC state) as a function of strain; given this, results at high strain (where both H_c2 and T_c are greatly enhanced) can be included in this analysis, making the evidence for singlet pairing considerably stronger.

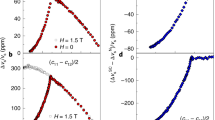
• (7) There is a discontinuity at T_c in the elastic modulus c₆₆ associated with the shear B_2g (ϵ_xy) strain, as inferred from ultrasound experiments^16,17. While the elastic moduli associated with A_1g compressional strains exhibit discontinuities at all second-order phase transitions, such a discontinuity in a shear elastic constant is most straightforwardly associated with a two-component SC order parameter²⁵. This follows from the requirement that a gauge-invariant bilinear can be constructed from the order parameter that transforms as xy under the point group operations—such a bilinear cannot be constructed for any one-component SC order parameter but can be constructed for a number of two-component order parameters. It is also important to note that no discontinuity has been observed in the elastic modulus associated with B_1g (${\epsilon }_{{x}^{2}-{y}^{2}}$) strain.

• (8) There is new μSr data which shows that for moderate values of stress along the x-direction (approximately 1 GPa, which translates to 0.9% of ${\epsilon }_{{x}^{2}-{y}^{2}}$ strain and 0.3% of ${\epsilon }_{{x}^{2}+{y}^{2}}$ strain¹⁷), that T_trsb(ϵ) = 1.0 K is substantially below T_c(ϵ) = 1.4 K²⁶. However, the interpretation of this split transition is made somewhat subtle by the observation that in high-resolution specific heat measurements, while the critical anomaly at T_c(ϵ) is still clear and relatively sharp and of the expected magnitude, no thermodynamic signature of any feature associated with a transition at T_trsb(ϵ) has been detected²⁷.

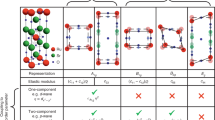
Despite a long history of interpreting results in SRO in terms of a p-wave order parameter (or more technically, an odd parity order parameter) and of the existence of a variety of other experimental results that provide circumstantial support to this idea, we will interpret the new NMR results as ruling this out²⁸. Focusing on possible singlet (even parity) SC states, consistent with the tetragonal symmetry of the crystal there is one possible symmetry-related two-component state, which corresponds to $\left\{{d}_{xz},{d}_{yz}\right\}$ (E_g) pairing, and four possible single-component states, corresponding to ${d}_{{x}^{2}-{y}^{2}}$ (B_1g), ${g}_{xy({x}^{2}-{y}^{2})}$ (A_2g), s (A_1g) and d_xy (B_2g).

We discard the symmetry-related two-component option (E_g)^29,30,31 from consideration for two reasons: First, the thermal conductivity and STM indicate vertical line nodes while these states have symmetry-protected horizontal line nodes. This is not entirely definitive, since such a state could have accidental vertical line nodes as well, but this seems a rather unnatural occurrence. Second, regarding the non-on-site pairing E_g proposal²⁹, such a state would have a vanishing pair-wave function for two electrons in the same Ru-O plane, which seems implausible on theoretical grounds, given the extreme quasi-two-dimensional (quasi-2D) nature of the Fermi surfaces. Regarding the local pairing proposal that involves the multi-orbital nature of the ruthenates^30,31, it would produce a jump in the elastic modulus for both the ${\epsilon }_{{x}^{2}-{y}^{2}}$- and ϵ_xy-type strain, whereas only the latter shows a discontinuity in experiments. Moreover, there is currently no clearly established signature of the predicted Bogoliubov–de Gennes (BdG) Fermi surface that arises in such a state.

Arguments discriminating among the remaining options are slightly more subtle. The ${d}_{{x}^{2}-{y}^{2}}$ and ${g}_{xy({x}^{2}-{y}^{2})}$ have symmetry-protected vertical line nodes along the (1,1,0) direction, while for any of the other cases, such nodes would necessarily be accidental nodes. It is not yet clear how precisely the observed line nodes are aligned with this symmetry axis—the more precise the experimental constraints on this, the more solid is the identification of these as the relevant states.

Having focused on two distinct one-dimensional representations, the natural next step would be to determine which one is favored. However, several of the observations summarized above require a two-component order parameter—specifically 5, 7, and 8. We are thus driven to assume that there is an accidental near-degeneracy between ${d}_{{x}^{2}-{y}^{2}}$ and ${g}_{xy({x}^{2}-{y}^{2})}$ pairing, i.e., we assume that SRO happens to be fine-tuned close to the boundary between a regime in which one of these is dominant and the other in which the other dominates.

Landau–Ginzburg treatment

Thus, in the following, we will assume that, at zero applied strain, SRO happens to be tuned to a multi-critical point at which these two SC states have (nearly) the same T_c. Depending on other details, the SC phase below T_c can have various patterns of broken symmetry. This is most easily explored by considering the Landau–Ginzburg effective free energy density expressed in terms of the complex (charge 2e) scalar fields, D and G, that represent the local value of the pair-fields of the stated symmetries:

$$\frac{{\mathcal{H}}}{T}={V}_{0}(D,G)+{V}_{1}(G,D)+K+\ldots,$$

(1)

where V₀ includes the terms in the effective potential (through quartic order in the fields) in the absence of disorder, external strain (i.e., it assumes tetragonal symmetry), and under the assumption of an exact Z₂ symmetry between the D and G orders, while V₁ includes to quadratic (leading) order in the field terms related to breaking of this accidental Z₂ symmetry, as well as the effects of disorder and externally applied strain (breaking of tetragonal symmetry), K is a quadratic form in the gauge invariant gradients of the order parameter, $(-i\overrightarrow{\nabla }-2\overrightarrow{A})D$ and $(-i\overrightarrow{\nabla }-2\overrightarrow{A})G$, and … refers to higher-order terms in powers of the fields and their derivatives. Specifically,

$$\begin{array}{l}{V}_{0}(D,G)=\frac{{\alpha }_{0}}{2}\left[\,{\left|D\right|}^{2}+{\left|G\right|}^{2}\,\right]+\frac{{\gamma }_{0}}{4}{\left[{\left|D\right|}^{2}+{\left|G\right|}^{2}\right]}^{2}\\ \qquad\qquad +\frac{{\gamma }_{1}}{4}{\left[{\left|D\right|}^{2}-{\left|G\right|}^{2}\right]}^{2}+\frac{{\gamma }_{2}}{4}{\left[{D}^{\star }G+{G}^{\star }D\right]}^{2}\end{array}$$

(2)

and

$${V}_{1}(D,G)=-\frac{{h}_{0}(\overrightarrow{r})}{2}\left[\,{\left|D\right|}^{2}+{\left|G\right|}^{2}\,\right]-\frac{{h}_{1}(\overrightarrow{r})}{2}\left[\,{\left|D\right|}^{2}-{\left|G\right|}^{2}\,\right]\,-\frac{{h}_{2}(\overrightarrow{r})}{2}\left[\,{D}^{\star }G+{G}^{\star }D\right]$$

(3)

Note that V₀ has an enlarged SO(4) symmetry for the special case in which γ₁ = γ₂ = 0.

Here the principal T dependence is incorporated in a T dependence of α₀, such that it changes from positive to negative as T drops from above to below T_c. The multi-critical point that serves as the focus point for our analysis arises when h₁ = 0; otherwise, the mean value of h₁ encodes the preference for one or the other form of pairing, with d-wave pairing favored for h₁ > 0. Below T_c, the nature of the SC state is determined by the signs and relative magnitudes of the quartic terms. To simplify the discussion, we will consider the case in which γ₀ is positive and larger in magnitude than the remaining terms. In the uniform SC state when h₁ = 0, the preferred form of ordering is determined by the relative sign and magnitude of γ₁ and γ₂. For γ₁ < 0 and γ₂ > γ₁, the SC state is either pure d or pure g and thus preserves all spatial symmetries as well as time-reversal symmetry. The case that will be of primary interest here is that in which γ₁ > 0 and γ₂ > 0, so the SC state breaks both time-reversal symmetry as well as some lattice symmetries; we refer to this as a TRSB SC, and it corresponds to ${d}_{{x}^{2}-{y}^{2}}\pm i{g}_{xy({x}^{2}-{y}^{2})}$ pairing. Finally, if γ₁ > γ₂ and γ₂ < 0, the SC state breaks various lattice symmetries but preserves time-reversal symmetry; this is a nematic superconductor, which has two possible symmetry-related states ${d}_{{x}^{2}-{y}^{2}}\pm {g}_{xy({x}^{2}-{y}^{2})}$, depending on the relative sign of the two components. Turning to the terms that appear in V₁, h₀ has the interpretation as a local T_c, h₁ as the local deviation from multi-criticality (i.e. a local preference for d or g), and h₂ has the symmetry of a random local strain, ϵ_xy. Importantly, such a local strain favors one orientation of the nematic order over the other. In the absence of an externally applied strain, the configuration (or spatial) average of all the random fields can be assumed to vanish, $\overline{{h}_{j}(\overrightarrow{r})}=0$, but in the presence of applied strain,

$$\overline{{h}_{j}(\overrightarrow{r})}={\Lambda }_{j}^{a}\,{\epsilon }_{a}+{\Lambda }_{j}^{a,b}{\epsilon }_{a}{\epsilon }_{b}+\ldots ,$$

(4)

where a sum over a is implicit, ${\Lambda }_{j}^{a}$ and ${\Lambda }_{j}^{ab}$ are appropriate coupling constants, the indices a and b (which are implicitly summed over) label the components of the strain tensor—which we decompose according to symmetry as a = s for A_1g (although in a tetragonal system, there are properly two distinct components of A_1g strain), a = (x² − y²) for B_1g, and a = xy for B_2g, and … indicates higher-order terms in powers of the strain. All components of ${\Lambda }_{j}^{a}=0$ by symmetry other than ${\Lambda }_{0}^{s}$, ${\Lambda }_{1}^{s}$, and ${\Lambda }_{2}^{xy}$. Similarly, all terms in ${\Lambda }_{j}^{ab}=0$ other than the diagonal terms, ${\Lambda }_{0}^{a,a}$ and ${\Lambda }_{1}^{a,a}$ (for any a), and the off-diagonal term, ${\Lambda }_{2}^{s,xy}={\Lambda }_{2}^{xy,s}$. In other words, there generically is a shift of the mean T_c and of the splitting between the d- and g-wave order that is linear in the isotropic strain and quadratic in each component of the shear strain. However, the degeneracy between ${d}_{{x}^{2}-{y}^{2}}+{g}_{xy({x}^{2}-{y}^{2})}$ and ${d}_{{x}^{2}-{y}^{2}}-{g}_{xy({x}^{2}-{y}^{2})}$ is lifted only in the presence of non-zero B_2g strain. The detailed shape and even topology of the resulting phase diagrams in the T–strain plane depend on the relative magnitudes of various parameters in the Landau–Ginzburg free energy; representative phase diagrams as a function of strain (assuming degeneracy between d and g at zero strain) are shown in Fig. 1.

Fig. 1: Superconducting phase diagram.

Schematic phase diagrams as a function of T and various components of the strain. In keeping with the present scenario, we assume that the D and G wave orders are essentially degenerate at zero strain. All panels were simulated with LG parameters γ₀ = 2, γ₁ = 1, γ₂ = 0.5. a is for symmetric (A_1g) strain. Note that the shape and even the topology of the phase diagram depends on the relative sign and magnitude of the various couplings ${\Lambda }_{j}^{a}$ and ${\Lambda }_{j}^{ab}$; here, for purposes of illustration, we took ${\Lambda }_{0}^{a}=-0.086,\,{\Lambda }_{1}^{a}=0.035,\,{\Lambda }_{0}^{a,a}=-0.025$, and ${\Lambda }_{1}^{a,a}=0.021$, where a = x² + y². b is for B_1g shear strain, where the explicitly shown phase boundaries correspond to ${\Lambda }_{0}^{b,b}=-0.04$ and ${\Lambda }_{1}^{b,b}=0.028$ with b = (x² − y²). c is for B_2g shear strain. Here, to linear order in the strain, the shape of the phase diagram is insensitive to the assumed parameters, here chosen to be ${\Lambda }_{0}^{c,c}=-0.02,\,{\Lambda }_{1}^{c,c}=0.01$, and ${\Lambda }_{2}^{c}=0.014$, where c = xy.

When we come to discuss disorder, we will define the root mean squared disorder strengths, σ_j, as

$$\nu \int\ d\overrightarrow{r}\,\overline{\left[{h}_{i}(\overrightarrow{r})-\overline{{h}_{i}}\right]\,\left[{h}_{j}(\overrightarrow{0})-\overline{{h}_{j}}\right]}\equiv {\delta }_{i,j}{\sigma }_{j}^{2}$$

(5)

(where ν is the volume of a unit cell). Because the most relevant disorder is likely that associated with inhomogeneous strain, it may be important to consider the range of the disorder correlations as well.

Quasiparticle properties and BCS considerations

While we are free to normalize the order parameter fields that appear in the Landau–Ginzburg effective field theory in any way we like, the same freedom does not pertain when we relate these fields to the gap parameter that governs the quasiparticle spectrum. Interpreting the various possible states through the lens of the BdG equations of BCS mean-field theory, we relate the gap parameter to the order parameter fields according to

$$\Delta (\overrightarrow{k})={e}^{i\theta }\,\left[D\,{F}_{d}(\overrightarrow{k})\,+{e}^{i\phi }G\,{F}_{g}(\overrightarrow{k})\right],$$

(6)

where θ is the overall SC phase, ϕ is the relative phase between the d- and g-wave components, and where we normalize the real dimensionless gap functions ${F}_{a}(\overrightarrow{k})$ so that ${\rm{Max}}[{F}_{a}(\overrightarrow{k})]=1$; thus D and G are, respectively, the maximum gap in the d- and g-wave state, respectively. F_a can have an arbitrarily complicated $\overrightarrow{k}$ dependence (depending on microscopic details), so long as they transform in the desired fashion under the crystalline symmetries. In keeping with the spirit of the Landau–Ginzburg approach, at least in a range of T near to T_c, we can imagine that all the singular T and strain dependences in the problem are inherited from those of the order parameter fields, D and G. From here, as usual, it follows (still assuming the validity of BCS mean-field theory) that the quasiparticle spectrum is

$$E(\overrightarrow{k})=\sqrt{{\left[\varepsilon (\overrightarrow{k})-\mu \right]}^{2}+{\left|\Delta (\overrightarrow{k})\right|}^{2}},$$

(7)

where $\varepsilon (\overrightarrow{k})$ is the normal state (Fermi liquid) dispersion.

At the level of BCS mean-field theory, once the values of D(T) and G(T) are determined, a host of dynamic and thermodynamic quantities can be computed in the usual way. One particularly important quantity is the jump in the specific heat at the various transitions. Consider, for example, the case in which $\overline{{h}_{1}}>0$ and γ₁, γ₂ > 0, so that upon lowering the temperature there is first a transition at T_c to a pure d-wave SC state, and then at a lower temperature, T_trsb < T_c, a transition to a ${d}_{{x}^{2}-{y}^{2}}+i{g}_{xy({x}^{2}-{y}^{2})}$ state. If we assume the simplest possible mean-field dependence of the gaps

$$D(T)={D}_{0}\sqrt{1-\frac{T}{{T}_{{\rm{c}}}}}\quad {\rm{for}}\,T\, < \,{T}_{{\rm{c}}}$$

(8)

$$G(T)={G}_{0}\sqrt{1-\frac{T}{{T}_{{\rm{trsb}}}}} \quad {\rm{for}}\, T \, < \, {T}_{{\rm{trsb}}}\,<\,{T}_{{\rm{c}}},$$

(9)

the specific heat jump at T_c can be expressed as

$$\frac{\Delta {C}_{{\rm{sc}}}}{{T}_{{\rm{c}}}}={\left(\frac{{D}_{0}}{{T}_{{\rm{c}}}}\right)}^{2}\left[\left[\left(-\frac{\partial f}{\partial E}{\left|{F}_{d}\right|}^{2}\right)\right]\right]={\left(\frac{{D}_{0}}{{T}_{{\rm{c}}}}\right)}^{2}\,\rho ({E}_{{\rm{F}}})\,\langle {\left|{F}_{d}\right|}^{2}\rangle \,$$

(10)

and the specific heat jump at T_trsb as

$$\frac{\Delta {C}_{{\rm{trsb}}}}{{T}_{{\rm{trsb}}}}={\left(\frac{{G}_{0}}{{T}_{{\rm{trsb}}}}\right)}^{2}\,\rho ({E}_{{\rm{F}}})\,\langle {\left|{F}_{g}\right|}^{2}A\left(z\right)\rangle =\frac{\Delta {C}_{{\rm{sc}}}}{{T}_{{\rm{c}}}}{\left(\frac{{G}_{0}}{{T}_{{\rm{trsb}}}}\right)}^{2}\,{\left(\frac{{T}_{{\rm{c}}}}{{D}_{0}}\right)}^{2}{\mathcal{F}}\left(\frac{{T}_{{\rm{trsb}}}}{{T}_{{\rm{c}}}},\frac{{D}_{0}}{{T}_{{\rm{c}}}}\right)$$

(11)

where 〈f〉 and $\left[\left[f\right]\right]$ signify, respectively, the average of f over the Fermi surface and over the Brillouin zone,

$$A(z)={\int \nolimits_{0}^{\infty}}\frac{{\rm{d}}x}{{\cos}\,{\rm{h}}^{2}\sqrt{{x}^{2}+{z}^{2}}},\qquad z=\frac{{F}_{d}}{2}\frac{{D}_{0}}{{T}_{{\rm{trsb}}}}\sqrt{1-\frac{{T}_{{\rm{trsb}}}}{{T}_{{\rm{c}}}}},$$

(12)

${E}_{d}(\overrightarrow{k})$ is the dispersion in the pure d-wave SC state, and ${\mathcal{F}}$ is a dimensionless function defined implicitly in Eq. (11).

In Fig. 2, we have computed ${\mathcal{F}}$ as a function of T_trsb/T_c for a band structure corresponding to nearest-neighbor hopping on a square lattice with a mean electron density n = 1.38, per site and assumed F_a have the simplest forms consistent with symmetry, ${F}_{d}=(1/2)\left[\cos ({k}_{x})-\cos ({k}_{y})\right]$ and ${F}_{g}=(3\sqrt{3}/4)\sin ({k}_{x})\sin ({k}_{y})\left[\cos ({k}_{x})-\cos ({k}_{y})\right]$, and a typical mean-field value of D₀/T_c = 2.5. For comparison, we have performed the same calculation for the case in which the second-order parameter is a simple s-wave, F_g → F_s = 1. It is striking that the specific heat jump is much smaller for the transition to the d + ig state, and especially so the smaller T_trsb/T_c. There are several contributing factors to this. First, because the d-wave gap grows so singularly with decreasing temperature below T_c, the total remaining entropy in the system is rapidly reduced relative to that in the normal state—this effect would apply for any “second” transition in the SC state. However, the effect is particularly dramatic due to the fact that the g-wave gap also has nodes in the one region of the Fermi surface that remains ungapped (nodal) in the d-wave SC state. Thus the density of thermally excited quasiparticles is only slightly (further) reduced upon entering the d + ig—TRSB phase.

Fig. 2: Specific heat jump.

Dimensionless magnitude, ${\mathcal{F}}$, of the specific heat jump at T_trsb with D₀/T_c = 2.5. (${\mathcal{F}}({T}_{{\rm{trsb}}}/{T}_{{\rm{c}}})$ is defined in Eq. (11).) The lower curve is for the case in which the transition is from a d-wave to a ${d}_{{x}^{2}-{y}^{2}}+i{g}_{xy({x}^{2}-{y}^{2})}$-wave SC; the upper is for a d-wave to a ${d}_{{x}^{2}-{y}^{2}}+is$-wave.

A plausible scenario

The set of experimental observations that we have enumerated above have, for some time, seemed difficult to reconcile with each other. With the assumption that SRO is tuned close to the conjectured multi-critical point, much of this seeming difficulty is readily eliminated. For $\overline{{h}_{1}}=0$, there is a single SC transition, and the SC state is unconventional, in keeping with points 1 and 2. The SC order is even parity, spin-singlet pairing, consistent with point 6. Because both the d- and the g-wave components of the order parameter are odd under any spatial transformation that exchanges k_x and k_y, consistent with point 3, the existence of nodal lines in the quasiparticle spectrum along the (1,1,0) direction is protected by symmetry, even in the TRSB SC phase; this is distinct from the case for any other order parameter symmetries that have been considered to date. Importantly, at the assumed multi-critical point, the d- and g-wave components of the order parameters behave like a two-component order parameter with precisely the requisite relative symmetries to account for point 7. Specifically, the bilinear formed of B_1g and A_2g order parameters is of the B_2g representation, thus producing a discontinuity in c₆₆ at T_c. This scenario also provides a natural explanation for why no discontinuity is seen in (c₁₁ − c₁₂)/2—the B_1g elastic modulus—since such a bilinear cannot be formed. This is in contrast with other two-component SC order parameters, such as d_xz,yz or p_x,y states, where a discontinuity in (c₁₁ − c₁₂)/2 is expected in general, and the lack of experimental evidence for such a discontinuity would have to be explained away in some other way.

Since T_c appears to be most strongly sensitive to B_1g strain, it is important to stress that no singular non-analytic changes in either T_c or T_trsb as a function of ${\epsilon }_{{x}^{2}-{y}^{2}}$ are expected. The principal effects of strain of this symmetry are analytic (i.e., quadratic) strain dependences of $\overline{{h}_{0}}$ and $\overline{{h}_{1}}$. There is no general reason for one sign of the effect, but both empirically and based on microscopic considerations related to the proximity of one band to a Lifshitz transition point, it is clear that h₀ (and hence T_c) must be a strongly increasing function of ${[{\epsilon }_{{x}^{2}-{y}^{2}}]}^{2}$. It is also reasonable to assume on microscopic grounds that h₁ is an increasing function of ${[{\epsilon }_{{x}^{2}-{y}^{2}}]}^{2}$, since the fact that the g-wave gap function vanishes at the van-Hove points implies that proximity to the Lifshitz transition likely favors d-wave over g-wave pairing. Consequently, as shown in Fig. 1, we expect that ${T}_{{\rm{c}}}-{T}_{{\rm{trsb}}} \sim +{[{\epsilon }_{{x}^{2}-{y}^{2}}]}^{2}$ and that for T_c > T > T_trsb, there is a d-wave-like SC followed by a lower T transition to a TRSB SC with ${d}_{{x}^{2}-{y}^{2}}+i{g}_{xy({x}^{2}-{y}^{2})}$-wave-like order. (Strictly speaking, in the presence of shear strain, the SC state should be classified by the representations of the orthorhombic point group, which is why we refer to the states as “d-wave like” and “g-wave like”). This all is broadly consistent with point 8.²

The TRSB in the SC state discussed as point 5 is consistent with the present scenario so long as we assume all γ_j > 0. Precisely at the point at which the two orders are degenerate, the onset of TRSB would occur simultaneously with T_c, consistent with present observations. However, as is exhibited in the various schematic phase diagrams in Fig. 1, any strain is expected to drive the system away from this fine-tuned condition, resulting in a phase diagram in which T_c > T_trsb, consistent with point 8. The fact that one set of the g-wave nodes coincides with the d-wave nodes means that the specific heat jump at the transition from a pure d-wave SC to a ${d}_{{x}^{2}-{y}^{2}}+i{g}_{xy({x}^{2}-{y}^{2})}$ state is significantly reduced, which may partially account for the fact that no signature of T_trsb has yet been observed in specific heat measurements. (Note, in a regime in which the higher T transition is to a pure g-wave SC, one would expect a stronger thermodynamic signature of the lower temperature transition to the ${d}_{{x}^{2}-{y}^{2}}+i{g}_{xy({x}^{2}-{y}^{2})}$ state since one set of g-wave nodes would be gapped below T_trsb.

There is good reason to expect small or even vanishing equilibrium currents in this state. Since the SC order of a ${d}_{{x}^{2}-{y}^{2}}+i{g}_{xy({x}^{2}-{y}^{2})}$ state preserves parity, it is non-chiral, i.e., the associated Bogoliubov bands have zero Chern number. Thus there is no topological reason to expect edge currents. Moreover, the fact that reflection through a mirror plane perpendicular to the (1,1,0) direction is respected even in the ${d}_{{x}^{2}-{y}^{2}}+i{g}_{xy({x}^{2}-{y}^{2})}$ state is sufficient to establish that edge currents must vanish at any surface that respects this symmetry.

However, despite these successes, one is hard-pressed in the context of the present scenario to simultaneously account for a portion of the observations in point 4 (no non-analytic ϵ_xy strain dependence of T_c in the limit of vanishing stain). To account for this in a consistent fashion, we invoke the effect of weak disorder that is equivalent to random local strains. Note that, while it is an established fact that the relevant materials are, to an extraordinary level of approximation, nearly perfectly crystalline, with normal state mean-free paths in excess of 1 μm (point 2), long-wave-length disorder (i.e., strain disorder) does not make much contribution to determining the mean-free path and is not expected to lead to a substantial reduction of T_c, even in an unconventional SC. Indeed, as discussed in point 4, there is some direct experimental evidence of the existence of the presence of random strain²³.

There are several different scenarios that can (at least roughly) reconcile the remaining observations by incorporating the effects of weak, random strain—that is to say non-zero σ_j as defined in Eq. (5). We plan to address this issue in a forthcoming work. In general, for the same reasons discussed in ref. ³² in the context of an assumed two-component p-wave order parameter, such disorder rounds out any non-analytic cusp-like strain dependence of T_c. The easiest limit in which to illustrate this is one in which the random strains are very long range correlated, so one can think of the system as consisting of essentially macroscopic regions with different strains. In any region with a non-zero value h₁, the accidental degeneracy between d and g is lifted, so even a local measurement of T_c versus strain would see analytic dependence. In regions with approximately zero h₁, but non-zero h₂, a cusp would be expected in the ϵ_xy dependence of T_c measured locally. However, even in this case, the global onset of superconductivity would be determined by the point at which SC regions percolate, which would have no such cusp.³ One would also expect strain disorder to further reduce both the magnitude and the sharpness of any thermodynamic signature of the transition to the TRSB state in the case in which T_c is measurably larger than T_trsb.

Aspects of a microscopic picture

Because the normal state of SRO is a good Fermi liquid, and because the SC phase transition appears to be mean-field like, it makes sense to think about the mechanism of SC from a weak-coupling BCS perspective. Various studies using an asymptotically exact weak-coupling approach to the problem taking into account only on-site interactions have found that the SRO band structure is conducive to SC states with p-wave symmetry and d${}_{{x}^{2}-{y}^{2}}$-wave symmetry³³,³⁴. Similar conclusions have been drawn on the basis of a random phase approximation ansatz³⁵ and multi-orbital functional renormalization group studies, which better account for the strong antiferromagnetic fluctuations seen in neutron scattering experiments on SRO^36,37. In all cases, the pair-wave function approximately vanishes on site, thus avoiding the effects of a repulsive on-site Hubbard U. Given the uncertainty concerning the correct relative magnitudes of the various interactions, and the intrinsic issues concerning the applicability of such approaches to real materials (where interactions are never weak), even though the p-wave instability is often found to be dominant, it would be difficult to argue strongly on purely theoretical grounds which of these is preferred. However, as far as we know, no previous study of SRO has found indication of a significant tendency to pairing in a g-wave channel.

However, in a related study, the effect of a repulsive nearest-neighbor repulsion, V, on the character of the weak coupling SC for the Hubbard model on a square lattice was analyzed³⁸. In the range of doping in which the dominant pairing instability is in the ${d}_{({x}^{2}-{y}^{2})}$ channel at V = 0, there is a transition to a g-wave state for V greater than a critical value, V_c ~ U²ρ(E_F). This is natural in the sense that the pair wave-function in the g-wave state not only vanishes on-site but also on any pair of nearest-neighbor sites. Thus, for V = V_c, precisely the sort of accidental degeneracy we have invoked arises. (We are currently in the process of extending this analysis to the case of the SRO band structure (in preparation).) Alternatively, even though probably more contrived than the latter microscopic reasoning, a proximity of ${d}_{({x}^{2}-{y}^{2})}$-wave and g-wave pairing propensity had been found in an effective 2D electronic model inspired by the ruthenates, which was assumed to be subject to three-dimensional phonon coupling³⁹.

Another important insight from the weak coupling approach concerns the form of the gap function. All such calculations^{33,36,40,41,42} indicate a tendency toward pair-wave functions with substantially more complex structure than the minimal functions we considered above. In fact, deep gap minima not required by symmetry arise ubiquitously in such studies. Such “accidental near-nodes” were invoked in earlier attempts to reconcile p_x + ip_y and d + is SC states with experiments that suggest the existence of line nodes. The possibility of ${d}_{{x}^{2}-{y}^{2}}+is$ pairing near a point of accidental degeneracy of the two ordering tendencies has been considered previously in the context of iron pnictides⁴³ and more recently in the context of SRO⁴⁴. While in our present scenario, there are symmetry-protected true line nodes even in the ${d}_{{x}^{2}-{y}^{2}}+i{g}_{xy({x}^{2}-{y}^{2})}$ SC phase that would be absent in its ${d}_{{x}^{2}-{y}^{2}}+is$-wave cousin, it is possible that further structure of the gaps could be invoked to produce near-nodes at the requisite locations (We also plan to address this in future studies (in preparation)).

Discussion

Experimental issues that require further study

One of the strongest pieces of evidence for TRSB is the onset of the Kerr effect. On symmetry grounds, the Kerr effect vanishes in any state that does not break time-reversal symmetry and all vertical mirror plane symmetries. While a ${d}_{{x}^{2}-{y}^{2}}+i{g}_{xy({x}^{2}-{y}^{2})}$ SC breaks time-reversal symmetry, it preserves mirror symmetry through the planes perpendicular to (1,1,0) and (1,−1,0). Since the Kerr measurements are performed in an experimental geometry that likewise preserves these mirror symmetries, the proposed state, by itself, cannot account for the observed Kerr signal. Disorder, especially the sort of strain disorder we have already invoked, generically breaks these mirror symmetries (but not time-reversal symmetry). Consequently, we conjecture that the observed Kerr measurements are likely consistent with the present scenario, but this is an issue that deserves further analysis.

A variety of other experimental observations need to be addressed. Evidence of triplet pairing has been adduced from experiments on 214/113 strontium ruthenate heterostructure tunneling⁴⁵, of odd-parity pairing from phase-sensitive Josephson tunneling²⁰, of horizontal line nodes from field-dependent specific heat measurements⁴⁶, and of half quantum vortices from cantilever magnetometry⁴⁷. All these observations pose some challenge to be reconciled with our ansatz and thus deserve further analysis and revisiting from both an experimental and a theoretical viewpoint.

Proposals for future experiments

Because the proposed degeneracy between d and g is accidental, it is not plausible that it would turn out to be exact under conditions of zero strain and zero disorder. Thus we would expect there to be a small but non-zero splitting between T_c and T_trsb—however, if this is small, it might be difficult to detect under circumstances in which the root mean square variance of h₀ or h₁ (σ₀ or σ₁) produce variations of T_c and T_trsb that are larger than the intrinsic splitting. A possibly more directly testable aspect of this proposal, however, is that the application of any strain—regardless of its symmetry—would be expected to enhance this splitting. Specifically, in the absence of disorder, and under the assumption that the degeneracy is effective exact at zero strain, we would expect a strain-induced splitting

$${T}_{{\rm{c}}}-{T}_{{\rm{trsb}}}=\sqrt{\delta {T}_{1}^{2}+\delta {T}_{2}^{2}}$$

(13)

$$\delta {T}_{1} \sim \left|{\Gamma }_{1}^{s}{\epsilon }_{s}+{\Gamma }_{1}^{s,s}{\epsilon }_{s}^{2}\right|+{\Gamma }_{1}^{xy,xy}{\epsilon }_{xy}^{2}+{\Gamma }_{1}^{{x}^{2}-{y}^{2},{x}^{2}-{y}^{2}}{\epsilon }_{{x}^{2}-{y}^{2}}^{2}$$

$$\delta {T}_{2} \sim \left|{\Gamma }_{2}^{xy}{\epsilon }_{xy}+{\Gamma }_{2}^{xy,s}{\epsilon }_{xy}{\epsilon }_{s}\right|$$

(14)

In particular, the prediction that a symmetry preserving strain, ϵ_s, will lead to a splitting of the transition directly reflects the assumption that it is an accidental degeneracy—rather than a symmetry protected one—that is responsible for the two-component character of the order.

Similarly, disorder (especially short-range correlated disorder) is expected to have a substantial impact on T_c for any unconventional SC. In the present case, because they are not symmetry related, it should have a different effect on the d- and g-wave components, thus leading to a split transition. Since the g-wave order has more (symmetry related) nodes on the Fermi surface, one would probably expect disorder to suppress the g-wave component more strongly, thus leading to a case in which there is pure d-wave pairing below T_c and a lower temperature transition to a ${d}_{{x}^{2}-{y}^{2}}+i{g}_{xy({x}^{2}-{y}^{2})}$ SC at T_trsb < T_c.

Methods

All technical aspects of our analysis are coherently presented in the “Results” and “Discussion” section.