Charge fractionalization in quantum wires

Abstract

Although the unit of charge in nature is a fundamental constant, the charge of individual quasiparticles in some low-dimensional systems may be fractionalized. Quantum one-dimensional (1D) systems, for instance, are theoretically predicted to carry charge in units smaller than the electron charge e. Unlike 2D systems, the charge of these excitations is not quantized and depends directly on the strength of the Coulomb interactions. For example, in a 1D system with momentum conservation, it is predicted that the charge of a unidirectional electron that is injected into the wire decomposes into right- and left-moving charge excitations carrying fractional charges f₀e and (1−f₀)e respectively^1,2. f₀ approaches unity for non-interacting electrons and is less than one for repulsive interactions. Here, we provide the first experimental evidence for charge fractionalization in one dimension. Unidirectional electrons are injected at the bulk of a wire and the imbalance in the currents detected at two drains on opposite sides of the injection region is used to determine f₀. Our results elucidate further^3,4 the collective nature of electrons in one dimension.

Main

Charge fractionalization in one dimension is already predicted for the spinless Luttinger model^1,2. The charge fraction f₀ is given by

where g_c is the Luttinger-liquid interaction parameter. For a galilean invariant system, g_c=v_F/v_c, where v_F is the bare Fermi velocity and v_c is the velocity of charge excitations. Roughly, g_c≈(1+U/2ɛ_F)^−1/2, where U is the Coulomb interaction energy and ɛ_F is the Fermi energy. In spinfull one-dimensional (1D) systems, charge fractionalization occurs in addition to spin–charge separation, which has been recently confirmed by spectroscopy and tunnelling experiments^4,5,6.

Observing interaction effects in 1D systems using transport experiments is a considerable challenge. For example, the d.c. two-terminal conductance with ideal contacts is universal and given by G=G₀≡2e²/h, independent of interactions^7,8,9,10,11. Shot-noise measurements have been useful in detecting fractional charge in 2D systems^12,13,14. However, low-frequency shot-noise measurements in an ideal wire would only reveal the physics of the Fermi-liquid contacts, remaining insensitive to fractionalization¹⁵. Although both noise and conductance should reveal interaction effects at frequencies exceeding v_F/g_cL∼10¹⁰ Hz, where the excitation wavelength is shorter than the wire segment^16,17,18, these frequencies are difficult to explore experimentally at low temperatures.

Initial experimental indication of electron fractionalization in one dimension is provided by angle-resolved photo-emission spectroscopy measurements on stripe-ordered cuprate materials⁵. Recent theoretical studies have proposed transport experiments aimed at detecting the same physics in quantum wires. Generally, these involve the realization of multi-terminal geometries, including: (1) local injection of electrons into a wire, where high-frequency noise correlations are expected¹⁸; (2) a four-probe geometry, measuring voltage shot noise due to an impurity¹⁹; (3) studying the d.c. I(V) curves in the presence of a bulk contact²; and (4) measuring the suppression of Aharonov–Bohm interference between two weakly coupled wires²⁰.

Here, we realize another multi-terminal geometry: we use a parallel-wire system previously applied to the study of spin–charge separation^3,4 and localization in one dimension²¹. Using momentum conservation in the tunnelling process between the two wires, we inject unidirectional electrons into the bulk of a wire, with fractionalization resulting in currents detected on both sides of the injection region. The current asymmetry AS≡(I_R−I_L)/(I_R+I_L), where I_R(L) is the current detected on the right (left), depends on the extent of fractionalization, but also on details of the coupling at the drains. We evaluate the effect of drain coupling by measuring the two-terminal conductance G_2T between the right and left drains, finding that G_2T/G₀=AS. We argue, on the basis of a theoretical model, that this observed equality proves that the tunnelling electron charge fractionalizes as predicted by theory.

The double quantum-wire sample is shown in Fig. 1a. Details about the sample and measurement technique are given in the Supplementary Information. The three-terminal geometry shown in the figure requires biasing two gates (G₁, G₂). The gates deplete the upper wire and leave the lower wire continuous, defining a finite central junction of length L_S=10–40 μm, and a semi-infinite junction on each side. The short junction serves as the source and the long junctions 1 and 3 as drains. We measure the differential tunnelling conductance ∂ I_T/∂ V_SD between the source and each drain using standard lock-in techniques. Typically dV_SD is 14 μV and the frequency is a few hertz. The measurements are carried out in a ³He refrigerator at T=0.25 K.

Figure 1: Measurement set-up.

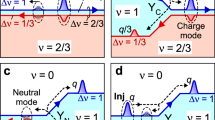
a, Cleaved-edge-overgrowth sample. Both the upper wire (UW; blue) and the lower wire (LW; green) form on the cleaved edge, facing the page. The upper wire is at the edge of a populated 2DEG (light blue) serving as a contact, through ohmic contacts O₁, O₂ and O₃. Two-terminal geometry is realized by biasing gate G₁ to deplete the upper wire, so that transport takes place by tunnelling into the lower wire and back via tunnel junctions 1 and 3. The three-terminal geometry is realized by depleting the upper wire using both gates G_1,2, which define a finite source junction. Contact O₂ is biased, and d.c. current to drains O₁, O₃ is measured. Magnetic field B applied perpendicular to the cleave plane enables momentum control of tunnelling. b, Phenomenological model: junctions 1 and 3 are characterized by parameter β. In junction 1, the chemical potential of the outgoing lower-wire charge mode y₁ depends on the incoming potential w₁ and the upper-wire potential V₁. The same holds for junction 3. In the three-terminal geometry, current I_S is injected at the source. Note: V_1,3 are the upper-wire electron potentials at the junction, in equilibrium with the 2DEG.

It is instructive to describe tunnelling between the wires in terms of their energy–momentum dispersions. Magnetic field B has the effect of shifting both dispersions relative to each other by ℏq_B=e B d along the momentum axis, as seen in Fig. 2a, which depicts their relative positions for various magnetic fields. For V_SD=0, both dispersions have the same electrochemical potential. Typically at B=0 the two 1D dispersions do not overlap (i), as the wires have different densities, and tunnelling is suppressed. Applying a field B⁻ shifts the dispersions to overlap near one of the Fermi points (ii), enabling tunnelling between co-propagating electrons. The high field crossing of the two dispersions, where electrons tunnel between counter-propagating modes is marked as B⁺ (iv,v) where B^±=ℏ|k_F^UW±k_F^LW| (with k_F^UW(LW) being the upper (lower) wire Fermi momenta). A key feature of this measurement geometry is that at B=B^±, electrons with a well-defined momentum state, near the Fermi point, are added to the lower wire. Typically each wire is populated by several sub-bands, but tunnelling between different sub-bands is suppressed by near-orthogonality³, so that each sub-band j contributes a single pair of peaks, denoted B_j^±.

Figure 2: Three-terminal asymmetry measurement.

a, Annotations depicting the dispersion arrangement for each major feature. Blue (red)—single mode in the lower (upper) wire. The upper wire is represented by the dispersions of one 1D mode and the 2DEG (depicted by rotated dispersion), and the lower wire by one 1D mode (the dispersions are presented by parabolae as an illustration, but in reality are more complex owing to electron–electron interactions). (i) B=0; (ii) B=B⁻; (iii) 2D–1D tunnelling (iv) B=+B⁺; (v) B=−B⁺. The red circle represents the injected electrons. Note that because the upper-wire density is larger than the lower-wire density, at B=B⁻ right-movers are injected. At B=B⁺, left-movers are always injected. b, Differential conductance at the right and left drains versus B. Current is detected whenever populated states in one wire overlap unpopulated states in the other. The wide features around B=±2 T are associated with tunnelling from the upper 2DEG to the lower wire. The sharp features at B=±6.5 T=±B⁺ are associated with the overlap of counter-propagating 1D states in both wires. When B=+B⁺, left-moving electrons are injected to the lower wire, and the majority of the current is detected at the left drain. At B=−B⁺, the majority of the current is detected at the right. The right/left versus B^± symmetry attests to the geometrical symmetry of the right and left drains.

In Fig. 2b, the right and left differential conductances ∂ I_R/∂ V_SD and ∂ I_L/∂ V_SD for L_S=10 μm are plotted versus B. As B is scanned from zero to positive fields, small, sharp peaks corresponding to co-propagating electrons tunnelling between sub-bands j=1,2 are first encountered at B_1,2⁻. The wide feature at 1 T<B<3 T results from tunnelling between the populated 2D electron gas (2DEG) in the upper quantum well and the lower wire (Fig. 2a(iii)). Further increasing the field, we finally encounter the B⁺ feature at B=6.5 T. To check whether the original directionality of the injected electrons is conserved, we now compare the conductance at both drains. Pronounced directional asymmetry emerges near the B⁺ feature: at B=+B⁺ left-moving electrons are injected into the lower wire (Fig. 2a(iv)), and the current detected at the left drain is indeed significantly stronger than on the right. Exactly opposite values appear at B=−B⁺, attesting to the geometric symmetry of the sample. A similar effect appears near the B⁻ features, but is more difficult to observe as the differential conductance is small relative to a strong background signal.

The effect observed near −B⁺ is quantified by an asymmetry parameter AS≡(I_R−I_L)/(I_R+I_L); the deviation from perfect asymmetry cannot a priori be attributed to fractionalization as the wire is not perfect, and microscopic effects such as backscattering can suppress AS by distributing the charge evenly in the wire before it has the chance to be detected. Moreover, complicated processes associated with coupling of the interacting wire with the non-interacting leads also take place in the drains and may lead to a smaller overall asymmetry. To isolate fractionalization physics from such microscopic effects, we measure the two-terminal conductance G_2T between the left and right drains. G_2T, being independently sensitive to these microscopic processes, enables us to extract the extent of fractionalization from AS. To demonstrate this we use a model (the geometry of which is shown in Fig. 1b) assuming a single sub-band is occupied in the lower wire. The model is based on Luttinger-liquid theory as in our system g_c≈0.4–0.5 (see the Supplementary Information for the method of evaluating g_c and a discussion justifying the use of a single-sub-band model).

The chemical potentials V_1,3 in the upper wire (subscript indicates junction) are set by the 2DEG that couples to both right- and left-moving upper-wire modes²². According to Luttinger-liquid theory, we may define separate chemical potentials for right- and left-moving lower-wire charge modes on each side of the central junction, denoted y_1,3, w_1,3 respectively. These are defined so that the current (right-moving) at any point is given by I=g_cG₀(y−w), whereas w+y is determined by the charge density, such that in equilibrium, where I=0, y and w are equal to the electron chemical potential V. With these definitions, we find that a right-moving charge excitation will affect the local value of y, but leave w unchanged, and vice versa. At the two end contacts, if the currents are small enough so that linear response applies, we must have y₁=β V₁+γ w₁,w₃=β V₃+γ y₃, where the parameters β and γ must satisfy β+γ=1 so that y=w=V in equilibrium. We have assumed here that the two junctions have identical parameters. We note without limiting the generality of the model, that β accounts for both backscattering occurring in the lower wire as well as any process associated with the coupling of the lower wire to the Fermi-liquid leads.

For the two-terminal conductance, no current enters the lower wire at the centre contact, so if there is no scattering there, we must have w₁=w₃ and y₁=y₃, and we compute G_2T=I/(V₃−V₁). This yields G_2T=g_cG₀β/(2−β). We note that the g_c dependence is a consequence of the boundary conditions at equilibrium. We also note that theoretically β<1/(2−g_c) and correspondingly G_2T≤G₀. For the three-terminal conductance, we set V₁=V₃=0, and require that I_R+I_L=I_S, where I_S is the injected current, I_R=g_cG₀(y₃−w₃) is the net right-moving current in the right half of the wire and I_L=g_cG₀(w₁−y₁) is the left-moving current in the left half of the wire.

At B=−B⁺, where the centre contact injects right-moving electrons, if we assume that an (unknown) fraction f of each electron charge travels to the right, this means that g_cG₀(y₃−y₁)=I_Sf and g_cG₀(w₁−w₃)=I_S(1−f).

Solving for AS=(I_R−I_L)/(I_R+I_L), we obtain:

and hence the ratio:

at least for a single-mode wire. This is a fundamental result: it implies that regardless of the microscopic details, it is sufficient to measure G_2T, AS and g_c under the same conditions to extract f.

We therefore proceed to measure G_2T between contacts O₁ and O₃ (Fig. 1a). This requires tuning the voltage of a single gate (G₂ or G₁ in the figure) to deplete the upper wire. As coupling to the lower wire is via tunnelling, G_2T depends on B, and should be maximal when B=B⁺. G_2T versus V_G scans are shown in Fig. 3a, showing line scans taken at different magnetic fields close to B⁺. For V_G=−1.58 V, conductance through the upper wire is suppressed. For −1.76<V_G<−1.58 V, current flows through the lower wire, coupled by junctions 1, 3. For each line scan, G_2T(B) is taken as the maximal value in this range and is shown as a circle in Fig. 3b. The result seems to fit a lorentzian, possibly related to variations of the density or of the tunnelling rate along the wire.

Figure 3: Two-terminal conductance scans.

a, G_2T versus V_G, for 4.825 T<B<5.75 T. The lower-wire conductance step is defined between V_G=−1.58 V, where the last upper-wire mode closes, and V_G=−1.76 V, where the lower wire closes. Coupling to the lower wire is done via junctions 1, 3 (Fig. 1a). The height of the step increases as B approaches B⁺. At each B, the data point G_2T(B) is defined as the maximal value in the range marked by the two vertical lines. b, G_2T versus B, as extracted from a. The solid line is a lorentzian fit. B<B⁺ scans are omitted from a for clarity.

We study the ratio G_2T/AS by comparing G_2T(B⁺) and AS(B⁺) at different wire densities. Density is controlled either by biasing a side gate, evaporated over the cleave plane, or by shining infrared light on the sample. The results are plotted in Fig. 4. In the observed density range, G_2T seems to depend linearly on n_L, the line intercepting G_2T(n_L)=0 at a finite density of n_L=20 μm⁻¹. The mechanism underlying this dependence is not understood. Superimposing the asymmetry results on this plot yields the key experimental finding of this work: AS(n_L) lies on top of the G_2T(n_L) line, showing that G_2T=AS in all of these cases. Only few AS data points are presented because this measurement imposes a stringent requirement: the density distribution along the sample has to be very smooth, so that the density in the source junction would be identical to the densities in both drain junctions. This implies that the maximal tunnelling rate appearing at B=B⁺ will occur at the same magnetic field everywhere. The inset to Fig. 4 shows that G_2T=AS even when the density distribution is not perfectly smooth: in these cases, the B⁺ feature appearing in the asymmetry scan reflects the local density at the source junction, marked B_S⁺, and the B⁺ feature of the two-terminal measurement reflects density in larger regions at the drains. The AS result is therefore taken at B_S⁺ and should be compared with G_2T at the same field. This is done by superimposing a data point AS(B_S⁺) on a plot of G_2T(B), taken at the same conditions. To present compiled data from different scans, where the height and width of the G_2T(B) lorentzian are different, we normalize each lorentzian to unity height and width, and apply the same transformation to the respective AS(B_S⁺) data point, verifying that AS(B_S⁺)=G_2T(B_S⁺).

Figure 4: G_2T and AS, plotted versus lower-wire density n_L for three different samples.

G_2T: circles; AS: triangles. The line is a linear fit. Density control: sample 13#1—side gate; 10#4, 11#1—illumination. Inset: AS versus B_S⁺ (circles); G_2T(B) lorentzian (line). To present compiled data from different densities, where lorentzian width and height vary, we normalized each lorentzian to unity width and height. The AS versus B_S⁺ data point is then subject to the same normalization (see text).

The compiled measurements presented in Fig. 4 show that the result G_2T=AS is robust: it holds for different samples, at different densities, and even when the sample has an uneven density distribution. Returning now to equation (1), we have (2f−1)=g_c, confirming that the fractionalization factor is f=(g_c+1)/2, as theoretically predicted by Luttinger-liquid theory¹ for an ideal momentum-conserving directional injector. As 0.4<g_c<0.5, we conclude that the fractionalization ratios are in the range of 0.7<f<0.75.