Abstract
Percolation on a one-dimensional lattice and fractals, such as the Sierpinski gasket, is typically considered to be trivial, because they percolate only at full bond density. By dressing up such lattices with small-world bonds, a novel percolation transition with explosive cluster growth can emerge at a non-trivial critical point. There, the usual order parameter, describing the probability of any node to be part of the largest cluster, jumps instantly to a finite value. Here we provide a simple example in the form of a small-world network consisting of a one-dimensional lattice which, when combined with a hierarchy of long-range bonds, reveals many features of this transition in a mathematically rigorous manner.
Similar content being viewed by others
Introduction
The percolation properties1 of networks are of significant interest—without percolation, any large-scale transport or communication through the network ceases. Much research has been dedicated to the understanding of percolation on randomly grown, complex networks2. Yet, the engineering of artificial networks with well-controlled features seems desirable. Indeed, there has been considerable interest in the properties of spatial networks, linking real-world geometry with small-world effects3,4,5. In particular, networks possessing hierarchical features4,6,7,8,9,10 relate to actual transport systems such as for air travel, routers and social interactions. Certain hierarchical networks, with a self-similar structure, have been shown to exhibit novel features8,11,12,13,14,15. To these, we add here an unprecedented discontinuous transition in the formation of an extensive cluster for ordinary, random-bond addition. Such an extensive cluster is said to percolate, as it contains a finite fraction of all nodes. Remarkably, this discontinuous transition can be derived 'exactly' with recursive methods, as shown below.
For a random network that allows bonds between any pair of nodes, the possibility of a discontinuous ('explosive') percolation transition has recently attracted considerable attention16,17,18,19,20,21,22,23,24,25,26,27,28. Such a transition raises the prospect that a minute increase in the bond density p of a network can suddenly make a large fraction of all nodes accessible, for instance, for the spreading of a contagion29. Yet, all proposed mechanisms for such a transition require 'correlated' bond additions16. Although further simulations of the dynamics of such correlated cluster formation21,22,23,24,25,26,27,28 seemed to support the existence of a discontinuity, evidence against it17,18,19,20 finally mounted into a general proof of the impossibility of explosive percolation for any of the proposed mechanisms30. In contrast to these efforts, we study ordinary (uncorrelated) bond additions, but on networks with a recursive, hierarchical structure to induce such an explosive percolation dynamics. Understanding of explosive cluster formation will be significantly advanced when the discontinuity can be studied rigorously by simply adding bonds randomly to these networks.
Results
Probability of a spanning cluster
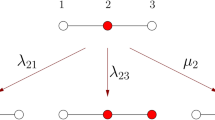
In our discussion, we focus on a simple example of a hierarchical network that is shown in Fig. 1. In its hierarchical construction, networks from preceding generations are merged for successive generations for ever larger networks. The probability for an end-to-end path of the most elementary network at n=0, a single bond, is Tn=0=p. By merging two networks of generation n side-by-side and adding a long-range bond to obtain a network of generation n+1, we recursively determine the probability Tn+1. This analysis is but one example of the real-space renormalization group31.
(The network is displayed at full bond density, p=1.) In (n=0)-th generation, the network consists of a single bond between two endnodes (open circles). The probability for an end-to-end path is obviously Tn = 0 = p. In successive generations, n + 1= 1,2,..., two sub-networks from the previous generation n are merged together with the endpoints connected by a new long-range bond (shaded arcs). There is an end-to-end path with probability Tn + 1, if either the new long-range bond exists (probability p, irrespective of Tn) or both previous sub-networks are present (probability (1−p)T2n), leading to equation (1). In each generation n the network has N = 2n + 1 nodes and E = 2n+1 − 1 bonds for an average degree 2E/N ~ 4 for large n.
The probabilities for an end-to-end path satisfy the recursion

as is explained in Fig. 1. In the limit of infinitely large networks, we obtain for any p, the probability for such an end-to-end connection,  , from the stationary solutions of equation (1), called 'fixed points'. Setting
, from the stationary solutions of equation (1), called 'fixed points'. Setting  in equation (1) yields a horizontal line of fixed points T*≡1 for all p, as well as arising line of fixed points,
in equation (1) yields a horizontal line of fixed points T*≡1 for all p, as well as arising line of fixed points,

Both lines intersect at p = 1 / 2. Further analysis shows11 that equation (2) is the stable solution for all 0 < p < 1/2 that describes the actual behaviour of large networks. That is, very large networks possess an end-to-end connection with a finite probability approaching 0 < T* (p) < 1. However, for 1/2⩽ p⩽ 1, the horizontal line is the only physical and stable solution such that a connection exists with certainty, T*=1.
Origin of the percolation transition
The phenomenology of percolation on hierarchical networks is quite distinct from that of lattices11,12,13,14. Specifically, on a lattice both, an end-to-end path and an extensive cluster, arise with certainty above the same critical bond density pc. Each node attains a finite probability P∞ (p > pc) > 0 to be connected to the spanning cluster. In contrast, hierarchical networks may have two transitions at a lower and an upper bond density, pl< pu. Below the lower transition pl, all clusters remain finite and no end-to-end paths exists. Above the upper transition pu, there is an extensive cluster and a certain end-to-end path, as on any lattice. But, both transitions delimit an interval p∈(pl, pu) that contains fractal (sub-extensive) clusters with a finite probability T* for an end-to-end path, as given by equation (2). These clusters each harbour a vanishing fraction of all nodes; however, they diverge in size with NΨ, defining a new fractal exponent 0⩽ Ψ (p) < 113. Accordingly, the order parameter1,31 P∞ becomes non-zero only at pu, making it the thermodynamically correct transition point, pc=pu. In the present network, it is pl=0 and pu = 1/2; more elaborate networks with exact but non-trivial pl and pu are discussed elsewhere11.
We note that the simultaneous emergence of an extensive cluster with end-to-end paths seems to be special for 'flat' geometries. Hierarchical networks possess what is called a hyperbolic geometry10, for which most nodes are close to the periphery, similar to a tree, with many root-to-end paths. Correspondingly, parabolic networks would be very prone to clustering in the bulk with few paths to any peripheral node, that is, an extensive cluster would emerge before paths that access the periphery arise.
Construction of the order parameter
To reveal the nature of the transition, the probability T*(p) alone provides insufficient information. In addition, we have to derive the average size 〈 smax〉n of the largest cluster and

as the proper order parameter1 from cluster-generating functions. Thus, we introduce two basic quantities: the probability ti(n) (p) that both endnodes are connected to the same cluster of size i, and the probability si,j(n) (p) that the left endnode is connected to a cluster of size i and the right endnote to a different cluster of size j. The corresponding generating functions, to provide the average cluster size, are defined as


and are depicted in Fig. 2. Tn(x) represents clusters with an effective bond between the endnodes whereas Sn(x,y) represents those that fail to provide such a bond. The following steps, while subtle, only entail elementary manipulations that result in three coupled but linear recursions. Although we provide enough details here to reproduce the intermediate steps in a few lines, we have implemented those steps also as a Mathematica script provided in the Supplementary Software. Therein lies the advantage of our present example: The discontinuity can be obtained exactly and with ease.
The recursion relations for these generating functions are obtained in Fig. 3 by considering all possible configurations on three nodes, similar to Fig. 1 but now also taking cluster sizes into account. For each configuration, the type of effective bond between each of the nodes is checked, see Fig. 2, and these bonds are assigned a value Tn(x) or Sn(x, y), depending on the type of cluster each represents. As in Fig. 1, small-world bonds are merely assigned the probability p or 1−p for being present or not. Marking the increment in cluster size, the inner node provides a factor of x or y for its adjacent cluster, or unity if it remains isolated. The contribution of each configuration to the next generation is the product of the weights of the three bonds and of the intermediate node; all eight of these are determined in Fig. 3. From Fig. 3, we read off the recursions
All diagrams contributing to  in the nth real-space recursion group step are shown. The remaining endnodes (always-open circles) are not counted in the generating functions; the (black) connecting nodes increment the cluster size, accounted for by a factor of x or y. The contribution of each configuration is: (a)
in the nth real-space recursion group step are shown. The remaining endnodes (always-open circles) are not counted in the generating functions; the (black) connecting nodes increment the cluster size, accounted for by a factor of x or y. The contribution of each configuration is: (a)  , (b)
, (b)  , (c)
, (c)  , (d)
, (d)  , (e)
, (e)  , (f)
, (f)  , (g)
, (g)  , and (h)
, and (h)  . As tallied up in equations (6,7), configurations (a)–(e) span end-to-end and contribute to T n+1 (x), while (f)-(h) do not span and contribute to S n + 1 (x, y).
. As tallied up in equations (6,7), configurations (a)–(e) span end-to-end and contribute to T n+1 (x), while (f)-(h) do not span and contribute to S n + 1 (x, y).


initiated with  . Naturally, both equations reduce to equation (1) for x = y = 1 where
. Naturally, both equations reduce to equation (1) for x = y = 1 where  .
.
The recursions in equations (6,7) contain more information than is needed here, and we simplify them in terms of functions of a single variable x. We define the functions Σn(x) ≡ Sn (x,x) and Sn (x) ≡ Sn(x,1) = Sn(1,x) that, combined into a more efficient vector notation V = [T,Σ,S], lead to

with a function-vector F of non-linear components

As needed in equation (3), the mean size 〈 smax〉n of the cluster connected to the endnodes results from the first moment of the generating functions. These are obtained via their first derivative in x at x=1,

for a network of size N = 2n + 1 → ∞.
Analysis of the recursions for the mean cluster size
The mean size of the largest cluster, as needed in equation (3) to construct the order parameter, is obtained by Taylor-expanding equation (8) to first order in ɛ ≡ 1 − x → 0. To zeroth order, each component in equation (8) evaluated at x=1 reproduces equation (1) again. To order ɛ, we find an linear inhomogeneous recursion for  , dropping the now-redundant argument x=1,
, dropping the now-redundant argument x=1,

with the Jacobian matrix

and the inhomogeneity from differentiating for x explicitly

In equations (12) and (13) we neglected the index n on  and its components to simplify the presentation. They depend on n through
and its components to simplify the presentation. They depend on n through  . Since each network at n=0 only consists of endnodes, which are not counted, all clusters are initially empty, that is,
. Since each network at n=0 only consists of endnodes, which are not counted, all clusters are initially empty, that is,  .
.
For large n at x=1, that is, near the fixed point  , it is easy to show that the inhomogeneity in equation (11) is subdominant, leaving a linear homogeneous system with constant coefficient-matrix
, it is easy to show that the inhomogeneity in equation (11) is subdominant, leaving a linear homogeneous system with constant coefficient-matrix  . The largest eigenvalue λ of this matrix provides the dominant contribution for each component of
. The largest eigenvalue λ of this matrix provides the dominant contribution for each component of  . We obtain λ between the transitions,
. We obtain λ between the transitions,  , by applying equation (2) for T* in the matrix. Via equation (10), it is
, by applying equation (2) for T* in the matrix. Via equation (10), it is  , which yields the fractal exponent
, which yields the fractal exponent

The largest eigenvalue always remains  , which implies that the order parameter P∞ in equation (3) vanishes for
, which implies that the order parameter P∞ in equation (3) vanishes for  .
.
Above and at the transition,  , it is T*=1 and equation (12) provides uniformly λ=2, as the largest eigenvalue (that is, Ψ≡1), indicating percolation in form of an extensive cluster. For a continuous transition,
, it is T*=1 and equation (12) provides uniformly λ=2, as the largest eigenvalue (that is, Ψ≡1), indicating percolation in form of an extensive cluster. For a continuous transition,  . In contrast, equation (11) can be shown rigorously to provide a monotone increasing sequence for Tn′, exactly at p = pc = 1/2 and for any p above (see Supplementary Software). Therefore, the order parameter is positive definite even exactly at p=pc, as displayed in Fig. 4. In fact, the continuity of P∞ (p) is interrupted merely because T*≡ 1 suddenly becomes an 'unstable' fixed point of equation (1) below pc. There, the stable branch transitions to equation (2) that lacks extensive clusters, Ψ < 1. Hence, it is the intersection of two stable branches of fixed points T* at pu that causes a discontinuous transition. Such intersections of lines of fixed points is generic in hierarchical networks11, whereas fixed points for percolation on lattices always remain 'isolated'.
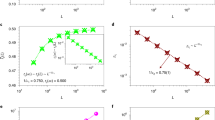
. In contrast, equation (11) can be shown rigorously to provide a monotone increasing sequence for Tn′, exactly at p = pc = 1/2 and for any p above (see Supplementary Software). Therefore, the order parameter is positive definite even exactly at p=pc, as displayed in Fig. 4. In fact, the continuity of P∞ (p) is interrupted merely because T*≡ 1 suddenly becomes an 'unstable' fixed point of equation (1) below pc. There, the stable branch transitions to equation (2) that lacks extensive clusters, Ψ < 1. Hence, it is the intersection of two stable branches of fixed points T* at pu that causes a discontinuous transition. Such intersections of lines of fixed points is generic in hierarchical networks11, whereas fixed points for percolation on lattices always remain 'isolated'.
P∞ (p) is evaluated after n = 10k iterations of the recursions in equation (11) with k = 1,...,5,, displayed from left to right. This corresponds to system sizes of up to  nodes. It evolves slowly into a discontinuity at
nodes. It evolves slowly into a discontinuity at  . Convergence is slowest just below pc, as finite-size corrections decay as
. Convergence is slowest just below pc, as finite-size corrections decay as  from equation (14).
from equation (14).
Discussion
We have shown that a hierarchy of small-world bonds grafted onto a one-dimensional lattice can result in an explosive percolation transition, even if bonds are added sequentially in an uncorrelated manner. The discontinuous transitions found in hierarchical networks are unique as alternative models, based on correlated bond additions, have been proven to fail30. At this point, the precise conditions to be imposed on the hierarchy of long-range bonds for obtaining this transition are not entirely clear. However, in each example we have examined, the addition of small-world bonds converted an initially finitely ramified network into an infinitely ramified network to provide pc< 1, as several other networks demonstrate11. In a finitely ramified network, by definition1, the removal of just a finite number of bonds can separate off extensive clusters in the limit of large systems, N → ∞, resulting in pc = 1. In contrast, studies of hierarchical systems with small-world bonds imposed on a priori infinitely ramified 2d-lattices11,12,14 seem to result in infinite-order transitions instead, which have been observed in many other networks32.
Additional information
How to cite this article: Boettcher, S. et al. Ordinary percolation with discontinuous transitions. Nat. Commun. 3:787 doi: 10.1038/ncomms1774 (2012).
References
Stauffer, D. & Aharony, A. Introduction to Percolation Theory 2nd edn (CRC Press, Boca Raton, 1994).
Barabasi, A.- L. Linked: How Everything is Connected to Everything Else and What it Means for Business, Science, and Everyday Life (Plume Books, 2003).
Watts, D. J. & Strogatz, S. H. Collective dynamics of 'small-world' networks. Nature 393, 440–442 (1998).
Boguñá, M., Krioukov, D. & Claffy, K. C. Navigability of complex networks. Nature Phys. 5, 74–80 (2009).
Barthelemy, M. Spatial networks. Phys. Rep. 499, 1–101 (2011).
Trusina, A., Maslov, S., Minnhagen, P. & Sneppen, K. Hierarchy measures in complex networks. Phys. Rev. Lett. 92, 178702 (2004).
Andrade, J. S., Herrmann, H. J., Andrade, R. F. S. & da Silva, L. R. Apollonian networks: Simultaneously scale-free, small world, Euclidean, space filling, and with matching graphs. Phys. Rev. Lett. 94, 018702 (2005).
Hinczewski, M. & Berker, A. N. Inverted Berezinskii-Kosterlitz-Thouless singularity and high-temperature algebraic order in an ising model on a scale-free hierarchicallattice small-world network. Phys. Rev. E 73, 066126 (2006).
Boettcher, S., Gonçalves, B. & Guclu, H. Hierarchical regular small-world networks. J. Phys. A: Math. Theor. 41, 252001 (2008).
Krioukov, D., Papadopoulos, F., Kitsak, M., Vahdat, A. & Boguñá, M. Hyperbolic geometry of complex networks. Phys. Rev. E 82, 036106 (2010).
Boettcher, S., Cook, J. L. & Ziff, R. M. Patchy percolation on a hierarchical network with small-world bonds. Phys. Rev. E 80, 041115 (2009).
Berker, A. N., Hinczewski, M. & Netz, R. R. Critical percolation phase and thermal Berezinskii-Kosterlitz-Thouless transition in a scale-free network with short-range and long-range random bonds. Phys. Rev. E 80, 041118 (2009).
Nogawa, T. & Hasegawa, T. Monte Carlo simulation study of the two-stage percolation transition in enhanced binary trees. J. Phys. A: Math. Theor. 42, 145001 (2009).
Hasegawa, T., Sato, M. & Nemoto, K. Generating-function approach for bond percolation in hierarchical networks. Phys. Rev. E 82, 046101 (2010).
Boettcher, S. & Brunson, C. T. Fixed point properties of the Ising ferromagnet on the Hanoi networks. Phys. Rev. E 83, 021103 (2011).
Achlioptas, D., D'Souza, R. M. & Spencer, J. Explosive percolation in random networks. Science 323, 1453–1455 (2009).
da Costa, R. A., Dorogovtsev, S. N., Goltsev, A. V. & Mendes, J. F. F. Explosive percolation transition is actually continuous. Phys. Rev. Lett. 105, 255701 (2010).
Grassberger, P., Christensen, C., Bizhani, G., Son, S.- W. & Paczuski, M. Explosive percolation is continuous, but with unusual finite size behavior. Phys. Rev. Lett. 106, 225701 (2011).
Nagler, J., Levina, A. & Timme, M. Impact of single links in competitive percolation. Nature Phys. 7, 265–270 (2011).
Lee, H. K., Kim, B. J. & Park, H. Continuity of the explosive percolation transition. Phys. Rev. E 84, 020101 (2011).
Araujo, N. A. M. & Herrmann, H. J. Explosive percolation via control of the largest cluster. Phys. Rev. Lett. 105, 035701 (2010).
Friedman, E. J. & Landsberg, A. S. Construction and analysis of random networks with explosive percolation. Phys. Rev. Lett. 103, 255701 (2009).
Rozenfeld, H. D., Gallos, L. K. & Makse, H. A. Explosive percolation in the human protein homology network. Eur. Phys. J. B 75, 305–310 (2010).
Radicchi, F. & Fortunato, S. Explosive percolation: a numerical analysis. Phys. Rev. E 81, 036110 (2010).
Cho, Y. S., Kahng, B. & Kim, D. Cluster aggregation model for discontinuous percolation transition. Phys. Rev. E 81, 030103(R) (2010).
D'Souza, R. M. & Mitzenmacher, M. Local cluster aggregation models of explosive percolation. Phys. Rev. Lett. 104 (2010).
Araujo, N. A. M., Andrade Jr., J. S., Ziff, R. M. & Herrmann, H. J. Tricritical point in explosive percolation. Phys. Rev. Lett. 106, 095703 (2011).
Manna, S. S. & Chatterjee, A. A new route to explosive percolation. Physica A 390, 177–182 (2011).
Balcan, D., Colizza, V., Goncalves, B., Hu, H., Ramasco, J. J. & Vespignani, A. Multiscale mobility networks and the spatial spreading of infectious diseases. Proc. Natl Acad. Sci. USA 106, 21484–21489 (2009).
Riordan, O. & Warnke, L. Explosive percolation is continuous. Science 333, 322–324 (2011).
Plischke, M. & Bergersen, B. Equilibrium Statistical Physics, 2nd edn (World Scientifc, Singapore, 1994).
Dorogovtsev, S. N., Goltsev, A. V. & Mendes, J. F. F. Critical phenomena in complex networks. Rev. Mod. Phys. 80, 1275–1335 (2008).
Acknowledgements
S.B. thanks M. Paczuski, P. Grassberger, and the entire Complex Science Group at University of Calgary for helpful discussions. This work has been partially supported by grant DMR-0812204 from the National Science Foundation.
Author information
Authors and Affiliations
Contributions
S.B. and R.M.Z. developed the idea for this research; S.B. and V.S. worked out the formalism; and V.S. implemented the formalism, interpreted the results, and conducted numerical tests in close collaboration with S.B.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Software
Mathematica code (ZIP 56 kb)
Rights and permissions
About this article
Cite this article
Boettcher, S., Singh, V. & Ziff, R. Ordinary percolation with discontinuous transitions. Nat Commun 3, 787 (2012). https://doi.org/10.1038/ncomms1774
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms1774
This article is cited by
-
The dynamic nature of percolation on networks with triadic interactions
Nature Communications (2023)
-
Percolation in networks with local homeostatic plasticity
Nature Communications (2022)
-
Percolation in Media with Columnar Disorder
Journal of Statistical Physics (2017)
-
Percolation Phase Transition of Surface Air Temperature Networks under Attacks of El Niño/La Niña
Scientific Reports (2016)
-
Two Types of Discontinuous Percolation Transitions in Cluster Merging Processes
Scientific Reports (2015)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

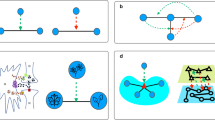


 , the open circles represent the endnodes, shaded areas indicate clusters that either span (Tn) or do not span (Sn) between the endnodes. Clusters that do not reach an endnode are ignored.
, the open circles represent the endnodes, shaded areas indicate clusters that either span (Tn) or do not span (Sn) between the endnodes. Clusters that do not reach an endnode are ignored.
