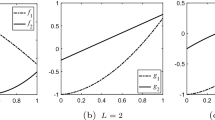
Abstract
Vector optimization problems are a significant extension of multiobjective optimization, which has a large number of real life applications. In vector optimization the preference order is related to an arbitrary closed and convex cone, rather than the nonnegative orthant. We consider extensions of the projected gradient gradient method to vector optimization, which work directly with vector-valued functions, without using scalar-valued objectives. We provide a direction which adequately substitutes for the projected gradient, and establish results which mirror those available for the scalar-valued case, namely stationarity of the cluster points (if any) without convexity assumptions, and convergence of the full sequence generated by the algorithm to a weakly efficient optimum in the convex case, under mild assumptions. We also prove that our results still hold when the search direction is only approximately computed.
Similar content being viewed by others
References
C.D. Aliprantis, M. Florenzano, V.F. Martins da Rocha, and R. Tourky, “General equilibrium in infinite security markets,” Preprint, Université de Paris 1, 2002.
C.D. Aliprantis, M. Florenzano, and R. Tourky, “General equilibrium analysis in ordered topological vector spaces,” Preprint, Université de Paris 1, 2002.
Ya.I. Alber, A.N. Iusem, and M.V. Solodov, “On the projected subgradient method for nonsmooth convex optimization in a Hilbert space,” Mathematical Programming, vol. 81, pp. 23-37, 1998.
V.A. Bereznyev, V.G. Karmanov, and A.A. Tretyakov, “The stabilizing properties of the gradient method,” USSR Computational Mathematics and Mathematical Physics, vol. 26, pp. 84-85, 1986.
D. Bertsekas, Nonlinear Programming, Athena Scientific: Belmont, 1995.
R. Burachik, L.M. Graña Drummond, A.N. Iusem, and B.F. Svaiter, “Full covergence of the steepest descent method with inexact line searches,” Optimization, vol. 32, pp. 137-146, 1995.
R. Correa and C. Lemaréchal, “Convergence of some algorithms for convex minimization,” Mathematical Programming, vol. 62, pp. 261-275, 1993.
N.O. Da Cunha and E. Polak, “Constrained minimization under vector-valued criteria in finite dimensional spaces,” Journal of Mathematical Analysis and Applications, vol. 19, pp. 103-124, 1967.
J. Fliege and B.F. Svaiter, “Steepest descent methods for multicriteria optimimization,” Mathematical Methods of Operations Research, vol. 51, pp. 479-494, 2000.
E.N. Gafni and D. Bertsekas, “Convergence of a gradient projection method,” Technical Report LIDS-P-1201, Laboratory for Information and Decision Systems, M.I.T., 1982.
T. Gal and T. Hanne, “On the development and future aspects of vector optimization and MCDM,” in Multicriteria Analysis. J. Clímaco (Ed.), Springer: Berlin, 1997, pp. 130-145.
A.M. Geoffrion, “Proper efficiency and the theory of vector maximization,” Journal of Mathematical Analysis and Applications, vol. 22, pp. 618-630, 1968.
E. Golstein and N. Tretyakov, Modified Lagrange Functions, Moscow, 1989.
L.M. Graña Drummond and B.F. Svaiter, “A steepest descent method for vector optimization,” Technical Report A2001/21, IMPA, Rio de Janeiro, 2001.
J.-B. Hiriart Urruty and C. Lemaréchal, Convex Analysis and Minimization Algorithms, Springer: Berlin, 1993.
J.P. Ignizio, Goal Programming and Extensions. D.C. Heath and Co., 1976.
A.N. Iusem and B.F. Svaiter, “A proximal regularization of the steepest descent method,” RAIRO, Recherche Opérationelle, vol. 29, no. 2, pp. 123-130, 1995.
J. Jahn, Mathematical Vector Optimization in Partially Ordered Linear Spaces, Verlag Peter D. Lang: Frankfurt, 1986.
J. Jahn, “Optimality conditions for set-valued optimization problems. Set valued optimization,” Mathematical Methods of Operations Research, vol. 48, pp. 187-200, 1998.
K. Kiwiel and K.G. Murty, “Convergence of the steepest descent method for minimizing quasi convex functions,” Journal of Optimization Theory and Applications, vol. 89, pp. 221-226, 1996.
D.T. Luc, Theory of Vector Optimization, Lecture Notes in Economy and Mathematic Systems 319. Springer: Berlin, 1989.
Y.E. Nesterov, Effective Methods in Nonlinear Programming, Moscow, 1989.
B.T. Polyak, Introduction to Optimization, Optimization Software: New York, 1987.
R.T. Rockafellar, Convex Analysis, Princeton University Press: New Jersey, 1970.
D.J. White, “A bibliography on the applications of mathematical programming multiple objective methods,” Journal of the Operational Research Society, vol. 41, pp. 669-691, 1990.
W.I. Zangwill, Nonlinear Programming: A Unified Approach, Prentice Hall: New Jersey, 1969.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Drummond, L.G., Iusem, A. A Projected Gradient Method for Vector Optimization Problems. Computational Optimization and Applications 28, 5–29 (2004). https://doi.org/10.1023/B:COAP.0000018877.86161.8b
Issue Date:
DOI: https://doi.org/10.1023/B:COAP.0000018877.86161.8b