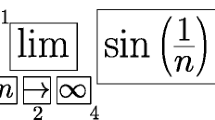Skip to main content
SpringerLink
Log in

Letting the Intuitive bear on the Formal; A Didactical Approach for the Understanding of the Limit of a Sequence

  • Published:
Educational Studies in Mathematics Aims and scope Submit manuscript

Abstract

This theoretical paper provides: (1) a presentation of some tasks that maybe regarded as typical sources for forming students' intuitions and first understandings about limiting processes of real sequences, (2) an analysis of the formal definition of limit via identifying roles for each symbol that occurs to achieve a mental image firmly consonant with the definition, and (3) a description of how this mental imagery may be used to re-examine the validity of some intuitive beliefs. In particular a persistent issue found in (1) is that the sources encourage an intuitive image of a sequence as having an ultimate term associated with the limit; it is this belief that is mostly discussed in (3).

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

REFERENCES

  • Artigue, M.: 1991, ‘Analysis’, in D. Tall (ed.), Advanced Mathematical Thinking, Kluwer Academic Publishers, Dordrecht, pp. 168–198.

    Google Scholar 

  • Binmore, K.G.: 1977, Mathematical Analysis, A Straightforward Approach, Cambridge University Press, Cambridge, pp. 26–27.

    Google Scholar 

  • Boyer, C.B.: 1939, The History of the Calculus and its Conceptual Development, reprinted by Dover, New York, 1959.

    Google Scholar 

  • Brousseau, G.: 1986, ‘Fondements et methodes de la didactique des mathematiques’, Recherches en Didactique des Mathematiques 7(2), 33–115.

    Google Scholar 

  • Brousseau, G.: 1989, ‘Le contrat didactique: Le milieu’, Recherches en Didactique des Mathematiques 9(3), 309–336.

    Google Scholar 

  • Burenkov, V.I. and Terarykova, T.V.: 1996, ‘Overcoming difficulties in learning limits’ in the Book of Abstracts of Short Presentations ICME 8, Sevilla.

  • Cornu, B.: 1981, ‘Apprentissage de la notion de limite: modeles spontanes et modeles propes’, Actes du Cinquieme Colloque du Groupe Internationale PME, Grenoble, 322–326.

  • Cornu, B.: 1983, Apprentissage de la notion de limite: conceptions et obstacles, These de doctorat de troisieme cycle, L'Universite Scientifique et Medicale de Grenoble.

  • Cornu, B.: 1991, ‘Limits’, in D. Tall (ed.), Advanced Mathematical Thinking, Kluwer Academic Publishers, Dordrecht, pp. 153–166.

    Google Scholar 

  • Cottrill, J., Dubinsky, E., Nichols, D., Schwingendorf, K., Thomas, K. and Vidakovic, D.: 1996, ‘Understanding the limit concept: Beginning with a coordinated process scheme’, Journal of Mathematical Behavior 15, 167–192.

    Article  Google Scholar 

  • Davis, P.J. and Hersh, R.: 1981, The Mathematical Experience, Birkhauser, Boston.

    Google Scholar 

  • Davis, R.B. and Vinner, S.: 1986, ‘The notion of limit: Some seemingly unavoidable misconceptional stages’, Journal of Mathematical Behavior 5(3), 281–303.

    Google Scholar 

  • Downs, M. and Mamona-Downs, J.: 2000, ‘On graphic representation of differentiation of real functions’, THEMES in Education 1(2), 173–198.

    Google Scholar 

  • Dubinsky, Ed, Elterman, F. and Gong, K.: 1988, ‘The student's construction of quantification’, For the Learning of Mathematics 8, 44–51.

    Google Scholar 

  • Fischbein, E., Tirosh, D. and Hess, P.: 1979, ‘The intuition of infinity’, Educational Studies in Mathematics 10, 3–40.

    Article  Google Scholar 

  • Gardiner, A.: 1982, Infinite Processes Background to Analysis, Springer-Verlag, New York.

    Google Scholar 

  • Khinchin, A.Ya.: 1968, The Teaching of Mathematics, (Essays by A. Ya. Khinchin edited by B.V. Gnedenko), The English University Press, pp. 23–24.

  • Kline, M.: 1972, Mathematical Thought from Ancient to Modern Times, Oxford University Press, New York, pp. 35–37.

    Google Scholar 

  • Lakoff, G. and Nunez, R.E.: 2000, Where Mathematics Comes From, Basic Books.

  • Mamona, J.: 1987, Students Interpretations of Some Concepts of Mathematical Analysis, Unpublished Ph.D. Thesis, Faculty of Mathematical Studies, University of Southampton.

  • Mamona, J.: 1990, ‘Sequences and series - Sequences and functions: Students' confusions’, International Journal of Mathematical Education in Science and Technology 21(2), 333–337.

    Google Scholar 

  • Mamona-Downs, J. and Downs, M.: 2000, ‘Advanced mathematical thinking with a special reference to reflection on mathematical structure’, to appear in Lyn English (Chief Ed.), Handbook of International Research in Mathematics Education, Lawrence Erlbaum Ass., NJ.

    Google Scholar 

  • Nunez, R.: 1993, ‘Big and small infinities: Psychocognitive aspects’, Proceedings of PME 17, Tsukuba, Japan, II, 121–128.

    Google Scholar 

  • Nunez, R.: 1994, ‘Subdivision and small infinities: Zeno, paradoxes and cognition’, Proceedings of PME 18, Lisbon, Portugal, III, 368–375.

    Google Scholar 

  • Orton, A.: 1980, A Cross-sectional Study of the Understanding of Elementary Calculus in Adolescents and Young Adults, Unpublished Ph.D. Thesis, Leeds University.

  • Pinto, M.M.F.: 1996, ‘Students use of quantifiers’ Paper presented to the Advanced Mathematical Thinking Group of PME 20, Valencia, Spain.

  • Pinto, M.M.F. and Tall, D.O.: 2001, ‘Following students development in a traditional university classroom’, Proceedings of the 25th Conference of the International Group of Mathematics Education 4, 57–64. Utrecht, The Netherlands.

  • Robinson, A.: 1966, Non-Standard Analysis, Amsterdam, North-Holland.

  • Schoenfeld, A.: 1992, ‘Learning to think mathematically: Problem solving, metacognition, and sense making in mathematics’, in D. Grouws (ed.), Handbook of research on mathematics teaching and learning, Macmillan and National Council of Teachers of Mathematics, New York, pp. 334–370.

    Google Scholar 

  • Schwarzenberger, R.L.E. and Tall, D.O.: 1978, ‘Conflicts in the learning of real numbers and limits’, Mathematics Teaching 8(2), 44–49.

    Google Scholar 

  • Sierpinska, A.: 1987, ‘Humanities students and epistemological obstacles related to limits’, Educational Studies in Mathematics 18, 371–397.

    Article  Google Scholar 

  • Sierpinska, A.: 1990, ‘Some remarks on understanding in mathematics’, For the Learning of Mathematics 10(3), 24–36.

    Google Scholar 

  • Sullivan, K.: 1976, ‘The teaching of elementary calculus: an approach using infinitesimals’, American Mathematical Monthly 83(5), 370–375.

    Article  Google Scholar 

  • Szydlik, J.E.: 2000, ‘Mathematical beliefs and conceptual understanding of the limit of a function’, Journal for Research in Mathematics Education 31(3), 258–276.

    Article  Google Scholar 

  • Tall, D.O.: 1980a, ‘Intuitive infinitesimals in the calculus’, Abstracts of short communications, ICME IV, Berkeley, page C5.

    Google Scholar 

  • Tall, D.O.: 1980b, ‘The notion of infinite measuring numbers and its relevance in the intuition of infinity’, Educational Studies in Mathematics 11, 271–284.

    Article  Google Scholar 

  • Tall, D.: 1992, ‘The transition to advanced mathematical thinking: Functions, limits, infinity and proof’, in D. Grouws (ed.), Handbook of Research on Mathematics Teaching and Learning, Macmillan and National Council of Teachers of Mathematics, New York, pp. 495–511.

    Google Scholar 

  • Tall, D.O. and Vinner, S.: 1981, ‘Concept image and concept definition in mathematics with particular reference to limits and continuity’, Educational Studies in Mathematics 12(2), 151–169.

    Article  Google Scholar 

  • Vinner, S.: 1987, ‘Continuous functions-images and reasoning in college students’, Proceedings of PME 11, Montreal, Canada. III, pp. 177–183.

    Google Scholar 

  • Vinner, S.: 1991, ‘The role of definitions in the teaching and learning of mathematics’, in D. Tall (ed.), Advanced Mathematical Thinking, Kluwer Academic Publishers, Dordrecht, pp. 65–81.

    Google Scholar 

  • Williams, S.R.: 1991, ‘Models of limit held by college calculus students’, Journal for Research in Mathematics Education 22(3), 237–251.

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. University of Macedonia, 156 Egnatia str., P.O. Box 1591, 540 06, Greece

    Joanna Mamona-Downs

Authors
  1. Joanna Mamona-Downs
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Mamona-Downs, J. Letting the Intuitive bear on the Formal; A Didactical Approach for the Understanding of the Limit of a Sequence. Educational Studies in Mathematics 48, 259–288 (2001). https://doi.org/10.1023/A:1016004822476

Download citation

  • Issue Date:

  • DOI: https://doi.org/10.1023/A:1016004822476

Search

Navigation