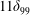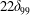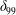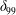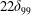1 Introduction
Laminar–turbulent transition in boundary layers is a fundamental topic, the understanding of which has special significance in science and engineering. However, modelling the transition process from laminar to turbulent flow poses considerable theoretical and numerical challenges due to the complex nature of the nonlinear breakdown, disparate length and time fluctuations arising and uncertainties regarding the inflow or so-called receptivity process (Morkovin Reference Morkovin and Wells1969). In a flat-plate boundary layer, laminar–turbulent transition can be triggered by growth of small-amplitude perturbations, such as Tollmien–Schlichting (TS) waves. The linear stage of the TS disturbance evolution can be described by the Orr–Sommerfeld (OS) equation (Orr Reference Orr1907). Since the existence of TS waves was experimentally verified by Schubauer & Skramstad (Reference Schubauer and Skramstad1948), there have been numerous detailed theoretical and numerical studies undertaken, to corroborate experimental observations of the transition process. While good agreement of eigenvalues based theory with experiment was achieved quite early (Schubauer & Skramstad Reference Schubauer and Skramstad1948), the use of linear and nonlinear theories to predict the breakdown process and precisely where transition occurred remained elusive, until the realisation that the environment (initial conditions) played a crucial role in the transition modelling and hence turbulence tripping process. A presently accepted tenant of the main actors involved in the transition processes are receptivity, linear eigenmode growth and nonlinear breakdown. TS waves and their evolution is now known to be influenced by multiple physical factors such as non-parallelism, free-stream environment, surface geometry and surface roughness. To correctly predict where and how transition occurs, such complexity are therefore required to be included in the modelling.
1.1 Natural transition
Receptivity is the initial stage of the natural transition process, which consists of the transformation of environmental disturbances, such as acoustic (sound), vorticity (turbulence) in isolation or in collaboration with small-scale surface features, giving birth to perturbations within the boundary layer. The aim of receptivity analysis is to assess the initial state of the disturbance, vis-à-vis its amplitude, frequency and phase within the boundary layer. Ruban (Reference Ruban1984) and Goldstein (Reference Goldstein1985) investigated the interaction of free-stream disturbances with an isolated steady hump within the viscous sublayer of a triple-deck region. The basic mechanism involves the process of resonance existing between the environmental length and time scales matching those from linear stability derived eigenmodes; i.e. small surface geometrical variations coupled with acoustic fluctuations in the free stream, say.
These initial works worked with undistorted base flows, where the surface roughness (i.e. hump) was assumed small. Experiments by Corke, Sever & Morkovin (Reference Corke, Sever and Morkovin1986) on randomly distributed roughness suggested that the rapid growth of TS waves on the rough wall was not attributable to the inflectional instability of the base flow due to roughness, but claimed that the growth was due to the continual excitation of TS waves by free-stream turbulence. In such a situation, at least two issues arise: (i) additional receptivity and generation of alternative TS waves, which may then interact with the pre-existing TS disturbance(s); and (ii) interaction between pre-existing TS waves and the distorted base flow. With a large enough height/depth scale, a localised roughness element can cause flow separation and so far, there is no theoretical framework to describe amplification of TS waves based on asymptotic analysis. Wu & Hogg (Reference Wu and Hogg2006) using a linearised lower-deck assumption, investigated this scenario where the base flow was distorted by a localised small-amplitude wall imperfection. However, Xu et al. (Reference Xu, Sherwin, Hall and Wu2016) suggest that applicability of Wu & Hogg (Reference Wu and Hogg2006) results, apply to rather stringent conditions and requires roughness height/depth scale to be extremely small. Theoretical studies of the interaction between the TS wave and a truly distorted base flow have received less attention. Ruban, Bernots & Kravtsova (Reference Ruban, Bernots and Kravtsova2016) recently considered within a strict asymptotic framework a large enough hump in a transonic boundary layer, forming a separation bubble, and the consequent generation of the TS wave; however a pre-existing TS wave convecting through the bubble and the consequent effect was not investigated.
In a flat-plate boundary layer, the problem of using direct numerical simulation (DNS) to investigate the interaction between a 2-D separation bubble and the TS wave dates back to the 1980s. Gruber, Bestek & Fasel (Reference Gruber, Bestek and Fasel1987) prescribed a locally decelerated external velocity field at the free-stream boundary to generate the bubble, and hence simulated the spatial development of the TS wave. The nearly explosive growth of disturbance amplitudes was observed. Van-Dam & Elli (Reference Van-Dam, Elli, Hussaini, Kumar and Streett1992) generated the bubble by reducing the velocity of the upper boundary in a short region and found strong nonlinear interaction between the TS wave and bubble, which consequently changed the structure of the bubble and the TS wave. Rist, Maucher & Wagner (Reference Rist, Maucher, Wagner, Desideri, Hirsch, Le-Tallec, Pandolfi and Periaux1996) and Rist & Maucher (Reference Rist and Maucher2002) observed that the primary growth of 2-D disturbances via the TS instability mechanism in the boundary layer upstream of the separation location may undergo a gradual switchover into an inviscid amplification similar to the Kelvin–Helmholtz mechanism. Häggmark, Bakchinov & Alfredsson (Reference Häggmark, Bakchinov and Alfredsson2000) experimentally studied a 2-D separation bubble on a flat plate and found the bubble highly susceptible to high frequency 2-D instability waves for both natural and forced conditions; with exponential growth rate of wave disturbances in the bubble. Rist (Reference Rist, Lin, Phillips and Valentine1993) suggested a 3-D oblique mode breakdown rather than a secondary instability of finite-amplitude 2-D waves. More recently, Marxen & Rist (Reference Marxen and Rist2010) numerically investigated laminar–turbulent transition in laminar separation bubbles and emphasised the importance of large-scale coherent structures for bubble size and the reattachment process. Further, Marxen, Lang & Rist (Reference Marxen, Lang and Rist2013) considered the convective primary amplification of a forced 2-D perturbation which initiated the formation of essentially 2-D large-scale vortices in the bubble. Embacher & Fasel (Reference Embacher and Fasel2014) considered unforced and forced laminar separation bubbles for a local analysis of primary and secondary instability. They found that for the unforced separation bubble, a global instability which occurs only in the nonlinear regime gives rapid rise of 2-D disturbances which surpassed the convective growth predicted by linear theory. In these papers (see also Alam & Sandham Reference Alam and Sandham2000), the separation bubbles were generated by either decreasing the free-stream velocity or by the prescription of an artificial adverse pressure gradient. The latter approach is known to have an additional impact on instability of the boundary layer.
1.2 Motivation of the present research and definition of the problem
The essential issue is that when a laminar separation bubble arises, it generally destabilises the flow, and may undergo rapid transition to turbulence, even at rather low Reynolds numbers. The general concept is that separation provokes an increase in velocity perturbations and TS destabilisation, the flow may breakdown within the separation region, close to it or further downstream of the bubble. Two-dimensional laminar bubbles have been investigated in detail, equivalent 3-D bubbles less so. In this paper, we consider 3-D separation bubbles caused by localised 3-D indentations, in an otherwise flat-plate boundary layer. The focus of the work is to explore how a pre-existing 2-D Tollmien–Schlichting disturbance, is altered, interacts and develops three-dimensionality as it convects through the 3-D separation bubble. The schematic computational domain is illustrated in figure 1. The purpose is to establish a clear understanding of TS disturbance development and sensitivity to convecting through localised reversed flow 3-D regions formed by 3-D surface indentations.
Figure 1. Overview of the 3-D computational set-up with the Blasius profile at the inflow and positions of the disturbance strip (double dashed lines) and indentation (grey shading area).
$x_{c}$
denotes the streamwise centre position of indentation. (The parameter definitions can be found in tables 1 and 2.)
The numerical study complements the experimental campaign conducted in the Gaster Laboratory at City University London. The very low turbulence intensity (less than 0.01 %) of the tunnel, is ideally suited to investigate and thus generate controlled TS waves, as opposed to undesired disturbances generated by high turbulence and acoustic fluctuations arising in more noisier tunnels. In the computational study, a line source is used to generate spanwise-uniform TS waves. In the experiments, the TS wave is excited from a point source using Gaster and Grant’s technique (Gaster & Grant Reference Gaster and Grant1975). For simplicity, and to better elucidate the physics, only one frequency of the TS wave is considered, more complex initialisation and white noise excitations are for a future study; having gained insight from the scenario investigated in this paper. The forced single TS disturbance study, we believe provides significant insight in understanding the 3-D TS laminar separation bubble, 3-D base flow distortion interaction problem.
In the next section we introduce the governing equations and definitions. The numerical strategy and configurations are provided in § 3. In § 4, primarily the linear development of the TS disturbance convecting and interacting with a 3-D separation bubble is investigated and compared with experiments. Fully nonlinear calculations are then conducted to gain a better understanding of the effect of the indentation on laminar–turbulent onset. Finally in § 5 conclusions from the work are highlighted.
2 Mathematical formulation
2.1 Fully nonlinear and linearised Navier–Stokes equations
Following the usual notation, in an inertial coordinate system, the non-dimensional incompressible Navier–Stokes equations (NSEs) and continuity equation are given as follows
$$\begin{eqnarray}\displaystyle & \unicode[STIX]{x2202}_{t}u_{i}^{\prime }-Re^{-1}\unicode[STIX]{x2202}_{j}^{2}u_{i}^{\prime }+u_{j}^{\prime }\unicode[STIX]{x2202}_{j}u_{i}^{\prime }+\unicode[STIX]{x2202}_{i}p^{\prime }=0,\quad \text{in }\unicode[STIX]{x1D6FA}^{\prime }, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \unicode[STIX]{x2202}_{j}u_{j}^{\prime }=0,\quad \text{in }\unicode[STIX]{x1D6FA}^{\prime }, & \displaystyle\end{eqnarray}$$
$u_{i}^{\prime }$
is one component of velocity field along the
$i$
th direction,
$\unicode[STIX]{x2202}_{t}$
denotes the derivative with respect to time,
$\unicode[STIX]{x2202}_{j}$
(or
$\unicode[STIX]{x2202}_{x_{j}}$
) is the
$j$
th direction spatial derivative,
$Re$
is the Reynolds number defined by
$LU_{\infty }/\unicode[STIX]{x1D708}$
where
$L$
is the distance from the leading edge,
$\unicode[STIX]{x1D708}$
is the kinematic viscosity and
$p$
is the pressure. For a domain
$\unicode[STIX]{x1D6FA}^{\prime }\in \mathbb{R}^{2}$
(
$i=1,2$
),
$(x_{1}^{\prime },x_{2}^{\prime })=(x^{\prime },y^{\prime },z^{\prime })$
and
$(u_{1}^{\prime },u_{2}^{\prime })=(u^{\prime },v^{\prime })$
. For a domain
$\unicode[STIX]{x1D6FA}^{\prime }\in \mathbb{R}^{3}$
(
$i=1,2,3$
),
$(x_{1}^{\prime },x_{2}^{\prime },x_{3}^{\prime })=(x^{\prime },y^{\prime })$
and
$(u_{1}^{\prime },u_{2}^{\prime },u_{3}^{\prime })=(u^{\prime },v^{\prime },w^{\prime })$
.
Considering a steady state solution
$\bar{u}_{i}^{\prime }$
of (2.1) and a small perturbation
$\tilde{u} _{i}^{\prime }$
such that
$u_{i}^{\prime }=\bar{u}_{i}^{\prime }+\tilde{u} _{i}^{\prime }$
and dropping the second-order terms in
$\tilde{u} _{i}^{\prime }$
, equation (2.1) are linearised as follows
$$\begin{eqnarray}\displaystyle & \unicode[STIX]{x2202}_{t}\tilde{u} _{i}^{\prime }-Re^{-1}\unicode[STIX]{x2202}_{j}^{2}\tilde{u} _{i}^{\prime }+\bar{u}_{j}^{\prime }\unicode[STIX]{x2202}_{j}\tilde{u} _{i}^{\prime }+\tilde{u} _{j}^{\prime }\unicode[STIX]{x2202}_{j}\bar{u}_{i}^{\prime }+\unicode[STIX]{x2202}_{i}\tilde{p}^{\prime }=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \unicode[STIX]{x2202}_{j}\tilde{u} _{j}^{\prime }=0. & \displaystyle\end{eqnarray}$$
$\tilde{u} _{i}^{\prime }$
in a boundary layer.
In the flat-plate simulations undertaken, with the assumptions of relatively large
$Re$
and no pressure gradient, the base flow can be approximated by the well-known Blasius equation (Schlichting Reference Schlichting1968), which has the following streamwise and vertical velocity profiles
$$\begin{eqnarray}\bar{u}_{B}=U_{\infty }f^{\prime }(\unicode[STIX]{x1D702})\quad \text{and}\quad \bar{v}_{B}=\frac{1}{2}\sqrt{\frac{\unicode[STIX]{x1D708}U_{\infty }}{x}}(\unicode[STIX]{x1D702}f^{\prime }(\unicode[STIX]{x1D702})-f(\unicode[STIX]{x1D702})),\end{eqnarray}$$
where
$f(\unicode[STIX]{x1D702})$
denotes the dimensionless streamfunction and the dimensionless coordinate
$\unicode[STIX]{x1D702}$
is defined by
$y/\unicode[STIX]{x1D6FF}_{x}$
(
$\unicode[STIX]{x1D6FF}_{x}:=\sqrt{\unicode[STIX]{x1D708}x/U_{\infty }}$
). For a flat-plate boundary layer,
$\bar{u}_{B}$
and
$\bar{v}_{B}$
can be regarded as a steady state solution (
$\bar{u}^{\prime },\bar{v}^{\prime }$
) of (2.1).
Under the assumption of streamwise parallel flow in two dimensions, the perturbation assumes the normal form
$$\begin{eqnarray}(\tilde{u} ^{\prime },\tilde{v}^{\prime },\tilde{p}^{\prime })=(\hat{u} ^{\prime },\hat{v}^{\prime },\hat{p}^{\prime })\exp (\text{i}(\unicode[STIX]{x1D6FC}^{\prime }\cdot x^{\prime }-\unicode[STIX]{x1D714}^{\prime }\cdot t))+\text{c.c.},\end{eqnarray}$$
where
$\unicode[STIX]{x1D6FC}^{\prime }$
and
$\unicode[STIX]{x1D714}^{\prime }$
denote wavenumber and frequency of a perturbation, respectively. The mode
$(\hat{u} ^{\prime },\hat{v}^{\prime },\hat{p}^{\prime })$
in (2.4) can be obtained by solving the well-known Orr–Sommerfeld eigenvalue problem.
Generally, for an unstable frequency
$\unicode[STIX]{x1D714}\in \mathbb{R}^{+}$
, assuming that the TS mode is dependent on both
$x^{\prime }$
and
$y^{\prime }$
, the TS wave envelope is defined by the absolute maximum amplitude of the TS wave as follows
$$\begin{eqnarray}A^{\prime }(x^{\prime },z^{\prime })=\max \{|\tilde{u} ^{\prime }(x^{\prime },y^{\prime },z^{\prime },t)|:\forall y^{\prime }\in [0,\infty ),\forall ~t\in \mathbb{R}^{+}\}.\end{eqnarray}$$
2.2 Mapping from a deformed surface to a flat surface
A flexible strategy to handle surface deformation is to employ a coordinate transformation which maps a deforming domain to a non-deforming one. Considering a temporal- and single-spatial-parameter-dependent mapping, the transformation has been successfully used to simulate flow/structure interaction (Newman & Karniadakis Reference Newman and Karniadakis1997; Evangelions Reference Evangelions1999). As a simplification, Darekar & Sherwin (Reference Darekar and Sherwin2001) did not consider temporal dependence but only single-spatial-parameter dependence and simulated flow past a square-section cylinder with a wavy stagnation face. Here, we consider a 3-D time-independent surface deformation mapping from
$\unicode[STIX]{x1D6FA}^{\prime }$
to
$\unicode[STIX]{x1D6FA}$
, defined by
$$\begin{eqnarray}x=x^{\prime },\quad y=y^{\prime }-\unicode[STIX]{x1D701}(x^{\prime },z^{\prime }),\quad z=z^{\prime },\end{eqnarray}$$
where
$\unicode[STIX]{x1D701}(\cdot ,\!\cdot )$
is the streamwise–spanwise vertical displacement of the surface. Accordingly, the velocity components and pressure are transformed as follows (Serson, Meneghini & Sherwin Reference Serson, Meneghini and Sherwin2016):
$$\begin{eqnarray}u=u^{\prime },\quad v=v^{\prime }-u^{\prime }\unicode[STIX]{x2202}_{x^{\prime }}\unicode[STIX]{x1D701}-w^{\prime }\unicode[STIX]{x2202}_{z^{\prime }}\unicode[STIX]{x1D701},\quad w=w^{\prime },\quad p=p^{\prime }.\end{eqnarray}$$
We introduce following differential operators:
$$\begin{eqnarray}D_{t}\equiv \unicode[STIX]{x2202}_{t}+u_{j}\unicode[STIX]{x2202}_{j},\quad \unicode[STIX]{x2202}_{x^{\prime }}\equiv \unicode[STIX]{x2202}_{x}-\unicode[STIX]{x1D701}_{x}\unicode[STIX]{x2202}_{y},\quad \unicode[STIX]{x2202}_{y^{\prime }}\equiv \unicode[STIX]{x2202}_{y},\quad \unicode[STIX]{x2202}_{z^{\prime }}\equiv \unicode[STIX]{x2202}_{z}-\unicode[STIX]{x1D701}_{z}\unicode[STIX]{x2202}_{y}.\end{eqnarray}$$
The NSEs (2.1) are thus transformed as follows:
$$\begin{eqnarray}\displaystyle & \unicode[STIX]{x2202}_{t}u_{i}-Re^{-1}\unicode[STIX]{x2202}_{j}^{2}u_{i}+u_{j}\unicode[STIX]{x2202}_{j}u_{i}+\unicode[STIX]{x2202}_{i}p={\mathcal{A}}_{i},\quad \text{in }\unicode[STIX]{x1D6FA}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \unicode[STIX]{x2202}_{j}u_{j}=0,\quad \text{in }\unicode[STIX]{x1D6FA}. & \displaystyle\end{eqnarray}$$
${\mathcal{A}}_{i}$
denotes the additional acceleration introduced by the non-inertial transformation along the
$i$
th direction and is dependent on
$\{u_{j}\}_{j=1}^{d}$
,
$p$
and
$\unicode[STIX]{x1D701}$
. The definition of
${\mathcal{A}}_{i}$
(or
${\mathcal{A}}_{x_{i}}$
) is given in appendix A.
The localised surface deformation
$\unicode[STIX]{x1D701}(\cdot ,\cdot )$
is defined by
$$\begin{eqnarray}\unicode[STIX]{x1D701}(x,z)=\left\{\begin{array}{@{}ll@{}}-{\displaystyle \frac{h}{2}}(\cos (2\unicode[STIX]{x03C0}\cdot r/\unicode[STIX]{x1D706})+1),\quad & r\leqslant \unicode[STIX]{x1D706}/2,\\ 0,\quad & r>\unicode[STIX]{x1D706}/2,\end{array}\right.\end{eqnarray}$$
where
$h$
is the amplitude and
$\unicode[STIX]{x1D706}$
is a length scale. The radial parameter
$r$
is defined by
$r=\sqrt{(x^{\prime }-x_{c}^{\prime })^{2}+(z^{\prime }-z_{c}^{\prime })^{2}}$
where
$(x_{c}^{\prime },z_{c}^{\prime })$
is the centre position of the surface deformation in
$x^{\prime }-z^{\prime }$
plane.
3 Numerical strategy and flow configurations
A spectral/
$hp$
element discretisation, implemented in the Nektar
$++$
package with support of
$h$
(grid size) refinement and/or
$p$
(polynomial order) refinement, is used to solve the nonlinear as well as the linearised Navier–Stokes equations. A stiffly stable splitting scheme is adopted which decouples the velocity and pressure fields; time integration is achieved by a second-order accurate implicit–explicit scheme (Karniadakis, Israeli & Orszag Reference Karniadakis, Israeli and Orszag1991; Cantwell et al.
Reference Cantwell, Moxey, Comerford, Bolis, Rocco, Mengaldo, Grazia, Yakovlev, Lombard and Ekelschot2015).
For the 2-D calculations, a convergence study by
$p$
-type refinement was performed to confirm mesh independence. In the 3-D calculations, a spectral element discretisation is used only in the
$x$
–
$y$
plane, while a Fourier expansion is adopted in the spanwise
$z$
-direction. Hence, along the spanwise direction, periodic boundary conditions are specified. For 3-D base flow generation and fully nonlinear calculations, independence of spanwise Fourier modes is performed to guarantee that independence of mesh and modes is achieved. The independence validations guarantee that for the largest depth
$h$
, the
$L^{2}$
relative errors of the shear stress on wall was of order
$O(10^{-5})$
.
For base flow generation, in the whole computational domain, the
$L^{2}$
relative error of velocity fields is less than
$10^{-6}$
, which is defined by
$$\begin{eqnarray}\Vert \unicode[STIX]{x2202}_{t}^{d}u_{i}\Vert _{0}/\Vert u_{i}\Vert _{0}\cdot T_{c}\leqslant 10^{-6},\end{eqnarray}$$
where
$\Vert \,\cdot \,\Vert _{0}$
means the standard
$L^{2}$
norm,
$\unicode[STIX]{x2202}_{t}^{d}$
denotes the discrete temporal derivative and
$T_{c}$
is the convective time scale. Once base flows are obtained, the linearised Navier–Stokes equations (LNSEs) are employed to address amplification of spanwise-uniform 2-D TS waves and deformation of
$A^{\prime }(x^{\prime },z^{\prime })$
within indentation.
Mesh and Fourier modes used for base flow generation are kept the same as used by direct numerical calculations. For direct numerical calculations in § 4.3, based on the parameters given in table 1, different spectral elements and Fourier modes are used. For
$\unicode[STIX]{x1D706}=81$
mm and
$\unicode[STIX]{x1D706}=40.5$
mm, the spanwise direction was assumed to be periodic and discretised by 180 and 160 Fourier modes, while the streamwise and wall-normal planes discretised using 5425 and 4876 elements, respectively. A polynomial expansion of degree 5 is imposed in the streamwise direction. The wall-normal grid is stretched by the function
$y^{\prime }=68\unicode[STIX]{x1D6FF}_{x}L(1+\unicode[STIX]{x1D709})/(2L+68(1-\unicode[STIX]{x1D709}))$
where
$\unicode[STIX]{x1D709}\in [-1,1]$
.
Table 1. Physical parameters:
$x_{i}$
and
$x_{o}$
denote the computational domain inlet and outlet positions, respectively;
$x_{c}$
is the centre position of indentations;
$f$
is the frequency of perturbation in hertz;
$\unicode[STIX]{x1D706}$
and
$h$
denote width and depth of indentations, respectively;
$L_{x}$
,
$L_{y}$
and
$L_{z}$
are scales of the domain
$\unicode[STIX]{x1D6FA}$
along
$x$
,
$y$
and
$z$
directions.
For 2-D calculations, the domain considered is the streamwise symmetric plane of the 3-D indentation. In the latter, the domain
$\unicode[STIX]{x1D6FA}^{\prime }$
is symmetric with respect to the plane
$z^{\prime }=0$
. Steady base flows are firstly computed by solving fully nonlinear NSEs. Following this, upstream small in amplitude perturbations (suction/blowing) ahead of the indentation is imposed to generate the purely 2-D linear TS disturbance, whose evolution is then followed over the deformed (from 2-D Blasius) indentation base flow. Subsequently by increasing the magnitude of the initial forcing a nonlinear response arises, and this leads to full transitional flows (see § 4.3).
Figure 2. Positions of the inlet
$x_{i}^{\prime }$
(
$+$
) and indentation centre
$x_{c}^{\prime }$
(●) and the outlet
$x_{o}^{\prime }$
(
$\times$
). The horizontal dashed line indicates the physical frequency at which experiments are conducted. The solid dark line indicates the neutral stability curve of the flat-plate boundary layer. The modified neutral stability curves are shown by the coloured lines for 2-D base flows computed for the case
$\unicode[STIX]{x1D706}=162$
mm; arrow indicates the direction of increasing depth
$h=0.18$
, 0.36, 0.81, 2.17 mm.
The experiment was conducted at a free-stream unit Reynolds number,
$Re=1.2\times 10^{6}$
, with the reference free-stream velocity
$U_{\infty }=18~\text{m}~\text{s}^{-1}$
. The centre of the indentation defined by (2.10) was located at 0.649 m from the leading edge of the flat plate. The centres of individual indentations are fixed with respect to the flat-plate boundary layer height and investigations are done by only varying geometrical parameters of depth and radial extent. Experimental measurements discussed herein are for two configurations: A (
$\unicode[STIX]{x1D706}=81$
mm and
$h=1.620$
mm) and C (
$\unicode[STIX]{x1D706}=81$
mm and
$h=2.170$
mm) of Group 1 presented in table 1. Numerical data were also collected for
$\unicode[STIX]{x1D706}=162$
mm and
$h=2.17$
mm, and complementing 2-D and 3-D base flows computed too. In figure 2, how the neutral stability curves are modified from the pure Blasius flow result (the solid dark line) by 2-D indentation depth changes are shown by the coloured lines. Based on this preliminary analysis, the experiments TS disturbance was generated by point source excitation, at a frequency
$f=172$
Hz (
${\mathcal{F}}=2\unicode[STIX]{x03C0}f\unicode[STIX]{x1D708}/U_{\infty }^{2}\times 10^{6}=50$
), located 0.375 m from the leading edge. Since the TS wavelength
$\unicode[STIX]{x1D706}_{TS}$
at the indention centre
$x_{c}^{\prime }$
was computed to be approximately 34 mm, identified cases of interest were deemed to be
$\unicode[STIX]{x1D706}=81$
and
$\unicode[STIX]{x1D706}=40.5$
mm (i.e. table 1), giving the ratios of
$\unicode[STIX]{x1D706}$
to the TS wavelength
$\unicode[STIX]{x1D706}/\unicode[STIX]{x1D706}_{TS}=2.38$
and
$\unicode[STIX]{x1D706}/\unicode[STIX]{x1D706}_{TS}=1.19$
, respectively. Hot-wire traverses were made through the laminar boundary layer within a streamwise experimental domain ranging from
$x=0.45$
m to 1.0 m, where the mean and fluctuating streamwise velocity components were captured. The fluctuating streamwise velocity components were obtained from a Fourier transform of the hot-wire signal, filtered at a band-pass frequency of 2 Hz–2 kHz.
All physical parameters, at which simulations were conducted for the two indentations, are given in table 1; equivalent non-dimensional quantities are given in table 2. The inlet position
$x_{i}^{\prime }$
is located at 0.1 m where the zero pressure gradient Blasius base flow is applied. This is sufficiently far from the centre (0.649 m) of indentations and ensures that indentations’ size and distorted base flow has little influence on the inlet Blasius velocity profile imposed.
Table 2. Non-dimensional parameters:
$Re_{\unicode[STIX]{x1D6FF}_{i}^{\ast }}$
and
$Re_{\unicode[STIX]{x1D6FF}_{o}^{\ast }}$
denote the inlet and outlet displacement thickness Reynolds numbers, respectively;
$Re_{\unicode[STIX]{x1D6FF}_{o}^{\ast }}$
is the displacement thickness Reynolds number at the centre position of indentations;
${\mathcal{F}}$
denotes the non-dimensional frequency;
$\unicode[STIX]{x1D706}/\unicode[STIX]{x1D6FF}_{99}$
,
$h/\unicode[STIX]{x1D6FF}_{99}$
,
$L_{x}/\unicode[STIX]{x1D6FF}_{99}$
,
$L_{y}/\unicode[STIX]{x1D6FF}_{99}$
and
$L_{z}/\unicode[STIX]{x1D6FF}_{99}$
are non-dimensionalisation of the physical quantities
$\unicode[STIX]{x1D706}$
,
$h$
,
$L_{x}$
,
$L_{y}$
and
$L_{z}$
. The reference scale
$\unicode[STIX]{x1D6FF}_{99}$
used, is the zero pressure gradient boundary layer Blasius thickness value at
$x_{c}$
.
4 Results
For convenience, regarding the definition of the separation bubble assumed in this paper, the upper limit of the separation bubble is taken as the line of streamwise zero velocity (Ward Reference Ward1963).
Figure 3. Relative indentation variation and associated separation bubble topological change in the plane
$z^{\prime }=0$
for the 3-D cases with
$\unicode[STIX]{x1D706}=81$
mm. For each
$h$
, the coloured dashed lines indicate the closed curves defined by
$\unicode[STIX]{x1D6E4}=\{(x^{\prime },y^{\prime }):\bar{u}^{\prime }(x^{\prime },y^{\prime },z^{\prime }=0)=0\}$
. The arrow indicates expansion of separation bubble extent with increasing
$h$
(corresponding to table 1 parameters of Group 1).
4.1 Steady base flows
4.1.1 Velocity fields
In figure 3, changes to the 3-D indentation geometry and associated separation bubbles in the physical plane
$z^{\prime }=0$
are shown, for
$\unicode[STIX]{x1D706}=81$
mm. To obtain a better physical appreciation of the size of these indentation we also show the indentation in physical non-stretched coordinates at the top of this figure. Although the geometry factor
$h$
varies by small increments (0.275 mm), the separation bubble topology shows drastic variation. In figure 4, the comparison between 2-D and 3-D base flows in the plane
$z^{\prime }=0$
is given for the larger indentation detailed in table 1. Differences in the topological shapes between the 2-D and 3-D separation bubbles do arise, as noted by the solid lines. Figure 4(a,c,e) highlights that for different indentation depths, the 2-D separation bubbles have a similar shape but are of different sizes. However, from figures 3 and 4(b,d,f), we observe that the shapes of the 3-D separation bubbles in the symmetrical planes strongly depend on the indentation depth
$h$
. For the 2-D separation bubbles, the upper interfaces of the bubbles are slightly concave, but for the 3-D separation bubbles the upper interfaces are almost flat. Moreover, even for the largest depth
$h$
, the 2-D separation bubble is completely confined within the indentation region, whereas for the largest 3-D indentation depth the recirculation bubble extends beyond the plane
$y^{\prime }=0$
. For the first depth, they were similar. Some moderate differences appear at the intermediate depth and the largest one is very different. Yet noting figure 4(f), the contour lines of 3-D streamwise velocity fields are significantly different and are highly deformed at the tip of the separation bubble. The vertical velocity is also enhanced in this region.
Figure 4. Comparison of 2-D base flows (a,c,e) and 3-D base flows in the planes
$z^{\prime }=0$
(b,d,f). (a,b)
$h=1.620$
mm; (c,d)
$h=1.895$
mm; (e,f)
$h=2.170$
mm. The parameter
$\unicode[STIX]{x1D706}$
is fixed and equals 81 mm. The solid dark lines indicate the closed curves defined by
$\unicode[STIX]{x1D6E4}=\{(x^{\prime },y^{\prime }):\bar{u}^{\prime }(x^{\prime },y^{\prime },z^{\prime }=0)=0\}$
.
$\bar{u}^{\prime }$
(iso-lines) and
$\bar{v}^{\prime }$
(coloured contours) are normalised by the free-stream velocity magnitude. (See table 1 for the parameters of Cases A–C of Group 1).
In figure 5, base flows in the symmetric planes for the smaller
$\unicode[STIX]{x1D706}=40.5$
mm indentations are shown. For the 2-D indentations, separation bubbles have quite similar shapes to the
$\unicode[STIX]{x1D706}=81$
mm results. In planes
$z^{\prime }=0$
, for all
$h$
values, the 3-D separation bubbles occupy most of indentation compared with the corresponding 2-D cases. For the medium and largest depth cases, and similar to the
$\unicode[STIX]{x1D706}=81$
,
$h=2.17$
mm case, the tip of the separation bubble protrudes through the plane
$y^{\prime }=0$
and around this protruding tip, there exists a local region with a stronger vertical velocity, in contrast to the 2-D counterparts.
The appearance of the separation bubble with a protruding tip appears to have a strong effect on the instability of the boundary layers. We return to this point in § 4.2.
Figure 5. Comparison of 2-D base flows (a,c,e) and 3-D base flows in the planes
$z^{\prime }=0$
(b,d,f). (a,b)
$h=1.620$
mm; (c,d)
$h=1.895$
mm; (e,f)
$h=2.170$
mm. The solid dark lines indicate the closed curves defined by
$\unicode[STIX]{x1D6E4}=\{(x^{\prime },y^{\prime }):\bar{u}^{\prime }(x^{\prime },y^{\prime },z^{\prime }=0)=0\}$
. The parameter
$\unicode[STIX]{x1D706}$
is fixed and equals 40.5 mm.
$\bar{u}^{\prime }$
(iso-lines) and
$\bar{v}^{\prime }$
(coloured contours) are normalised by the free-stream velocity magnitude. (See table 1 for the parameters of Cases A–C of Group 2).
Figure 6. Comparison of
$\unicode[STIX]{x2202}\bar{u}^{\prime }/\unicode[STIX]{x2202}\unicode[STIX]{x1D702}|_{w}$
on the wall: (a,c,e)
$\unicode[STIX]{x1D706}=81$
mm; (b,d,f)
$\unicode[STIX]{x1D706}=40.5$
mm. (a,b), (c,d) and (e,f) indicate the cases
$h=1.620$
, 1.895 and 2.170 (mm), respectively. (Solid line)
$r=\unicode[STIX]{x1D706}/2$
; (dark dashed line) positive values; (white dashed line) non-positive values (
$\unicode[STIX]{x2202}u^{\prime }/\unicode[STIX]{x2202}\unicode[STIX]{x1D702}|_{w}\leqslant 0$
). The outermost white dashed lines indicate
$\unicode[STIX]{x2202}u^{\prime }/\unicode[STIX]{x2202}\unicode[STIX]{x1D702}|_{w}=0$
.
4.1.2 Properties of wall shear stress
For convenience, we introduce the following rescaled definitions:
$$\begin{eqnarray}\hat{z}\equiv z/\unicode[STIX]{x1D706},\quad \text{and}\quad \hat{x}\equiv (x-x_{c})/\unicode[STIX]{x1D706},\end{eqnarray}$$
where the values of
$\unicode[STIX]{x1D706}$
and
$x_{c}$
are given in table 1. In figure 6, contour plots of
$\unicode[STIX]{x2202}\bar{u}^{\prime }/\unicode[STIX]{x2202}\unicode[STIX]{x1D702}|_{w}$
(with suffix ‘
$w$
’ denoting the wall) are given for
$\unicode[STIX]{x1D706}=81$
and 40.5 mm. The white contour lines with non-positive values indicate the region where the flows are reversed, while the outermost white dashed lines denotes where
$\unicode[STIX]{x2202}\bar{u}^{\prime }/\unicode[STIX]{x2202}\unicode[STIX]{x1D702}|_{w}=0$
. The topological shapes of
$\unicode[STIX]{x2202}\bar{u}^{\prime }/\unicode[STIX]{x2202}\unicode[STIX]{x1D702}|_{w}$
contour lines change notably with increasing
$h$
. For
$\unicode[STIX]{x1D706}=81$
mm cases, as the depth increases contours of negative shear (white dashed lines) change shape from an oval-type pattern to a more ‘arrowhead’ pattern which points towards the location where the recirculation zone penetrates into the
$y^{\prime }=0$
plane. This protrusion of the recirculation bubble into the main stream flow leads to a low shear region behind the protrusion region causing the positive (red) shear regions to be subdivided, in the spanwise symmetry plane, leading to a horizontal line of low (light blue) shear. A similar ‘arrowhead’ feature appears to have been established for all of the shear patterns in the smaller
$\unicode[STIX]{x1D706}=40.5$
mm width indentation cases. The ratio
$h/\unicode[STIX]{x1D706}$
appears to be a possible characterising parameter for the ‘arrowhead’ formation.
Figure 7. Comparisons of streamwise growth rate
$\unicode[STIX]{x1D6FC}_{{\mathcal{E}}}^{\prime }$
contours (a,c,e) and rescaled TS amplitude
$|\tilde{u} ^{\prime }(x^{\prime },y^{\prime },z^{\prime })|/A^{\prime }(x_{neutral}^{\prime },z^{\prime })$
contours (b,d,f) where
$A^{\prime }(x_{neutral}^{\prime },z^{\prime })$
means amplitude of TS waves at the lower branch of the neutral stability curve. The parameter
$\unicode[STIX]{x1D706}=81$
mm. (a,b)
$h=1.620$
mm; (c,d)
$h=1.895$
mm; (e,f)
$h=2.170$
mm. In (a,c,e), the black dashed lines indicate destabilisation of TS waves and the white dashed lines indicate stabilisation of TS waves (
$-\unicode[STIX]{x1D6FC}_{\text{i}}^{\prime }\leqslant 0$
). The solid circles are the curves of
$r=\unicode[STIX]{x1D706}/2$
. In (b,d,f), the red dashed lines indicate the interfaces of the regions enclosed by
$\unicode[STIX]{x1D6E4}=\{(x^{\prime },y^{\prime }):\bar{u}^{\prime }(x^{\prime },y^{\prime },z^{\prime }=0)=0\}$
.
Figure 8. Comparisons of streamwise growth rate
$\unicode[STIX]{x1D6FC}_{{\mathcal{E}}}^{\prime }$
contours (a,c,e) and rescaled TS amplitude
$|\tilde{u} ^{\prime }(x^{\prime },y^{\prime },z^{\prime })|/A^{\prime }(x_{neutral}^{\prime },z^{\prime })$
contours (b,d,f) where
$A^{\prime }(x_{neutral}^{\prime },z^{\prime })$
means amplitude of TS waves at the lower branch of the neutral stability curve. The parameter
$\unicode[STIX]{x1D706}=40.5$
mm. (a,b)
$h=1.620$
mm; (c,d)
$h=1.895$
mm; (e,f)
$h=2.170$
mm. In (a,c,e), the black dashed lines indicate destabilisation of TS waves and the white dashed lines indicate stabilisation of TS waves (
$-\unicode[STIX]{x1D6FC}_{\text{i}}^{\prime }\leqslant 0$
). The solid circles are the curves of
$r=\unicode[STIX]{x1D706}/2$
. In (b,d,f), the red dashed lines indicate the interfaces of the regions enclosed by
$\unicode[STIX]{x1D6E4}=\{(x^{\prime },y^{\prime }):\bar{u}^{\prime }(x^{\prime },y^{\prime },z^{\prime }=0)=0\}$
.
4.2 Results of linear instability analysis
4.2.1 Growth properties of primary linear instability modes
As shown in the previous section, the properties of the base flows are strongly dependent on geometrical parameters of the indentations. The appearance of the separation bubble will obviously change the instability of the boundary layers. A direct impact is that when the TS waves enter the separation bubble region, the spanwise-uniform 2-D TS modes evolve into 3-D linear instability modes and in the symmetrical planes, the 3-D mode structures are quite different from the standard 2-D TS modes. As we shall demonstrate, the growth rates of these 3-D linear instability modes depend on the local profile of streamwise velocity in
$y$
and are most energetic when the top of the recirculation zone interacts with the location of the incoming TS wave. In figures 7(a,c,e) and 8(a,c,e), we show the growth rate contours of the perturbation fields. The growth rate, which is different from the definition in (2.4), is defined based on the perturbation energy integral
$$\begin{eqnarray}\unicode[STIX]{x1D6FC}_{{\mathcal{E}}}^{\prime }=\frac{\unicode[STIX]{x1D6FF}_{x}}{{\mathcal{E}}}\frac{\text{d}{\mathcal{E}}}{\text{d}x^{\prime }},\quad \text{where }{\mathcal{E}}=\int _{w}^{\infty }(|\tilde{u} ^{\prime }|^{2}+|\tilde{v}^{\prime }|^{2}+|\tilde{w}^{\prime }|^{2})\,\text{d}y^{\prime }.\end{eqnarray}$$
In figure 7(a,c,e), the 3-D growth rate contours, for
$\unicode[STIX]{x1D706}=81$
mm, have distinct changes in contour colour levels which are clearly dependent on the changes in depth
$h$
. In the (red) regions, the growth rates increase towards the centre symmetry plane where they have maximal growth; moreover growth rates increase with increasing depth
$h$
. For
$h=1.620$
and 1.895 mm, there are two regions where the growth rates of the 3-D linear instability modes decrease: one within the indentation and another downstream of the indention. The 3-D modes’ stabilisation phenomena in these two regions are due to different phenomena. For
$h=1.620$
mm, the stabilisation regions have two local minima, but for
$h=1.895$
mm, in each stabilisation region, there are two local minima and the downstream stabilisation region has a thin wedge-like extension which divides the downstream destabilisation region into two separate regions. For
$h=2.170$
mm, the stabilisation regions shrink into a very narrow region and downstream has a long distance thin extension about the symmetry plane. For the shorter
$\unicode[STIX]{x1D706}=40.5$
mm, compared to
$\unicode[STIX]{x1D706}=81$
mm case, figure 8(a,c,e) shows that the red colour levels in the stabilisation regions within the indentations have no notable changes, with
$h$
varying. While downstream of the indentations, the extent of the stabilisation regions become less pronounced. Moreover within the indentation region, with increasing
$h$
, destabilisation effects become strong and this phenomenon is similar to results given in figure 7(a,c,e); however, the variation in overall topological structure of the destabilisation regions for
$\unicode[STIX]{x1D706}=40.5$
mm appear to be only slowly varying.
Normalised amplitudes of the disturbance profiles
$|\tilde{u} ^{\prime }(x^{\prime },y^{\prime },z^{\prime })|/A^{\prime }(x_{neutral}^{\prime },z^{\prime })$
, in the symmetry plane
$z^{\prime }=0$
, are shown in figures 7(b,d,f) and 8(b,d,f); the TS wave amplitude at the neutral stability point is
$A^{\prime }(x_{neutral}^{\prime },z^{\prime })$
). Observe that with an increase of the separation bubbles’ reach, the disturbance modes’ amplitudes increase from
$O(10^{2})$
to
$O(10^{4})$
, i.e. a factor of 100. In contrast, for the shorter
$\unicode[STIX]{x1D706}=40.5$
mm indentation, the amplitudes increase by a factor of 10, for increasing depth. Moreover, from figure 7(b,d,f) we observe that downstream of the indentations, disturbance maximum (i.e. the red shaded regions) migrates to being located further away from the surface for increasing
$h$
. Similar phenomenon for
$\unicode[STIX]{x1D706}=40.5$
mm can be observed from figure 8(b,d,f), but this disturbance maximum migration away from the surface is less clear than that for
$\unicode[STIX]{x1D706}=81$
mm case.
4.2.2 Modification of the linear instability modes
Above growth properties of the linear instability modes and the normalised linear instability modes’ amplitudes in the symmetry planes
$z^{\prime }=0$
were presented. Here, we consider modification of the linear instability modes within the separation bubbles and the modes’ destabilisation mechanism. In order to address shapes of the linear instability modes, we introduce the following locally normalised quantities:
$$\begin{eqnarray}|\tilde{u} ^{\prime }(x^{\prime },y^{\prime },z^{\prime })|/A^{\prime }(x^{\prime },z^{\prime })\end{eqnarray}$$
and
$$\begin{eqnarray}|\tilde{u} _{c}^{\prime }|=|\tilde{u} ^{\prime }(x^{\prime },y^{\prime },z^{\prime })|/A^{\prime }(x^{\prime },z^{\prime })|_{x^{\prime }=x_{c}^{\prime }}.\end{eqnarray}$$
Figure 9. Comparisons of
$|\tilde{u} ^{\prime }(x^{\prime },y^{\prime },z^{\prime })|/A^{\prime }(x^{\prime },z^{\prime })$
contours (a,c,e) in the planes
$z^{\prime }=0$
and corresponding TS mode profiles
$|\tilde{u} _{c}^{\prime }|=|\tilde{u} ^{\prime }(x^{\prime },y^{\prime },z^{\prime })|/A^{\prime }(x^{\prime },z^{\prime })$
and
$|\tilde{v}_{c}^{\prime }|=|\tilde{v}^{\prime }(x^{\prime },y^{\prime },z^{\prime })|/A^{\prime }(x^{\prime },z^{\prime })$
(b,d,f) at
$x^{\prime }=x_{c}^{\prime }$
in the planes
$z^{\prime }=0$
. The parameter
$\unicode[STIX]{x1D706}=81$
mm. (a,b)
$h=1.620$
mm; (c,d)
$h=1.895$
mm; (e,f)
$h=2.170$
mm. In (a,c,e), the dashed lines indicate the interfaces of the regions enclosed by
$\unicode[STIX]{x1D6E4}=\{(x^{\prime },y^{\prime }):\bar{u}^{\prime }(x^{\prime },y^{\prime },z^{\prime }=0)=0\}$
and in (b,d,f), the solid lines indicate the profiles of
$|\tilde{u} _{c}^{\prime }|$
and the dashed lines indicate the profiles of
$\bar{u}_{c}^{\prime }$
. In (b,d,f),
$\times$
symbols indicate the experimental results of
$|\tilde{u} _{c}^{\prime }|$
and
$\circ$
indicates the position where
$\bar{u}_{c}^{\prime }=0$
.
Figure 10. Experimental results of
$|\tilde{u} ^{\prime }(x^{\prime },y^{\prime },z^{\prime })|/A^{\prime }(x^{\prime },z^{\prime })$
contours in the planes
$z^{\prime }=0$
, which correspond to the cases
$h=1.620$
and 2.170 mm with
$\unicode[STIX]{x1D706}=81$
mm.
Figure 11. Comparisons of
$|\tilde{u} ^{\prime }(x^{\prime },y^{\prime },z^{\prime })|/A^{\prime }(x^{\prime },z^{\prime })$
contours (a,c,e) in the planes
$z^{\prime }=0$
and corresponding TS mode profiles
$|\tilde{u} _{c}^{\prime }|=|\tilde{u} ^{\prime }(x^{\prime },y^{\prime },z^{\prime })|/A^{\prime }(x^{\prime },z^{\prime })$
and
$|\tilde{v}_{c}^{\prime }|=|\tilde{v}^{\prime }(x^{\prime },y^{\prime },z^{\prime })|/A^{\prime }(x^{\prime },z^{\prime })$
(b,d,f) at
$x^{\prime }=x_{c}^{\prime }$
in the planes
$z^{\prime }=0$
. The parameter
$\unicode[STIX]{x1D706}=40.5$
mm. (a,b)
$h=1.620$
mm; (c,d)
$h=1.895$
mm; (e,f)
$h=2.170$
mm. In (a,c,e), the dashed lines indicate the interfaces of the regions enclosed by
$\unicode[STIX]{x1D6E4}=\{(x^{\prime },y^{\prime }):\bar{u}^{\prime }(x^{\prime },y^{\prime },z^{\prime }=0)=0\}$
and in (b,d,f), the solid lines indicate the profiles of
$|\tilde{u} _{c}^{\prime }|$
and the dashed lines indicate the profiles of
$\bar{u}_{c}^{\prime }$
and
$\circ$
indicates the position where
$\bar{u}_{c}^{\prime }=0$
.
In figure 9, linear disturbance structures for
$\unicode[STIX]{x1D706}=81$
mm are shown. From figure 9(a,c,e), we observe that within the indentations, the disturbances have two maxima for
$y^{\prime }/\unicode[STIX]{x1D6FF}_{x}<2$
, which are typically different from the original TS form calculated in conventional Blasius profiles. At the start positions of the separation bubbles, a lower maximum ‘sprouts’ from the main maximum and develops in the separation bubbles. By taking local mode profiles at the centre positions of the indentations, we clearly observe three maxima for the first two profiles in figure 9(b,d,f). For the third profile, because the dominant maximum value of the profile is very much greater than the other two, the third maximum at the edge of the boundary layer becomes less distinct but still exists, weakly. Moreover, the amplitude of the lower maximum decreases with increasing
$h$
relative to the upper maximum lobe. Another interesting phenomenon is that when the separation bubble size increases and the upper interface moves towards the main stream, the disturbance maximum becomes more and more concentrated around the intermediate peak and the other two maxima become less distinct. This property is also indicated by the instability mode profiles’ change given in figure 9(b,d,f). Meanwhile, we observe that the most amplified position of the instability mode is located at the peak vertical position of the incoming TS mode profile.
Figure 10 shows the experimental results of
$|\tilde{u} ^{\prime }(x^{\prime },y^{\prime },z^{\prime })|/A^{\prime }(x^{\prime },z^{\prime })$
for the cases
$h=1.620$
and 2.170 mm; these are to be compared with their numerical counterparts shown in figure 9(a,c,e). Quantitative agreement is achieved in the bulk of the flow, with qualitative consistency between numerics and experiment within the bubble. The near-wall maximum lobe is resolved both in the experiment and the numerical simulation. There are however, inaccuracies involved in measurement close to the surface, due to difficulties of hot-wire probe positioning along the curved, indented surface. Hence, there exists an offset (0.33 mm off the surface normal), where measurements closer in to the surface were not taken; this is the reason for the missing data just off the surface arising in figure 10.
In figure 11 (
$\unicode[STIX]{x1D706}=40.5$
mm) similar phenomena to figure 9 are observed, however, the near-wall maxima are much less than the intermediate peaks compared to the
$\unicode[STIX]{x1D706}=81$
mm results. As already commented upon, the changes of the separation bubbles size and the upper interface positions for the
$\unicode[STIX]{x1D706}=40.5$
mm indentation vary only weakly for each
$h$
variation. This points to the possibility, that as the indentation depth keeps on increasing, the bulk of the flow and disturbances at some stage become insensitive to any further increases of indentation depth. The distance from the upper interface of the separation bubble to the wall plays a key role in amplifying and modifying the linear perturbation profile.
Nayfeh, Ragab & AI-Maaitah (Reference Nayfeh, Ragab and AI-Maaitah1988) investigating the instability of flows around a smooth hump, observed that ahead of the separation region, the eigenfunction has the character typical of TS waves with two maxima, a large one at the critical layer and a smaller maximum peak at the edge of the boundary layer. In the separation region, the eigenfunctions developed a third peak at the inflection point of the base flow profile. Dovgal, Kozlov & Michalke (Reference Dovgal, Kozlov and Michalke1994), inducing a separation bubble by a rectangular hump in a 2-D boundary layer, observed TS modes turned into eigen-oscillations of the separation bubble and featured three maxima. These and other works on boundary layers with separation bubbles thus indicate, the dominant peaks of the disturbances are located at the critical layer, these peaks increase with distance from the separation point and achieve maximum values which can be attributed to the critical layer. Häggmark et al. (Reference Häggmark, Bakchinov and Alfredsson2000) experimentally studied a 2-D separation bubble on a flat plate by means of hot-wire anemometry and found that the streamwise velocity disturbances for both natural and forced cases exhibited three maxima; Diwan & Ramesh (Reference Diwan and Ramesh2009) experimental results confirmed this observation.
From the above, we know that although the instability modes in the separation bubbles are modified, the amplitude of the ‘sprouting’ lower maximum peak is less than that of the main maximum. The linear instability is still dominated by the intermediate value located around the position defined by the peak position of the original TS mode profile.
4.2.3 Destabilisation mechanism
Figure 12. Normalised profiles of base flow and the instability modes in the symmetrical plane for the case
$h=2.170$
mm with
$\unicode[STIX]{x1D706}=81$
mm: (a) dark dashed line indicates the
$N$
-factor and solid vertical lines are normalised streamwise velocity profiles; (b) the vertical lines indicate the normalised local instability mode profiles. In both figures, the red dashed lines indicate the interface of the separation bubble.
The dominant transition mechanism in separated shear layers has been broadly investigated as a research focus in many studies. The more recent research demonstrated that the primary instability mechanism in a separation bubble is inflectional in nature (Diwan & Ramesh Reference Diwan and Ramesh2009). In figure 12, normalised streamwise components of the base flow and the perturbation in the symmetric plane for
$\unicode[STIX]{x1D706}=81$
mm are shown. Ahead of the separation bubble, the base flow possesses the similarity structure of the Blasius profile, then from inception of the separation bubble, the streamwise component of the base flow starts to develop a free shear layer. The profiles in the separation bubble are dependent on the distance from the wall (or the depth parameter
$h$
). Betchov & Criminale (Reference Betchov and Criminale1967) suggested that the distance of the inflection point from the wall is an important parameter in dictating the inflectional instability in a shear layer. This conclusion was confirmed by Taghavi & Wazzan (Reference Taghavi and Wazzan1974) and Nayfeh, Ragab & Masad (Reference Nayfeh, Ragab and Masad1990). A common conclusion is that as the distance of the inflection point from the wall is increased, the growth rates are also increased and the base flow profiles become more unstable. From figure 12, we observe that in the confined separation bubble, the inflection point position from the wall is determined by the parameter
$h$
, which turns out to determine the formation of the shear layer. Therefore, the obtained growth rates and the tremendous amplification of the instability modes are strongly influenced by
$h$
. For the cases we studied, the upstream boundary layers are convectively unstable and the disturbances from there get advected downstream into the indentation regions. The seed of the inflectional instability is the upstream TS wave. Figure 12(b,d,f) shows the modification of the incoming TS wave as it progresses through the indentation region. Observe that in front of the separation point, the instability modes still possess the shape of the original TS mode profile. As the upstream instability modes propagate towards the separation point, the instability mode shapes are modified progressively and become gradually transformed into the modes typical of inflectional instability. The near-wall local maxima of the profiles become smaller and smaller and the inflection instability takes over the dominant role for the boundary layer instability. Figures 7 and 8, strongly suggest that in the symmetrical plane, the local dramatic amplification of the incoming instability modes is attributed to the inflectional instability.
4.2.4 Energy concentration of disturbances in planes
$x^{\prime }=x_{c}^{\prime }$
From the discussions in §§ 4.2.2 and 4.2.3, we believe that the spanwise form of the separation bubbles induce the phenomenon of localised perturbation energy focusing in the indentations. We now consider the instability modes’ contour shapes in the spanwise planes
$x^{\prime }=x_{c}^{\prime }$
; with reference to the
$\unicode[STIX]{x1D706}=81$
mm case.
In figure 13, contours of
$|\tilde{u} ^{\prime }(x^{\prime },y^{\prime },z^{\prime })|/A^{\prime }(x_{neutral}^{\prime },z^{\prime })$
are shown for each
$h$
. Energy focusing of the disturbance structure in the
$x^{\prime }=x_{c}^{\prime }$
planes clearly arises. The energy focusing regions lie above the upper interfaces of the separation bubbles. With increasing
$h$
, the focusing regions become more concentrated, and strength of the amplitudes of
$|\tilde{u} ^{\prime }(x^{\prime },y^{\prime },z^{\prime })|/A^{\prime }(x_{neutral}^{\prime },z^{\prime })$
become greater. Cusp-like interfaces of the separation bubbles develop, which appears to correlate to the cusp-like interface shape, where energy concentration accumulates at the cusp tip. This energy focusing can be explained by the discussions in §§ 4.2.2 and 4.2.3. The developing cusp structures cause the upper interface positions of the separation bubbles to grow monotonically towards the mean streams as
$z^{\prime }\rightarrow 0$
. Therefore, the distances from the upper interfaces of the separation bubbles to the wall increase and the amplification of the disturbance becomes stronger and stronger when slice position of
$|\tilde{u} ^{\prime }(x^{\prime },y^{\prime },z^{\prime })|/A^{\prime }(x_{neutral}^{\prime },z^{\prime })$
moves towards
$z^{\prime }=0$
. A sharper cusp leads to formation of a more concentrated streamwise ‘spike’ in the disturbance structure. As a direct consequence the amplitude of the disturbance is maximised in the plane
$z^{\prime }=0$
. This is consistent with the growth rate contours given in figure 7 where at
$z^{\prime }=0$
, TS modes have their largest growth rates.
The existence of the concentrated energy region is supported by the experimental results shown in figure 14; note at the indentation centre along the spanwise plane, case
$h=1.62$
mm, shows close agreement with the numerical results. With increasing depth, greater concentration of energy within a small spatial extent is also replicated in the experiment. However, numerical results predict a much finer/sharper spike in amplitude compared to the experiment. For the deeper
$h=2.17$
mm indentation, the sharp concentrated tip in the energy above the bubble was not replicated by the experiment. This may be due to the lack of spanwise resolution in the measurements, in addition to nonlinear phenomenon.
Figure 13. Comparison of
$|\tilde{u} ^{\prime }(x^{\prime },y^{\prime },z^{\prime })|/A^{\prime }(x_{neutral}^{\prime },z^{\prime })$
in the
$y{-}z$
planes at
$x^{\prime }=x_{c}^{\prime }$
contours where
$A^{\prime }(x_{neutral}^{\prime },z^{\prime })$
means amplitude of TS waves at the lower branch of the neutral stability curve. The parameter
$\unicode[STIX]{x1D706}=81$
mm. (a)
$h=1.620$
mm; (b)
$h=1.895$
mm; (c)
$h=2.170$
mm. The red dashed lines indicate the interfaces of the regions enclosed by
$\unicode[STIX]{x1D6E4}=\{(y^{\prime },z^{\prime }):\bar{u}^{\prime }(x^{\prime }=x_{c}^{\prime },y^{\prime },z^{\prime })=0\}$
(zero streamwise velocity line).
Figure 14. Experimental results of
$|\tilde{u} ^{\prime }(x^{\prime },y^{\prime },z^{\prime })|/A^{\prime }(x_{neutral}^{\prime },z^{\prime })$
which correspond to the results given in figure 13 for the case
$h=1.620$
mm (a) and the case
$h=2.170$
mm (b). The parameter
$\unicode[STIX]{x1D706}=81$
mm.
Figure 15. Comparisons of streamwise disturbance envelops in the planes
$z^{\prime }=0$
: (a) between 2-D (dashed lines) and 3-D (solid lines) results for
$\unicode[STIX]{x1D706}=81$
mm; (b) between 2-D (dashed lines) and 3-D (solid lines) results for
$\unicode[STIX]{x1D706}=40.5$
mm. The arrow indicates the
$h$
increasing direction from
$h=1.620$
to 2.170 (mm). The lines with the same colour have the same depth
$h$
.
$N$
means the
$N$
-factor defined by
$\log (A^{\prime }(x^{\prime },z^{\prime }=0)/A^{\prime }(x^{\prime }=x_{neutral}^{\prime },z^{\prime }=0))$
where
$A^{\prime }(x^{\prime }=x_{neutral}^{\prime },z^{\prime }=0)$
is the maximum TS amplitude value at the neutral position of the lower branch of the neutral stability curve. The streamwise extension of the grey shaded area indicates the region where the indentations with
$\unicode[STIX]{x1D706}=81$
(mm) are located. The streamwise extension of the olive shaded area indicates the region where the indentations with
$\unicode[STIX]{x1D706}=40.5$
(mm) are located.
Figure 16. Comparison of
$N$
-factor contours. The parameter
$\unicode[STIX]{x1D706}=81$
mm. (a)
$h=1.620$
mm; (b)
$h=1.895$
mm; (c)
$h=2.170$
mm. The dark dashed lines with the given values indicate the contour lines’ values of
$N$
.
4.2.5
$N$
-factors
$N$
-factors are a convenient means to ascertain how large a disturbance has become relative to some initial reference (van Ingen Reference van Ingen1956; Smith & Gamberoni Reference Smith and Gamberoni1956). We define
$N=\log (A^{\prime }(x^{\prime },z^{\prime })/A^{\prime }(x_{neutral}^{\prime },z^{\prime }))$
, with
$A^{\prime }(x_{neutral}^{\prime },z^{\prime })$
the TS amplitude value at the neutral stability curve. The results are summarised in figures 15 and 16.
Figure 15(a), shows the 2-D and 3-D comparison of
$N$
-factors along the symmetry plane for
$\unicode[STIX]{x1D706}=81$
mm. As noted from figure 4, for the smallest
$h$
(
$=$
1.620 mm), the 2-D separation bubble is larger than the 3-D separation bubble in the symmetry plane and as a consequence the 2-D
$N$
-factor profile is greater than the equivalent 3-D
$N$
-factor profile in the indentation region. For
$h=1.895$
mm and
$x<0.8$
, the amplitude of the 2-D
$N$
-factor profile is less than the 3-D
$N$
-factor profile and when
$x>0.8$
, the 2-D
$N$
-factor profile is greater than the 3-D
$N$
-factor profile. The downstream stabilisation of the disturbance predicted by the
$N$
-factor evolution is of course, a direct consequence of the negative growth rates arising in figure 7. For the case
$h=2.17$
mm, amplitude of the 3-D
$N$
-factor profile is greater than that of the 2-D
$N$
-factor profile and generally exceeds 8.
$N$
-factors of the order of 8 generally imply the likelihood of strong nonlinear interactions leading to the onset or triggering of laminar–turbulent transition.
In figure 15(b),
$N$
-factors between 2-D and 3-D indentations for
$\unicode[STIX]{x1D706}=40.5$
mm case are compared. Here, the 3-D
$N$
-factors are greater within the indentation region, for all depths, than the equivalent 2-D results. Much further downstream, the 2-D
$N$
-factors grow and exceed the 3-D
$N$
-factor values. For all depths, the 2-D/3-D
$N$
-factors are less than
$8$
in the indentations, and the 2-D
$N$
-factors display little variation with varying
$h$
. Note that the growth rates return to the flat-plate (Blasius) case beyond the 2-D indentation shape variation. Here, clearly a non-varying flow field (as evidenced by little change in separation bubble shape) has been established, and consequently the instability of the flow also displays little variation.
Comparing
$N$
-factors of the
$\unicode[STIX]{x1D706}=81$
and 40.5 mm cases, observe that within the indentation, the magnitudes of
$N$
-factor profiles for
$\unicode[STIX]{x1D706}=40.5$
mm are greater than the
$\unicode[STIX]{x1D706}=81$
mm results; case
$h=2.17$
mm excepted. The strongest destabilisation corresponds to the
$h=2.17$
,
$\unicode[STIX]{x1D706}=81$
mm case.
Figure 16 shows spanwise values of the
$N$
-factors in the computational domain for varying
$h$
with
$\unicode[STIX]{x1D706}=81$
mm. Overall, increasing depth prompts the onset of laminar–turbulent transition. Behind the indentations, we observe that the area of the wedge-like region bounded by the large
$N$
-factor contours moves upstream towards the indentation for increasing
$h$
. For the cases
$h=1.62$
and 1.895 mm, the
$N$
-factor criteria predicts that the transition onset is located far downstream of the indentation. In the case
$h=2.17$
mm, transition onset occurs within the indentation regions if the traditional transition criteria is adopted.
4.3 Nonlinear results
Although the classical transition onset is obtained by estimating the
$N$
-factor criteria contour lines, we cannot claim that the onset of laminar–turbulent transition does occur. Linear theory has the weakness that the initial forcing amplitude can be scaled out of the problem. The actual process of laminar tripping to turbulence is of course inherently nonlinear, and as stated in the introduction initial forcing magnitude and environment is a key component in transition onset location. We next, very briefly, touch upon direct numerical simulations to further investigate the corresponding laminar–turbulent transition onset, under the single frequency disturbance scenario investigated in this paper. Moreover, only the
$\unicode[STIX]{x1D706}=81$
mm case is discussed.
We consider the spanwise-uniform 2-D TS waves excited by time-dependent blowing and suction at
$x=0.25$
m (
$Re_{\unicode[STIX]{x1D6FF}_{d}^{\ast }}=942.5$
) and the amplitude is set to
$0.002\,\%U_{\infty }$
. To ensure reliability of results, time integration of the fully nonlinear Navier–Stokes equations was over 20 convective time scales. Figures 17 and 18, summarise the outcome of the simulations, and show iso-surfaces of the pressure fields with respect to different
$h$
. For each case, we use the same iso-surface levels according to global and local values of maximum and minimum pressure, respectively.
Figure 17. Comparison of laminar–turbulent transition onsets for different
$h$
in a large domain. The parameter
$\unicode[STIX]{x1D706}=81$
mm. (a)
$h=1.620$
mm; (b)
$h=1.895$
mm; (c)
$h=2.170$
mm. The iso-surfaces are generated by pressure fields. The red dashed lines indicate the contour lines with the transition criteria
$N$
-factor 6. The solid circles indicate the indentation boundaries
$r=\unicode[STIX]{x1D706}/2$
.
Figure 18. Comparison of laminar–turbulent transition onsets for different
$h$
in a local domain around indentation. The parameter
$\unicode[STIX]{x1D706}=81$
mm. (a)
$h=1.620$
mm; (b)
$h=1.895$
mm; (c)
$h=2.170$
mm. The iso-surfaces are generated by pressure fields. The red dashed lines indicate the contour lines with the transition criteria
$N$
-factor 6. The solid circles indicate the indentation boundaries
$r=\unicode[STIX]{x1D706}/2$
.
From figure 17(a), we observe that onset occurs earlier than that predicted by the
$N=6$
transition criteria; though displaying quite complex nonlinearity, transition onset appears to take place downstream of the indentation. For cases
$h=1.895$
and 2.170 (mm), the
$N$
-factor values vary rapidly, and within the confines of the indentation, attain values of 6 and higher, particularly along the symmetry plane, along which they are maximal. From figure 18, we observe that the
$N$
-factor criteria are good indicators of transition onset or at very least of likely occurrence of strong nonlinear processes taking place. Note that the transition onset for the
$h=2.17$
mm case is slightly earlier, closer to the indentation lip, than that for
$h=1.895$
mm depth. Though
$N=6$
values are attained within the indentation regions in both cases, the highly nonlinear complex structures indicative of flow breakdown occur just downstream of the indentation. This conclusion can also be deduced from figure 15. The
$\unicode[STIX]{x1D6EC}$
-like structures arising in figure 17 are directly generated by the focusing of the instability modes perturbation energy discussed in § 4.2.4, which are essentially attributed to the cusp-like upper interfaces of the separation bubbles in the planes
$x_{c}^{\prime }$
and their non-uniform amplification effect on oncoming perturbations (see figure 13).
Though inflectional profiles in the steady base flow arise, existence of these on their own does not lead to transition. In our base flows, for the confined thin separation bubbles arising (figure 12) maximum destabilisation, due to the inflectional flow, takes place as the TS disturbance convects over the indentation region. Provided nonlinearity during this stage is still not strong enough to bring about flow breakdown, the subsequent effects downstream of the separation bubble are weak, especially since the inflection point moves close to the wall as the base flow adjusts back to ‘Blasius-like’ flow. The inflectional instability being weak, its propensity to accentuate disturbances is thus weak too downstream of the indentation. If the inflow forcing in the wall disturbance strip flow is zero, no laminar–turbulent transition arises. In order to validate this argument, for the case with
$h=2.17$
mm, we removed the disturbance forcing after 20 convective time scales and continued the computation for another 40 convective time scale, the flow returned back to only the steady base flow state and displayed little temporal variations. This is different from the phenomenon observed in the DNS simulations of Spalart & Strelets (Reference Spalart and Strelets2000), where the laminar boundary layer was made to separate by way of aspiration through an opposite boundary. With subsequent elimination of the incoming disturbances, transition was then found to take place by the so-called ‘transition by contact’ mechanism.
As a final remark, the likelihood of nonlinear processes arising in the near-wall region of the deepest indentation is high due to the rapid destabilisation predicted by numerics and we believe this is another reason for some of the discrepancies between experiment and computation in figures 9(a,c,e) and 10. Linear theory derived
$N$
-factors rapidly reach values of
$7$
and higher within the indentations (note figure 15). Power spectra of the hot-wire signal (not presented in this paper) showed the emergence of harmonics indicating the presence of nonlinear effects. The magnitude of the point forcing in the experiment was set at quite a low value, however this could not be reduced indefinitely, to ensure a linear response throughout the spatial extent of the measurement range. Below a certain level this was then equivalent to the tunnel background level making discernment of TS structure ahead of the indentation quite difficult. In addition to attributing the discrepancy between experiment and the numerics to the linearised Navier–Stokes equations treatment, there are some uncertainties in the hot-wire measurements too. Only a single component probe was used for the hot-wire measurements, data collected within the indentation will have been compromised due to presence of three-dimensional flow as well as probe mechanism interacting and interfering with the reversed flow in the bubble.
5 Conclusions
In this paper, we studied the influence of a 3-D indentation on the instability of a boundary layer. The study was performed using both linear analysis and nonlinear calculations. We only consider the interaction of spanwise-uniform 2-D TS waves with two different types of 3-D indentations. For each type, we fix the maximum radial length scale
$\unicode[STIX]{x1D706}$
in
$x$
–
$z$
planes and changed the depth scale
$h$
. For the parameters investigated, separation bubbles are present in the indentation regions for both 2-D and 3-D cases. Some numerical findings were compared with experimental results and good agreement was obtained of the most influential flow features.
With variation of depth
$h$
significant differences in the symmetry plane arise in the topological shapes of the 3-D separation bubbles compared with the equivalent 2-D separation bubble shape. The destabilisation impact of the 3-D separation bubbles is different from that of the 2-D separation bubbles. For 2-D cases, the upper interfaces of the bubbles are concave, but for 3-D cases they are nearly flat. In the spanwise plane across
$x_{c}^{\prime }$
(the indentation centre coordinate), with increasing
$h$
, cusp-like structures develop on the upper interfaces of the separation bubbles. Furthermore, the 3-D separation bubbles occupy more space within the indentations as depth increases, and develop protrusions at the bubble tips which extend into the main stream. Once a certain
$h/\unicode[STIX]{x1D706}$
threshold is exceeded, the occurrence of the separation bubble protrusions are common for the 3-D cases, and this phenomenon does not arise in the equivalent 2-D cases. The appearance of the protrusion leads to considerable destabilisation of the flow. The cusp-like structure focusses the instability modes’ energy at the cusps’ tip. This leads to considerable amplification of the emergent 3-D structure.
The transformation of the incoming TS modes and their massive destabilisation over the indentations is attributed to an inflectional instability mechanism coming into play. The indentation depth determines the upper interfaces of the 3-D separation bubbles and influences the distance of the inflection point from the wall. The observed phenomena are attributed to the inflectional instability mechanism arising between the main stream and the separation bubble. The strength of the inflection point and the amplitude of the initial forcing dictate whether transition will take place. The simplistic
$N$
-factors analysis, provides a reasonable indication of the likelihood of the emergent 3-D structure undergoing tripping to turbulence. The results of DNS demonstrates that the likelihood of laminar–turbulent transition occurring within the indentations is highest since the most destabilised plane is the symmetry plane. Flow destabilisation is inextricably linked to the parameters of the surface indentation, in terms of depth and aspect ratio (
$h/\unicode[STIX]{x1D706}$
). Linear analysis, by way of
$N$
-factors may be used to ascertain the propensity of the disturbance to undergo tripping, however the precise details and processes are inherently nonlinear and dependent on the magnitude of the initial forcing applied to the disturbances.
Acknowledgements
The authors acknowledge support from Innovate UK grant 113001. Aspects of the research was supported by the Engineering and Physical Sciences Research Council (EPSRC) grant EP/I037946/1. Acknowledgements are also due to the United Kingdom Turbulence Consortium (UKTC) under grant EP/L000261/1 as well as EPSRC for access to ARCHER UK National Supercomputing Service. S.J.S. additionally acknowledges Royal Academy of Engineering support under their research chair scheme. The authors thank the reviewers for a number of helpful and constructive suggestions for the manuscript. Data supporting this publication can be obtained from https://sites.google.com/site/oadatasci/indent.
Appendix A. Definition of
${\mathcal{A}}_{i}$
${\mathcal{A}}_{i}$
denotes the additional acceleration along the
$i$
th direction in (2.9), which is detailed as follows
$$\begin{eqnarray}\displaystyle {\mathcal{A}}_{x} & = & \displaystyle \unicode[STIX]{x2202}_{x}\unicode[STIX]{x1D701}\unicode[STIX]{x2202}_{y}p+Re^{-1}[\unicode[STIX]{x2202}_{x^{\prime }}^{2}u-\unicode[STIX]{x2202}_{x}^{2}u],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{A}}_{y} & = & \displaystyle -[\unicode[STIX]{x2202}_{t}(u\unicode[STIX]{x2202}_{x}\unicode[STIX]{x1D701}+w\unicode[STIX]{x2202}_{z}\unicode[STIX]{x1D701})+(u\unicode[STIX]{x2202}_{x}+v\unicode[STIX]{x2202}_{y}+w\unicode[STIX]{x2202}_{z})(u\unicode[STIX]{x2202}_{x}\unicode[STIX]{x1D701}+w\unicode[STIX]{x2202}_{z}\unicode[STIX]{x1D701})]\nonumber\\ \displaystyle & & \displaystyle +\,Re^{-1}[\unicode[STIX]{x2202}_{x^{\prime }}^{2}(v+u\unicode[STIX]{x2202}_{x}\unicode[STIX]{x1D701}+w\unicode[STIX]{x2202}_{z}\unicode[STIX]{x1D701})+\unicode[STIX]{x2202}_{z^{\prime }}^{2}(v+u\unicode[STIX]{x2202}_{x}\unicode[STIX]{x1D701}+w\unicode[STIX]{x2202}_{z}\unicode[STIX]{x1D701})-(\unicode[STIX]{x2202}_{x}^{2}+\unicode[STIX]{x2202}_{z}^{2})v]\nonumber\\ \displaystyle & & \displaystyle +\,Re^{-1}[\unicode[STIX]{x2202}_{y}^{2}(u\unicode[STIX]{x2202}_{x}\unicode[STIX]{x1D701}+w\unicode[STIX]{x2202}_{z}\unicode[STIX]{x1D701})],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{A}}_{z} & = & \displaystyle \unicode[STIX]{x2202}_{z}\unicode[STIX]{x1D701}\unicode[STIX]{x2202}_{y}p+Re^{-1}[\unicode[STIX]{x2202}_{z^{\prime }}^{2}w-\unicode[STIX]{x2202}_{z}^{2}w].\end{eqnarray}$$
$\unicode[STIX]{x1D701}(\cdot ,\cdot )$
is a function of
$x$
and
$z$
(or
$x^{\prime }$
and
$z^{\prime }$
), we have the following: 
$$\begin{eqnarray}D_{t}(u_{i}\unicode[STIX]{x2202}_{i}\unicode[STIX]{x1D701})=-[\unicode[STIX]{x2202}_{t}(u\unicode[STIX]{x2202}_{x}\unicode[STIX]{x1D701}+w\unicode[STIX]{x2202}_{z}\unicode[STIX]{x1D701})+(u\unicode[STIX]{x2202}_{x}+v\unicode[STIX]{x2202}_{y}+w\unicode[STIX]{x2202}_{z})(u\unicode[STIX]{x2202}_{x}\unicode[STIX]{x1D701}+w\unicode[STIX]{x2202}_{z}\unicode[STIX]{x1D701})].\end{eqnarray}$$
Equation (A 1b ) can be rewritten in the following form:
$$\begin{eqnarray}{\mathcal{A}}_{y}=-D_{t}(u_{i}\unicode[STIX]{x2202}_{i}\unicode[STIX]{x1D701})+Re^{-1}[\unicode[STIX]{x2202}_{x^{\prime }}^{2}(v+u_{i}\unicode[STIX]{x2202}_{i}\unicode[STIX]{x1D701})+\unicode[STIX]{x2202}_{z^{\prime }}^{2}(v+u_{i}\unicode[STIX]{x2202}_{i}\unicode[STIX]{x1D701})-(\unicode[STIX]{x2202}_{x}^{2}+\unicode[STIX]{x2202}_{z}^{2})v+\unicode[STIX]{x2202}_{y}^{2}(u_{i}\unicode[STIX]{x2202}_{i}\unicode[STIX]{x1D701})].\end{eqnarray}$$
Open access
