Hostname: page-component-76fb5796d-skm99 Total loading time: 0 Render date: 2024-04-28T11:20:34.646Z Has data issue: false hasContentIssue false
  • English
  • Français

VIII.—The Schrödinger Equation with a Periodic Potential

Published online by Cambridge University Press:  14 February 2012

M. S. P. Eastham
M. S. P. Eastham
Affiliation:
Department of Mathematics, Chelsea College of Science and Technology, University of London.
Get access Rights & Permissions [Opens in a new window]

Synopsis

The differential equation

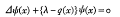
in N dimensions is considered, where q(x) is periodic. When N = 1, it is known that the conditional stability set coincides with the spectrum and that these also coincide with two other sets involving eigenvalues of associated eigenvalue problems. These results have been proved by means of the Floquet theory and the discriminant. Here an alternative proof is given which avoids the Floquet theory and which applies to the general case of N dimensions.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 69 , Issue 2 , 1971 , pp. 125 - 131
Copyright
Copyright © Royal Society of Edinburgh 1971

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

References to Literature

1.Eastham, M. S. P., 1967. “Gaps in the essential spectrum associated with singular differential operators”, Q. Jl Math., 18, 155–168.CrossRefGoogle Scholar
2.Eastham, M. S. P., 1968. “On the limit points of the spectrum”, J. Lond. Math. Soc., 43, 253–260.CrossRefGoogle Scholar
3.Eastham, M. S. P., 1970. Theory of ordinary differential equations. London: Van Nostrand Reinhold.Google Scholar
4.Gelfand, I. M., 1950. “Eigenfunction expansions for an equation with periodic coefficients”, Doklady Akad. Nauk. SSSR, 73, 1117–1120.Google Scholar
5.Glazman, I. M., 1965. Direct methods of qualitative spectral analysis of singular differential operators. Jerusalem: I.P.S.T.Google Scholar
6.Kato, T., 1966. Perturbation theory for linear operators. Berlin: Springer.Google Scholar
7.Lidskii, V. B., 1961. “Eigenfunction expansions for equations with periodic coefficients”, Appendix VIII in the Russian edition of (10).Google Scholar
8.Magnus, W., and Winkler, S., 1966. Hill's equation. New York: Interscience.Google Scholar
9.Peierls, R. E., 1955. Quantum theory of solids. Oxford Univ. Press.Google Scholar
10.Titchmarsh, E. C., 1958. Eigenfunction expansions, Part II. Oxford Univ. Press.Google Scholar