Hostname: page-component-848d4c4894-pftt2 Total loading time: 0 Render date: 2024-05-31T06:07:01.326Z Has data issue: false hasContentIssue false
  • English
  • Français

INVARIANCE OF THE COEFFICIENTS OF STRONGLY CONVEX FUNCTIONS

Part of: Geometric function theory

Published online by Cambridge University Press:  23 November 2016

D. K. THOMAS  and
SARIKA VERMA
D. K. THOMAS*
Affiliation:
Department of Mathematics, Swansea University, Singleton Park, SwanseaSA2 8PP, UK email d.k.thomas@swansea.ac.uk
SARIKA VERMA
Affiliation:
Department of Mathematics, DAV University, Jalandhar, Punjab 144012, India email sarika.16984@gmail.com
*
✉d.k.thomas@swansea.ac.uk
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

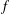Let the function $f$ be analytic in 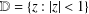$\mathbb{D}=\{z:|z|<1\}$ and given by 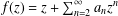$f(z)=z+\sum _{n=2}^{\infty }a_{n}z^{n}$. For 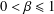$0<\unicode[STIX]{x1D6FD}\leq 1$, denote by 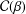${\mathcal{C}}(\unicode[STIX]{x1D6FD})$ the class of strongly convex functions. We give sharp bounds for the initial coefficients of the inverse function of 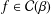$f\in {\mathcal{C}}(\unicode[STIX]{x1D6FD})$, showing that these estimates are the same as those for functions in 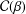${\mathcal{C}}(\unicode[STIX]{x1D6FD})$, thus extending a classical result for convex functions. We also give invariance results for the second Hankel determinant 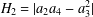$H_{2}=|a_{2}a_{4}-a_{3}^{2}|$, the first three coefficients of 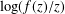$\log (f(z)/z)$ and Fekete–Szegö theorems.

Keywords

univalent functionsinvarianceinverse coefficientsstrongly starlike and convex functionsHankel determinantlogarithmic coefficientsFekete–Szegö

MSC classification

Primary: 30C45: Special classes of univalent and multivalent functions (starlike, convex, bounded rotation, etc.)
Secondary: 30C50: Coefficient problems for univalent and multivalent functions
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 95 , Issue 3 , June 2017 , pp. 436 - 445
Copyright
© 2016 Australian Mathematical Publishing Association Inc. 

References

Ali, R. M., ‘Coefficients of the inverse of strongly starlike functions’, Bull. Malays. Math. Sci. Soc. (2) 26 (2003), 63–71.Google Scholar
Ali, R. M. and Singh, V. A., ‘On the fourth and fifth coefficients of strongly starlike functions’, Results Math. 29 (1996), 197–202.CrossRefGoogle Scholar
Brannan, D. A., Clunie, J. and Kirwan, W. E., ‘Coefficient estimates for a class of starlike functions’, Canad. J. Math. XXII(3) (1970), 476–485.CrossRefGoogle Scholar
Hayman, W. K., ‘On the second Hankel determinant of mean univalent functions’, Proc. Lond. Math. Soc. (3) 3(18) (1968), 77–94.CrossRefGoogle Scholar
Janteng, A., Halim, S. and Darus, M., ‘Hankel determinants for starlike and convex functions’, Int. J. Math. Anal. 1(13) (2007), 619–625.Google Scholar
Libera, R. J. and Zlotkiewicz, E. J., ‘Coefficient bounds for the inverse of a function with derivative in O’, Proc. Amer. Math. Soc. 87(2) (1983), 251–257.Google Scholar
Löwner, C., ‘Untersuchungen uber schlichte konforme Abbildungen des Einheitskreises I’, Math. Ann. 89 (1923), 103–121.CrossRefGoogle Scholar
Noonan, J. W. and Thomas, D. K., ‘On the second Hankel determinant of areally mean p-valent functions’, Trans. Amer. Math. Soc. 223(2) (1976), 337–346.Google Scholar
Pommerenke, Ch., ‘On the Hankel determinants of univalent functions’, Mathematika 16(13) (1967), 108–112.CrossRefGoogle Scholar