Hostname: page-component-848d4c4894-p2v8j Total loading time: 0.001 Render date: 2024-05-31T07:23:56.125Z Has data issue: false hasContentIssue false
  • English
  • Français

THE DE BRUIJN–NEWMAN CONSTANT IS NON-NEGATIVE

Part of: Zeta and $L$-functions: analytic theory

Published online by Cambridge University Press:  06 April 2020

BRAD RODGERS  and
TERENCE TAO Open the ORCID record for TERENCE TAO [Opens in a new window]
BRAD RODGERS
Affiliation:
Department of Mathematics and Statistics, Queen’s University, Kingston, ON K7L 3N6, Canada; brad.rodgers@queensu.ca
TERENCE TAO
Affiliation:
Department of Mathematics, UCLA, Los Angeles, CA 90095, USA; tao@math.ucla.edu

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For each 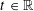$t\in \mathbb{R}$, we define the entire function

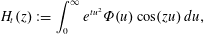$$\begin{eqnarray}H_{t}(z):=\int _{0}^{\infty }e^{tu^{2}}\unicode[STIX]{x1D6F7}(u)\cos (zu)\,du,\end{eqnarray}$$
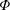where $\unicode[STIX]{x1D6F7}$ is the super-exponentially decaying function
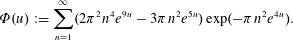$$\begin{eqnarray}\unicode[STIX]{x1D6F7}(u):=\mathop{\sum }_{n=1}^{\infty }(2\unicode[STIX]{x1D70B}^{2}n^{4}e^{9u}-3\unicode[STIX]{x1D70B}n^{2}e^{5u})\exp (-\unicode[STIX]{x1D70B}n^{2}e^{4u}).\end{eqnarray}$$
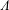 Newman showed that there exists a finite constant $\unicode[STIX]{x1D6EC}$ (the de Bruijn–Newman constant) such that the zeros of 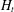$H_{t}$ are all real precisely when 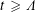$t\geqslant \unicode[STIX]{x1D6EC}$. The Riemann hypothesis is equivalent to the assertion $\unicode[STIX]{x1D6EC}\leqslant 0$, and Newman conjectured the complementary bound 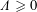$\unicode[STIX]{x1D6EC}\geqslant 0$. In this paper, we establish Newman’s conjecture. The argument proceeds by assuming for contradiction that 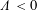$\unicode[STIX]{x1D6EC}<0$ and then analyzing the dynamics of zeros of 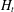$H_{t}$ (building on the work of Csordas, Smith and Varga) to obtain increasingly strong control on the zeros of 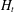$H_{t}$ in the range 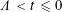$\unicode[STIX]{x1D6EC}<t\leqslant 0$, until one establishes that the zeros of 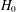$H_{0}$ are in local equilibrium, in the sense that they locally behave (on average) as if they were equally spaced in an arithmetic progression, with gaps staying close to the global average gap size. But this latter claim is inconsistent with the known results about the local distribution of zeros of the Riemann zeta function, such as the pair correlation estimates of Montgomery.

MSC classification

Primary: 11M06: $zeta (s)$ and $L(s, chi)$
Type
Number Theory
Information
Forum of Mathematics, Pi , Volume 8 , 2020 , e6
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2020

References

Abramowitz, M. and Stegun, I.A., Handbook of Mathematical Functions (Dover, New York, 1965).Google Scholar
Bourgain, J., ‘Global wellposedness of defocusing critical nonlinear Schrödinger equation in the radial case’, J. Amer. Math. Soc. 12(1) (1999), 145–171.CrossRefGoogle Scholar
Broughan, K., Equivalents of the Riemann Hypothesis, Vol. 2, Analytic Equivalents, Encyclopedia of Mathematics and its Applications, 165 (Cambridge University Press, Cambridge, 2017).Google Scholar
de Bruijn, N. C., ‘The roots of trigonometric integrals’, Duke J. Math. 17 (1950), 197–226.CrossRefGoogle Scholar
Chang, A., Mehrle, D., Miller, S. J., Reiter, T., Stahl, J. and Yott, D., ‘Newman’s conjecture in function fields’, J. Number Theory 157 (2015), 154–169.CrossRefGoogle Scholar
Conrey, J. B., Ghosh, A., Goldston, D., Gonek, S. M. and Heath-Brown, D. R., ‘On the distribution of gaps between zeros of the zeta-function’, Q. J. Math. 36 (1985), 43–51.CrossRefGoogle Scholar
Conrey, J. B., Ghosh, A. and Gonek, S. M., ‘A note on gaps between zeros of the zeta function’, Bull. Lond. Math. Soc. 16(4) (1984), 421–424.CrossRefGoogle Scholar
Csordas, G., Norfolk, T. S. and Varga, R. S., ‘A lower bound for the de Bruijn–Newman constant 𝛬’, Numer. Math. 52 (1988), 483–497.CrossRefGoogle Scholar
Csordas, G., Odlyzko, A. M., Smith, W. and Varga, R. S., ‘A new Lehmer pair of zeros and a new lower bound for the De Bruijn–Newman constant Lambda’, Electron. Trans. Numer. Anal. 1 (1993), 104–111.Google Scholar
Csordas, G., Ruttan, A. and Varga, R. S., ‘The Laguerre inequalities with applications to a problem associated with the Riemann hypothesis’, Numer. Algorithms 1 (1991), 305–329.CrossRefGoogle Scholar
Csordas, G., Smith, W. and Varga, R. S., ‘Lehmer pairs of zeros, the de Bruijn–Newman constant 𝛬, and the Riemann hypothesis’, Constr. Approx. 10(1) (1994), 107–129.CrossRefGoogle Scholar
Erdős, L., Schlein, B. and Yau, H.-T., ‘Universality of random matrices and local relaxation flow’, Invent. Math. 185(1) (2011), 75–119.CrossRefGoogle Scholar
Ki, H., Kim, Y. O. and Lee, J., ‘On the de Bruijn–Newman constant’, Adv. Math. 22 (2009), 281–306.CrossRefGoogle Scholar
Lehmer, D. H., ‘On the roots of the Riemann zeta-function’, Acta Math. 95 (1956), 291–298.CrossRefGoogle Scholar
Montgomery, H. L., ‘The pair correlation of zeros of the zeta function’, inAnalytic Number Theory (Proceedings of Symposia in Pure Mathematics, Vol. XXIV, St. Louis Univ., St. Louis, MO, 1972) (American Mathematical Society, Providence, RI, 1973), 181–193.Google Scholar
Montgomery, H. L. and Vaughan, R. C., Multiplicative Number Theory. I. Classical Theory, Cambridge Studies in Advanced Mathematics, 97 (Cambridge University Press, Cambridge, 2007).Google Scholar
Newman, C. M., ‘Fourier transforms with only real zeroes’, Proc. Amer. Math. Soc. 61 (1976), 246–251.Google Scholar
Norfolk, T. S., Ruttan, A. and Varga, R. S., A Lower Bound for the de Bruijn–Newman Constant 𝛬 II, (eds. Gonchar, A. A. and Saff, E. B.) Progress in Approximation Theory (Springer, New York, 1992), 403–418.Google Scholar
Odlyzko, A. M., ‘An improved bound for the de Bruijn–Newman constant’, Numer. Algorithms 25 (2000), 293–303.CrossRefGoogle Scholar
Pólya, G., ‘Über trigonometrische Integrale mit nur reelen Nullstellen’, J. Reine Angew. Math. 58 (1927), 6–18.Google Scholar
Polymath, D. H. J., ‘Effective approximation of heat flow evolution of the Riemann 𝜉 function, and a new upper bound for the de Bruijn–Newman constant’, Res. Math. Sci. 6 (2019), 3, Paper No. 31, 67 pp.CrossRefGoogle Scholar
te Riele, H. J. J., ‘A new lower bound for the de Bruijn–Newman constant’, Numer. Math. 58 (1991), 661–667.CrossRefGoogle Scholar
Saouter, Y., Gourdon, X. and Demichel, P., ‘An improved lower bound for the de Bruijn–Newman constant’, Math. Comp. 80 (2011), 2281–2287.CrossRefGoogle Scholar
Stein, E. M. and Shakarchi, R., Complex Analysis, Vol. 2 (Princeton University Press, Princeton, NJ, 2010).Google Scholar
Stopple, J., ‘Notes on Low discriminants the generalized Newman conjecture’, Funct. Approx. Comment. Math. 51(1) (2014), 23–41.CrossRefGoogle Scholar
Stopple, J., ‘Lehmer pairs revisited’, Exp. Math. 26(1) (2017), 45–53.CrossRefGoogle Scholar
Tao, T., Nonlinear Dispersive Equations: Local and Global Analysis, CBMS Regional Conference Series in Mathematics, 106 (American Mathematical Society, Providence, RI, 2006), Published for the Conference Board of the Mathematical Sciences, Washington, DC.CrossRefGoogle Scholar
Tao, T. and Vu, V. H., Additive Combinatorics, Vol. 105 (Cambridge University Press, Cambridge, 2006).CrossRefGoogle Scholar
Titchmarsh, E. C., The Theory of the Riemann Zeta-function, 2nd edn (Oxford University Press, Oxford, 1986), (revised by D. R. Heath-Brown).Google Scholar