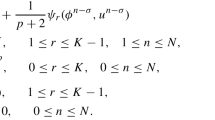On averaged exponential integrators for semilinear wave equations with solutions of low-regularity

Abstract

In this paper we introduce a class of second-order exponential schemes for the time integration of semilinear wave equations. They are constructed such that the established error bounds only depend on quantities obtained from a well-posedness result of a classical solution. To compensate missing regularity of the solution the proofs become considerably more involved compared to a standard error analysis. Key tools are appropriate filter functions as well as the integration-by-parts and summation-by-parts formulas. We include numerical examples to illustrate the advantage of the proposed methods.

1 Introduction

In this paper we are interested in solving abstract wave equations of the form

$$\begin{aligned} q''(t) = - L q(t) + G(t, q(t)),\quad t \in [0,t_{\mathrm {end}}], \quad q(0) = q_0, \quad q'(0) = q'_0, \end{aligned}$$

(1.1)

in some Hilbert space $H$ where L is a positive, self-adjoint operator and G is a sufficiently regular nonlinearity (e.g., Fréchet-differentiable). Such equations arise in many physical models. A prominent example is the cubic wave equation

$$\begin{aligned} \partial _t^2 q(t,x) = \partial _x^2 q(t,x) + q(t,x)^3 , \qquad (t,x) \in [0,t_{\mathrm {end}}] \times I \end{aligned}$$

posed on some interval $I \subseteq {\mathbb {R}}$ and equipped with appropriate initial and boundary conditions.

Our aim is to construct and investigate time integration schemes for (1.1) under physically realistic assumptions, in particular finite energy conditions. Hence, the solution will in general be of low regularity and we thus restrict ourselves to second-order schemes. Clearly, a standard time integrator (e.g., a Runge–Kutta scheme or an exponential integrator) can only be applied to an abstract evolution equation if it is unconditionally stable due to the unbounded operator L.

In the finite dimensional case ($\dim H< \infty$), unconditionally stable integrators (in the sense that L does not cause any restriction on the time step) for this equation were already considered in [8, 12, 17, 24]. Such exponential (or trigonometric) integrators were shown to be second-order convergent while only assuming a finite-energy condition. This was somewhat surprising since usually, second-order (exponential) schemes need two bounded time derivatives of the solution in the error analysis. The key ingredient are certain matrix functions that act as filters. The effect of these filters is that they remove resonances in the local error, which, in contrast to a standard error analysis, enforce cancellation effects in the global error. In fact one can prove that local and global error are of the same order if the filters are chosen appropriately.

Recently, in [2, 3] we presented a completely new technique to prove related results for ordinary differential equations by reformulating a trigonometric integrator as a Strang splitting applied to a modified problem. Using ideas from [20, 21], a specific representation of the local error was derived, which allowed us to separate terms of order three (which can be treated in a standard way) and the leading local error term, which is of order two only. A carefully adapted Lady Windermere’s fan argument is employed to treat these terms in the global error accumulation.

In this paper we prove error bounds for different classes of exponential integrators applied to an evolution equation (1.1) in a unified way. More precisely, we characterize the structure of the defects and the properties of filter functions which allow second-order convergence under a finite-energy condition in different abstract frameworks (i.e., in different function spaces), which define the assumptions on L, G, and the initial data. Within this framework we can handle various boundary conditions.

We point out that our results are not restricted to globally Lipschitz continuous functions G, but also apply to locally Lipschitz ones that satisfy certain growth conditions. Our analysis thus covers the class of nonlinearities for which the existence of a classical solution can be guaranteed. In particular, this includes polynomial nonlinearities up to a certain degree which is determined by the spatial dimension and the corresponding Sobolev embeddings. In the one-dimensional case such equations with periodic boundary conditions and arbitrary high polynomial degree have been studied in [9] for nonlinearities with Lipschitz properties on a whole scale of Sobolev spaces. However, this rich structure is not available in our general framework and, in contrast to our work, well-posedness cannot be guaranteed.

Further work on exponential integration schemes for the time-integration of semilinear wave equations was conducted in [1] where a sine-Gordon equation is studied and the difficulties arise in the proper treatment of a single constant $c\rightarrow \infty$ which induces high oscillations in time. In the paper [10] the approach from [9] was extended and in the one-dimensional case a quasilinear wave equation with periodic boundary conditions was studied. However, they assume smooth coefficients and high regularity for the analysis. Exponential splitting schemes for linear evolution equations have been analyzed in [15]. The error estimates depend on commutator bounds that are not available in our scenario. Finally, we point out that we do not address long-term behavior as in [4, 6].

The paper is organized as follows. In Sect. 2, we give an informal overview over the methods of interest, the main concepts, and the main results and also present numerical examples illustrating the main results of our work. In particular, the necessity of using averaging techniques in the regime of low-regularity is shown.

The informal overview is made rigorous in Sect. 3, where we introduce the analytic framework and a functional calculus which allows us to define the operator-valued filters and ensures well-posedness of the problem as well as of the schemes.

We further state the assumptions on the operator L, the nonlinearity G, and the initial data that on the one hand will guarantee the well-posedness of (1.1) and on the other hand allow to carry out the error analysis.

In Sect. 4 we characterize filter functions which allow to prove that the exact solution of the original problem and the solution of the averaged problem only differ up to terms of order $\tau ^2$, where $\tau >0$ denotes the step size. Section 5 provides a characterization of numerical methods in terms of the structure of their defects, which are necessary to derive error bounds.

Finally, Sects. 6 and 7 contain our main results the error bounds for one-step and for multistep methods, respectively.

2 Informal overview of methods, concepts and results

Before we present the analytical framework necessary to formulate our results rigorously, we first give an informal overview of the methods of interest, the main concepts, and the main results. In the finite dimensional case $\dim H < \infty$ (which is not the situation of interest in this paper), all the approximations presented are well-defined and the statements valid. However, for evolution equations posed in appropriate function spaces, this is no longer true unless additional assumptions are imposed. Since some of them are rather technical, we postpone them to Sect. 3.

2.1 Problem statement: Second-order differential equation

Let L be a linear, self-adjoint, and positive-definite operator on $H$ and $G: [0,t_{\mathrm {end}}] \times H\rightarrow H$. We consider the differential equation

$$\begin{aligned} q''(t) = - L q(t) + G(t, q(t)),\quad t \in [0,t_{\mathrm {end}}], \quad q(0) = q_0, \quad q'(0) = q'_0, \end{aligned}$$

and assume that the solution q satisfies the finite-energy condition

$$\begin{aligned} \langle L q(t), q(t) \rangle _H + \langle q'(t), q'(t) \rangle _H \le K^2 \qquad \text{for } t \in [0,t_{\mathrm {end}}] \,, \end{aligned}$$

(2.1)

where $\langle \cdot ,\cdot \rangle _H$ denotes the inner product on H. In first-order formulation, the differential equation can be written as

$$\begin{aligned} u'(t) = A u(t) + f(t,u(t)) , \qquad u = \begin{pmatrix} q \\ q' \end{pmatrix}, \end{aligned}$$

(2.2)

with

$$\begin{aligned} A = \begin{pmatrix} 0 &{} I \\ -L &{} 0 \end{pmatrix}, \qquad f(t , u) = \begin{pmatrix} 0 \\ G (t, q) \end{pmatrix} \,, \end{aligned}$$

and inner product

$$\begin{aligned} \langle u_1 , u_2 \rangle = \langle q_1 , q_2 \rangle _H + \langle L^{-1} q'_1 , q'_2 \rangle _H \,. \end{aligned}$$

Obviously, A is skew-adjoint with respect to $\langle \cdot ,\cdot \rangle$ and hence has a purely imaginary point spectrum.

2.2 Methods

In the following we shortly present four different types of methods to discretize equation (2.2) in time with a constant stepsize $\tau >0$.

2.2.1 Strang splitting

The exact flows $\varphi _\tau ^A$ and $\varphi _\tau ^{f}$ of the two subproblems

$$\begin{aligned} \begin{pmatrix} t' \\ u' \end{pmatrix} = \begin{pmatrix} 1 \\ A u \end{pmatrix} ,\qquad \begin{pmatrix} t' \\ u' \end{pmatrix} = \begin{pmatrix} 0 \\ f(t,u) \end{pmatrix}, \end{aligned}$$

are given explicitly by

$$\begin{aligned} \varphi _\tau ^A \begin{pmatrix} t_{0} \\ u_{0} \end{pmatrix} = \begin{pmatrix} t_0+ \tau \\ e^{\tau A} u_0 \end{pmatrix} ,\qquad \varphi _\tau ^{f}\begin{pmatrix} t_{0} \\ u_{0} \end{pmatrix} = \begin{pmatrix} t_0 \\ u_0 + \tau f(t_0,u_0) \end{pmatrix} \,. \end{aligned}$$

We consider the Strang splitting in the variants $\bigl (A,f,A\bigr )$ and $\bigl (f,A,f\bigr )$ given by

$$\begin{aligned} \begin{pmatrix} t_{n+1} \\ u_{n+1} \end{pmatrix}&= \varphi _{\tau / 2}^A \circ \varphi _\tau ^{f} \circ \varphi _{\tau / 2}^A \begin{pmatrix} t_{n} \\ u_{n} \end{pmatrix} \,, \end{aligned}$$

(2.3a)

$$\begin{aligned} \begin{pmatrix} t_{n+1} \\ u_{n+1} \end{pmatrix}&= \varphi _{\tau / 2}^{f} \circ \varphi _\tau ^A \circ \varphi _{\tau / 2}^{f} \begin{pmatrix} t_{n} \\ u_{n} \end{pmatrix} \,, \end{aligned}$$

(2.3b)

respectively. Note that the $\bigl (f,A,f\bigr )$variant (2.3b) is equivalent to a trigonometric integrator without filter functions, see, e.g., [13, XIII.2.2].

2.2.2 Corrected Lie Splitting

Next we consider the second-order corrected Lie splitting given by

$$\begin{aligned} \begin{aligned} u_{n+1}&= e^{\tau A} \bigl ( u_n + \tau f\big ( t_{n+1/2}, u_n \big ) + \tfrac{\tau ^2}{2} r \big ( t_{n+1/2}, u_n \big ) \bigr ) \end{aligned} \end{aligned}$$

(2.4)

with the correction term

$$\begin{aligned} r(t , u) :=J_{f}\big ( t , u \big ) \begin{pmatrix} 0 \\ A u \end{pmatrix} - Af\big (t , u \big ) . \end{aligned}$$

It is inspired by a fourth-order method of this type proposed in [22, 4.9.3 (c)]. Note that in the linear case, where $f(t,u) = F u$, the correction term reduces to the commutator

$$\begin{aligned} r (t , u) = F A u - A F u = \left[ F, A \right] u \, . \end{aligned}$$

Hence, one can consider (2.4) as an approximation to the method

$$\begin{aligned} u_{n+1} = e^{\tau A} e^{\tau F} e^{\tfrac{\tau ^2}{2} \left[ F, A \right] } u_n \,, \end{aligned}$$

which was considered in [26, (3.37)].

2.2.3 Exponential Runge–Kutta methods

General two-stage exponential Runge–Kutta methods are of the form

$$\begin{aligned} \begin{aligned} {U_n}=&\; e^{c_2 \tau A } u_n + c_2 \tau \varphi _1( c_2 \tau A ) f\big (t_n, u_n\big ), \\ u_{n+1} =&\; e^{\tau A } u_n + \tau b_1(\tau A ) f\big (t_n, u_n\big ) + \tau b_2(\tau A ) f\big (t_n + c_2 \tau , {U_n}\big ) \,, \end{aligned} \end{aligned}$$

(2.5)

where $c_2 \in (0,1]$ is a given quadrature node. Recall that the $\varphi$-functions are defined as

$$\begin{aligned} \varphi _{k+1} (z) :=\int \limits _0^1 e^{(1-s) z } \frac{s^k}{k !} \,ds,\quad k \ge 0. \end{aligned}$$

If the coefficient functions $b_1,b_2$ satisfy

$$\begin{aligned} \begin{aligned} b_1(z) + b_2(z)&= \varphi _1(z), \qquad c_2 b_2(0)&= \frac{1}{2} \,, \end{aligned} \end{aligned}$$

the method is second-order convergent for parabolic problems, see [18, Theorem 4.3.]. Popular choices are $c_2 = \frac{1}{2}$, $b_1 = 0$ or $c_2 = 1$, $b_2(z) = \varphi _2(z)$. All our results also apply to the symmetric, but implicit exponential Runge–Kutta scheme from [5, Example 2.1] and to ERKN methods, e.g., those considered in [28]. The necessary modifications are straightforward so that we omit the details.

2.2.4 Exponential multistep methods

The two-step exponential multistep method from [19, (2.7)]

$$\begin{aligned} \begin{aligned} u_{n+1} =&\; e^{\tau A} u_n+\tau \varphi _1(\tau A) f\left( t_n, u_n \right) \\&+\tau \varphi _2(\tau A) \left( f\left( t_n, u_n \right) - f\left( t_{n-1}, u_{n-1} \right) \right) , \quad n\ge 1 \,, \\ u_1 =&\; e^{\tau A} \left( u_0 + \tau f\left( t_0, u_0 \right) \right) \,, \end{aligned} \end{aligned}$$

(2.6)

is derived from the variation-of-constants formula for the exact solution of (1.1) by approximating the nonlinearity f in the integral term by an interpolation polynomial using the last two approximations $u_{n-1}, u_n$.

In a similar manner we consider a method that was used in [7, (B 4)], namely

$$\begin{aligned} \begin{aligned} u_{n+1}&= e^{2 \tau A} u_{n-1} + 2 \tau e^{ \tau A} f( t_n, u_n) \,, \\ u_1&= e^{\tau A} \bigl ( u_0 + \tau f( t_0, u_0) \bigr ) \,. \end{aligned} \end{aligned}$$

(2.7)

For $A = 0$ it reduces to an explicit Nyström method, cf. method (1.13’) in [14].

2.3 Averaged differential equation

Let $\chi = \phi ,\psi :i {\mathbb {R}}\rightarrow {\mathbb {R}}$ be even (i.e., $\chi (-z) = \chi (z)$) and analytic functions satisfying $\chi (0) = 1$. Then we define

$$\begin{aligned} {\widetilde{\chi }}= \chi ( i \tau L^{1/2}) \end{aligned}$$

and an averaged nonlinearity

$$\begin{aligned} {\widetilde{G}}(t,q) :={\widetilde{\psi }}G(t, {\widetilde{\phi }}q) \, . \end{aligned}$$

Using the block diagonal operators

$$\begin{aligned} \varPhi = \begin{pmatrix} {\widetilde{\phi }}&{} 0 \\ 0 &{} {\widetilde{\phi }}\end{pmatrix}, \qquad \varPsi = \begin{pmatrix} {\widetilde{\psi }}&{} 0 \\ 0 &{} {\widetilde{\psi }}\end{pmatrix} \,, \end{aligned}$$

we consider the averaged differential equation

$$\begin{aligned} {\widetilde{u}}'(t) = A {\widetilde{u}}(t) + {\widetilde{f}}(t,{\widetilde{u}}(t)), \qquad {\widetilde{f}}(t , {\widetilde{u}}) = \varPsi f(t , \varPhi {\widetilde{u}}) = \begin{pmatrix} 0 \\ {\widetilde{G}}(t, {\widetilde{q}}) \end{pmatrix} \,. \end{aligned}$$

(2.8)

The averaging is done such that the solution ${\widetilde{u}}$ of (2.8) also satisfies a finite-energy condition (2.1) (with a modified constant ${\widetilde{K}}$, which is independent of $\tau$ and n, cf., Lemma 4.2 below). In Theorem 4.1, we provide sufficient conditions on $\psi , \phi$ such that

$$\begin{aligned} \left\Vert u(t)-{\widetilde{u}}(t) \right\Vert \le C \tau ^2, \qquad t \in [0,t_{\mathrm {end}}], \end{aligned}$$

where $\left\Vert \cdot \right\Vert$ denotes the norm induced by $\langle \cdot ,\cdot \rangle$.

Remark 2.1

We only consider fixed stepsizes in this paper. Introducing variable stepsizes would require the investigation of a whole family of averaged problems (2.8). In addition, our analysis below would involve a much higher technical effort.

2.4 Averaged methods

The main idea is to apply one of the numerical methods to the averaged equation (2.8) instead of the original one (2.2). Equivalently, one could modify the numerical scheme in an appropriate way using filter functions. This is illustrated in Fig. 1.

Fig. 1

Different ways to construct an approximation $u_n$ of the solution $u(t_n)$ of the original equation (2.2) and the solution ${\widetilde{u}}(t_n)$ of the averaged equation (2.8)

Since the solutions of (2.2) and (2.8) only differ by terms of order $\tau ^2$, one might hope for second-order accuracy if the method is of order two at least. In fact we will later see that in the case of evolution equations, this intuition is not always justified, i.e., order reduction might appear. The main goal in this paper is to characterize the numerical methods, the assumptions on L and G, and the choice of the filter functions which lead to second-order error bounds.

2.5 Main results

Our main results, which are detailed in Theorem 6.2 for exponential one-step methods and in Sect. 7 for exponential multistep methods, are the following error bounds.

• (a) The Strang splitting, the exponential Runge–Kutta, and the exponential multistep methods applied to the original equation (2.2) satisfy

  $$\begin{aligned} \Vert u(t_n) -u_n \Vert \le C_1 \tau \,. \end{aligned}$$

• (b) All methods of Sect. 2.2 applied to the averaged equation (2.8) with appropriate filters $\phi ,\psi$ satisfy

  $$\begin{aligned} \Vert u(t_n) -u_n \Vert \le C_2 \tau ^2 \,. \end{aligned}$$

The constants $C_1, C_2$ only depend on the initial value $u_0$, the finite energy K, properties of G, and $t_{\mathrm {end}}$, but not on n and $\tau$.

The strategy to prove these bounds is to split the error into two terms, namely

$$\begin{aligned} \left\Vert u(t_n)-u_n \right\Vert \le \left\Vert u(t_n)-{\widetilde{u}}(t_n) \right\Vert + \left\Vert {\widetilde{u}}(t_n)-u_n \right\Vert . \end{aligned}$$

(2.9)

The first term is bounded by Theorem 4.1, the second by Theorem 6.1 or Corollaries 7.1, and 7.2, respectively. A crucial step is to show that the averaged solution inherits the regularity of the original solution, which is done in Lemma 4.2.

2.6 Numerical example

In this section we illustrate the effect of averaging within numerical methods by approximating the solution of a variant of the sine-Gordon equation given on the torus ${\mathbb {T}}= {\mathbb {R}}/ ( 2 \pi {\mathbb {Z}})$ by

$$\begin{aligned} q''(t) = \varDelta q (t) - q (t) + m_a \sin ( m_i \, q(t) ) \, q(t), \end{aligned}$$

(2.10)

with $t \in [0,1]$ and $m_i,m_a \in L^{\infty }({\mathbb {T}})$. Note that for $q \in L^2({\mathbb {T}})$ and

$$\begin{aligned} G(q) (x) :=m_a(x) \sin ( m_i(x) \, q ) \, q \,, \end{aligned}$$

we have G(q) in $L^2({\mathbb {T}})$, but even for $q \in H^1({\mathbb {T}})$ we cannot expect $G(q) \in H^\epsilon ({\mathbb {T}})$ for any $\epsilon >0$. Hence, the analysis of [9, 10] does not apply to such non-smooth nonlinearities. For the spatial discretization, we used a Fourier spectral method in order to control the regularity of the solution. The initial values $(q_0,v_0) \in H^1({\mathbb {T}}) \times L^2({\mathbb {T}})$ are constructed such that

$$\begin{aligned} (q_0,v_0)\in H^{1}({\mathbb {T}}) \times L^2({\mathbb {T}}) \setminus H^{1+\epsilon }({\mathbb {T}}) \times H^{\epsilon }({\mathbb {T}}) \end{aligned}$$

for $\epsilon = 10^{-6}$, see [16] for details.

Fig. 2

Discrete $L^\infty \Big ( [0,1],L^2({\mathbb {T}}) \times H^{-1} ({\mathbb {T}})\Big )$ error (on the y-axis) of the numerical solution of (2.10) plotted against the step size $\tau$ (on the x-axis) with N grid points. The gray lines indicate order one (dotted) and two (dashed)

In Fig. 2 we computed the approximate solution with the Strang splitting variant (2.3a), i.e., $\bigl (A,{\widetilde{f}},A\bigr )$, with filters (blue, dots)

$$\begin{aligned} \phi (z) = \psi (z) = \mathop {\mathrm {sinhc}}(\tfrac{z}{2}) = \tfrac{1}{2} \Big ( \varphi _1(\tfrac{z}{2}) + \varphi _1(- \tfrac{z}{2}) \Big ) \end{aligned}$$

(2.11)

and without filters, i.e., $\phi =\psi =1$, (red, crosses) with $N= 2^j$, $j=9,10,11$, spatial grid points. The codes are available from the authors on request. We observe order reduction of the non-averaged scheme to order one in the stiff regime, while in the non-stiff regime, the two errors of both schemes are quite close. The non-stiff regime is characterized by time steps $\tau$ for which $\varphi _1(\tau A)$ is invertible for all $\tau < \tau _0$. Since $\left\Vert A \right\Vert \approx N/2$, this is true for $\tau _0 \approx 4 \pi / N$. For abstract evolution equations, only the stiff regime is relevant, i.e., the limit $N\rightarrow \infty$.

3 Analytical framework

We fix some notation for the rest of the paper. For Hilbert spaces X, Y, $\langle \cdot ,\cdot \rangle \,=\,\langle \cdot ,\cdot \rangle _X$ denotes the scalar product on X and ${\mathcal {B}}(X,Y)$ the set of all bounded operators $T:X\rightarrow Y$ equipped with the standard operator norm $\Vert T \Vert _{Y\leftarrow X}$. Further, $C^k (X,Y)$ is the space of all k-times Fréchet-differentiable functions from X to Y. We write $W^{k,p}(\varOmega )$, $k\in {\mathbb {N}}_0$, $1\le p \le \infty$, for the Sobolev space of order k with all (weak) derivatives in $L^p(\varOmega )$ and abbreviate $H^k(\varOmega ) :=W^{k,2}(\varOmega )$. For multi-indices $\alpha ,\beta \in {\mathbb {N}}^\ell$ we write $\alpha \le \beta$ if $\alpha _i \le \beta _i$ for all $i=1,\dots ,\ell$.

3.1 Second-order equation

Let H be a real, separable Hilbert space and $L :{\mathcal {D}}(L) \subseteq H \rightarrow H$ be a positive, self-adjoint operator with compact resolvent. We consider the abstract second-order evolution equation (1.1) in H. To reformulate it as a first-order system we use the intermediate space $V = {\mathcal {D}}(L^{1/2})$ with

$$\begin{aligned} {\mathcal {D}}(L)\hookrightarrow V\hookrightarrow H, \qquad \left\Vert v \right\Vert _{V} = \left\Vert L^{1/2} v \right\Vert _{H} , \end{aligned}$$

with dense and compact embeddings, in particular, there is a constant $C_{\rm emb}$ such that

$$\begin{aligned} \left\Vert v \right\Vert _{H} \le C_{\rm emb}\left\Vert v \right\Vert _{V} , \ v \in V, \qquad \left\Vert q \right\Vert _{V} \le C_{\rm emb}\left\Vert q \right\Vert _{{\mathcal {D}}(L)} , \ q \in {\mathcal {D}}(L)\,. \end{aligned}$$

(3.1)

We exemplify the abstract framework considered in the rest of the paper by a class of semilinear wave equations.

Example 3.1

We consider the semilinear evolution equation (1.1) in the following setting:

• (a) $\emptyset \ne \varOmega \subseteq {\mathbb {R}}^d$ is a convex, bounded Lipschitz domain with $d\in \{1,2,3\}$.

• (b) $L = -\mathop {\mathrm {div}} ( {\mathbf {A}} \nabla )$ with uniformly positive definite ${\mathbf {A}}\in L^{\infty }(\varOmega )^{d\times d}$.

• (c) For $g :[0,t_{\mathrm {end}}] \times \varOmega \times {\mathbb {R}}\rightarrow {\mathbb {R}}$ there is some $\alpha = ( \alpha _t , \alpha _x, \alpha _y ) \in {\mathbb {N}}^3$ such that all partial derivatives $\partial ^\beta g$, $\beta \le \alpha$, exist, are continuous in t and y and bounded in x.

• (d) There is $\gamma >1$ and a constant $C_\text{g}>0$ such that for all $(t,x,y) \in [0,t_{\mathrm {end}}] \times \varOmega \times {\mathbb {R}}$ we have

  $$\begin{aligned} \begin{aligned} | g(t,x,y) | , |\partial _t g(t,x,y) |&\le C_\text{g} \bigl (1 + |y|^\gamma \bigr ) \,, \\ |\partial _y g(t,x,y) |&\le C_\text{g} \bigl (1 + |y|^{\gamma -1} \bigr ) \,. \end{aligned} \end{aligned}$$

  (3.2a)

  For the corrected Lie Splitting (2.4) we assume in addition

  $$\begin{aligned} |\partial _{yy} g(t,x,y) | & \le C_\text{g} \bigl (1 + |y|^{\gamma -1} \bigr ). \end{aligned} $$

  (3.2b)

  For $(t,x) \in [0t_{\mathrm {end}}] \times \varOmega$ and $q \in V$ we define

  $$\begin{aligned} G(t,q) (x) :=g(t,x,q(x)) . \end{aligned}$$

In Table 1 at the end of this section, details for different choices of H are presented for these problems.

In the following we recall sufficient conditions on the nonlinearity G to guarantee well-posedness of the equation and to establish the error analysis presented in Sects. 4, 5, 6, and 7.

Assumption 3.2

(Well-posedness) For G we have $G \in C^1([0,t_{\mathrm {end}}] \times V, H)$, i.e., G is Fréchet-differentiable with Fréchet-derivative $J_{G}(t,q) \in {\mathcal {B}}\bigl ([0,t_{\mathrm {end}}] \times V, H\bigr )$ for all $q \in V, t\in [0,t_{\mathrm {end}}]$.

The most subtle assumption is given now. It states the necessary regularity for G evaluated at a sufficiently smooth function.

Assumption 3.3

(Regularity of G evaluated at a smooth function) For $q \in C^1([0,t_{\mathrm {end}}] , V) \cap C([0,t_{\mathrm {end}}] , {\mathcal {D}}(L))$ we have

$$\begin{aligned}&t \,\,\mapsto\, \,G(t,q(t)) \in C^1 \left( [0,t_{\mathrm {end}}], V\right) \text{ with } \frac{d}{dt} G(t,q(t)) = J_{G}(t,q(t)) \begin{pmatrix} 1 \\ q'(t) \end{pmatrix} \,, \\&t \,\,\mapsto\, \,J_{G}(t,q(t)) \in C^1 \left( [0,t_{\mathrm {end}}], {\mathcal {B}}\left( [0,t_{\mathrm {end}}] \times V, H\right) \right) \text{ with }C>0\text{ such that } \quad \\ \end{aligned}$$

(A1)

$$\begin{aligned} \Big \Vert \frac{d}{dt} J_{G}(t,q(t)) \Big \Vert _{ H\leftarrow [0,t_{\mathrm {end}}] \times V} \le C,\quad C = C \left( \left\Vert q(t) \right\Vert _{{\mathcal {D}}(L)} , \left\Vert q'(t) \right\Vert _{V} \right) \end{aligned}$$

(A2)

The next assumption states bounds of G and $J_{G}$. We point out that the dependency of the constants arising from different radii is crucial for the error analysis.

Assumption 3.4

(Regularity of G) There are constants $C = C(r)$ such that for given $r_V,r_L>0$ and q with $\left\Vert q \right\Vert _{V} \le r_V$, $\left\Vert q \right\Vert _{{\mathcal {D}}(L)} \le r_L$, $p \in V$, and $t\in [0,t_{\mathrm {end}}]$ the following inequalities are satisfied:

$$\begin{aligned} \left\Vert G(t,q) \right\Vert _{V}&\le C(r_L), \end{aligned}$$

(A3)

$$\begin{aligned} \Big \Vert J_{G}(t,q) \begin{pmatrix} s \\ p \end{pmatrix} \Big \Vert _{H}&\le C(r_V) \left( \left| s \right| + \left\Vert p \right\Vert _{V} \right) , \end{aligned}$$

(A4a)

$$\begin{aligned} \Big \Vert J_{G}(t,q) \begin{pmatrix} s \\ p \end{pmatrix} \Big \Vert _{V}&\le C(r_L) \left( \left| s \right| + \left\Vert p \right\Vert _{V} \right) . \end{aligned}$$

(A4b)

For the corrected Lie Splitting (2.4) we assume in addition for $\left\Vert p_i \right\Vert _{V} \le r_{V}, \; i= 1, \; 2,$

$$\begin{aligned} \Big \Vert (J_{G}(t,{p_{1}} - J_{G}(t,{p_{2}}) \begin{pmatrix} 0 \\ q \end{pmatrix} \Big \Vert _{H}&\le C(r_{L}, r_{V}) \left\Vert {{p_{1}} - {p_{2}}} \right\Vert _{V} . \end{aligned}$$

Remark 3.5

Note that shifting G to $G + c I$ for some $c\in {\mathbb {R}}$ does not affect the validity of Assumptions 3.2 to 3.4. Hence, we can also treat positive semidefinite operators L by applying a shift.

In Table 1 the main example 3.1 is specified more precisely. We collected three examples where we stated for a given Hilbert space $H$ the dimension d of the domain $\varOmega$ and additional assumptions on the data such that Assumptions 3.2 to 3.4 are satisfied. All examples are posed with homogeneous Dirichlet boundary conditions. By possibly shifting L, we can also treat Neumann, Robin, or periodic boundary conditions.

Higher order Sobolev spaces $H= H^k(\varOmega )$, $k\ge 2$, can be handled as well but the spaces and conditions for the operators and parameters become more complicated.

Table 1 Overview on examples

Remark 3.6

Note that from Assumption 3.2 and the chain rule one can only conclude that

$$\begin{aligned} t \,\,\mapsto\,\, G(t,q(t)) \in C^1 \left( [0,t_{\mathrm {end}}], H\right) \end{aligned}$$

instead of (A1).

• (a) In Example 3.1 the additional regularity $q \in C([0,t_{\mathrm {end}}] , {\mathcal {D}}(L))$ is sufficient to verify the Assumption (A1).

• (b) For $G \in C^1([0,t_{\mathrm {end}}] \times V, V)$ the chain rule immediately yields Assumption (A1). However, in Example 3.1 with $H = H^{-1}(\varOmega )$ and $V = L^2(\varOmega )$, this would imply that G is already affine-linear, see [11, Sect. 3]. Hence, not even the function $q \,\mapsto\, \sin (q)$ would be covered by the analysis.

3.2 First-order equation

We consider the first-order formulation (2.2) of equation (1.1) on the separable Hilbert space $X= V\times H$. The skew-adjoint operator A is given on its domain ${\mathcal {D}}(A) = {\mathcal {D}}(L) \times V$. Hence, A is the generator of a unitary group $\left( e^{t A} \right) _{t\in {\mathbb {R}}}$. We call u a classical solution of (2.2) on $[0,t^*)$ if u solves (2.2), $u(0) = u_0$, and

$$\begin{aligned} u \in C^1([0,t_{\mathrm {end}}] , X) \cap C([0,t_{\mathrm {end}}] , {\mathcal {D}}(A)) \end{aligned}$$

(3.3)

for any $t_{\mathrm {end}}< t^*$. The Assumptions 3.2 to 3.4 are translated into this setting by means of the following three lemmas. The first one provides a classical solution of (2.2) by standard semigroup theory. All statements in the lemmas directly follow from the special structure of f and the assumptions in Sect. 3.1.

Lemma 3.7

(Well-posedness) Let G satisfy Assumption 3.2. Then $f:[0,t_{\mathrm {end}}] \times X\rightarrow X$ defined in (2.2) satisfies $f\in C^1([0,t_{\mathrm {end}}] \times X, X)$ with Fréchet derivative $J_{f}\bigl ( t, u \bigr ) \in {\mathcal {B}}\left( [0,t_{\mathrm {end}}] \times X, X\right)$ for all $u \in X$ and $t\in [0,t_{\mathrm {end}}]$.

The following lemma shows differentiability of f in the stronger ${\mathcal {D}}(A)$ norm.

Lemma 3.8

(Regularity of $f$ evaluated at a smooth function) Let G satisfy Assumption 3.3and u satisfy (3.3). Then we have

$$\begin{aligned} t&\,\,\mapsto\,\, f\bigl ( t, u(t) \bigr ) \in C^1 \left( [0,t_{\mathrm {end}}], {\mathcal {D}}(A)\right) \text{ with } \frac{d}{dt}\,\, f\bigl ( t, u(t) \bigr ) = J_{f}\bigl ( t, u(t) \bigr ) \begin{pmatrix}1 \\ u'(t) \end{pmatrix} \end{aligned}$$

(A1′)

$$\begin{aligned} t&\,\,\mapsto\,\, J_{f}\bigl ( t, u(t) \bigr ) \in C^1 \left( [0,t_{\mathrm {end}}], {\mathcal {B}}\left( [0,t_{\mathrm {end}}] \times X, X\right) \right) \text{ with }C>0\text{ such that } \\&\Big \Vert \frac{d}{dt} J_{f}\bigl ( t, u(t) \bigr ) \Big \Vert _{X\leftarrow [0,t_{\mathrm {end}}] \times X} \le C \left( \left\Vert A u(t) \right\Vert , \left\Vert u'(t) \right\Vert \right) \,. \end{aligned}$$

(A2′)

The next Lemma contains two Lipschitz properties of f which easily follow from the corresponding bound on the derivative. They are crucial for the forthcoming error analysis.

Lemma 3.9

(Regularity of $f$) Let G satisfy Assumption 3.4. Then there are constants $C = C(r)$ such that for given $r_X,r_A>0$ and $u_i$ with $\left\Vert u_i \right\Vert \le r_X$, $\left\Vert u_i \right\Vert _{{\mathcal {D}}(A)} \le r_A$, $i=1,2$, $v \in X$, and $t\in [0,t_{\mathrm {end}}]$ the following inequalities are satisfied:

$$\begin{aligned} \left\Vert f(t,u_1) \right\Vert _{{\mathcal {D}}(A)}&\le C(r_A) , \end{aligned}$$

(A3′)

$$\begin{aligned} \Big \Vert J_{f}(t,u_1) \begin{pmatrix} s \\ v \end{pmatrix} \Big \Vert&\le C(r_X) \left( \left| s \right| + \left\Vert v \right\Vert \right) , \end{aligned}$$

(A4a′)

$$\begin{aligned} \Big \Vert J_{f}(t,u_1) \begin{pmatrix} s \\ v \end{pmatrix} \Big \Vert _{{\mathcal {D}}(A)}&\le C(r_A) \left( \left| s \right| + \left\Vert v \right\Vert \right) , \end{aligned}$$

(A4b′)

$$\begin{aligned} \Big \Vert f(t,u_1) - f(t,u_2) \Big \Vert&\le C\left( r_X\right) \left\Vert u_1-u_2 \right\Vert , \end{aligned}$$

(A5a′)

$$\begin{aligned} \left\Vert f(t,u_1) - f(t,u_2) \right\Vert _{{\mathcal {D}}(A)}&\le C\left( r_A \right) \left\Vert u_1-u_2 \right\Vert . \end{aligned}$$

(A5b′)

For the corrected Lie Splitting (2.4) we further have for $\left\Vert v_i \right\Vert \le r_X$, $i=1,2,$

$$\begin{aligned} \Big \Vert \left(J_{f}(t,v_1) - J_{f}(t,v_2)\right) \begin{pmatrix} 0 \\ u_{1} \end{pmatrix} \Big \Vert &\le C\left( r_A, r_X \right) \left\Vert v_1-v_2 \right\Vert . \end{aligned}$$

Lemma 3.7 guarantees local well-posedness of (2.2), see [23, Thm. 6.1.5]. Our error analysis only requires assumptions on the data, which then implies the following regularity of the solution.

Proposition 3.10

Let Assumption 3.2be satisfied and take an initial value $u_0\,\in \,{\mathcal {D}}(A)$. Then there exists a time $t^* > 0$ and a classical solution of (2.2) on $[0,t^* )$ satisfying (3.3). Hence, for every $0<t_{\mathrm {end}}<t^*$ there exists a constant $K>0$ with

$$\begin{aligned} \max \, \left\{ \left\Vert Au (t) \right\Vert , \left\Vert u'(t) \right\Vert \right\} \le K, \qquad t \in [0,t_{\mathrm {end}}] . \end{aligned}$$

(3.4)

In the following we refer to (3.4) as the generalized finite-energy condition.

Remark 3.11

• (a) Note that for $u=\bigl (q, q' \bigr )$ in the situation of Example 3.1 with $H = H^{-1}(\varOmega )$, the generalized finite energy condition implies

  $$\begin{aligned} \left\Vert Au (t) \right\Vert ^2 = \left\Vert q \right\Vert _{{\mathcal {D}}(L)} ^2 + \left\Vert q' \right\Vert _{V} ^2 = \big \Vert {\mathbf {A}}^{1/2} \, \nabla q \big \Vert _{L^2} ^2 + \left\Vert q' \right\Vert _{L^2} ^2 \le K^2 \,. \end{aligned}$$

  This corresponds to the finite energy condition used in [8, 12, 17, 24].

• (b) The bound (3.4) also implies

  $$\begin{aligned} \left\Vert u' (t) \right\Vert ^2 = \left\Vert q' \right\Vert _{V} ^2 + \left\Vert q'' \right\Vert _{H} ^2 \le K^2 \,. \end{aligned}$$

3.3 Filter

From the compact resolvent property of L and the compact embeddings we can infer that also A has a compact resolvent. Hence, A admits an orthonormal basis of eigenvectors

$$\begin{aligned} (\phi _k)_{k\in M}, \quad A \phi _k = i \lambda _k \phi _k, \quad \phi _k \in \bigcap \limits _{j\in {\mathbb {N}}} {\mathcal {D}}(A^j) \,, \end{aligned}$$

where $M\subseteq {\mathbb {N}}$ and $\lambda _k \in {\mathbb {R}}$. Any $x\in X$ can thus be represented as

$$\begin{aligned} x = \sum \limits _{k \in M} \alpha _k \phi _k, \quad \alpha _k = \langle x, \phi _k \rangle _{X} \,, \end{aligned}$$

with the equivalence

$$\begin{aligned} x \in {\mathcal {D}}(A) \iff \sum \limits _{k \in M} | \lambda _k \alpha _k |^2 <\infty \,. \end{aligned}$$

This enables us to define the following functional calculus on the set

$$\begin{aligned} {\mathcal {C}}_b \left( i {\mathbb {R}}\right) :=\{ h :i {\mathbb {R}}\rightarrow {\mathbb {C}}\mid h \text{ is continuous and }\Vert h\Vert _{\infty } < \infty \} \,, \end{aligned}$$

see [25, Theorem 5.9]. It leads to the following properties of operator functions.

Theorem 3.12

Let $A:{\mathcal {D}}(A) \rightarrow H$ be a skew-adjoint operator on a separable Hilbert space $X$ with compact resolvent. Then the map $\varPsi _A :{\mathcal {C}}_b \left( i {\mathbb {R}}\right) \rightarrow {\mathcal {L}}(X)$,

$$\begin{aligned} h \,\mapsto\, {\left\{ \begin{array}{ll} h(A):X\rightarrow X\\ x = \sum \limits _{k \in M} \alpha _k \phi _k \,\mapsto\, h(A)x = \sum \limits _{k \in M} h(i \lambda _k) \alpha _k \phi _k \end{array}\right. } \end{aligned}$$

satisfies the following properties:

• (a) $\varPsi _A$ is linear

• (b) $\left\Vert h(A) \right\Vert _{X\leftarrow X} \le \Vert h\Vert _\infty$

• (c) $(g h) (A) = g(A) h(A)$

• (d) For $x\in {\mathcal {D}}(A)$ it holds $h(A)x \in {\mathcal {D}}(A)$ and $A h(A)x = h(A) Ax$

For the construction of the integrators we make use of filter functions.

Definition 3.13

Let $\chi \in {\mathcal {C}}_b \left( i {\mathbb {R}}\right)$. We call $\chi$ a filter of order m, $m=1,2$, if the following properties are satisfied. There exist $\vartheta , \varTheta \in {\mathcal {C}}_b \left( i {\mathbb {R}}\right)$ such that for all $z\in i{\mathbb {R}}$

$$\begin{aligned} |\chi (z)|&\le 1 \,, \end{aligned}$$

(F1)

$$\begin{aligned} 1 - \chi (z)&= z^m \vartheta (z) \,, \end{aligned}$$

(F2)

$$\begin{aligned} z \chi (z)&= (e^{z} - 1) \varTheta (z)\,. \end{aligned}$$

(F3)

In addition, for $m=2$, $\chi$ is symmetric, i.e.

$$\begin{aligned} \chi (z)&= \chi (-z) \,. \end{aligned}$$

(F4)

Note that (F3) is equivalent to $\chi (z) = \varphi _1(z) \varTheta (z)$.

By Theorem 3.12 we can define a corresponding class of filter operators that we later use in the averaged schemes.

Theorem 3.14

Let $\tau >0$ and $\chi \in {\mathcal {C}}_b \left( i {\mathbb {R}}\right)$ be a filter of order m with $\vartheta ,\varTheta$ from Definition 3.13. Then we have

$$\begin{aligned} \begin{array}{llll} & {Boundedness:}& \quad \Vert \chi ( \tau A) \Vert_{X\leftarrow X} \le 1& \qquad \qquad \mathrm{(OF1)} \\ & & \quad \left\Vert \vartheta ( \tau A) \right\Vert _{X\leftarrow X} \le \Vert \vartheta \Vert _\infty , \quad \left\Vert \varTheta ( \tau A) \right\Vert_{X\leftarrow X} \le \Vert \varTheta \Vert _\infty & \\ & {Smoothing:} & \quad \chi (\tau A) :X\rightarrow {\mathcal {D}}(A)\, { is\, continuous\, with}& \qquad \qquad \mathrm{(OF2)}\\ & & \quad \left\Vert \tau A \chi ( \tau A) \right\Vert _{X\leftarrow X} \le 2 \, \Vert \varTheta \Vert _\infty & \\ & {Consistency:}& \quad \vartheta (\tau A) :X\rightarrow {\mathcal {D}}(A^m),& \\ & & \quad I - \chi (\tau A) = \left( \tau A \right) ^m \vartheta (\tau A)& \qquad \qquad \mathrm{(OF3)}\\ & {Cancelation:}& \quad (\tau A) \chi (\tau A) = (e^{\tau A} - I) \varTheta (\tau A) & \qquad \qquad \mathrm{(OF4)}\\ & {Block\, structure:}& \quad {For} \; m=2 \,{ and }\, i\in \{1,2\},& \\ & & \quad \pi _i x = 0 \ { implies } \ \pi _i \chi (\tau A)x = 0.& \qquad \qquad \mathrm{(OF5)}\\ \end{array} \end{aligned}$$

Here, $\pi _i:X\rightarrow X$ denotes the projection onto the i-th component.

Proof

The properties (OF1), (OF3), (OF4) directly follow from the functional calculus and (OF2) is a direct consequence of (OF4). To prove (OF5), we use the fact that we can approximate $\chi$ uniformly on $i{\mathbb {R}}$ by even rational functions as $\lim _{x\rightarrow \pm \infty } \chi (i x)=\,0$, see [27, Sect. 1.6]. Hence, the assertion is true since it is easily verified for functions of the type

$$\begin{aligned} z\,\mapsto\, \frac{z^2}{z^2 - \delta },\qquad z\,\mapsto\, \frac{1}{z^2 - \delta } \end{aligned}$$

with some $\delta > 0$. $\square$

Remark 3.15

• (a) An example for $m=2$ is the short average filter proposed in [8] that we used in (2.11). We note that in this example $\chi (i x) = \mathop {\mathrm {sinc}}(\tfrac{x}{2})$ holds for all $x\in {\mathbb {R}}$, which relates our filters to the ones considered in [13, Chapter XIII.].

• (b) We further obtain $\left\Vert \tau A \vartheta (\tau A) \right\Vert _{X\leftarrow X}^2 \le 2 \Vert \vartheta \Vert _\infty$ for $m=2$ as

  $$\begin{aligned} |z \vartheta (z)|^2 = |z^2 \vartheta (z)| \, |\vartheta (z)| \le 2 \Vert \vartheta \Vert _\infty \quad \text{for all} \quad z\in i{\mathbb {R}}\,. \end{aligned}$$

4 Averaged problem

In this section we bound the difference between the solution ${\widetilde{u}}$ of the averaged equation (2.8) and the solution u of (2.2). Note that by Proposition 3.10, a unique classical solution ${\widetilde{u}}$ of (2.8) exists since the assumptions on $f$ also hold for ${\widetilde{f}}$.

In order to apply (A5a′) we define $r_X$ via

$$\begin{aligned} \max \limits _{t\in [0,t_{\mathrm {end}}] } \left\Vert u(t) \right\Vert \le C_{\rm emb}K =:\,\,\tfrac{1}{2} r_X \end{aligned}$$

with $C_{\rm emb}$ defined in (3.1) and K in (2.1).

Theorem 4.1

Let Assumptions 3.2, to 3.4be valid and consider the averaged nonlinearity ${\widetilde{f}}$ defined in (2.8) with second-order filters. Then there is a $\tau _0>0$ and a constant $C_{{\rm av}}>0$ such that for all $\tau \le \tau _0$

$$\begin{aligned} \left\Vert u(t) - {\widetilde{u}}(t) \right\Vert \le C_\text{av}\tau ^2, \qquad 0 \le t \le t_{\mathrm {end}}\,. \end{aligned}$$

(4.1)

The constant $C_\text{av}$ and $\tau _0$ depend on $r_X$, $u_0$, $t_{\mathrm {end}}$, the finite energy K defined in (2.1), the filter functions, and the embedding constant $C_{\rm emb}$, but not on $\tau$.

In particular, ${\widetilde{u}}$ exists on $[0,t_{\mathrm {end}}]$ and is bounded by

$$\begin{aligned} \max \limits _{t\in [0,t_{\mathrm {end}}] } \left\Vert {\widetilde{u}}(t) \right\Vert \le \tfrac{3}{4} r_X \,. \end{aligned}$$

Proof

Let $\widetilde{t^*}>0$ be the maximal existence time of ${\widetilde{u}}$ and define

$$\begin{aligned} t_0 :=\sup \{ s \in (0,\widetilde{t^*}) \mid \max \limits _{t\in [0,s] } \left\Vert {\widetilde{u}}(t) \right\Vert \le r_X \} \,. \end{aligned}$$

We first observe that for $t\le \min \{ t_0, t_{\mathrm {end}}\}$ the variation-of-constants formula yields

$$\begin{aligned} u(t) - {\widetilde{u}}(t)&= \int _0^t e^{(t-s) A} \left( f\big (s, u(s)\big ) - {\widetilde{f}}\big (s , {\widetilde{u}}(s) \big ) \right) \, ds \nonumber \\&= I_1(t) + I_2(t) + \int _0^t e^{(t-s) A} \left( {\widetilde{f}}\big (s, u(s) \big ) - {\widetilde{f}}\big (s , {\widetilde{u}}(s) \big ) \right) \, ds \end{aligned}$$

(4.2)

with

$$\begin{aligned} I_1(t)&= \int _0^t e^{(t-s) A} \left( I - \varPsi \right) f\big (s , u(s)\big ) \, ds, \\ I_2(t)&= \int _0^t e^{(t-s) A} \varPsi \left( f\big (s ,u(s)\big ) - f\big (s , \varPhi u(s)\big ) \right) \, ds . \end{aligned}$$

By Assumption (A5a′) and since $t\le t_0$, the third term in (4.2) is bounded by

$$\begin{aligned} \Big \Vert \int _0^t e^{(t-s) A} \left( {\widetilde{f}}\big (s, u(s) \big ) - {\widetilde{f}}\big (s, {\widetilde{u}}(s) \big ) \right) \, ds \Big \Vert \le C\big ( r_X \big ) \int _0^t \left\Vert u(s) - {\widetilde{u}}(s) \right\Vert \, ds . \end{aligned}$$

It remains to prove

$$\begin{aligned} \left\Vert I_j(t) \right\Vert \le C \tau ^2 , \qquad j=1,2, \end{aligned}$$

(4.3)

since these bounds are sufficient to apply a Gronwall lemma which shows the assertion for all $t\le \min \{ t_0, t_{\mathrm {end}}\}$.

To bound $I_1$ we use integration-by-parts and (OF3) to obtain

$$\begin{aligned} \begin{aligned} I_1(t)&= \tau ^2 \int _0^t e^{(t-s) A} A^2 \vartheta (\tau A) f\big (s , u(s)\big ) \, ds \\&= \tau ^2 \left[ - e^{(t-s) A} A \vartheta (\tau A) f\big (s, u(s)\big ) \right] _0^t \\&\quad + \tau ^2 \int _0^t e^{(t-s) A} A \vartheta (\tau A) J_{f}\big (s, u(s)\big ) \begin{pmatrix} 1 \\ u'(s) \end{pmatrix} \, ds , \end{aligned} \end{aligned}$$

where we used that $f\big (s,u(s)\big )$ is differentiable in $X$. By Assumptions (A3′), (A4b′), and the bound (3.4) on $u'$ we have

$$\begin{aligned} \begin{aligned} \left\Vert A f\big (s, u(s)\big ) \right\Vert \le C\left( K\right) , \qquad \Big \Vert A J_{f}\big (s, u(s)\big ) \begin{pmatrix} 1 \\ u'(s) \end{pmatrix} \Big \Vert \le C\left( K\right) . \end{aligned} \end{aligned}$$

This proves (4.3) for $j=1$.

Using the notation ${\mathbf {u}}(s,\sigma ) = \sigma u(s) + (1-\sigma ) \varPhi u(s)$ and the differentiability (A1′) of $f$ we get

$$\begin{aligned} I_2(t)&= \int _0^t e^{(t-s) A} \varPsi { \left( f\big (s,u(s)\big ) - f\big (s,\varPhi u(s)\big ) \right) } \, ds \\&= \int _0^t \int _0^1 e^{(t-s) A} \varPsi \tfrac{d}{d \sigma }\,\, f\big (s,{\mathbf {u}}(s,\sigma ) \big ) \,d\sigma \, ds \\&= \int _0^t \int _0^1 e^{(t-s) A} \varPsi J_{f}\big (s,{\mathbf {u}}(s,\sigma ) \big ) \begin{pmatrix} 0 \\ \left( I - \varPhi \right) u(s) \end{pmatrix} \,d\sigma \, ds \\&= \int _0^t \int _0^1 e^{(t-s) A} \varPsi J_{f}\big (s, {\mathbf {u}}(s,\sigma ) \big ) \begin{pmatrix} 0 \\ \left( I - \varPhi \right) e^{s A} u_0 \end{pmatrix} \,d\sigma \, ds\\&\quad + \int _0^t \int _0^1 e^{(t-s) A} \varPsi J_{f}\big (s,{\mathbf {u}}(s,\sigma ) \big ) \begin{pmatrix} 0 \\ \left( I - \varPhi \right) \int \limits _0^s e^{(s-\theta ) A} f\big (\theta , u(\theta ) \big ) \end{pmatrix} \, d\theta \,d\sigma \, ds \\&=I_{2,1}(t) + I_{2,2}(t). \end{aligned}$$

By (OF3) and integration-by-parts, the first term can be rewritten as

$$\begin{aligned} \begin{aligned} I_{2,1}(t) = & \tau ^2 \left[ \int _0^1 e^{(t-s) A} \varPsi J_{f}\big (s, {\mathbf {u}}(s,\sigma ) \big ) \begin{pmatrix} 0 \\ \vartheta (\tau A) e^{s A} A u_0 \end{pmatrix} \,d\sigma \right] _0^t \\&+ \tau ^2 \int _0^t \int _0^1 e^{(t-s) A} A \varPsi J_{f}\big (s, {\mathbf {u}}(s,\sigma ) \big ) \begin{pmatrix} 0 \\ \vartheta (\tau A) e^{s A} A u_0 \end{pmatrix} \,d\sigma \, ds\\&- \tau ^2 \int _0^t \int _0^1 e^{(t-s) A} \varPsi \tfrac{d}{ds}\,\, J_{f}\big (s, {\mathbf {u}}(s,\sigma ) \big ) \begin{pmatrix} 0 \\ \vartheta (\tau A) e^{s A} A u_0 \end{pmatrix} \,d\sigma \, ds \,. \end{aligned} \end{aligned}$$

Hence, we have $\left\Vert I_{2,1}(t) \right\Vert \le C \tau ^2$ by (A2′), (A4a′), and (A4b′).

By assumption (A1′) we also have

$$\begin{aligned} \begin{aligned} \int \limits _0^s e^{(s-\theta ) A} f\big (\theta , u(\theta ) \big ) d\theta&\in {\mathcal {D}}(A), \\ \quad A \int \limits _0^s e^{(s-\theta ) A} f\big (\theta , u(\theta ) \big ) d\theta&= \int \limits _0^s e^{(s-\theta ) A} A f\big (\theta , u(\theta ) \big ) d\theta . \end{aligned} \end{aligned}$$

Again integration-by-parts and Assumptions (A1′) and (A4b′) yield the desired bound (4.3). Using (4.1) for $t\le \min \{ t_0, t_{\mathrm {end}}\}$ we obtain for $\tau \le \tau _0$

$$\begin{aligned} \max \limits _{s\in [0,t ] } \left\Vert {\widetilde{u}}(s) \right\Vert \le \max \limits _{s\in [0,t ] } \left\Vert u(s) \right\Vert + C_\text{av}\tau ^2 \le \tfrac{3}{4} r_X \,. \end{aligned}$$

This proves $t_0 \ge t_{\mathrm {end}}$ and hence (4.1) holds on $[0,t_{\mathrm {end}}]$ for all $\tau \le \tau _0$. $\square$

In the next lemma we show that ${\widetilde{u}}$ inherits the regularity of u uniformly in $\tau$.

Lemma 4.2

Let Assumptions 3.2to 3.4be valid. Then there is a $\tau _0>0$ and a constant ${\widehat{C_\text{av}}}>0$ such that for all $\tau \le \tau _0$

$$\begin{aligned} \left\Vert A u(t) - A {\widetilde{u}}(t) \right\Vert \le {\widehat{C_\text{av}}} \tau , \quad 0 \le t \le t_{\mathrm {end}}. \end{aligned}$$

(4.4)

In particular, ${\widetilde{u}}$ satisfies the generalized finite-energy condition uniformly in $\tau \le \tau _0$, i.e.,

$$\begin{aligned} \max \left\{ \left\Vert A{\widetilde{u}}(t) \right\Vert , \left\Vert {\widetilde{u}}'(t) \right\Vert \right\}&\le {\widetilde{K}}, 0 \le t \le t_{\mathrm {end}}, \end{aligned}$$

(4.5)

where $\tau _0$ and the constants ${\widehat{C_\text{av}}}$ and ${\widetilde{K}}$ depend on $r_X$, $u_0$, $t_{\mathrm {end}}$, the finite energy K defined in (2.1), the filter functions, and the embedding constant $C_{\rm emb}$, but not on $\tau$.

Proof

We proceed as in the proof of Theorem 4.1 and define $t_0$ by

$$\begin{aligned} t_0 :=\sup \{ s \in (0,t_{\mathrm {end}}] \mid \max \limits _{t\in [0,s] } \left\Vert A {\widetilde{u}}(t) \right\Vert \le 2 K \} \,. \end{aligned}$$

For $0 \le t \le t_0$, (4.1), (4.2), and (A5b′) imply

$$\begin{aligned} \left\Vert A u(t) - A {\widetilde{u}}(t) \right\Vert&= \Big \Vert \int _0^t A e^{(t-s) A} \left( f\big (s,u(s) \big ) - {\widetilde{f}}\big (s,{\widetilde{u}}(s) \big ) \right) \, ds \Big \Vert \\&\le \left\Vert A I_1(t) \right\Vert + \left\Vert A I_2(t) \right\Vert + C \left( 2 K \right) \int _0^t \left\Vert u(s) - {\widetilde{u}}(s) \right\Vert \, ds \\&\le \left\Vert A I_1(t) \right\Vert + \left\Vert A I_2(t) \right\Vert + \tau ^2 t C \left( 2 K \right) C_\text{av}. \end{aligned}$$

With Remark 3.15, similar arguments as before yield ${\mathcal {O}}(\tau )$ bounds for $\left\Vert A I_1(t) \right\Vert$ and $\left\Vert A I_2(t) \right\Vert$. By possibly reducing $\tau _0$ we obtain the result for $0 \le t \le t_{\mathrm {end}}$. This immediately implies the first bound in (4.5) and the second bound is then obtained from (2.8). $\square$

Remark 4.3

Note that Theorem 4.1 and Lemma 4.2 remain true for $\varPsi = I$ as for this choice $I_1(t) = 0$ and the proof does not require (F3). This case is of interest for methods (2.5) and (2.6).

5 Abstract assumptions on the methods

In this section we characterize the classes of methods which are covered by our error analysis.

We recall that u denotes the solution of the original problem (2.2) and ${\widetilde{u}}$ the solution of the averaged problem (2.8). Further, we denote the numerical flow by $S_\tau$ and the defect by $\delta _n$, i.e., a one-step method is given by

$$\begin{aligned} u_{n+1} = S_\tau (t_n, u_n),\qquad \delta _n = S_\tau \bigl ( t_n, {\widetilde{u}}(t_n) \bigr ) - {\widetilde{u}}(t_{n+1}). \end{aligned}$$

(5.1)

We start with an assumption on the stability of the method.

Assumption 5.1

(Stability) The method applied to (2.8) is stable in the sense that for all $v \in \mathcal{D}(A),\; w \in X$, $t \ge 0$,

$$\begin{aligned} S_\tau (t,v) - S_\tau (t,w) = e^{\tau A} \left( v-w\right) + \tau {\mathcal {J}}\left( t,v,w\right) , \end{aligned}$$

(5.2)

where ${\mathcal {J}}: {\mathbb {R}}\times \mathcal{D}(A) \times X\rightarrow X$ is bounded by

$$\begin{aligned} \left\Vert {\mathcal {J}}\left( t, v,w\right) \right\Vert \le C_{\mathcal {J}}\left( \left\Vert v \right\Vert_{\mathcal{D}(A)} ,\left\Vert w \right\Vert \right) \left\Vert v-w \right\Vert ,\qquad t\in [0,t_{\mathrm {end}}]. \end{aligned}$$

(5.3)

Next, we consider the consistency.

Assumption 5.2

(Consistency for order one) The method applied to the original equation (2.2) satisfies Assumption 5.1 (with $\phi =\psi =1$) and its defect (5.1) satisfies

$$\begin{aligned} \left\Vert \delta _n \right\Vert \le C \tau ^2 \,, \end{aligned}$$

where $C>0$ is independent of $\tau$ and n.

For second-order methods, our analysis requires a particular structure of the defect. Before we state this in an abstract way, we briefly motivate it. Most of the methods we consider are constructed from the variation-of-constants formula

$$\begin{aligned} {\widetilde{u}}(t_{n+1}) = e^{\tau A } {\widetilde{u}}(t_n) + \tau \int \limits _0^1 e^{(1-s) \tau A} {\widetilde{f}}(t_n+\tau s , {\widetilde{u}}(t_n+\tau s)) \,ds \,, \end{aligned}$$

(5.4)

where only the integral term is approximated. Hence, this defect can be expressed as some quadrature error that contains the second derivative in s of

$$\begin{aligned} f_1(s)= \tau {\widetilde{f}}(t_n+\tau s , {\widetilde{u}}(t_n+\tau s)) \qquad \text{ or } \qquad f_2(s) = e^{(1-s) \tau A} f_1(s) \,, \end{aligned}$$

(5.5)

depending on the precise method. Terms of order $\tau ^3$ do not cause any difficulties. However, terms of lower order exist which, in general, require more careful treatment. From $f_1$ we obtain the second-order term

$$\begin{aligned} \tau ^2 J_{{\widetilde{f}}}\big ( t_n + \tau s , {\widetilde{u}}(t_n + \tau s )\big ) \begin{pmatrix} 0 \\ \left( \tau A \varPhi \right) A {\widetilde{u}}(t_n + \tau s ) \end{pmatrix} \end{aligned}$$

(5.6)

and $f_2$ gives in addition the term

$$\begin{aligned} \tau ^2 \left( \tau A \varPsi \right) e^{(1-s) \tau A} A f(t_n+\tau s , \varPhi {\widetilde{u}}(t_n + \tau s )) . \end{aligned}$$

(5.7)

For these terms property (OF4) needs to be used in order to carry over the local convergence order to the global error. Similar terms are obtained for the defect of the splitting scheme (2.4). Together with the integral in (5.4), equations (5.7) and (5.6) give rise to the following general structure of $\delta _n$.

Assumption 5.3

(Structure of defects for order two) The defect $\delta _n$ defined in (5.1) of a numerical method applied to the averaged equation (2.8) is of the form

$$\begin{aligned} \delta _n = \delta _n^{(1)} + \delta _n^{(2)} + D_n \end{aligned}$$

(5.8)

with $\left\Vert D_n \right\Vert \le C \tau ^3$, where the constant $C>0$ is independent of $\tau$ and n. In addition, one of the following sets of conditions is satisfied:

• (a) If $\phi ,\psi$ are filters of order 2, then there exist $w_n \in X$ and a linear map $W_n:X\rightarrow {\mathcal {D}}(A)$ which satisfy

  $$\begin{aligned}& \left\Vert w_n \right\Vert\le C , &&\Big \Vert \frac{1}{\tau } \big ( w_{n+1} - w_{n} \bigr ) \Big \Vert\le C , \end{aligned}$$

  (5.9a)
  $$\begin{aligned} &\left\Vert W_n \right\Vert _{X\leftarrow X} \le C ,&\Big \Vert \frac{1}{\tau } \bigl (W_{n+1} - W_n\bigr ) \Big \Vert\le C , \end{aligned}$$

  (5.9b)
  $$\begin{aligned} &\left\Vert A W_n \right\Vert _{X\leftarrow X}\le C , &&&&&&&&&&&&&\end{aligned}$$

  (5.9c)

  with a constant C which is independent of $\tau$ and n such that $\delta _n^{(i)}$ can be written as

  $$\begin{aligned} \delta _n^{(1)} = \tau ^2 \bigl (\tau A \varPsi \bigr ) w_n\,, \qquad \delta _n^{(2)} = \tau ^2 W_n \bigl (\tau A \varPhi \bigr ) A {\widetilde{u}}(t_n) \,, \end{aligned}$$

  (5.10)

• (b) If $\psi =1$ and $\phi$ is a filter of order 2, then (5.9) and (5.10) hold with $w_n = 0$ for all n.

Remark 5.4

From (5.9) and (OF2) one can directly derive $\left\Vert \delta _n \right\Vert \le C \tau ^2$. However, this would only yield a suboptimal first-order bound in the global error.

The following proposition embeds the methods presented in Sect. 2.2 in the abstract framework.

Proposition 5.5

Let Assumptions 3.2 to 3.4 be satisfied.

• (a) The Strang splitting methods (2.3a) and (2.3b) applied to the averaged equation (2.8) satisfy Assumptions 5.1, 5.2, and 5.3 (a).

• (b) The second-order variant of the Lie splitting (2.4) applied to the averaged equation (2.8) satisfies Assumptions 5.1and 5.3 (a).

• (c) The exponential Runge–Kutta method (2.5) applied to the averaged equation (2.8) satisfies Assumptions 5.1, 5.2, and 5.3 (b).

Proof

Assumption 5.1 is easily verified for all schemes. We only prove part (a) for the Strang splitting $\bigl (A,{\widetilde{f}},A\bigr )$ as the statement for the $\bigl ({\widetilde{f}},A,{\widetilde{f}}\bigr )$ variant and part (c) can be adapted from this proof. We comment on part (b) below.

Let $t_{n+\xi } :=t_n + \tau \xi$, ${\widetilde{u}}_{n+\xi } :={\widetilde{u}}(t_{n+\xi } )$, and ${\widetilde{f}}_{n+\xi } :={\widetilde{f}}(t_{n+\xi } ,{\widetilde{u}}_{n+\xi } )$. Since we can write the scheme as

$$\begin{aligned} S_\tau \bigl (t_n, {\widetilde{u}}_n \bigr ) = e^{\tau A} {\widetilde{u}}_n + \tau e^{\frac{\tau }{2} A} {\widetilde{f}}\big (t_{n+1/2}, e^{\frac{\tau }{2} A} {\widetilde{u}}_n \big ), \end{aligned}$$

the defect is given by

$$\begin{aligned} \delta _n&= e^{\tau A} {\widetilde{u}}_n + \tau e^{\frac{\tau }{2} A} {\widetilde{f}}\big ( t_{n+1/2}, e^{\frac{\tau }{2} A} {\widetilde{u}}_n \big ) - {\widetilde{u}}_{n +1} \\&= \tau e^{\frac{\tau }{2} A} {\widetilde{f}}\big ( t_{n+1/2}, e^{\frac{\tau }{2} A} {\widetilde{u}}_n \big ) - \int \limits _0^{\tau } e^{(\tau -\xi ) A} {\widetilde{f}}_{n+\xi } \,d\xi \\&= {\widehat{I}}_1 + {\widehat{I}}_2, \end{aligned}$$

where

$$\begin{aligned} {\widehat{I}}_1&= \tau e^{\frac{\tau }{2} A} {\widetilde{f}}_{n+1/2} - \int \limits _0^{\tau } e^{(\tau -\xi ) A} {\widetilde{f}}_{n+\xi } \,d\xi \\ {\widehat{I}}_2&= \tau e^{\frac{\tau }{2} A} \bigl ( {\widetilde{f}}\big ( t_{n+1/2}, e^{\frac{\tau }{2} A} {\widetilde{u}}_n \big ) - {\widetilde{f}}_{n+1/2}\bigr ) \,. \end{aligned}$$

${\widehat{I}}_1$ is the quadrature error of the midpoint rule. It can be written in terms of the Peano kernel $\kappa _2$ as

$$\begin{aligned} \begin{aligned} {\widehat{I}}_1&= \tau \int \limits _0^{1} \kappa _2(\xi ) \frac{d^2}{d \xi ^2} \Bigl ( e^{(1-\xi ) \tau A} {\widetilde{f}}_{n+\xi } \Bigr ) \,d\xi \\&= \tau ^3 \int \limits _0^{1} \kappa _2(\xi ) e^{(1-\xi ) \tau A} A^2 \varPsi f(t_{n+\xi } , \varPhi {\widetilde{u}}_{n+\xi }) \,d\xi \\&\quad + \tau ^3 \int \limits _0^{1} \kappa _2(\xi ) e^{(1-\xi ) \tau A} \varPsi J_{f}\big ( t_{n+\xi } ,\varPhi {\widetilde{u}}_{n+\xi }\big ) \begin{pmatrix} 0 \\ A \varPhi A {\widetilde{u}}_{n+\xi } \end{pmatrix} \,d\xi + {\widehat{D}}^{(1)}_n \end{aligned} \end{aligned}$$

with $\left\Vert {\widehat{D}}^{(1)}_n \right\Vert \le C \tau ^3$. Again using the variation-of-constants formula, (OF2), (A5a′), and (A5b′) we obtain

$$\begin{aligned} \begin{aligned} {\widehat{I}}_1&= \tau ^3 \int \limits _0^{1} \kappa _2(\xi ) e^{(1-\xi ) \tau A} A^2 \varPsi f(t_{n+\xi } , \varPhi e^{\xi \tau A} {\widetilde{u}}_n ) \,d\xi \\&\qquad + \tau ^3 \int \limits _0^{1} \kappa _2(\xi ) e^{(1-\xi ) \tau A} \varPsi J_{f}\big ( t_{n+\xi } ,\varPhi {\widetilde{u}}_{n+\xi }\big ) \begin{pmatrix} 0 \\ A \varPhi A e^{\xi \tau A} {\widetilde{u}}_n \end{pmatrix} \,d\xi + {\widehat{D}}_n \\&=:\tau ^3 A \varPsi w_n + \tau ^3 W_n A \varPhi A {\widetilde{u}}_n + {\widehat{D}}_n \,, \end{aligned} \end{aligned}$$

with $\big \Vert {\widehat{D}}_n \big \Vert \le C \tau ^3$.

To bound ${\widehat{I}}_2$ recall that ${\widetilde{f}}$ only depends on the first component of ${\widetilde{u}}$. Using (A5a′), the variation-of-constants formula, and $\pi _1 {\widetilde{f}}_{n+1/2} = 0$, we have

$$\begin{aligned} \left\Vert {\widetilde{f}}\big ( t_{n+1/2}, e^{\frac{\tau }{2} A} {\widetilde{u}}_n \big ) - {\widetilde{f}}_{n+1/2} \right\Vert&= \left\Vert {\widetilde{f}}\big ( t_{n+1/2}, \pi _1 e^{\frac{\tau }{2} A} {\widetilde{u}}_n \big ) - {\widetilde{f}}\big ( t_{n+1/2}, \pi _1 {\widetilde{u}}_{n+1/2} \big ) \right\Vert \\&\le C(r_X) \left\Vert \pi _1 \Bigl ( e^{\frac{\tau }{2} A} {\widetilde{u}}_n - {\widetilde{u}}_{n+1/2}\Bigr ) \right\Vert \\&= C(r_X) \Big \Vert \pi _1 \Bigl (\tfrac{\tau }{2} {\widetilde{f}}_{n+1/2}- \int \limits _0^{\tau /2} e^{(\tau /2-\xi ) A} {\widetilde{f}}_{n+\xi } \,d\xi \Bigr ) \Big \Vert \\&\le C \tau ^2 \,, \end{aligned}$$

since this is just a quadrature error of the (right) rectangular rule.

The properties (5.9a) to (5.9c) follow directly from Lemma 3.9. Using the first order Peano kernel $\kappa _1$, Assumption 5.2 is verified by writing

$$\begin{aligned} \begin{aligned} {\widehat{I}}_1&= \tau \int \limits _0^{1} \kappa _1(\xi ) \frac{d}{d \xi } \Bigl ( e^{(1-\xi ) \tau A} {\widetilde{f}}_{n+\xi }\Bigr ) \,d\xi \end{aligned} \end{aligned}$$

as this yields $\big \Vert {\widehat{I}}_1 \big \Vert \le C \tau ^2$ for $\psi = \phi =1$ by (A1′) and (A3′).

We briefly comment on the scheme (2.4). The defect can be written as

$$\begin{aligned} \begin{aligned} \delta _n&= e^{\tau A} \Bigl ( {\widetilde{u}}_{n} + \tau {\widetilde{f}}\big ( t_{n+1/2}, {\widetilde{u}}_{n}\big ) + \tfrac{\tau ^2}{2} r \big ( t_{n+1/2}, {\widetilde{u}}_{n} \big ) \Bigr ) - {\widetilde{u}}_{n+1} \\&= \int \limits _0^{\tau } \tfrac{d}{d\xi } \Bigl ( e^{\xi A} \bigl ( {\widetilde{u}}_{n+1-\xi }+ \xi {\widetilde{f}}\big ( t_{n+1/2}, {\widetilde{u}}_{n+1-\xi }\big ) + \tfrac{\xi ^2}{2} r \big ( t_{n+1/2}, {\widetilde{u}}_{n+1-\xi }\big ) \bigr ) \Bigr ) \,d\xi \\&= \int \limits _0^{\tau } e^{\xi A} \Bigl ( {\widetilde{f}}\big ( t_{n+1/2}, {\widetilde{u}}_{n+1-\xi }\big ) - {\widetilde{f}}_{n+1-\xi } \Bigr ) \,d\xi \\&\qquad + \int \limits _0^{\tau } \tfrac{\xi ^2}{2} e^{\xi A} \Bigl ( \tfrac{d}{d\xi } r \big ( t_{n+1/2}, {\widetilde{u}}_{n+1-\xi }\big ) + A r \big ( t_{n+1/2}, {\widetilde{u}}_{n+1-\xi }\big ) \Bigr ) \,d\xi \\&= {\widehat{I}}_3 + {\widehat{I}}_4 \,. \end{aligned} \end{aligned}$$

In the first term ${\widehat{I}}_3$ we add and subtract $\tau e^{\tau /2 A} {\widetilde{f}}_{n+1/2}$ and get the quadrature error of the midpoint rule. The term ${\widehat{I}}_4$ admits a similar structure as in ${\widehat{I}}_1$ and hence Assumption 5.3 can be verified as before. $\square$

Remark 5.6

We note that method (2.4) applied to the original equation (2.2) does not satisfy Assumption 5.2.

6 Main result for exponential one-step methods

The following result is the last step towards our main Theorem 6.2. It states the global error of a numerical integrator applied to the averaged equation (2.8) with suitable filters satisfying our assumptions (e.g., all the methods of Sect. 2.2) is second order accurate. As before, u denotes the solution of the original problem (2.2) and ${\widetilde{u}}$ the solution of the averaged problem (2.8).

Theorem 6.1

(Global error of the averaged problem) Let Assumptions 3.2to 3.4be fulfilled. Moreover, let $(u_n)_n$ be the numerical approximations of a scheme applied to the averaged equation (2.8) that satisfies Assumptions 5.1and 5.3. Then there is a $\tau _0>0$ and a constant $C_\text{e}>0$ such that for all $\tau \le \tau _0$

$$\begin{aligned} \left\Vert u_n - {\widetilde{u}}(t_n) \right\Vert \le C_\text{e}\, \tau ^2, \qquad 0 \le t_n = n\tau \le t_{\mathrm {end}}. \end{aligned}$$

The constant $C_\text{e}$ and $\tau _0$ depend on $u_0$, $t_{\mathrm {end}}$, the finite energy K defined in (2.1), the filter functions, and the embedding constant $C_{\rm emb}$, but are independent of $\tau$ and n.

Proof

The proof makes use of the error recursion from [12] and adapts techniques from Theorem 5.3 in [2].

Due to definition (5.1) of the defect $\delta _n$, the global error ${\widetilde{e}}_n = {\widetilde{u}}(t_n) - u_n$ can be written as

$$\begin{aligned} {\widetilde{e}}_{n+1} = S_\tau (t_n , {\widetilde{u}}(t_n)) - S_\tau (t_n, u_n) - \delta _n. \end{aligned}$$

By Assumption 5.1, the global error satisfies

$$\begin{aligned} {\widetilde{e}}_{n+1} = e^{(n+1) \tau A} {\widetilde{e}}_0 + \tau \sum _{j=0}^n e^{(n-j) \tau A} {\mathcal {J}}\bigl (t_j, {\widetilde{u}}(t_j) , u_j \bigr ) - \sum _{j=0}^n e^{(n-j)\tau A} \delta _j. \end{aligned}$$

(6.1)

The error bound follows from a discrete Gronwall lemma, once we established the bound

$$\begin{aligned} \Big \Vert \sum _{j=0}^n e^{(n-j) \tau A} \delta _j \Big \Vert \le C_\delta \tau ^2 \end{aligned}$$

(6.2)

with a constant $C_\delta$ being independent of $\tau$ and n.

The proof is done by induction on n. For $n=0$, the statement is obviously true. Hence we assume that for all $0\le k \le n$ it holds

$$\begin{aligned} \left\Vert u_k \right\Vert \le r_X, \qquad \left\Vert u_k - {\widetilde{u}}(t_k) \right\Vert \le C_\text{e}\, \tau ^2,\qquad C_\text{e}:=C_\delta \, e^{C_{\mathcal {J}}( {\widetilde{K}}, r_X ) t_{\mathrm {end}}} \,. \end{aligned}$$

By Assumption 5.3, the defect is split into three parts, which motivates to write

$$\begin{aligned} \sum _{j=0}^n e^{(n-j) \tau A} \delta _j = {\widetilde{e}}_{n+1}^{(1)} + {\widetilde{e}}_{n+1}^{(2)} + {\widetilde{e}}_{n+1}^{(D)}, \end{aligned}$$

where

$$\begin{aligned} {\widetilde{e}}_{n+1}^{(\ell )} = \sum _{j=0}^n e^{(n-j) \tau A} \delta _j^{(\ell )},\quad \ell = 1,2, \qquad {\widetilde{e}}_{n+1}^{(D)} = \sum _{j=0}^n e^{(n-j) \tau A} D_j. \end{aligned}$$

Since $\left\Vert D_j \right\Vert \le C\tau ^3$ and $n\tau \le t_{\mathrm {end}}$ we easily see

$$\begin{aligned} \Big \Vert {\widetilde{e}}_{n+1}^{(D)} \Big \Vert = \Big \Vert \sum _{j=0}^n e^{(n-j) \tau A} D_j \Big \Vert \le C\tau ^2. \end{aligned}$$

To bound ${\widetilde{e}}_{n+1}^{(\ell )}$, $\ell =1,2$, we define

$$\begin{aligned} E_n = \sum _{j=0}^{n} e^{j \tau A} \qquad \text{and} \qquad F_n = \sum _{j=0}^{n} {\widetilde{u}}(t_j). \end{aligned}$$

Summation-by-parts, Assumption 5.3, and (OF4) yield

$$\begin{aligned} \sum _{j=0}^n e^{(n-j) \tau A} \delta _j^{(1)}&= E_{n} \delta _0^{(1)} + \sum _{j = 0}^{n-1} E_{n-j-1} \bigl (\delta _{j+1}^{(1)} - \delta _j^{(1)} \bigr ) \\&= \tau ^3 E_{n} A \varPsi w_{0} \ + \tau ^3 \sum _{j = 0}^{n-1} E_{n-j-1} A \varPsi \bigl (w_{j+1} - w_{j}\bigr ) \\&= \tau ^2 E_{n} (e^{\tau A} - I) \varTheta _\varPsi w_{0} \\&\quad + \tau ^2 \Bigl ( \tau \sum _{j=0}^{n-1} E_{n-j-1} (e^{\tau A} - I) \varTheta _\varPsi \frac{1}{\tau } \bigl ( w_{j+1} - w_{j}\bigr ) \Bigr ). \end{aligned}$$

To bound $E_j(e^{\tau A} - I)$ we exploit a telescopic sum to get

$$\begin{aligned} \left\Vert E_j(e^{\tau A} - I) \right\Vert = \Big \Vert \sum _{k=0}^{j} e^{k \tau A} (e^{\tau A} - I) \Big \Vert = \left\Vert e^{(j+1) \tau A} - I \right\Vert \le 2. \end{aligned}$$

Together with (5.9a) and (OF4) this yields (6.2) for $\delta _j^{(1)}$ instead of $\delta _j$.

Next we consider ${\widetilde{e}}_{n+1}^{(2)}$. Again, Assumption 5.3, summation-by-parts, and (OF4) with $\chi = \varPhi$ yield

$$\begin{aligned} \sum _{j=0}^n e^{(n-j) \tau A} \delta _j^{(2)}&= \tau ^3 W_{n} A \varPhi A F_n + \tau ^3 \sum _{j=0}^{n-1} e^{(n-j) \tau A} \bigl ( W_{j} - e^{ -\tau A} W_{j+1} \bigr ) A \varPhi A F_j \\&= \tau ^2 W_{n} \varTheta _\varPhi (e^{\tau A} - I) A F_n \\&\quad + \tau ^2 \Bigl ( \tau \sum _{j=0}^{n-1} e^{(n-j) \tau A} \frac{1}{\tau } \bigl ( W_{j} - e^{-\tau A} W_{j+1} \bigr ) \varTheta _\varPhi (e^{\tau A} - I) A F_j \Bigr ). \end{aligned}$$

Here, we have

$$\begin{aligned} \begin{aligned} \frac{1}{\tau } \bigl ( W_{j} - e^{ -\tau A} W_{j+1} \bigr ) = \frac{1}{\tau } e^{ -\tau A} \bigl ( W_{j} - W_{j+1} \bigr ) - \frac{1}{\tau } (e^{-\tau A} - I) W_{j}. \end{aligned} \end{aligned}$$

The terms can be estimated by (5.9b) and (5.9c)

$$\begin{aligned} \Big \Vert \frac{1}{\tau } e^{ -\tau A} \bigl ( W_{j} - W_{j+1} \bigr ) \Big \Vert _{X\leftarrow X}&= \Big \Vert \frac{1}{\tau } \bigl ( W_{j} - W_{j+1} \bigr ) \Big \Vert _{X\leftarrow X} \le C , \\ \Big \Vert \frac{1}{\tau } (e^{-\tau A} - I) W_{j} \Big \Vert _{X\leftarrow X}&= \Big \Vert \varphi _1(-\tau A) A W_{j} \Big \Vert _{X\leftarrow X} \le C , \end{aligned}$$

since $\left| \varphi _1(z) \right| \le 1$ for $z \in i{\mathbb {R}}$.

Next we consider $(e^{\tau A} - I) A F_j$ for $j\le n$. After adding the exact solution we apply the variation-of-constants formula, (A3′), and (4.5), which gives

$$\begin{aligned} \Big \Vert (e ^{\tau A} - I) A F_j \Big \Vert&= \Big \Vert A \sum _{k=0}^j (e^{\tau A} {\widetilde{u}}(t_k) - {\widetilde{u}}(t_k+ \tau ) ) + A \sum _{k=0}^j ( {\widetilde{u}}(t_k+ \tau ) - {\widetilde{u}}(t_k)) \Big \Vert \\&= \Big \Vert \sum _{k=0}^j \int _0^\tau e^{(\tau - s)A} A {\widetilde{f}}({\widetilde{u}}(t_k + s)) \, ds + A ({\widetilde{u}}(t_{j+1}) - {\widetilde{u}}_0) \Big \Vert \\&\le t_{\mathrm {end}}C({\widetilde{K}})+ 2{\widetilde{K}}. \end{aligned}$$

This yields (6.2) for $\delta _j^{(2)}$ instead of $\delta _j$ and together with the results above proves (6.2).

Finally, (5.3), (6.1), (6.2), and ${\widetilde{e}}_0 = 0$ give

$$\begin{aligned} \left\Vert {\widetilde{e}}_{n+1} \right\Vert&= \Big \Vert \tau \sum _{j=0}^n e^{(n-j) \tau A} {\mathcal {J}}\bigl ( t_j, {\widetilde{u}}(t_j) , u_j \bigr ) - \sum _{j=0}^n e^{(n-j)\tau A} \delta _j \Big \Vert \\&\le C_\delta \tau ^2 + \tau \sum _{j=1}^n C_{\mathcal {J}}({\widetilde{K}} , r_X ) \left\Vert {\widetilde{e}}_j \right\Vert \,. \end{aligned}$$

A discrete Gronwall Lemma thus yields

$$\begin{aligned} \left\Vert {\widetilde{e}}_{n+1} \right\Vert&\le \tau ^2 \, C_\delta \, e^{C_{\mathcal {J}}( {\widetilde{K}} , r_X ) t_{\mathrm {end}}} = C_\text{e}\tau ^2 , \\ \left\Vert u_{n+1} \right\Vert&\le \left\Vert {\widetilde{u}}(t_{n+1}) \right\Vert + \left\Vert {\widetilde{e}}_{n+1} \right\Vert \le \tfrac{3}{4} r_X + C_\text{e}\tau ^2 \le r_X \end{aligned}$$

for $\tau \le \tau _0 \le \tfrac{1}{2} \bigl (\tfrac{r_X}{C_\text{e}}\bigr )^{1/2}$ and the induction is closed.$\square$

Our main result is the following theorem.

Theorem 6.2

Let Assumptions 3.2to 3.4be fulfilled. Further let $(u_n)_n$ be the numerical approximations of a scheme that satisfies Assumptions 5.1and 5.3.

• (a) If the method also satisfies Assumptions 5.2and is applied to the original equation (2.2), then there is a $\tau _0>0$ and a constant $C_1>0$ such that for all $\tau \le \tau _0$

  $$\begin{aligned} \left\Vert u_n - u(t_n) \right\Vert \le C_1 \tau , \qquad 0 \le t_n = n\tau \le t_{\mathrm {end}}\,. \end{aligned}$$

• (b) Let $\phi ,\psi$ such that Assumption 5.3is satisfied. Then there is a $\tau _0>0$ and a constant $C_2>0$ such that for all $\tau \le \tau _0$

  $$\begin{aligned} \left\Vert u_n - u(t_n) \right\Vert \le C_2 \tau ^2, \qquad 0 \le t_n = n\tau \le t_{\mathrm {end}}, \end{aligned}$$

  if the method is applied to the averaged equation (2.8).

The constants $C_1,C_2$ and $\tau _0$ depend on $u_0$, $t_{\mathrm {end}}$, the finite energy K defined in (2.1), the filter functions, and the embedding constant $C_{\rm emb}$, but are independent of $\tau$ and n.

Proof

Part (a) follows directly from Assumption 5.2 and equation (6.1). For part (b), we simply combine Theorem 4.1 and Theorem 6.1 by the triangle inequality (2.9). $\square$

7 Main result for exponential multistep methods

We briefly indicate how to extend the developed theory to the exponential multistep methods of Sect. 2.2.4. The first-order convergence as in part (a) of Theorem 6.2 is easily shown. To get second order, Assumption 5.1 needs to be modified.

For method (2.6), we denote the numerical flow by $S_\tau (t,v_n,v_{n-1})$ and obtain

$$\begin{aligned} S_\tau (t,v_n,v_{n-1}) - S_\tau (t,w_n,w_{n-1}) = e^{\tau A} \bigl (v_n-w_n\bigr ) + \tau {\mathcal {J}}_n, \end{aligned}$$

where ${\mathcal {J}}_n = {\mathcal {J}}\bigl (t,v_n,v_{n-1},w_n,w_{n-1}\bigr )$ is bounded by

$$\begin{aligned} \begin{aligned} \left\Vert {\mathcal {J}}_n \right\Vert&\le C_{\mathcal {J}}\bigl ( \left\Vert v_n \right\Vert ,\left\Vert w_n \right\Vert \bigr ) \left\Vert v_n-w_n \right\Vert \\&\quad +C_{\mathcal {J}}\bigl ( \left\Vert v_{n-1} \right\Vert ,\left\Vert w_{n-1} \right\Vert \bigr ) \left\Vert v_{n-1}-w_{n-1} \right\Vert ,\quad t\in [0,t_{\mathrm {end}}]. \end{aligned} \end{aligned}$$

This yields the following convergence result.

Corollary 7.1

Let Assumptions 3.2to 3.4be valid. Consider the numerical approximations $(u_n)_n$ from (2.6) applied to the averaged equation (2.8) with $\psi = 1$ and a filter $\phi$ of order 2. Then there is a $\tau _0>0$ and a constant $C>0$ such that for all $\tau \le \tau _0$

$$\begin{aligned} \left\Vert u(t_n) -u_n \right\Vert \le C \tau ^2 , \qquad 0 \le t_n = n \tau \le t_{\mathrm {end}}, \end{aligned}$$

where C and $\tau _0$ depend on $u_0$, $t_{\mathrm {end}}$, the finite energy K defined in (2.1), the filter functions, and the embedding constant $C_{\rm emb}$, but are independent of $\tau$ and n.

Proof

We first employ Theorem 4.1 and Lemma 4.2, so again it remains to prove the error in approximating the filtered solution. As in the proof of [19, Thm. 4.3] the defect stems from a quadrature error that yields the dominant terms as in (5.6). Considering the defect

$$\begin{aligned} \delta _n = S_\tau \bigl (t_n, {\widetilde{u}}(t_n), {\widetilde{u}}(t_{n-1}) \bigr ) - {\widetilde{u}}(t_{n+1}) \,, \end{aligned}$$

Assumption 5.3 (b) is satisfied and a slight modification of the proof of Theorem 6.1 yields the assertion. $\square$

For method (2.7) we have

$$\begin{aligned} S_\tau (t,v_n,v_{n-1}) - S_\tau (t,w_n,w_{n-1}) = e^{2 \tau A} \bigl (v_{n-1}-w_{n-1}\bigr ) + \tau {\mathcal {J}}_n \end{aligned}$$

where ${\mathcal {J}}_n={\mathcal {J}}\left( t,v_n,w_n\right)$ is bounded by

$$\begin{aligned} \begin{aligned} \left\Vert {\mathcal {J}}_n \right\Vert&\le C_{\mathcal {J}}\bigl ( \left\Vert v_n \right\Vert ,\left\Vert w_n \right\Vert \bigr ) \left\Vert v_n-w_n \right\Vert ,\quad \forall t\in [0,t_{\mathrm {end}}]. \end{aligned} \end{aligned}$$

In order to apply the techniques from above we define the modification

$$\begin{aligned} \begin{aligned} \chi _2: {\mathcal {C}}_b \bigl ( i {\mathbb {R}}\bigr ) \rightarrow {\mathcal {C}}_b \bigl ( i {\mathbb {R}}\bigr ), \quad \chi (\cdot ) \,\mapsto\, \chi (2\cdot ) \,, \end{aligned} \end{aligned}$$

and can state the following result.

Corollary 7.2

Let Assumptions 3.2to 3.4be valid and u be the classical solution of (2.2).

Consider the numerical approximations $(u_n)_n$ from (2.7) applied to the averaged equation (2.8) with filters $\chi _2\psi ,\chi _2 \phi$ where $\psi ,\phi$ are filters of order 2. Then there is a $\tau _0>0$ and a constant $C>0$ such that for all $\tau \le \tau _0$

$$\begin{aligned} \left\Vert u(t_n) -u_n \right\Vert \le C \tau ^2 , \qquad 0 \le t_n = n \tau \le t_{\mathrm {end}}, \end{aligned}$$

where C and $\tau _0$ depend on $u_0$, $t_{\mathrm {end}}$, the finite energy K defined in (2.1), the filter functions, and the embedding constant $C_{\rm emb}$, but are independent of $\tau$ and n.

Proof

Since the method stems from a midpoint rule applied to the variation-of-constants formula the defect is again given with dominant terms similar to (5.6) and (5.7). If we resolve the error recursion, we only obtain every second defect and the propagation is driven by $e^{2 \tau A}$. As $e^{z}$ in (F3) is replaced by $e^{2 z}$, this can be combined to conclude the assertion similar to the proof of Theorem 6.1. $\square$