1 Introduction

The tube hydroforming (THF) process is a cutting-edge manufacturing process for sheet as well as tube forming with applications in various sectors such as pharmaceutics, chemical, aerospace, and automotive industries with better quality and competitive manufacturing cost of the products. The hydroforming process is an alternative manufacturing process for conventional manufacturing and also propose product can be manufactured in competitive price and time with weight reduction. The AISI316L material characterization has studied under different flow and friction conditions. The study is focused on stress concentration reduction so that punch life can be enhanced [1]. Industries are attracting towards tube hydroforming technology because this technology has ability to manufacture intricate size and shapes of the tubes for high and low weights steel. The research focus was on process and forming parameters estimation (such pressure, yielding, ultimate and calibration points etc.) during copper tube forming under axial loading condition [2]. It is seen that the success of THF depends on feed and pressure parameters in which the reliability of FE model in hydroforming is studied. The reliability of FE model was depending on the material properties and seen that the hydroforming performed by numerical analysis was more accurate and simpler than trial–error method [3], whereas, the bulging of tube component was mainly affected by the internal pressure and axial feeding [4]. The THF (tube hydroforming) process has many advantages over the conventional manufacturing process such as improved component quality, reduction in weight and lower manufacturing costs [5]. Many researchers performed comparative study of experimental and numerical study under free bulge and calibration conditions [6].

Omar et al. [7] studied the strain path for weld as well base metal during tube bulging. Also, observed improvement in structural strength and stiffness through optimized section geometry, lower tooling cost due to fewer parts, fewer secondary operations, tight dimensional tolerances, low spring-back and reduced scrap [8]. The performance of tube hydroforming process is highly dependent on process parameters such as internal pressure, axial feeding, friction, etc. without any type of defects. Therefore, the forming parameters must be determined carefully [9]. Now a day the tube hydroforming process is rapidly implemented in many industrial applications for bulging of tube in desired die cavity. The advantages over the conventional methods are higher strength to weight ratio and lower price. The applications in automotive and aerospace industries such as engine cradle, chassis components, seat frames, exhaust manifolds, structural body and power transmission components, T, X and Y fittings manufacturing [3, 10].

The hydroforming process is employed for manufacturing of tubular parts with the objective as vehicle weight reduction [11]. The Tube hydroforming was used frequently in automotive and aerospace Industries. The process gives better product quality within less production expenses. The T-shape tubular part is used for tube hydroforming parameters optimization such as axial feed, counter force and forming pressure by employing ANN (Artificial Neural Network) and Finite element analysis (FEA) [12]. The Goodwin forming limit diagram (FLD) diagram has been widely used for the representation of formability analysis of material for seamless and ERW tube. The parameters such as microstructure, mechanical behaviour is studied for various laser welded and ERW tube material [13]. FEA was employed for the analysis of formability parameters to study the effect on various heat affect zone (HAZ), weld zone and base metal regions. It was also found necking near weld zone for seamed weld tube [14].

The seamed, laser welded and electric resistance welded (ERW) tubes have been widely used in automotive vehicles and so on. Also found that laser welded tube has better formability for diameter to thickness ratio as compared with ERW tube. FEA is commonly used in auto industries for analysis of process and forming parameters to improve product quality as well as to reduce product design and development time. The FEA is also helpful to analyse formability parameters of complex geometries [15]. The researcher has proposed 0.92 new necking criteria for prediction of necking in sheet and tube deformed components [16]. An initially FLC was introduced by Keeler and Backofen [17]. THF is a widespread technique in metal forming process, which can produce lightweight tubes or tube components with complex cross sections [18, 19]. The researcher has investigated the parameters such as microstructure, deformation behaviour and mechanical properties of the annealed pure copper material for double branched tube component [20]. In this process, it is possible to manufacture the intricate or complex geometry parts or components. The effect of friction and forming pressures on formability parameters was studied. Also, found that the uniform thickness distribution in both low- and high-pressure hydroforming processes. The friction has more and less sensitive parameter in both high- and low-pressure tube hydroforming respectively [21]. The loading and die geometry input parameters were considered for the formability study for SS304 material and the strain paths were predicted under the free and fixed conditions [22]. The various diameter and thickness geometry parameters were used for the comparative study of formability parameters on seamless and welded tubes. It was also found that the formability increased in both tube geometries [23]. The effect of corner radius and coefficient of friction on thickness distribution and bulge height was studied by FEA. The numerical and analytical results were observed in good agreement for formability parameters [24]. The necking points of bulged tube were used to construct the forming limit stress diagram (FLSD) based on principle stresses [25]. THF process is a special manufacturing process used to produce tubular structural components. Many researchers have found optimum parameters of tube hydroforming process to attain the maximum bulge height with distinguish parameters such as internal pressure, axial feed and coefficient of friction conditions. Also, found that the maximum bulge height is possible when the pressure is more and feed rate is less and the bulge height is minimum when the feed rate is more and pressure is less [26]. The forming pressures were predicted by applying implicit and explicit FEA tool. The explicit tool has better deformation properties by comparing with implicit solver [27]. The researcher has constructed forming limit diagram for QSTE340 seamed tube material. The theoretical and numerical comparative models were developed for the construction of left and right side of the forming limit diagram (FLD) respectively [28]. The analytical model was employed for the prediction of forming pressure. The analytically predicted results are verified with experimental for free bulging behaviour of tube [29]. The simple and complex strain paths were constructed by employing Swift’s diffused necking and Hill’s necking criterions. The experimental strain paths were compared and validated [30]. The tubular components are manufactured with axial feed and internal pressure in tube hydroforming process. The tube was fed into the die setup and the axial feeds were applied till the bursting of tube so that the effective process parameters can be analysed. The forming limit curve (FLC) has been widely applied for the analysis of hydro formability parameter representations. The researcher has main focus on the study on laser seamed tube. There are three types of test methods such as free bulging and elliptical bulging, hydroforming limit test. These test methods were applied on laser welded and electric resistance welded tubes (ERW). The cracking failure defect has been analysed on both seamed and ERW tubes during bulging of tube. The FLC analysis demonstrates that the laser welded tube exhibits a better hydro-formability than that of the ERW tube under same input conditions [3, 22, 31, 32]. The sensitivity analysis of thickness variations during tube bulging was studied [33], whereas a novel FLD diagram was developed for nonlinear loading paths under fixed and free conditions [34]. The tailor welded tubes were developed with various thicknesses components for hydroforming experimentation and also concluded that seam weld issues are resolved in tailor weld tube [35]. The wrinkling defects are analysed on magnesium alloy material under the axial feed condition and also predicted the variations in between deformation and axial feed by simulation [36]. The strain non-uniform index and forming limit diagram are good methods to identify the defect free components by simulation [37]. The fracture and necking parameters were analysed numerically and observed that the static pressure was increased which led to shifting the fracture area from P to C type shaped tubes [38], whereas the forming limit diagram was drawn at necking points of bulged tube with experimentation and simulation on AL-7020-T6 material grade [39].

Various researchers studied the process and forming parameters during bulging of tube. Day by day fuel consumption in automotive sector is increasing due to heavy weight of materials. Hence it required to reduce the weight of components or vehicle. The fuel consumption can be minimized by reducing weight of the vehicle or by adopting advanced manufacturing techniques. Also, it is found that the ferrite and austenite grade material is not used for tube hydroforming process. The common bulging tube defects are observed to be wrinkling, buckling, spring-back and fracture or necking. Hence the purpose of this study is to improve the bulging and minimize the thinning ratio so that manufacturing processes will be improved in industries. This research focuses on hydroforming process, formability and process parameters design for replacing the conventional tube bending, welding and cutting operations. The paper is organised as follows; the significance of study with brief literature review is presented in Sect. 1. Section 2 present materials used and methodology adopted. Section 3 highlight the theoretical study followed. Sections 4 and5 focuses on numerical analysis and experimental worked performed. Whereas results and discussion is presented in depth in Sect. 6 and in last concluding remark is given.

2 Materials and methodology

The AISI304 grade material is regularly used for manufacturing of home equipment, medical instruments, boilers and measuring instruments, whereas AISI409L grade material is used in two and three-wheelers exhaust system, catalytic converter and muffler systems. The chemical composition (wt.%) of the material under consideration is shown in Table 1. The tubes were prepared by using plane sheet metal with 1.5 mm thicknesses. Tube procurement parameters are presented in Table 2. The specimen’s preparations and the details of the used tube dimensions for tube hydroforming process is shown in Table 3. It is the selection and design of parameters for numerical and experimental study. The tube geometry parameters like tube diameter, length to diameter ratio and the feed type have been used. Therefore, 3 tubes for similarity check are defined and out of which consistency were checked for at least 2 experiments and it is set that it must have same necking for the success of the bulging tube.

Table 1 Chemical composition of materials
Full size table
Table 2 Tube procurement parameters
Full size table
Table 3 Tube dimensions
Full size table

2.1 Mechanical and material parameters

The mechanical and material properties have important role in tube hydroforming process. The simulation model was designed in FEA based Pamstamp software which is dedicated for metal forming analysis using two types of grades as shown in Table 4. The specimens are prepared as per the ASTM E8 standard for tensile test. The testing was performed on UTM (universal testing machine) computerized control machine along with feedback system. The maximum load capacity of the machine was 250kN.The load was applied gradually on specimen to find the true stress strain curve. The anisotropy material properties are calculated by using mathematical Eqs. (1–4). The strain hardening exponent value shows the formability and stretchability in tube bulging.

$$\overline{r} = \frac{{r_{0} + r_{90} + 2 \times r_{45} }}{4}$$
(1)
$$\Delta r = \frac{{r_{0} + r_{90} - 2 \times r_{45} }}{2}{ }$$
(2)
$$\overline{n} = \frac{{n_{0} + n_{90} + 2 \times n_{45} }}{4}$$
(3)
$$\overline{k} = \frac{{k_{0} + k_{90} + 2 \times k_{45} }}{4}$$
(4)

where \(\overline{r}\) = planar anisotropy, \(\Delta r\) = normal anisotropy, \(\overline{n}\) = avg. strain hardening exponent, \(\overline{k}\) = avg. strength coefficient, \(r_{0}\) (parallel), \(r_{45}\) (diagonal) and \(r_{90}\) (perpendicular) = rolling directions.

Table 4 Material and mechanical properties
Full size table

3 Theoretical study

3.1 Plastic strain-based Hill criterion

The anisotropic yield function employed to calculate failure strains in plane stress during simulation as shown in following equation. The Hill’s yield criterion [40] and its coefficients are measured based on anisotropy property along the three different directions such as 0, 45 and 90 in degrees.

$$f_{\sigma } = \sqrt {(\sigma_{22} - \sigma_{33} )^{2} \times F + (\sigma_{33} - \sigma_{11} )^{2} \times G + (\sigma_{11} - \sigma_{22} )^{2} \times H + 2 \times L \times \sigma_{23}^{2} + 2 \times M \times \sigma_{31}^{2} + 2 \times N \times \sigma_{12}^{2} }$$
(5)

whereas the various coefficients of the Hill criteria are presented by Eq. (6).

$$H = \frac{{r_{0} }}{{1 + r_{0} }},F = \frac{H}{{r_{90} }},G = \frac{H}{{r_{0} }},N = \frac{{\left( {r_{90} + r_{0} } \right) \times \left( {2r_{45} + 1} \right)}}{{2*r_{90} \times \left( {1 + r_{0} } \right)}}$$
(6)

3.2 North American deep drawing research group (NADDRG)

The (NADDRG) criteria [41] is employed to estimate the FLD points in real time situations. The FLD is a combination of two lines passing by a point (f10) in the plane-strain state. The lines are drawn at left and right side of FLD with slopes of about 45° and 20° respectively. The Eq. (7) present the requisites of engineering strain for estimating the forming limit strain f10.

$$\in_{10} = \left( {\frac{{23.3 + 14.13*t_{o} }}{0.12}} \right) \times n$$
(7)

whereas, to—original blank thickness (mm), n—strain hardening exponent

3.3 Thickness gradient necking criterion (TGNC)

Initially this criterion is established from simulation for forming limit strains findings. In THF, the critical neck is seen by the nearness of a basic neighbourhood thickness gradient in the tube. Such an impression of the neck is autonomous of the strain path, forming rate and the tube metal (material properties). The critical neighbourhood thickness gradient Rcritical, exists at the on—set of an obvious nearby neck. After beginning of deformation of the tube, a thickness gradient, “RTG” creates in the deformation tube as presented by Eq. (8).

$$R_{TG} = \frac{{t_{n} }}{{t_{n - 1} }}$$
(8)

where \(R_{TG}\) = thickness gradient, \(t_{n}\) = necking element thickness, \(t_{n - 1}\) = neighboring element thickness.

As the tube starts bulging (forming), the thickness gradient continues to reduce from original value of 1.5. The thickness gradient goes on decrease at the on—set of localized necking and at a certain stage called diffused necking, it reaches to a critical value. From the work of Kumar et al. [16], Nandedkar [42] and Reddy et al. [43], the Rcri is experimentally estimated as 0.92. If Rcri is less than or equal to 0.92, the tube specimen is considered as necked.

$$R_{critical} = \frac{{t_{n} }}{{t_{n - 1} }} \le 0.92$$

4 Numerical analysis

The Finite Element Analysis (FEA) procedure was developed for the simulation of tube bulging, in Pamstamp software. Basically, there are three stages of simulation such as Pre-processing-Input, Solver and Post processing-output as shown in Fig. 1.

Fig. 1
figure 1

Steps of simulation

Full size image

The explicit FEA based Pamstamp software have steps which are followed during simulation. The input parameters are material properties, boundary conditions along the two different directions such as unidirectional and bidirectional. The anisotropy yield base model was solved i.e. Hill criteria. The output or post-processing parameters such as strain distribution, thinning etc. were measured at necking point and it was done before the fracture of the components. The simulation model was developed in CAD solid work tool. Then, the CAD files imported in FEA environment. The obtained 3D solid model and tube loading position on lower die are shown in Fig. 2. Solid model shows the upper die, lower die in Fig. 2, left and right piston as well as coordinate frames. The friction coefficient used in between the contact surfaces of dies and punch is taken as 0.008.

Fig. 2
figure 2

Simulation setup and tube loading position on lower die

Full size image

5 Experimentation procedure

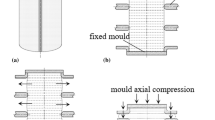
The block diagram of tube hydroforming process is shown in Fig. 3. The tube is loaded in between upper and lower dies, and then axial or fixed feed is applied to the both ends of the tube. Here, in hydroforming process an intensifier has an important role to develop required pressure inside the tube so that created inside pressure should be exerted inside the tube area and then tube bulged into die set cavity. The strain paths of the bulging tube were sensed in computer system and its further process to analyse the forming parameters. The process parameters such as pressure and axial feeds affect the material behaviour and quality of the components. The pressure and feed ranges from 0 to 0.05 GPa and 0–3 mm respectively.

Fig. 3
figure 3

Block diagram of tube hydroforming setup

Full size image

The micro hardness of tube is measured according to ASTM E-92-82standard. The locations of hardness measurements are also shown in right hand side of the Fig. 4. After hardness measurement it was found that AISI409L furnished higher hardness properties than AISI304. It means that AISI409L difficult to form in desired size and shape as compared to AISI304 grade material.

Fig. 4
figure 4

Measured micro hardness (Experimentally)

Full size image

For experimentation tubes required as shown in Fig. 5 are used and prepared as per requirement. The operational and experiementation steps are presented in flowchart as shown in Fig. 6. The die set are loaded on machine as per the design of experimentation (DOE) planning and tubes were loaded between the upper and lower dies. After applying all conditions,the tube bulging started. The deformation at neck position recorded with all required parameters.The complete tube hydroforming setup is shown in Fig. 7.The left and right pistons are used to apply axial or fixed conditions to both ends of the tubes. The pressure intensifier has major role for bulging of tubes. The necking specimens are shown in Fig. 8 along with bulging height and length. After bulging of a tube, the image of that tube is imported in ARGUS system for the measurement of the different strains. The bulged tube necking is observed in this system before fracture. The strain paths were recorded at necking point and which is before fracture and it is measured using using Digital Image Correlation techniques using speckle patterns drawn on the tube (Online DIC, ARAMIS). The specimens have shown after fracture.

Fig. 5
figure 5

Prepared specimen

Full size image
Fig. 6
figure 6

Experimentation procedure flowchart

Full size image
Fig. 7
figure 7

Experimental setup

Full size image
Fig. 8
figure 8

Bulging of tubes of a axial, b fixed feed for AISI304

Full size image

6 Results and discussion

6.1 Numerical analysis

The strength of the weld metal is very less as compared with base metal and due to this less strength, the weld metal fails suddenly. The formability parameter L/D has major impact on thinning or thickness of bulge tube or failure of a tube. In both case failures occurred along the axial direction. In lower L/D ratio less thinning is found as compared to higher L/D ratio and it means better formability in higher L/D ratio.

The FEA tool is helpful to find the approximate forming parameters such as strain path, thinning, etc. of tube metal deformation during tube hydroforming process. In base metal thinning has started from 16.3 to 44.6% under the axial feed condition. The maximum and minimum thinning observed in L/D = 2, 3 and L/D = 1respectively. However, in weld metal it was observed that thinning varies from 7.7 to 18.6% under fixed feed condition. The thinning is directly proportional to L/D ratio in both fixed and axial conditions as shown in Table 5.

Table 5 FEA AISI304 grade material of bulging tubes for base and weld metal
Full size table

In base metal thinning started from 13.1 to 14.8% under the axial feed condition. The maximum and minimum thinning observed in L/D = 3 and L/D = 1 respectively. However, in weld metal it is observed that thinning varies from 6.8 to 8.5% under fixed feed condition. The thinning is directly proportional to L/D ratio in both fixed and axial conditions as shown in Table 6. By comparing it is observed that, AISI304 grade material is best suitable for tube hydroforming. The greater L/D ratio gives the better bulging or uniform bulging. For L/D = 1 failure occurs in base metal which is nearer to the weld line and for L/D = 2,3 failures observed nearer to the weld line for both axial and fixed feed conditions.

Table 6 FEA AISI409L grade material of bulging tubes for base and weld metal
Full size table

6.2 Experimental test

The strain paths for base and weld metal of AISI304 and AISI409L has been recorded as shown in Fig. 9.Required load for weld material is more as compared to base metal for both material grades. The material fracture at ultimate tensile strength point which is commonly shortens tensile elongation. The fracture or necking point is at ultimate tensile strength and load needed for weld material is higher by comparing with the base metal because the surface of the weld strip is harden during the welding process. After ultimate point plastic deformation were continued and due to this reason, the elongation is more but practically the necking or fracture or last point is ultimate point.

Fig. 9
figure 9

Strain paths for weld and base metal

Full size image

The strain paths were measured for weld and base metal as shown in Fig. 11. The engineering and true stress strain curves for base and weld metal of AISI304 and AISI409L are shown in Fig. 10 respectively. The experimental true stress–strain curves data are used for simulation and further development in metal forming. The true stress–strain curve has more surface area as compared to engineering curve because this area is used for the study of formability parameters of any sheet or tube metal forming. The engineering curves or values are used to calculate true stress–strain curve and following relations (Eq. 10) used.

$$\begin{gathered} \sigma_{True} = \sigma_{engg} \left( {\varepsilon_{engg} + 1} \right) \hfill \\ \varepsilon_{True} = \ln (\varepsilon_{engg} + 1) \hfill \\ \end{gathered}$$
(10)

whereas, \(\sigma_{True}\) = true stress in MPa, \(\varepsilon_{True}\) = true strain in %, \(\sigma_{engg}\) = engineering stress, \(\varepsilon_{engg}\) = engineering strain.

Fig. 10
figure 10

Stress and strain path for AISI304 and AISI409L material

Full size image

The experimental results (FLD) have been compared with mathematical FLD model and FEA simulation FLD results. The predictions have made for two grades such as AISI304 and AISI409L materials. The comparisons were made in between austenitic and ferritic stainless steels. The result shows the Austenitic stainless steel has better formability as compared to ferritic stainless steel. The Simulation Hill 98 plasticity law based on hardening curve which was Hollomon, law gives the little bit upper boundary for all FLD curves as shown in Fig. 11. The simulated results show a closed match with mathematical and experimental analyses. By comparing the results among the three FLD, it is observed that the sufficient level of accuracy under axial and fixed feed conditions. Second quadrant shows the axial feed conditions or uniaxial direction for L/D = 1 and FLD points are moving towards the plane strain condition for L/D = 2, 3. In axial and fixed feed conditions the negative and positive minor strains are observed respectively.

Fig. 11
figure 11

Theoretical, numerical and experimental forming limit diagram (FLD)

Full size image

Initially the tube is placed inside the die cavity and then hydraulic pressure is applied to bulge the tube. The deformed tube is taken in ARGUS software tool for the measurement of major or minor strain or strain measurement. The bulged tube by experimentally and the tube become elliptical deformation. The major and minor strain paths were recorded by optical strain measuring ARGUS software. At actual grid method is used at necking point for measuring both dimensions or directly we can take major and minor strain values at this particular necking point by drawing a tangent method. The strain limit diagram was obtained experimentally. Initially the tube was kept under the loading position and then loading stopped, as bursting occurred. After bursting, the major and minor diameters of the ellipse near the crack were measured and then represented on forming limit diagram (FLD). The major and minor engineering strains were calculated by using Eq. (11) and diameters were measured on the profile projector machine.

$$\begin{gathered} {\text{e}}_{{{\text{major}}}} = \frac{{{\text{d}}_{{{\text{major}}}} - {\text{d}}_{{{\text{initial}}}} }}{{{\text{d}}_{{{\text{initial}}}} }} \hfill \\ {\text{e}}_{{\min {\text{or}}}} = \frac{{{\text{d}}_{{\min {\text{or}}}} - {\text{d}}_{{{\text{initial}}}} }}{{{\text{d}}_{{{\text{initial}}}} }} \hfill \\ \end{gathered}$$
(11)

whereas, \(e_{major}\) = major engineering strain, \(e_{\min or}\) = minor engineering strain, \(d_{major}\) = major diameter, \(d_{\min or}\) = minor diameter, \(d_{initial}\) = initial diameter of circle.

Equation (11) is used find the major and minor strain based on major and minor diameter of the ellipse and which are used to draw FLD diagram. While estimating these two strain paths the circular element is converted into elliptical element and deformation can be used to calculate the strain paths. The power hardening law or material model equation was used to model the tube behaviour and the Holloman equation [44] as written by Eq. (12).

$$\overline{{\sigma_{Y} }} = K \times (\overline{\varepsilon })^{n}$$
(12)

whereas \(\overline{{\sigma_{Y} }}\) = effective stress along Y direction, K = strength coefficient, \(\overline{\varepsilon }\) = effective plastic strain, n = strain hardening exponent. The tubes are prepared (Fig. 5) as per requirement with data presented in Table 7.

Table 7 Tube preparation for experimentation
Full size table

The conditions (Fig. 12) were applied for experimental work as axial and fixed feed condition. In axial feed condition the feed was given from 0 to 3 mm along the both ends. But in case of fixed feed condition feed was given from 0 to 0.001 mm respectively. From, experimentation tube bulging was takes place in both dimensions such as length and diameter. Here F and Pi parameters represents the feed applied in axial direction and internal pressure developed for tube bulging. In fixed condition case both ends were fixed by using fixed plungers and pressure were applied inside through the opening of the left and right plungers. The bulge height can be improved by feeding the material along the axial direction and increasing the internal pressure uniformly and also thinning can be minimized by maintaining the uniform pressure inside the tube. Also, higher formability in axial feed condition is observed as compared to fixed feed condition. The bulge height is improved in L/D = 3 ratio with axial feed condition. By comparing the three L/D ratio it is observed that maximum bulge height in L/D = 2 ratio and minimum in L/D = 1 ratio. In this research feasibility of tube hydroforming process is studied and crosschecked for the ferrite and austenite steel grades.

Fig. 12
figure 12

Axial and fixed feed [22]

Full size image

From Figs. 13, 14 and 15 it is observed that maximum bulging was observed when L/D = 3 in both cases. The variation in simulation and experimental results was observed to be 8–17%. But in fewer samples it is observed to be more than 17% which is not shown in these plots. During comparative study between two materials, it was observed that AISI304 grade material has maximum formability strength. The affected formability parameters were studied for both axial and fixed feed condition. The L/D formability strain path was studied and found in L/D = 1near weld and is greater than one in base metal at necking point. The minimum strain paths were found in base metal during L/D = 2 and 3 and that was away from weld or greater than 90 degree. In axial feed it is found that maximum thinning was 40% and 15% in base and weld metal respectively for AISI304 material. Again, in axial feed it is found that maximum thinning was 14.8% and 8.5% in base and weld metal respectively for AISI409L material.

Fig. 13
figure 13

Variation of bulge height with axial and fixed feed

Full size image
Fig. 14
figure 14

Variation of thinning with axial and fixed feed

Full size image
Fig. 15
figure 15

Axial and fixed feed versus bulging length

Full size image

Compressive stress was developed in axial feed condition along the axial direction whereas tensile stress was developed in fixed feed condition along the axial stress. With the axial feed condition the unidirectional or minimum strain path was found when compared with the fixed feed condition. Leakage in axial feed condition leads to lesser bulge height. Due to leakage problem the results are summarized as bellows.

In axial feed condition it is that observed maximum bulge height or better formability because the material feeding was done along the axial direction, but due to leakage issue less bulge height is obtained in axial feed condition. The bulging has a certain limit up to necking point and at this point formability parameters are measured before fracture. Bulge height is higher than it feeds lesser material to compensate the necking at the bulged portion. So that, the bulging of the tube component decreases with increase in bulge height. Figure 16 shows the distinguish parameters such as bulge height with respect to pressure. The axial and fixed feed shows the better formability till the specific point, after that the axial feed gives the better formability in corner radius fills of a bulge tube. The internal pressure has major process parameters for the better formability properties. AISI304 grade material observed the high pressure required for higher bulge height as compared with AISI409L.

Fig. 16
figure 16

Feed versus pressure and bulge height

Full size image

Generally, the mechanical properties are used for numerical analysis. Hence Hill-1948 yield criterion and Holloman’s law are considered for the present study and obtained results are compared with existing literature shown in Table 8. Different test along the rolling directions 0°, 45° and 90° were used to analyze the effect of plastic anisotropy. The axial and fixed feed conditions are applied to predict the formability parameters.

Table 8 Comparative analysis
Full size table

7 Conclusions

In this paper as per objective the simulated model results are compared with mathematical model and then required experimental work was performed on various tube dimensions. From investigations it is observed that the mathematical models and simulated model shows sufficient level of accuracy for austenitic and ferritic stainless steel in unidirectional conditions. The three types of predictions show better correlation among each other. The influencing or interacting parameters are considered for tube metal part manufacturing through material optimization, formability and process parameters, alternative material selection for vehicle, weight reduction, product quality improvement and customer satisfaction.

The simulation and experimental analyses show sufficient level of quality and good curve fitting with maximum variation of 17%. AISI304 grade material shows better formability as compared to AISI409L, lead to highly suitable material for tube hydroforming components. The L/D ratio forming parameter has major impact on quality of the forming because L/D = 3 ratio has more uniform formability as compared to L/D = 1. The forming parameters such as thinning, FLD, L/D ratio and bulge height are in good agreement obtained numerically and experimentally. From experimental investigation it is observed that the internal pressure plays significant role to get optimum quality of the components or products. The maximum thinning was observed in fixed feed condition as compared to axial feeding for both materials. The better formability parameters are found for AISI304, hence this material is suitable for hydroforming process. This research can be extended further for the improvements of the formability parameters at room and high temp also.