Effect of bridge pier diameter on maximum depth of scour impacts on the environment

Abstract

This study uses a physical experimental model to investigate the scale effect of cylindrical bridge piers on local scour. Non-dimensional public relations are developed after determining the effective parameters. Experiments are carried out to estimate the maximum scour depth around cylindrical piers with 10, 20, 30, 40, 60 and 100 mm in diameter in a laboratory channel for well-sorted gradation of sediment particles. The average diameters of sediment particles are 0.5 and 0.7 mm under clear water conditions and the relative speeds are 0.67, 0.76, 0.86 and 0.95. Scour around the piers of Naderi and Fifth Bridges in Ahvaz is measured and the results are compared to the physical model results. This indicates that for the piers of less than 30 mm in diameter, the relative scour depth is just a function of the particle Froude Number. In addition to this, it is related to the ratio of the pier diameter to the flow depth for larger piers. The actual data collected from the mentioned bridges pier scour are compared to the physical experimental results. Accordingly, it is observed that the physical experimental results are highly agree with the actual one.

1 Introduction

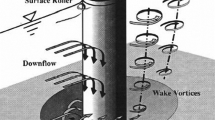
Investigation of the scour phenomenon is very important. The scour around structures such as bridges pier or bridge abutments or embankment need to be controlled otherwise, this could lead to irreparable damages. The instability of bridge piers is one of irreversible damages caused by the scour. Without applying an appropriate solution, it eventually leads to the demolition of the structure. Therefore, a study on the mechanism of the scour occurrence and the effective parameters on the amount of scour are a necessity [36]. Bridge piers across the river divert river flow, which results in scour around the piers. Every year, scour results in slippage of the bridge piers during flooding and the destruction of bridges is occurred. This cuts avenues for assistance in these regions and highlights the requirement for major study of this phenomenon. The prediction of scour and its consideration during the design of bridges and implementation of design policies are crucial to the control and reduction of local scour [38]. Scour creates holes around piers and undermine the stability of the bridge. The force of the water flow against the pier and the separation of the stream lines are the main causes of scour around piers [9]. The pressure gradient resulting from the force of water against the pier diverts the surface stream lines of water downward toward the substrate in foreside of the bridge pier (or abutment). The flow of water hits the substrate and digs into it, then clashes with the mainstream, creating a horseshoe vortex. Horseshoe vortices are more active in foreside of the bridge pier. The separation of the flow by the pier increases the height of the water behind the pier. The shear stress increases behind the pier and forms the vortices. Surveys indicate that horseshoe vortices and down flow play a major role in the development of scour around piers [4]. Previous research has shown that the technique of local scour near bridge piers are very complex [26]. Bridge pier scour refers to the removal of sediment particles around pier. The obstruction caused by the pier creates a horseshoe vortex, which is characterized by intense turbulence and high shear stresses, often bringing about scouring of the sediment bed. In certain situations, the pier-scour hole may develop to such an extent that could become a threat to the integrity of the bridge foundation. This sometimes leads to the complete demise of the entire structure as well [17]. In fact, it is not practical for a physical model of local scour around pier to satisfy all these similarities because of extremely complicated flow conditions. In scour modelling, inertial, gravitational, vortices and viscous forces are very significant for defining similarity [16].

Ahmad and Khassaf [1] also have done several experiments on local scour and different shapes piers experimentally. The diameter of pier in this study was 8 cm. The results display that the depth of scour depends on the foundation level and the pier shape. Bradimarte et al. [3] were done a wide range of experiments on bridge pier scour. By doing this, the dynamic and mechanic characteristics of local scour were analyzed. Briaud [7] 94 had done several examinations in a flume that was full of clays and sands. Some of the experiments were bigger than the laboratory-scale. Furthermore, based on the collected data, on equations for R²-coefficent that varies between 0.8 and 0.9 were obtained. In consequence, the last depth of scour around the pier was calculated. Ravi et al. [31] had used air injection to decreases scour around the bridge pier. The tests were done in a clear-water with cohesive sediments in bed. It was observed that air injection can reduce scour effect by 30%. Generally hydraulic researchers have done many experiments to investigate the local scour around bridge piers and develop empirical equations to estimate the maximum scour depth. However, due to different laboratory conditions and limitations on data collection, specifically in small-scale laboratory flumes, most of the empirical equations for determining depth have a great deal of uncertainty and substantial limitations [33,34,35,36,37]. Ataie-Ashtiani and Beheshti [2] investigated local scour for different diameter pier arrangements and with different bridge pier spacings. It was observed that, increasing and decreasing the space and pier diameter between the two piers, respectively, could result in scour depth. Breusers [6] addressed the effect of pier diameter on scour while holding the other parameters constant. He changed the pier diameter for different depths of flow and sizes of sediment particles in the bed. The conclusion explains that the ratio of flow depth to diameter of pier has a direct relationship with maximum scour depth. He proposed a relationship for estimating relative scour depth as ${{d_{s} } \mathord{\left/ {\vphantom {{d_{s} } D}} \right. \kern-\nulldelimiterspace} D} = f\left( {{{y_{0} } \mathord{\left/ {\vphantom {{y_{0} } D}} \right. \kern-\nulldelimiterspace} D}} \right)$, where d_s is scour depth, D is diameter and y₀ is depth of flow. Jane [17] studied the scour around cylindrical bridge piers in clear water and concluded that scour increases as the upstream Froude Number increases. He presented a formulation based on previous studies as ${{d_{s} } \mathord{\left/ {\vphantom {{d_{s} } D}} \right. \kern-\nulldelimiterspace} D} = f\left( {{{y_{0} } \mathord{\left/ {\vphantom {{y_{0} } {D,F_{r} }}} \right. \kern-\nulldelimiterspace} {D,F_{r} }}} \right)$ where F_r is the Froude Number. Raudkivi and Ettema [30] assessed cylindrical bridge piers scour in clear water and using uniform grain particles in the bed. They found that bed sediment particle size distribution, average particle diameter size and pier diameter have significant effects on the maximum local scour. Their results confirm that the relative depth of flow depends on the average particle size of bed particles. To investigate cylindrical piers and invariable sediment beds with different particles size a channel was used. Kothyari concluded that the most scour depth devaluation as the size of the foundation matter increases under constant hydraulic conditions and that pier diameter was effective at 5–15% on scour depth [18]. Ettema et al. [13] used a channel to investigate the effects of pier scale on piers using a uniform bed of sediment particles with an average size of 0.7 mm and cylindrical piers with different diameters. The results showed that the maximum depth of scour occurs in front of a pier and scour depth is lower than 15–20%. Mueller et al. [28] evaluated the experimental results for scour depth from field studies on piers of large bridges. The results confirmed that the data for an in vitro model for the prediction of maximum scour depth was similar to data from field studeis. Ram Babu et al. [29] investigated various experimental techniques to measure scour around cylindrical bridge piers. They used a laboratory channel. Maximum scour depth was investigated in cohesive soils. They found that increasing the flow velocity from 0.199 to 0.328 m/s can increase the development of scour around all piers. Simaro et al. [35] examined flow parameters for pier scour. They tested cylindrical piers in a uniform bed of sediment particles with an average size of 0.8 mm and showed that scour depth is dependent on the pace of flow toward the pier and factors such as pier diameter and the size of bed sediment particles. Lanca et al. [21] predicted scour depth around cylindrical piers made of Plexiglas. In addition, they used the average size of the sediment particles as a variable. It was concluded that upstream flow depth has a direct effect on the scour depth. Sheppard et al. [34] predicted maximum scour depth around the pier and assessed cylindrical bridge piers in clear water condition as well as an invariable bed of sediment particles in the laboratory of the United States Geological. A reservoir was in the hydroelectric power plant that supplied the water flow in their channel. Then, it was observed that the maximum water depth occurs in the maximum pier diameter and this effects on the scour depth in steady hydraulic conditions. Lee and Sturm [22] have done a range of experiments on different pier diameters and sediment. They concluded, that the maximum scour depth around the cylindrical pier is related to the diameter of the pier and sediment particles in the bed. It was observed that, the scour depth is always more than the real one around the bridge piers. Considering the fact that, the scour depth around the piers by using the piers scale effect of the laboratory model was examined in this study. Also, investigating the erosion pattern around the bridge piers in different flow conditions, different types of non-cohesive sand particles and maximum scour depth were proposed in this paper as well. Accordingly, the current study experimentally examined the influence of the scale of cylindrical piers on local scour and compared it with actual measurements. The main purpose of this study is to provide an appropriate scale for experimental studies regarding the bridge piers. Methodology, laboratory facilities, related Figures and Tables will be shown further in the paragraphs below (Fig. 1 and Table 1).

Table 1 Previous studies on the bridge pier scour

2 Materials and methods

2.1 Dimensional analysis

The dimensionless parameters were determined to identify effective parameters for scour and explained the relationship between them using the Buckingham dimensional analysis method. The effective parameters in local scour around bridge pier are: d_s maximum scour depth, y flow depth, B channel width, D pier diameter, V flow velocity, D₅₀ average sediment diameter, g gravity, t time, ρ water density, ρ_s sediment density, v water viscosity, C_D pier shape factor and σ sediment standard deviation. Therefore, dimensionless quantities are $\pi_{1} = \frac{V}{{g^{\frac{1}{2}} y^{\frac{1}{2}} }},\;\pi_{2} = \frac{V}{{g^{\frac{1}{2}} y^{\frac{3}{2}} }},$ $\pi_{3} = \frac{D}{y},\;\pi_{4} = \frac{{D_{50} }}{y},$ $\pi_{5} = \frac{B}{y},\;\pi_{6} = \frac{{d_{s} }}{y},$ $\pi_{7} = \frac{{\rho_{s} }}{\rho },\;\pi_{8} = \frac{{g^{\frac{1}{2}} t}}{{y^{\frac{1}{2}} }}$, $\pi_{9} = C_{D} ,\;{\text{and}}\;\pi_{10} = \sigma$. Note that, the fix parameters were neglected initially in the modeling because all the piers were of the same type. So, the dimensionless equation was determined as show in Eq. (1):

$$ {\raise0.7ex\hbox{${d_{s} }$} \!\mathord{\left/ {\vphantom {{d_{s} } D}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$D$}} = f(F{}_{r},\;R_{e} ,\;{{D_{50} } \mathord{\left/ {\vphantom {{D_{50} } D}} \right. \kern-\nulldelimiterspace} D},\;{D \mathord{\left/ {\vphantom {D {y_{0} }}} \right. \kern-\nulldelimiterspace} {y_{0} }},G_{s} $$

(1)

where ${{d_{s} } \mathord{\left/ {\vphantom {{d_{s} } D}} \right. \kern-\nulldelimiterspace} D}$ the proportion of is scour depth to pier diameter, $F_{r}$ is the Froude Number of flow, $R_{e}$ is the Reynolds Number of flow, ${{D_{50} } \mathord{\left/ {\vphantom {{D_{50} } D}} \right. \kern-\nulldelimiterspace} D}$ is the proportion of average size of sediment particles to pier diameter, ${D \mathord{\left/ {\vphantom {D {y_{0} }}} \right. \kern-\nulldelimiterspace} {y_{0} }}$ is the ratio of pier diameter to flow depth and $G_{s}$ indicates the relative density of particles. Since, under the conditions of the experiment, the Reynolds Number ranged from 15,400 to 22,235.2, which reflects turbulent flow, the Reynolds Number was eliminated from Eq. (1) [8]. ${{F_{r} ,\;D_{50} } \mathord{\left/ {\vphantom {{F_{r} ,\;D_{50} } D}} \right. \kern-\nulldelimiterspace} D}\;{\text{and}}\;G_{s} - 1$ were combined and the particle Froude Number $F_{rg} = {V \mathord{\left/ {\vphantom {V {\left( {g\left( {G_{s} - 1} \right)D_{50} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {g\left( {G_{s} - 1} \right)D_{50} } \right)}}^{0.5}$ was used to extract the relations (V is flow velocity and g is acceleration caused by gravity). The final equation is simplified as:

$$ {{d_{s} } \mathord{\left/ {\vphantom {{d_{s} } {D = f\left( {F_{rg} ,\;{D \mathord{\left/ {\vphantom {D {y_{0} }}} \right. \kern-\nulldelimiterspace} {y_{0} }}} \right)}}} \right. \kern-\nulldelimiterspace} {D = f\left( {F_{rg} ,\;{D \mathord{\left/ {\vphantom {D {y_{0} }}} \right. \kern-\nulldelimiterspace} {y_{0} }}} \right)}} $$

(2)

2.2 Field measurement

The Karun river is one of the largest and longest rivers in Iran and a watershed of the Persian Gulf. Field data was collected around the Naderi Bridge and Fifth Bridge piers across the Karun river in Ahwaz. The field measurements were recorded and the relations were compared. This was done to determine equation providing the response are similar to the field data. An echo-sounder was used to measure the depth of scour. Also, an echo-sounder was used to measure the depth around the piers as well. The scour depth was then considered to field scour depth. Flow conditions on the day of measurement of scour depth at the Naderi and Fifth Bridge piers are shown in (Table 2).

Table 2 Field data from Ahwaz-Karun River Station (Naderi Bridge and Fifth Bridge)

2.3 Lab facilities and experiment method

The experiments were done in a channel 6 m in length, 0.72 m in width, 0.6 m in depth with a longitudinal slope of nearly zero in the Physical and Hydraulic Models laboratory of the Water Sciences Engineering Faculty at Shahid Chamran University of Ahvaz. The channel walls were made of toughened glass with a thickness of 10 mm. The flow from the water supply tank was conveyed in a tank at the beginning of the channel using an impeller pump at a maximum flow rate of 25 L/s. To remove inlet turbulence, a mesh plate was used in the inlet of channel. After exiting the channel, the flow enters an output baffle tank then a pipe 8″ in diameter to return to the water supply tank. The flow depth was controlled using a sliding gate which was located at the end of the channel. Figure 2 shows different views of the experimental channel.

Fig. 1

Flow and scour pattern around a cylindrical pier: a view of flow around a bridge pier in the bed flume when hits an obstacle

Fig. 2

a Definition sketch of bridge pier arrangement: hydraulic flume with sample of experimental b schematic of experimental channel with bridge pier in the bed material (looking downstream) c bridge pier in experimental tested

2.4 Experimental set-up

Achieving the correct maximum scour depth requires consideration of the effective factors. To avoid the lateral effects of the channel walls on local scour and select the maximum diameter of the pier, criteria such as ${D \mathord{\left/ {\vphantom {D {B\langle 0.16}}} \right. \kern-\nulldelimiterspace} {B\langle 0.16}}$ [30] and ${D \mathord{\left/ {\vphantom {D {B\langle 0.15}}} \right. \kern-\nulldelimiterspace} {B\langle 0.15}}$ [27,28,29,30,31,32,33,34] were considered. D is pier diameter in the bed and B is the channel width. A ratio of 0.13 was chosen to establish the above criteria. Cylindrical wooden piers with diameters of 10, 20, 30, 40, 60 and 100 mm were used (Fig. 2c). Since the diameter of the piers for the Naderi and Fifth Bridges is 1500 mm, the piers used for the scale model bridge were 1/150, 1/75, 1/50, 1/37.5, 1/25 and 1/15 of the field values. Breusers and Raudkivi [4] stated that, to prevent roughness at the substrate surface at the velocities close to the critical bed shear stress, D₅₀ > 0.7 mm should be used; for sediment with D₅₀ < 0.7 mm the roughness should be at flow paces greater than > 0.6 V_c (V_c is critical velocity of bed material movement). To neglect non-uniformity of the bed material, the geometric standard deviation (SD) of sediment particles should be 1.1 to 1.5; however, such particles should not large enough to cover the scour hole. Sheppard et al. [34] showed the scour depth decreased at D/D₅₀ = 12. Lee and Sturm [22] reported a minimum equal to 20. The experimental zone was 0.7 × 2 m in area and 10 cm in thickness of bed materials in the middle of the channel with the model piers located at a distance of 1 m from the entrance. The simulated bed was filled two types of non-cohesive sand with average diameters of 0.5 and 0.7 mm, and geometric standard deviation of 1.18 and 1.22, respectively. Upstream of the study area was filled with coarse grain material to develop flow in the area of the experiment and prevent local erosion caused by a change in roughness. A Laser meter with a precision of 1 mm was used to profile sediment removal and measure the depth of scour. The Dietz theory [6] states that the scour depth increases relatively as the flow depth increases as y₀, so ${D \mathord{\left/ {\vphantom {D {y_{0} }}} \right. \kern-\nulldelimiterspace} {y_{0} }}$ lower than 0.4. If the relative flow depth is deep enough, surface vortices will not interact with horseshoe vortices and relative flow depth will not affect scour depth [12]. ${D \mathord{\left/ {\vphantom {D {y_{0} }}} \right. \kern-\nulldelimiterspace} {y_{0} }}\langle 0.7$ was carefully observed so the depth of the hole was not influenced by flow depth [24]. It is also important when determining depth of flow to observe maximum shear stress to create maximum scour depth in clear water conditions. Since local scour depend on sediment and erosion deposition, a different evolution in hole scouring is expected. In clear water, the scour depth increases slowly until it becomes stable. In order to assess scour conditions in clear water state ${V \mathord{\left/ {\vphantom {V {V_{C} }}} \right. \kern-\nulldelimiterspace} {V_{C} }} \le 1$ was considered which in this relation V is the mean velocity upstream of the bridge and $V_{C}$ is the critical velocity [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32]. The model was designed for scour in clear water. Melville and Chew [25] stated that, when the relative velocity is 0.3 < V/V_c < 1, scour occurs in clear water state. The critical flow velocity on the removable bed and the absence of the piers was calculated in several steps by establishing a constant flow rate of 25 l/s and gradual decreasing the depth of flow. In all experiments, constant depths of 16 and 15 cm were selected. Table 3 shows the flow conditions of the experiment.

Table 3 Hydraulic conditions for testing in lab

Scour occurs over time until it reaches equilibrium state. Melville and Chew and Dey et al. [11,12,13,14,15,16,17,18,19,20,21,22,23,24,25] found that the time to equilibrium of scour was related to flow conditions, geometry and bed material parameters. Researchers have attempted to standardize calculation of time to reach equilibrium. Ettema [12] found that the time to reach equilibrium state for scour in a 4 h period produced an increase in scour depth of ≤ 1 mm. Kumar et al. [19] measured scour from the beginning of a 3 h experiment and found it to be ≤ 1 mm. In this study, to determine the maximum time for experimental testing, a 300 min test was conducted at a flow rate of 25 L/s (relative velocity: V/V_c = 0.95). The scour depth was measured in front of each pier every 5 min for the first hour, every 15 min for the second hour and every half-hour for the third hour and over. When maximum scour occurred and changes in scour became negligible over time, the experimental was stopped. Figure 3a and b show the variation of times scour depth for different size of the piers and two case of bed material.

Fig. 3

Variation of scour depth versus time in the different piers diameter a 0.5 mm bed material, b 0.7 mm bed material

3 Results and discussion

In all experiments, after confirming the vertical position of the pier, the flow rate and depth were adjusted. Vortices immediately appeared around the pier and rapid scouring occurred. Shortly after the start of the experiment, upon the formation of a scour hole, deposits rising out of the hole were transmitted downstream by the secondary flow. A total of 48 experiments for each diameter cylindrical piers were carried out at relative velocities of 0.95, 0.86, 0.76 and 0.67 corresponding to the upstream Froude Numbers for each bed material size in clear water (Table 4).

Table 4 Scour depth versus pier diameter (d_s/D) under constant hydraulic conditions

Dimensional analysis was used to find the parameters of changes in parameters and the mathematical relationships were developed using nonlinear multivariate regression analysis in SPSS software to predict maximum depth of scour. After multiple analyses, the following relations in tables Eqs. (3) to (8) in (Table 5) were extracted which R² is the correlation coefficient between values and α is the significant level of value dispersion. In the Fig. 4 the scour geometry were shown for two cases in which Fig. 4a is the scour pattern around pier that pier diameter was 100 mm in ${V \mathord{\left/ {\vphantom {V {V_{c} }}} \right. \kern-\nulldelimiterspace} {V_{c} }} = 0.95$ and the size of bed 0.7 mm material cases. Figure 4b also shows the scour pattern around pier that the pier diameter was 60 mm in ${V \mathord{\left/ {\vphantom {V {V_{c} }}} \right. \kern-\nulldelimiterspace} {V_{c} }} = 0.95$ and the size of bed 0.5 mm material cases. If there is an obstacle in front of the water flow, the study of horseshoe vortex around the pier would be substantial. In fact, when an obstacle such as bridge pier is in the front part of the stream, therefore, considering the water flow condition will be important [20]. According to Fig. 4a and b, if the flow of water is hit by a bridge pier and passes it, then the horseshoe vortex would transfer sediments around the bridge pier to downstream of the flume. In consequence, scour will create a hole around the bridge piers based on the sediment movement. If the power of the water stream increases, more sediment will be transferred. In addition, the maximum depth of scour occurs in front of the bridge pier, and the scour hole would be symmetrical around the pier on both sides. Moreover, scour depth will decrease to downstream, and sediment will be collected at the back of the pier as well. Furthermore, scour volume will rise when the pier diameter increases, in consequence the hole around the bridge pier would be greater. The contours shown on related figures are erosion lines $\left( {Z\langle 0} \right)$, sedimentation lines $\left( {Z\rangle 0} \right)$ and the bed level $\left( {Z = 0} \right)$. More recently, experimental studies also have shown sediment transport rate [10,11,12,13,14, 23].

Table 5 The equations for bridge pier scour this study

Fig. 4

Influence of different dimensions of bridge pier in the reduction of scour depth: Scour hole was drawn with Surfer software a 0.7 mm bed material, b 0.5 mm bed material

Figure 5 compares the measured (d_s/D) values (vertical axis) and the calculated (d_s/D) using Eqs. (3) to (8) (horizontal axis) which were acquired by the measured values of experiments under different experimental conditions and a wide range of parameters. The dispersion of points when compared to line 45 of Fig. 5 shows that the experimental and computational values were relatively well correlated. The data have set in the 40% error range with Pearson Method. The R² values for the experimental and computational results for Eqs. (3) to (8) were 0.91, 0.95, 0.92, 0.9, 0.93 and 0.97, respectively, which demonstrate satisfactory compliance.

Fig. 5

Comparison of measured and calculated relative scour depth (d_s /D) using Eqs. (3) to (8)

The equations extracted using the maximum depth from field observations were compared with field data to determine which relationship produced responses that were closest to the actual values. The flows recorded on the field observation day (Table 2) were obtained using Eqs. (3) to (8) (Table 5). Table 6 shows that the 30 mm pier for the 1/50 scale model compared to the field records can be considered the most appropriate basis for the scale model. It was necessary to alter the other bases to make them closer to scale. Figure 6 shows scour hole around Naderi and Fifth Bridges in 2 m from the river sedimentation bed that measurements were around the bridge pier. The data are real data from river bed for drawing scour hole around the piers that the data measured with echo-sounder.

Table 6 Results of field results versus those from Eqs. (3) to (8)

Fig. 6

Bed topography in the field: scour hole around bridge pier in Karon river- (Ahwaz) a Naderi bridge pier b Fifth bridge pier

Figure 7 shows the measured d_s/D versus pier diameter for different particle Froude Numbers. It was necessary to use the same hydraulic conditions to compare the laboratory and field values. Figure 8 shows the measured and calculated d_s/D for the Naderi Bridge and the particle Froude Number of Fifth Bridge (F_rg).

Fig. 7

Changes in measured (d_s/D) versus diameter of pier for different F_rg

Fig. 8

Changes in (d_s/D) for measured values from Naderi and Fifth Bridges for F_rg = 2

As it can be seen, the relative scour depths of the piers of 10, 20 and 30 mm are similar to the relative scour depth at the Naderi and Fifth Bridges. This shows that piers with diameters of less than 30 mm had relative scour depths similar to field measurement and indicates that Eqs. (3) to (5) are suitable for calculation of (d_s/D). Mod lines piers with diameters of more than 30 mm showed relative scour depths are below those of the Naderi and Fifth Bridges. It was necessary to find the coefficient $\left( {{D \mathord{\left/ {\vphantom {D y}} \right. \kern-\nulldelimiterspace} y}_{0} } \right)^{\alpha }$ from relations (6) to (8) using equation $\left( {{{d_{s} } \mathord{\left/ {\vphantom {{d_{s} } D}} \right. \kern-\nulldelimiterspace} D}} \right)_{p} = \left( {{{d_{s} } \mathord{\left/ {\vphantom {{d_{s} } D}} \right. \kern-\nulldelimiterspace} D}} \right)_{m} \times \left( {{D \mathord{\left/ {\vphantom {D {y_{0} }}} \right. \kern-\nulldelimiterspace} {y_{0} }}} \right)^{\alpha }$ is shows in Table 5, and use it in the equations to make it closer to the relative scour depth of the 40, 60 and 100 mm mod lines piers under field conditions. Figure 9 shows (d_s/D) versus the diameter of the tested piers after modification of the relations. It was shown after modification that the relative scour depth of piers tested under field conditions was similar to the relative scour depth of the Naderi and Fifth Bridges. Figure 10 also shows the changes in relative scour depth after correction of the relations compared to the field conditions for a particle Froude Number equal to 2.

Fig. 9

Changes in (d_s/D) versus pier diameter after modification of proposed relations at F_rg = 2

Fig. 10

Relative scour depth change after modification of relations versus field conditions

Figure 11 compares (d_s /D) are made using experimental values (vertical axis) and (d_s/D) using Eqs. (3) to (5) for 10, 20 and 30 mm piers and modified Eqs. (9) to (11) for 40, 60 and 100 mm piers (horizontal axis). R² for the laboratory and computational values were 0.79, 0.74, 0.87, 0.88, 0.89 and 0.9, respectively.

Fig. 11

Comparison of measured and calculated (d_s/D) using relations (3) to (5) and modified relations (9) to (11)

4 Discussion

The main cause of concern about the stability of bridge pier is the occurrence of scour around the piers. Therefore, there is an interest in finding reliable ways to reduce and control local scour depth. Local scour around a cylindrical bridge pier results from the down flow at the upstream face of the pier and the horseshoe vortex (HSV) at the base of the pier. Separation of the flow at the sides of the pier also creates the so-called wake vortices. These vortices are unstable and shed alternatively from each side of the pier. They act as little tornadoes lifting the sediment particles from the bed and form a scour hole around of the pier. Countermeasures for local scour at bridge piers can be grouped in two categories: armoring devices and flow-altering methods. This study is done with the purpose of examination of the effect of bridge pier’s dimension in the scour hole. Failure of bridges because of scouring is a common occurrence. In each year, a significant amount of money is spent to repair or reconstruct bridges which their piers or abutments have been damaged. Because of failure experiences, many researchers have worked on scour phenomena during the last decades. Consequently, two selected researches have been used that their experimental results are almost matched to that of the current study.

4.1 Comparison of results with those of previous studies

Figure 12 compares the effect of the present research [measured (d_s/D)] with scour equations proposed by Breusers [5] and Jane [17]. If (d_s/D) is a one-parameter function of F_rg $\left( {{{d_{s} } \mathord{\left/ {\vphantom {{d_{s} } {D\infty F_{rg} }}} \right. \kern-\nulldelimiterspace} {D\infty F_{rg} }}} \right)$ and if D > 30 mm, then (d_s/D) is a function of two parameters such as F_rg and pier diameter to depth of flow $\left( {{{d_{s} } \mathord{\left/ {\vphantom {{d_{s} } {D\infty F_{rg} ,{{\,D} \mathord{\left/ {\vphantom {{\,D} {y_{0} }}} \right. \kern-\nulldelimiterspace} {y_{0} }}}}} \right. \kern-\nulldelimiterspace} {D\infty F_{rg} ,{{\,D} \mathord{\left/ {\vphantom {{\,D} {y_{0} }}} \right. \kern-\nulldelimiterspace} {y_{0} }}}}} \right)$. Table 7 shows the correlation coefficients between values. After achieving the scour depths based on the equation, we compared our study to other researches with similar hydraulic conditions. Accordingly, two equations from Breusers [5] and Jain [15] were considered in this study, which were written in the below table. It was concluded that the Reynolds number is almost in laminar flow condition in diameter of 10 and 20 mm. On the other hand, the Reynolds number is in turbulent flow condition for other cylindrical bridge pier. Therefore, pier with a scale of < 1.5 has almost maximum scour depth like scour depth in the field. If the cylindrical bridge pier diameter increases, so the Reynolds number $\left( {R_{e} = {{VD} \mathord{\left/ {\vphantom {{VD} \mu }} \right. \kern-\nulldelimiterspace} \mu }} \right)$ will rise and the boundary layer would develop mostly around the bridge pier. Table 7 shows that $R^{2}$ connection between the lab data in the present paper (Table 4) and the researcher’s data in their equation with current hydraulic conditions (Fig. 12), which has been extracted via statistical methods.

Fig. 12

Comparison of measured and calculated (d_s/D)

Table 7 R² for this study and previous studies

5 Conclusion

The current paper hypothesis is finding the proper pier through comparing a wide range of field data which its performance will be better than other ones in the same conditions. The tests are carried out for six cylindrical bridge piers (D) with diameter of 10, 20, 30, 40, 60 and 100 mm in condition of clear water in a laboratory flume with the mean bed particles measure of 0.5 mm and 0.7 mm. Therefore, in this research cylindrical shape bridge pier was selected and the effects of piers diameters and particle Froude Number were investigated on scour development. It was observed that, the maximum velocity occur near the piers, since the down flow developed the significant secondary currents, so this and generated vortex can be considered as effective parameters on the bridge scour. The results show that in all pier diameters, the maximum scour depth increases to the Froud Number. In addition, statistical analysis shows that piers 30 mm in diameter and a scale of 1/50 of field values is recommended as suitable. If this scale is used under experimental conditions, the results will be approximately consistent with field measurement values. The effect of pier diameter and scale agreement with the field conditions suggests that the (d_s/D) of piers with a diameter of < 30 mm are similar to that for the (d_s/D) of piers in the field. The relations for piers of 10 and 20 mm indicate that (d_s/D) is a one-parameter function of F_rg and provided appropriate predictions. The relative scour depth for pier diameter > 30 mm was lower than (d_s/D) in compare with the field data. By finding the power of α in the coefficient ${D \mathord{\left/ {\vphantom {D {y_{0} }}} \right. \kern-\nulldelimiterspace} {y_{0} }}$ and multiplying it by the common equations for piers with 40, 60 and 100 mm diameters, it is possible that produce similar (d_s /D) relative to scour depth in the field. The (d_s/D) in these piers are two-parameter function including the F_rg and the ratio of pier diameter to depth of flow. These equations was insufficient between the measured (d_s/D) and the values from the relations provided by Breusers and Jane and confirms the positive results for the proposed method. In most cases, due to the limitations in the process of building a bridge, the circular cross-section bridge piers will be used. In this manuscript, this kind of bridge piers have been tested as well. On the other hand, the equipment used in this study could not measure dynamic behavior and momentarily scour. In consequence, the study on the non-circular cross-sections bridge piers and the momentarily scour around the bridge piers can be discussed in the future works.