Dynamical Behaviour of an Infected Predator-Prey Model with Fear Effect

Abstract

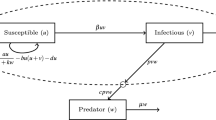
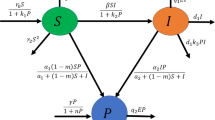
In this article, we have presented an infected predator-prey model with Holling type II functional response where the predator population is divided into two sub-classes, namely susceptible and infected due to disease. Here, we have assumed that the fear induced by susceptible and infected predators are of different levels. Well-posedness of the model system along with persistence criterion and the conditions of local stability of each equilibrium point have been established. Direction of Hopf bifurcation near the interior equilibrium point has been investigated. From model analysis, it is observed that fear induced by both susceptible and infected predators jointly determine dynamical complexity of the system. Fear induced by susceptible predators enhances the stable coexistence of the system whereas high amount of fear induced by infected predators destabilizes the system. It is also observed that the ratio of the birth rate of prey and the level of fear induced by both the susceptible and infected predators actively determine the topological behaviour of the system. We have performed comprehensive and meticulous numerical simulations to verify and validate the analytical findings of our model system, and finally, the article is ended up with a conclusion.

Appendix

$A_1$: The detailed calculation of Permanence of Sect. 3.3 The supremum value $Q_1,Q_2,Q_3$, according to Standard Comparison theorem, can be obtained as a positive solutions of the following system of equations

$$\begin{aligned}&x\left( r-d_1-\frac{c_2z}{b_1+x}\right) =0, \end{aligned}$$

(7.1)

$$\begin{aligned}&\quad y\left( \frac{c_3x}{b_1}-d_2\right) =0, \end{aligned}$$

(7.2)

$$\begin{aligned}&\quad z\left( \frac{c_4x}{b_1}+ay-d_3\right) =0. \end{aligned}$$

(7.3)

Solving the above system of equations, we get $x=\frac{b_1d_2}{c_3}=Q_1,~ y=\frac{c_3d_3-c_4d_2}{ac_3}=Q_2,~ z=\frac{b_1(c_3+d_2)(r-d_1)}{c_2c_3}=Q_3.$ Interestingly, inequalities (3.4), (3.5), (3.6) can be written in the following form

$$\begin{aligned}&\frac{\text {d}x}{\text {d}t}\ge x\left( \frac{r}{1+k_1Q_2+k_2Q_3}-mx-d_1-\frac{(c_1Q_2+c_2Q_3)}{b_1}\right) , \end{aligned}$$

(7.4)

$$\begin{aligned}&\quad \frac{\text {d}y}{\text {d}t}\ge y\left( \frac{c_3x}{b_1+Q_1}-az-d_2\right) , \end{aligned}$$

(7.5)

$$\begin{aligned}&\quad \frac{\text {d}z}{\text {d}t}\ge z\left( \frac{ay}{1+bQ_3}-d_3\right) . \end{aligned}$$

(7.6)

Similarly, we get $x=\frac{s_1}{s_2}=q_1, y=\frac{d_3\{c_2c_3+bb_1(c_3+d_2)(r-d_1)\}}{ac_2c_3}=q_2, ~z=\frac{c_3^2s_1-b_1d_2s_2(c_3+d_2)}{b_1s_2(c_3+d_2)}=q_3,$ and $s_1=a^2c_2c_3^2b_1r-\{ac_2c_3+k_1c_2(c_3d_3-c_4d_2)+ab_1k_2(c_3+d_2)(r-d_1)\}\{ab_1c_3d_1+c_1(c_3d_3-c_4d_2)+ab_1(c_3+d_2)(r-d_1)\}$, $s_2=mab_1c_3\{ac_2c_3+k_1c_2(c_3d_3-c_4d_2)+ab_1k_2(c_3+d_2)(r-d_1)\}$. Now, $Q_1$ is always positive, $Q_2>0 ~\mathrm {if}~ c_3d_3>c_4d_2$, $Q_3, q_2>0$ as $r>d_1$ and $q_3$ will be positive if $\frac{s_1}{s_2}>\frac{b_1d_2(c_3+d_2)}{c_3^2}$ which consequently satisfies the positivity of $q_1$.

$A_2$:The detailed calculation of direction and stability of Hopf bifurcation of Sect. 5.2

$$\begin{aligned} g_{11}&= \frac{1}{4}\left[ \left( \frac{\partial ^2 H_1}{\partial x_1^2}+\frac{\partial ^2 H_2}{\partial y_1^2}\right) +i\left( \frac{\partial ^2 H_2}{\partial x_1^2}+\frac{\partial ^2 H_1}{\partial y_1^2}\right) \right] \\&=\frac{1}{4N}\big [\left\{ {Q_1}_{x_1 x_1}p_{22}-{Q_2}_{x_1 x_1}p_{12}+u_1{Q_3}_{x_1 x_1}+u_5{Q_1}_{y_1 y_1}-u_6{Q_2}_{y_1 y_1}+u_2{Q_3}_{y_1 y_1} \right\} \\&\quad +i\big \{u_5{Q_1}_{x_1 x_1}-u_6{Q_2}_{x_1 x_1}+u_2{Q_3}_{x_1 x_1}\\&\quad +p_{22}{Q_1}_{y_1 y_1}-p_{12}{Q_2}_{y_1 y_1}+u_4{Q_3}_{y_1 y_1}\big \}\big ],\\ g_{02}&=\frac{1}{4}\left[ \left( \frac{\partial ^2 H_1}{\partial x_1^2}\right. \right. \\&\left. \left. \quad -\frac{\partial ^2 H_1}{\partial y_1^2}-2\frac{\partial ^2 H_2}{\partial x_1\partial y_1}\right) +i\left( \frac{\partial ^2 H_2}{\partial x_1^2}-\frac{\partial ^2 H_2}{\partial y_1^2}+2\frac{\partial ^2 H_1}{\partial x_1\partial y_1}\right) \right] \\&=\frac{1}{4N}\big [\left\{ {Q_1}_{x_1 x_1}p_{22}-{Q_2}_{x_1 x_1}p_{12}\right. \\&\left. \quad +u_1{Q_3}_{x_1 x_1}-({Q_1}_{y_1 y_1}p_{22}-{Q_2}_{y_1 y_1}p_{12}\right. \\&\left. \quad +u_1{Q_3}_{y_1 y_1})-2(u_5{Q_1}_{x_1 y_1}-u_6{Q_2}_{x_1 y_1}+u_2{Q_3}_{x_1 y_1}) \right\} \\&\quad +i\big \{u_5{Q_1}_{x_1 x_1-u_6{Q_2}_{x_1 x_1}+u_2{Q_3}_{x_1 x_1}-(u_5{Q_1}_{y_1 y_1}-u_6{Q_2}_{y_1 y_1}+u_2{Q_3}_{y_1 y_1}) +2({Q_1}_{x_1 y_1}p_{22}-{Q_2}_{x_1 y_1}p_{12}+u_4{Q_3}_{x_1 y_1})}\big \}\big ],\\ g_{20}&=\frac{1}{4}\left[ \left( \frac{\partial ^2 H_1}{\partial x_1^2}-\frac{\partial ^2 H_1}{\partial y_1^2}+2\frac{\partial ^2 H_2}{\partial x_1\partial y_1}\right) +i\left( \frac{\partial ^2 H_2}{\partial x_1^2}-\frac{\partial ^2 H_2}{\partial y_1^2}-2\frac{\partial ^2 H_1}{\partial x_1\partial y_1}\right) \right] \\&= \frac{1}{4N}\big [\left\{ {Q_1}_{x_1 x_1}p_{22}-{Q_2}_{x_1 x_1}p_{12}\right. \\&\left. \quad +u_1{Q_3}_{x_1 x_1}-({Q_1}_{y_1 y_1}p_{22}-{Q_2}_{y_1 y_1}p_{12}+u_1{Q_3}_{y_1 y_1})+2(u_5{Q_1}_{x_1 y_1}-u_6{Q_2}_{x_1 y_1}+u_2{Q_3}_{x_1 y_1}) \right\} \\&\quad +i\big \{u_5{Q_1}_{x_1 x_1-u_6{Q_2}_{x_1 x_1}+u_2{Q_3}_{x_1 x_1}-(u_5{Q_1}_{y_1 y_1}-u_6{Q_2}_{y_1 y_1}+u_2{Q_3}_{y_1 y_1}) -2({Q_1}_{x_1 y_1}p_{22}-{Q_2}_{x_1 y_1}p_{12}+u_4{Q_3}_{x_1 y_1})}\big \}\big ],\\ G_{21}&=\frac{1}{8}\left[ \left( \frac{\partial ^3 H_1}{\partial x_1^3}+\frac{\partial ^3 H_1}{\partial x_1\partial y_1^2}+\frac{\partial ^3 H_2}{\partial x_1^2\partial y_1}+\frac{\partial ^3 H_2}{\partial y_1^3}\right) +i\left( \frac{\partial ^3 H_2}{\partial x_1^3}+\frac{\partial ^3 H_2}{\partial x_1\partial y_1^2}-\frac{\partial ^3 H_1}{\partial x_1^2\partial y_1}-\frac{\partial ^3 H_1}{\partial y_1^3}\right) \right] \\&= \frac{1}{8N}\big [\big \{({Q_1}_{x_1 x_1 x_1}p_{22}-{Q_2}_{x_1 x_1 x_1}p_{12}\\&\quad +u_1{Q_3}_{x_1 x_1 x_1})+({Q_1}_{x_1 y_1 y_1}p_{22}-{Q_2}_{x_1 y_1 y_1}p_{12}+u_1{Q_3}_{x_1 y_1 y_1})+(u_5{Q_1}_{x_1 x_1 y_1}-u_6{Q_2}_{x_1 x_1 y_1}\\&\quad +u_2{Q_3}_{x_1 x_1 y_1})+(u_5{Q_1}_{y_1 y_1 y_1}-u_6{Q_2}_{y_1 y_1 y_1}\\&\quad +u_2{Q_3}_{y_1 y_1 y_1}) \big \} +i\big \{u_5{Q_1}_{x_1 x_1 x_1}-u_6{Q_2}_{x_1 x_1 x_1}+u_2{Q_3}_{x_1 x_1 x_1}+(u_5{Q_1}_{x_1 y_1 y_1}-u_6{Q_2}_{x_1 y_1 y_1}\\&\quad +u_2{Q_3}_{x_1 y_1 y_1})-({Q_1}_{x_1 x_1 y_1}p_{22}-{Q_2}_{x_1 x_1 y_1}p_{12}+u_1{Q_3}_{x_1 x_1 y_1})- ({Q_1}_{y_1 y_1 y_1}p_{22}-{Q_2}_{y_1 y_1 y_1}p_{12}+u_1{Q_3}_{y_1 y_1 y_1}) \big \}\big ], \\ \omega&=-\frac{\partial H_1}{\partial y_1}=-\frac{1}{N}[{Q_1}_{y_1}p_{22}-{Q_2}_{y_1}p_{12}+u_1{Q_3}_{y_1}], \\ h_{11}&=\frac{1}{4}\left[ \left( \frac{\partial ^2 H_3}{\partial x_1^2}+\frac{\partial ^2 H_3}{\partial y_1^2}\right) \right] \\&=\frac{1}{4N}[(-{Q_1}_{x_1 x_1}p_{22}+{Q_2}_{x_1 x_1}p_{12}\\&\quad +u_3{Q_3}_{x_1 x_1})+(-{Q_1}_{y_1 y_1}p_{22}+{Q_2}_{y_1 y_1}p_{12}+u_3{Q_3}_{y_1 y_1})],\\ h_{20}&=\frac{1}{4}\left[ \left( \frac{\partial ^2 H_3}{\partial x_1^2}-\frac{\partial ^2 H_3}{\partial y_1^2}-2i\frac{\partial ^2 H_3}{\partial x_1 \partial y_1}\right) \right] \\&=\frac{1}{4N}[(-{Q_1}_{x_1 x_1}p_{22}+{Q_2}_{x_1 x_1}p_{12}\\&\quad +u_3{Q_3}_{x_1 x_1})+(-{Q_1}_{y_1 y_1}p_{22}+{Q_2}_{y_1 y_1}p_{12}+u_3{Q_3}_{y_1 y_1})-2i(-{Q_1}_{x_1 y_1}p_{22}+-{Q_2}_{x_1 y_1}p_{12}\\&\quad +u_3{Q_3}_{x_1 y_1})],\\ M_5&= \frac{\partial H_3}{\partial z_1}=-{Q_1}_{z_1}p_{22}+{Q_2}_{z_1}p_{22}+u_3{Q_3}_{z_1}. \end{aligned}$$

To find the value of $\omega _{11}$ and $\omega _{20}$, we have to solve,

$$\begin{aligned} M_5 \omega _{11} =-h_{11},~ (N-2i\omega )\omega _{20}=-h_{20}, \end{aligned}$$

Additionally,

$$\begin{aligned} G_{110}&= \frac{1}{2}\left[ \left( \frac{\partial ^2 H_1}{\partial x_1 \partial z_1}+\frac{\partial ^2 H_2}{\partial y_1 \partial z_1}\right) \right. \\&\left. \quad +i\left( \frac{\partial ^2 H_2}{\partial x_1 \partial z_1}-\frac{\partial ^2 H_1}{\partial y_1 \partial z_1}\right) \right] , \\&= \big [ \big \{{Q_1}_{x_1 z_1}p_{22}-{Q_2}_{x_1 z_1}p_{12}+u_1{Q_3}_{x_1 z_1}\\&\quad +u_5{Q_1}_{y_1 z_1}-u_6{Q_2}_{y_1 z_1}+u_2{Q_3}_{y_1 z_1} \big \}+i\big \{(u_5{Q_1}_{x_1 z_1}-u_6{Q_2}_{x_1 z_1}+u_2{Q_3}_{x_1 z_1})-({Q_1}_{y_1 z_1}p_{22}\\&\quad -{Q_2}_{y_1 z_1}p_{12}+u_4{Q_3}_{y_1 z_1}) \big \} \big ],\\ G_{101}&= \frac{1}{2}\left[ \left( \frac{\partial ^2 H_1}{\partial x_1 \partial z_1}-\frac{\partial ^2 H_2}{\partial y_1 \partial z_1}\right) +i\left( \frac{\partial ^2 H_2}{\partial x_1 \partial z_1}+\frac{\partial ^2 H_1}{\partial y_1 \partial z_1}\right) \right] , \\&= \big [ \big \{{Q_1}_{x_1 z_1}p_{22}-{Q_2}_{x_1 z_1}p_{12}+u_1{Q_3}_{x_1 z_1}\\&\quad -(u_5{Q_1}_{y_1 z_1}-u_6{Q_2}_{y_1 z_1}+u_2{Q_3}_{y_1 z_1}) \big \}+i\big \{(u_5{Q_1}_{x_1 z_1}-u_6{Q_2}_{x_1 z_1}+u_2{Q_3}_{x_1 z_1})\\&\quad +({Q_1}_{y_1 z_1}p_{22}-{Q_2}_{y_1 z_1}p_{12}+u_4{Q_3}_{y_1 z_1}) \big \} \big ],\\ g_{21}&= G_{21}+2G_{110}\omega _{11}+G_{101}\omega _{20}. \end{aligned}$$

where $u_1=p_{12}p_{23}-p_{13}p_{22},~u_2=p_{21}p_{13}-p_{11}p_{23},~u_3=p_{11}p_{22}-p_{12}p_{21},~u_4=p_{12}p_{23}-p_{13}p_{23},~u_5=p_{23}-p_{21},~u_6=p_{13}-p_{11},~u_7=p_{22}-p_{21}.$ Now, let us consider $g_1=1+k_1y^*+k_2z^*,~g_2=b_1+x^*,~g_3=1+bz^*,~g_4=k_1p_{21}+k_2p_{31},~g_5=k_1p_{22}+k_2p_{32},~g_6=k_1p_{23}+k_2p_{33}$ so that ${Q_1}_{x_1 x_1}=\frac{2rg_4(g_4x^*-g_1p_{11})}{g_1^3}-2mp_{11}^2+\frac{2p_{11}p_{21}c_1(x^*-g_2)}{g_2^2}+\frac{2b_1p_{11}^2c_1y^*}{g_2^3}$. Similarly, the other expressions related with the terms $g_{11},~g_{02},~g_{20},~G_{21},~\omega ,~h_{11},~h_{20},~M_5,~G_{110},~G_{101},~g_{21}$ can be obtained from the partial derivative of $Q_i,~i=1,2,3$ w.r.t. $x_1,y_1,z_1$ at the interior equilibrium point $E^*(x^*,y^*,z^*)$ (for details see Hassard et al. 1981; Khajanchi 2017)