Introduction

Monkeypox is a severe viral zoonotic disease (i.e., animal-to-human infection) that occurs sporadically, primarily in rural areas in Central and Western Africa, near tropical rainforests. This is caused by the monkeypox virus within the Poxviridae family that belongs to the genus Orthopoxvirus (Durski et al. 2018; Jezek et al. 1988). The genus Orthopoxvirus also comprises variola virus (the origin of smallpox), vaccinia virus (used for the eradication of smallpox in the vaccine), and cowpox virus (used in the earlier vaccine). Monkeypox virus is mainly transmitted to humans from wild animals such as rodents and primates, but transmission often occurs from humans to humans. Human to human transmission has been linked to respiratory droplets and contact with bodily fluids, a contaminated patient’s environment or items, and a skin lesion on an infected individual (Alakunle et al. 2020). Monkeypox virus has emerged as the most common orthopox virus after the eradication of the smallpox (Kantele et al. 2016). Fever, headache, muscle aches, backache, swollen lymph nodes, chills, and weariness are some of the symptoms that some individuals who may have contracted monkeypox experience. Up to a tenth of those infected with monkeypox die, with the majority of deaths happening in children under the age of ten (Nguyen et al. 2021).

Monkeypox was identified in 1958 when two pox-like disease outbreaks occurred in monk colonies held for study, hence the term ’monkeypox. The first human case was reported in the Democratic Republic of Congo in 1970 during a time of increased attempts to eradicate the smallpox. Among other Central and Western African countries like Cameroon, Gabon, Cote d’Ivoire, Liberia, Central African Republic, Congo, South Sudan and Sierra Leone, monkeypox has since been identified in humans. The first proof of monkeypox outbreaks in humans outside of Africa was a 2003 outbreak in the US. Monkeypox importation was later recognized in the United Kingdom and Israel. Mortality rate ranged from 1 percent to 10 percent in occurrences, with most deaths arising in younger populations (Ladnyj et al. 1972; CDC 2003). Monkeypox’s incubation period is typically about 6–16 days but can vary from 5 to 21 days. There are two facets of the contagious era, with an initial intrusive duration in the first 5 days, where the main signs are fever, lymphadenopathy (lymph node swelling), back pain, extreme headache, myalgia (muscle ache) and serious asthenia (energy shortage). A maculopapular rash (flat-based skin lesions) occurs 1–3 days after the onset of fever, and grows into small fluid-filled blisters (vesicles), which are pus-filled and then crust over in about ten days (Hutson et al. 2013).

Presently, there are no clear treatments available for monkeypox infection, though numerous novel antivirals, such as Brincindofovir, Tecovirimat and vaccinia immue globulin can be used to control the spread of the disease. There has been a significant increase in monkeypox in the last decade, associated with the decrease in herd immunity to smallpox. Vaccination against smallpox has been shown to be successful at 85 percent in the prevention of monkeypox but is no longer regularly available since global eradication of smallpox. The post-exposure vaccine can help prevent or decrease the severity of the disease (Rimoin et al. 2010; Meyer et al. 2020).

The disease has been given little attention in the past and this has contributed to insufficient knowledge on its mechanisms of transmission. Nevertheless, few studies have tried to research dynamics of monkeypox virus using a mathematical modelling technique. Study in Bhunu and Mushayabasa (2011) provides the basis for transmission analysis of pox-like dynamics of monkeypox virus as a case study. In Bhunu et al. (2009), the authors have shown that with the planned treatment intervention, the disease will be eradicated from both human and non-human primates in due time. The dynamics of monkeypox virus in human host and rodent with the stability analysis is studied in Usman and Adamu (2017). Other significant contributions can be found in TeWinkel (2019), Somma et al. (2019), Bankuru et al. (2020), Grant et al. (2020). Having gone through several works on the monkeypox virus and its mechanisms of transmission, we found that none considered the combination of isolated, exposed compartments in the human subpopulation and the effects of that contact rate with rodent population. Our aim is to investigate the various factors that could lead to reduction in the disease transmission and the effects of such factors on the basic reproduction number.

The rest of this paper is structured as follows: Method which includes model formulation and analysis are described in “Method” section. Next, “ Backward bifurcation” section consists of the numerical simulations and results, discussion of results is given in “Results”, “Discussion” sections. Finally, in “Conclusion” section, we have provided conclusions of this article. Table 1 shows a detailed description of the parameters, while the model’s compartmental flow diagram is shown in Fig. 1.

Method

We propose a deterministic compartmental model on the transmission dynamics of monkeypox consisting of two populations that is, humans and rodents. The human population is further subdivided into five compartments, susceptible humans \(S_{\rm h}(t)\), exposed humans \(E_{\rm h}(t)\), infected humans \(I_{\rm h}(t)\), isolated humans \(Q_{\rm h}(t)\) and recovered humans \(R_{\rm h}(t)\). The rodent population is subdivided into three compartments, susceptible rodents \(S_{\rm r}(t)\), exposed rodents \(E_{\rm r}(t)\) and infected rodents \(I_{\rm r}(t)\). Recruitment into human population is at a rate \(\theta _{\rm h}\). \(\beta _1\) is the effective contact rate with the probability of human been infected with the virus per contact with an infected rodent and \(\beta _2\) is the product of effective contact rate and the probability of human been infected with monkey pox virus after getting in contact with infectious human. The proportion of exposed individuals moving to highly infected class is \(\alpha _2\) while the proportion identified is \(\alpha _1\). After medical diagnosis, some suspected cases are confirmed, where others were not detected and returned back to susceptible humans a rate \(\varphi \). The suspected cases are treated and moved to recovered class at a rate \(\tau \). The recovery rate for human is at a rate \(\gamma \). Natural death occurs in the humans and rodents population at the rates \(\mu _{\rm h}\) and \(\mu _{\rm r}\) respectively. \(\beta _3\) is the effective contact rate with the probability of rodent been infected per contact with infected rodent. The infected rodent population decreased by natural mortality rate \(\mu _{\rm r}\) or by disease induced death rate \(\delta _r\). The transition among various compartments considered in the model is illustrated in Fig. 1, the model is governed by the following set of nonlinear differential equations below:

$$\begin{aligned} \begin{aligned} \frac{{\rm d}S_{\rm h}}{{\rm d}t}&=\theta {_{\rm h}}-\frac{(\beta _1I_{\rm r}+\beta _2 I_{\rm h})\ S_{\rm h}}{N_{\rm h}} -\mu _{\rm h}\ S_{\rm h}+\varphi Q_{\rm h} \\ \frac{{\rm d}E_{\rm h}}{{\rm d}t}&=\frac{(\beta _1I_{\rm r}+\beta _2 I_{\rm h})\ S_{\rm h}}{N_{\rm h}} -(\alpha _1+\alpha _2+\mu _{\rm h}\ )\ E_{\rm h} \\ \frac{{\rm d}I_{\rm h}}{{\rm d}t}&=\alpha _1\ E_{\rm h}-(\mu _{\rm h}+\delta _{\rm h}+\gamma )\ I_{\rm h }\\ \frac{{\rm d}Q_{\rm h}}{{\rm d}t}&=\alpha _2\ E_{\rm h}-(\varphi +\tau +\delta _{\rm h}+\mu _{\rm h}\ )\ Q_{\rm h} \\ \frac{{\rm d}R_{\rm h}}{{\rm d}t}&=\gamma I_{\rm h}+\tau Q_{\rm h}-\mu _{\rm h}\ R_{\rm h} \\ \frac{{\rm d}S_{\rm r}}{{\rm d}t}&=\theta _{\rm r}-\frac{\beta _3\ S_{\rm r}\ I_{\rm r}}{N_{\rm r}} -\mu _{\rm r}\ S_{\rm r} \\ \frac{{\rm d}E_{\rm r}}{{\rm d}t}&=\frac{\beta _3\ S_{\rm r}\ I_{\rm r}}{N_{\rm r}} -(\mu _{\rm r}+\alpha _3)E_{\rm r} \\ \frac{{\rm d}I_{\rm r}}{{\rm d}t}&=\alpha _3\ E_{\rm r}-(\mu _{\rm r}+\delta _{\rm r})I_{\rm r} \end{aligned} \end{aligned}$$
(1)
Fig. 1
figure 1

Schematic representation of the model

Full size image

The model analysis

For the human population, \(N_{\rm h}=S{_{\rm h}}+E{_{\rm h}}+I{_{\rm h}}+Q{_{\rm h}}+R{_{\rm h}}\), the differential equation is given as:

$$\begin{aligned} ({\rm d}N{_{\rm h}})/{\rm d}t=\theta {_{\rm h}}-\delta {_{\rm h}}\ I{_{\rm h}}-\mu {_{\rm h}}\ N{_{\rm h}} \end{aligned}$$
(2)

Also, for the rodent population

\(N{_{\rm r}}=S{_{\rm r}}+E{_{\rm r}}+I{_{\rm r}}\), and the corresponding differential equations is given as:

$$\begin{aligned} ({\rm d}N{_{\rm r}})/{\rm d}t=\theta {_{\rm r}}-(\mu{_{\rm r}}+\theta{_{\rm r}})N{_{\rm r}} \end{aligned}$$
(3)

Theorem 1

Let \(\left( S{_{\rm h}},E{_{\rm h}},I{_{\rm h}},Q{_{\rm h}},R{_{\rm h}},S{_{\rm r}},E{_{\rm r}},R \right) \) be the solution of 1 with the initial conditions in a biologically feasible region \({\Gamma }={\Gamma }{_{\rm h}}\times {\Gamma }{_{\rm r}}\) with:

$$\begin{aligned} {\Gamma }{_{\rm h}}={S{_{\rm h}},E{_{\rm h}},I{_{\rm h}},Q{_{\rm h}},R{_{\rm h}}\in R_+^5:N{_{\rm h}}\le \frac{\theta {_{\rm h}}}{\mu {_{\rm h}}} } \end{aligned}$$
(4)

and

$$\begin{aligned} {\Gamma }{_{\rm r}}={S{_{\rm r}},E{_{\rm r}},R{_{\rm r}}\in R_+^3:N{_{\rm r}}\le \frac{\theta{_{\rm r}}}{\mu{_{\rm r}}}} \end{aligned}$$
(5)

Then \({\Gamma }\) is non-negative invariant

Following the approach of Somma et al. (2019), we have that:

$$\begin{aligned} 0\le N{_{\rm h}}\ (t)\le N{_{\rm h}}\ (0)\ell ^{-\mu {_{\rm h}}\ (t)}+\frac{\theta {_{\rm h}}}{\mu{_{\rm r}}} \left( 1-\ell ^{-\mu {_{\rm h}}\ (t)}\right) \end{aligned}$$
(6)

also

$$\begin{aligned} N{_{\rm r}}\ (t)\le N{_{\rm r}}\ (0)\ell ^{-(\mu{_{\rm r}}+\theta )t}+\frac{\theta{_{\rm r}}}{\mu{_{\rm r}}} \left( 1-\ell ^{-(\mu{_{\rm r}}+\theta )t}\right) \end{aligned}$$
(7)

Hence, the set \({\Gamma }\) is positive invariant and for t.

Monkeypox-free equilibrium state

This occurs in the absence of disease. Thus, in the absence of infection, we set \(E{_{\rm h}},I{_{\rm h}},Q{_{\rm h}},R{_{\rm h}},E{_{\rm r}}\) and \(I{_{\rm r}}\) to zero in 1 and the resulting solution gives the monkeypox-free equilibrium states given as:

$$\begin{aligned} {\Phi }_{\rm MFE} \ (S{_{\rm h}}^*,E{_{\rm h}}^*,I{_{\rm h}}^*,Q{_{\rm h}}^*,R{_{\rm h}}^*,S{_{\rm r}}^*\ E{_{\rm r}}^*,I{_{\rm r}}^*) \end{aligned}$$
(8)

Endemic equilibrium

This occurs when the infection persist in the population represented by \({\Phi }_{\rm MEE} \left( S^*{_{\rm h}},E^*{_{\rm h}},I^*{_{\rm h}},Q^*{_{\rm h}},R^*{_{\rm h}},S^*{_{\rm r}}, E^*{_{\rm r}},I^*{_{\rm r}} \right) \). Thus,

$$\begin{aligned} S^*{_{\rm h}}= & {} \frac{k_1 k_3 \theta {_{\rm h}}}{\mu {_{\rm h}} k_1 k_3-\alpha _2 \varphi \phi {_{\rm h}}+k_1 k_3 \phi {_{\rm h}} } \nonumber \\ E^*{_{\rm h}}= & {} \frac{k_3 \phi {_{\rm h}} \theta {_{\rm h}}}{\mu {_{\rm h}} k_1 k_3-\alpha _2 \varphi \phi {_{\rm h}}+k_1 k_3 \phi {_{\rm h}} } \nonumber \\ I^*{_{\rm h}}= & {} \frac{ k_3 \alpha _1 \phi {_{\rm h}} \theta {_{\rm h}}}{k_2 (\mu {_{\rm h}} k_1 k_3-\alpha _2 \varphi \phi {_{\rm h}}+k_1 k_3 \phi {_{\rm h}})} \nonumber \\ Q^*{_{\rm h}}= & {} \frac{\alpha _2 \phi {_{\rm h}} \theta {_{\rm h}}}{\mu {_{\rm h}} k_1 k_3-\alpha _2 \varphi \phi {_{\rm h}}+k_1 k_3 \phi {_{\rm h}} } \nonumber \\ R^*{_{\rm h}}= & {} \frac{(\alpha _1 \gamma k_3+\alpha _2 k_2 \tau )\phi {_{\rm h}} \theta {_{\rm h}}}{\mu {_{\rm h}} k_2 (\mu {_{\rm h}} k_1 k_3-\alpha _2 \varphi \phi {_{\rm h}}+k_1 k_3 \phi {_{\rm h}})} \nonumber \\ S^*{_{\rm r}}= & {} \frac{\theta{_{\rm r}}}{\mu{_{\rm r}}+\phi{_{\rm r}} } \nonumber \\ E^*{_{\rm r}}= & {} \frac{\theta{_{\rm r}}}{k_4 (\mu{_{\rm r}}+\phi{_{\rm r}})}\nonumber \\ I^*{_{\rm r}}= & {} \frac{\phi{_{\rm r}} \alpha _3 \theta{_{\rm r}}}{k_4 k_5 (\mu{_{\rm r}}+\phi{_{\rm r}})} \end{aligned}$$
(9)

where \(k_1=\alpha _1+\alpha _2+\mu {_{\rm h}}\), \(k_2=\mu {_{\rm h}}+\delta {_{\rm h}}+\gamma ,\) \(k_3=\varphi +\tau +\delta {_{\rm h}}+\mu {_{\rm h}}\), \(k_4=\mu{_{\rm r}}+\alpha _3\), \(k_5=\mu{_{\rm r}}+\delta{_{\rm r}}\), \(\phi {_{\rm h}}=\frac{\beta _1\ I^*{_{\rm r}}+\beta _2\ I^*{_{\rm h}}}{N{_{\rm h}}}\), \(\phi{_{\rm r}}=\frac{\beta _3\ I^*{_{\rm r}}}{N{_{\rm r}}}\).

Basic reproduction number

In our proposed model 1, compartments \(S{_{\rm h}}\), \(R{_{\rm h}}\) and \(S{_{\rm r}}\) are the disease free states whereas the compartments \(E{_{\rm h}}, I{_{\rm h}}, Q{_{\rm h}}, E{_{\rm r}}\) and \(I{_{\rm r}}\) are the infection class.

Hence the monkeypox-free equilibrium state can be given as:

$$\begin{aligned} {\Phi }_{\rm MFE} = \left( \frac{\theta {_{\rm h}}}{\mu {_{\rm h}}},0,0,0,0,\frac{\theta{_{\rm r}}}{\mu{_{\rm r}}},0,0\right) \end{aligned}$$
(10)

The basic reproduction number is one of the critical parameters to examine the long-term behaviour of an epidemic. It can be defined as the number of secondary cases produced by a single infected individual in its entire life span as infectious agent. We have used next-generation matrix technique explained in Diekmann et al. (2010), Peter et al. (2020), to obtain the expression of reproduction number \(R_0\). It was first introduced by Driessche and Watmough van den Driessche and Watmough (2008), where this technique is discussed in detail for the estimation of \(R_0\). Also, there are various articles available in literature where the next-generation matrix technique has been used to estimate the expression for the basic reproduction number (Samui et al. 2020; Kumar et al. 2021).

The model system 1 can be written as:

$$\begin{aligned} \frac{{\rm d}x}{{\rm d}t}= & {} {\mathcal {F}}(x) - {\mathcal {V}}(x) \\ {\mathcal {F}}= & {} \begin{pmatrix} 0 \\ (\frac{\beta _1 I{_{\rm r}}+\beta _2 I{_{\rm h}}}{N{_{\rm h}}})S{_{\rm h}} \\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ \end{pmatrix}\nonumber \\ {\mathcal {V}}= & {} \begin{pmatrix} -\theta {_{\rm h}} + \frac{(\beta _1I{_{\rm r}}+\beta _2I{_{\rm h}})S{_{\rm h}}}{N{_{\rm h}}}+\mu {_{\rm h}}S{_{\rm h}}-\varphi Q{_{\rm h}} \\ (\alpha _1+\alpha _2+\mu {_{\rm h}})E{_{\rm h}} \\ -\alpha _1E{_{\rm h}}+(\mu {_{\rm h}}+\delta {_{\rm h}}+\gamma )I{_{\rm h}} \\ -\alpha _2E{_{\rm h}}+(\varphi +\tau +\delta {_{\rm h}}+\mu {_{\rm h}})Q{_{\rm h}} \\ -\gamma I{_{\rm h}}-\tau Q{_{\rm h}}+\mu {_{\rm h}} R{_{\rm h}} \\ -\theta{_{\rm r}}+\frac{\beta _3S{_{\rm r}}I{_{\rm r}}}{N{_{\rm r}}}+\mu{_{\rm r}}S{_{\rm r}} \\ -\frac{\beta _3S{_{\rm r}}I{_{\rm r}}}{N{_{\rm r}}}+(\mu{_{\rm r}}+\alpha _3)E{_{\rm r}} \\ -\alpha _3E{_{\rm r}}+(\mu{_{\rm r}}+\delta{_{\rm r}})I{_{\rm r}} \\ \end{pmatrix}\nonumber \end{aligned}$$
(11)

Progression from \(E{_{\rm h}}\) to \(I{_{\rm h}}\) or \(Q{_{\rm h}}\) are not considered to be new infections, but rather the progression of infected individuals through various compartments. Hence, the transmissions matrix F and transitions matrix V can be given as :

$$\begin{aligned} F= & {} \begin{pmatrix} 0 &{} \beta _2 &{} 0 &{} \beta _1 \\ 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 \\ \end{pmatrix}\\ V= & {} \begin{pmatrix} \alpha _1+\alpha _2+\mu {_{\rm h}} &{} 0 &{} 0 &{} 0\\ -\alpha _1 &{} \mu {_{\rm h}}+\delta {_{\rm h}}+\gamma &{} 0 &{} 0\\ -\alpha _2 &{} 0 &{} \varphi \tau +\delta {_{\rm h}}+\mu {_{\rm h}} &{} 0\\ 0 &{}0 &{} 0 &{} \mu{_{\rm r}}+\delta{_{\rm r}}\\ \end{pmatrix} \end{aligned}$$

For simplicity, let \(\Upsilon _1 = \alpha _1+\alpha _2+\mu {_{\rm h}}, \Upsilon _2=\mu {_{\rm h}}+\delta {_{\rm h}}+\gamma , \Upsilon _3 = \varphi \tau +\delta {_{\rm h}}+\mu {_{\rm h}} \) and \(\Upsilon _4 = \mu{_{\rm r}}+\delta{_{\rm r}}\)

Now:

$$\begin{aligned} V^{-1} = \frac{1}{\Upsilon _1\Upsilon _2\Upsilon _3\Upsilon _4}\begin{pmatrix} \Upsilon _2\Upsilon _3\Upsilon _4 &{} 0 &{} 0 &{}0 \\ \alpha _1 \Upsilon _3\Upsilon _4 &{} \Upsilon _1\Upsilon _3\Upsilon _4 &{} 0 &{} 0\\ \alpha _2\Upsilon _2\Upsilon _4 &{} 0 &{} \Upsilon _1\Upsilon _2\Upsilon _4 &{} 0\\ 0 &{} 0 &{} 0 &{} \Upsilon _1\Upsilon _2\Upsilon _3\\ \end{pmatrix} \end{aligned}$$
(12)

Now, after much simplification we obtain:

$$\begin{aligned} {\rm FV}^{-1} = \frac{1}{\Upsilon _1\Upsilon _2\Upsilon _3\Upsilon _4} \begin{pmatrix} \beta _2\alpha _1\Upsilon _3\Upsilon _4 &{} 0 &{} 0 &{} \beta _1 \Upsilon _1\Upsilon _2\Upsilon _3 \\ 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0\\ \end{pmatrix} \end{aligned}$$
(13)

Now, the basic reproduction number is defined as the largest eigenvalue (spectral radius) of the next generation matrix \({\rm FV}^{-1}\) and can be obtained as:

$$\begin{aligned} R_0 = \rho ({\rm FV}^{-1}) = \frac{\beta _2\alpha _1\Upsilon _3\Upsilon _4 }{\Upsilon _1\Upsilon _2\Upsilon _3\Upsilon _4} = \frac{\beta _2\alpha _1}{\Upsilon _1\Upsilon _2} \end{aligned}$$
(14)

Hence,

$$\begin{aligned} R_0 = \frac{\alpha _1\beta _2}{(\alpha _1+\alpha _2 +\mu {_{\rm h}})(\mu {_{\rm h}}+\delta {_{\rm h}}+\gamma )} \end{aligned}$$
(15)

Stability of disease-free equilibrium

To obtain the conditions for the global stability for \(E_0\), we have used the approach set out in Castillo-Chavez and Song (2004), which states that if the model system can be written in the following form:

$$\begin{aligned} \begin{aligned} \frac{{\rm d}X}{{\rm d}t}&=F(X,Z) \\ \frac{{\rm d}Z}{{\rm d}t}&=G(X,Z), G(X,0)=0 \end{aligned} \end{aligned}$$
(16)

here \(X \in R^n\) are the uninfected individuals and \(Z\in R^m\) describes the infected individuals. According to this notation, the disease-free equilibrium is given by \(Q_0=(X_0,0)\). Now, the following two conditions guarantees the global stability of the disease free equilibrium.

K1 ::

For \(\frac{{\rm d}X}{{\rm d}t}=F(X,0)\), \(X_0\) is globally asymptotically stable.

K2 ::

\(G(X,Z)=BZ-{\hat{G}}(X,Z)\) where \({\hat{G}}(X,Z)\ge 0\) for \(X,Z \in \Omega \).

here \(B=D_zG(X_0,0)\) is a M-matrix and \(\Omega \) is the feasible of the model. The following theorem then defines the global stability of \(E_0\).

Lemma 1

The equilibrium point \(Q_0=(X_0,0)\) is a globally asymptotically stable when \(R_0\le 1\) and assumptions \(K_1\) and \(K_2\) are satisfied.

Now, the following theorem establishes the global stability of the disease free equilibrium \(E_0\) for our proposed model system.

Theorem 2

The DFE point \(E_0\) is globally asymptotically stable provided \(R_0\le 1\).

Proof

First, we will prove \(K_1\) as:

$$\begin{aligned} F(X,0)= \begin{bmatrix} \theta {_{\rm h}}-\mu {_{\rm h}} S{_{\rm h}}\\ -\mu {_{\rm h}}R{_{\rm h}}\\ \theta{_{\rm r}}-\mu{_{\rm r}}S{_{\rm r}}\\ -(\mu{_{\rm r}}+\alpha _3)E{_{\rm r}}\\ \end{bmatrix} \end{aligned}$$

The characteristic polynomial of F(X, 0) is:

$$\begin{aligned} (\lambda +\mu {_{\rm h}})^2(\lambda +\mu{_{\rm r}})(\lambda +\mu{_{\rm r}}+\alpha _3) \end{aligned}$$
(17)

\(\Rightarrow \lambda _1 =\lambda _2= -\mu {_{\rm h}} \), \( \lambda _3 = -\mu{_{\rm r}} \) and \(\lambda _4 = -\mu{_{\rm r}} -\alpha _3\).

Hence, \(X = X_0\) is globally asymptotically stable.

Now, we have:

$$\begin{aligned} G(X,Z)= & {} BZ - {\hat{G}}(X,Z) \end{aligned}$$
(18)
$$\begin{aligned}= & {} \begin{bmatrix} -(\alpha _1+\alpha _2+\mu {_{\rm h}}) &{} \frac{\beta _2S^0{_{\rm h}}}{N{_{\rm h}}} &{} 0 &{} \frac{\beta _1S^0{_{\rm h}}}{N{_{\rm h}}} \\ \alpha _1 &{} -(\mu {_{\rm h}}+\delta {_{\rm h}}+\gamma ) &{} 0 &{} 0\\ \alpha _2 &{} 0 &{} -(\varphi +\tau +\delta {_{\rm h}}+\mu {_{\rm h}}) &{} 0\\ 0 &{} 0 &{} 0 &{} \mu{_{\rm r}}+\delta{_{\rm r}}\\ \end{bmatrix}\\&\times \begin{bmatrix} E{_{\rm h}}\\ I{_{\rm h}}\\ Q{_{\rm h}}\\ I{_{\rm r}}\\ \end{bmatrix} - \begin{bmatrix} (\frac{\beta _2(S^0{_{\rm h}}-S{_{\rm h}})+\beta _1(S^0{_{\rm h}}-S{_{\rm h}})}{N{_{\rm h}}})E{_{\rm h}} \\ 0\\ 0\\ \alpha _3E{_{\rm r}}\\ \end{bmatrix}\nonumber \end{aligned}$$
(19)

Here, one can easily observe that B satisfies all conditions explained in K2. \(\square \)

Stability of endemic equilibrium

We will use the Routh–Hurwitz criterion to prove the local stability of the endemic equilibria. Here, we will derive the conditions under which the endemic equilibria is locally asymptotically stable.

The Jacobian matrix about the endemic equilibria \(\phi _{\rm MEE}\) is given as :

$$\begin{aligned} J = \begin{bmatrix} a_{11} &{}0 &{} a_{13}&{} a_{14} &{} 0 &{} 0 &{}0 &{} a_{18} \\ a_{21} &{} a_{22} &{} a_{23} &{}0&{}0&{}0&{}0&{}a_{28}\\ 0 &{} a_{32} &{} a_{33} &{} 0 &{}0 &{}0 &{}0 &{}0 \\ 0 &{} a_{42} &{} 0 &{} a_{44} &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} a_{53} &{} a_{54} &{} a_{55} &{} 0 &{} 0 &{} 0\\ 0 &{}0 &{} 0 &{} 0 &{} 0&{} a_{66} &{} 0 &{} a_{68}\\ 0 &{}0 &{} 0 &{} 0 &{} 0&{} a_{76} &{} a_{77} &{} a_{78}\\ 0 &{}0 &{} 0 &{} 0 &{} 0&{} 0 &{} a_{87} &{} a_ {88}\\ \end{bmatrix} \end{aligned}$$

Here,

$$\begin{aligned} \begin{aligned}&a_{11} = -\left( \frac{\beta _1I{_{\rm r}}+\beta _2 I{_{\rm h}}}{N{_{\rm h}}}\right) -\mu {_{\rm h}} \quad a_{13} = -\frac{\beta _2 S{_{\rm h}}}{N{_{\rm h}}} \\&a_{14} = \phi \quad a_{18}=-\frac{\beta _1S{_{\rm h}}}{N{_{\rm h}}} \\&a_{21}=\frac{\beta _1I{_{\rm r}}+\beta _2I{_{\rm h}}}{N{_{\rm h}}} \quad a_{22}=-(\alpha _1+\alpha _2+\mu {_{\rm h}}) \\&a_{23}=\frac{\beta _2S{_{\rm h}}}{N{_{\rm h}}} \quad a_{28}=\frac{\beta _1S{_{\rm h}}}{N{_{\rm h}}} \\&a_{32}=\alpha _1 \quad a_{33}=-(\mu {_{\rm h}}+\delta {_{\rm h}}+\gamma )\\&a_{42}=\alpha _2 \quad a_{44}= -(\varphi +\tau +\delta {_{\rm h}}+\mu {_{\rm h}})\\&a_{53}=\gamma \quad a_{54}=\tau \quad a_{55}=-\mu {_{\rm h}}\\&a_{66}=-(\mu{_{\rm r}}+\frac{\beta _3I{_{\rm r}}}{N{_{\rm r}}}) \quad a_{68}=-\frac{\beta _3 S{_{\rm r}}}{N{_{\rm r}}} \\&a_{76}=\frac{\beta _3I{_{\rm r}}}{N{_{\rm r}}} \quad a_{77}=-(\mu{_{\rm r}}+\alpha _3)\\&a_{78}=\frac{\beta _3S{_{\rm r}}}{N{_{\rm r}}} \quad a_{87}= \alpha _3 \quad a_{88}= -(\mu{_{\rm r}}+\delta{_{\rm r}}) \end{aligned} \end{aligned}$$

The characteristic equation of J is given as:

$$\begin{aligned} \begin{aligned}&\frac{1}{N{_{\rm h}} N{_{\rm r}}}\Big [\left( -x-\mu {_{\rm h}}\right) (-\phi \alpha _2 \left( I{_{\rm r}} \beta _1+I{_{\rm h}} \beta _2\right) \\&\quad \left( x+\gamma +\delta {_{\rm h}}+\mu {_{\rm h}}\right) + \left( -x-\tau - \varphi -\delta {_{\rm h}}-\mu {_{\rm h}}\right) \\&\quad \left( S{_{\rm h}} \alpha _1 \beta _2 \left( x+\mu {_{\rm h}}\right) -\left( x+\alpha _1+\alpha _2+\mu {_{\rm h}}\right) \right. \\&\quad \left. \left( x+\gamma +\delta {_{\rm h}}+\mu {_{\rm h}}\right) \left( I{_{\rm r}} \beta _1+I{_{\rm h}} \beta _2+N{_{\rm h}} \left( x+\mu {_{\rm h}}\right) \right) \right)\bigg )\\&\quad \left( S{_{\rm r}} \alpha _3 \beta _3 \left( x+\mu{_{\rm r}}\right) -\left( x+\alpha _3+\mu{_{\rm r}}\right) \right. \\&\quad \left. \left( I{_{\rm r}} \beta _3+N{_{\rm r}} \left( x+\mu{_{\rm r}}\right) \right) \left( x+\left( \mu{_{\rm r}}+\delta{_{\rm r}}\right) \right) \right) \Big ]=0 \end{aligned} \end{aligned}$$
(20)

which can be further written as:

$$\begin{aligned}&x^8+A_1x^7 +A_2 x^6+A_3x^5+A_4x^4\nonumber \\&\quad +A_5x^3+A_6x^2+A_7x+A_8 = 0 \end{aligned}$$
(21)

where \(A_i\)’s are the coefficients of \(x^{8-i}\) \(; i=1,2,\ldots 8\) after converting the polynomial in standard form.

Note: To obtain the condition for the stability of \(\phi _{\rm MEE}\) we will made the following substitution:

$$\begin{aligned} \begin{aligned}&P = \frac{A_1A_2-A_0A_3}{A_1}, \quad Q=\frac{A_1A_4-A0A_5}{A_1}, \\&R=\frac{A_1A_6-A_0A_7}{A_1}, \quad S= A_8 , \\&P^*=\frac{pA_3-A_1Q}{P}, \quad Q^*=\frac{PA_5-A_1R}{P},\\&R^*=\frac{PA_7-A_1S}{P}, \quad M = \frac{P^*Q-PQ^*}{P^*} ,\\&N= \frac{P^*R-PR^*}{P^*}, \quad T= \frac{P^*S}{P^*},\\&M^*=\frac{MQ^*-P^*N}{M} , \quad N^*=\frac{MR^*-P^*T}{M}, \\&X=\frac{M^*N-MN^*}{M^*}. \quad \end{aligned} \end{aligned}$$

Hence, we can conclude this section by the following theorem:

Theorem 3

The endemic equilibrium point \(\phi _{\rm MEE}\) is locally asymptotically stable provided \(R_0 > 1\) and following conditions are satisfied:

$$\begin{aligned} \begin{aligned}&A_1> 0. \\&A_1A_2> A_3. \\&A_1A_2A_3+A_0A_1A_5> A_0A^2_3+A^2_1A_4 \\&P^*Q>PQ^* \quad MQ^*>P^*N \quad M^*N>MN^* \quad XN^*>TM^* \end{aligned} \end{aligned}$$
(22)

Backward bifurcation

The analysis conducted in the previous section on the occurrence of endemic equilibrium \(E^*\) suggests the probability of backward bifurcation. It can be defined as the state when a stable endemic equilibrium coexist with with a stable disease-free equilibrium when the associated reproduction number is less than unity. We use the center manifold based result (theorem 4.1) given in Castillo-Chavez and Song (2004), to check the occurrence of backward bifurcation.

Let:

$$\begin{aligned}&S{_{\rm h}} = y_1,\quad E{_{\rm h}} = y_2,\quad I{_{\rm h}} = y_3,\quad Q{_{\rm h}} = y_4,\\&R{_{\rm h}} = y_5,\quad S{_{\rm r}} = y_6,\quad E{_{\rm r}} = y_7,\quad I{_{\rm r}} = y_8. \end{aligned}$$

Consider, \(U = \left( y_1,y_2, y_3, y_4, y_5, y_6, y_7, y_8, \right) ^T\), then the given system (1) can be written as:

$$\begin{aligned} \frac{{\rm d}U}{{\rm d}t} = \left( f_1, f_2, f_3, f_4, f_5, f_6, f_7, f_8 \right) ^T \end{aligned}$$
(23)

where,

$$\begin{aligned} \begin{aligned} f_1&= \theta {_{\rm h}} - \frac{(\beta _{1} y_8+\beta _2 y_3)S{_{\rm h}}}{N{_{\rm h}}} -\mu {_{\rm h}} y_1+\phi y_4 \\ f_2&= \frac{(\beta _{1} y_8+\beta _2 y_3)S{_{\rm h}}}{N{_{\rm h}}} - (\alpha _1 +\alpha _2+\mu {_{\rm h}})y_2 \\ f_3&= \alpha _1 y_2 - (\mu {_{\rm h}}+\delta {_{\rm h}}+\gamma ) y_3 \\ f_4&= \alpha _2 y_2 - (\varphi +\tau +\delta {_{\rm h}}+\mu {_{\rm h}})y_4 \\ f_5&= \gamma y_3 + \tau y_4-\mu {_{\rm h}} y_5 \\ f_6&= \theta{_{\rm r}} - \frac{\beta _3 y_6y_8}{N{_{\rm r}}} - \mu{_{\rm r}} y_6 \\ f_7&= \frac{\beta _3 y_6y_8}{N{_{\rm r}}} - (\mu{_{\rm r}}+\alpha _3)y_7 \\ f_8&= \alpha _3 y_7 - (\mu{_{\rm r}}+\delta{_{\rm r}})y_8 \end{aligned} \end{aligned}$$
(24)

From the expression of \(R_0\), we can observe that \(R_0\) is highly influenced by \(\beta _2\), the product of effective contact rate and the probability of human been infected with monkey pox virus after getting in contact with infectious human. Therefore, we will consider \(\beta _2\) as our bifurcation parameter.

Hence , when \(R_0 = 1\), we have:

$$\begin{aligned} \beta ^*_{2} = \frac{(\alpha _1+\alpha _2+\mu {_{\rm h}})(\mu {_{\rm h}}+\delta {_{\rm h}}+\gamma )}{\alpha _1} \end{aligned}$$
(25)

Now, the above system at monkeypox-free equilibrium state \(\phi _{\rm MFE}\) is given by:

$$\begin{aligned} J_0 ( \phi _{\rm MFE}, \beta _{2}^*)= \begin{bmatrix} -\mu {_{\rm h}} &{} 0 &{} -\beta _2 &{}0 &{}0 &{}0 &{} 0 &{} -\beta _1 \\ 0 &{} -A_1 &{} \beta _2 &{} 0 &{}0 &{}0 &{}0 &{} \beta _1 \\ 0 &{} \alpha _1 &{} -A_2 &{}0 &{}0 &{}0 &{}0 &{}0 \\ 0 &{} \alpha _2 &{} 0 &{} -A_3 &{} 0 &{}0 &{}0 &{}0 \\ 0 &{} 0 &{} \gamma &{} \tau &{} -\mu {_{\rm h}} &{} 0 &{} 0 &{}0 \\ 0 &{} 0&{} 0 &{} 0 &{} 0 &{} -\mu{_{\rm r}} &{} 0 &{} 0 \\ 0 &{} 0&{} 0 &{} 0 &{} 0 &{} 0 &{} -A_4 &{} \beta _3 \\ 0 &{} 0&{} 0 &{} 0 &{} 0 &{}0 &{} \alpha _3 &{} -A_5 \\ \end{bmatrix} \end{aligned}$$

Clearly, ‘0’ is an eigenvalue of \(J_0 ( \phi _{\rm MFE}, \beta _{2}^*)\). Let \(W = \left( w_1, w_2, w_3, w_4, w_5, w_6, w_7, w_8 \right) \) be the associated right eigenvector corresponding to zero eigenvalue, and can be attained by simplifying:

$$\begin{aligned} \begin{array}{l} -\mu {_{\rm h}} w_1-\beta _2w_3 - \beta _1 w_8 = 0 \\ -A_1w_2 + \beta _2 w_3 + \beta _1 w_8 = 0 \\ \alpha _1 w_2 - A_2 w_3 = 0 \\ \alpha _2 w_2 - A_3 w_4 = 0 \\ \gamma w_3 + \tau w_4 - \mu {_{\rm h}} w_5 = 0 \\ -\mu{_{\rm r}} w_6 - \beta _3 w_8 = 0 \\ -A_4w_7 +\beta _3 w_8 = 0 \\ \alpha _3w_7 - A_5 w_8 = 0 \\ \end{array} \end{aligned}$$
(26)

On evaluation, W can be given as:

$$\begin{aligned} \begin{aligned}&w_1 =-\frac{A_1A_2}{\alpha _1\mu {_{\rm h}}} \quad w_2 = \frac{A_2}{\alpha _1} \quad w_3 = 1 \\&w_4 = \frac{\alpha _2 A_2}{\alpha _1 A_3} \quad w_5 = \frac{1}{\mu {_{\rm h}}}\left( \gamma +\frac{\tau \alpha _2 A_2}{\alpha _1 A_3}\right) \\&w_6 = \frac{\beta _3 }{\beta _1 \mu{_{\rm r}}}\left( \frac{A_1A_2}{\alpha _1}+\beta _2\right) \\&w_7 = -\frac{A_5}{\alpha _3\beta _1}\left( \frac{A_1A_2}{\alpha _1}+\beta _2\right) \quad w_8 = -\frac{1}{\beta _1}\left( \frac{A_1A_2}{\alpha _1}+\beta _2\right) \end{aligned} \end{aligned}$$

Now, let \(V = \left( v_1, v_2, v_3, v_4, v_5, v_6 , v_7, v_8 \right) \) be the associated left eigenvector of \(J_0\) corresponding to zero eigenvalue and satisfying \(V.W = 0\). Then V can be given as :

$$\begin{aligned} \begin{aligned}&v_1 = 0, \\&v_2 = \left( \frac{A_2}{\alpha _1}+\frac{\beta _2}{A_2}-(\left( \frac{A_1A_3}{\alpha _1}+\beta _2\right) \right. \\&\qquad \left. . \frac{1}{\left( \frac{A_4A_5}{\alpha _3}-\beta _3\right) }\times \left( \frac{A_5}{\alpha _3}+\frac{\beta _2}{A_2}\right) \right) ^{-1}, \\&v_3 = \frac{\beta _2}{A_2}.v_2, \quad v_4=v_5=v_6=0,\\&v_7 = \frac{\beta _1}{\left( \frac{A_4A_5}{\alpha _3}-\beta _3\right) }.v_2, \quad v_8 = \frac{\beta _2}{A_2}.v_7 \end{aligned} \end{aligned}$$

As discussed in theorem 4.1 (Castillo-Chavez and Song 2004), we have:

$$\begin{aligned} a= & {} \sum _{k,i,j=1}^{8} v_k w_i w_j \frac{\partial ^2f_k}{\partial y_i\partial y_j}\left( \phi _{\rm MFE},\beta ^*_2\right) \end{aligned}$$
(27)
$$\begin{aligned} b= & {} \sum _{k,i=1}^8 v_k w_i \frac{\partial ^2f_k}{\partial y_i\partial \beta _2}\left( \phi _{\rm MFE},\beta ^*_2\right) \end{aligned}$$
(28)

Algebraic calculations shows that:

$$\begin{aligned} \frac{\partial ^2f_2}{\partial x_1x_3}= & {} \frac{\beta _2}{N{_{\rm h}}} = \frac{\partial ^2f_2}{\partial x_3x_1} \quad \frac{\partial ^2f_2}{\partial x_1x_8} = \frac{\beta _1}{N{_{\rm h}}} = \frac{\partial ^2f_2}{\partial x_8x_1} \\ \frac{\partial ^2f_7}{\partial x_8x_6}= & {} \frac{1}{N{_{\rm r}}} = \frac{\partial ^2f_7}{\partial x_6x_8} \end{aligned}$$

Now, substituting all the above values in the expressions for ‘a’ and ‘b’, we obtain:

$$\begin{aligned} a\,\,=\,\, & {} \frac{2v_2w_1}{N{_{\rm h}}}(w_3\beta _2+w_8\beta _1)+2v_7 \frac{w_6w_8}{N{_{\rm r}}} \end{aligned}$$
(29)
$$\begin{aligned} b= & {} v_2.w_2.\frac{\theta }{\mu {_{\rm h}} N{_{\rm h}}} \end{aligned}$$
(30)

Now, to persist backward bifurcation in the proposed model, both the values of ‘a’ and ‘b’ has to be simultaneously positive.

Results

A sensitivity analysis determines how different values of an independent variable affect a particular dependent variable under a given set of assumptions (Kalyan et al. 2021; Victorr et al. 2020). The normalized forward sensitivity index of a variable to a parameter is the ratio of the relative change in the variable to the relative change in the parameter. When variable is a differentiable function of the parameter, the sensitivity index may be alternatively defined using partial derivatives. The parameter values have been taken from literature as given in Table 1.

Table 1 Parameter values used for the simulations
Full size table

Since the basic reproduction number \(R_0\) helps us to predict the future course of the disease, the sensitivity analysis is performed to understand which parameters involved in the model effect the value of \(R_0\) relatively more. We have used the following expression of the sensitivity for \(R_0\) which depends upon parameter v.

$$\begin{aligned} \psi _v^{R_0}= \frac{v}{R_0} \times \frac{\partial R_0}{\partial v} \end{aligned}$$
(31)

A negative index of sensitivity shows that the parameter and \(R_0\) are inversely proportional. A positive sensitivity index, however, denotes that the value of \(R_0\) increases with an increase in the value of the parameter concerned.

The estimated sensitivity indices for \(R_0\) are presented in Table 2. From Table 2, we can see that an increase in the values of \(\alpha _2\), \(\mu {_{\rm h}}\), \(\delta {_{\rm h}}\) and \(\gamma \) will results in a decrease in the value of \(R_0\). On the another hand, an increase in the value of \(\alpha _1\) and \(\beta _2\) will increase the monkey-pox cases.

Table 2 Sensitivity index of parameters
Full size table
Fig. 2
figure 2

Surface plot showing simultaneous impact of \(\alpha _1\) and \(\alpha _2\) on \(R_0\)

Full size image
Fig. 3
figure 3

Surface plot showing simultaneous impact of \(\alpha _1\) and \(\beta _2\) on \(R_0\)

Full size image
Fig. 4
figure 4

Surface plot showing simultaneous impact of \(\beta _2\) and \(\alpha _2\) on \(R_0\)

Full size image
Fig. 5
figure 5

Surface plot showing simultaneous impact of \(\mu {_{\rm h}}\) and \(\gamma \) on \(R_0\)

Full size image
Fig. 6
figure 6

Variation in infected population over time for different values of \(\alpha _1\); proportion of humans exposed to infection

Full size image
Fig. 7
figure 7

Variation in infected population over time for different values of \(\delta {_{\rm h}}\); disease induced death rate of humans

Full size image
Fig. 8
figure 8

Variation in infected population over time for different values of \(\gamma \); recovery rate of humans

Full size image
Fig. 9
figure 9

Variation in infected population without any isolated interventions

Full size image

Discussion

The basic reproduction number is a crucial parameter in disease dynamics which gives us major information about the disease. To understand the effect of various disease transmission parameters on the basic reproduction number, we have obtained the surface plots showing variation of \(R_0\) with sensitive parameters. From Fig. 2, it can be observed that as the value of \(\alpha _2\) increases, it leads to reduced disease transmission. Similarly, it can be easily seen from Fig. 3 that contact rate with rodent population directly affects the transmission of monkey-pox. Similarly, the simultaneous effect of \(\beta _2, \alpha _2, \mu {_{\rm h}}\) and \(\gamma \) on the basic reproduction number has been shown in Figs. 4 and 5.

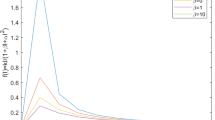
Further, we have performed numerical experiments to detect effect of change in sensitive parameters on the number of infected individuals. This has been investigated in Figs. 6, 7 and 8. Now we have incorporated a compartment \(Q{_{\rm h}}\) in the model, which consists of the isolated proportion of the infected humans. Through numerical simulations, we have shown how the infected population would behave in the absence of isolated interventions. In Fig. 9, we show that the isolation of infected individuals helps to reduce disease transmission.

Conclusion

A non-linear compartmental model has been proposed to understand the transmission of Monkey pox disease. The proposed model consist of eight mutually exclusive compartments. The human population has been divided into five compartments, where we has introduced the exposed \((E{_{\rm h}})\) and isolated human \((Q{_{\rm h}})\) compartments along with standard compartments of exposed population \((E{_{\rm h}})\), infected humans \((I{_{\rm h}})\) and recovered humans \((R{_{\rm h}})\). Similarly, the rodent population is also divided into three compartments; exposed \((E{_{\rm r}})\), susceptible \((S{_{\rm r}})\) and infected rodents \((I{_{\rm r}})\). Further, we have established the fundamental properties of the proposed model.

Basic reproduction number has been estimated using next-generation matrix technique. The proposed model exhibit two equilibrium points; disease free equilibrium point and endemic equilibrium point. We have obtained the stability conditions for both of the equilibrium points. Further, the existence of the endemic equilibrium implies the possibility of the backward bifurcation. We have also derived the condition for the existence of the backward bifurcation. Further we have shown the sensitivity of various parameters involved in the model. The sensitivity index has been provided in Table 2. We found that \(\alpha _2\), which is human to human contact rate is the most sensitive parameter in the transmission of the disease. Also, with the help of numerical simulations, we have shown the simultaneous effect of various parameters on the basic reproduction number \(R_0\). Our analysis suggests that isolation of infected humans helps to reduce disease transmission. It is, therefore, realised from the simulation that isolation of the infected humans, is playing significant roles in the management and control of monkeypox virus.