Introduction

Soil is functionally a non-renewable resource; while topsoil develops over centuries, the world’s growing human population is actively depleting the resource over decades. As a non-renewable resource and the basis for 97 % of all food production (Pimentel 1993), strategies to prevent soil depletion are critical for sustainable development. Significant literature exists documenting the magnitude of the soil erosion problem. Between 30 and 50 % of the world’s arable land is substantially impacted by soil loss (Pimentel 1993), which directly affects rural livelihoods (Lal 1985; Kerr 1997) in addition to indirectly affecting aquatic resources (Ochumba 1990; Eggermont and Verschuren 2003), lake/river sediment dynamics (Kelley and Nater 2000; Walling 2000), global carbon cycling (Duxbury 1995; Lal 2003), aquatic and terrestrial biodiversity (Harvey and Pimentel 1996; Alin et al. 2002) and ecosystem services (Tinker 1997; Pimentel and Kounang 1998). Severe soil degradation has been documented throughout sub-Saharan Africa (Lal 1985; Pimentel 1993; Oostwoud and Bryan 2001; Lufafa et al. 2002), resulting in declining functional capacity (Zobisch et al. 1995; Gachene et al. 1997), ultimately affecting poverty and food security (Sanchez et al. 1997).

It is estimated that about 80 % of the current degradation on agricultural land in the world is caused by soil erosion due to water (Angima et al. 2003). Soil erosion is a major problem throughout the world. Globally, 1964.4 M ha of land is affected by human-induced degradation (UNEP 1997). Of this, 1903 M ha are subjected to aggravated soil erosion by water and another 548.3 M ha by wind. Average soil erosion rate in Asia is 16.6 Mg/ha/year and Asia ranks second in soil loss rate followed by South America (22.1 Mg/ha/year) (Walling and Webb 1983). One estimate puts the loss of top soil by water action at 1200 m tones every year in India which costs Rs 12,000 crores annually (Vohra 1985). In the present century about 70 % of the total people of the world depend on agriculture. Therefore, this issue of soil loss is one of the burning topics of discussion. In India population pressure is very high (16 % of the world’s population) and about 80 % of the population relies on agriculture tilling land as many time as possible and therefore, soil erosion from agricultural land is maximum. This soil loss impacted on agricultural production in very significant scale. It is estimated that India suffers an annual loss of 13.4 million tones in the production of major cereal, oilseed and pulse crops due to water erosion equivalent to about $ 2.51 billion (Sharda et al. 2010). As per harmonized data base on land degradation, 120.72 million ha area is affected by various forms of land degradation in India with water erosion being the chief contributor (68.4 %) (Maji 2007). The National Bureau of Soil Survey and Land Use Planning (Sehgal and Abrol 1994) data show that nearly 3.7 million ha suffer from nutrient loss and/or depletion of organic matter.

Considering the importance of protecting and restoring the soil resource, it is increasingly been recognized by the world community (Lal 1998; Barford et al. 2001; Lal 2001). Sustainable management of soil received strong support at the Rio summit in 1992 and its Agenda 21 (UNCED 1992), UN Framework Convention on Climate Change (UNFCCC 1992) and Articles 3.3 and 3.4 of the Kyoto Protocol (UNFCCC 1997), the 1994 UN Framework Convention to Combat Desertification (UNFCD 1996). This attempt is not confined within summits and pacts, many a scholars have produced a good number of articles of decision value in this field addressing estimation of soil erosion by Walling and Webb (1983), Lal (2003), Lin et al. (2002), Amore et al. (2004), Lanuzaa and Paningbatan (2010) and Prasannakumar et al. (2012) vulnerability and risk of soil erosion by Milevski (2008), Boardman et al. (2009) and Sharda et al. (2013), application of geospatial techniques for estimating soil erosion Baigorria and Romero (2007), developing soil erosion based models and factor calibration for modeling by Williams et al. (1984), Flanagan and Nearing (1995), Santhi et al. (2001), Foster et al. (2003), Turpin et al. (2005), Santhi et al. (2006), Pandey et al. (2009) etc. Present river basin is majorly composed with fragile laterite soil and old lateritic alluvium. At the same time this basin is agriculturally dominated (cropping intensity is 172 %). So, addressing soil erosion issues is indespensible. In this present paper, attempt has been taken to identify soil erosion potential areas of river Chandrabhaga, a sub tributary of Mayurakshi river. Quantification of soil erosion volume and measurement of surface lowering rates etc. in different soil erosion vulnerable zones have been for validating this model.

Study sites

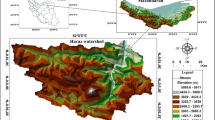
Chandraghaga river (length: 26 km) basin, covering an area 119 sq km, is a sub basin of Mayurakshi river system located mainly over the western plateau fringe(Chottanagpur) blocks (administrative unit) of Birbhum district namely Rajnagar, Dubrajpur and Suri. Entire basin area comes under rarh tract (Bagchi and Mukerjee 1983) with secondary laterite formation (Chakrabarty 1970) mainly carried by some of the rivers coming from Chottanagpur plateau (Jha1997, Jha and Kapat 2003, 2009). Elevation of this basin ranges from 150 (at the source region) to 24 m (at confluence). Average slope, measured as per Wentworth’s method (1930), is 2–3 % whereas it is <1 % in the confluence segment. Geologically 60 % of the basin area in the upper catchment is composed with granitic gneissic rock of Pleistocene age overlain by weathered coarse grain lateritic regolith and soil and 30 % of area at the lower catchment is made with newer alluvium of Holocene period (Fig. 1) (GSI 1985) (Fig. 2).

Fig. 1
figure 1

Drainage network and basin over geological setting of the study area; square box indicates sites used for RUSLE; this layer created after generating spatial vulnerable soil loss model and same is then imposed on study area map

Full size image
Fig. 2
figure 2

Landsat image based land use land cover (LULC) of Chandrabhaga river basin

Full size image

The thickness of alluvium increases toward eastern part of the basin and it ranges from 12 to 20 m and groundwater yield potentialities of aquifers from also increases eastward with a rate about 5–15 m3/h (Ray and Shekhar 2009). No such significant lineaments are existing there. The water table is moderately deep (5–10 mbgl) with moderately high seasonal fluctuation (Mukherjee et al. 2007). Few locally confined aquifer structure are found in this basin.

Parts of the confluence area is cladded with sick immature sal (shorearobusta) dominated forest. Two to three decades ago, parts of the upper catchment were also captured by same type of forest but it is already deforested. Most part of the basin area is dominated by agricultural land with poor qualities of soil fertility and soil moisture (during pre monsoon 8–11 %). Average annual rainfall of this basin as gauged by Suri meteorological station is 1444.432 mm. High degree of seasonality of rainfall is reflected by 82 % rainfall during the months of June to September. Rainfall analysis since 1980–2013 focused that there is no significant trend of rainfall as also indicated by linear regression model (y − 2.137x + 5704) and coefficient of determination (R2 = 0.005). This trend is identical with the general trend of rainfall in India as estimated by many a scholars viz. Jagannathan and Parthasarathy (1973), Chaudhary and Abhyankar (1979), Kumar et al. (2005) and Dash et al. (2007) etc. reported that in all India scale there is no significant change of rainfall in last 110 years excepts few regional pockets (Sinha Ray and De 2003). Average potential evaporation of this area since 1901–2014 is 73.45 mm/year (IMD 2015).

Materials and methods

Raster based estimation of soil vulnerability analysis

In the first step, all data were registered into Universal Transverse Mercator projection northern zone 45 datum WGS 84. The base map of the study area was prepared from Survey of India (SOI) topographical maps (sheet no. 73 M/5 and 73 M/9) on 1:50,000 scale. The drainage network or stream link map for the study area were prepared from manual digitized of scanned SOI toposhets that has been used as stream link layer and stream junction prepared thereafter. The rainfall distribution map was prepared form District Planning Map, NATMO. The soil texture map was collected from the National Bureau of Soil Survey and Land Use Planning (NBSS and LUP) Regional Centre, Kolkata, India. The texture groups of soil have been integrated into GIS environment into percentage value of sand. The Shuttle Radar Topography Mission Digital Elevation Model (SRTM DEM v3, 1-arc sec) was used to create the relief zone and flow accumulation maps using spatial analyst tool in ArcGIS. The Land Use Land Cover (LULC) was prepared from Landsat OLI image collected from US Geological Survey (USGS) Global Visualization Viewer (Path/row: 139/43). Supervised classification was done using the maximum likelihood classifier algorithm of ERDAS Imagine (v. 9.1) for LULC classification. High resolution QuickBird images available in GoogleEarth for 18th April, 2013 and 17th February, 2014 combined with field based ground control points were utilized for both training area selection and for the evaluation of map accuracy. The overall accuracy of Landsat derived LULC map is 87.6 % with corresponding Kappa statistics of 0.84. The LULC of the Chandraghaga basin is classified in six land use classes: settlement, damping ground, vegetation, agriculture, fallow land, riparian zone.

Any model for computing potential soil loss in an area must deals with a large number of variables, i.e. parameters concerning vegetation, crop management, soil, relief, slope and climate. When available spatial data are geo-referenced and can be put in the form of maps, Geographic Information Systems (GIS) allow simpler and faster data and parameter management. Therefore, GIS can make soil erosion studies easier, especially when repeated applications of similar and complex procedures are required.

For estimating soil loss, several methods and models have produced by troops of scholars. The development of Universal Soil Loss Equation (USLE) (Wischmeir and Smith 1978), Modified Universal Soil Loss Equation (MUSLE) (Williams 1975), a revised version of the empirical-based USLE the Revised Universal Soil Loss Equation (RUSLE) (Renard et al. 1991, 1997), RUSLE 1.06 (Toy and Foster 1998), RUSLE1.06c (US Department of agriculture, Agricultural Research Service and National Sediment Laboratory 2003), RUSLE2 (USDA-NRCS 2008), Water Erosion Prediction Project (WEPP) (Flanagan and Nearing 1995) etc. are some land mark methods for detecting soil loss prone areas or estimation of soil loss. Another approach follows multicriteria evaluation of potential soil erosion risk zones.

For nearly two decades, a number of multi-attribute (or multi-criteria) evaluation methods have been implemented in the GIS environment for land suitability evaluation, including WLC and its variants (Carver 1991; Eastman 1997) and the analytic hierarchy process (Banai 1993). There are two fundamental classes of multi-criteria evaluation methods in GIS: the Boolean overlay operations (non-compensatory combination rules) and the weighted linear combination (WLC) method (compensatory combination rules). They have been the most often used approaches for different sorts of land-use suitability analysis (Heywood et al. 1995; Jankowski 1995; Barredo et al. 2000; Beedasy and Whyatt 1999; Malczewski 2004). These approaches can be generalized within the framework of the ordered weighted averaging (OWA) (Asproth et al. 1999; Jiang and Eastman 2000; Makropoulos and Butler. 2005; Malczewski et al. 2003; Malczewski and Rinner 2005).

The WLC is a simple additive weighting based on the concept of a weighted average (Eastman 2006). The decision maker directly assigns weights of “relative importance” to each attribute map layer. A total score is then obtained for each alternative by multiplying the importance weight assigned for each attribute by the scaled value given to the alternative on that attribute, and summing the products over all attributes. OWA is a family of multi-criteria combination procedures (Yager 1988). It involves two sets of weights: the weights of relative criterion importance and the order (or OWA) weights. Although OWA is a relatively new concept (Yager 1988), there have been several applications of this approach in the GIS environment (Asproth et al. 1999; Jiang and Eastman 2000; Mendes and Motizuki 2001; Araujo and Macedo 2002; Malczewski et al. 2003; Rashed and Weeks 2003; Calijuri et al. 2004; Makropoulos and Butler 2005; Rinner and Malczewski 2002). All those applications use the conventional (quantitative) OWA. Specifically, research into GIS, OWA has so far focused on the procedures that require quantitative specification of the parameters associated with the OWA operators.

In the present study six parameters with proper database have been selected as map layers viz. (1) slope, (2) soil texture, (3) NDVI, (4) drainage frequency, (5) rainfall, (6) proximity to stream link. Among these layers initially proximity to stream link layer was in vector form. As this process executes on the basis of raster based weighted linear combination, these vector layers have been converted into raster maps using either distance mapping techniques (e.g. proximity to stream link) using spatial analyst tool in ArcGIS software or grid based raster surface like DEM (e.g. rainfall layer, drainage frequency layer, soil texture layer) in ERDAS Imagine Software. Each attribute (map layer) is categorized into ten equal classes and ranking 1–10 (adopting 10 point scale) considering the fact that greater rank will reflect greater soil erosion vulnerable zones. To fulfill this purpose, all these attributes have been reclassified into 10 classes and ranked accordingly. The logic behind ranking to intra attribute classes from 1 to 10 is described in Table 2. Weightage of each attribute has been defined subjectively (see Table 2) considering the role of those in the study area. Rank of all sub classes under each attribute is then multiplied by the defined weight of each individual attribute. This function can be presented using the following formula.

$${\text{WLC}} = \sum\limits_{j = 1}^{n} {a_{ij} w_{j} }$$

Where, aij = ith rank of jth attribute; wj = weightage of jth attribute.

This weighted linear combination has been done using raster calculator tool in Arc GIS environment (Table 1).

Table 1 Modes of ranking of the intra sub class of parameters and distribution of priority based weightage
Full size table

Logic behind weight distribution

For weight distribution of the selected parameters, knowledge based method of weighting following Islam and Sado (2002), Sanyal and Lu (2006), Drobne and Lisec (2009) and Mondol and Pal (2015) have been done. Total considered weight in this work is supposed to 1.

Slope drives soil erosion in positive direction and plays one of the most dominant role therefore 0.2 weight has been assigned.

Soil texture inherently determines erodibility and cohesiveness of soil. Coarse texture soil is highly fragile and in this river basin coarse textured laterite soil inspires to provide weightage of 0.25.

Drainage frequency or density is one of the dominant parameters which act as major erosion vector. Frequent drainage fuels more erosion and therefore, 0.15 weights has been given.

NDVI represents canopy area which protects soil in different ways. In general, as the protective canopy of land cover increases, soil erosion decreases (Elwell and Stocking 1976). It protects soil from direct rainfall and tightly binds soil particles. Considering its multidimensional importance much weight (0.2) is being provided.

As most of the rainfall (82 %) happens during monsoon months (June to September), rainfall intensity factor influences to provide 0.1 weight. But overall spatial variation is very low over the basin and hence, relatively less weight has been assigned.

Association of streams can positively influence soil erosion and has been assigned 0.10 weight. As it is a pedimental river basin and drained by mostly 1st and 2nd order streams so variation in this regard is meager.

Soil loss estimation framework

Along with raster based weighted linear combination method, Revised Universal Soil Loss Equation (RUSLE) (Renard et al. 1991, 1997) based soil loss has been:

$${\text{A}} = {\text{R}} \times {\text{K}} \times {\text{LS}} \times {\text{C}} \times {\text{P}}$$
$${\text{A}} = {\text{Soil}}\;{\text{loss}}$$
$${\text{L}} = {\text{Slope}}\;{\text{length}}\;{\text{factor}}\;\left( {\text{m}} \right)$$
$${\text{S}} = {\text{Slope}}\;{\text{gradient}}\;{\text{factor}}\;\left( \% \right)$$
$${\text{C}} = {\text{Cropping}}/{\text{land}}\;{\text{use}}\;{\text{management}}$$
$${\text{P}} = {\text{Soil}}\;{\text{erosion}}\;{\text{control}}\;{\text{practice}}\;{\text{factor}}$$
$${\text{LS}} = {\text{Length}}\;{\text{gradient}}\;{\text{factor}}$$

R is the rainfall and runoff factor by geographic location, is calculated using the following equation:

$$R = 38.5 + 0.35 \times Pr$$

Where, Pr is average annual precipitation of the study areaK and LS values of the respective areas have been calculated following Robert (2000).

To quantify soil loss rate over different erosion prone areas of spatial soil loss vulnerable areas as being produced through WCL method, 22 sample sites (0.25 km × 0.25 km area each) 7 from extremely vulnerable area and 5 each from other three vulnerable areas (see Fig. 1) have been selected and these sites are distributed over the basin considering factors of dominance. Actually, these sites have been selected from spatial soil erosion vulnerability model as a separate data layer and overlaid on the map of study area to avoid another similar kind of map inserting sample sites. For estimating A value R, K, LS, C and P values for each site has been calculated as per defined method.

Measuring framework for surface lowering

Dataset for actual surface lowering rate has been taken from Ghosh (2015) and Ghosh et al. (2015) for validating soil spatial soil erosion vulnerable model. Pegging operation, since 2011–2014, on 40 sites (see Fig. 1) has been done by those scholars for calculating surface lowering rate.

Results and discussion

Individual status of the selected parameters

Before integrating all six data layers, spatial status of individual parameter can be quantized. Specifically, in each data layers percentage of area may come under potent erosion vulnerable may help to understand the nature of control on each parameter on final integrated map layer. In slope dataset, average slope variation is very negligible, but 3.14 % area with relatively greater slope (2.58–4.38 %) in the upper catchment and proximate areas of the water divide; in soil texture dataset proportion of sand greater than 60 % covers greater than 37.61 % of the basin and they are mainly concentrated adjacent to the water divide areas and gully heads areas of the basin (Fig. 3); 32.76 % of the basin area mainly in the upper catchment is characterized by high drainage frequency (4–8 streams/sq km) (Fig. 5); in rainfall dataset, 27.5 % area receives rainfall greater than 1400 mm annually mainly in the upper catchment (Fig. 6); in stream link proximity dataset 39.68 % area covers very proximate stream links association (Fig. 7); in NDVI dataset, 63 % area is bare and concentrated majorly within middle and lower catchment. Land use land cover (LULC) of 1985 shows that more percentage of area was covered with mainly sal forest. From all these datasets it is evident that all the potential area in each individual dataset is not concentrated in same spatial unit i.e. there is inter parameter spatial multi-directionality. Therefore, for generating final conclusion, integration of datasets is required (Figs. 2, 4, 8, 9).

Fig. 3
figure 3

Slope map shown in percentage

Full size image
Fig. 4
figure 4

Soil texture (proportion of sand)

Full size image
Fig. 5
figure 5

Normalized differential vegetation index

Full size image
Fig. 6
figure 6

Drainage frequency

Full size image
Fig. 7
figure 7

Average annual rainfall

Full size image
Fig. 8
figure 8

Stream link proximity map

Full size image
Fig. 9
figure 9

Raster calculator with selected parameters and their respective weightage

Full size image

Weighted compositing of the raster datasets for delineation of potential soil erosion vulnerable areas

The vulnerability map (Fig. 10) shows the relative ranking of the erosion potential sites, generated by weighted linear combination mapping, according to the importance of concerned criteria. The vulnerability scores indicate soil erosion susceptibility. High vulnerability scores indicate that the site is highly susceptible for soil loss. According to the overall suitability score (Fig. 10) 19.87 % of the total basin area is very extremely vulnerable (score 5.66–8.0), 30.07 % is highly vulnerable (score 4.70–5.65), 23.21 % is moderately vulnerable (score 3.76–4.69), and 26.83 % is less vulnerable for potential soil erosion (see Table 2). Extremely vulnerable areas are concentrated mainly in upper and middle catchments of the basin. Sparse vegetation, frequent gully association, coarse sand texture i.e. more proportionality of sand, association of streams explain more erosion propensity in this area. Most of the extremely erosive areas are located within granitic gneissic area with coarse lateritic fragile soil. Over the time, squeezing vegetation area (21 % loss since 1979–2014), decaying vegetation quality (lowering of NDVI value), uprooting trees etc. have highly inflated soil erosion. Lateritic soil is naturally fragile because of its inherent constraints of acidity, nutrient loss, chemical impairment, crusting, water erosion and poor water holding capacity as these are highly weathered and leached soil and enriched with oxides of iron and aluminum in tropics (Jha and Kapat 2003, 2009) and therefore the region with deep lateritic content instigates more erosion. Chemical analysis of laterite samples of this area indicates that Fe2O3 varies antipathetically with Al2O3 and the ratio of Fe2O3 and Al2O3 is 1:0.2–1:2.01. Ti2O3 has a slight good and direct relationship with Fe2O3. The presence of anatese probably accounts for appreciable amount of TiO3 (1.5–5.0 %) in this laterite. Such chemical composition with least biomass availability in soil is in fact highly erosive. High seasonal variability of rainfall (Coefficient of variation = 98.04 %) encourage strong wetting and drying of soil and it often causes vulnerability of soil loss. Apart from all these, strong riling and gulling is another major vector of strong rate vulnerability of soil loss specifically in upper part of the rill and gully heads and in fat, these areas contribute more soil erosion (Kar and Bandopadhyay 1974; Bandopadhyay 1987; Jha and Kapat 2009).

Fig. 10
figure 10

Potential soil erosion vulnerable areas

Full size image
Table 2 Area under different surface water suitability zones
Full size table

Estimated soil loss

RUSLE based estimation of soil loss in different potential soil loss areas (indicated in Fig. 1) is described in Table 2. In extremely vulnerable soil loss areas, estimated soil loss is 21.78 Mg/ha/year followed by 9.45 Mg/ha/year in the highly vulnerable areas. Very minimum rate of soil erosion (2.25 Mg/ha/year) is found in 26.83 % basin area. This fact proves that overall grading as made using WLC method in Fig. 10 is down to earth. Average (spatial) estimated soil erosion is 9.12 Mg/ha/year. Total estimated annual soil loss as per this equation is 105525.9 Mg/year out of this 54.48 % lost amount is contributed by the extremely vulnerable areas (Table 2). Although this highly soil erosive areas are imposed over granitic and gneissic surface, but pedimental regolith contributes such friable soil for erosion.

Actual soil loss

Results of actual soil loss in different vulnerable areas indicate accordant characters with spatial vulnerability of soil loss model. Surface lowering rate is maximum (2.5 mm/year) in the extremely vulnerable soil erosion areas and very low rate of surface lowering is noticed in less (0.4 mm/year) vulnerable areas (vide Table 2). These information obviously validate both spatial model and RUSLE based estimation of soil loss.

In fine, it can be said that such spatial vulnerability of soil loss model can provide decision support regarding where soil protection plan should be implemented in priority basis. Adoption of suitable measures in the erosion hotspot areas is essential to protect rampant nutrient rich top soil loss in such agriculturally dominated areas.