1 Introduction

In life science and engineering studies such as medicine, biomedical sciences, bio-statistics, communication, computer engineering, reliability, survival analysis, and life testing, statistical models play an indispensable role in studying the natural phenomena that occur in such fields of study. Probability models are used to model and characterize natural life phenomena. In probability studies, extending the classical probability models becomes necessary due to the natural events that occur and require higher dimensional data analysis and complex decisions. Whereas the traditional models cannot efficiently model such natural phenomena, especially when the failure rates are non-monotone. Thus, the practitioners proposed many ways of adding new parameter(s) to manipulate the existing traditional model and improve their quality and flexibility to provide higher accuracy so that the exploration of lifetime data can be assessed better. Data exploration in lifetime studies is one of the keys to analyzes real-world, enabling us to measure, predict, and explain quantities of interest that arise in the fields of artificial intelligence, big data analysis, data mining, biomedical sciences, business studies, and communication with the aid of several powerful tools in probability and statistical concepts, programming, optimization, algorithms, and computational techniques; for more studies, one can see [1,2,3,4].

Topp Leone (TL) model was introduced in [5], the model is defined on finite support \(w\in (0,1)\) with the cumulative distribution function (cdf),

$$\begin{aligned}H(w)=w^\alpha (2-w)^\alpha , \;\;\, \alpha >0.\end{aligned}$$

TL possesses a bathtub failure rate and has only one parameter; it has a closed-form of the cumulative distribution function, unlike beta distribution. This model has received comprehensive study and applications in sciences and social sciences such as biology, economics, ecology, etc. One can see [6] for the moments properties of the TL. [7] provides some stochastic ordering results and reliability studies of the TL. [8] discussed the Bayesian estimation of the TL under trimmed samples. [9] provided the recurrence relations for the moments of order statistics from the TL without any restrictions on the shape parameter and many relations when the shape parameter is an integer. [10] derived some explicit algebraic expressions for the single and product moments of order statistics from TL, and gave an identity about single moments of the order statistics. [11] proposed the use of maximum likelihood and uniformly minimum variance unbiased estimation procedures for the stress–strength reliability parameter from TL for the problem on both complete and left censored data, also considering the interval estimation of the reliability parameter. [12] develops a Bayesian estimation in the context of non-informative priors for the shape parameter of the mixture of TL distributions for a censored data set. Under the assumption of the known scale parameter of the TL, [13] provided Bayes and empirical Bayes estimates of the unknown parameter under non-informative and suitable conjugate priors and under the assumption of squared and linear-exponential error loss functions, also concluded that the proposed estimates are minimax and admissible. [14] constructed the Bayesian point and interval estimation for the shape parameter of the TL under lower k-record values. [15] discussed the moments of dual generalized order statistics from TL-weighted Weibull and its characterization.

Recently, [16] proposed a new inverted Topp–Leone distribution called the Kies inverted Topp–Leone with its applications to COVID-19 mortality rates in the United Kingdom and Canada. [17] introduced the odd Weibull inverted Topp–Leone distribution with its application to COVID-19 mortality rates in the United Kingdom and Canada. [18] introduced the type I half-logistic Nadarajah-Haghighi distribution and illustrated its good performance in fitting the COVID-19 mortality rates data from California, USA. [19] proposed exponentiated Gumbel–Weibull-Logistic and provided its application to Nigeria’s COVID-19 infections data. [20] estimated the daily recovery cases from COVID-19 in Egypt using power-odd generalized exponential Lomax distribution. [21] provided some statistical inferences based on the exponentiated exponential model that aided in assessing covid-19 cases in Kerala. [22] compared the performance of some lifetime models, including the Weibull model, using COVID-19 data from Pakistan. Among others.

TL has tractable close form properties, but it is not flexible enough to cover a wide range of practical applications, especially in lifetime data analysis. But, the demand for flexible lifetime models in practice is increasing due to the inability of the classical ones and rapid progress in applied statistical studies, biomedical sciences, engineering, computer sciences, reliability, econometrics, etc. Thus, researchers are encouraged to extend classical models to more flexible ones capable of modelling various failure rates that occur in lifetime analysis. TL families of distributions have been extended to a generator of distributions by various authors, and their positive impact has been discussed comprehensibly in the literature. For example, [23,24,25] proposed various Topp–Leone-G (TLG) family, [26] introduced the generalized Topp–Leone-G (GTLG), [27] type II Topp–Leone-G (TIITLG), [28] type II generalized Topp–Leone-G (TIIGTG), [29] power Topp–Leone-G (PwTLG), [30] Type II power Topp–Leone-G (TIIPTLG), [31] extended Topp–Leone -G (ETLG), G–fixed–Topp–Leone (GFTL) [32], exponentiated Generalized Topp Leone-G (EGTLG) [33], Marshall–Olkin Topp Leone-G (MOTLG) [34], Topp–Leone odd log-logistic-G (TLOLLG) [35], and Topp–Leone Marshall–Olkin-G (TLMOG) [36], among other.

In probability and statistical studies, the generators of probability models have significantly contributed to the literature regarding distribution theory and led to numerous useful tools in mathematical and statistical theory and practice. Here, we proposed a new extension of the Topp–Leone generator of distributions (NETLG) as an additional tool for statistical studies. This work aims to introduce another flexible generator of distributions from the TL that can accommodate various failure rates and can be used to model different kinds of skewed data. An additional parameter was employed to the usual TLG by applying a function involving exponential and natural logarithm. The additional power parameter allows the tuning of the model functions for better flexibility and provides some new statistical viewpoints for modelling data. Any valid baseline model can be chosen to propose a new flexible member of the NETLG model; the new model can provide more flexible shapes of the density and failure rates in comparison to parent distribution; the new generator’s special models have the capability to provide a better fit than some other existing alternative models. Moreover, different probability models serve different purposes and represent different data generation processes. In addition, we want to investigate some of the important mathematical and statistical properties regarding the new model to present a closed-form and convenient representation of the model properties with the aid of several mathematical techniques, computational algorithms, and computer packages for numerical assessment. Finally, two applications of the NETLG family to COVID 19 data are used to illustrate its importance in practice.

In Sect. 2, we derived the new model and discussed some important properties. In Sect. 3, maximum likelihood estimation (MLE), least-square estimation (SLE), and percentile estimation (PE) are proposed for the parameter estimation and assessed by simulation studies. Section 4 provides an application of the new model family for illustration. In Sect. 5, the conclusion.

2 New Extension of the Topp–Leone-G Models (NETLG) and Its Properties

Let \(G(x;\xi )\) be any valid baseline cumulative distribution function, \(x\in {\mathbb {R}},\) and \(\xi \) is a vector of parameters, the cumulative distribution function (cdf) of some Topp–Leone-G families are given in Table 1:

Table 1 Some Topp–Leone-G families
Full size table

In this work, we proposed the new extended Topp–Leone generator of distributions (NETLG) due to the idea in [37]. The perspective of this model derivation is innovative and will have broader academic value. No doubt, the studies related to this model will provide tools for extending several mathematical results in probability and mathematical statistics. The additional parameter provides more flexibility to the new model than other existing TL families. It is a fact that different distributions serve different purposes and represent different data generation processes; thus, our new model provided a new means of data generating processes and a Monte Carlo simulation process. The cumulative distribution function of the new extended Topp–Leone generator of distributions (NETLG) is given by

$$\begin{aligned} F(x)=e^{-\alpha \left( -\log G(x;\xi ) \right) ^\beta } \,\left( 2-e^{- \left( -\log G(x;\xi ) \right) ^\beta } \right) ^\alpha , \alpha , \beta >0. \end{aligned}$$
(1)

If \(\beta =1\) we have the Topp–Leone-G model [23]. The corresponding probability density function (pdf) is given by

$$\begin{aligned} f(x)= & {} 2\alpha \beta \frac{g(x;\xi )}{G(x;\xi )} \left( -\log G(x;\xi ) \right) ^{\beta -1} e^{-\alpha \left( -\log G(x;\xi ) \right) ^{\beta }}\,\left( 1-e^{-\left( -\log G(x;\xi ) \right) ^\beta } \right) \nonumber \\ {}{} & {} \left( 2-e^{- \left( -\log G(x;\xi ) \right) ^\beta } \right) ^{\alpha -1}, \end{aligned}$$
(2)

where \(g(x;\xi )\) is the corresponding pdf of the baseline cdf \(G(x;\xi )\). The survival function and hazard rate function (hrf) of the NETLG for \(\beta ,\, \alpha >0\) are given by

$$\begin{aligned} s(x)=1-e^{-\alpha \left( -\log G(x;\xi ) \right) ^\beta } \,\left( 2-e^{-\left( -\log G(x;\xi ) \right) ^\beta } \right) ^\alpha , \end{aligned}$$
(3)

and

$$\begin{aligned} h(x){} & {} =2\alpha \beta \frac{g(x;\xi )}{G(x;\xi )}\nonumber \\ {}{} & {} \frac{\begin{matrix} \left( -\log G(x;\xi ) \right) ^{\beta -1} e^{-\alpha \left( -\log G(x;\xi ) \right) ^{\beta }}\,\left( 1-e^{-\left( -\log G(x;\xi ) \right) ^\beta } \right) \left( 2-e^{- \left( -\log G(x;\xi ) \right) ^\beta } \right) ^{\alpha -1}\end{matrix}}{1-e^{-\alpha \left( -\log G(x;\xi ) \right) ^\beta } \,\left( 2-e^{-\left( -\log G(x;\xi ) \right) ^\beta } \right) ^\alpha },\nonumber \\ \end{aligned}$$
(4)

respectively.

The asymptotic properties of the NETLG model are discussed below.

Lemma 1

Let \(X\sim \)NETLG; then we have the following asymptotic.

$$\begin{aligned} F(x)&\sim 2e^{-\alpha \left( -\log G(x;\xi ) \right) ^\beta } \;\;as\; G \rightarrow 0, \end{aligned}$$
(5)
$$\begin{aligned} s(x)&\sim \alpha \left( 1-e^{-\left( -\log G(x;\xi ) \right) ^\beta } \right) ^2 \sim \alpha \left( -\log G(x;\xi ) \right) ^{2\beta } \;\; as\; G\rightarrow 1, \nonumber \\ f(x)&\sim 2\alpha \beta g(x;\xi ) \left( -\log G(x;\xi ) \right) ^{\beta -1}\,\left( 1-e^{-\left( -\log G(x;\xi ) \right) ^\beta } \right) \;\; as\; G\rightarrow 1 , \nonumber \\ h(x)&\sim \frac{2\beta g(x;\xi ) \left( -\log G(x;\xi ) \right) ^{\beta -1}}{\left( 1-e^{-\left( -\log G(x;\xi ) \right) ^\beta } \right) } \;\; as\; G\rightarrow 1, \nonumber \\ f(x)&\sim 4\alpha \beta \frac{g(x;\xi )}{G(x;\xi )} \left( -\log G(x;\xi ) \right) ^{\beta -1}\,e^{-\alpha \left( -\log G(x;\xi ) \right) ^\beta }\;\; as\; G\rightarrow 0. \nonumber \\ \end{aligned}$$
(6)

The quantile of distribution has many uses in theoretical studies and statistics applications. Quantile function serves as a tool for parameter estimation and simulation. The quantile function of the NETLG can be derived as

$$\begin{aligned} Q(u)=G^{-1}\left( e^{-\left[ -\log \left( 1-\sqrt{1-u^{\frac{1}{\alpha }}}\right) \right] ^{1/\beta }}\right) ,\;\;0\le u\le 1. \end{aligned}$$
(7)

In particular, \(Q(\frac{1}{2})\) is the median. The skewness and kurtosis of the NETLG can be discussed by the Bowley’s skewness (B), and Moor’s kurtosis (M) defined respectively as

$$\begin{aligned}B=\frac{Q(\frac{3}{4})-2Q(\frac{2}{4})+Q(\frac{1}{4})}{Q(\frac{3}{4} )-Q(\frac{1}{4})}\end{aligned}$$

and

$$\begin{aligned} M=\frac{Q(\frac{7}{8})-Q(\frac{5}{8})+Q(\frac{3}{8})-Q(\frac{1}{8})}{Q( \frac{6}{8})-Q(\frac{2}{8})} .\end{aligned}$$

2.1 Stochastic Ordering

Stochastic ordering is another aspect of probability theory that allows us to discuss some of the relative characters of distributions. There are various means by which we might say that a random variable X is smaller than a random variable Y. However, in stochastic ordering, we say that X is stochastically smaller than Y denoted as \(X \prec _{st}Y\). There are many other stochastic orders such as likelihood, hazard, etc., for details one can see [38] among others. Here, we obtained the likelihood ordering result for NETLG under some possible conditions. Let a random variable \(X_1\) with pdf \(f_1(x)\) and \(X_2\) having pdf \(f_2(x)\), then \(X_1\) is said to be smaller than \(X_2\) in the likelihood ratio order \((denoted\; X_1 \prec _{lr} X_2 )\) if \(f_1 (x)/f_2(x)\) is decreasing in x.

Proposition 1

Let \(X_1\) be a random variable having \(NETLG_1(\alpha _1,\beta ,\xi )\) and random variable \(X_2\) having \(NETLG_2(\alpha _2,\beta ,\xi )\), then, \(X_1 \prec _{lr} X_2\) if \(\alpha _1\le \alpha _2\).

Proof

We show that \(f_1 (x)/f_2(x)\) is decreasing.

$$\begin{aligned} \frac{f_1(x;\alpha _1,\beta ,\xi )}{f_2(x;\alpha _2,\beta ,\xi )}=\frac{\alpha _1}{\alpha _2} e^{-{(\alpha _1-\alpha _2)} \left( -\log G(x;\xi ) \right) ^{\beta }} \, \left( 2-e^{- \left( -\log G(x;\xi ) \right) ^\beta } \right) ^{\alpha _1-\alpha _2}, \end{aligned}$$

and

$$\begin{aligned} \frac{\partial }{\partial x}\frac{f_1(x;\alpha _1,\beta ,\xi )}{f_2(x;\alpha _2,\beta ,\xi )}&=2\frac{\alpha _1}{\alpha _2}\beta (\alpha _1-\alpha _2)\frac{g(x;\xi )}{G(x;\xi )} \left( -\log G(x;\xi ) \right) ^{\beta -1}\,e^{-{(\alpha _1-\alpha _2)} \left( -\log G(x;\xi ) \right) ^{\beta }} \\&\times \,\left( 1-e^{- \left( -\log G(x;\xi ) \right) ^\beta } \right) \, \left( 2-e^{- \left( -\log G(x;\xi ) \right) ^\beta } \right) ^{\alpha _1-\alpha _2-1}, \end{aligned}$$

thus, \(\frac{\partial }{\partial x}\frac{f_1(x;\alpha _1,\beta ,\xi )}{f_2(x;\alpha _2,\beta ,\xi )}\le 0\) if \(\alpha _1\le \alpha _2 \). \(\square \)

2.2 Series Representation of the pdf

The series representation of the NETLG could make it easier for us to compute some properties of the NETLG. But we need the following expansions. For \(|z|\le 1\) and \(b>0\) real and non integer,

$$\begin{aligned} (1-z)^{b-1}=\sum _{i=0}^\infty \frac{(-1)^i \Gamma (b)}{i! \Gamma (b-i)} z^i. \end{aligned}$$
(8)

Also, for a power series to the power of \(n\in {\mathbb {N}}\) we need:

Lemma 2

([39])  For a given power series of the form \(\sum _{k=0}^\infty a_k x^k\), let n be a positive integer, then,

$$\begin{aligned} \left( \sum _{k=0}^\infty a_k x^k\right) ^n=\sum _{k=0}^\infty c_k x^k, \end{aligned}$$

where \(c_0=a_0^n\), \(c_m=\frac{1}{m\,a_0}\sum _{k=1}^m(kn-m+k) a_k c_{m-k}\) for \(m\ge 1\).

Form the (2); the following expressions can be presented in a series form by using (8) as

$$\begin{aligned}&e^{-\alpha \left( -\log G(x;\xi ) \right) ^{\beta }}\left( 1-e^{-\left( -\log G(x;\xi ) \right) ^\beta } \right) \,\left( 2-e^{- \left( -\log G(x;\xi ) \right) ^\beta } \right) ^{\alpha -1}\nonumber \\&\quad =\sum _{i,k=0}^\infty \sum _{j=0}^{i+1}\omega _{i,j,k}\,\left( -\log G(x;\xi ) \right) ^{\beta k}, \end{aligned}$$
(9)

where, \(\omega _{i,j,k}=\frac{(-1)^{j+k}\alpha ^k(j+1)^k\Gamma (\alpha )\genfrac(){0.0pt}1{i+1}{j}}{i!\,k! \Gamma (\alpha -1)}\), therefore, (2) can be presented as

$$\begin{aligned} f(x)= & {} \sum _{i,k=0}^\infty \sum _{j=0}^{i+1}\omega _{i,j,k}^* \frac{g(x;\xi )}{G(x;\xi )} \left( -\log G(x;\xi ) \right) ^{\beta (k+1)-1}\nonumber \\ {}= & {} \sum _{i,k=0}^\infty \sum _{j=0}^{i+1}\omega _{i,j,k}^* \,\tau _k(x;\beta ,\xi ), \end{aligned}$$
(10)

where, \(\omega _{i,j,k}^*=\frac{2\alpha \beta (-1)^{j+k}\alpha ^k(j+1)^k\Gamma (\alpha )}{i!\,k! \Gamma (\alpha -1)}\genfrac(){0.0pt}1{i+1}{j}\) and \(\tau _k(x;\beta ,\xi ) =\frac{g(x;\xi )}{G(x;\xi )} (-\log G(x;\xi ))^{\beta (k+1)-1}\). Further, for an integer \(\beta (k+1)-1\) we can proceed and simplify \((-\log G(x;\xi ))^{\beta (k+1)-1}\) in (10) by some algebra as

$$\begin{aligned} \left( -\log G(x;\xi ) \right) ^{\beta (k+1)-1}&=\sum _{l=0}^{\beta (k+1)-1}\genfrac(){0.0pt}1{\beta (k+1)-1}{l}\left( -\log G(x;\xi )-1 \right) ^l,\\&=1+\sum _{l=1}^{\beta (k+1)-1}\genfrac(){0.0pt}1{\beta (k+1)-1}{l}\left( \sum _{n=0}^\infty w_{n} (G(x;\xi )-1)^n \right) ^l, \end{aligned}$$

where \(w_0=-1\), and  \(w_{n}=\frac{(-1)^n}{n}\), therefore, we can apply the lemma 2 in above to get

$$\begin{aligned} \left( -\log G(x;\xi ) \right) ^{\beta (k+1)-1}=1+\sum _{l=1}^{\beta (k+1)-1}\genfrac(){0.0pt}1{\beta (k+1)-1}{l} \sum _{n=0}^\infty c_{n} (G(x;\xi )-1)^n, \end{aligned}$$

where \(c_0=w_0^n\), and \(c_{m}=\frac{1}{m w_0}\sum _{n=1}^m (ln-m+n)w_n\,c_{m-n}\), hence,

$$\begin{aligned} \left( -\log G(x;\xi ) \right) ^{\beta (k+1)-1}&=1+\sum _{l=1}^{\beta (k+1)-1} \sum _{n=0}^\infty d_{k,v,n}\, G^v(x;\xi ), \end{aligned}$$
(11)

where \(d_{k,v,n}=\sum _{v=0}^n \genfrac(){0.0pt}1{\beta (k+1)-1}{l}\genfrac(){0.0pt}1{n}{v} c_{n}(-1)^{n-1}\), thus, by putting (11) in (10) we have

$$\begin{aligned} f(x)=\sum _{i,k=0}^\infty \sum _{j=0}^{i+1}\omega _{i,j,k}^* \frac{g(x;\xi )}{G(x;\xi )} +\sum _{i,k,n=0}^\infty \sum _{l=1}^{\beta (k+1)-1} \sum _{j=0}^{i+1}\omega _{i,j,k}^* \,d_{k,v,n}\,g(x;\xi ) \, G^{v-1}(x;\xi ), \nonumber \\ \end{aligned}$$
(12)

2.3 Moments

Let X follow the NETLG distributions, the \(r^{th}\) moment of X can be obtained from \(\mu _r=E[X^r]=\int _{-\infty }^\infty x^r f(x)dx\). The moments can be computed directly from the (10) as

$$\begin{aligned} \mu _r=\sum _{i,k=0}^\infty \sum _{j=0}^{i+1}\omega _{i,j,k}^* \,\int _{-\infty }^{\infty }\,x^r\,\tau _k(x;\beta ,\xi )\,dx, \end{aligned}$$
(13)

where \(\omega _{i,j,k}^* \) and \(\tau _k(x;\beta ,\xi )\) are given previously in (10). In other way, we can compute the moment from (12) given by

$$\begin{aligned} \mu _r=\sum _{i,k=0}^\infty \sum _{j=0}^{i+1}\omega _{i,j,k}^* \int _{-\infty }^\infty x^r \frac{g(x;\xi )}{G(x;\xi )} dx +\sum _{i,k,n=0}^\infty \sum _{l=1}^{\beta (k+1)-1} \sum _{j=0}^{i+1}v^{-1} \omega _{i,j,k}^* \,d_{k,v,n}\,E_v[X^r], \end{aligned}$$

where \(\omega _{i,j,k}^*\) given in (12),  \(d_{k,v,n}\) in (11), and \(E_v[X^r]\) is the \(r^{th}\) moment of the exponentiated baseline distribution \(G^v(x;\xi )\) distribution.

Next, we consider the incomplete moments used in computation the mean deviations, income inequalities, and moments of residual life. The incomplete moment of X defined as \(I_r(t)=\int _{-\infty }^t x^r f(x)dx\) from (10) can take the following form

$$\begin{aligned} I_r(t)=\sum _{i,k=0}^\infty \sum _{j=0}^{i+1}\omega _{i,j,k}^* \int _{-\infty }^t x^r \tau _k(x;\xi ) \,dx, \end{aligned}$$
(14)

where \(\tau _k(x;\xi )\) is given in the equation (10). The first incomplete moment \(I_1(t)\), i.e when \(r=1\), is a tool for computing the mean deviations about the mean \(\delta _1(X)\) and the mean deviations about median \(\delta _2(X)\) defined by

$$\begin{aligned}\delta _1(X)=2\mu _1 F(\mu _1)-2I_1(\mu _1)\;\;\; and \;\;\, \delta _2(X)=\mu _1-2 I_1(M), \end{aligned}$$

where \(\mu _1\) is the firs moment of X i.e, \(\mu _1\); \(M=Q(0.5)\) from (7); and F(.) is the cdf in (1).

The Lorenz and Bonferroni curves are computed using \(I_1(t)\). For a random variable X and a given probability p, the Lorenz and Bonferroni curves are defined by \(L(p)=(\mu _1)^{-1}I_1(q)\) and \(B(q)=(p\mu _1)^{-1}I_1(q)\) respectively, and \(q=Q(p)\) from (7).

Moreover, \(I_1(t)\) can be used to compute the two mean of residual life, i.e, the mean residual life defined by \(M(t)=E(X-t|X>t)\), or, \(M(t)=\int _0^\infty \frac{s(x+t)}{s(t)}dx\), where s(t) is the survival function of X, and the mean reverse residual life defined by \(m(t) = E(t-X|X\le t)\), or \(m(t)= \int _0^t \frac{F(x)}{F(t)} dx\), where F(.) is the cdf of X. These measures are applied in the determination of the distributions of the extreme values.

2.4 Stress–Strength Reliability

In practice, a good design of a system is so that the system can resist the assumed stress to be applied. Assume that a component possesses stress X and is subjected to a strength Y, then parameter \(R=P(Y<X)\) discusses the system performance. It is called the stress–strength parameter in reliability studies. The system will fail when the applied stress is higher than the assumed system strength. We can find some applications of R in various fields in [40, chap. 7]. R has been discussed by many researchers in the literature through various perspectives. For example, let X and Y be an independent random variables, then: normal distribution (N) [41, 42], Weibull (W) [43,44,45], exponential (E) [46], generalized exponential (GE) [47], beta-Erlang truncated exponential (BETE) [48], Poisson-odd generalized exponential family (POGE) [49], generalized logistic (GL) [50], Poisson-generalized half logistic (PGHL) [51], generalized exponential Poisson (GEP) [52], Poisson half logistic (PHL) [53], exponentiated sine Weibull (ESW) [54], extended cosine Weibull (ECSW) [55], among others.

Let X and Y be independent random variables, having the density \(f_1(x;\alpha _1, \beta ,\xi )\) and Y with cdf \(F_2(y;\alpha _2,\beta , \xi )\) from NETLG, then, the stress–strength reliability parameter is \(R=P(Y<X)=\int _{-\infty }^\infty \, f_1(x) \,F_2(x) dx.\) Therefore,

$$\begin{aligned} R=\int _{-\infty }^\infty&2\alpha _1 \beta \frac{g(x;\xi )}{G(x;\xi )} \left( -\log G(x;\xi ) \right) ^{\beta -1} e^{-{(\alpha _1+\alpha _2)} \left( -\log G(x;\xi ) \right) ^{\beta }}\\&\times \left( 1-e^{-\left( -\log G(x;\xi ) \right) ^\beta } \right) \left( 2-e^{- \left( -\log G(x;\xi ) \right) ^\beta } \right) ^{\alpha _1+\alpha _2-1}\, dx, \end{aligned}$$

hence,

$$\begin{aligned} R= \frac{\alpha _1}{\alpha _1+\alpha _2}\int _{-\infty }^\infty f(x;\alpha _1+\alpha _2,\beta ,\xi )dx=\frac{\alpha _1}{\alpha _1+\alpha _2}. \end{aligned}$$

2.5 Entropy

Entropy is the degree of disorder or randomness in a system. Here, we computed the Renyi entropy of the NETLG families defined by \({Re(\rho )}={(1-\rho )^{-1}}{\log \left[ {\int _{-\infty }^{\infty }}{f^\rho (x)}dx\right] }\), where \(\rho >0\) and \(\rho \ne {1}\). We started by simplify the expression of \(f^\rho (x)\) as:

$$\begin{aligned} f^\rho (x)&=2^\rho \alpha ^\rho \beta ^\rho \frac{g^\rho (x;\xi )}{G^\rho (x;\xi )} \left( -\log G(x;\xi ) \right) ^{\rho (\beta -1)} e^{-\alpha \rho \left( -\log G(x;\xi ) \right) ^{\beta }}\nonumber \\&\times \left( 1-e^{-\left( -\log G(x;\xi ) \right) ^\beta } \right) ^\rho \, \left( 2-e^{- \left( -\log G(x;\xi ) \right) ^\beta } \right) ^{\rho (\alpha -1)}, \end{aligned}$$
(15)

we can simplify the following expression obtained from the above equation as

$$\begin{aligned}&e^{-\alpha \rho \left( -\log G(x;\xi ) \right) ^{\beta }}\left( 1-e^{-\left( -\log G(x;\xi ) \right) ^\beta } \right) ^\rho \,\left( 2-e^{- \left( -\log G(x;\xi ) \right) ^\beta } \right) ^{\rho (\alpha -1)} \nonumber \\&\quad =\sum _{i,j,k=0}^\infty \phi _{i,j,k}\,\left( -\log G(x;\xi ) \right) ^{\beta k}, \end{aligned}$$
(16)

where, \(\phi _{i,j,k}=\genfrac(){0.0pt}1{\rho (\alpha -1)}{i}\genfrac(){0.0pt}1{i+\rho }{j} \frac{(-1)^{j+k} (\alpha \rho +j)^k }{k!}\), thus, by substituting the above series in (15) we get

$$\begin{aligned} f^\rho (x)=2^\rho \alpha ^\rho \beta ^\rho \sum _{i,j,k=0}^\infty \phi _{i,j,k}\, \frac{g^\rho (x;\xi )}{G^\rho (x;\xi )} \left( -\log G(x;\xi ) \right) ^{\beta (k+\rho )-\rho }, \end{aligned}$$

hence, the Renyi entropy of the NETLG families can be obtained from

$$\begin{aligned} {Re(\rho )}={(1-\rho )^{-1}}{\log \left[ \! 2^\rho \alpha ^\rho \beta ^\rho \sum _{i,j,k=0}^\infty \phi _{i,j,k}\, \int _{-\infty }^{\infty }\,\frac{g^\rho (x;\xi )}{G^\rho (x;\xi )} \left( -\log G(x;\xi ) \right) ^{\beta (k+\rho )-\rho }\,dx\! \right] }. \end{aligned}$$

2.6 Order Statistics

Let \(X_{1}, X_{2}, \cdots , X_{n}\), \(n\ge 1\), be an ordered sample obtained from NETLG families with cdf F(x) and pdf f(x), then, the density function of the \(i^{th}-\)order statistics is represented by \(f_{i:n}(x)\) and define by

$$\begin{aligned} f_{i:n}(x)=\frac{f(x)}{B(i,n-i+1)} \sum _{j=0}^{n-i}\genfrac(){0.0pt}1{n-i}{j} (-1)^j F^{i+j-1}(x). \end{aligned}$$

Simplifying \(F^{i+j-1}(x)\) in above, we have

$$\begin{aligned} F^{i+j-1}(x)=e^{-\alpha (i+j-1) \left( -\log G(x;\xi ) \right) ^\beta } \,\left( 2-e^{- \left( -\log G(x;\xi ) \right) ^\beta } \right) ^{\alpha (i+j-1)}, \end{aligned}$$

thus, the density function of the \(i^{th}-\)order statistics be comes the mixture of the NETLG\((\alpha (i+j),\beta ,\xi )\) as

$$\begin{aligned} f_{i:n}(x)=\frac{1}{(i+j)\,B(i,n-i+1)} \sum _{j=0}^{n-i}\genfrac(){0.0pt}1{n-i}{j} (-1)^j f(x;\alpha (i+j),\beta ,\xi ). \end{aligned}$$
(17)

The \(r^{th}\) moments of the \(i^{th}-\)order statistics can be computed from (17) by considering (13) as

$$\begin{aligned} E[X_{i:n}^r]=\frac{1}{(i+j)\,B(i,n-i+1)} \sum _{j=0}^{n-i}\genfrac(){0.0pt}1{n-i}{j} (-1)^j E[X^r]_{f_{[\alpha (i+j),\beta ,\xi ]}}, \end{aligned}$$

where \(E[X^r]_{f_{[\alpha (i+j),\beta ,\xi ]}}\) is the expectation of NETLG families with respect to the density \(f(x;\alpha (i+j),\beta ,\xi )\).

The asymptotic distributions for the extreme order statistics \(X_{1:n}\) and \(X_{n:n}\) from NETLG families can be discussed according to the details in [56, chap. 8], among others.

2.7 A Special Member of the NETLG Families

A special member of the NETLG is derived and discussed in this subsection, namely the new extended Topp–Leone exponential (NETLE) distributions.

2.7.1 New Extended Topp–Leone Exponential (NETLE)

Let the baseline density in (2) be exponential distribution with parameter \(\lambda >0\), having cdf and pdf given by \(G(x;\lambda )=1- e^{-\lambda x}\) and \(g(x;\lambda )=\lambda e^{-\lambda x}\) respectively, \(x>0\). The density (f(x)) and the hazard (h(x)) functions of the NETLE are given by

$$\begin{aligned} f(x)&=\frac{2\alpha \beta \lambda e^{-\lambda x}}{(1-e^{-\lambda x})} \left( -\log (1-e^{-\lambda x}) \right) ^{\beta -1} e^{-\alpha \left( -\log (1-e^{-\lambda x}) \right) ^\beta } \left( 1-e^{- \left( -\log (1-e^{-x}) \right) ^\beta } \right) \nonumber \\&\qquad \times \left( 2-e^{- \left( -\log (1-e^{-x}) \right) ^\beta } \right) ^{\alpha -1}, \end{aligned}$$
(18)
$$\begin{aligned} h(x)&=\frac{2\alpha \beta \lambda e^{-\lambda x}}{(1-e^{-\lambda x})} \left( -\log (1-e^{-\lambda x}) \right) ^{\beta -1} e^{-\alpha \left( -\log (1-e^{-\lambda x}) \right) ^\beta }\nonumber \\&\quad \times \frac{\left( 1-e^{- \left( -\log (1-e^{-x}) \right) ^\beta } \right) \left( 2-e^{- \left( -\log (1-e^{-x}) \right) ^\beta } \right) ^{\alpha -1}}{1-e^{-\left( -\log (1-e^{-\lambda x}) \right) ^\beta }\left( 2-e^{- \left( -\log (1-e^{-x}) \right) ^\beta } \right) ^{\alpha }}. \end{aligned}$$

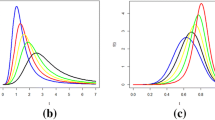
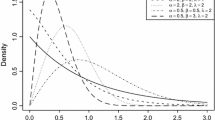
Figures 1 and 2 show the plots of the density and hazard functions of the NETLU for some parameter values.

Fig. 1
figure 1

Plots of the density and hazard rate function of the NETLE distribution

Full size image
Fig. 2
figure 2

Plots of the hazard rate function of the NETLE distribution

Full size image

Let be a random variable X follow NETLE, then the quantile function of X is given by

$$\begin{aligned} Q_{NETLE}(u)=-\lambda ^{-1} \log (1-q(u,\alpha ,\beta )), 0\le u\le 1,\end{aligned}$$

where \(q(u,\alpha ,\beta )=e^{-\left[ -\log \left( 1-\sqrt{1-u^{\frac{1}{\alpha }}}\right) \right] ^{1/\beta }}\).

Figure 3 illustrated that the B-skewness and M-kurtosis of the NETLE; notice that both the B skewness and M kurtosis are independent of \(\lambda \). The skewness decreases in \(\alpha \) and unimodal in \(\beta \), while the kurtosis decreases in \(\alpha \) and increases in \(\beta \).

Fig. 3
figure 3

Plots of the B-skewness and M-kurtosis of the NETLE distribution

Full size image

Proposition 2

Let \(X\sim \)NETLE with pdf in (18), then,

  1. 1.

    For a very large \(t>0\), i.e, as \({t\rightarrow \infty }\) the asymptotic of the mean residual life is given by

    $$\begin{aligned}M(t)\sim \frac{1}{2\lambda \beta }. \end{aligned}$$
  2. 2.

    For a very small \(t>0\), i.e, as \({t\rightarrow 0}\) the asymptotic of the mean reverse residual life for \(\beta =1\) is

    $$\begin{aligned}m(t)\sim \frac{t}{\alpha +1}. \end{aligned}$$

Proof

  1. 1.

    The asymptotic of the survival function of NETLE can be obtained from (6) as \(s(x)\sim \alpha \left( -\log \left( 1-e^{-\lambda x} \right) \right) ^{2\beta }\sim e^{-\lambda x} \;\;as \;x \,\rightarrow \,\infty ,\) therefore, as \(\;t \,\rightarrow \,\infty \) we have \(M=\int _0^\infty \frac{s(x+t)}{s(t)}dx\sim \int _0^\infty e^{-2\lambda \beta x} dx =\frac{1}{2\lambda \beta }. \)

  2. 2.

    As \({x\rightarrow 0}\) the cdf of NETLE from (5) for \(\beta =1\) become: \(F(x)\sim 2\left( 1-e^{-\lambda x} \right) ^\alpha \sim 2\lambda ^\alpha x^\alpha \), therefore, as \({t\rightarrow 0}\), \(m(x)=\int _0^t \frac{F(x)}{F(t)} dx \sim t^{-\alpha } \int _0^t x^{\alpha } dx = \frac{t}{\alpha +1} \).

\(\square \)

Proposition 3

Let \(X_1\le X_2\le , \ldots ,\le X_n,\) be from NETLE with pdf in (18), let \(B_n=(X_{n:n}-a_n)/b_n\), then, \(B_n{\mathop {\rightarrow }\limits ^{d}} B\) implies that

$$\begin{aligned} \lim _{n\rightarrow \infty } P(B_n\le x)=G(x)=e^{-{e^{-x}}}, \end{aligned}$$

for every valid \(x\in \Re \) of G(x). \(a_n=F^{-1}(1-{n^{-1}})\) and \(b_n=E[X-a_n|X>a_n]\) from theorem 8.3.4 of [56].

Proof

From theorem 8.3.2 of [56], we used \(\lim _{t \rightarrow \infty } \frac{s(t+xE(X-t |X>t))}{s(t)}\), based on the theorem 2 number 1., \(M(t)\sim \frac{1}{2\lambda \beta }\) as \(t \rightarrow \infty \), thus, \(\lim _{t \rightarrow \infty } \frac{s(t+xE(X-t|X>t))}{s(t)} \sim \lim _{t \rightarrow \infty } \frac{e^{-2\lambda \beta \left( t+\frac{x}{2\lambda \beta } \right) }}{e^{-\lambda \beta t}}=e^{-x}\). \(\square \)

Proposition 4

Let \(X_1\le X_2\le , \ldots ,\le X_n,\) be from NETLE with pdf in (18), let \(B_n^*=(X_{1:n}-a_n^*)/b_n^*\), then, for \(\beta =1\), \(B_n^*{\mathop {\rightarrow }\limits ^{d}} B^*\) is implies that

$$\begin{aligned} \lim _{n\rightarrow \infty } P(B_n^*\le x)=G^*(x; \theta )=1-e^{-e^x}, \end{aligned}$$

for every valid \(x\in \Re ^+\) of \(G^*(x)\), thus, \(a_n^*=F^{-1}(\frac{1}{n})\) and \(b_n^*=E(a_n^*-X|X\le a_n^*)\) from the theorem 8.3.6 of [56].

Proof

From theorem 8.3.6 of [56] we can consider \(\lim _{t \rightarrow 0} \frac{F(t+xE(t-X|X \le t))}{F(t)}\). Based on the Theorem 2 number 2., the asymptotic of \(E(t-X|X \le t)\) for \(\beta =1\) as \(\lim _{t \rightarrow 0}\) is \(m(t)\sim \frac{t}{\alpha +1}\), thus, \(\lim _{t \rightarrow 0} \frac{F(t+xE(t-X|X \le t))}{F(t)} \sim \lim _{t \rightarrow 0} \frac{2 \lambda ^\alpha (t+\frac{tx}{\alpha +1})^\alpha }{2 \lambda ^\alpha t^\alpha }=\left( 1+\frac{x}{\alpha +1}\right) ^\alpha \rightarrow e^x \;\;as \,\,\alpha \rightarrow \infty \). \(\square \)

3 Model Parameter Estimation

The parameters of the NETLG are estimated using the method of maximum likelihood estimation (MLE), least-square estimation (SLE), and percentile estimation (PE). The performance of the techniques is examined by simulation studies using NETLE.

3.1 Maximum Likelihood Estimation (MLE)

Let \(X_1, \ldots , X_n\) be a random sample of size n from the NETLG. Let \(\Theta =(\alpha ,\beta , \xi )^T\) be a vector of parameters, with the MLEs as \({\hat{\Theta }}=({\hat{\alpha }}, {\hat{\beta }}, {\hat{\xi }})^T\). The \({\hat{\Theta }}\) can be computed by the maximization of the log-likelihood function \((\ell (\Theta ))\) in Eq. (19).

$$\begin{aligned} \ell (\theta )&=n\log 2+n\log \alpha +n\log \beta +\sum _{i=1}^n \log g(x_i;\xi )-\sum _{i=1}^n \log G(x_i;\xi )\nonumber \\&+(\beta -1) \sum _{i=1}^n \log \left( -\log G(x_i;\xi ) \right) -\alpha \sum _{i=1}^n \left( -\log G(x_i;\xi ) \right) ^\beta \nonumber \\&+ \sum _{i=1}^n \log \left( 1-e^{- \left( -\log G(x_i;\xi ) \right) ^\beta } \right) +(\alpha -1) \sum _{i=1}^n \log \left( 2-e^{- \left( -\log G(x_i;\xi ) \right) ^\beta } \right) \end{aligned}$$
(19)

In other way, by solving the nonlinear system given below in (20) to (22).

$$\begin{aligned} \frac{\partial \ell }{\partial \alpha }=&\frac{n}{\alpha }-\sum _{i=1}^n \left( -\log G(x_i;\xi ) \right) ^\beta +\alpha \sum _{i=1}^n \log \left( 2-e^{- \left( -\log G(x_i;\xi ) \right) ^\beta } \right) \end{aligned}$$
(20)
$$\begin{aligned} \frac{\partial \ell }{\partial \beta }=&\frac{n}{\beta }+\sum _{i=1}^n \log \left( -\log G(x_i;\xi ) \right) -\alpha \sum _{i=1}^n\,\left( -\log G(x_i;\xi ) \right) ^\beta \, \log \left( -\log G(x_i;\xi ) \right) \nonumber \\&+\sum _{i=1}^n \frac{e^{- \left( -\log G(x_i;\xi ) \right) ^\beta } \left( -\log G(x_i;\xi ) \right) ^\beta \log \left( -\log G(x_i;\xi ) \right) }{1-e^{- \left( -\log G(x_i;\xi ) \right) ^\beta }}\nonumber \\&+(\alpha -1) \sum _{i=1}^n \frac{e^{- \left( -\log G(x_i;\xi ) \right) ^\beta }\,\left( -\log G(x_i;\xi ) \right) ^\beta \, \log \left( -\log G(x_i;\xi ) \right) }{2-e^{- \left( -\log G(x_i;\xi ) \right) ^\beta }} \end{aligned}$$
(21)
$$\begin{aligned} \frac{\partial \ell }{\partial \xi }=&\sum _{i=1}^n \frac{g^\xi (x_i;\xi )}{g(x_i;\xi )}-\sum _{i=1}^n \frac{G^\xi (x_i;\xi )}{G(x_i;\xi )}-(\beta -1)\beta \sum _{i=1}^n \frac{\left( -\log G(x_i;\xi ) \right) ^{\beta -1}\,G^\xi (x_i;\xi )}{\left( -\log G(x_i;\xi ) \right) ^\beta \, G(x_i;\xi )} \nonumber \\&+\alpha \beta \sum _{i=1}^n \frac{\left( -\log G(x_i;\xi ) \right) ^{\beta -1}\,G^\xi (x_i;\xi )}{ G(x_i;\xi )}\nonumber \\&-\beta \sum _{i=1}^n \frac{e^{- \left( -\log G(x_i;\xi ) \right) ^\beta }\,\left( -\log G(x_i;\xi ) \right) ^{\beta -1}\, G^\xi (x_i;\xi )}{\left( 1-e^{- \left( -\log G(x_i;\xi ) \right) ^\beta } \right) \, G(x_i;\xi )} \nonumber \\&-(\alpha -1)\beta \sum _{i=1}^n \frac{e^{- \left( -\log G(x_i;\xi ) \right) ^\beta }\,\left( -\log G(x_i;\xi ) \right) ^{\beta -1}\, G^\xi (x_i;\xi )}{\left( 2-e^{- \left( -\log G(x_i;\xi ) \right) ^\beta } \right) \, G(x_i;\xi )}. \end{aligned}$$
(22)

Where \(g^\xi (x_i;\xi )\) and \(G^\xi (x_i;\xi )\) are the partial derivative with respect to \(\xi \). Under the usual condition for the parameters in the interior of the \((\alpha ,\beta , \xi )\) space but not on the boundary, The asymptotic distribution of \(({\hat{\Theta }}-\Theta )\) as \(n\rightarrow \infty \) is the multivariate normal distribution with zero means and covariance matrix \({\textbf {I}}^{-1}(\Theta )\). The asymptotic behavior is also valid as \({\textbf {I}}(\Theta )=\lim _{n\rightarrow \infty }n^{-1} {\textbf {J}}_n(\Theta )\), where \({\textbf {J}}_n(\Theta )\) is a unit information matrix evaluated at \({\hat{\Theta }}\), and \(J(\Theta )= \left( {\partial ^2 \ell (\Theta )}/{\partial {\Theta }\partial {\Theta ^T}}\right) \).

3.2 Least Square Method (LSE)

Let \(X_{1}<,...,<X_{n}\) be an ordered random sample of size n from NETLG families of distributions. The LSEs for the vector of parameters \(\Theta =(\alpha , \beta , \xi )^T\), i.e \({\bar{\Theta }}=({\bar{\alpha }}, {\beta }, {\bar{\xi }})^T\) can be obtained by minimizing \(L(\Theta )\) given by,

$$\begin{aligned} L(\Theta )=\sum _{i=1}^n \left( e^{-\alpha \left( -\log G(x_i;\xi ) \right) ^\beta } \,\left( 2-e^{- \left( -\log G(x_i;\xi ) \right) ^\beta } \right) ^\alpha -\frac{i}{n+1} \right) ^2, \end{aligned}$$

or by the solution of the following nonlinear equations, which can be done numerically using R software, among others.

$$\begin{aligned} \frac{\partial L}{\partial \alpha }&=2\sum _{i=1}^n \left( e^{-\alpha \left( -\log G(x_i;\xi ) \right) ^\beta } \,\left( 2-e^{- \left( -\log G(x_i;\xi ) \right) ^\beta } \right) ^\alpha -\frac{i}{n+1} \right) \\&\times F(x_i)\left[ \log \left( 2- e^{- \left( -\log G(x_i;\xi ) \right) ^\beta }\right) - \left( -\log G(x_i;\xi ) \right) ^\beta \right] \\ \frac{\partial L}{\partial \beta }&=2\sum _{i=1}^n \left( e^{-\alpha \left( -\log G(x_i;\xi ) \right) ^\beta } \,\left( 2-e^{- \left( -\log G(x_i;\xi ) \right) ^\beta } \right) ^\alpha -\frac{i}{n+1} \right) \\&\times F(x_i) \left( -\log G(x_i;\xi ) \right) ^\beta \log \left( -\log G(x_i;\xi ) \right) \left[ \frac{e^{- \left( -\log G(x_i;\xi ) \right) ^\beta }}{\left( 2- e^{- \left( -\log G(x_i;\xi ) \right) ^\beta }\right) }- \alpha \right] \\ \frac{\partial L}{\partial \xi }&=2\alpha \beta \sum _{i=1}^n \left( e^{-\alpha \left( -\log G(x_i;\xi ) \right) ^\beta } \,\left( 2-e^{- \left( -\log G(x_i;\xi ) \right) ^\beta } \right) ^\alpha -\frac{i}{n+1} \right) \\&\times F(x_i) \left( -\log G(x_i;\xi ) \right) ^{\beta -1} \frac{G^\xi (x_i;\xi )}{G(x_i;\xi )} \left[ 1-\frac{e^{- \left( -\log G(x_i;\xi ) \right) ^\beta }}{\left( 2- e^{- \left( -\log G(x_i;\xi ) \right) ^\beta }\right) }\right] \end{aligned}$$

3.3 Percentile Estimation (PE)

The quantle of the NETLG in (7) can be used for parameter estimation. Let \(X_{1},X_{2},...,X_{n}\) be an ordered random sample of size n from NETLG families of distributions, the unknown parameters \(\Theta =(\alpha , \beta , \xi )^T\) can be estimated by equating the sample percentile points to the population percentile points. Let \(u_i\) denotes an estimate of \(F(x_{i:n})\), then the percentile estimators \({\tilde{\Theta }}=({\tilde{\alpha }},{\tilde{\beta }}, {\tilde{\xi }})^T\) can be obtained by minimizing (23) or by the solution of the \(\frac{\partial P}{\partial \alpha }=\frac{\partial P}{\partial \beta }=\frac{\partial P}{\partial \xi }=0\).

$$\begin{aligned} P(\Theta )=\sum _{i=1}^n \left( x_{i:n} -G^{-1}\left( e^{-\left[ -\log \left( 1-\sqrt{1-u_i^{\frac{1}{\alpha }}}\right) \right] ^{1/\beta }}\right) \right) ^2. \end{aligned}$$
(23)

3.4 Simulation Studies

Simulation studies are conducted to examine the performances of the different parameter estimation techniques by discussing their bias and mean square error (MSE) of the estimators. A moderate sample size of \(N=1000\) is generated each of sizes \(n = 30, 60, 90,\cdots 300\), from the NETLE for some chosen parameters values. The computations ware perform using the R3.5.3-software [57]. The resulting simulation studies is given in Fig. 4, 5, 6 and 7. The results from the figures indicated that both the MLE, LSE, and PE performed consistently as expected, and an increase in the sample sizes decreases the MSE, the bias appears negative in some cases. Thus, we can conclude that these three techniques can be enough for the parameter estimation of the NETLE and the other NETLG distributions.

Fig. 4
figure 4

Plots of the bias and MSE of the simulated data for \(\alpha =2.5 , \beta =1.5, \lambda =0.5 \)

Full size image
Fig. 5
figure 5

Plots of the bias and MSE of the simulated data for \(\alpha =0.8 , \beta =0.9, \lambda =0.5 \)

Full size image
Fig. 6
figure 6

Plots of the bias and MSE of the simulated data for \(\alpha =1.5 , \beta =1.2, \lambda =1.1\)

Full size image
Fig. 7
figure 7

Plots of the bias and MSE of the simulated data for \(\alpha =1.9, \beta =0.9, \lambda =1.0\)

Full size image

4 Real Data Illustration

We illustrated the advantages and flexibility of the NETLG families using NETLE distribution and compared its performance with some other popular models using two real data set. We estimated the competing models by maximum likelihood and compared fit using the Akaike Information Criterion (AIC), Bayesian Information Criterion (BIC), and Consistent Akaike Information Criterion (CAIC), Kolmogorov Smirnov (KS), Anderson-Darling (AD), and Cramer-von Mises (CvM) measures. The model with the smallest value of these measures fitted the data better. The competing models are the extended Topp–Leone exponential (ExTLE) [31], extended Erlang-truncated exponential (ExETE) [58], Poisson Topp–Leone exponential (PTLE) [59], generalized exponential Poisson (GEP) [60], Topp–Leone exponential (TLE) [23], Topp–Leone generalized inverted exponential (TLGIE) [61], generalized exponential (GE) [62], beta exponential (BE) [63], beta Erlang-truncated exponential (BETE) [48], and exponential (E) distribution.

4.1 Data I

The first data consist of the daily new deaths due to COVID-19 in New Jersey, USA, from March 12, 2020 to July 25, 2021, extracted from https://www.worldometers.info/coronavirus/usa/new-jersey/. The data: 1, 1, 2, 5, 2, 6, 5, 8, 19, 21, 22, 31, 37, 24, 42, 79, 100, 206, 124, 226, 81, 98, 259, 308, 222, 263, 284, 189, 106, 409, 398, 409, 365, 260, 150, 198, 425, 352, 413, 214, 279, 86, 121, 449, 372, 518, 352, 231, 162, 74, 386, 318, 297, 171, 150, 165, 88, 226, 210, 248, 231, 126, 121, 94, 161, 176, 120, 151, 111, 64, 18, 48, 162, 81, 141, 115, 84, 24, 58, 139, 114, 87, 73, 80, 87, 88, 112, 97, 56, 108, 42, 56, 63, 62, 41, 38, 29, 14, 36, 55, 52, 33, 45, 34, 27, 5, 17, 41, 52, 24, 22, 23, 50, 64, 106, 31, 50, 6, 30, 23, 43, 31, 20, 20, 5, 2, 2, 23, 33, 18, 13, 17, 16, 18, 15, 9, 10, 6, 3, 6, 3, 13, 3, 10, 11, 2, 5, 4, 15, 2, 31, 9, 7, 9, 1, 2, 2, 7, 2, 6, 8, 4, 3, 7, 5, 15, 9, 6, 5, 3, 22, 7, 11, 5, 9, 4, 4, 5, 8, 9, 4, 5, 4, 2, 1, 3, 9, 10, 3, 5, 4, 13, 7, 3, 3, 3, 4, 3, 7, 5, 7, 3, 7, 2, 1, 17, 12, 4, 4, 2, 4, 3, 18, 16, 17, 8, 12, 2, 10, 17, 15, 10, 6, 9, 1, 2, 16, 23, 16, 10, 12, 4, 10, 22, 12, 19, 25, 28, 15, 14, 38, 36, 36, 24, 32, 17, 16, 46, 59, 36, 27, 38, 11, 20, 84, 56, 62, 45, 42, 23, 15, 87, 111, 77, 59, 61, 29, 24, 86, 125, 66, 51, 50, 28, 26, 106, 139, 81, 47, 23, 19, 39, 115, 188, 82, 106, 32, 34, 38, 120, 124, 110, 99, 86, 173, 113, 34, 113, 87, 24, 16, 51, 136, 86, 109, 59, 17, 22, 132, 115, 81, 82, 72, 29, 30, 70, 109, 100, 93, 77, 24, 23, 93, 147, 79, 64, 47, 13, 13, 31, 135, 89, 62, 50, 24, 17, 104, 99, 69, 46, 46, 14, 21, 48, 128, 42, 30, 36, 16, 17, 45, 133, 46, 40, 34, 15, 22, 41, 79, 31, 27, 31, 40, 7, 61, 50, 38, 28, 24, 7, 15, 82, 75, 30, 24, 11, 9, 14, 51, 49, 34, 42, 33, 12, 25, 50, 59, 47, 43, 40, 9, 18, 45, 65, 30, 27, 39, 13, 19, 61, 49, 20, 25, 34, 12, 16, 42, 49, 33, 27, 22, 11, 10, 28, 43, 25, 26, 20, 9, 14, 23, 32, 23, 17, 14, 7, 9, 25, 34, 14, 12, 16, 6, 5, 7, 28, 6, 12, 8, 6, 5, 1, 31, 6, 2, 2, 3, 5, 11, 12, 7, 4, 4, 2, 3, 15, 18, 6, 12, 4, 3, 3, 6, 13, 5, 5, 5, 1, 4, 13, 3, 3, 5, 4, 4, 7, 11, 2, 2, 5, 3, 6, 12, 5, 2, 4, 5, 2, 4, 6, 3, 2, 5, 7, 3, 1, 8, 11, 4, 7, 5, 5, 4, 9, 6, 7, 9.

The results obtained from these measures and the estimators are provided in the Table 2. The results show that NETLE has the smallest value of the AIC, BIC, CAIC, KS, AD and CvM; thus NETLE provides a good representation of the data better than the other competing TL families and extensions exponential. Thus, NETLE can be recommended as a good model for modeling COVID-19 data and other studies in various fields of applied statistics. Figure 8 shows the plots of the (a) histogram with the fitted NETLE, PTLE, and TLE densities and (b) empirical cdf with fitted NETLE, PTLE, and TLE cdfs for the New Jersey data. Figure 9 is quantile-quantile plots of the NETLE, PTLE, and TLE for the New Jersey data set, it can be seen from the quantile-quantile plots that NETLE has more quantiles laying on the straight line.

Table 2 MLEs, L, AIC, BIC, CAIC, KS, AD, and CvM for the New Jersey data set
Full size table
Fig. 8
figure 8

Plots of the a histogram with the fitted NETLE, PTLE and TLE densities, and b empirical cdf with fitted NETLE, PTLE and TLE cdfs for the New Jersey data

Full size image
Fig. 9
figure 9

Plots of the quantile-quantile plots of the NETLE(left), PTLE(middle) and TLE(right) for the New Jersey data set

Full size image

4.2 Data II

The second data is the daily new deaths due to COVID-19 in California, USA, collected from March 12, 2020 to September 30, 2020. The data was extracted from https://www.worldometers.info/coronavirus/usa/california/. The data: 1, 1, 1, 5, 4, 3, 4, 1, 10, 6, 11, 14, 17, 12, 25, 12, 14, 35, 30, 24, 41, 44, 28, 33,54, 64, 61, 25, 46, 44, 53, 55, 80, 86, 89, 105, 28, 48, 73, 120, 103, 71, 91, 32, 58, 85, 75, 89, 80, 75, 24, 71, 92, 74, 81, 91, 64, 26, 61, 97, 89, 80, 104, 55, 79, 32, 103, 86, 106, 69, 71, 31, 19, 43, 102, 82, 97, 74, 27, 47, 72, 61, 63, 72, 66, 29, 23, 95, 97, 71, 47, 72, 27, 30, 85, 79, 74, 65, 67, 24, 48, 69, 96, 79, 64, 33, 32, 42, 104, 82, 98, 63, 29, 19, 75, 118, 150, 137, 102, 73, 26, 46, 138, 125, 127, 121, 91, 12, 57, 119, 155, 156, 134, 90, 27, 92, 169, 175, 113, 191, 136, 38, 108, 196, 169, 148, 188, 103, 67, 87, 182, 160, 186, 151, 75, 19, 98, 179, 164, 134, 166, 146, 18, 104, 149, 142, 140, 144, 67, 35, 80, 144, 157, 167, 152, 65, 22, 33, 72, 154, 99, 172, 71, 52, 75, 152, 105, 90, 99, 73, 31, 53, 123, 117, 88, 132, 51, 21, 34, 150, 107.

Table 3 provide the resulting test of the competing models. The NETLE provides a better fit to the data set than the other models because NETLE has the smallest values of all the measures. Figure 10 shows the plots of the (a) histogram with the fitted NETLE, PTLE, and TLE densities and (b) empirical cdf with fitted NETLE, PTLE, and TLE cdfs for the California data set. Figure 11 is quantile-quantile plots of the NETLE, PTLE, and TLE for the California data set. In addition, Fig. 11 displayed that the quantiles of the NETLE are laying on the straight line better than the PTLE and TLE, which indicates the good performance of our new model.

Table 3 MLEs, L, AIC, BIC, CAIC, KS, AD, and CvM for the California data set
Full size table
Fig. 10
figure 10

Plots of the a histogram with the fitted NETLE, PTLE and TLE densities, and b empirical cdf with fitted NETLE, PTLE and TLE cdfs for the California data

Full size image
Fig. 11
figure 11

Plots of the quantile-quantile plots of the NETLE (left), PTLE (middle), and TLE (right) for the California data set

Full size image

5 Conclusion

This paper proposes and studies a new extension of the Topp–Leone family of distributions. The model’s important mathematical and statistical properties are derived such as stochastic ordering, model series representation, moments, stress–strength reliability parameter, Renyi entropy, order statistics, and the moment of residual life. A new member of NETLG called new extended Topp–Leone exponential (NETLE) is derived; we study its skewness and kurtosis, quantile, residual life, reverse residual life, and extreme value distributions. The model parameter estimation is conducted by maximum likelihood estimation (MLE), least-square estimation (LSE), and percentile estimation (PE). The performance of the MLE, LSE, and PE is examined by simulation studies from the NETLE by discussing the estimators’ bias and mean square error (MSE), and the result was very good, as their MSE decreased with the increase in the sample size. In the end, we compare the performance of the NETLE in practice with some other popular models using two sets of daily new deaths due to COVID-19 data from California and New Jersey, USA, and our new model performs better than the other existing models as measured by some model selection criteria and goodness of fit statistics. For further studies, several special models can be derived and investigated, and different methods of estimation of the models can be considered, such as Bayesian analysis under various prior, regression analysis, survival analysis, the stress–strength reliability estimation under various viewpoints, and other applied studies due to the flexibility of the proposed family. However, the properties and characterizations of some special members of the model may require some complicated mathematical ideas such as special integrals and series representations which may lead to many useful mathematical tools. We hope that the new model will attract wider applications in various fields of studies.