1 Introduction

Erosion–corrosion can be described as the wear caused by combined action of mechanical process of solid particle erosion and electrochemical process of corrosion [1]. Erosion–corrosion-related problems occur in power plants, oil and gas processing, and chemical plants where there is an interaction between solid particles, corrosive fluid, and a target material [2–5]. The interactions between erosion and corrosion are complex and both processes can either complement each other and accelerate the material removal rate or may suppress the total wear rate [6, 7].

Change in erosion rate due to corrosion or change in corrosion rate because of erosion factor is called synergism [2, 3]. In fact, synergy is described as the additional wear rate experienced by a metal under the combined action of erosion and corrosion [3, 8]. Synergy is said to be positive when the total wear rate due to erosion–corrosion is higher than the sum of wear rates due to pure erosion and pure corrosion. Negative synergism occurs when erosion–corrosion rate is lower than sum of pure erosion and pure corrosion rates [3, 7, 9]. Synergy can be obtained numerically through Eq. (1):

$$S \, = \, T \, {-} \, \left( {W_{\text{o}} + \, C_{\text{o}} } \right),$$
(1)

where T is the total wear rate due to erosion–corrosion, W o is the wear rate due to pure erosion (i.e., with cathodic protection of target material in erosion–corrosion process), C o is the wear rate due to pure corrosion (i.e., with no erosion effects), and S is the additional wear rate due to synergistic effects [3, 7, 9, 10]. S could be further divided into two subdivisions as

$$S \, = \, \Delta W_{\text{c}} + \, \Delta C_{\text{w}} ,$$
(2)

in which ΔW c is the change in erosion rate because of corrosive media and ΔC w is the change in corrosion rate due to erosion [10].

From Eqs. (1), (2), and (3a) could be obtained:

$$T \, = \, W_{\text{o}} + \, \Delta W_{\text{c}} + \, C_{\text{o}} + \, \Delta C_{\text{w}} ,$$
(3a)

where

$$W_{\text{o}} + \, \Delta W_{\text{c}} = \, W_{\text{c}} ,$$
(3b)
$$C_{\text{o}} + \, \Delta C_{\text{w}} = \, C_{\text{w}} .$$
(3c)

The term W o + ΔW c shows the erosion part of the material loss rate, and the term C o + ΔC w represents the corrosion part of the material loss [10]. Therefore,

$$T \, = \, W_{\text{c}} + \, C_{\text{w}} ,$$
(4)

W c is called the total wear component of T and C w is called the total corrosion component of T.

Interaction between erosion and corrosion is very important for designers and researchers to understand the macro- and micro-mechanism of these two processes when selecting materials for any engineering applications [3, 7]. For example, corrosion can enhance erosion rate through dissolution of work hardened layer or erosion can increase material tendency for passive layer formation and thus suppressing corrosion rate [11]. The extent of erosion–corrosion is dependent on a wide range of variables, including the solid sand particle factors (hardness, density, size, and shape), target material (hardness, metallographic structure, strength, ductility, and toughness), and the environment (erosive particle concentration, slurry composition, flow velocity, temperature, and impact angle) [12].

Extensive studies have been conducted to understand the effect of various variables on erosion–corrosion behavior of materials. For example, for ductile materials, it has been shown that erosion–corrosion has a maximum rate at low impingement angles ranging from 15° to 30° [13, 14]. Oka et al. [14] investigated erosion–corrosion behavior of some materials and showed that for pure aluminum alloy maximum erosion–corrosion rate occurred at impingement angle near to 30°.

Among the engineering alloys, aluminum and its alloys have attracted much attention. The excellent combination of lightweight, high strength to weight ratio, great corrosion resistance, and reasonable cost has made aluminum and its alloys one of the most commonly used metal groups [15]. The high corrosion resistance, especially to seawater and marine atmospheres, is the primary advantage of 5000 series aluminum alloy [16]. For example, AA5052 alloy with 2.5 wt% magnesium and 0.1 wt% chromium shows a good compromise between mechanical resistance, formability, fatigue resistance, and corrosion resistance. AA5052 alloy is widely used in marine applications where makes it vulnerable to erosion–corrosion due to mechanical action of sands and electrochemical corrosion of seawater [15–17]. Erosion–corrosion behavior of various aluminum alloys has been investigated [18–21]. However, to our knowledge, there was no study on the erosion–corrosion behavior of AA5052 alloy. Moreover, synergistic effects including effect of erosion on corrosion and corrosion on erosion are important parameters in total erosion–corrosion material loss which can be different in various materials and working conditions [2, 3, 9].

In this study, the erosion–corrosion behavior of AA5052 aluminum alloy has been investigated in 3.5 wt% NaCl solution at various impingement angles of 25°–90°. Pure erosion and erosion–corrosion tests were performed to study the synergistic effects of erosion and corrosion including change in erosion rate because of corrosive media (ΔW c) and the change in corrosion rate due to erosion (ΔC w).

2 Experimental Procedure

Samples, 5 mm × 5 mm in cross-section (i.e., an exposed area of 0.25 cm2), made of AA5052 aluminum alloy with a composition of Al–2.02%Mg–0.51%Fe–0.13%Si–0.003%Cr and a hardness of 30 HV30 were used in the tests. The surface of the specimens was ground up to 1200 SiC paper.

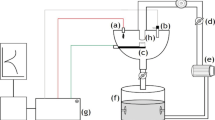
A slurry electrolyte of 3.5 wt% NaCl solution containing SiO2 with an average size of 250–500 μm as eroding particles was used in the tests. Pure erosion and erosion–corrosion tests were performed using a jet impingement rig that could pump the erosive–corrosive media through a nozzle on the sample surface at controlled velocities and impingement angles. Figure 1 shows a schematic setup of the erosion–corrosion rig. The nozzle with a diameter of 8 mm (i.e., an area of 0.50 cm2) could erode the whole area of the sample at any impingement angle. The distance between the jet nozzle and the specimen surface was adjusted to be about 5 mm at impingement angle of 90°.

Fig. 1
figure 1

Schematic of erosion–corrosion setup, 1 electro pump, 2 reference electrode in capillary, 3 counter electrode, 4 sample, 5 nozzle, 6 slurry entrance to the container, 7 potentiostat, and 8 exit valve

Full size image

At a specific concentration of impinging particles, the number of impacted particles on the surface of the sample decreased as the impingement angle decreased. Therefore, the erosion and erosion–corrosion rates were normalized based on the number of impacted particles on the sample surface. In order to obtain the normalized values, the erosion and erosion–corrosion rates were divided by the sinθ, where θ is the impingement angle, as shown in Fig. 2 [22].

Fig. 2
figure 2

Effect of impingement angle on the number of impacted particles on the surface of sample at a normal incident and b oblique angle of θ [22]

Full size image

Pure erosion and erosion–corrosion tests were performed at a jet velocity of 3 m/s, sand concentration of 90 g/l, and different impingement angles of 25°–90° for test duration of 30 min. Erosion–corrosion tests were conducted at open circuit potential (OCP) without applying any external potential.

Pure erosion tests were performed with applying a constant voltage of one volt negative to OCP of the samples according to ASTM G119-09 standard [10]. The OCP of the alloy was measured in the first 60 s of each test and the cathodic voltage was then applied using a 302N Autolab potentiostat/galvanostat. Before and after each test, samples were cleaned with acetone using ultrasonic cleaner and weighted using a precision balance with an accuracy of 0.1 mg. For more accuracy, all the tests were repeated for at least three times.

Potentiodynamic polarization tests were conducted in stagnant solution, flow corrosion (i.e., flow of the solution over the sample with no mechanical action of erodent particles) and during erosion–corrosion process using the potentiostat/galvanostat apparatus to obtain pure corrosion rate and corrosion rate during erosion–corrosion process according to ASTM G102-04 standard [23]. The tests were performed at potential range of −250 to +1000 mV versus OCP with scan rate of 2 mV/s. The counter and reference electrodes were graphite and saturated Ag/AgCl in a capillary, respectively. After obtaining the pure corrosion, pure erosion and erosion–corrosion rates, the synergistic effect (S) was calculated using Eq. (1). Electrochemical corrosion rate during erosion–corrosion process (C w) was obtained according to polarization curves. ΔC w was then calculated by subtracting C o from C w [i.e., Eq. (3c)] [10], and using Eq. (2) ΔW c was also calculated. The eroded surfaces were characterized using SEM to investigate the erosion mechanisms and analysis of surface layer formed on the erosion–corrosion samples.

3 Results and Discussion

Figure 3 shows the polarization curve for AA5052 aluminum alloy in a stagnant 3.5 wt% NaCl solution. As could be seen in Fig. 3, a passivation occurred at anodic branch of the diagram. This passive layer, usually Al2O3·3H2O [24], is a protective layer against corrosion and is the reason for low corrosion rates at many environments such as seawater [17]. The corrosion current density was graphically obtained [24] from polarization curve in Fig. 3 and was about 3.15 × 10−6 A/cm2. Using stern-geary equation in accordance with ASTM G102-04 [23], a pure corrosion rate (i.e., C o) of about 10−3 mg/cm2 h was calculated.

Fig. 3
figure 3

Polarization curve for stagnant corrosion of AA5052 alloy in 3.5 wt% NaCl solution

Full size image

Figure 4 shows pure erosion (W o) and erosion–corrosion (T) rates as a function of impingement angle at a jet velocity of 3 m/s and sand concentration of 90 g/l. Figure 4 shows that maximum pure erosion and erosion–corrosion rates occurred at an impingement angle of 30° and minimum of these rates occurred at an impingement angle of 90°. Differences between the rates of erosion–corrosion in 30° and 90° impingement angles could be due to change in the erosion mechanisms. At impingement angle of 30° material loss through cutting was the dominant erosion mechanism, whereas at impingement angle of 90° material loss mostly occurred via plastic deformation and work hardening due to the normal particle impacts [25–28].

Fig. 4
figure 4

Pure erosion (W o), erosion–corrosion (T) and synergism (S) rates versus impingement angle for AA5052 aluminum alloy at a jet velocity of 3 m/s and sand concentration of 90 g/l after 30 min of erosion

Full size image

Figure 5 shows SEM images of pure erosion and erosion–corrosion samples eroded at impingement angles of 30° and 90°. Figure 5a, c shows that erosion features like raised lips and wear tracks were present in the direction of erosion in both pure erosion and erosion–corrosion samples eroded at impingement angle of 30°. At any impingement angle, particle impact on the surface of the sample may be divided into tangential and normal stress components. Tangential stress component of the impacts, which was dominant at low impingement angles around 30°, plastically deformed the surface through cutting and created wear tracks and raised edges. The formation and the subsequent removal of the edges by particle impacts could lead to a higher erosion rate at impingement angle of 30° for both pure erosion and erosion–corrosion as shown in Fig. 4.

Fig. 5
figure 5

SEM images of AA5052 alloy eroded at a jet velocity of 3 m/s: pure erosion at impingement angle of a 30° and b 90° and erosion–corrosion at impingement angle of c 30° and d 90°

Full size image

At higher impingement angles, the normal component of impact forces became dominant [25, 26]. Figure 5b and d shows the eroded surfaces of the alloy at an impingement angle of 90°. The figure shows plastic deformation of the surface with raised edges around the impact. A higher impact energy could be transferred from sand to the surface at the normal angle and induce a thicker work hardened layer on the surface [28]. This could be a reason for the lower erosion rate at normal angle as shown in Fig. 4.

Figure 4 also shows synergism rates (S) at different impingement angles calculated from Eq. (1). Comparing the corrosion rate obtained from Fig. 3 with the pure erosion (W 0) and erosion–corrosion rates (T) of Fig. 4 reveals that corrosion rate (C o) of the alloy in a stagnant solution was only about 0.06 % of the erosion and erosion–corrosion rates and could be neglected in calculating synergism values. Figure 4 shows a negative synergism at all impingement angles. The energy dispersive spectrometry (EDS) analysis of samples eroded at impingement angles of 30° and 90° is shown in Table 1. The analysis of the as-received and pure corrosion (i.e., corroded sample under a stagnant solution after 30 min) surfaces is also presented in Table 1. The table shows a higher amount of oxygen on the surface of erosion–corrosion and pure corrosion samples as compared to pure erosion and as-received samples. This could indicate the formation of a thicker protective oxide layer on the surface of erosion–corrosion and pure corrosion samples. High oxygen content on the erosion–corrosion surface of aluminum alloys was also observed by others [9, 20] and was attributed to the existence of a protective oxide layer on the surface. At the velocity of 3 m/s, it seems that the energy of the impacted particles was not high enough to totally remove the protective oxide layer formed on the erosion–corrosion surface, i.e., removal rate of protective oxide layer by sand erosion was lower than the formation rate of this layer. Therefore, this layer could increase the material resistance against impacted sands in erosion–corrosion compared to pure erosion tests, which resulted in a negative synergism as shown in Fig. 4.

Table 1 EDS analysis of the alloy at various test conditions in wt%
Full size table

Polarization curves of AA5052 aluminum alloy during erosion–corrosion tests at impingement angles of 25°, 30°, 45°, and 90° were obtained to measure the pure corrosion rates in the erosion–corrosion conditions. A similar trend in polarization curves was obtained at various impingement angles and, therefore, the polarization curves of the alloy at typical impingement angles of 30° and 90° are only shown in Fig. 6. For comparison, the polarization curves of the alloy in a stagnant solution (i.e., the same as Fig. 3) and flow corrosion (i.e., with no mechanical action of sand particles) at a jet velocity of 3 m/s are also presented in Fig. 6. The corrosion current densities, the corrosion rates, and the corrosion potentials (E corr) were obtained from the polarization curves and are shown in Table 2. The table indicates close values of the corrosion rates at various impingement angles. This could suggest that at a jet velocity of 3 m/s, the impact angle did not affect the corrosion behavior of AA5052 as was also suggested by Zhang [9]. The table also shows that the corrosion rate in the flow condition is about 30 times of that in the stagnant condition. Because of fluid flow, more oxygen as a corrosive agent could reach the surface, and therefore oxygen reduction occurred with higher rates. This could result in a higher corrosion rate during the flow compared to the stagnant condition shown in Fig. 6.

Fig. 6
figure 6

Polarization curves of AA5052 aluminum alloy during various test conditions

Full size image
Table 2 i corr and E corr of the alloy at various test conditions obtained from polarization curves shown in Fig. 6
Full size table

An almost same trend was observed in the anodic branch of polarization curves in various conditions in Fig. 6. This could also confirm the existence of a protective and passive layer (i.e., Table 1), which was durable enough during particle impacts under the erosion–corrosion conditions. Existence of the passive layer on the surface could be a reason for close corrosion rates in flow and erosion–corrosion conditions shown in Fig. 6. This protective layer could also be responsible for very close E corr obtained in Fig. 6. Furthermore, as mentioned before, this layer could be a reason for lower erosion–corrosion compared to pure erosion rates, which resulted in negative synergisms obtained in Fig. 4. Indeed, sand particle impacts did not have any remarkable effect on the corrosion behavior of AA5052 aluminum alloy at a jet velocity of 3 m/s. It could be suggested that at a jet velocity of 3 m/s the corrosion behavior of the alloy during erosion–corrosion process was mainly controlled by oxygen replenishment of the eroding surface.

Table 3 shows various factors that affect the erosion–corrosion rate as obtained in Eqs. (1), (2), and (3a) at a jet velocity of 3 m/s, sand concentration of 90 g/l, and impingement angles of 25°, 30°, 45°, and 90°. The total wear component (W c) was more than 94 % of the total material loss rate (T) at all impingement angles. This indicated that erosion was the dominant material loss mechanism in the erosion–corrosion of AA5052 aluminum alloy at a jet velocity of 3 m/s. Table 3 also shows that W c was lower than the pure erosion rate (W o). This means that ΔW c (i.e., change in erosion rate because of corrosive media) was negative. Negative ΔW c revealed that corrosion has suppressed erosion rate probably due to a protective film formation discussed earlier. Although corrosion rate during erosion–corrosion (C w) was very low compared to erosion–corrosion rates, the high absolute values of ΔW c revealed that corrosion had a large effect on the erosion rate and could not be neglected in erosion–corrosion processes.

Table 3 Material loss rates and synergy factorsa at various impingement angles in mg/cm2 h
Full size table

Table 3 also shows that W c (i.e., W o + ΔW c) was about 30 and 52 % lower than the pure erosion rate, W o, at impingement angles of 30° and 90°, respectively. This might suggest a higher effect of corrosion in erosion–corrosion process at angle of 90° than the 30°. Table 3 also shows little change in ΔC w (i.e., change in corrosion rate due to erosion) at various impingement angles. This could be attributed to the very low effect of sand impingement on the corrosion behavior of the alloy as discussed for polarization curves in Fig. 6.

4 Conclusions

The effect of impingement angle on the pure erosion and the erosion–corrosion behavior of AA5052 aluminum alloy was studied in 3.5 wt% NaCl solution and following results were obtained:

  1. (1)

    Maximum pure erosion and erosion–corrosion rates occurred at impingement angle of 30° and minimum of these rates occurred at impingement angle of 90°.

  2. (2)

    Negative synergism was obtained at all studied impingement angles, which could be attributed to the formation of protective oxide layer on the surface of erosion–corrosion samples.

  3. (3)

    The existence of the protective oxide layers was confirmed by both the EDS analysis of the erosion and erosion–corrosion surfaces and the polarization curves during erosion–corrosion tests.

  4. (4)

    Polarization curves showed similar corrosion rates in flow and erosion–corrosion tests that were also higher than the stagnant condition. This could suggest that oxygen reduction rather than sand erosion was responsible for the higher corrosion rates.