1 Introduction

It is recognized by many studies that the combustor is the least efficient system in power plants (Markatos and Mukerjee 1981; Shah and Markatos 1987; Stanciu et al. 2007; Khaldi and Adouane 2011). In order to improve the efficiency of the combustion system, it is necessary to identity the physical and chemical mechanisms responsible for thermodynamic irreversibilities. The contribution of each mechanism can be determined by calculating its entropy generation rate, (Liakos et al. 2000; Bejan 2002; Yapici et al. 2005a; Rakopoulos and Giakoumis 2006). Wherefore, the basic equations expressing the distributions of velocity, temperature and species concentrations are used to deduce the local entropy generation rate (Datta 2000; Yapici et al. 2005b; Lior et al. 2006). The review paper of Som and Datta (2008) outlined all the works dealing with computing entropy production in combustion processes covering different fuel types (liquid, gaseous and solid), different configurations (confined, unconfined), different flame types (premixed, non-premixed) and different flow regimes (laminar, turbulent). Laminar flames were considered at first by various researchers (e.g. Datta 2000; Stanciu et al. 2001a; Yapici et al. 2004; Som and Datta 2008) showing that the thermal diffusion, chemical reaction, mass diffusion and the viscous dissipation represent, in order of enumeration, the predominant sources of entropy generation rate. Few works were interested in turbulent flames despite their fundamental role in actual combustors. Stanciu et al. (2001a, 2007) and Yapici et al. (2004, 2005a) works are based on the standard k-ε model for modeling turbulence and strong irreversible chemical reaction assumptions, i.e., one-step or two-steps exothermic reactions or fast-chemistry reaction. The numerical analysis of Yapici et al. (2004, 2005b) was limited to computing uniquely the thermal and viscous contributions in the entropy generation; the former dominates largely the last. The computation of Stanciu et al. (2001a, 2007) divided the entropy field in mean part and turbulent part. The important result is that at whole the turbulent fluctuations are the major source of entropy generation; in decreasing volumetric rate, the main contributors are chemical, thermal conduction and mass diffusion (Stanciu et al. 2001b, 2007).

The present study is interested in the calculation of thermodynamic irreversibilities occurring in turbulent combustion process in a coaxial jets burner. This combustor configuration was the focus of numerous experimental as well as numerical investigations because of its relatively simple geometry and its representativeness of gas turbine burners. The study is based on the k-ε turbulence model and it considers a two-step combustion reaction. The local entropy generation rate is calculated taking into account all the mechanisms responsible of entropy generation, i.e., viscous friction, heat conduction, species diffusion and chemical reaction. Besides, the effects of the preheating of the inlet fuel and air factor of mixture on entropy generation are analyzed. All the simulations are carried by the software Fluent.

2 Burner Configuration

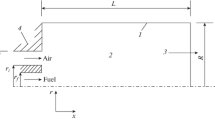
The present study is a continuation of previous numerical investigations of Bouras et al. (2010, 2012) based on the experimental work of Owen et al. (1976), where the interest was on turbulent diffusion flame characterization in the coaxial jet combustor configuration (Owen et al. 1976; Pierce and Moin 2004). The burner depicted in Fig. 1 and considered in the experimental study consists of a coaxial jet discharging into a cylindrical chamber pressurized to 3.8 atm. The burner is of radius R4 = 0.06115m and length L = 1m and is with isothermal walls of 500K. The fuel (CH4) is issued from the inner jet with radius R1 = 0.03157m, at a velocity V1 = 0.987 m/s and at temperature T1 = 300K, while the preheated air at temperature T2 = 750K is supplied from the annular jet of external radius R3 = 0.04685m at a velocity V2 = 20.63 m/s.

Fig. 1
figure 1

Schematic of the burner

Full size image

This work consists a two-dimensional (2D) study of the entropy generation in diffusion flame. We produced the geometry and meshes by GAMBIT, and the chosen meshes are of quadrilateral type, where the selected grid is smoothed in the region nearby the solid walls of the burner and at the level of interaction of air and CH4, in order to accommodate more information in solid boundary and flame zone. The volume contained approximately 40.000 cells, the size of a cell ranged from 4.87E-09 m2 to 1.52E-04 m2.

3 Governing Equations

The simulation of combustion in the burner is assumed steady, turbulent and axisymmetric. According to these assumptions, the set of equations suitable for the adopted combustion model are the following (Stanciu et al. 2001a; Yapici et al. 2005a; Stanciu et al. 2007; Som and Datta 2008):

$$ \mathrm{Continuity}:\kern1em \frac{\partial }{\partial {x}_i}\left(\rho {u}_i\right)=0 $$
(1)

and: ρ:Density; u i : velocity components.

$$ \mathrm{Momentum}\kern1.25em \frac{\partial }{\partial {x}_i}\left(\rho {u}_i{u}_j\right)=-\frac{\partial p}{\partial {x}_j}+\frac{\partial {\tau}_{ij}}{\partial {x}_j} $$
(2)

and: u j : velocity components; p: Pressure; τ: Shear stress tensor; x i : Cartesian coordinate.

$$ \mathrm{Energy}:\kern1.25em \frac{\partial }{\partial {x}_i}\left(\rho {u}_ih\right)={u}_i\frac{\partial p}{\partial {x}_i}+{\tau}_{ij}\frac{\partial {u}_i}{\partial {x}_j}+\frac{\partial }{\partial {x}_i}{\lambda}_{eff}\frac{\partial T}{\partial {x}_i}-\frac{\partial }{\partial {x}_i}\left({\displaystyle \sum_{k=1}^n\rho {y}_k{U}_{k,i}}{h}_k\right) $$
(3)

and: h: Enthalpy; T: Temperature; λ: Thermal conductivity; y: Mass fraction of chemical species.

$$ \mathrm{Species}:\kern1.25em \frac{\partial }{\partial {x}_i}\left(\rho {u}_i{y}_k\right)=\frac{\partial^2\rho {D}_k{y}_k}{\partial {x^2}_i}+{\dot{\omega}}_k $$
(4)

and: D:Coefficient of mass diffusion; ω:Arrhenius terms.

$$ \mathrm{Thermodynamic}\ \mathrm{status}:\kern1.25em p=\rho RT{\displaystyle \sum_{k=1}^n\frac{y_k}{M_k}} $$
(5)

and: M k :Mass Molar; R: Constant of ideal gas.

$$ \mathrm{Turbulence}\ \mathrm{kineticenergy},\ k:\kern1.5em \frac{\partial }{\partial {x}_i}\left(\rho {u}_ik\right)=\frac{\partial }{\partial {x}_j}\left(\mu +\frac{\mu_t}{\sigma_k}\right)\frac{\partial k}{\partial {x}_j}+{G}_k-\rho \varepsilon +{S}_k $$
(6)
$$ \mathrm{Dissipationrate},\ \varepsilon :\kern1.75em \frac{\partial }{\partial {x}_i}\left(\rho {u}_i\varepsilon \right)=\frac{\partial }{\partial {x}_j}\left(\mu +\frac{\mu_t}{\sigma_{\varepsilon }}\right)\frac{\partial \varepsilon }{\partial {x}_j}+{C}_{1\varepsilon}\frac{\varepsilon }{k}{G}_{\varepsilon }-{C}_{2\varepsilon}\rho \frac{\varepsilon }{k}+{S}_{\varepsilon } $$
(7)

where: μ: Viscosity and C 1ε  = 1.44, C 2ε  = 1.92, σ k  = 1.0, σ ε  = 1.3 are k-Ɛ turbulence model constant.

The combustion reaction is modeled with a two-step reaction mechanism where the production and the combustion of carbon monoxide (CO) are taken into account. In the first stage, methane is oxidized into carbon monoxide and water vapor, and in the second, carbon monoxide is oxidized into carbon dioxide. The reaction mechanism takes place according to the constraints of chemistry, and is defined by stoichiometric equations (Som and Datta 2008; Yapici et al. 2004):

$$ \mathrm{Reaction}\ 1:\kern0.75em C{H}_4+\frac{3}{2}{O}_2\to CO+2{H}_2O\kern1.25em \left(\mathrm{step}\ 1\right) $$
(8a)
$$ \mathrm{Reaction}\ 2:\kern1.5em CO+\frac{1}{2}{O}_2\to C{O}_2\kern1em \left(\mathrm{step}\ 2\right). $$
(8b)

Once the computations are made, the results obtained are exploited to calculate the local entropy generation rate, as follows (Stanciu et al. 2001b; Rakopoulos and Kyritsis 2001; Yapici et al. 2005b; Som and Datta 2008):

$$ {\dot{S}}_{gen}={\left({\dot{S}}_{gen}\right)}_f+{\left({\dot{S}}_{gen}\right)}_h+{\left({\dot{S}}_{gen}\right)}_d+{\left({\dot{S}}_{gen}\right)}_{ch} $$
(9)

where:

$$ {\left({\dot{S}}_{gen}\right)}_f:\ \mathrm{Fluid}\ \mathrm{friction}\ \mathrm{volumetric}\ \mathrm{entropy}\ \mathrm{generation}\ \mathrm{rate},\ {\left({\dot{S}}_{gen}\right)}_f=\frac{\mu_{eff}}{T}\frac{\partial {u}_i}{\partial {x}_j}\frac{\partial {u}_i}{\partial {x}_j}>0 $$
(10)
$$ {\left({\dot{S}}_{gen}\right)}_h:\ \mathrm{Heat}\ \mathrm{transfer}\ \mathrm{volumetric}\ \mathrm{entropy}\ \mathrm{generation}\ \mathrm{rate},\ {\left({\dot{S}}_{gen}\right)}_h=\frac{\lambda_{eff}}{T^2}\frac{\partial T}{\partial {x}_j}\frac{\partial T}{\partial {x}_j}>0 $$
(11)
$$ {\left({\dot{S}}_{gen}\right)}_d:\mathrm{Diffusion}\ \mathrm{of}\ \mathrm{species}\ \mathrm{volumetric}\ \mathrm{entropy}\ \mathrm{generation}\ \mathrm{rate},\ {\left({\dot{S}}_{gen}\right)}_d={\displaystyle \sum_{k=1}^n\rho {D}_k}\frac{R_k}{y_k}\frac{\partial {y}_k}{\partial {x}_i}\frac{\partial {y}_k}{\partial {x}_i}>0 $$
(12)
$$ {\left({\dot{S}}_{gen}\right)}_{ch}:\ \mathrm{Chemical}\ \mathrm{reaction}\ \mathrm{volumetric}\ \mathrm{entropy}\ \mathrm{generation}\ \mathrm{rate},\ {\left({\dot{S}}_{gen}\right)}_{ch}=\frac{\dot{\omega}}{T}{\displaystyle \sum_{k=1}^n\left({\gamma}_k^{\prime }-{\gamma}_k^{{\prime\prime}}\right)}{\mu}_k>0 $$
(13)

and: μ k : Chemical potential; γ: Stoichiometric coefficient.

We used FLUENT-CFD package to resolve the governing equations mentioned previously. We note that the SIMPLEC algorithm is used for pressure velocity coupling. And, the convergence criteria for solving equations are equal to 10−3. This investigation shows two types of results. The first one is the validation of computational profiles of axial velocity and temperature field with experimental data for methane fueled coaxial jet combustor (Owen et al. 1976; Pierce and Moin 2004), and the second one, the obtained results are exploited to evaluate the entropy generation rate for different cases of flows.

4 Results and Discussion

4.1 Numerical Validation

The primary quantities were tested against experimental data that used the length R and the velocity U normalized by the injector radius (R ≡ R3) and the inlet bulk velocity of air (U ≡ V2).

4.1.1 Axial Velocity

Figure 2 presents the comparison of computational and experimental radial profile of axial velocity. Indeed, the velocity fields achieve significantly better agreement with the experiment at two measurement stations x/R = 0.14 and x/R = 4.67. The mean axial velocity ranges from about u/U = −0.15 to 1.1, where the maximum is located in the flame zone. The negative values of velocity are present close to the wall in the recirculating region and in the center of the burner: a brutal variation in the section of the burner results in the creation of the recirculating zones what can be explained by the significant negative values observed close to the wall. In addition, the difference between the inlet velocity of CH4 and air produces the second zone of recirculation, which appears at the center of the combustion chamber. The meeting of the two inlet flows is characterized by high mixture level generated by the shearing where the flame stabilized in this region (Bouras et al. 2010, 2012; Pierce and Moin 2004). The zone of the flame is the seat of the great values of velocity. In particular, the position of peak velocity is reproduced well by the present numerical computation. Furthermore, in the recirculating region and the flame holder, the agreement is satisfactory.

Fig. 2
figure 2

Radial profiles of normalized axial velocity

Full size image

4.1.2 Temperature

The comparisons of the predicted radial profiles of temperature with those of experiments at two measurement stations, x/R = 4.52 and x/R = 5.20, are shown in Fig. 3. Temperature is a quantity that is derived from the energy equation by assuming isothermal walls and neglecting thermal radiation. The high values of the temperature are located within the reaction zone around the center of the burner; away the temperature decreases to achieve the wall temperature. Indeed, the numerical temperature profiles give similar experimental trends but with overestimation, especially near the center of the burner. The expected overprediction of temperature can be attributed to three factors: i) ignoring of thermal radiation in the numerical simulation, ii) experimental uncertainty, especially in regions with large temperature fluctuations, and iii) difficulty to ensure perfectly the experiment condition of isothermal water-cooled walls at 500K (Bouras et al. 2010, 2012; Pierce and Moin 2004).

Fig. 3
figure 3

Radial profiles of Temperature

Full size image

4.2 Entropy Generation Analysis

Figure 4 illustrates the pie chart of the entropy generation rates produced by all the mechanisms involved in the combustion process. The total generated entropy is about 140 W/K. Chemical reaction (52 %) is the first producer of entropy. In the second order comes the heat conduction which is responsible of 38 %. Therefore, species diffusion transfers have moderate part (10 %). The effect of viscosity friction is negligible regarding the generation of thermodynamic irreversibilities.

Fig. 4
figure 4

Pie charts of entropy generation

Full size image

4.2.1 Effect of Preheating Fuel on Entropy Generation

In this part of work, we performed a detailed numerical analysis for the study of entropy generation considering the preheated CH4 at the inlet, using the mathematical equations presented previously (Eqs. 9, 10, 11, 12 and 13). Figure 5 illustrates the obtained entropy generation sources rates for different CH4 inlet temperatures. It has been shown that the total rate of entropy generation becomes large in the region of high temperature gradient. The chemical reaction accounted for the maximum entropy generation in CH4 flame, while thermal diffusion contributed in the second largest one after the entropy generation due to the chemical reaction. The contribution of diffusion species gives less impact comparatively to two previous sources. However, the effect of the viscous dissipation on the total entropy generation is negligible. Moreover, the preheated fuel in a stoichiometric, CH4–air, flame has given a reduction in the total entropy generation rate by approximately 0.4 % with the difference of 10°C of temperature relatively to the reference flow. However, the effect of the preheated fuel on the total entropy generation was found to be much smaller, and the effect of the viscous dissipation negligible. So, the total entropy generation decreases with the increase of inlet temperature of fuel (CH4).

Fig. 5
figure 5

Effect of preheating fuel on entropy generation

Full size image

4.2.2 Effect of air Factor on Entropy Generation

Air factor, λ, is defined as the relation between the actual air fuel ratio and the stoichiometry air fuel ratio. Based on this definition, we can distinguish the type of the reactive mixture: λ = 1.0 is at stoichiometry, rich mixtures λ < 1.0, and lean mixtures λ > 1.0. In this section, the effect of air factor on the creation of thermodynamic irreversibilities in the combustion chamber is analyzed for each process of entropy generation contribution as shown in Fig. 6. The air factor, λ, varies from 0.5 to 1.3. The combustors of gas turbines run always with air excess regime where the air factor is greater than 1(λ >1). The first result is that the total entropy generated by the combustion process increases with increasing air factor, in deficit air as well as in excess air regimes. Entropy production due to heat conduction increases monotonously over all the range of air factor. The variation is more rapid in the air excess regime. The entropy generation caused by chemical reaction has two trends; at first, it increases in the air deficit regime (λ < 1) and then decreases slowly in the air excess regime. The increasing entropy generation due to heat conduction and that due to the decreasing chemical reaction meet at air factor equal to 1.3. Moreover, in air excess regime the burner is diluted by air, noncombustible. Thus, an amount of heat combustion released in the burner is absorbed by nonparticipating matter in the combustion reaction. This causes the average level of flame temperature falling lower than its level obtained at stoichiometry fuel/air mixture. Among all the considered mechanisms, entropy generation due to heat conduction is more sensible versus air factor; it shows a more rapid variation because its dependency to temperature squared, in accordance with Eq. (11).

Fig. 6
figure 6

Effect of air factor on entropy generation

Full size image

5 Conclusions

The aim of the paper is the assessment of the thermodynamic inefficiencies occurring during combustion processes. Through entropy generation analysis, we were able to identify the role of every physical and chemical mechanism involved in generating thermodynamic irreversibilities. The analysis is based on the numerical simulation, by the software Fluent, of a typical combustion system. The case study consists of a turbulent diffusion flame burning in a cylindrical burner; a configuration representative of gas turbine combustors. At first, the results, in terms of velocity, temperature and species fields are compared to experimental reference data. Then, it appears that chemical reaction and heat transfer are the more important processes responsible for thermodynamic irreversibilities; they are responsible, respectively, for 50 and 40 % of entropy generation rate. The species diffusion has a moderate role, around 10 %, while the irreversibilities generated by viscous friction are negligible. Preheating of the inlet fuel has a positive impact on the total thermodynamic irreversibilities associated to the combustion process by reducing the entropy generation rate due to heat transfer. Air excess has negative impact on the efficiency of combustion processes. It increases considerably the share and dominance of heat conduction in generating entropy.