Coupling the discrete element method and solid state diffusion equations for modeling of metallic powders sintering

Abstract

A novel discrete element method-based approach for modeling of solid state sintering of spherical metallic powder is presented. It tackles the interplay between the thermodynamical mass transport effects arising in the vicinity of the grain boundary between the particles and their mechanical interaction. To deal with the former, an elementary model is used that describes the behavior of the matter flow at the grain boundary such that neck growth and shrinkage are properly captured. The model solves a set of partial differential equations which drive the changes of the corresponding geometry parameters. Their evolution is transformed into the equivalent normal sintering force arising in each sinter neck. To capture the mechanical interaction of particles due to their rearrangement resulting from the geometry changes of each individual contact, the entire assembly is modeled as an assembly of 2-nodal structural elements with 6 degrees of freedom per node. The stiffness properties are estimated employing the approximations from the bonded DEM. The numerical implementation then constitutes a two-step staggered solution scheme, where these models are applied sequentially. The performed benchmarks reveal the plausibility of the proposed approach and exhibit good agreement of both neck growth and shrinkage rates obtained in the numerical simulations with the experimental data.

1 Introduction

Multiple modern numerical techniques target simulation of sintering process at different scales. Molecular dynamics (MD) [1, 2] is most suitable for nanoscale modeling of assemblies which contain very few particles. For handling larger domains, continuous finite element method (FEM) models based on the solid mechanics [3] or mass transport equations [4] can be used. A substantial progress has been recently made in applying diffuse interface methods for sintering simulations [5,6,7], thanks to their robustness and scalability. They are based on Cahn–Hilliard and Alen–Cahn partial differential equations [8, 9] which describe the mass transport processes of the matter and evolution of the phases. However, these are unable to capture properly shrinkage of an assembly due to the absence of the advection terms. The Wang’s approach [10] is the most common option to introduce the densifying contributions into the phase-field partial differential equations. Due to lack of rigorous physical or mechanical theoretical foundation its practical usage is not straightforward since an additional set of parameters, which cannot be precomputed and may only be calibrated to fit the experimental data [11], emerges. To overcome this limitation, an alternative approach based on zero grain boundary force assumption has been recently derived [12]. Another limiting factor for applying FEM models for large-scale simulations is high computational costs. Though, with the aid of modern HPC computing, the phase-field models have become more efficient [13], they still require substantial computational resources if one wants to perform a simulation of an assembly of over a thousand of particles. Even if a modern cluster is at disposal, the energy costs should not be disregarded.

In comparison with the continuous FEM approaches, the kinematic Monte–Carlo [14, 15] and discrete element methods are less computationally demanding for sintering simulations at mesoscale. The latter has intensively evolved in the recent decades. The work of Jagota and Dawson [16] introduced the basic concepts of this family of models: The authors adapted the general particle dynamics simulations of Cundall and Strack [17] for the case of viscous micromechanical modeling of powder compacts. The basic formulation assumed particles to have only translational degrees of freedom and later was extended by Jagota and Scherrer [18] to account for rotational effects; thus, both forces and moments equilibrium are enforced for each sphere. Being firstly derived for 2-dimensional particle packings, these approaches were later generalized for 3D cases [19]. Parhami and McMeeking [20] adopted the ideas of Jagota, Dawson, and Scherrer to study the sintering behavior of 3-dimensional random networks of crystalline equisized powders. The underlying equations for the interaction of neighboring particles were developed by Swinkels and Ashby [21] and Bouvard and McMeeking [22]. As was exposed by Reidel et al. [23], the transport mechanism for densification and creep of the sintering powder compact is grain boundary diffusion that resulted in appearance of the normal stress driving densification process. Svoboda and Riedel [24] then further enhanced this idea balancing the grain boundary fluxes by and surface diffusion mechanisms. Requiring the normal stresses to be equilibrated by surface tension at the neck, they obtained the solution of the two mass transport equations that led to a linear relation between the sintering force transmitted by a contact and the normal relative velocity of the particles. This expression was directly used by Henrich et al. [25] in the DEM context. Dosta et al. [26] have recently shown that this model can result in very efficiently numerical implementations taking advantage of superior performance of the modern CUDA-based codes [27].

Martin et al. [28] enhanced the numerical method of Parhami and McMeeking introducing grain coarsening behavior. An efficient contact detection strategy was also added in their implementation. This model was later used to investigate which effects the presence of a substrate has on the microstructure of the constrained sintered films [29]. Martin et al. [30] later validated the developed discrete element method (DEM) framework using an in situ X-ray microtomography analysis of the sintered NaCl powder. Nosewicz et al. [31, 32] incorporated elastic interaction of particles in addition to the viscous effects for DEM simulations of both free and pressure-assisted sintering. Thanks to this enhancement of the particles contact model, it became possible to study sintering and postsintering residual stresses of particles collections [33]. Due to its elegance and efficiency, the approach of Nosewicz et al. got a lot of attention among the researchers: For instance, Iacobellis et al. [34] used it to model sintering of ceramic composite materials (ZrB$_2$–SiC), Matsuda [35] enhanced it with independent evaluation of the neck growth rate between two particles by means of the direct integration of the diffusion equation.

Despite having superior performance over the phase-field technique, DEM modeling of sintering still suffers from high computational costs compared to macroscale continuum mechanics-based models [3, 36, 37]. The need to use contact detection procedures and application of explicit time integration naturally limit computational efficiency of DEM approaches and hence reduce the number of simulated particles. Furthermore, most DEM- based sintering models employ the viscous model [20] in which a timestep decreases with the evolution of particle contact viscosity. The advantage of DEM with respect to continuum mechanics formulations (commonly implemented with FEM) is the capability of taking into account the particulate nature of the sintered material. This does not explicitly enter continuum mechanics rheological models, thus complicated and sometimes questionable assumptions on the structure of sintered material are required. To take advantage of both worlds (rigor of the DEM-based and performance of the continuum mechanics-based models), so-called multiscale formulations have been proposed. These approaches combine the results along different scales and have recently become efficient tools to model complex thermo-mechanical phenomena like sintering. In this context, Rojek et al. [38] applied their DEM model developed earlier not to run the entire simulation of the particles assembly but only to get its macroscopic properties (elastic and viscous moduli) which are then supplied to a more performance efficient continuum mechanics- based model. In its turn, the DEM model itself used the diffusion properties of material computed at the previous step using molecular dynamics simulations. This toolchain was then extended to the cases of pressure-assisted sintering by Nosewicz et al. [39]. Another multiscale, so-called integrated microstructure model, has been proposed by Raether et al. [40] where Monte–Carlo technique capturing diffusion processes was coupled with particle-based simulations responsible for handling rearrangements due to geometry changes.

A novel DEM staggered numerical scheme is presented in the current work. It couples the numerical solution of the solid state diffusion equations of individual contact pairs with the discrete element modeling of the entire particles assembly. The thermodynamically driven particles interaction is described differently in comparison with the existing approaches. The complete sintering interaction, i.e., mass transport mechanism of grain boundary diffusion and sintering driving force resulting from surface tension, in all the aforementioned formulations relies on the derivations of Bouvard and McMeeking [22] obtained from Coble’s assumptions [41] for the neck geometry, whereas the proposed approach employs the elementary model derived by Thomsen et al. [42] to quantify the mass transport effects between the two particles resulting in local geometry changes leading to rearrangements within the packing. To describe the geometry of a contact pair, this formulation introduces 7 variables (degrees of freedom) whose evolution is represented by the system of seven partial differential equations. According to the number of unknowns, within the text, this model is normally referred as the “7DOF model”. The approach of Thomsen et al. relies on the assumptions introduced by Herring [43] for the grain boundary diffusion mechanism which also constitute the foundation of the Swinkels’ and Ashby’s [21] expressions underlying the majority of the DEM sintering models. Though being quite convenient, the derived expressions of Bouvard and McMeeking [22] are strictly valid only for equisized particles while the 7DOF model underlying the proposed DEM approach has no such a limitation. The use of the 7DOF formulation provides another significant benefit: a simple and fast model calibration procedure. One can adjust the missing diffusion properties to fit the experimental data using not the entire DEM assembly but only the 7DOF model.

A cohesive bond model is adapted to describe the mechanical interaction between the particles. It is constructed such that not only a DEM framework can be used but also a structural FEM implementation can be designed in which, instead of dynamics, a quasi-static equilibrium of the assembly is analyzed allowing thus to avoid the use of explicit time integration techniques. The latter provides large marching timesteps that positively influences performance of numerical solutions.

Section 2 describes the basic concepts of the approach proposed herein and its essential ingredients: the part responsible for capturing the mass transport phenomenon, the methodology for converting its effects into the internal forces, and the 2-nodal structural finite element that models mechanical interaction of particles as an assembly of elastic links. The details of the numerical implementation, such as the transfer of variables values between the two steps of the solution procedure, generation of the initial packing, and the time marching strategies, are well presented in Sect. 3. The developed framework is then applied for numerical analysis of sintering of copper and titanium powder particles in Sect. 4, where the obtained results are compared with experiments. Since third-party data may contain hard to track errors and be subject to certain limitations not always explicitly disclosed in the papers, it is desirable (but not always possible) to operate with personal highly reliable experimental results. Taking advantage of having excellent research facilities at our center, the titanium benchmark uses the experimental data obtained previously [44] by our group for which all the conditions and possible limitations are known. Finally, Sect. 5 summarizes the model features and discloses the possible directions of its further development.

2 Staggered numerical model

2.1 Basic idea

The model developed by Thomsen et al. [42] is capable to simulate sintering of 2 particles only. To extend it applicability to packings with large number of particles, the following quasi-static DEM approach is proposed. Each individual particle is attached to a node having 6 degrees of freedom: 3 displacements and 3 rotations. The latter are represented by the Euler rotation vector. The packing is then discretized as an assembly of 2-nodal finite elements. Every contact pair is represented by a set containing 2 structural elements of different types. The first element wraps up the 7DOF model whose governing equations are resolved individually for each pair of particles thus describing the changes of geometry of the latter as all the contacts were independent from the each other. The results provided by the 7DOF model are converted into the sintering forces generated at the bonds which are then applied to the nodes.

When operating as an interconnected system, the contact pairs of the packing start acting on each other increasing or decreasing shrinkage rates at different parts of the packing due to mechanical interaction of particles via the growing necks. To capture this phenomenon, a second element is created for each contact pair. It estimates stiffness of the sintering bond from the geometry of the contacting particles and computes the reactive forces and moments arising at the neck thus eliminating unphysical kinematic mechanisms in the modeled packing. Contributions from both element types are then added to the global force vector and tangent matrix, and the obtained linear system of equations is solved in a regular manner.

Fig. 1

Two particles (7DOF) model

2.2 7DOF particles sintering model

The sintering force is introduced with the aid of the 7DOF model developed by Thomsen et al. [42, 44]. A short summary is provided herein and the reader is referred to the aforementioned works for more details. This model is based on a simple but computationally efficient geometrical approach of coupling the two particles via a pair of caps connected by two cones representing the neck. Seven degrees of freedom gathered in vector

$$\begin{aligned} \varvec{Y} = \begin{bmatrix} y_1&y_2&y_3&y_4&y_5&y_6&y_7 \end{bmatrix}^T \end{aligned}$$

(1)

and shown in Fig. 1a are introduced in order to describe the change of geometry of the contact pair due to the underlying mass transport mechanisms. The time derivative of each component $y_i$ of vector $\varvec{Y}$ is related to the change of a specific volume $V_i$ of the pair of particles via the chain rule as

$$\begin{aligned} {\dot{y}}_i = \dfrac{{\mathrm{d}} y_i}{{\mathrm{d}}t} = \dfrac{{\mathrm{d}} y_i}{{\mathrm{d}} V_i} \dfrac{{\mathrm{d}} V_i}{{\mathrm{d}} t} = \left( \dfrac{{\mathrm{d}} V_i}{{\mathrm{d}} y_i} \right) ^{-1} \dfrac{{\mathrm{d}} V_i}{{\mathrm{d}}t}. \end{aligned}$$

(2)

For solid state sintering, evaporation and condensation mass transports can be neglected [45] and the current model then captures (1) grain boundary, (2) surface, and (3) lattice diffusion which are of the primary importance for the present study. The complete set of possible diffusion paths arising in accordance with this assumption is shown in Fig. 1b, and the corresponding volume fluxes ${\dot{V}}_i$ are summarized in Table 1. These volume fluxes result in the following changes of the specific regions of the model:

$$\begin{aligned} \dfrac{{\mathrm{d}} V_1}{{\mathrm{d}} t}&= {\dot{V}}_{I\,A} + {\dot{V}}_{I\,B} + {\dot{V}}_{II\,A} + {\dot{V}}_{II\,B} + {\dot{V}}_{III\,A} \nonumber \\&+ {\dot{V}}_{III\,B} + {\dot{V}}_{IV\,A} + {\dot{V}}_{IV\,B}, \end{aligned}$$

(3a)

$$\begin{aligned} \dfrac{{\mathrm{d}} V_2}{{\mathrm{d}} t}&= -\left( {\dot{V}}_{V\,A} + {\dot{V}}_{VI\,A} \right) , \end{aligned}$$

(3b)

$$\begin{aligned} \dfrac{{\mathrm{d}} V_3}{{\mathrm{d}} t}&= {\dot{V}}_{V\,A} + {\dot{V}}_{IV\,A} - \left( {\dot{V}}_{III\,A} + {\dot{V}}_{IV\,A} \right) , \end{aligned}$$

(3c)

$$\begin{aligned} \dfrac{{\mathrm{d}} V_4}{{\mathrm{d}} t}&= -\left( {\dot{V}}_{I\,A} + {\dot{V}}_{II\,A} \right) , \end{aligned}$$

(3d)

$$\begin{aligned} \dfrac{{\mathrm{d}} V_5}{{\mathrm{d}} t}&= -\left( {\dot{V}}_{V\,B} + {\dot{V}}_{VI\,B} \right) , \end{aligned}$$

(3e)

$$\begin{aligned} \dfrac{{\mathrm{d}} V_6}{{\mathrm{d}} t}&= {\dot{V}}_{V\,B} + {\dot{V}}_{IV\,B} - \left( {\dot{V}}_{III\,B} + {\dot{V}}_{IV\,B} \right) , \end{aligned}$$

(3f)

$$\begin{aligned} \dfrac{{\mathrm{d}} V_7}{{\mathrm{d}} t}&= -\left( {\dot{V}}_{I\,B} + {\dot{V}}_{II\,B} \right) . \end{aligned}$$

(3g)

Table 1 Volume fluxes introduced in the two-particle model

It is assumed that the linear kinetic Fick’s law holds for the defined diffusion paths. This introduces then linear dependency between the density of the particle flux and the gradient of the chemical potential $\mu$. As pointed in [42], this general form of the first Fick’s law, for which the driving force is provided by the gradient of chemical potential rather than the gradient of concentration (which is a more common formulation), allows to compute the volume fluxes as

$$\begin{aligned} {\dot{V}}_i = - C_i \Omega \dfrac{D n}{k_{\mathrm{B}} T} \nabla \mu _i, \end{aligned}$$

(4)

where $\Omega$ is the atomic volume, n the density of mobile particles and $C_i$ is the cross-sectional area related to the corresponding volume flux (see Table 1), $k_{\mathrm{B}}$ is the Boltzmann constant and T is the temperature. The diffusion coefficient D is computed in accordance with the Arrhenius equation as

$$\begin{aligned} D = D_0 e^{-\frac{Q}{RT}}, \end{aligned}$$

(5)

where $D_0$ is the pre-exponential factor, Q is the activation energy, and R is the gas constant.

To resolve system (3), quantities $\mu _i$ have to be detailed. In general, the chemical potential is a partial derivative of the Gibbs free energy G with respect to the number of atoms N [43]:

$$\begin{aligned} \mu = \dfrac{\partial G}{\partial N}. \end{aligned}$$

(6)

For the ith region of the model this can be rewritten as

$$\begin{aligned} \mu _i = \dfrac{\partial G}{\partial N_i} = \dfrac{\partial G}{\partial V_i} \dfrac{\partial V_i}{\partial N_i} = \dfrac{\partial G}{\partial V_i} \Omega , \end{aligned}$$

(7)

where the definition of atomic volume $\Omega = \dfrac{\partial V_i}{\partial N_i}$ was substituted. The total free energy of the system for solid state sintering is mainly determined by the evolution of interfacial areas A and thus can be defined in the following form:

$$\begin{aligned} G = \gamma _s A_s + \gamma _{gb} A_{gb}, \end{aligned}$$

(8)

assuming $\gamma _s$ and $\gamma _{gb}$, the specific energies of the free surface and the grain boundary, are constant over the respecting interface regions. Substitution of (8) into (7) results in

$$\begin{aligned} \mu _i = \left( \gamma _s \dfrac{\partial A_s}{\partial V_i} + \gamma _{gb} \dfrac{\partial A_{gb}}{\partial V_i} \right) \Omega \end{aligned}$$

(9)

which in liaison with (4) allows one to resolve system (3). This set of equations can be integrated with any numerical scheme suitable for first-order differential equations. In the present work, the forth-order Runge–Kutta integration was chosen.

2.3 Sintering force

At a given time $t_i$, one can solve system (3) for each contact pair within the packing independently and obtain new positions of the centers of the contacting particles from variables $y_{4\,i}$ and $y_{7\,i}$. However, these solutions do not account for interactions of particles as an interconnected network of elastic elements. To handle this, actions generated by the mass transport mechanisms are converted into equivalent sintering forces and then applied to the entire assembly of particles in contactwise manner. To understand better these actions, one can think of an assembly of bars subject to cooling. Being cooled, individual bars contract resulting in appearance of compression forces in different parts of the structure which, as a whole, responds elastically to this loading. The current case is very similar, only the source of compression forces is different.

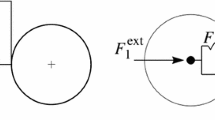
Likewise temperature-induced deformations can be converted into compression loading, the same can be done with sintering driven geometry changes. To do this, an equivalent bar of length $L_0$ having uniform cross section A [46, 47] is introduced as shown in Fig. 2. The axial force in the bar is computed from its axial deformation $\Delta L$ using the following classical expression [48]:

$$\begin{aligned} F_n = \dfrac{EA \Delta L}{L_0} \end{aligned}$$

(10)

with E being the Young’s modulus. The initial length of the bar is nothing but the distance between the centers of the particles at the initial configuration $t_0$:

$$\begin{aligned} L_0 = y_{4\,0} + y_{7\,0} \approx y_{2\,0} + y_{5\,0} = R_A + R_B, \end{aligned}$$

(11)

where $R_A$ and $R_B$ are the initial radii of the particles:

$$\begin{aligned} R_A&= y_{2\,0}, \end{aligned}$$

(12a)

$$\begin{aligned} R_B&= y_{5\,0}. \end{aligned}$$

(12b)

Compression is computed from the solution of system (3) as

$$\begin{aligned} \Delta L = \left( y_{4\,0} + y_{7\,0} \right) - \left( y_{4\,i} + y_{7\,i} \right) . \end{aligned}$$

(13)

The cross-section area of the equivalent bar is given by

$$\begin{aligned} A = \pi R_m^2, \end{aligned}$$

(14)

where $R_m$ is the arithmetic mean of the radii of contacting particles:

$$\begin{aligned} R_m = \dfrac{y_{2\,i} + y_{5\,i}}{2}. \end{aligned}$$

(15)

Given that at the earlier stage of sintering, which the 7DOF model is applicable to, regardless of the intensive growth of the neck, the radii of particles do not exhibit significant changes, the following simplification can be made for the bar geometry:

$$\begin{aligned} R_m = \dfrac{R_A + R_B}{2}, \end{aligned}$$

(16)

which barely alters the stiffness of the elastic element. It is then convenient to rewrite

$$\begin{aligned} F_n = \dfrac{\pi }{2} E R_m \Delta L. \end{aligned}$$

(17)

Fig. 2

Replacement of the two particles with an equivalent bar of constant cross section

The equivalent bar shown in Fig. 2 whose cross section is defined by (14) and (15) is a common option [47] for bonded DEM simulations and has proved to provide good agreement with experimental data in the context of fracture mechanics.

Expression (17) converts the changes of geometry induced in each contact pair by the mass transport mechanisms into the normal compression forces that can be deemed at this stage as external loading. To obtain response to this action, a special 2-nodal elastic link is described in the next section.

2.4 Cohesive bonding

A cohesive bond model is now introduced to capture the mechanical interaction between the particles. The approach proposed by Potyondy and Cundall [46] for modeling of cement joints has been presently adopted. According to this formulation, the contact pair is perceived as rigid spheres, whose centers are attached to nodes A and B as shown in Fig. 3, connected via an elastic link. The element local Cartesian coordinate system with unitary vectors $\varvec{e}_1$, $\varvec{e}_2$, $\varvec{e}_3$ is placed at the center of particle A and $x_3$-axis is directed toward the center of particle B.

Fig. 3

Two-nodal element representing bonded spherical particles

Elastic link at the particles grain boundary has tensile, shear, bending, and torsion stiffness. Therefore, the following small relative deformations arise at the bond:

• 1. $\varepsilon _1$, $\varepsilon _2$—shear displacements,

• 2. $\varepsilon _3$—tensile displacement,

• 3. $\gamma _1$, $\gamma _2$—bending rotations,

• 4. $\gamma _3$—torsional rotation.

These quantities can be gathered in the vector of local deformations

$$\begin{aligned} \varvec{y}_{\mathrm{link}} = \begin{bmatrix} \varvec{{\varepsilon }} \\ \varvec{{\gamma }} \end{bmatrix}, \end{aligned}$$

(18)

having

$$\begin{aligned} \varvec{{\varepsilon }}&= \begin{bmatrix} \varepsilon _1&\varepsilon _2&\varepsilon _3 \end{bmatrix}^T, \end{aligned}$$

(19a)

$$\begin{aligned} \varvec{{\gamma }}&= \begin{bmatrix} \gamma _1&\gamma _2&\gamma _3 \end{bmatrix}^T. \end{aligned}$$

(19b)

Local deformations at the bond are obtained from nodal displacements $\varvec{u}_A$, $\varvec{u}_B$ and rotations $\varvec{{\theta }}_A$, $\varvec{{\theta }}_B$. The latter are represented by the Euler rotation vector [49]. Displacements vector $\varvec{{\varepsilon }}$ can be derived from the element kinematics represented in Fig. 4. From the scheme one can easily write the following vector identity:

$$\begin{aligned} \varvec{l}_{A\,0} - \varvec{l}_{B\,0} = \varvec{u}_{A} + \varvec{l}_{A} - \varvec{{\varepsilon }} - \varvec{l}_{B} - \varvec{u}_{B}, \end{aligned}$$

(20)

where vectors

$$\begin{aligned} \varvec{l}_{A\,0}&= L_{A\,0} \varvec{e}_3 = y_{40} \varvec{e}_3, \end{aligned}$$

(21a)

$$\begin{aligned} \varvec{l}_{B\,0}&= -L_{B\,0} \varvec{e}_3 = - y_{70} \varvec{e}_3 \end{aligned}$$

(21b)

describe the distance from the particles center to the grain boundary center. At the deformed configuration they are rotated to new positions

$$\begin{aligned} \varvec{l}_{A}&= \varvec{Q}_A \varvec{l}_{A\,0}, \end{aligned}$$

(22a)

$$\begin{aligned} \varvec{l}_{B}&= \varvec{Q}_B \varvec{l}_{B\,0}. \end{aligned}$$

(22b)

The rotation tensors $\varvec{Q}_A$ and $\varvec{Q}_B$ are computed by the Euler–Rodrigues formula [50]:

$$\begin{aligned} \varvec{Q} = \varvec{I} + h_1 \left( \theta \right) \varvec{{\Theta }} + h_2 \left( \theta \right) \varvec{{\Theta }}^2, \end{aligned}$$

(23)

where the identity second-order tensor $\varvec{I}$, the trigonometric functions

$$\begin{aligned} h_1 \left( \theta \right) = \dfrac{\sin {\theta }}{\theta } \quad \text {and} \quad h_2 \left( \theta \right) = \dfrac{1}{2} \left( \dfrac{\sin {\theta /2}}{\theta /2} \right) ^2 \end{aligned}$$

(24)

and tensor $\varvec{{\Theta }}$ were introduced. The latter simply is the skew symmetric cross-product matrix of the vector $\varvec{{\theta }}$, i.e., $\varvec{{\Theta }} = \text {skew}\left( \varvec{{\theta }}\right)$.

Fig. 4

Kinematics of the sintering pair element

Expression (23) and, therefore, identity (20) are valid for arbitrarily large rotations. However, the rotations of the particles are rather small during sintering of realistic powder packings. Moreover, if an incremental approach is chosen for implementation (which is the case for the current work), the necessity of handling arbitrary rotations is even less important as within a given timestep rotations can be considered small even if the structure undergoes large motions during the entire simulation process [51]. In this case, the higher-order term can be omitted in (23) and identity (20) can then be simplified leading to a neat formula for computing the displacements at the bond:

$$\begin{aligned} \begin{aligned} \varvec{{\varepsilon }}&= \varvec{u}_{A} - \varvec{u}_{B} + \varvec{{\Theta }}_A \varvec{l}_{A\,0} - \varvec{{\Theta }}_B \varvec{l}_{B\,0} \\&= \varvec{u}_{A} - \varvec{u}_{B} - \varvec{L}_{A\,0} \varvec{{\theta }}_A + \varvec{L}_{B\,0} \varvec{{\theta }}_B, \end{aligned} \end{aligned}$$

(25)

where $\varvec{L}_{A\,0} = \text {skew}\left( \varvec{l}_{A\,0}\right)$ and $\varvec{L}_{B\,0} = \text {skew}\left( \varvec{l}_{B\,0}\right)$. Local rotations at the bond in this case are then evaluated by

$$\begin{aligned} \varvec{{\gamma }} = \varvec{{\theta }}_A - \varvec{{\theta }}_B. \end{aligned}$$

(26)

The link state vector $\varvec{y}_{\mathrm{link}}$ can be then extracted from the nodal displacements of the element with the aid of

$$\begin{aligned} \varvec{y}_{\mathrm{link}} = \varvec{H} \varvec{y}, \end{aligned}$$

(27)

where

$$\begin{aligned} \varvec{y} = \begin{bmatrix} \varvec{u}_A \\ \varvec{{\theta }}_A \\ \varvec{u}_B \\ \varvec{{\theta }}_B \end{bmatrix} \end{aligned}$$

(28)

and

$$\begin{aligned} \varvec{H} = \begin{bmatrix} \varvec{I} &{} -\varvec{L}_{A\,0} &{} -\varvec{I} &{} \varvec{L}_{B\,0} \\ \varvec{O} &{} \varvec{I} &{} \varvec{O} &{} -\varvec{I} \end{bmatrix} \end{aligned}$$

(29)

with $\varvec{O}$ being are a zero second-order tensor.

The reactive forces and moments arising at the bonding link are introduced as vector

$$\begin{aligned} \varvec{P}_{\mathrm{link}} = \begin{bmatrix} \varvec{F}_{\mathrm{link}} \\ \varvec{M}_{\mathrm{link}} \end{bmatrix} \end{aligned}$$

(30)

consisting of

$$\begin{aligned} \varvec{F}_{\mathrm{link}}&= \begin{bmatrix} F_1&F_2&F_3 \end{bmatrix}^T, \end{aligned}$$

(31a)

$$\begin{aligned} \varvec{M}_{\mathrm{link}}&= \begin{bmatrix} M_1&M_2&M_3 \end{bmatrix}^T. \end{aligned}$$

(31b)

The constitutive relation between $\varvec{y}_{\mathrm{link}}$ and $\varvec{P}_{\mathrm{link}}$ [46] is defined as

$$\begin{aligned} \varvec{P}_{\mathrm{link}} = \varvec{K}_{\mathrm{link}} \varvec{y}_{\mathrm{link}}, \end{aligned}$$

(32)

where the local stiffness matrix of the bond has been introduced:

$$\begin{aligned} \varvec{K}_{\mathrm{link}} = \begin{bmatrix} \varvec{K}_F &{} \\ &{} \varvec{K}_M \end{bmatrix} \end{aligned}$$

(33)

with

$$\begin{aligned} \varvec{K}_F&= \dfrac{1}{L_0} \begin{bmatrix} G A &{}&{} \\ &{} G A &{} \\ &{}&{} E A \end{bmatrix}, \end{aligned}$$

(34a)

$$\begin{aligned} \varvec{K}_M&= \dfrac{1}{L_0} \begin{bmatrix} E I &{}&{} \\ &{} E I &{} \\ &{}&{} G J \end{bmatrix}, \end{aligned}$$

(34b)

as frequently done in cohesive DEM approaches [52]. Here shear modulus

$$\begin{aligned} G = \dfrac{E}{2 \left( 1 + \nu \right) } \end{aligned}$$

(35)

is computed from elasticity modulus E and Poisson’s ration $\nu$; A, I, and J are the area, moment of inertia, and polar moment of inertia of the bond cross section. These are given in accordance with the proposal of Potyondy and Cundall [46] for the 3D version of the cement bond as

$$\begin{aligned} A&= \pi R_m^2, \end{aligned}$$

(36a)

$$\begin{aligned} I&= \dfrac{1}{4} \pi R_m^4, \end{aligned}$$

(36b)

$$\begin{aligned} J&= \dfrac{1}{2} \pi R_m^4, \end{aligned}$$

(36c)

where $R_m$ is computed using (16). Stiffness coefficients (33) are constant and do not account for the growth of the neck during sintering. However, as demonstrated by further numerical simulations (see Sect. 4), even such a simple choice renders the results which are in good agreement with the experimental data. Of course, more complex and accurate forms of $\varvec{K}_{\mathrm{link}}$ can be proposed which is the prospect of the authors’ future work. The plausibility of the adopted simplification has also been previously investigated in [46] where it was successfully applied for multiple numerical simulations whose results were verified by experiments.

The local force $\varvec{F}_{\mathrm{link}}$ and moments $\varvec{M}_{\mathrm{link}}$ arising at the bonding link are now transferred to nodes A and B by analyzing equilibrium of each particle within the contact pair. As can be seen from Fig. 5, the following static relations hold for particles A and B:

$$\begin{aligned} \varvec{F}_A&= \varvec{F}_{\mathrm{link}}, \end{aligned}$$

(37a)

$$\begin{aligned} \varvec{M}_A&= \varvec{M}_{\mathrm{link}} - \varvec{l}_{A\,0} \times \varvec{F}_{\mathrm{link}}, \end{aligned}$$

(37b)

$$\begin{aligned} \varvec{F}_B&= -\varvec{F}_{\mathrm{link}}, \end{aligned}$$

(37c)

$$\begin{aligned} \varvec{M}_B&= -\varvec{M}_{\mathrm{link}} + \varvec{l}_{B\,0} \times \varvec{F}_{\mathrm{link}} \end{aligned}$$

(37d)

which, after all the forces and moments are gathered in a single vector

$$\begin{aligned} \varvec{P} = \begin{bmatrix} \varvec{F}_A \\ \varvec{M}_A \\ \varvec{F}_B \\ \varvec{M}_B \end{bmatrix}, \end{aligned}$$

(38)

can be written in compact notation as

$$\begin{aligned} \varvec{P} = \varvec{H}^T \varvec{P}_{\mathrm{link}} \end{aligned}$$

(39)

and even further simplified with the aid of (27) and (32):

$$\begin{aligned} \varvec{P} = \varvec{H}^T \varvec{K}_{\mathrm{link}} \varvec{H} \varvec{y} \end{aligned}$$

(40)

Fig. 5

Static equilibrium of the sintering pair element

This expression allows instant computation of the element nodal forces and moments directly from the nodal displacements and rotations and can be readily implemented in any finite element framework. Expression (40) does not contain any nonlinear contribution which is the result of the previously made assumption regarding the displacements and rotations remaining small within a given timestep. This means that the entire DEM step is linear that positively affects the simulation time.

Note that the possibility of bonds breakage during sintering is not considered in the proposed model as these events, even if they happen, are negligible in comparison with the number of growing necks thanks to homogeneity and relatively high density of initial packings.

3 Implementation details

The model was prototyped in KRATOS Multiphysics framework [53] and then reimplemented in the in-house deal.ii [54]-based code. The results presented further are obtained using the latter implementation.

3.1 Correction of the inter-particles shrinkage

After performing the DEM step, the positions of the centers of particles of the jth contact pair differ from values $y_{4\,i}$ and $y_{7\,i}$ of the corresponding vector $\varvec{Y}_j$ at time $t_i$ and the latter have to be updated accordingly. To this end, the axial compression of the entire contact pair is computed as

$$\begin{aligned} \xi _3 = \left( \varvec{u}_A - \varvec{u}_B \right) \cdot \varvec{e}_3, \end{aligned}$$

(41)

which is then appended to values of $y_4$ and $y_7$ obtained at the previous timestep as

$$\begin{aligned} {\overline{y}}_{4\,i}&= y_{4\,i-1} + \dfrac{\Delta y_{4\,i}}{\Delta y_{4\,i} + \Delta y_{7\,i}} \xi _3, \end{aligned}$$

(42a)

$$\begin{aligned} {\overline{y}}_{7\,i}&= y_{7\,i-1} + \dfrac{\Delta y_{7\,i}}{\Delta y_{4\,i} + \Delta y_{7\,i}} \xi _3, \end{aligned}$$

(42b)

where quantity $\xi _3$ is distributed between $y_4$ and $y_7$ proportionally to their initial contributions to shrinkage at time $t_i$:

$$\begin{aligned} \Delta y_{4\,i}&= y_{4\,i-1} - y_{4\,i}, \end{aligned}$$

(43a)

$$\begin{aligned} \Delta y_{7\,i}&= y_{7\,i-1} - y_{7\,i}. \end{aligned}$$

(43b)

The alteration of the distance between the centers of particles of a given contact is then given by

$$\begin{aligned} \overline{\Delta L}_i = {\overline{y}}_{4\,i} + {\overline{y}}_{7\,i} - y_{4\,i} - y_{7\,i}. \end{aligned}$$

(44)

The isotropic shrinkage observable macroscopically during sintering implicitly introduces the homogeneity of densification inside a sinter body provided the contact pairs are randomly oriented. This means that for assemblies containing a large number of particles, quantity (44) should have Gaussian distribution.

3.2 Generation of initial packings

Discussion on the generation of initial packings for subsequent sintering simulations [25] itself could become a topic of an independent paper. An extensive study of this question is out of scope of the present work and a single quite simple but yet efficient approach to generate green bodies with initial relative density of $~\approx 60$% is proposed.

The generation procedure has to provide an isotropic configuration with irregular, realistic distributions of particles having relatively low porosity. The algorithm developed by Nosewicz et al. [55] fulfills these requirements and therefore is adopted herein with minor modifications. The main challenge at this stage is to provide such initial stress-free configuration of spherical particles that would have the maximum green density. Within the present work, the initial compact was constructed with the aid of DEM technique implemented in software package Yade [56]. At the initial step, a facet box is created and then a cloud of particles whose radii have predefined distribution around the mean value with the specified dispersion is generated inside. To this end, Yade function “makeCloud()” is used and by default it generates a uniform distribution of particles radii. However, a custom distribution, for instance, directly from experimental data, can be provided via its additional parameters.

Once the particles cloud has been generated, gravity is applied then along the $x_3$-axis such that all particles fall down to the lower part of the box. After equilibrium has been reached, the plane perpendicular to the $x_3$-axis is placed over to the uppermost particle of the compact covering the entire packing. Small constant velocities are then applied to this plane and to the other two planes perpendicular to it and to the remaining axes of the coordinate system performing thus triaxial compression of the packing until the relative density of $~\approx 60$% has been reached. Homogeneity of packings obtained with the aid of the proposed procedure will be verified further in the benchmark.

Fig. 6

Solution procedure of the proposed approach

3.3 Solution procedure

The previous sections disclose the key components of the proposed numerical model. Once they have been derived, the complete solution procedure can be assembled and its summary is presented as flowchart in Fig. 6. At the first step, the initial packing is generated and the kinematic boundary conditions are imposed as described in Sect. 3.2. Then the time loop is launched. At the beginning of each timestep, the packing is checked for appearance of new contacts. The 7DOF model is solved then for each jth contact pair performing a single Runge–Kutta step delivering new values of vector $\varvec{Y}_j$ as an output. This data is used to compute the sintering forces as detailed in Sect. 2.3 and the Newton–Raphson DEM solution step is executed thereafter. Once the step has been solved, the components of vectors $\varvec{Y}_j$ are updated as explained in Sect. 3.1. If the final time is not yet reached, another timestep is initiated.

In order to speed up computations, time control is introduced. Timestep $\Delta t_i$ is adjusted such that the optimal accuracy is reached at the Runge–Kutta integration step. Two slightly different strategies, reflected in Fig. 7, can be proposed to this end. According to the first one, the Runge–Kutta solution of system (3) is performed for all the contact pairs and then the integration error for each of them is computed. If the desired tolerance is not reached at least for a single pair, the results for all the contacts are rejected, timestep $\Delta t_i$ is reduced as

$$\begin{aligned} \Delta t_{i} = \dfrac{\Delta t_i}{\alpha } \end{aligned}$$

(45)

and the step is repeated. If the accuracy is reached with some margin, i.e.,

$$\begin{aligned} \max _{n=1,N} \epsilon _n < 0.1 \epsilon _{lim}, \end{aligned}$$

(46)

then the next timestep can be increased by a factor of $\alpha$:

$$\begin{aligned} \Delta t_{i+1} = \alpha \Delta t_i. \end{aligned}$$

(47)

This strategy ensures that both Runge–Kutta and DEM steps of the algorithm are solved with the highest possible accuracy. However, this approach inevitably suffers from frequent significant reductions of the timestep once a new contact pair has been detected. This happens since the growth of the neck between the two particles is particularly intensive when the contact has just been initiated. In order to capture the neck evolution at this very early stage, the timestep size has to be small enough and only then can be gradually increased preserving the accuracy. According to this algorithm, it turns out that the most recently detected contacts compromise the computational performance limiting the timestep globally for the entire packing while most of the contact pairs (those already having relatively large necks) could be handled with much larger $\Delta t$.

Fig. 7

Solution strategies for solving the 7DOF model at a given time $t_{i}$ with timestep $\Delta t_i$

An alternative approach preserves the global timestep and it instead subdivides $\Delta t_i$ separately for each nth contact pair when system (3) is solved. The global timestep size is increased via (47) if the number of contact pairs which required subdivision to meet the desirable integration accuracy is below 5% and decreased using (45) if this number exceeds 15%. The thresholds values can be varied to achieve an optimal ratio between computational speed and accuracy. The performance and reliability of the two strategies are assessed later in the subsequent section.

To allow the DEM step to be marched with a relatively large timestep, a Newton scheme is applied for the mechanical model to find its equilibrium. This means that a linear system of equations has to be solved at each iteration that requires the corresponding tangent matrix to be well-conditioned. To ensure its invertibility, certain kinematic boundary conditions have to be imposed on the particles assembly to prevent its spatial rigid body motions. To this end, those particles touching the principal planes Oxy, Oxz, and Oyz of the global coordinate system are constrained to remain on them during the simulation. In practice, specimens usually lie on a horizontal surface that also thanks to friction fixes them from sliding during sintering. Keeping this in mind, the proposed boundary conditions correlate well with reality: One of the three planes can be deemed as a horizontal foundation while the other two prevent rigid body motions of the particles assembly in the corresponding directions.

4 Numerical benchmarks

4.1 Numerical simulations of copper sintering

Table 2 Material properties of copper

Fig. 8

Packing of 805 copper particles

Fig. 9

Segmentation of a packing along the given axis for computing the relative density variation

Fig. 10

Variation of the relative density of the packing of 805 copper particles along axes x, y, z for segment width $q_s$ = 0.025 mm

At first, numerical simulations of copper sintering are performed to study the essential features of the proposed model. The benchmark is inspired by the thorough study performed by Thomsen et al. [42] in analyzing the experimental data of Kingery and Berg [62] and Wilson and Shewmon [63] in order to get the grain boundary and surface diffusion coefficients of copper. The material properties obtained therein and adopted currently are summarized in Table 2, elastic parameters for the corresponding sintering temperature are extracted from [61] by means of further extrapolation. Since in our model only the Poisson’s ratio affects the deformation of the particle composite, an arbitrary value could be assumed for the Young’s modulus. The latter could be explicitly removed from the corresponding formulas if the two structural elements described in Sects. 2.3 and 2.4 were mathematically merged in a single expression.

Fig. 11

Shrinkage of the cubic packing of the copper powder particles

Fig. 12

Comparing timestep for the two solution strategies for the sintering simulations of the cubic packing of the copper powder particles (with detection of new contacts)

Fig. 13

Average neck growth within the cubic packing of the copper powder particles

A nearly cubic packing of dimension $0.5\times 0.5\times 0.4$ mm shown in Fig. 8a containing 805 particles having mean diameter 50 $\upmu$m with dispersion 0.1 is sintered at temperature $T=1293$ K for 5000 seconds. To check if the obtained initial packing homogeneous, the relative density along the three global axes x, y, z was analyzed. To this end, over each of the axes the packing was divided into a number of equal laminae of length $q_s$ as shown in Fig. 9 and the relative density for each of them was computed as the ratio between the sum of volumes of the particles segments inside the lamina and the volume of the lamina itself:

$$\begin{aligned} \rho _{\text {rel}\;s} = \dfrac{V_{\text {particles}\;s}}{V_{\text {lamina}\;s}}. \end{aligned}$$

(48)

As can be seen from Fig. 10, where the variation of this quantity along the three axes is presented, the density is quite uniform and does not vary a lot in different directions across the packing. The drops of the density at the edges is explainable since there more voids are located between the particles.

One should not be confused with the final configuration of the packing in Fig. 8b: though it is quite similar to the initial one, by looking carefully at the axes it is possible to observe that the particles assembly densifies. Confirming this visual observation, Fig. 11 shows the shrinkage values of the packing along the 3 axes $\left( \dfrac{\Delta L_1}{L_{10}}, \; \dfrac{\Delta L_2}{L_{20}}, \; \dfrac{\Delta L_3}{L_{30}} \right)$ and compares them with the change of the distance between the particles centers $\dfrac{\Delta L}{L_0}$ obtained for a simple 2 particles system using the 7DOF model previously calibrated using the data from the particle row experiments from [62]. As seen from the plots in Fig. 11, the curves for the 3 directions agree with each other (that indirectly confirms the homogeneity of the generated initial packing) and also with the reference data. The existing difference arises due to the generated assembly of particles: In a spatial packing there are balancing interactions that do not exist in a row [64] where the overall change in length is just the sum of all center approaches. This explains why the shrinkage of the cube is lower than the shrinkage determined on the basis of the two-particle model or the experiments with particle rows. As will be shown in the next numerical benchmark, where the comparative data comes from experiments with spatially packed particles, the densification along the corresponding axis approaches the reference values.

Even if the graphs show that the formation of new contacts during sintering significantly increases densification, Fig. 11c demonstrates that quite accurate results can be already obtained even if detection of new contacts is disabled during numerical analysis. Such rapid preliminary simulations can provide a rough idea about the packing behavior which can be helpful when performing large number of batch parametric computations.

It is worth to compare the two strategies for time marching at the Runge–Kutta step described in Sect. 3.3. It turns out that the first and the second strategies provide very close results while the latter is almost two orders of magnitude faster than the former (1 h vs. $\approx$ 100 h on an Intel Core i7–8550U laptop). The reason of the drastic drop of performance for the first strategy can be seen in Fig. 12 exposing the change of the timestep size over the simulation process. The timestep can hardly reach its maximum possible value since whenever a new contact is detected, $\Delta t_i$is automatically reduced to meet the accuracy requirements. Note also that for the second strategy the maximum possible timestep is adjusted to be of an order of magnitude lower than for the first strategy, which is $\Delta t_{\text {max}}=10$ seconds, in order to avoid situations when numerous new contacts appear within a single solution step that could have introduced additional error in capturing properly the interplay between the contacts. Note, that as can be seen from Fig. 13, neck growth is less sensitive to the choice of the time marching strategy.

4.2 Numerical simulations of titanium sintering

Table 3 Temperature profiles and the average particle diameters of the experiments

As a second benchmark, numerical simulations reproducing the experimental data of Thomsen et al. [44, 65] for pure titanium are performed with the proposed technique. The samples are sintered using different heating profiles summarized in Table 3. As can be seen from the table, the particles sizes do not vary significantly across the experiments, so a single packing having mean diameter 64 $\upmu$m is chosen for numerical simulations in order not to repeat the packing generation step and save computational time. This assumption will introduce a bit more noticeable error for experiment E25B which was conducted for specimens having a larger mean diameter of the particles. The generated packing has normal distribution of particles diameters and reproduces the experimental data as explained in Sect. 3.2, see Fig. 15. The generated packing shown in Fig. 14a contains 3619 particles and has the dimensions of $0.75\times 0.75\times 1.5$ mm in order to check how the model works when the assembly is not cubic. For performance reasons, it was decided to stick to the aspect ratio 1:1:2 and not to go above that.

The properties of titanium used in the simulations are gathered in Table 4. The basic atomic properties of titanium and its surface and grain boundary energies along with the bulk diffusivity were taken from the literature. Surface and grain boundary diffusion prefactors and activation energies were identified by the authors in the previous work [65]. To this end, experimental data for the settings from Table 3 was used to calibrate the 7DOF model. Shrinkage of the entire sample was measured simply by micrometer screw. To obtain neck growth, specimens were broken and the fracture surfaces of the sinter necks were measured using scanning electron microscope. A simple particle swarm optimization algorithm followed by the gradient method was applied to adjust the diffusion coefficients for surface diffusion and grain boundary diffusion simultaneously for the 7DOF model to reproduce the experiments. To account for the phase transition of pure titanium at 1156K, the properties are switched from $\alpha$-phase to $\beta$-phase once the corresponding temperature has been reached.

Fig. 14

Packing of 3619 titanium particles

Fig. 15

Distribution of particles diameters in the experiments and numerical simulation

The Young’s modulus was set $E=57$ GPa and the Poisson ratio $\nu = 0.39$ as investigated in [66]. This data is provided for $\beta$-titanium at temperature $T=1273$ K. Due to lack of data regarding elastic properties of $\alpha$-titanium, Young’s modulus and Poisson ratio for this phase are said to be the same as for the $\beta$-phase.

Table 4 Material properties of titanium

As has just been mentioned, at low temperatures sintering process is not intensive and the neck growth and shrinkage evolution can be hardly observed. For this reason, the parts of the heating curve with temperatures lower than 793 K are truncated as shown in Fig. 17 in order to save computation time in the numerical simulations. Indeed, as can be seen in Fig. 17, where the neck growth and shrinkage were computed for 2 particles of diameter 66.6 $\upmu$m with the aid of the 7DOF model for the complete and truncated heating curves, such a deviation from the conditions of the original experiment is acceptable. The blue curves in Fig. 17 were offset along the x-axis by 24 minutes so that the results for the 2 different heating profiles could be visually easily compared.

Fig. 16

Heating profile

Fig. 17

Comparison of results obtained with the aid of 2- particle model for the full and reduced heating profiles

Fig. 18

Comparison of neck growth and shrinkage from simulation results and experimental data. The error bars represent the respective measurement uncertainties during the evaluation of the samples

Fig. 19

Results of the numerical simulations of experiment E14B: comparison of the 2-particle and DEM models

Figure 18 exposing neck growth and shrinkage at the end of the sintering process shows that the results of numerical simulations agree well with the experimental observations. One can notice that the behavior of the DEM model presented in Sect. 2 is strongly dependent on the underlying 7DOF model, as expected. Indeed, the 7DOF model can be calibrated alone firstly and then the obtained material diffusion properties can be directly used for analysis of large packings performed with the particles-based approach. Therefore, if the calibration step is not perfectly accurate (see larger deviations of shrinkage for experiments E23B, E24B, and E25B in Fig. 18b), the DEM model also suffers from this.

Good agreement is achieved not only for the final configurations but also over the entire time integration process. To demonstrate that, one of the experiments, E14B, is chosen for more detailed analysis. Figure 19 plots the evolutions of neck growth and shrinkage of the packing along the $x_3$-axis for the numerical integration performed with the second time marching strategy having the detection of new contacts enabled. The curves are nearly indistinguishable from those obtained by means of the 7DOF model for a simple 2 particles system. It is assumed that the narrow distribution of the particle size in the specimen is even necessary for the good agreements of the experimental data from particles collections with the simulation results from the 2-particle model. The fact that mechanical coupling used here nevertheless has an effect is illustrated by the histogram in Fig.  20. It shows the occurring deviations of the changes of the individual particle distances in the assembly from the changes of the distances previously calculated in each case with the 7DOF model demonstrating thus how the correction of variables $y_{4\,i}$ and $y_{7\,i}$ described in Sect. 3.1 performs. The distribution of quantity $\overline{\Delta L}_i$ computed for each jth contact at the selected timestep $t_i=30$ min is normal besides the very few outliers, as expected, confirming thus the plausibility of the proposed mechanism of coupling the thermodynamical and mechanical effects.

Having possibility to track during numerical analysis an individual particle and its neighborhood, one can compute the relative density of the assembly as the ratio between the sum of the volumes of the particles and the volume occupied by the packing:

$$\begin{aligned} \rho _\text {rel} = \dfrac{V_\text {particles}}{V_\text {packing}}. \end{aligned}$$

(49)

The corresponding curve is plotted in Fig. 22a for the case when the packing presented in Fig. 14a was sintered at temperature $T=1373$ K for 100 h instead of using the heating profile from Fig. 16, the obtained final configuration is shown in Fig. 14b. Qualitatively, the curves exhibit the same behavior as demonstrated by neck growth and shrinkage in Fig. 19. Note that with the current model, it is hardly possible to advance significantly further than the relative density of 0.8 due to the geometric restrictions of the 7DOF model and grain growth effect becoming more influencing on the densification process at the later stages of sintering. This phenomenon is currently not captured by the developed model.

The densification effect can be also clearly seen comparing microstructures in Fig. 21 for the initial and final configurations. The images are obtained building a cross-sectional plane passing through the mass center of the packing and having a normal vector $n=(1,0,0)$.

If new contacts are detected during numerical analysis, the evolution of the particles’ coordination number $n_c$ averaged over the entire packing can be also captured as shown in Fig. 22a. The dependency of the coordination number from the increase of the relative density plotted in Fig. 22b is close to linear that agrees well with the experimental studies of geometrical structure of disordered sphere packings performed by Aste et al. [72].

Fig. 20

Distribution of corrections of quantities $y_{4\,i}$ and $y_{7\,i}$ within the packing at time $t=30$ min for experiment E14B

Fig. 21

Microstructure at the cross-sectional plane with normal vector $n=(1,0,0)$ passing through the central point of the packing of 3619 titanium particles

Fig. 22

Analysis of densification of the titanium packing containing 3619 particles

5 Conclusion and discussion

The novel staggered quasi-static DEM scheme for simulating the early stage solid state sintering of metallic powder compacts has been presented. The proposed approach consists of the two main models capturing mass transport and mechanical phenomena independently with connections between them.

Diffusion behavior is tackled independently for each contact pair by the elementary 7DOF model of Thomsen et al. [42]. It takes into account the interplay of different transport mechanisms (lattice, surface, and grain boundary diffusion) to carefully capture neck growth and centers approach for an interacting pair of particles. The effects resulting from the corresponding changes in geometry are then converted into the equivalent forces which drive the compaction of the packing.

To capture the mechanical interaction of particles within the entire packing, the latter is represented as an assembly of structural finite elements replacing each contact pair by an elastic link. Translational and rotational degrees of freedom are defined per particle thus both force and moment equilibria are enforced. The link introduces local tensile, shear, bending, and torsion stiffness at the contact point of the two particles. To obtain the corresponding stiffness coefficients, the approximations used in the bonded DEM are employed. These relations setting up dependency between various stiffness components and the contact pair geometry are simple but yet efficient and render the formulation that is able to provide the numerical results which are in good agreement with experiments. However, this ingredient of the entire model can be improved with a more accurate description of the mechanical behavior of each pair of particles. For instance, stiffening of the grain boundary region due to neck growth is not accounted for in the present implementation. Besides that, the geometry details of the contact pair are currently hidden: The two spheres and the bond between them is effectively replaced by an equivalent bar with constant cross-sectional profile.

The underlying 7DOF model, thanks to its simplicity, can be relatively easy calibrated to fit the existing experimental data if some diffusion properties of a given material are absent, as described in [42] and later demonstrated in [44]. The obtained coefficients can be directly used in the proposed formulation without any further modification and rescaling.

The plausibility of the proposed model as well as the plausibility of the basic assumption of an instantaneous mechanical equilibrium, introduced by the same authors in [12], was demonstrated with the numerical benchmarks for both constant temperature and realistic varying heating profile. The obtained results for neck growth and shrinkage agree well with the existing experimental data for the early stage sintering of copper and titanium powder compacts.

The numerical solution procedure resembles a two-step staggered scheme, where at first the mass transport equations are resolved for each contact pair and then the particles rearrangement is obtained as the result of the arising sintering forces. The presented implementation is particularly efficient and is able to perform simulations of assemblies containing a few thousands particles even on an average modern computer within a reasonable amount of time. Since mass transport and mechanical behaviors are handled independently, the thermodynamical part of the model can be easily extended. For instance, mixtures of particles made of different materials or containing various impurities can be naturally treated. In this case, this information is accounted for each contact pair via its diffusion properties (getting them though itself is quite a challenging task, especially, for mixtures). Besides that, additional phenomena, like, for instance, heat transfer, as has been done by Teixeira et al. [73] for DEM sintering simulations too, can be added to the model to enhance its accuracy in predicting the densification rates.

However, the proposed approach is applicable to the early stage sintering only since grain growth phenomenon is not included in the formulation. The results obtained with the developed coupled model can be later used as an initial configuration for a subsequent phase-field simulation where grain coarsening is naturally captured with the Allen–Cahn equation [12]. The developed model in this sense can be perceived as a component of a larger toolchain being currently developed by the authors.