1 Introduction

Nanomaterials and nanostructures have been investigating recently for their innovative properties and features. The analysis and design of such materials and structures has increased rapidly in the last decades. Their application is extremely wide, and they can be used for different purposes [1,2,3,4]. Focusing on nanostructures several applications has been already presented in medicine [5], electronics [6], aerospace [7] and even in civil engineering [8,9,10]. The most common of such are nanoplates, nanoroads and nanobeams.

However, classical continuum mechanics [11, 12] is not sufficient to capture some effects which are present at the nanoscale and come from the influence of the microstructure on the macroscale, for instance, material constituent interactions create observable effects at the macroscale. As a matter of fact, it has been recently demonstrated that the behavior of nanostructures is affected by the material microstructure in [13,14,15], in addition, such effects have been also measured in experimental testing in [16, 17]. Alternatively to experimental testing, numerical modeling can be employed such as atomic models [18,19,20]. However, such modeling solutions are computationally expensive with respect to continuum mechanics. Therefore, the main aim of the present study is to consider a higher-order continuum mechanics model which is able to take into consideration a length scale effects. This is the most common approach considered in the so-called nonlocal theories [21,22,23,24], where the description of the structural object is dependent on one of more length scale parameters.

Several nonlocal theories have been presented in the scientific community through the years such as couple stress [25], modified couple stress [26, 27], integral type and micropolar [28,29,30], strain and stress gradient [31,32,33,34,35] and modified strain gradient [36, 37],

This work focuses on a second-order strain gradient theory which is a simple and effective approach to investigate nonlocal effects in nanostructures. In the present case, the nonlocal effect is embodied in a single length scale parameter \(\ell\) which multiplies the second gradient of the strain field; this leads to a stress field that is not only linearly dependent on the strain and also on its second gradient. This approach has been efficiently applied to isotropic [38] as well as composite structures [39]. Recent works on the static and dynamic analysis of nanostructures have been proposed. Timoshenko beam theory was combined with stress gradient theory for the bending phenomena of nanobeams made of functionally graded (FG) materials. Analogously Euler–Bernoulli beam theory has been used in [40] for the free and forced vibrations of nanobeams on elastic Pasternak foundation. Nonhomogeneous nanobeams on elastic medium have been analyzed with strain gradient effects by Civalek and Akgöz [41, 42]. Brischetto and co-workers used nonlocal theories for the study of composite plates and shells subjected to thermal, hygrometric and piezoelectric stress [43,44,45,46]. Nanoplate problems subjected to hygrothermal loads have been proposed in [47,48,49,50,51,52], using different nonlocal theories. Most common research works solve such nonlocal problems with analytical or semi-analytical methods which, in general, limit the analysis to simply supported conditions (for the Navier method [53]) or two sides supported and two arbitrary (for the Levy method [54]).

The aim of this study is to provide a trigonometric analytical and semi-analytical solutions to the bending problem of composite thin nanoplates subjected to hygrothermal using nonlocal second-order strain gradient theory. Sinusoidal and uniform loads for cross- and angle-ply laminates are studied, and for every uniform distribution considered also the convergence analysis for both displacement and stress fields is performed. This paper is structured as follows: after the introductory section, the theoretical background for Kirchhoff thin plates in hygrothermal environment is developed, using second-order strain gradient theory. Then, in order to validate the calculation code, implemented in MATLAB, various comparisons with the literature are reported [55,56,57,58]. After the comparisons, the results obtained for different lamination schemes and different types of loads are provided. Finally, remarks and conclusions are reported at the end of this paper.

2 Theoretical background

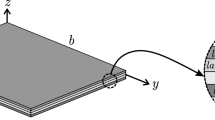
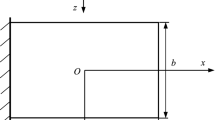
Consider a laminated thin nanoplate, modeled with the Kirchhoff plate theory, subjected to hygrothermal stresses [59]. The plate is composed of k orthotropic layers oriented at angles \(\theta _1\); \(\theta _2;\ldots ; \theta _k\). The thickness of the k-th oriented layer, along the z axis, is defined as \(h_k=z_{k+1}-z_k\).

Fig. 1
figure 1

Laminate general layout

Full size image

Introduced the reference system as in Fig. 1, we can define the displacement field of a generic point of the solid by means of the triad of displacement components U, V, W, which are functions of the coordinates (x, y, z).

$$\begin{aligned} \begin{Bmatrix} U \\ V \\ W \end{Bmatrix} = {\mathbb {I}}_3{\mathbf {u}} + z \begin{bmatrix} 0 &{}\quad 0 &{}\quad \frac{\partial }{\partial x} \\ 0 &{}\quad 0 &{}\quad \frac{\partial }{\partial y} \\ 0 &{}\quad 0 &{}\quad 0 \end{bmatrix} {\mathbf {u}} \end{aligned}$$
(1)

where \({\mathbf {u}} ^ {\top } = \begin{Bmatrix} u&\quad v&\quad w \end{Bmatrix}\) represent the components of the displacement vector of a generic point placed on the reference surface of the plate. \({\mathbb {I}}_3\) is the \(3\times 3\) identity matrix.

From this model, we can trace the relationships between displacement components and deformation components that make up the compatibility equations.

$$\begin{aligned} {\varvec{\varepsilon }}&= \begin{Bmatrix} \varepsilon _{xx} \\ \varepsilon _{yy} \\ \gamma _{xy} \end{Bmatrix}= \begin{Bmatrix} \varepsilon _{xx}^{(0)} \\ \varepsilon _{yy}^{(0)} \\ \gamma _{xy}^{(0)} \end{Bmatrix} + z \begin{Bmatrix} \varepsilon _{xx}^{(1)} \\ \varepsilon _{yy}^{(1)} \\ \gamma _{xy}^{(1)} \end{Bmatrix} \end{aligned}$$
(2)
$$\begin{aligned} {\varvec{\varepsilon }}&= {\varvec{\varepsilon }}^{(0)} + z{\varvec{\varepsilon }}^{(1)} =\left( {\mathbb {D}}^{(0)} + z{\mathbb {D}}^{(1)} \right) {\mathbf {u}} \end{aligned}$$
(3)

where the superscript \(^{(0)}\) stands for membrane strain whereas \(^{(1)}\) for bending strain, and

$$\begin{aligned} {\mathbb {D}}^{(0)}= \begin{bmatrix} \frac{\partial }{\partial x} &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad \frac{\partial }{\partial y} &{}\quad 0 \\ \frac{\partial }{\partial y} &{}\quad \frac{\partial }{\partial x} &{}\quad 0 \end{bmatrix}, \quad {\mathbb {D}}^{(1)}= \begin{bmatrix} 0 &{}\quad 0 &{}\quad -\frac{\partial ^2}{\partial x^2} \\ 0 &{}\quad 0 &{}\quad -\frac{\partial ^2}{\partial y^2} \\ 0 &{}\quad 0 &{}\quad -2\frac{\partial ^2}{\partial x \partial y} \end{bmatrix} \end{aligned}$$
(4)

We introduce the \(Q^{(k)}_{ij}\) representing the rigidity of the orthotropic k-th ply into the plate reference system. The stiffnesses relate the stress components to the strain components, allowing to write the constitutive equations, and are defined through the following relationships as a function of engineering constants

$$\begin{aligned} Q_{11}^{(k)}=\frac{E_{1}^{(k)}}{1-\nu _{12}^{(k)}\nu _{21}^{(k)}}, \quad Q_{22}^{(k)}=\frac{E_{2}^{(k)}}{1-\nu _{12}^{(k)}\nu _{21}^{(k)}}, \quad Q_{12}^{(k)}=\frac{\nu _{12}^{(k)}E_{2}^{(k)}}{1-\nu _{12}^{(k)}\nu _{21}^{(k)}}, \quad Q_{66}^{(k)}=G_{12}^{(k)} \end{aligned}$$
(5)

In order to know the mechanical behavior of nanoplates subjected to hygrothermal stress, we introduce the nonlocal elastic theory of second-order strain gradient. Therefore, the constitutive equations take the following form

$$\begin{aligned} \begin{Bmatrix} \sigma _{xx}^{(k)} \\ \sigma _{yy}^{(k)} \\ \sigma _{xy}^{(k)} \end{Bmatrix}&= \left( 1- \ell ^2 \nabla ^2 \right) \begin{bmatrix} \bar{Q}_{11}^{(k)} &{}\quad \bar{Q}_{12}^{(k)} &{}\quad \bar{Q}_{16}^{(k)} \\ \bar{Q}_{12}^{(k)} &{}\quad \bar{Q}_{22}^{(k)} &{}\quad \bar{Q}_{26}^{(k)} \\ \bar{Q}_{16}^{(k)} &{}\quad \bar{Q}_{26}^{(k)} &{}\quad \bar{Q}_{66}^{(k)} \end{bmatrix} \begin{Bmatrix} \varepsilon _{xx} \\ \varepsilon _{yy} \\ \gamma _{xy} \end{Bmatrix}\\&\quad \quad - \begin{bmatrix} \bar{Q}_{11}^{(k)} &{}\quad \bar{Q}_{12}^{(k)} &{}\quad \bar{Q}_{16}^{(k)} \\ \bar{Q}_{12}^{(k)} &{}\quad \bar{Q}_{22}^{(k)} &{}\quad \bar{Q}_{26}^{(k)} \\ \bar{Q}_{16}^{(k)} &{}\quad \bar{Q}_{26}^{(k)} &{}\quad \bar{Q}_{66}^{(k)} \end{bmatrix} \begin{Bmatrix} \alpha _{xx}^{(k)}\Delta T + \beta _{xx}^{(k)}\Delta C \\ \alpha _{yy}^{(k)}\Delta T + \beta _{yy}^{(k)}\Delta C \\ 2\alpha _{xy}^{(k)}\Delta T + 2\beta _{xy}^{(k)}\Delta C \end{Bmatrix} \end{aligned}$$
(6)

where \(\bar{Q}_{ij}^{(k)}\) are the classical reduced elastic stiffnesses [55] in the geometric reference plane. The same can be done for the hygrothermal properties of the material as

$$\begin{aligned} \alpha _{xx}^{(k)}&= \alpha _{1}^{(k)}\cos ^2{\theta ^{(k)}}+\alpha _{2}^{(k)}\sin ^2{\theta ^{(k)}},\quad \beta _{xx}^{(k)} = \beta _{1}^{(k)}\cos ^2{\theta ^{(k)}}+\beta _{2}^{(k)}\sin ^2{\theta ^{(k)}}\\ \alpha _{yy}^{(k)}&=\alpha _{1}^{(k)}\sin ^2{\theta ^{(k)}}+\alpha _{2}^{(k)}\cos ^2{\theta ^{(k)}} ,\quad \beta _{yy}^{(k)}=\beta _{1}^{(k)}\sin ^2{\theta ^{(k)}}+\beta _{2}^{(k)}\cos ^2{\theta ^{(k)}}\\ 2\alpha _{xy}^{(k)}&= 2\left( \alpha _{1}^{(k)}-\alpha _{2}^{(k)}\right) \sin {\theta ^{(k)}}\cos {\theta ^{(k)}} ,\quad 2\beta _{xy}^{(k)}=2\left( \beta _{1}^{(k)}-\beta _{2}^{(k)}\right) \sin {\theta ^{(k)}}\cos {\theta ^{(k)}} \end{aligned}$$
(7)

It is convenient to report the constitutive equation in matrix form as

$$\begin{aligned} {\varvec{\sigma }}^{(k)} =\left( 1- \ell ^2 \nabla ^2 \right) \bar{{\mathbf {Q}}}^{(k)} {\varvec{ \varepsilon }} - \bar{{\mathbf {Q}}}^{(k)} \left( {\varvec{\alpha }}^{(k)} T_0 + \frac{z}{h} {\varvec{\alpha }}^{(k)} T_1 + {\varvec{\beta }}^{(k)} C_0 + \frac{z}{h} {\varvec{\beta }}^{(k)} C_1 \right) \end{aligned}$$
(8)

where \(\ell\) is the nonlocal ratio and the operator \(\nabla ^2=\partial ^2/\partial x^2 + \partial ^2/\partial y^2\). The variation of hygrothermal loads along the thickness is governed by the following relationships

$$\begin{aligned} \Delta T&= T_0 + zT_1/h \\ \Delta C&= C_0 + zC_1/h \end{aligned}$$
(9)

where \(T_0\), \(C_0\) represent the constant distributions of temperature and humidity, analogously \(T_1\), \(C_1\) indicate the linear distributions of temperature and humidity. Note that all parameters are characterized by the same units since linear terms are multiplied by z/h.

By integrating the stresses along the thickness, we obtain:

$$\begin{aligned}&{\mathbf {N}} = \begin{Bmatrix} N_{xx} \\ N_{yy} \\ N_{xy} \end{Bmatrix}= \sum _{k=1}^{N_L} \int _{z_k}^{z_{k+1}} \begin{Bmatrix} \sigma _{xx}^{(k)} \\ \sigma _{yy}^{(k)} \\ \sigma _{xy}^{(k)} \end{Bmatrix}{\mathrm{d}}z\\&{\mathbf {M}} = \begin{Bmatrix} M_{xx} \\ M_{yy} \\ M_{xy} \end{Bmatrix}= \sum _{k=1}^{N_L} \int _{z_k}^{z_{k+1}} \begin{Bmatrix} \sigma _{xx}^{(k)} \\ \sigma _{yy}^{(k)} \\ \sigma _{xy}^{(k)} \end{Bmatrix}z\ {\mathrm{d}}z \end{aligned}$$
(10)

Introducing the \({\mathbf {A}}\), \({\mathbf {D}}\) and \({\mathbf {B}}\) matrices, called membrane stiffness matrix, bending stiffness matrix and bending-membrane coupling stiffness matrix,

$$\begin{aligned}&{\mathbf {A}}=\sum _{k=1}^{N_{L}}\int _{z_k}^{z_{k+1}} \bar{{\mathbf {Q}}}^{(k)} {\mathrm{d}}z=\sum _{k=1}^{N_{L}}\bar{{\mathbf {Q}}}^{(k)} \left( z_{k+1}-z_k \right) \\&{\mathbf {B}}=\sum _{k=1}^{N_{L}}\int _{z_k}^{z_{k+1}} \bar{{\mathbf {Q}}}^{(k)} z{\mathrm{d}}z=\frac{1}{2}\sum _{k=1}^{N_{L}} \bar{{\mathbf {Q}}}^{(k)}\left( z_{k+1}^2-z_k^2 \right) \\&{\mathbf {D}}=\sum _{k=1}^{N_{L}}\int _{z_k}^{z_{k+1}} \bar{{\mathbf {Q}}}^{(k)} z^2{\mathrm{d}}z =\frac{1}{3}\sum _{k=1}^{N_{L}}\bar{{\mathbf {Q}}}^{(k)} \left( z_{k+1}^3-z_k^3 \right) \end{aligned}$$
(11)

and vectors \({\mathbf {A}}^{\alpha }\), \({\mathbf {A}}^{\beta }\), \({\mathbf {B}}^{\alpha }\), \({\mathbf {B}}^{\beta }\), \({\mathbf {D}}^{\alpha }\) and \({\mathbf {D}}^{\beta }\) containing the hygrothermal properties of the material

$$\begin{aligned} {\mathbf {A}}^{\alpha }&=\sum _{k=1}^{N_{L}}\int _{z_k}^{z_{k+1}} \bar{{\mathbf {Q}}}^{(k)} {\varvec{\alpha }}^{(k)}{\mathrm{d}}z = \sum _{k=1}^{N_{L}}\bar{{\mathbf {Q}}}^{(k)} {\varvec{\alpha }}^{(k)} \left( z_{k+1}-z_k \right) \\ {\mathbf {B}}^{\alpha }&=\sum _{k=1}^{N_{L}}\int _{z_k}^{z_{k+1}} \bar{{\mathbf {Q}}}^{(k)} {\varvec{\alpha }}^{(k)}z\ {\mathrm{d}}z=\frac{1}{2}\sum _{k=1}^{N_{L}}\bar{{\mathbf {Q}}}^{(k)} {\varvec{\alpha }}^{(k)} \left( z_{k+1}^2-z_k^2\right) \\ {\mathbf {D}}^{\alpha }&=\sum _{k=1}^{N_{L}}\int _{z_k}^{z_{k+1}} \bar{{\mathbf {Q}}}^{(k)} {\varvec{\alpha }}^{(k)}z^2\ {\mathrm{d}}z=\frac{1}{3}\sum _{k=1}^{N_{L}}\bar{{\mathbf {Q}}}^{(k)} {\varvec{\alpha }}^{(k)} \left( z_{k+1}^3-z_k^3\right) \end{aligned}$$
(12)
$$\begin{aligned} {\mathbf {A}}^{\beta }&=\sum _{k=1}^{N_{L}}\int _{z_k}^{z_{k+1}} \bar{{\mathbf {Q}}}^{(k)} {\varvec{\beta }}^{(k)}{\mathrm{d}}z=\sum _{k=1}^{N_{L}}\bar{{\mathbf {Q}}}^{(k)} {\varvec{\beta }}^{(k)} \left( z_{k+1}-z_k \right) \\ {\mathbf {B}}^{\beta }&=\sum _{k=1}^{N_{L}}\int _{z_k}^{z_{k+1}} \bar{{\mathbf {Q}}}^{(k)} {\varvec{\beta }}^{(k)}z\ {\mathrm{d}}z=\frac{1}{2}\sum _{k=1}^{N_{L}}\bar{{\mathbf {Q}}}^{(k)} {\varvec{\beta }}^{(k)} \left( z_{k+1}^2-z_k^2 \right) \\ {\mathbf {D}}^{\beta }&=\sum _{k=1}^{N_{L}}\int _{z_k}^{z_{k+1}} \bar{{\mathbf {Q}}}^{(k)} {\varvec{\beta }}^{(k)}z^2{\mathrm{d}}z=\frac{1}{3}\sum _{k=1}^{N_{L}}\bar{{\mathbf {Q}}}^{(k)} {\varvec{\beta }}^{(k)} \left( z_{k+1}^3-z_k^3 \right) \end{aligned}$$
(13)

The stress characteristics as a function of the displacements take the following form

$$\begin{aligned} {\mathbf {N}}&= ({\mathbf {A}}{\mathbb {D}}^{(0)} + {\mathbf {B}}{\mathbb {D}}^{(1)}){\mathbf {u}}-\ell ^2\Big [{\mathbf {A}} \left( {\mathbb {D}}_{xx}^{(0)}+{\mathbb {D}}_{yy}^{(0)}\right) {\mathbf {u}} +{\mathbf {B}}\left( {\mathbb {D}}_{xx}^{(1)}+{\mathbb {D}}_{yy}^{(1)}\right) {\mathbf {u}}\Big ]+\nonumber \\&\quad -{\mathbf {A}}^{\alpha } T_0 - \frac{1}{h}{\mathbf {B}}^{\alpha } T_1 -{\mathbf {A}}^{\beta } C_0 - \frac{1}{h}{\mathbf {B}}^{\beta } C_1 \end{aligned}$$
(14)
$$\begin{aligned} {\mathbf {M}}&= ({\mathbf {B}}{\mathbb {D}}^{(0)} + {\mathbf {D}}{\mathbb {D}}^{(1)}){\mathbf {u}}-\ell ^2\Big [{\mathbf {B}}\left( {\mathbb {D}}_{xx}^{(0)} +{\mathbb {D}}_{yy}^{(0)}\right) {\mathbf {u}}+{\mathbf {D}}\left( {\mathbb {D}}_{xx}^{(1)} +{\mathbb {D}}_{yy}^{(1)}\right) {\mathbf {u}}\Big ]+\nonumber \\&\quad -{\mathbf {B}}^{\alpha } T_0 - \frac{1}{h}{\mathbf {D}}^{\alpha } T_1 -{\mathbf {B}}^{\beta } C_0 - \frac{1}{h}{\mathbf {D}}^{\beta } C_1 \end{aligned}$$
(15)

where subscripts \(_{xx}\), \(_{yy}\) represent second-order derivatives with respect to x and y applied to the operators defined in Eq. (4).

To obtain the balance equations we use the principle of virtual works \(\delta U + \delta V =0\), where \(\delta U\) is the variation of elastic energy and \(\delta V\) is the potential of external work done by applied forces.

$$\begin{aligned} \delta U&= \sum _{k=1}^{N_L} \int _{{\mathcal {A}}}\int _{z_k}^{z_{k+1}} \delta {\varvec{\varepsilon }}^{\top } {\varvec{\sigma }}^{(k)}\ {\mathrm{d}}z {\mathrm{d}}{\mathcal {A}}\\&=\sum _{k=1}^{N_L} \int _{{\mathcal {A}}}\int _{z_k}^{z_{k+1}} \left( {\mathbb {D}}^{(0)}\delta {\mathbf {u}}\right) ^{\top }{\varvec{\sigma }}^{(k)} + \left( {\mathbb {D}}^{(1)}\delta {\mathbf {u}}\right) ^{\top } z{\varvec{\sigma }}^{(k)}\ {\mathrm{d}}z {\mathrm{d}}{\mathcal {A}}\\&= \int _{{\mathcal {A}}}\left( {\mathbb {D}}^{(0)}\delta {\mathbf {u}}\right) ^{\top }{\mathbf {N}}+ \left( {\mathbb {D}}^{(1)}\delta {\mathbf {u}}\right) ^{\top } {\mathbf {M}}\ {\mathrm{d}}{\mathcal {A}} \end{aligned}$$
(16)

Integration by parts of the strain energy is

$$\begin{aligned} \delta U&= \int _{{\mathcal {A}}}\left( {\mathbb {D}}^{(0)}\delta {\mathbf {u}}\right) ^{\top }{\mathbf {N}}+ \left( {\mathbb {D}}^{(1)}\delta {\mathbf {u}}\right) ^{\top } {\mathbf {M}}\ {\mathrm{d}}{\mathcal {A}}\\&=\int _{{\mathcal {A}}}-\delta {\mathbf {u}}^{\top } \left( {\mathbb {D}}^{(0){\top }}{\mathbf {N}}\right) -\delta {\mathbf {u}}^{\top }\left( {\mathbb {D}}^{(1){\top }}{\mathbf {M}}\right) \ {\mathrm{d}}{\mathcal {A}} \\&\quad +\int _{\Gamma }\bigg [ \delta {\mathbf {u}}^{\top }\left( {\mathbf {n}}^{(0){\top }}{\mathbf {N}}\right) +\delta {\mathbf {u}}^{\top }\left( \left( {\mathbb {D}}^{(0)}{\mathbf {n}}^{(1)}\right) ^{\top }{\mathbf {M}}\right) -\delta {\mathbf {u}}^{\top }{\mathbb {D}}^{(2){\top }}\left( {\mathbf {n}}^{(0){\top }}{\mathbf {M}}\right) \bigg ]\ {\mathrm{d}}{\mathcal {S}} \end{aligned}$$
(17)

where

$$\begin{aligned} {\mathbf {n}}^{(0)}&=\begin{bmatrix} n_x &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad n_y &{}\quad 0 \\ n_y &{}\quad n_x &{}\quad 0 \end{bmatrix}, \quad {\mathbf {n}}^{(1)}=\begin{bmatrix} 0 &{}\quad 0 &{}\quad n_x \\ 0 &{}\quad 0 &{}\quad n_y \\ 0 &{}\quad 0 &{}\quad 0 \end{bmatrix}, \quad {\mathbb {D}}^{(2)}=\begin{bmatrix} 0 &{}\quad 0 &{}\quad \frac{\partial }{\partial x} \\ 0 &{}\quad 0 &{}\quad \frac{\partial }{\partial y} \\ 0 &{}\quad 0 &{}\quad 0 \end{bmatrix} \end{aligned}$$
(18)

Only transverse loads are applied to the plate, thus, potential of external work done by applied forces is

$$\begin{aligned} \delta V = -\int _{{\mathcal {A}}} {\mathbf {q}}^{\top }\delta {\mathbf {u}}\ {\mathrm{d}}{\mathcal {A}} \end{aligned}$$
(19)

where \({\mathbf {q}}= \begin{Bmatrix} 0&\quad 0&\quad q \end{Bmatrix}^{\top }\).

The balance equations and the boundary condition result to be

$$\begin{aligned}&{\mathbb {D}}^{(0){\top }}{\mathbf {N}} -{\mathbb {D}}^{(1){\top }}{\mathbf {M}}-{\mathbf {q}}=0 \end{aligned}$$
(20)
$$\begin{aligned}&{\mathbf {u}}=0 , \quad \left( {\mathbf {n}}^{(0){\top }}{\mathbf {N}}\right) - {\mathbb {D}}^{(2){\top }}\left( {\mathbf {n}}^{(0){\top }}{\mathbf {M}}\right) =0 \nonumber \\&\quad {\mathbb {D}}^{(2)}{\mathbf {u}}=0 \quad , \quad {\mathbf {M}}=0 \end{aligned}$$
(21)

Replacing Eqs. (14) and (15) in Eq. (20), the strong form of the problem is obtained.

3 Navier solution

In this section, we introduce the Navier displacements field for an orthotropic cross-ply and angle-ply laminate. The solution is obtained by substituting the Navier displacements field in the balance equation.

$$\begin{aligned} \begin{bmatrix} \hat{c}_{11}&{}\quad \hat{c}_{12}&{}\quad \hat{c}_{13}\\ \hat{c}_{12}&{}\quad \hat{c}_{22}&{}\quad \hat{c}_{23}\\ \hat{c}_{13}&{}\quad \hat{c}_{23}&{}\quad \hat{c}_{33} \end{bmatrix} \begin{Bmatrix} U_{mn} \\ V_{mn} \\ W_{mn} \end{Bmatrix}= \begin{Bmatrix} 0 \\ 0 \\ Q_{mn} \end{Bmatrix}+ \begin{Bmatrix} {\mathcal {F}}_{1,mn}^{{\mathrm{T}}} \\ {\mathcal {F}}_{2,mn}^{{\mathrm{T}}} \\ {\mathcal {F}}_{3,mn}^{{\mathrm{T}}} \end{Bmatrix} \end{aligned}$$
(22)

The coefficients \(\hat{c}_{ij}\) and \({\mathcal {F}}_{i,mn}^{{\mathrm{T}}}\) will be specified in the corresponding paragraphs for the specific case. Equation (22) can be solved by the method of static condensation. Consequently, the static solution is

$$\begin{aligned} W_{mn}&=\frac{1}{a_{mn}}\left[ Q_{mn}+{\mathcal {F}}_{3,mn}^{{\mathrm{T}}}+\frac{a_1}{a_0} {\mathcal {F}}_{1,mn}^{{\mathrm{T}}}+\frac{a_2}{a_0}{\mathcal {F}}_{2,mn}^{{\mathrm{T}}}\right] \\ U_{mn}&=\frac{1}{a_0}\left[ a_{1}W_{mn}+{\mathcal {F}}_{1,mn}^{{\mathrm{T}}}\hat{c}_{22} -{\mathcal {F}}_{2,mn}^{{\mathrm{T}}}\hat{c}_{12}\right] \\ V_{mn}&=\frac{1}{a_0}\left[ a_{2}W_{mn}-{\mathcal {F}}_{1,mn}^{{\mathrm{T}}}\hat{c}_{12} +{\mathcal {F}}_{2,mn}^{{\mathrm{T}}}\hat{c}_{11}\right] \end{aligned}$$
(23)

where

$$\begin{aligned} a_{mn}&=\hat{c}_{33}+\hat{c}_{13}\frac{a_1}{a_0}+\hat{c}_{23}\frac{a_2}{a_0}\\ a_{0}&=\hat{c}_{11}\hat{c}_{22}+\hat{c}_{12}\hat{c}_{12}\\ a_{1}&=\hat{c}_{12}\hat{c}_{23}+\hat{c}_{13}\hat{c}_{22}\\ a_{2}&=\hat{c}_{13}\hat{c}_{12}+\hat{c}_{11}\hat{c}_{23}. \end{aligned}$$
(24)

3.1 Cross-ply laminate

In this section, the analytical solution for cross-ply laminates is developed. The simply supported boundary condition for cross-ply laminates result to be:

$$\begin{aligned} u(x,0)=u(x,b)&=0\quad ;\quad v(0,y)=v(a,y)=0\\ w(x,0)=w(x,b)&=0\quad ;\quad w(0,y)=w(a,y)=0\\ \frac{\partial w}{\partial x}\bigg |_{(x,0)}&=\frac{\partial w}{\partial x}\bigg |_{(x,b)}=0 \quad ;\quad \frac{\partial w}{\partial y}\bigg |_{(0,y)}=\frac{\partial w}{\partial y}\bigg |_{(a,y)}=0 \end{aligned}$$
(25)

In order to satisfy the boundary condition, Navier displacements field is assumed to be

$$\begin{aligned} u(x,y)&=\sum _{m=1}^{\infty }\sum _{n=1}^{\infty } U_{mn}\cos {\alpha x}\sin {\beta y}\\ v(x,y)&=\sum _{m=1}^{\infty }\sum _{n=1}^{\infty } V_{mn}\sin {\alpha x}\cos {\beta y}\\ w(x,y)&=\sum _{m=1}^{\infty }\sum _{n=1}^{\infty } W_{mn}\sin {\alpha x}\sin {\beta y} \end{aligned}$$
(26)

A trigonometric development is also used for the mechanical and hygrothermal loads shown as

$$\begin{aligned} q(x,y)&= \sum _{m=1}^{\infty }\sum _{n=1}^{\infty } Q_{mn}\sin {\alpha x}\sin {\beta y} \end{aligned}$$
(27)
$$\begin{aligned} (T_{0}(x,y),T_{1}(x,y))&= \sum _{m=1}^{\infty }\sum _{n=1}^{\infty } \left( T_{0,mn},T_{1,mn}\right) \sin {\alpha x}\sin {\beta y} \end{aligned}$$
(28)
$$\begin{aligned} (C_{0}(x,y),C_{1}(x,y))&= \sum _{m=1}^{\infty }\sum _{n=1}^{\infty } \left( C_{0,mn},C_{1,mn}\right) \sin {\alpha x}\sin {\beta y} \end{aligned}$$
(29)

where \(\alpha ={m \pi }/{a}\) e \(\beta ={n \pi }/{b}\). The coefficients \(\hat{c}_{ij}\) for the cross-ply laminate are [39]

$$\begin{aligned} \hat{c}_{11}&=\alpha ^2A_{11}+\beta ^2 A_{66}+\ell ^2\left[ \alpha ^4A_{11}+\alpha ^2\beta ^2\left( A_{11}+A_{66}\right) +\beta ^4A_{66}\right] \\ \hat{c}_{12}&=\alpha \beta \left( A_{12}+A_{66}\right) +\ell ^2\left[ \alpha ^3\beta \left( A_{12}+A_{66}\right) +\alpha \beta ^3\left( A_{12}+A_{66}\right) \right] \\ \hat{c}_{13}&=-\alpha ^3B_{11}-\alpha \beta ^2\left( B_{12}+2B_{66}\right) \\&\quad -\ell ^2\left[ \alpha ^5B_{11}+\alpha ^3\beta ^2\left( B_{12}+ B_{11}+2B_{66}\right) +\alpha \beta ^4\left( B_{12}+2B_{66}\right) \right] \\ \hat{c}_{22}&=\beta ^2A_{22}+\alpha ^2A_{66} +\ell ^2\left[ \alpha ^2\beta ^2\left( A_{22}+A_{66}\right) +\alpha ^4A_{66}+\beta ^4A_{22}\right] \\ \hat{c}_{23}&=-\alpha ^2\beta \left( B_{12}+2B_{66}\right) -\beta ^3 B_{22}\\&\quad -\ell ^2\left[ \alpha ^4\beta \left( B_{12}+2B_{66}\right) +\alpha ^2\beta ^3\left( B_{22}+B_{12}+2B_{66}\right) +\beta ^5B_{22}\right] \\ \hat{c}_{33}&=\alpha ^4D_{11}+2\alpha ^2\beta ^2\left( D_{12}+2D_{66}\right) +\beta ^4D_{22}\\&\quad +\ell ^2\left[ \alpha ^6D_{11}+\alpha ^4\beta ^2\left( D_{11}+2D_{12}+4D_{66}\right) \right. \\&\quad \left. +\alpha ^2\beta ^4\left( D_{22}+2D_{12}+4D_{66}\right) +\beta ^6D_{22}\right] \end{aligned}$$
(30)

The hygrothermal load vector have the following form

$$\begin{aligned} {\mathcal {F}}_{1,mn}^{{\mathrm{T}}}&=-\alpha \Bigg [\left( A_{1}^{\alpha }T_{0,mn}+\frac{1}{h}B_{1}^{\alpha }T_{1,mn}\right) +\left( A_{1}^{\beta }C_{0,mn}+\frac{1}{h}B_{1}^{\beta }C_{1,mn}\right) \Bigg ]\\ {\mathcal {F}}_{2,mn}^{{\mathrm{T}}}&=-\beta \Bigg [\left( A_{2}^{\alpha }T_{0,mn}+\frac{1}{h}B_{2}^{\alpha }T_{1,mn}\right) +\left( A_{2}^{\beta }C_{0,mn}+\frac{1}{h}B_{2}^{\beta }C_{1,mn}\right) \Bigg ]\\ {\mathcal {F}}_{3,mn}^{{\mathrm{T}}}&=\alpha ^2\Bigg [\left( B_{1}^{\alpha }T_{0,mn}+\frac{1}{h}D_{1}^{\alpha }T_{1,mn}\right) +\left( B_{1}^{\beta }C_{0,mn}+\frac{1}{h}D_{1}^{\beta }C_{1,mn}\right) \Bigg ]\\&+\beta ^2\Bigg [\left( B_{2}^{\alpha }T_{0,mn}+\frac{1}{h}D_{2}^{\alpha }T_{1,mn}\right) +\left( B_{2}^{\beta }C_{0,mn}+\frac{1}{h}D_{2}^{\beta }C_{1,mn}\right) \Bigg ] \end{aligned}$$
(31)

The Navier solution for cross-ply laminate with simply supported boundary condition is valid only if: \(A_{16} = A_{26} = B_{16} = B_{26} = D_{16} = D_{26} = 0\); thus, it can be developed for laminates with a single generally orthotropic layer, symmetrically laminated plates with multiple specially orthotropic layers and antisymmetric cross-ply laminated plates.

3.2 Angle-ply laminate

In this section, the analytical solution for angle-ply laminates is developed. The simply supported boundary condition for angle-ply laminates results to be:

$$\begin{aligned} u(0,y)=u(a,y)=0\quad&;\quad v(x,0)=v(x,b)=0\\ w(x,0)=w(x,b)=0\quad&;\quad w(0,y)=w(a,y)=0\\ \frac{\partial w}{\partial x}\bigg |_{(x,0)}=\frac{\partial w}{\partial x} \bigg |_{(x,b)}=0 \quad&;\quad \frac{\partial w}{\partial y}\bigg |_{(0,y)}=\frac{\partial w}{\partial y}\bigg |_{(a,y)}=0 \end{aligned}$$
(32)

In order to satisfy the boundary condition, the Navier displacements field is assumed to be

$$\begin{aligned} u(x,y)&=\sum _{m=1}^{\infty }\sum _{n=1}^{\infty } U_{mn}\sin {\alpha x}\cos {\beta y}\\ v(x,y)&=\sum _{m=1}^{\infty }\sum _{n=1}^{\infty } V_{mn}\cos {\alpha x}\sin {\beta y}\\ w(x,y)&=\sum _{m=1}^{\infty }\sum _{n=1}^{\infty } W_{mn}\sin {\alpha x}\sin {\beta y} \end{aligned}$$
(33)

It is similar to what was done before the loads are (27), (28), (29).

The coefficients \(\hat{c}_{ij}\) for the angle-ply laminate are [39]

$$\begin{aligned} \hat{c}_{11}&=\alpha ^2A_{11}+\beta ^2 A_{66}+\ell ^2\left[ \alpha ^4A_{11}+\alpha ^2\beta ^2\left( A_{11}+A_{66}\right) +\beta ^4A_{66}\right] \\ \hat{c}_{12}&=\alpha \beta \left( A_{12}+A_{66}\right) +\ell ^2\left[ \alpha ^3\beta \left( A_{12}+A_{66}\right) +\alpha \beta ^3\left( A_{12}+A_{66}\right) \right] \\ \hat{c}_{13}&=-3\alpha ^2\beta B_{16}-\beta ^3B_{26}-\ell ^2\left[ 3B_{16}\left( \alpha ^4\beta +\alpha ^2\beta ^3\right) +B_{26}\left( \alpha ^2\beta ^3+\beta ^5\right) \right] \\ \hat{c}_{22}&=\beta ^2A_{22}+\alpha ^2A_{66} +\ell ^2\left[ \alpha ^2\beta ^2\left( A_{22}+A_{66}\right) +\alpha ^4A_{66}+\beta ^4A_{22}\right] \\ \hat{c}_{23}&=-\alpha ^3B_{16}-3\alpha \beta ^2B_{26}-\ell ^2\left[ B_{16}\left( \alpha ^5+\alpha ^3\beta ^2\right) +3B_{26}\left( \alpha \beta ^4+\alpha ^3\beta ^2\right) \right] \\ \hat{c}_{33}&=\alpha ^4D_{11}+2\alpha ^2\beta ^2\left( D_{12}+2D_{66}\right) +\beta ^4D_{22}\\&\quad +\ell ^2\big [\alpha ^6D_{11}+\alpha ^4\beta ^2\left( D_{11}+2D_{12}+4D_{66}\right) \\&\quad +\alpha ^2\beta ^4\left( D_{22}+2D_{12}+4D_{66}\right) +\beta ^6D_{22}\big ] \end{aligned}$$
(34)

The hygrothermal load vector have the following form:

$$\begin{aligned} {\mathcal {F}}_{1,mn}^{{\mathrm{T}}}&=-\beta \left[ \left( A_{3}^{\alpha }T_{0,mn} +\frac{1}{h}B_{3}^{\alpha }T_{1,mn}\right) +\left( A_{3}^{\beta }C_{0,mn} +\frac{1}{h}B_{3}^{\beta }C_{1,mn}\right) \right] \\ {\mathcal {F}}_{2,mn}^{{\mathrm{T}}}&=-\alpha \Bigg [\left( A_{3}^{\alpha }T_{0,mn} +\frac{1}{h}B_{3}^{\alpha }T_{1,mn}\right) +\left( A_{3}^{\beta }C_{0,mn} +\frac{1}{h}B_{3}^{\beta }C_{1,mn}\right) \Bigg ]\\ {\mathcal {F}}_{3,mn}^{{\mathrm{T}}}&=\alpha ^2\left[ \left( B_{1}^{\alpha }T_{0,mn} +\frac{1}{h}D_{1}^{\alpha }T_{1,mn}\right) +\left( B_{1}^{\beta }C_{0,mn} +\frac{1}{h}D_{1}^{\beta }C_{1,mn}\right) \right] \\&+\beta ^2\left[ \left( B_{2}^{\alpha }T_{0,mn}+\frac{1}{h}D_{2}^{\alpha }T_{1,mn}\right) +\left( B_{2}^{\beta }C_{0,mn}+\frac{1}{h}D_{2}^{\beta }C_{1,mn}\right) \right] \end{aligned}$$
(35)

The Navier solution for angle ply laminate with simply supported boundary condition is valid only if: \(A_{16} = A_{26} = B_{11} = B_{12} = B_{22} = B_{66} = D_{16} = D_{26} = 0\); thus, it can be developed for laminates with a single generally orthotropic layer, symmetrically laminated plates with multiple specially orthotropic layers and antisymmetric angle-ply laminated plates.

4 Results and discussion

In this section, the analytical solutions for cross- and angle-ply laminates subjected to thermal and hygrothermal loads are carried out. For each study case, the comparison between classical and nonlocal theory is shown. The properties of the material considered for the numerical solution are \(E_{1}=25\), \(E_{2}=1\), \(G_{12}=0.5\), \(\nu _{12}=0.25\), \(\alpha _{2}/\alpha _{1}=3\), \(\alpha _{1}=10^{-6}\), \(\beta _{1}=0\), \(\beta _{2}=0.44\). Please note that the units of measures are not reported because a consistent system of units has been used. The plates considered are rectangular with a ratio \(a/h=100\) and the total height of the laminate is kept constant independently of the number of plies from which it is composed. Initially, comparisons were made with the results found in the scientific literature. The formulas used to normalize the results and the point at which they are calculated are shown as

$$\begin{aligned} \bar{w}=w(a/2,b/2)\frac{ 10h}{\alpha _{1}T_{1}b^2},\quad&\quad \bar{\sigma }_{xy}= \frac{\sigma _{xy}(a,b,-h/2)}{E_{2}\alpha _{1}T_{1}b} \\ \bar{\sigma }_{xx}= \frac{\sigma _{xx}(a/2,b/2,-h/2)}{E_{2}\alpha _{1}T_{1}b},\quad&\quad \bar{\sigma }_{yy}= \frac{\sigma _{yy}(a/2,b/2,h/2)}{E_{2}\alpha _{1}T_{1}b} \end{aligned}$$
(36)

The results for comparison with references found in the literature were obtained considering a sinusoidal thermal load that varies linearly along the plate thickness \(\Delta T(x,y,z)=zT_{1}/h\).

Considering the effective disposition of the plies in terms of thermal properties of the material, it is possible to compare the values obtained with the values reported in the book [55] (Table 1) and in the article [58] (Table 2).

Table 1 Displacements (\(\bar{w}\)) of a cross-ply square plate simply supported, subjected to a sinusoidal temperature distribution
Full size table
Table 2 Displacements (\(\bar{w}\)) and stresses (\(\bar{\sigma }\)) of a cross-ply (0/90) square plate, simply supported, subjected to a sinusoidal temperature distribution
Full size table

If the effective disposition of the plies is not considered for thermal properties, the comparison with Zenkour (Tables 3, 4) can be carried out.

Table 3 Displacements (\(\bar{w}\)) of a cross-play square plate, simply supported, subjected to a sinusoidal temperature distribution, assuming that the thermal properties of the material do not depend on the effective disposition of the laminae (Zenkour, FPT, HPT and SPT) are the theories considered in [56])
Full size table
Table 4 Displacement \((\bar{w})\) of a laminate (0/90/0) for different kind of load and for different values of ratio a/b
Full size table

The validity of the code is demonstrated for sinusoidal loads and without nonlocal parameters. Subsequently, the analysis of the cross- and angle-ply laminates for different values of the ratio of nonlocality and different lamination schemes is discussed.

4.1 Cross-ply laminates

In Table 5, the results obtained for a sinusoidal thermal load with linear distribution along the plate thickness are shown. It is noted that the symmetrical laminates have the same behavior independently from the nonlocal parameter, while a significant reduction of displacements and an increase of normal stresses is observed as the ratio \((\ell /a)^2\) increases, for the tangential stress there is instead a decrease.

Table 5 Displacements (\(\bar{w}\)) and stresses (\(\bar{\sigma }\)) of a simply supported square cross-ply nanoplates, with different layout and for different values of nonlocal parameter, subjected to a sinusoidal temperature distribution \((T_{0}=0)\)
Full size table

In Fig. 2, the behavior of the antisymmetric plates, when the ratio between a and b sides and the nonlocal parameter vary, is analyzed. From the graphs, it is noted how the vertical displacement stabilizes after reaching the ratio \(a/b=1.5\) and also the reduction of the vertical displacement as the nonlocal parameter increases.

Fig. 2
figure 2

Displacements (\(\bar{w}\)) of cross-ply nanoplates (0/90) (a) and \((0/90)_2\) (b) subjected to sinusoidal thermal load, for different values of a/b ratio and nonlocal parameter \((\ell /a)^2\)

Full size image

Figure 3 represents the normal stresses in the two directions and the tangential in-plane stress, of the plate subjected to the sinusoidal thermal load with linear distribution along the thickness. The plates considered are squared with constant a/h ratio and composed by two and four crossed laminae, respectively. From these graphs, it can be observed how the normal stresses and the shear stress have different trends, when the nonlocal parameter increases the first ones registering an increase while the second ones show a decrease.

Fig. 3
figure 3

Stresses (\(\bar{\sigma }\)) of square plates (0/90) (a–c) and \((0/90)_2\) (d–f) subjected to sinusoidal thermal load, for different nonlocal parameters \((\ell /a)^2\)

Full size image

In order to study the uniform temperature distribution, it was necessary first to study the convergence of the solution by increase m and n because, unlike the sinusoidal distribution that represents a closed form solution, a sufficient number of trigonometric functions are needed to accurately approximate the load. Figure 4 shows in double logarithmic scale the relative error with respect to the expansion order used.

Fig. 4
figure 4

Relative error in logarithmic scale by varying n, m for the uniform thermal load

Full size image

The convergence analysis shows that \(m,n=199\) is an excellent approximation for \(\bar{w}\) and an acceptable solution in terms of \(\bar{\sigma }\), so this value was used in the following applications.

The vertical displacements of the plate subject to uniform thermal load (Table 6) are greater than the previous case.

Table 6 Displacements (\(\bar{w}\)) and stresses (\(\bar{\sigma }\)) of a simply supported square cross-ply nanoplates, with different layout and for different values of nonlocal parameter, subjected to a uniform temperature load distribution (\(m,n=1,3,5,\ldots ,199\); \(T_{0}=0\))
Full size table

In Fig. 5, the displacements as a function of the a/b ratio are shown, where in particular you can see the peak of the displacements for the ratio that assumes a value between 1.5 and 2 after which it undergoes a slight flexion and tends to stabilize, whereas with the nonlocal parameter other than zero, the vertical displacements after the peak do not stabilize but continue to decrease with increasing aspect ratios.

Fig. 5
figure 5

Displacements (\(\bar{w}\)) of cross-ply nanoplates (0/90) (a) and \((0/90)_2\) (b) subjected to uniform thermal load, for different values of a/b ratio and nonlocal parameter \((\ell /a)^2\)

Full size image

As for the sinusoidal thermal load, also for the uniform one there are the increase of normal stresses and the decrease of shear stress, these effects are well visible in Fig. 6.

Fig. 6
figure 6

Stresses (\(\bar{\sigma }\)) of square plates (0/90) (a–c) and \((0/90)_2\) (d–f) subjected to uniformal thermal load, for different nonlocal parameters \((\ell /a)^2\)

Full size image

Once the part related only to the thermal load has been completed, the combined load is analyzed, i.e., a distribution of temperature and a concentration of humidity acting simultaneously on the cross laminated plate. The values of the two loads acting on the plate are \(T_0=0,T_1=100\) and \(C_0=0 , C_1=3\times 10^{-4}\) and are both distributed linearly along the plate thickness (Fig. 7).

Fig. 7
figure 7

Displacements (\(\bar{w}\)) of cross-ply nanoplates (0/90) (a) and \((0/90)_2\) (b) subjected to sinusoidal hygrothermal load, for different values of a/b ratio and nonlocal parameter \((\ell /a)^2\)

Full size image
Table 7 Displacements (\(\bar{w}\)) and stresses (\(\bar{\sigma }\)) of a simply supported square cross-ply nanoplates, with different layout and for different values of nonlocal parameter, subjected to a sinusoidal hygrothermal load distribution (\(T_{0}=C_{0}=0\))
Full size table

In Fig. 8, the trend of normal and shear stresses is shown, along the thickness of two laminates that differ from each other for the number of plies, both subjected to hygrothermal load.

Fig. 8
figure 8

Stresses (\(\bar{\sigma }\)) of square plates (0/90) (a–c) and \((0/90)_2\) (d–f) subjected to sinusoidal hygrothermal load, for different nonlocal parameters \((\ell /a)^2\)

Full size image

As aforementioned, to study the uniform distribution it is necessary to perform the convergence analysis as shown in Fig. 9. This analysis is carried out both on the relative error on the displacements and on the stresses. It is underlined that the stresses result to have much lower precision in comparison to the displacements, for which a not large trigonometric expansion would be needed to obtain an accurate result.

Fig. 9
figure 9

Relative error in logarithmic by varying of n, m for uniform hygrothermal load

Full size image

In Fig. 10, according to what previously detected for the uniform load, the peak of the displacements around \(a/b=1.5\) and after a slight bending that tends to stabilize for the higher values of the a/b is observed.

Fig. 10
figure 10

Displacements (\(\bar{w}\)) of cross-ply nanoplates \((0/90)_2\) (a) and \((0/90)_2\) (b) subjected to uniform hygrothermal load, for different values of a/b ratio and nonlocal parameter \((\ell /a)^2\)

Full size image
Table 8 Displacements (\(\bar{w}\)) and stresses (\(\bar{\sigma }\)) of a simply supported square cross-ply nanoplates, with different layout and for different values of nonlocal parameter, subjected to an uniform hygrothermal load distribution (\(m,n=1,3,5,\ldots ,199\); \(T_{0}=C_{0}=0\))
Full size table

Finally in Fig. 11, the plots of normal and tangential stresses along the thickness of the laminates, with layout (0/90) and \((0/90)_2\), subjected to uniform hygrothermal load and for different values of the nonlocal parameter, are reported results are listed in Tables 7 and 8.

Fig. 11
figure 11

Stresses (\(\bar{\sigma }\)) of square plates (0/90) (a–c) and \((0/90)_2\) (d–f) subjected to uniform hygrothermal load, for different nonlocal parameter \((\ell /a)^2\)

Full size image

4.2 Angle-ply laminates

No values could be found in the literature for the antisymmetric angle-ply plates in order to carry out a comparison as previously done for cross-ply laminated plates. Except for the comparison with the literature values, the cases studied follow similar cases as in the previous section. The material properties also remain unchanged compared to the case of cross laminated plates.

It is analyzed the behavior of several angle-ply square plates subjected to a sinusoidal thermal load \((T_0=0 , T_1=1)\) distributed linearly along the thickness. The results, for the different layout and nonlocal parameter values, are presented in Table 9 and in Fig. 12.

Table 9 Displacements (\(\bar{w}\)) and stresses (\(\bar{\sigma }\)) of a simply supported square angle-ply nanoplates, with different layout and for different values of nonlocal parameter, subjected to a sinusoidal thermal load distribution (\(T_{0}=C_{0}=0\))
Full size table
Fig. 12
figure 12

Displacements (\(\bar{w}\)) of angle-ply nanoplates (− 45/45) (a) and \(({-}\,45/45)_2\) (b) subjected to sinusoidal thermal load, for different values of a/b ratio and nonlocal parameter \((\ell /a)^2\)

Full size image

Figure 13 depicts the normal and shear stresses for angle-ply nanoplates subjected to sinusoidal thermal load.

Fig. 13
figure 13

Stresses (\(\bar{\sigma }\)) of square plates (− 45/45) (a–c) and \(({-}\,45/45)_2\) (d–f) subjected to sinusoidal thermal load, for different nonlocal parameters \((\ell /a)^2\)

Full size image

To study the uniform temperature distribution, it was necessary to carry out a convergence analysis of the results, as it was done in the previous section. Figure 14 displays in double logarithmic scale the relative error as function of the trigonometric expansion considered. As for the case of the cross-ply nanoplates also here \(m,n=199\) is considered sufficient (as also indicated by Reddy [12] for elastic plates) for a good approximation of the results.

Fig. 14
figure 14

Relative error in logarithmic scale by varying of n, m for uniform thermal load

Full size image

Once again an increase is observed in the vertical displacement of the plate under the action of a uniform load compared to the sinusoidal thermal load (Fig. 15 and Table 10).

In Fig. 16, normal and shear in-plane stresses are shown along the thickness of the laminates, with layout (− 45/45) and \(({-}\,45/45)_2\), subjected to uniform thermal load and for different values of the nonlocal parameter.

Fig. 15
figure 15

Displacements (\(\bar{w}\)) of angle-ply nanoplates (− 45/45) (a) and \(({-}\,45/45)_2\) (b) subjected to uniform thermal load, for different values of a/b ratio and nonlocal parameter \((\ell /a)^2\)

Full size image
Table 10 Displacements (\(\bar{w}\)) and stresses (\(\bar{\sigma }\)) of a simply supported square angle-ply nanoplate, with different layout and for different values of nonlocal parameter, subjected to a uniform thermal load distribution (\(m,n=1,3,5,\ldots ,199\); \(T_{0}=C_{0}=0\))
Full size table
Fig. 16
figure 16

Stresses (\(\bar{\sigma }\)) of square plates (− 45/45) (a–c) and \(({-}\,45/45)_2\) (d–f) subjected to uniform thermal load, for different nonlocal parameter \((\ell /a)^2\)

Full size image

In the following, the case of plates subjected to both thermal load and hygrometric concentration is studied. The results of a sinusoidal distribution of the loads will be reported first (Figs. 17, 18 and Table 11) and then those related to the uniform distribution (Figs. 20, 21 and Table 12) with relative convergence analysis (Fig. 19). The material properties remain those already used for cross laminated plates.

Fig. 17
figure 17

Displacements (\(\bar{w}\)) of angle-ply nanoplates (− 45/45) (a) and \(({-}\,45/45)_2\) (b) subjected to sinusoidal hygrothermal load, for different values of a/b ratio and nonlocal parameter \((\ell /a)^2\)

Full size image
Fig. 18
figure 18

Stresses (\(\bar{\sigma }\)) of square plates (− 45/45) (a–c) and \(({-}\,45/45)_2\) (d–f) subjected to sinusoidal hygrothermal load, for different nonlocal parameter \((\ell /a)^2\)

Full size image
Fig. 19
figure 19

Relative error in logarithmic scale by varying of n, m for uniform hygrothermal load

Full size image
Fig. 20
figure 20

Displacements (\(\bar{w}\)) of angle-ply nanoplates (− 45/45) (a) and \(({-}\,45/45)_2\) (b) subjected to uniform hygrothermal load, for different values of a/b ratio and nonlocal parameter \((\ell /a)^2\)

Full size image
Fig. 21
figure 21

Stresses (\(\bar{\sigma }\)) of square plates (− 45/45) (a–c) and \(({-}\,45/45)_2\) (d–f) subjected to uniform hygrothermal load, for different nonlocal parameter \((\ell /a)^2\)

Full size image
Table 11 Displacements (\(\bar{w}\)) and stresses (\(\bar{\sigma }\)) of a simply supported square angle-ply nanoplates, with different layout and for different values of nonlocal parameter, subjected to a sinusoidal hygrothermal load distribution (\(T_{0}=C_{0}=0\))
Full size table
Table 12 Displacements (\(\bar{w}\)) and stresses (\(\bar{\sigma }\)) of a simply supported square angle-ply nanoplates, with different layout and for different values of nonlocal parameter, subjected to a uniform hygrothermal load distribution (\(m,n=1,3,5,\ldots ,199\); \(T_{0}=C_{0}=0\))
Full size table

5 Conclusions

This paper investigates the bending behavior of simply supported cross-ply and angle-ply nanoplates subjected to hygrothermal load using nonlocal strain gradient theory in combination with Kirchhoff plate theory. The analytical solution is obtained thanks to Navier displacement fields. Outcomes have been compared to other works wherever possible, showing good agreement. In the work, an increase in stiffness was observed after the introduction of the nonlocal parameter \(\ell\).

Many results are presented here for the first time. For sinusoidal distribution, the thermal and hygrothermal problems are developed for both cross- and angle-ply laminates, and for uniform distribution in addition to displacements and stresses outcomes, the convergence analysis is carried out. These results can be used as benchmark for further studies within the same topic.