Convolutional Neural Networks for Inference of Space Object Attitude Status

Abstract

Convolutional neural networks (CNNs) are utilized for the task of inferring the attitude status in terms of rotation rate of resident space objects (RSOs) using simulated light curve measurements. Research into the performance of CNNs on synthetic light curve data-sets has shown significant promise that has not yet translated into success when working with empirically collected light curves. This limitation appears to be due to a number of factors including: mixing of bidirectional reflectance distribution function (BRDF) signatures, the effects of sensor noise, and blurring due to atmospheric turbulence. A synthetic data-set of approximately 7500 light curves was generated that takes into account realistic BRDF signatures and environmental parameters. The RSO used in this study was texture mapped with three unique material BRDF signatures: silicon solar panel, glossy paint, and aluminum. A two-step BRDF model inversion of the Beard-Maxwell model was performed using empirically collected data-sets of these materials in order to physically derive the BRDF model parameters. The CNN was trained on light curves resulting from the RSO performing four different maneuvers: tumbling, accelerating in rotational rate, stabilizing, and inactive (or stable in rotation rate). The CNN achieved an overall classification accuracy of 86.2% across the four maneuver classes. A confusion matrix analysis of the different classes of maneuvers suggested that our model performed best when classifying tumbling and accelerating RSOs (94% accuracy) and worst at classifying inactive RSOs (60% accuracy). This performance limitation when classifying inactive RSOs is attributed to (1) back-scatter signatures and specular glints within the synthetic light curves of inactive satellites being mistaken as attitude maneuvers, and (2) low signal-to-noise ratio due to factors such as atmospheric blurring. These results suggest that CNNs have strong potential for aiding in the problem of classifying satellite attitude status from light curves, but that machine learning research must focus on developing training sets and pre-processing techniques that account for these complications.

Appendices

Appendix A: Light Curve Simulation

1.1 A.1 Propagation of Signal from RSO in Orbit to Telescope Aperture

The total irradiance, $M_\mathrm{orbit}$, in units of $\mathrm{Watts/m^2}$ onto a facet of an RSO in orbit can be obtained by modeling the sun as an idealized blackbody and assuming that the sun is an isotropic point source [6]:

$$\begin{aligned} M_\mathrm{orbit} = \int _{\lambda _L}^{\lambda _U} \left( \frac{r_\mathrm{sun}^2}{ (1 \, \mathrm{AU})^2 } \right) \frac{2 \pi h c^2}{\lambda ^5 \left[ \exp \left( \frac{hc}{\lambda K_B T_\mathrm{sun}} \right) - 1 \right] } \, d\lambda \, , \end{aligned}$$

(11)

where $T_\mathrm{sun}$ is the temperature of the sun, $K_B$ is Boltzmann’s constant, c is the speed of light, $\lambda$ is the wavelength of interest, h is Planck’s constant, $1 \, AU$ is the mean earth-sun distance and $r_{sun}$ is the radius of the sun. The wavelength-dependent irradiance was integrated over the upper ($\lambda _U$) and lower transmission ($\lambda _L$) bounds of the spectral filter of interest to give the wavelength-independent irradiance in this equation.

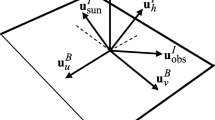
We assume that the distance between facets along the RSO is sufficiently small relative to the RSO-to-sun distance, $R_\mathrm{RSO/sun}(t)$, that $M_\mathrm{orbit}$ can be considered constant over all RSO facets. The radiance, $L_{\mathrm{orbit}_j}$, leaving the $j^{th}$ facet of the RSO body into a given observer direction ($\theta _r(t) \, , \phi _r(t)$) can be written according to:

$$\begin{aligned} L_{orbit_j} (t, \theta _r(t) \, , \phi _r(t)) = M_{orbit} \, \rho _j \Big ( \theta _i(t) \, , \phi _i(t) \, ; \theta _r(t) \, , \phi _r(t) \Big ) \left\langle \hat{n}^B_j (t) \cdot \hat{s}^B (t) \right\rangle \, , \end{aligned}$$

(12)

where ($\theta _i(t) \, , \phi _i(t)$) is the time-dependent direction of the sun relative to the facet in the body-frame, $\hat{n}^B_j$ is the unit normal vector denoting the orientation of the $j^{th}$ facet relative to the body frame, $\hat{s}^B$ is the unit normal vector specifying the solar orientation in the body frame, and $\rho _j$ is the observer/illumination direction dependent BRDF of the $j^{th}$ facet’s material. Note that the BRDF of spacecraft materials has been shown to be highly dependent on wavelength [4, 46], but is taken to be averaged over the range of the spectral filter [$\lambda _L \, , \lambda _U$] in this study. The observer-illuminator geometry parameters $\Big ( \theta _i(t) \, , \phi _i(t) \, ; \theta _r(t) \, , \phi _r(t) \Big )$ are all time-dependent due to the attitude and orbit of the RSO, but for simplicity, the time dependence will be dropped from this point forward.

The average irradiance onto an observing telescope aperture due to the $j^{th}$ facet, $E_{ap_j}$, in units of Watts/m$^2$ can then be written by taking into account the solid angle subtended by the RSO:

$$\begin{aligned} E_{ap_j} (t \, ; \theta _i \, , \phi _i \, ; \theta _r \, , \phi _r) = L_{\mathrm{orbit}_j} (t, \theta _r \, , \phi _r) \tau _\mathrm{atm}(\theta _r) \left( \frac{A_j}{R_\mathrm{RSO/obs}(t)^2} \right) \left\langle \hat{n}^B_j(t) \cdot \hat{o}^B(t) \right\rangle \, , \end{aligned}$$

(13)

where $\hat{o}^B$ is the unit normal vector specifying the observer orientation in the body frame, $A_j$ is the surface area of the $j^{th}$ facet, $\tau _\mathrm{atm}(\theta _r)$ is the zenith-angle dependent atmospheric transmittance, and $R_\mathrm{RSO/obs}(t)$ is the time dependent distance of the RSO to the observer telescope aperture.

In order to obtain the total expected irradiance, $E_{ap}$, onto the aperture, the signal due to all facets is summed:

$$\begin{aligned} E_{ap} (t \, ; \theta _i \, , \phi _i \, ; \theta _r \, , \phi _r) = \sum \limits _j E_{ap_j} (t \, ; \theta _i \, , \phi _i \, ; \theta _r \, , \phi _r) \end{aligned}$$

(14)

The flux due to a point source that reaches the focal plane, $\varPhi _\mathrm{FPA}$, in units of [Watts] can be written according to:

$$\begin{aligned} \varPhi _\mathrm{FPA}(t) = E_{ap} (t \, ; \theta _i \, , \phi _i \, ; \theta _r \, , \phi _r) \tau _\mathrm{opt}(\bar{\lambda }) \left( \frac{\pi D_{ap}^2}{4} \right) \end{aligned}$$

(15)

where $\tau _\mathrm{opt}(\bar{\lambda })$ is the average optical transmittance of the filter over the bandpass of interest, $D_{ap}$ is the aperture diameter, and $\bar{\lambda } = (\lambda _L + \lambda _U )/2$ is the average wavelength under consideration.

The signal can then be converted to units of $e^-$/second by taking into account the wavelength of bandpass of interest and the quantum efficiency of the focal plane array electronics [49]:

$$\begin{aligned} q_{S0}(t) = \varPhi _{FPA}(t) \left( \frac{\bar{\lambda }}{hc} \right) \, QE(\bar{\lambda }) \end{aligned}$$

(16)

1.2 A.2 Propagation of Energy From Sky Background Onto Focal Plane Array

By assuming that the sky background is an extended source, we can derive the spectral irradiance onto a pixel along the focal plane array according to the following equation for a telescope of $f_\# = f/D_{ap}$ , where f is the focal length of the telescope [10]:

$$\begin{aligned} E_\mathrm{sky} = \frac{L_\mathrm{sky} \, \pi \tau _\mathrm{optics} ( \bar{\lambda } ) }{(1+4 f_\#^2) } \end{aligned}$$

(17)

where $L_\mathrm{sky}$ is the photon radiance at the telescope aperture due to background sky pollution in units of photons/s/m$^2$/sr [10]:

$$\begin{aligned} L_\mathrm{sky} = M_\mathrm{orbit} \left( \frac{\bar{\lambda }}{hc} \right) \left( \frac{180}{\pi } \right) ^2 3600^2 \, \, 10^{-0.4(I_\mathrm{sky} + m_{v_0})} \end{aligned}$$

(18)

In the above equation $m_{v_{0}}$ is the magnitude of the Vega star which serves as the magnitude-zero source [6], and $I_\mathrm{sky}$ is the local background sky radiant intensity due to light pollution, moonlight, and starlight in units of visual magnitude per arcsec$^2$.

A final expression for the photon flux per pixel due to sky background, $q_{p, \mathrm{sky}}$, in units of $e^-$/pixel/second can be written as [49]:

$$\begin{aligned} q_{p, \mathrm{sky}} = \frac{L_\mathrm{sky} \, \pi \tau _\mathrm{optics} ( \bar{\lambda }) QE(\bar{\lambda }) p^2 }{(1+4 f_\#^2) } \, , \end{aligned}$$

(19)

where p is the pixel pitch.

1.3 A.3 Energy Loss Due to Atmospheric Turbulence Blur and Sampling

Inhomogeneities in the temperature of air within the atmosphere cause refractive index variations over the path from the surface of the earth to space. This refractive index gradient along the propagation path causes light to be received in a large variety of angles of incidence at the optical aperture [59]. Over short integration time scales (on the order of a few milliseconds), propagation through a turbulent atmosphere leads to phenomena such as image dancing, while over long time scales (on the order of hundreds of milliseconds) many dancing resolved images are collected which leads to image blurring [18]. Long-term blurring effects on imagery collected from optical telescopes arise primarily due to the effects of atmospheric turbulence on the phase rather than the amplitude of the propagating wavefront [32]. Consequently, in an imaging context, it can be assumed that energy is conserved when examining the effects of atmospheric turbulence on the received irradiance at the telescope aperture.

A plane wave approximation is met when the path length difference from an RSO in orbit to points along the extent of the observer aperture is negligible compared to the wavelength [59]:

$$\begin{aligned} D_{ap} \ll \sqrt{\bar{\lambda } \, R_\mathrm{RSO/obs}(t) } \end{aligned}$$

(20)

For the observer-to-RSO distances and optical wavelengths considered in this paper, Eq. 20 is met and a plane wave treatment is used.

For a plane wave, the full-width half maximum (FWHM) of the point spread function (PSF) due to atmospheric seeing is approximately parameterized by the wavelength-dependent Fried parameter of the atmosphere at a wavelength of 500 nm, $r_0(\theta _r)$: [18]. The value of $r_0$ is non-linearly dependent on the observation zenith angle, $\theta _r$. The equation for the dependence of the Fried parameter on zenith angle for a plane wave under the assumption of a constant atmospheric turbulence profile is given by [18]:

$$\begin{aligned} r_0(\theta _r) = 2.1 \left[ 1.46 \sec (\theta _r) \left( \frac{2\pi }{500 \, \mathrm{nm}} \right) ^2 C_n^2 \right] ^{-3/5} \end{aligned}$$

(21)

where $C_n^2$ is the altitude-independent refractive index structure constant. Equation 21 has been empirically shown to be valid for observing zenith angles up to 45 degrees [32].

For a moving RSO, the number of pixels occupied by the RSO along the sensor focal plane, m(t), grows according to:

$$\begin{aligned} m( t) = m_0(t) + \frac{\sqrt{m_0(\lambda , t)} \, \omega \, t_\mathrm{int}}{\mathrm{IFOV}} \, , \end{aligned}$$

(22)

where IFOV is the instantaneous field of view of a pixel on the sensor focal plane in units of radians/pixel, $m_0(\lambda , t)$ is the number of pixels initially subtended by the RSO, $t_\mathrm{int}$ is the integration time of the telescope system, and $\omega$ is the angular velocity of the RSO in units of rad/sec under the assumption of a telescope operating in stare mode [10]. The IFOV of the telescope is defined by $\mathrm{IFOV} = 2 \arctan (p/2f)$, where p is the pixel pitch, and f is the lens focal length.

The wavelength dependent number of pixels occupied by an RSO of projected area $A_{SO}$ at a distance $R_\mathrm{RSO/obs}(t)$ to the telescope can then be approximately defined as [10]:

$$\begin{aligned} m_0(t) = \left( \frac{A_{S0}}{R_\mathrm{RSO/obs}(t) \times \mathrm{IFOV}} + \frac{1}{\mathrm{IFOV}} \left( \frac{ \bar{\lambda } }{r_0(\theta _r)} \right) \right) ^2 \end{aligned}$$

(23)

Equation 23 gives the number of pixels across which the signal due to the RSO will be smeared. However, algorithms for calculating light curves will normally only integrate over a small rectangular transect that is aligned along the streak of the light curve in a collected image. In this paper, we assume that the rectangular extent has a transverse side length of $\Delta l$. The total number of pixels over which a light curve extraction algorithm will integrate is then given by:

$$\begin{aligned} m_{\varDelta l} = \varDelta l \, \left( m_0(t) \right) \end{aligned}$$

(24)

The fractional amount of energy lost due to the sampling algorithm of a streak detector can then be approximately calculated by $m_{\Delta l} / m(\lambda , t)$.

In this study, the parameter $r_0$ is defined for the site of interest at zenith angle $\theta _r = 0$ degrees using measures of atmospheric seeing obtained from previous studies [9, 32]. Equation 21 is then inverted to determine $C_n^2$ and the resultant value is used to infer the value of $r_0(\theta _r)$ for the RSO geometries over the light curve time series.

1.4 A.4 Noise Terms

The instantaneous Signal-to-Noise Ratio (SNR) of an RSO observed by a telescope on the ground can be derived by modeling a number of noise terms, including (1) the photon arrival process on the telecope’s CCD as a Poisson process, (2) dark current of sensor electronics, and (3) read noise in the process of conversion from analog to digital units. By assuming a constant background noise spectral signature, the instantaneous SNR can be written as [48]:

$$\begin{aligned} \mathrm{SNR}(t) = \frac{q_{SO}(t) t_\mathrm{int}}{\sqrt{q_{SO}(t) t_\mathrm{int} + 2 m(t) [q_{p,\mathrm{dark}} + q_{p,sky}]t_\mathrm{int} + q_\mathrm{read}/n^2}} \, , \end{aligned}$$

(25)

where $q_{p,dark}$ is the dark noise of the CCD [$e^-/\mathrm{pixel/s}$], $q_\mathrm{sky}(\lambda )$ is the wavelength-dependent sky signature reaching a pixel of the focal plane [$e^-/s$], $q_\mathrm{read}$ is the read noise of the sensor electronics [$e^-/\mathrm{pixel/s}$], $t_\mathrm{int}$ is the sensor integration time, m(t) is the wavelength- and time- dependent number of pixels occupied by the RSO along the focal plane, and n is a pixel binning factor.

The mean and variance of a Poisson distribution representing the photon arrival rate are equal to the rate parameter of the distribution [10]. Using this representation in combination with the assumption of independence of the random variable noise terms in Eq. 25, the mean and variance of the received light curve signal, $s_r(t)$, in units of electrons can be written as a Gaussian distribution following [48]:

$$\begin{aligned} \mu _{r}(t)= & {} \left( \frac{m_{\Delta l}}{m(t)} \right) q_{SO} t_\mathrm{int}\nonumber \\ \sigma ^2_{r}(t)= & {} \left( \frac{m_{\Delta l}}{m(t)} \right) q_{SO} t_\mathrm{int} + m_{\Delta l} \left[ q_{p,\mathrm{dark}} + q_{p,\mathrm{sky}} \right] t_\mathrm{int} + q_\mathrm{read}/n^2 \, , \end{aligned}$$

(26)

where the term $m_{\varDelta l} / m(t)$ is meant to signify the loss of a percentage of RSO signal due to the sampling of the light streak algorithm. Using Eq. 26, the instantaneous signal received due to the RSO for a given light track is derived as a random variable that is meant to simulate the combined effects of motion blur, optical blur, and noise due to the electronics of the system.

This term can be converted into Digital Counts (DC) by using knowledge of the full-well depth of sensor in units of electrons, $N_\mathrm{well}$, and of the dynamic range of the system in units of bits, $N_{DR} = 2^b$. Under this assumption, the received signal in units of electrons can be converted into digital counts according to:

$$\begin{aligned} DC_r(t) = \mathbf{int} \left( \frac{s_r(t) \, N_{DR}}{N_\mathrm{well}} \right) \end{aligned}$$

(27)

where the integer operator truncates the signal and further contributes to the noise of the received signal.

Appendix B: Beard–Maxwell BRDF Model Parameters

In Eq. 7, the incident and exitant polar angles are specified by the time series of solar, observer, and macro-facet orientations within the body frame:

$$\begin{aligned} \theta _i= & {} \left\langle \hat{n}^B_j (t) \cdot \hat{s}^B (t) \right\rangle \nonumber \\ \theta _r= & {} \left\langle \hat{n}^B_j (t) \cdot \hat{o}^B (t) \right\rangle \, \, , \end{aligned}$$

(28)

The half-angle between the incident and exitant directions ($\theta _n$) and the phase angle of the solar-observer geometry ($\beta$) are written respectively as:

$$\begin{aligned} \theta _n= & {} \cos ^{-1} \left( \frac{\cos \theta _i + \cos \theta _r}{2 \, \cos \beta } \right) \end{aligned}$$

(29)

$$\begin{aligned} \beta= & {} \frac{1}{2} \cos ^{-1} \left[ \cos \theta _i \, \cos \theta _r + \sin \theta _i \, \sin \theta _r \, \cos (\phi _r - \phi _i)\right] \end{aligned}$$

(30)

The term $R_f(\beta ; \, n, \, k)$ denotes the effective Fresnel reflectance of a material with complex index of refraction of $n^* = n \, + \, i k$, perpendicular reflectance coefficient of $r_s$, and parallel reflectance coefficient of $r_p$. The values of n and k capture the wavelength dependency of first surface reflection in terms of the index of refraction and extinction coefficients of the material [39]. In this study, the values of the Beard–Maxwell model are fit over a broad bandpass such that the values of n and k are considered to be averaged over wavelength:

$$\begin{aligned} R_f(\beta ; \, n, \, k)= & {} \frac{1}{2} \left( |r_s( n^*)|^2 + |r_p( n^*)|^2 \right) \nonumber \\ r_s( n^*)= & {} \frac{\cos \beta - \sqrt{(n^{*})^2 - \sin ^2 \beta }}{ \cos \beta \sqrt{(n^{*})^2 - \sin ^2 \beta }}\nonumber \\ r_p( n^*)= & {} \frac{(n^{*})^2\cos \beta - \sqrt{(n^{*})^2 - \sin ^2 \beta }}{ (n^{*})^2 \cos \beta + \sqrt{(n^{*})^2 - \sin ^2 \beta }} \, \, , \end{aligned}$$

(31)

The term $\rho _{fs}(\theta _n)$ denotes the first-surface reflectance. This term represents light being reflected in the specular direction off of a collection of micro-facets determined by a Cauchy distribution that make up the texture of the $j^{th}$ macro-facet pointing in direction $\hat{n}^B_j (t)$ [42, 56]:

$$\begin{aligned} \rho _{fs}(\theta _n) = \frac{R_f(\beta = 0; \, n, \, k) \, B}{ 4 \, \cos ^3 \theta _n \left[ \sigma ^2 + \tan ^2 \theta _n \right] } \, , \end{aligned}$$

(32)

where $\sigma$ is the mean square value of the micro-facet slope normal directions of the distribution, and B is a scaling parameter meant to fit the overall magnitude of the specular reflectance.

The shadowing and obscuration term, $S(\theta _n, \, \beta )$, accounts for the height distribution of the micro-facets. This function was derived according to fitting free parameters using empirical data [39]. This function, can be written as [42]:

$$\begin{aligned} S(\theta _n, \, \beta ) = \frac{1 + \frac{ \theta _n }{ \varOmega } \exp ^{-2 \beta / \psi }}{1 + \frac{\theta _n}{\varOmega }} \end{aligned}$$

(33)

where the free parameters $\varOmega$ and $\psi$ modify the falloff of the shadowing function in the forward-scattered and back-scattered directions, respectively.

Finally, the terms $\rho _D$ and $\rho _V$ represent the diffuse and directional volumetric reflectance of the material, respectively. Note that in the original Beard–Maxwell model, only one volumetric component was utilized [39]. In the enhanced version of the model used in this study both the Lambertian reflectance, $\rho _D$, and the directional diffuse reflectance, $\rho _V$, are used as fitting parameters [56].