1 Introduction

Chaos is described as a nonlinear extremely complex phenomenon found in nature featuring the high sensitivity to the initial conditions. These features are defined as butterfly effect, the term coined by Lorenz in 1963. Chaos theory is widely applicable to various fields of applied sciences and engineering, for instance, secure communication [1], biomedical engineering [2], machine learning, circuits [3], finance models [4], jerk systems [5], weather models [6], neural networks [7], oscillations [8], robotics [9], chemical reactions [10], encryption [11], ecological models [12], etc. Consequently, chaos theory has become one of the most appealing fields for researchers and engineers in recent times.

Historically, chaos theory dates back to the remarkable work of Poincare [13] established in 1890s while dealing with three-body problem to stabilize the solar system. In fact, he advocated the qualitatively behaviour, using geometric quantitatively to display the universal configuration of all solutions. Despite the observations made by Poincare [13], the first formal introduction of chaos in a deterministic system was proposed by Lorenz [14]. Lorenz observed that simple meteorological models depicted sensitive dependence on the initial conditions, known as butterfly effect, which established that chaos theory is widely applicable in other interdisciplinary areas also. Though the fundamental work on chaos synchronization had been carried by [15], the rapid growth in the field was seen after the phenomenal work of Ott et al. [16]. However, the concept of chaos synchronization was first introduced by Pecora and Carroll [17], wherein they performed synchronization of two identical chaotic systems based on master–slave composition which was unknown for the past 3 decades. Later on, many researchers carried forward the pioneered work of Pecora and Carroll and it has been established that chaos synchronization is also achievable for non-identical chaotic systems possessing absolutely different initial conditions.

In the available literature, a variety of synchronization techniques have been introduced and executed on many chaotic systems to gain stability. These include complete synchronization [18], lag synchronization [19], anti-synchronization [20], hybrid synchronization [21], projective synchronization [22], hybrid projective synchronization [23], modified projective synchronization [24], combination synchronization [25], combination–combination (C–C) synchronization [26], compound synchronization [27] and so on.

Up to now, numerous chaos control techniques have been formulated to attain chaos control and synchronization, for example, active control [28], sliding mode control [29], adaptive control [30], optimal control [31], back stepping design [32], impulsive control [33], time-delay feedback control [34], etc.

A hyperchaotic (HC) system is characterized as a chaotic system having more than two positive Lyapunov exponents. Rossler [35] introduced the first classical HC system in the year 1979. Over the past few decades, a variety of classical HC systems have been emerged and investigated, for example, Lorenz system, Liu system, Chen system, Lu system, Cai system, Pehlivan system, Tigan system, Nikolov system, Sundarapandian system, Vaidyanathan system, etc.

Chaos synchronization among chaotic systems using adaptive control method (ACM) was introduced by Hubler [36] in 1989 for the first time. Synchronization of Rossler like system and Chua’s circuit has been studied by using ACM in Ref. [37]. Also, adaptive control technique is studied to synchronize modified Chua’s circuit system in Ref. [38]. Mainieri and Rehaceh firstly [39] formulated the notion of projective synchronization while synchronizing chaotic systems in 1999. In Ref. [1], projective synchronization and chaos in secure communication is studied. Further, in Ref. [40], complex projective synchronization between complex chaotic systems is discussed. Sun et al. [26] first proposed the C–C synchronization scheme while synchronizing four identical or non-identical chaotic systems via active control method in 2012. A detailed study of C–C synchronization between four non-identical chaotic systems with uncertain parameters using sliding mode control is described in Ref. [41]. Further in Ref. [42], C–C synchronization among four complex nonlinear chaotic systems is studied and also particular cases, for instance, projective synchronization and combination synchronization, are mentioned. Moreover, a generalized methodology of C–C synchronization between n-dimensional chaotic fractional order nonlinear dynamical systems is developed in Ref. [43]. Here, the scheme discussed in Ref. [26] is extended to C–C synchronization between four n-dimensional fractional order nonlinear chaotic systems. Also, complex C–C synchronization among four newly constructed complex chaotic systems is discussed in Ref. [44]. In Ref. [45], chaos analysis and C–C synchronization of new HC systems having no equilibria are studied. Furthermore, C–C synchronization is generalized to n-dimensional time-delay nonlinear chaotic systems using robust adaptive sliding mode control in Ref. [46]. Also, in Ref. [47], C–C anti-synchronization between four identical fractional order HC systems is discussed. Further, C–C phase synchronization between different fractional order complex nonlinear chaotic systems via active control is studied in Ref. [48]. Also, finite-time combination synchronization among three non-identical chaotic systems is discussed in Ref. [49]. Moreover, combination synchronization between three different order chaotic systems via active backstepping technique is studied in [50].

Considering the aforementioned studies about C–C synchronization, our paper aims to investigate a hybrid projective combination–combination synchronization (HPCCS) among four non-identical HC systems via ACM. Moreover, based on (LST), we formulate an adaptive control law (ACL) with an estimated parameter update law. Our approach has potentiality and is advantageous. If chaos synchronization can be controlled efficiently, then it may be easily possible to achieve significantly higher quality achievements for information processing and secure communications. The HPCCS scheme among four non-identical HC systems of integer order using ACM has not yet been explored till now. This shows the novelty of this presented research work.

Our studies are structured as follows: in Sect. 2, some necessary definitions and basic notations are presented to be used within this paper. Section 3 deals with the methodology of ACM. Section 4 contains the basic structured features of the considered HC systems. Section 5 investigates the HPCCS scheme via ACM strategy. Numerical simulations are executed to verify the obtained analytical results of the proposed scheme in Sect. 6 . Also, a comparative analysis has been discussed. Lastly, some conclusions are drawn in Sect. 7

2 Preliminaries

In this section, we initially describe the procedure to achieve C–C synchronization according to master–slave configuration among four non-identical integer order HC systems with two master systems and two slave systems which are requisites for the subsequent sections.

The two master systems and two slave systems are expressed as

$$\begin{aligned} \dot{x_1}= \,&\ f_1(x_1)\eta _1+F_1(x_1), \end{aligned}$$
(1)
$$\begin{aligned} \dot{x_2}= \,&\ f_2(x_2)\eta _2+F_2(x_2), \end{aligned}$$
(2)
$$\begin{aligned} \dot{y_1}=\,&\ g_1(y_1)\theta _1+G_1(y_1)+u_1, \end{aligned}$$
(3)
$$\begin{aligned} \dot{y_2}=\,&\ g_2(y_2)\theta _2+G_2(y_2)+u_2, \end{aligned}$$
(4)

where \(x_1=(x_{11},x_{12}, \ldots ,x_{1n})^T\in R^n\), \(x_2=(x_{21},x_{22}, \ldots ,x_{2n})^T\in R^n\), \(y_1=(y_{11},y_{12}, \ldots ,y_{1n})^T\in R^n\), \(y_2=(y_{21},y_{22}, \ldots ,y_{2n})^T\in R^n\) are the state vectors of master and slave systems (1), (2), (3) and (4), respectively, \(f_1,f_2,g_1,g_2: R^n \rightarrow R^n\) are four nonlinear continuous functions, \(\eta _1=(\eta _{11},\eta _{12}, \ldots ,\eta _{1p_1})^{T}\) is a \(p_1\times 1\) unknown parameter vector of the first master system (1), \(\eta _2=(\eta _{21},\eta _{22}, \ldots ,\eta _{2p_2})^{T}\) is a \(p_2\times 1\) unknown parameter vector of the second master system (2), \(\theta _1=(\theta _{11},\theta _12, \ldots .,\theta _{1p_3})^{T}\) is a \(p_3\times 1\) unknown parameter vector of the first slave system (3), \(\theta _2=(\theta _{21},\theta _{22}, \ldots .,\theta _{2p_3})^{T}\) is a \(p_4\times 1\) unknown parameter vector of the second slave system (4), \(u_1= (u_{11},u_{12}, \ldots ,u_{1n})\in R^n\), \(u_2= (u_{21},u_{22}, \ldots ,u_{2n})\in R^n\) are the suitable controllers which are to be designed.

Definition 2.1

If there exist four constant matrices \(P,Q,R,S \in R^{n}\times R^{n}\) and \(R\ne 0\) or \(S\ne 0\) such that

$$\begin{aligned} lim_{t \rightarrow \infty } \Vert e\Vert =lim _{t \rightarrow \infty } \Vert (Px_1+Qx_2-Ry_1-Sy_2)\Vert =0, \end{aligned}$$

the combination of two master systems (1) and (2) is said to perform C–C synchronization with the combination of two slave systems (3) and (4) and \(\Vert .\Vert \) denotes the matrix norm.

Remark 2.2

The constant matrices P, Q, R and S are called the scaling matrices. In addition, P, Q, R, S can be extended as matrices of functions of state variables \(x_1,x_2,y_1\) and \(y_2\).

Remark 2.3

If \(R=0\) or \(S=0\), then C–C synchronization problem turns out to be the combination synchronization problem.

Remark 2.4

The combination synchronization problem will be converted into the chaos control problem for \(P=Q=R=0\) or \(P=Q=S=0\).

Remark 2.5

If \(R=S=-I\) and \(P=Q=-\alpha I\), for \(\alpha =1\) it turns into C–C complete synchronization and for \(\alpha =-1\) it will be reduced to C–C anti-synchronization. Combination of complete and anti-synchronization makes HPCCS. Thus, the HPCCS error takes the form:

$$\begin{aligned} e=(y_1+y_2)-\alpha _i(x_1+x_2), \end{aligned}$$
(5)

where \(\alpha =\mathrm{diag}(\alpha _1,\alpha _2, \ldots ,\alpha _n)\).

Remark 2.6

Definition 2.1 displays that the combination of master systems and slave systems can be expanded to three or more chaotic systems. Further, master systems and slave systems of the C–C synchronization scheme can be identical or non-identical.

3 Methodology of adaptive control method

Consider the chaotic (or HC) master system and the corresponding chaotic (or HC) slave system as

$$\begin{aligned} {\dot{x}}=&f_1(x)+f_2(x)\eta , \end{aligned}$$
(6)
$$\begin{aligned} {\dot{y}}=&g_1(y)+g_2(y)\beta +u, \end{aligned}$$
(7)

where \(x=(x_{1},x_{2}, \ldots ,x_{n})^T\), \(y=(y_{1},y_{2}, \ldots ,y_{n})^T\) are the state vectors, \(u=(u_i,i=1,2, \ldots ,n)\in R^{n}\) is the controller vector , \(f_1,g_1: R^n \rightarrow R^n\) are non-linear continuous vector functions, \(f_2: R^n \rightarrow R^{n\times m_1}\), \(g_2: R^n \rightarrow R^{n\times m_2}\) are matrix. \(\eta \in R^{m_1}\), and \(\beta \in R^{m_2}\) are non-linear parameter vectors.

Suppose error is described as

$$\begin{aligned} e(t)=y(t)-x(t), \end{aligned}$$

where \(e(t)=(e_i; i=1,2, \ldots ,n)^T\) is the error function and \(\Vert .\Vert \) represents the vector norm.

It follows that

$$\begin{aligned} \dot{e}(t)=\dot{y}(t)-\dot{x}(t). \end{aligned}$$

Using (6) and (7), the error dynamics becomes

$$\begin{aligned} \dot{e}(t)=g_1(y)+g_2(y)\beta +u-f_1(x)-f_2(x)\eta . \end{aligned}$$

Now, we design appropriate control function u and parameter update laws accordingly to ensure that master and slave systems with unknown parameters approach to desired synchronization state.

For that the controller is chosen as

$$\begin{aligned} u=-g_1(y)-g_2(y){\hat{\beta }} +f_1(x)+f_2(x){\hat{\eta }}-ke, \end{aligned}$$

where \({\hat{\eta }}(t)\), \({\hat{\beta }}(t)\) are the estimated values of unknown parameter vectors, respectively, and k is an arbitrarily chosen positive number known as gain constant.

The parameter update laws are described as

$$\begin{aligned} {\dot{\hat{\eta }}}= & {} -[f_2(x)]^Te+k_{\eta }{\tilde{\eta }} \\ {\dot{\hat{\beta }}}= & {} [g_2(y)]^Te+k_{\beta }{\tilde{\beta }}, \end{aligned}$$

where \({\tilde{\eta }}=\eta -{\hat{\eta }}\) and \({\tilde{\beta }}=\beta -{\hat{\beta }}\).

Choosing the Lyapunov function as

$$\begin{aligned} V(t)=\frac{1}{2}(e^{T}e+{\tilde{\eta }}^{T}{\tilde{\eta }}+{\tilde{\beta }}^{T}{\tilde{\beta }}). \end{aligned}$$

The derivative of V is written as

$$\begin{aligned} \dot{V}(t)&= e^{T}\dot{e}+{\tilde{\eta }}^{T}(-\dot{{\hat{\eta }}})+{\tilde{\beta }}^{T}(-\dot{{\hat{\beta }}}) \\&= e^{T}[g_2(y){\tilde{\beta }}-f_2(x){\tilde{\eta }}-ke]-{\tilde{\eta }}^{T}[-[f_2(x)]^Te+k_\eta {\tilde{\eta }}]-{\tilde{\beta }}^{T}[[g_2(y)]^Te+k_\beta {\tilde{\beta }}]\\&= e^{T}g_2(y){\tilde{\beta }}-e^{T}f_2(x){\tilde{\eta }}-ke^{T}e+{\tilde{\eta }}^{T}[f_2(x)]^T e-k_{\eta }{\tilde{\eta }}^{T}{\tilde{\eta }}- {{\tilde{\beta }}}^T[g_2(y)]^Te -k_{\beta } {\tilde{\beta }}^{T}{\tilde{\beta }} \\&=-ke^{T}e-k_{\eta } {\tilde{\eta }}^{T}{\tilde{\eta }}- k_{\beta } {\tilde{\beta }}^{T}{\tilde{\beta }}-[{\tilde{\eta }}^{T} [f_2(x)]^{T}e]^{T}+{\tilde{\eta }}^{T} [f_2(x)]^{T}e+[{\tilde{\beta }}^{T}[g_2(y)]^{T}e]^T-{\tilde{\beta }}^T [g_2(y)]^{T}e \\&=-ke^{T}e-k_{\eta } {\tilde{\eta }}^{T}{\tilde{\eta }}- k_{\beta } {\tilde{\beta }}^{T}{\tilde{\beta }} \\&<0, \end{aligned}$$

which establishes that \(\dot{V}\) is negative definite.

In accordance with LST, the error dynamical system is globally and asymptotically stable in the neighbourhood of the equilibrium points.

4 System description

Wang et al. [51] introduced the HC system:

$$\begin{aligned} \dot{x}_{11}= \,&a_1(y_{11}-x_{11})+w_{11}\nonumber \\ \dot{y}_{11}= \,&c_1x_{11}-y_{11}-x_{11}z_{11}\nonumber \\ \dot{z}_{11}= \,&x_{11}y_{11}-b_1z_{11}\nonumber \\ \dot{w}_{11}= \,&y_{11}z_{11}+d_1w_{11}, \end{aligned}$$
(8)

where \(x_{11},y_{11},z_{11},w_{11}\) are the states variables for the system (8) and for the system parameters \(a_1=10,b_1=8/3,c_1=28,d_1=-1\), the system (8) displays HC behaviour as discussed in Ref. [51].

Lu et al. [52] announced the HC system:

$$\begin{aligned} \dot{x}_{21}= \,&a_2(y_{21}-x_{21})+w_{21}\nonumber \\ \dot{y}_{21}= \,&-x_{21}z_{21}+c_2y_{21}\nonumber \\ \dot{z}_{21}= \,&x_{21}y_{21}-b_2z_{21}\nonumber \\ \dot{w}_{21}= \,&x_{21}z_{21}+d_2w_{21}, \end{aligned}$$
(9)

where \(x_{21},y_{21},z_{21},w_{21}\) are the state variables for the system (9) and for the system parameters \(a_2=36,b_2=3,c_2=20,d_2=1.3\), the system (9) exhibits HC behaviour as proven in Ref. [52].

Zheng et al. [53] proposed the HC system:

$$\begin{aligned} \dot{x}_{31}= \,&a_3(y_{31}-x_{31})+w_{31}\nonumber \\ \dot{y}_{31}= \,&b_3x_{31}+x_{31}z_{31}+c_3y_{31}+w_{31}\nonumber \\ \dot{z}_{31}= \,&-x_{31}x_{31}-d_3z_{31}\nonumber \\ \dot{w}_{31}= \,&-h_{3}y_{31}, \end{aligned}$$
(10)

where \(x_{31},y_{31},z_{31},w_{31}\) are the state variables for system (10) and for the system parameters \(a_3=20,b_3=14,c_3=10.6,d_3=2.8, h_{3}=4\), the system (10) shows HC behaviour as studied in Ref. [53].

Wei et al. [54] found the HC system:

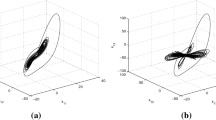
$$\begin{aligned} \dot{x}_{41}= \,&a_4(y_{14}-x_{14})\nonumber \\ \dot{y}_{41}= \,&-x_{41}z_{41}-c_4y_{41}+d_4w_{41}\nonumber \\ \dot{z}_{41}= \,&b_{4}+x_{41}y_{41}\nonumber \\ \dot{w}_{41}= \,&-h_{4}y_{41}, \end{aligned}$$
(11)

where \(x_{41},y_{41},z_{41},w_{41}\) are the state variables for the system (11) and for the system parameters \(a_4=10,b_4=25,c_4=-2.5,d_4=1,h_4=1\), system (11) depicts HC behaviour as shown in Ref. [54]. In addition, Fig. 1 and Fig. 2 display 2-D and 3-D phase portraits respectively of the aforementioned four hyperchaotic systerms.

In the next section, we shall present the HPCCS scheme using ACM.

5 Illustrative example

In this section, we discuss the ACL and the parameter estimation update law to stabilize the HC systems. For convenience, the systems (8) and (9) are treated as the master systems and the systems (10) and (11) are treated as the slave systems with controllers may be written as

$$\begin{aligned}&\dot{x}_{31}= a_3(y_{31}-x_{31})+w_{31}+u_{11}\nonumber \\&\dot{y}_{31}= b_3x_{31}+x_{31}z_{31}+c_3y_{31}+w_{31}+u_{12}\nonumber \\&\dot{z}_{31}= -x_{31}x_{31}-d_3z_{31}+u_{13}\nonumber \\&\dot{w}_{31}= -h_{3}y_{31}+u_{14}, \end{aligned}$$
(12)
$$\begin{aligned}&\dot{x}_{41}= a_4(y_{14}-x_{14}+u_{21}\nonumber \\&\dot{y}_{41}= -x_{41}z_{41}-c_4y_{41})+d_4w_{41}+u_{22}\nonumber \\&\dot{z}_{41}= b_{4}+x_{41}y_{41}+u_{23}\nonumber \\&\dot{w}_{41}= -h_{4}y_{41}+u_{24}, \end{aligned}$$
(13)

where \(u_{11}, u_{12}, u_{13}, u_{14}, u_{21}, u_{22},u_{23},u_{24}\) are the adaptive control inputs to be designed using ACM.

We define the HPCCS errors as

$$\begin{aligned} e_{11}= \,&x_{41}+x_{31}-\alpha _1 (x_{11}+x_{21})\nonumber \\ e_{12}= \,&y_{41}+y_{31}-\alpha _2 (y_{11}+y_{21})\nonumber \\ e_{13}= \,&z_{41}+z_{31}-\alpha _3 (z_{11}+z_{21})\nonumber \\ e_{14}= \,&w_{41}+w_{31}-\alpha _4 (w_{11}+w_{21}). \end{aligned}$$
(14)

The HPCCS error dynamics takes the form:

$$\begin{aligned}&\dot{e_{11}}= \dot{x_{41}}+\dot{x_{31}}-\alpha _1 (\dot{x_{11}}+\dot{x_{21}})\nonumber \\&\dot{e_{12}}= \dot{y_{41}}+\dot{y_{31}}-\alpha _2 (\dot{y_{11}}+\dot{y_{21}})\nonumber \\&\dot{e_{13}}= \dot{z_{41}}+\dot{z_{31}}-\alpha _3 (\dot{z_{11}}+\dot{z_{21}})\nonumber \\&\dot{e_{14}}= \dot{w_{41}}+\dot{w_{31}}-\alpha _4 (\dot{w_{11}}+\dot{w_{21}}). \end{aligned}$$
(15)

Substituting the equations of master systems (8)–(9) and slave systems (12)–(13) in (15), the error dynamics transforms to

$$\begin{aligned} \dot{e_{11}}= \,&a_3(y_{31}-x_{31})+w_{31}-\alpha _1 a_1(y_{11}-x_{11})-\alpha _1w_{11}+a_4(y_{41}-x_{41})\nonumber \\&-\alpha _1 a_2(y_{21}-x_{21})-\alpha _1 w_{21}+u_{11}+u_{21}\nonumber \\ \dot{e_{12}}= \,&b_{3}x_{31}+x_{31}z_{31}+c_3y_{31}+w_{31}-\alpha _2( c_1x_{11}-y_{11}-x_{11}z_{11})\nonumber \\&-x_{41}z_{41}-c_4y_{41}+d_4w_{41}-\alpha _2(-x_{21}z_{21}+c_2y_{21})+u_{12}+u_{22}\nonumber \\ \dot{e_{13}}= \,&-x_{31}x_{31}-d_3z_{31}-\alpha _3( x_{11}y_{11}-b_1z_{11})\nonumber \\&-b_4+x_{41}y_{41}-\alpha _3(x_{21}y_{21}-b_2z_{21})+u_{13}+u_{23}\nonumber \\ \dot{e_{14}}= \,&-h_{3}y_{31}-\alpha _4( -y_{11}z_{11}+d_1w_{11})-h_{4}y_{41}\nonumber \\&-\alpha _4(x_{21}z_{21}+d_2w_{21})+u_{14}+u_{24}. \end{aligned}$$
(16)

The adaptive controllers are defined as

$$\begin{aligned} u_{11}+u_{21}= \,&-\hat{a_3}(y_{31}-x_{31})-w_{31}+\alpha _1 \hat{a_1}(y_{11}-x_{11})+\alpha _1 w_{11}-k_1e_{11}\nonumber \\&-\hat{a_4}(y_{41}-x_{41})+\alpha _1 \hat{a_2}(y_{21}-x_{21})+\alpha _1 w_{21}\nonumber \\ u_{12}+u_{22}= \,&-\hat{b_3}x_{31}-x_{31}z_{31}-\hat{c_3}y_{31}-w_{31}+\alpha _2 (\hat{c_1}x_{11}-y_{11}-x_{11}z_{11})\nonumber \\&-k_2e_{12}+x_{41}z_{41}+\hat{c_4}y_{41}-\hat{d_4}w_{41}+\alpha _2 (-x_{21}z_{21}+\hat{c_2}y_{21})\nonumber \\ u_{13}+u_{23}= \,&x_{31}x_{31}+\hat{d_3}z_{31}+\alpha _3(x_{11}y_{11}-\hat{b_1}z_{11})-k_{3}e_{13}+\hat{b_4}-x_{41}y_{41}\nonumber \\ {}&+\alpha _3(x_{21}y_{21}-\hat{b_2}z_{21})\nonumber \\ u_{14}+u_{24}= \,&\hat{h_3}y_{31}+\alpha _4(-y_{11}z_{11}+\hat{d_1}w_{11})-k_{4}e_{14}+\hat{h_4}y_{41}\nonumber \\ {}&+\alpha _4(x_{21}z_{21}+\hat{d_2}w_{21}), \end{aligned}$$
(17)

where \(k_1,k_2,k_3\) and \(k_4\) are positive gain constants.

Putting the values of controllers (17) in error dynamics (16), we get

$$\begin{aligned} \dot{e_{11}}= \,&(a_3-{\hat{a}}_3)(y_{31}-x_{31})-\alpha _1 (a_1-{\hat{a}}_1)(y_{11}-x_{11})+(a_4-{\hat{a}}_4)(y_{41}-x_{41})\nonumber \\&-\alpha _1 (a_2-{\hat{a}}_2)(y_{21}-x_{21})-k_1e_{11}\nonumber \\ \dot{e_{12}}= \,&(b_3-{\hat{b}}_3)x_{31}+(c_3-{\hat{c}}_3)y_{31}-\alpha _2(c_1-{\hat{c}}_1)x_{11}-(c_4-{\hat{c}}_4)y_{41}\nonumber \\&+(d_4-{\hat{d}}_4)w_{41}-\alpha _2 (c_2-{\hat{c}}_2)y_{21}-k_2e_{12}\nonumber \\ \dot{e_{13}}= \,&-(d_3-{\hat{d}}_3)z_{31}+\alpha _3(b_1-{\hat{b}}_1)z_{11}-(b_4-{\hat{b}}_4)+\alpha _3(b_2-{\hat{b}}_2)z_{21}\nonumber \\&-k_3e_{13}\nonumber \\ \dot{e_{14}}= \,&-(h_3-{\hat{h}}_3)y_{31}-\alpha _4(d_1-{\hat{d}}_1)w_{11}-(h_4-{\hat{h}}_4)y_{41}-\alpha _4(d_2-{\hat{d}}_2)w_{21}\nonumber \\&-k_4e_{14}. \end{aligned}$$
(18)

We define parameter estimation error as follows:

$$\begin{aligned}&\tilde{a_1}=a_1-\hat{a_1},\tilde{a_2}=a_2-\hat{a_2},\tilde{a_3}=a_3- \hat{a_3},\tilde{a_4}=a_4-\hat{a_4},\tilde{b_1}=b_1-\hat{b_1}, \tilde{b_2}=b_2-\hat{b_2}, \nonumber \\&\tilde{b_3}=b_3-\hat{b_3},\tilde{b_4}=b_4-\hat{b_4} \tilde{c_1}=c_1-\hat{c_1},\tilde{c_2}=c_2-\hat{c_2},\tilde{c_3}= c_3-\hat{c_3},\tilde{c_4}=c_4-\hat{c_4},\nonumber \\&\tilde{d_1}=d_1-\hat{d_1},\tilde{d_2}=d_2-\hat{d_2},\tilde{d_3}=d_3- \hat{d_3},\tilde{d_4}=d_4-\hat{d},\tilde{h_3}=h_3-\hat{h_3},\tilde{h_4}=h_4-\hat{h_4}. \end{aligned}$$
(19)

From Eqs. (18) and (19), we obtain

$$\begin{aligned} \dot{e_{11}}= \,&\tilde{a_3}(y_{31}-x_{31})-\alpha _1 \tilde{a_1}(y_{11}-x_{11})+\tilde{a_4}(y_{41}-x_{41})\nonumber \\&-\alpha _1 \tilde{a_2}(y_{21}-x_{21})-k_1e_{11}\nonumber \\ \dot{e_{12}}= \,&\tilde{b_{3}}x_{31}+\tilde{c_3}y_{31}-\alpha _2\tilde{c_1}x_{11}-\tilde{c_4}y_{41}+\tilde{d_4}w_{41}-\alpha _2 \tilde{c_2}y_{21}-k_2e_{12}\nonumber \\ \dot{e_{13}}= \,&-\tilde{d_3}z_{31}+\alpha _3\tilde{b_1}z_{11}-\tilde{b_4}+\alpha _3\tilde{b_2}z_{21}-k_3e_{13}\nonumber \\ \dot{e_{14}}= \,&-\tilde{h_{3}}y_{31}-\alpha _4\tilde{d_1}w_{11}-\tilde{h_{4}}y_{41}-\alpha _4\tilde{d_2}w_{21}-k_4e_{14}. \end{aligned}$$
(20)

Next, we consider the candidate for Lyapunov function given by

$$\begin{aligned} V = \,&\frac{1}{2}[e_{11}^2+e_{12}^2+e_{13}^2+e_{14}^2+\tilde{a_1}^2+\tilde{a_2}^2+\tilde{a_3}^2+\tilde{a_4}^2\nonumber \\ {}&+\tilde{b_1}^2+\tilde{b_2}^2+\tilde{b_3}^2+\tilde{b_4}^2+\tilde{c_1}^2+\tilde{c_2}^2+\tilde{c_3}^2\nonumber \\ {}&+\tilde{c_4}^2+\tilde{d_1}^2+\tilde{d_2}^2+\tilde{d_3}^2+\tilde{d_4}^2+\tilde{h_3}^2+\tilde{h_4}^2], \end{aligned}$$
(21)

which is a positive definite function. Differentiating V along the trajectories of (21), we obtain

$$\begin{aligned} {\dot{V}}= \,&e_{11}\dot{e_{11}}+e_{12}\dot{e_{12}}+e_{13}\dot{e_{13}}+e_{14}\dot{e_{14}}-\tilde{a_1}\dot{\hat{a_1}}-\tilde{a_2}\dot{\hat{a_2}}-\tilde{a_3}\dot{\hat{a_3}}-\tilde{a_4}\dot{\hat{a_4}}\nonumber \\ {}&-\tilde{b_1}\dot{\hat{b_1}}-\tilde{b_2}\dot{\hat{b_2}}-\tilde{b_3}\dot{\hat{b_3}}-\tilde{b_4}\dot{\hat{b_4}}-\tilde{c_1}\dot{\hat{c_1}}\nonumber \\ {}&-\tilde{c_2}\dot{\hat{c_2}}-\tilde{c_3}\dot{\hat{c_3}}-\tilde{c_4}\dot{\hat{c_4}}-\tilde{d_1}\dot{\hat{d_1}}\nonumber \\ {}&-\tilde{d_2}\dot{\hat{d_2}}-\tilde{d_3}\dot{\hat{d_3}}-\tilde{d_4}\dot{\hat{d_4}}-\tilde{h_3}\dot{\hat{h_3}}-\tilde{h_4}\dot{\hat{h_4}}. \end{aligned}$$
(22)

In view of (22), we define the parameter estimation laws as follows:

$$\begin{aligned} \dot{\hat{a_1}}= \,&-\alpha _1(y_{11}-x_{11})e_{11}+k_5{\tilde{a}}_1 \nonumber \\ \dot{\hat{a_2}}= \,&-\alpha _1(y_{21}-x_{21})e_{11}+k_6{\tilde{a}}_2 \nonumber \\ \dot{\hat{a_3}}= \,&(y_{31}-x_{31})e_{11}+k_7{\tilde{a}}_3 \nonumber \\ \dot{\hat{a_4}}= \,&(y_{41}-x_{41})e_{11}+k_8{\tilde{a}}_4 \nonumber \\ \dot{\hat{b_1}}= \,&\alpha _3z_{11}e_{13}+k_9{\tilde{b}}_1\nonumber \\ \dot{\hat{b_2}}= \,&\alpha _3z_{12}e_{13}+k_{10}{\tilde{b}}_2\nonumber \\ \dot{\hat{b_3}}= \,&x_{31}e_{12}+k_{11}{\tilde{b}}_3\nonumber \\ \dot{\hat{b_4}}= \,&-e_{13}+k_{12}{\tilde{b}}_4\nonumber \\ \dot{\hat{c_1}}= \,&-\alpha _2x_{11}e_{12}+k_{13}{\tilde{c}}_1 \nonumber \\ \dot{\hat{c_2}}= \,&-\alpha _2y_{21}e_{12}+k_{14}{\tilde{c}}_2 \nonumber \\ \dot{\hat{c_3}}= \,&y_{31}e_{12}+k_{15}{\tilde{c}}_3 \nonumber \\ \dot{\hat{c_4}}= \,&-y_{41}e_{12}+k_{16}{\tilde{c}}_4 \nonumber \\ \dot{\hat{d_1}}= \,&\alpha _4w_{11}e_{14}+k_{17}{\tilde{d}}_1\nonumber \\ \dot{\hat{d_2}}= \,&\alpha _4w_{12}e_{14}+k_{18}{\tilde{d}}_2\nonumber \\ \dot{\hat{d_3}}= \,&-z_{31}e_{13}+k_{19}{\tilde{d}}_3\nonumber \\ \dot{\hat{d_4}}= \,&w_{41}e_{12}+k_{20}{\tilde{d}}_4\nonumber \\ \dot{\hat{h_3}}= \,&-y_{31}e_{14}+k_{21}{\tilde{h}}_3\nonumber \\ \dot{\hat{h_4}}= \,&-y_{41}e_{14}+k_{22}{\tilde{h}}_4. \end{aligned}$$
(23)

Theorem 5.1

The non-identical HC systems (8)–(9) and (12)–(13) are globally and asymptotically hybrid projective C–C synchronized for all initial states under the defined ACLs (17) and the parameter update law (23), where \(k_i,i=1,2,3 \ldots ,22\) are positive gain constants.

Proof

The Lyapunov function V defined by Eq. (21) is a positive definite function. Inserting the error dynamics (20) and using parameter update laws (23) into (22), the time derivative of V is obtained as

$$\begin{aligned} {\dot{V}}=&-k_1e_{11}^2-k_2e_{12}^2-k_3e_{13}^2-k_4e_{14}^2-k_5\tilde{a_1}^2-k_6\tilde{a_2}^2\nonumber \\ {}&-k_7\tilde{a_3}^2-k_8\tilde{a_4}^2-k_9\tilde{b_1}^2-k_10\tilde{b_2}^2-k_11\tilde{b_3}^2-k_12\tilde{b_4}^2\nonumber \\ {}&-k_{13}\tilde{c_1}^2-k_{14}\tilde{c_2}^2-k_{14}\tilde{c_3}^2-k_{15}\tilde{c_4}^2-k_{16}\tilde{d_1}^2\nonumber \\ {}&-k_{17}\tilde{d_2}^2-k_{18}\tilde{d_3}^2-k_{19}\tilde{d_4}^2-k_{20}\tilde{h_3}^2-k_{21}\tilde{h_4}^2. \end{aligned}$$
(24)

This shows that \(\dot{V}<0\) which ensures that \(\dot{V}\) is negative definite in \(\hbox {R}^{22}\).

Fig. 1
figure 1

Phase portraits of hyperchaotic systems a \(x_{11}-z_{11}\)-plane, b \(x_{21}-y_{21}\)-plane, c \(x_{31}-z_{31}\)-plane, d \(z_{41}-w_{41}\)-plane

Full size image

Thus, according to LST, we deduce that the HPCCS error \(e(t)\rightarrow 0\) asymptotically as \(t\rightarrow \infty \) for all initial conditions \(e(0)\in R^4\). Hence, the proof is complete. \(\square \)

6 Numerical simulation

In this section, we demonstrate the numerical simulations in order to check the effectivity and feasibility of the investigated approach. To achieve this, fourth order Runge–Kutta method has been used. For the simulation procedure, the parameter values are taken as \(a_1=10, b_1=8/3, c_1=28,\) \(d_1=-1, a_2=36, b_2=3, c_2=20, d_2=1.3, a_3=20,\) \(b_3=14, c_3=10.6, d_3=2.8, h_3=4, a_4=10, b_4=25,\) \( c_4=-2.5, d_4=1, h_4=1\). The initial conditions for the master systems and slave systems are arbitrarily chosen as \((x_{11}(0), y_{11}(0), z_{11}(0), w_{11}(0))=(-1,1,-1,1)\), \((x_{21}(0), y_{21}(0), z_{21}(0), w_{21}(0))=(5,8,-1,-3)\), \((x_{31}(0), y_{31}(0), z_{31}(0),w_{31}(0))=(5,4,7,2)\), \((x_{41}(0), y_{41}(0),z_{41}(0),w_{41}(0))=(0.2,0.1,0.75,-2)\). The control gains are selected as \(k_i=4\) for \(i=1,2, \ldots ,22\).

Fig. 2
figure 2

Phase portraits of hyperchaotic systems in a \(x_{11}-y_{11}-z_{11}\) space, b \(x_{21}-y_{21}-z_{21}\) space, c \(x_{31}-y_{31}-z_{31}\) space, d \(x_{41}-y_{41}-z_{41}\) space

Full size image
Fig. 3
figure 3

Complete synchronization of hyperchaotic systems a between \(x_{11}(t)+x_{21}(t)\) and \(x_{31}(t)+x_{41}(t)\), b between \(y_{11}(t)+y_{21}(t)\) and \(y_{31}(t)+y_{41}(t)\), c between \(z_{11}(t)+z_{21}(t)\) and \(z_{31}(t)+z_{41}(t)\), d between \(w_{11}(t)+w_{21}(t)\) and \(w_{31}(t)+w_{41}(t)\), e synchronization errors \(e_{11}\), \(e_{12}\), \(e_{13}\), \(e_{14}\), f parameter estimation

Full size image
Fig. 4
figure 4

Anti-synchronization of hyperchaotic systems a between \(x_{11}(t)+x_{21}(t)\) and \(x_{31}(t)+x_{41}(t)\), b between \(y_{11}(t)+y_{21}(t)\) and \(y_{31}(t)+y_{41}(t)\), c between \(z_{11}(t)+z_{21}(t)\) and \(z_{31}(t)+z_{41}(t)\), d between \(w_{11}(t)+w_{21}(t)\) and \(w_{31}(t)+w_{41}(t)\), e synchronization errors \(e_{11}\), \(e_{12}\), \(e_{13}\), \(e_{14}\), f parameter estimation

Full size image
Fig. 5
figure 5

HPCCS of hyperchaotic systems a between \(x_{11}(t)+x_{21}(t)\) and \(x_{31}(t)+x_{41}(t)\), b between \(y_{11}(t)+y_{21}(t)\) and \(y_{31}(t)+y_{41}(t)\), c between \(z_{11}(t)+z_{21}(t)\) and \(z_{31}(t)+z_{41}(t)\), d between \(w_{11}(t)+w_{21}(t)\) and \(w_{31}(t)+w_{41}(t)\), e HPCCS errors \(e_{11}\), \(e_{12}\), \(e_{13}\), \(e_{14}\), f parameter estimation

Full size image

Case 1. Let us assume the scaling matrix \(\alpha \) with \(\alpha _1=\alpha _2=\alpha _3=1\). In this case, we achieve complete C-C synchronization with master systems (8)–(9) and slave systems (12)–(13). The trajectories of master and slave systems with the control inputs are depicted in Fig. 3a–d. Further, initial states for error system are obtained as \((e_{11},e_{12},e_{13}, e_{14})=(1.2,-4.9,9.75,2)\). The convergence of synchronization error e(t) to zero as t approaches infinity as displayed in Fig. 3e shows that the HPCCS among two master systems and two slave systems has been achieved via ACM. Moreover, Fig. 3f displays that the estimated parameters converge to their respective original values asymptotically with time. Thus, the proposed HPCCS scheme between master and slave systems is verified computationally.

Fig. 6
figure 6

HPCCS error convergence portrait

Full size image

Case 2. When the scaling matrix \(\alpha \) is taken as \(\alpha _1=\alpha _2=\alpha _3=\alpha _4=-1\), then we achieve C–C anti-synchronization between the master systems (8)–(9) and the slave systems (12)–(13). Figure 4a–d exhibits the trajectories of master and slave variables with the control inputs. Also, initial states for error system are obtained as \((e_{11},e_{12},e_{13}, e_{14})=(9.2,13.1,5.75,-2)\). The convergence of synchronization error e(t) to zero as t approaches infinity as exhibited in Fig. 4e establishes that the HPCCS among two master systems and two slave systems is achieved via ACM. Further, Fig. 4f displays that the estimated parameters converge to their respective original values asymptotically with time. Thus, the proposed HPCCS scheme between master and slave systems is justified computationally.

Case 3. In this case, we achieve HPCCS scheme of master and slave systems by choosing the scaling matrix \(\alpha \) with \(\alpha _1=2,\alpha _2=-3, \alpha _3=3,\alpha _4=-2\). Figure 5a–d displays the trajectories of master and slave variables with the control inputs. Further, initial states for error system are obtained as \((e_{11},e_{12},e_{13}, e_{14})=(-2.8,31.1,13.75,-4)\). The convergence of synchronization error e(t) to zero as t approaches infinity as depicted in Fig. 5e ensures that the HPCCS among two master systems and two slave systems is achieved via ACM. Further, Fig. 5f exhibits that the estimated parameters converge to their respective original values asymptotically with time. Thus, the proposed HPCCS scheme between master and slave systems is ensured computationally.

A comparison analysis between the proposed HPCCS scheme and the earlier published work.

In Ref. [26], author used nonlinear active control to investigate the C–C synchronization between four identical Lu systems and non-identical chaotic systems where it is noticed that the synchronization is obtained at \(t=5\) (approx.) and \(t=4.8\) (approx.), respectively. Also, author adopted sliding mode control approach in Ref. [41] to achieve C–C synchronization among four different systems with uncertain parameters, here it has been found that synchronization error is converging to zero at \(t=2.4\) (approx.). Further, in Ref. [42], author studied C–C synchronization among four complex nonlinear chaotic systems where it has been recorded that the error synchronization is realized at \(t=5\) (approx.). Also in Ref. [45], author applied ACM to achieve C–C synchronization between four identical HC systems where it noted that the synchronization state is attained at \(t=5.1\) (approx.). Moreover, in Ref. [46], author utilized robust adaptive sliding mode control to generalize the C–C synchronization of n-dimensional chaotic systems with time delay in which the synchronization is obtained at \(t=4.9\) (approx.). Also in Ref. [48], author discussed phase synchronization between different complex chaotic systems of fractional order, by this procedure, the C–C synchronization has been carried out at \(t=4.5\) (approx.). Furthermore, in Ref. [55], author proposed ACM to study complex modified hybrid function projective synchronization between different complex chaotic systems with unknown complex parameters, where it has been seen that the desired synchronization is obtained at \(t=4.5\) (approx.). Apart from the above-described studies, we have investigated the HPCCS scheme among four non-identical HC systems using ACM in which it has been found that the synchronization occurs at \(t=1.2\) (approx.) as shown in Fig. 6. Hence, in comparison to the above discussed techniques, the synchronization time in our investigated scheme is much lesser which in turn shows the vitality and effectivity of the considered methodology.

7 Conclusion

In this paper, we have investigated the HPCCS scheme among four non-identical HC systems via ACM. The analytical expressions of control inputs and the parameter update laws are obtained in accordance with Lyapunov stability theory. Numerical simulations are demonstrated to check the effectivity and correctness of the theoretical results analysed by using MATLAB. Remarkably, the experimental outcomes and theoretical results are both in excellent compatibility. It is noticed that numerous synchronization schemes, viz., chaos control problem, combination synchronization, projective synchronization, etc. become the particular cases of C–C synchronization. In our study, the synchronization error takes less time to converge to zero which implies that our proposed scheme is more preferred over earlier published work. The considered synchronization scheme may be used in secure communications and information processing with several applications in biological, social and physical systems.