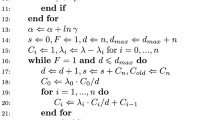EM estimation for bivariate mixed poisson INAR(1) claim count regression models with correlated random effects

Abstract

This article considers bivariate mixed Poisson INAR(1) regression models with correlated random effects for modelling correlations of different signs and magnitude among time series of different types of claim counts. This is the first time that the proposed family of INAR(1) models is used in a statistical or actuarial context. For expository purposes, the bivariate mixed Poisson INAR(1) claim count regression models with correlated Lognormal and Gamma random effects paired via a Gaussian copula are presented as competitive alternatives to the classical bivariate Negative Binomial INAR(1) claim count regression model which only allows for positive dependence between the time series of claim count responses. Our main achievement is that we develop novel alternative Expectation-Maximization type algorithms for maximum likelihood estimation of the parameters of the models which are demonstrated to perform satisfactory when the models are fitted to Local Government Property Insurance Fund data from the state of Wisconsin.

1 Introduction

Over the past decade, there has been a growing literature on bivariate (and/or multivariate) claim count regression models which can efficiently capture the dependence between claims from the same policy and/or different coverages bundled into a single policy. The interested reader is referred to Refs. [1,2,3,4,5,6,7, 9, 11, 13, 15, 23,24,25, 28, 29], among many others.

Pechon et al. [23] proposed the use of bivariate mixed Poisson count regression models, with correlated random effects for capturing the interactions between the different coverages purchased by members of the same household. In particular, Pechon et al. [23] considered the bivariate Poisson-Gamma (BPGGA) regression model with Gaussian copula and the bivariate Poisson-Lognormal (BPLN) regression model. In the former model the random effects are distributed according to two Gamma distributions with unit means and the dependence between the random effects is introduced by means of a Gaussian bivariate copula whereas in the latter model these random effects are distributed according to the bivariate Lognormal mixing distribution. Bermúdez et al. [4], following the setup of Pedeli and Karlis ([26] and [27]), were the first to derive a bivariate Poisson integer-valued autoregressive process of order 1 (BINAR(1)) claim count regression model which can account both for cross-sectional and temporal dependence between multiple claim types. The model they developed was employed for addressing the ratemaking problem of pricing an insurance contract in the case of positively correlated claims from different types of coverage in non-life insurance. Finally, Bermúdez and Karlis [5] built on the previous paper by using a multivariate INAR(1) (MINAR(1)) regression model based on the Sarmanov family of distributions. The MINAR(1) regression models based on the Sarmanov family of distributions are also restricted to a positive correlation structure between the claim count response variables. However, it enjoys some advantages compared to a different approach which can allow for both positive and negative correlations by using copulas for the specification of the joint distribution of the innovations. See, for instance, Refs. [8, 17, 18, 20,21,22] among others. Firstly, it avoids identifiability issues which may arise when a continuous copula distribution is paired with discrete marginals, see Ref. [12]. As is well known, the lack of identifiability means that it cannot be guaranteed that model fitting is unique and this may lead to problems in statistical inference, for example, one might receive no meaningful values for the standard errors of the parameters. Secondly, the computational intensity for discrete copula-based models increases as the dimension of the model increases and hence, as is also mentioned by the authors, their approach, which relies on the use of the Sarmanov family, provides models that are less computationally intensive to estimate and can still have a reasonable range for positive dependence structure between the claim count responses.

In this study, we introduce a family of bivariate mixed Poisson INAR(1) claim count regression models with correlated random effects for modelling the dependence structure between times series of different types of claim counts from the same and/or different types of coverage. The bivariate mixed Poisson INAR(1) regression models with correlated random effects are a broad class of models which can accommodate overdispersion, which is a direct consequence of unobserved heterogeneity due to systematic effects in the data, and correlations of different signs and magnitude. For demonstration purposes, we consider the bivariate mixed Poisson INAR(1) claim count regression models which are derived by using the bivariate Lognormal and Gaussian copula paired with gamma marginals as mixing densities, which we refer to as BINAR(1)-LN and BINAR(1)-GGA claim count regression models respectively. Both models can be regarded as extensions of the classical bivariate Negative Binomial INAR(1) claim count regression model with a shared gamma random effect, which we refer to as BINAR(1)-GA claim count regression model, in the sense that they provide more flexibility for modelling overdispersed bivariate time series of count data compared to the BINAR(1)-GA model which is derived by pre-imposing the restrictive positive correlation assumption between time series of different claim types of claim counts, since in some cases negative correlations may be of interest as well. Furthermore, unlike previous copula-based count regression models for which identifiability issues can arise when a continuous copula distribution is paired with discrete marginals, in the proposed family of models identifiability of the bivariate distribution of the innovations is guaranteed by imposing a unit mean constraint for the Gamma continuous mixing densities which are paired with a Gaussian copula.

The main contributions we make are as follows:

• Firstly, before we introduce the time series components, we present a unified framework for statistical inference via the Expectation-Maximization (EM) algorithm for the BPGA, BPLN and BPGGA regression models.¹

• Secondly, we develop novel EM type algorithms for maximum likelihood (ML) estimation of the BINAR(1)-GA, BINAR(1)-LN and BINAR(1)-GGA regression models, which has not been explored in the literature so far. The main reason for this is because the joint distribution of the innovations cannot be written in closed form in either model and hence its maximization is not possible via standard numerical optimization as is done in Refs. [4, 5, 17, 26, 27].

The rest of the paper is organized as follows. Section 2 presents the model specifications for the bivariate mixed Poisson regression models we consider and describes their ML estimation via the EM algorithm. Section 3 presents the derivation of their INAR(1) extensions that we first proposed herein and outlines the EM type algorithms we developed for statistical inference. Section 4 presents our empirical analysis which is based on the LGPIF dataset. Concluding remarks are given in Sect. 5. The interpretation of abbreviations used in the paper and some other technical details are provided in Appendix A.1.

2 The bivariate mixed Poisson regression model

2.1 Model specifications

The bivariate Poisson mixture is constructed by two independent Poisson random variables conditional on a random effect vector (or scalar) $\varvec{\theta } = (\theta _1, \theta _2)$ such that $N^{(i)} \sim Pois(\lambda _{i,t} \theta _i), \ i = 1,2$. The bivariate mixed Poisson regression is then constructed by further allowing the rate $\lambda _i$ to be modelled as functions of explanatory variables $\textbf{z}_{i,t}$ such that $\lambda _{i,t} = \exp \{ \textbf{z}_{i,t}^T \varvec{\beta }_i\}$. Denote the mixing density function of the random effect as $f_{\varvec{\phi }}(\varvec{\theta })$ parametrized by $\varvec{\phi }$. To avoid the identifiability issue, we have to restrict the expectation $\mathbb {E}[\theta _i]$ to be a fixed constant. One usually lets $\mathbb {E}[\theta _i] = 1$ so that $\varvec{\lambda }_t:= (\lambda _{1,t},\lambda _{2,t})$ will fully explain the frequency of a event and $\varvec{\phi }$ will explain the variation and correlation of the whole bivariate sequence. In the following, we will discuss three different mixing densities, univariate gamma (shared random effect), bivariate Lognormal and Gaussian copula paired with Gamma marginals.

• (a) Univariate Gamma density

  In this case, the bivariate mixed Poisson regression model shares the same random effect $N^{(i)}_t \sim Pois(\lambda _{i,t} \theta ) \ i = 1,2$. Denote the mixing density function as $f_{\phi }(\theta ) = f_{\varvec{\phi }}(\varvec{\theta })$ and it has following expression

  $$\begin{aligned} f_{\phi }(\theta ) = \frac{\phi ^{\phi }}{\Gamma (\phi )} \theta ^{\phi -1} e^{-\phi \theta }, \end{aligned}$$

  (1)

  which has unit mean and variance $\frac{1}{\phi }$. Then the unconditional probability mass function $f_{PG}(\textbf{k},t)$ of $\textbf{N}_t:= (N_t^{(1)}, N^{(2)}_t)$ can be written down in a closed form

  $$\begin{aligned} \begin{aligned} f_{PG}(\textbf{k},t)&= \frac{\lambda _{1,t}}{k_1!} \frac{\lambda _{2,t}}{k_2!} \int _0^{\infty } e^{-(\lambda _{1,t} + \lambda _{2,t})\theta } \theta ^{k_1 + k_2} f_{\phi }(\theta ) d \theta \\&= \frac{\Gamma (\phi + k_1 + k_2)}{\Gamma (\phi ) \Gamma (k_1 + 1) \Gamma (k_2 + 1)} \frac{\phi ^{\phi }\lambda _{1,t}^{k_1} \lambda _{2,t}^{k_2}}{(\phi + \lambda _{1,t} + \lambda _{2,t})^{\phi + k_1 + k_2}}. \end{aligned} \end{aligned}$$

  (2)

• (b) Bivariate Lognormal density

  Suppose now the random vector $\varvec{\epsilon } = (\epsilon _1, \epsilon _2)$ follows bivariate normal distribution, with mean vector $(-\frac{\phi _1^2}{2}, -\frac{\phi _2^2}{2})$ and covariance matrix $\Sigma$

  $$\begin{aligned} \Sigma = \begin{bmatrix} \phi _1^2 &{} \rho \phi _1 \phi _2 \\ \rho \phi _1 \phi _2 &{} \phi _2^2 \end{bmatrix} \end{aligned}$$

  (3)

  Then the random effect vector $\varvec{\theta } = e^{\varvec{\epsilon }} = (e^{\epsilon _1}, e^{\epsilon _2})$ has Lognormal distribution with unit mean. Denote the density function of $\varvec{\epsilon }$ as $f^N_{\Sigma }$ and $f^{LN}_{\Sigma }$ for Lognormal density. Then they have the following expressions

  $$\begin{aligned} f^N_{\Sigma } (\varvec{\epsilon }){} & {} = \frac{1}{2\pi \sigma _1\sigma _2 \sqrt{1-\rho ^2}} \\{} & {} \quad \times \exp \left\{ -\frac{1}{2(1-\rho ^2)} \left[ \left( \frac{\epsilon _1 + 0.5 \sigma _1^2}{\sigma _1} \right) ^2 \right. \right. \\{} & {} \quad \left. \left. - 2\rho \left( \frac{\epsilon _1 + 0.5 \sigma _1^2}{\sigma _1} \right) \left( \frac{\epsilon _2 + 0.5 \sigma _2^2}{\sigma _2} \right) \right. \right. \\{} & {} \quad \left. \left. + \left( \frac{\epsilon _2 + 0.5 \sigma _2^2}{\sigma _2} \right) ^2 \right] \right\} \\ f_{\varvec{\phi }}(\varvec{\theta })= & {} \frac{1}{\theta _1\theta _2} f^N_{\Sigma } (\log \varvec{\theta }) = f^{LN}_{\Sigma } (\varvec{\theta }). \end{aligned}$$

  The unconditional distribution $f_{PLN}(\textbf{k}, t)$ of $\textbf{N}_t$ is expressed as a double integral

  $$\begin{aligned} f_{PLN}(\textbf{k},t){} & {} = \int _{0}^{\infty } \int _{0}^{\infty } \frac{\lambda _{1,t}^{k_1}}{k_1!}\frac{\lambda _{2,t}^{k_2}}{k_2!} e^{-\lambda _{1,t} \theta _1} e^{-\lambda _{2,t} \theta _2} \theta _1^{k_1} \theta _2^{k_2}f^{LN}_{\Sigma }(\varvec{\theta }) d\theta _1 d\theta _2\nonumber \\{} & {} =\int _{R} \int _{R}\frac{\lambda _{1,t}^{k_1}}{k_1!}\frac{\lambda _{2,t}^{k_2}}{k_2!} \exp \{-\lambda _{1,t} e^{\epsilon _1} -\lambda _{2,t} e^{\epsilon _2} + k_1\epsilon _1 + k_2\epsilon _2 \}\nonumber \\{} & {} \qquad f^{N}_{\Sigma }(\varvec{\epsilon })d\epsilon _1 d\epsilon _2. \end{aligned}$$

  (4)

  All the double integrals with respect to Lognormal density $f^{LN}_{\Sigma }$ can be transformed into double integrals with respect to normal density $f^{N}_{\Sigma }$ so that they can be evaluated by Gauss-Hermite quadrature. See details in the Appendix A.2.

• (c) Gaussian copula paired with Gamma marginals

  Suppose now the random vector $\varvec{\theta }$ is distributed as a meta Gaussian copula such that its marginals are two independent Gamma random variables with parameter $(\phi _1,\phi _2)$ respectively. Define uniform random vector $\textbf{u} = (F_{\phi _1}(\theta _1), F_{\phi _2}(\theta _2))$. The distribution function $F_{GC}(\varvec{\theta })$ and density function $f_{GC}(\varvec{\theta })$ can be written as

  $$\begin{aligned} \begin{aligned} F_{GC}(\varvec{\theta })&= C_{\rho }(\textbf{u}) = F_{\rho }(\Phi ^{-1}(u_1), \Phi ^{-1}(u_2)) \\ f_{\varvec{\phi }}(\varvec{\theta })&= f_{GC}(\varvec{\theta }) = \frac{f_{\rho }(\Phi ^{-1}(u_1), \Phi ^{-1}(u_2))}{ f_{sn}(\Phi ^{-1}(u_1)) f_{sn}(\Phi ^{-1}(u_1)) } f_{\phi _1}(\theta _1) f_{\phi _2}(\theta _2) \\&:= c_{\rho }(\textbf{u}) f_{\phi _1}(\theta _1) f_{\phi _2}(\theta _2), \end{aligned} \end{aligned}$$

  (5)

  where $f_{\rho }(.,. ), F_{\rho }(.,.)$ are the density function and cumulative distribution of bivariate normal random variable with the following expression

  $$\begin{aligned} f_{\rho }(x_1,x_2) = \frac{1}{2\pi \sqrt{1-\rho ^2}} \exp \left\{ -\frac{1}{2} \frac{x_1^2 - 2\rho x_1 x_2 + x_2^2}{1-\rho ^2} \right\} . \end{aligned}$$

  (6)

  The $\Phi (x)$ is the cdf of standard normal random variable with $\Phi ^{-1}(x)$ as its quantile function and $f_{sn}(x)$ is the density function of the standard normal random variable. Finally, $f_{\phi _i}(x)$ and $F_{\phi _i}(x)$ are the pdf and cdf of Gamma density function defined in 1 for $i = 1,2$. Then a bivariate Poisson Gamma random vector is constructed as $N_t^{(i)} \sim Pois(\lambda _{i,t} \theta _i), i=1,2$ with probability mass function $f_{PGC}(\textbf{k},t)$ such that

  $$\begin{aligned} f_{PGC}(\textbf{k},t){} & {} {=} \frac{\lambda _{1,t}^{k_1}}{k_1 !} \frac{\lambda _{2,t}^{k_2}}{k_2 !} \int _{0}^{\infty }\int _{0}^{\infty } \exp \{{-}\lambda _{1,t} \theta _1 {-} \lambda _{2,t}\theta _2 \} \theta _1^{k_1} \theta _2^{k_2} f_{GC}(\theta _1,\theta _2) d\theta _1 d\theta _2 \nonumber \\{} & {} = \frac{\lambda _{1,t}^{k_1}}{k_1 !} \frac{\lambda _{2,t}^{k_2}}{k_2 !} \int _{0}^{1}\int _{0}^{1} e^{-\lambda _{1,t} F^{-1}_{\phi _1}(u_1) - \lambda _{2,t} F^{-1}_{\phi _2}(u_2)} \nonumber \\{} & {} \qquad F^{-1}_{\phi _1}(u_1)^{k_1} F^{-1}_{\phi _2}(u_2)^{k_2} c_{\rho }(u_1,u_2) d u_1 d u_2. \end{aligned}$$

  Then the double integral can be evaluated by Gauss-Legendre quadrature. See details in Appendix A.3.

2.2 The EM algorithm

For statistical inference of above model, the classical maximum likelihood estimation is not straightforward to apply because the log likelihood function

$$\begin{aligned} \begin{aligned} \ell (\Theta ) = \sum _{t=1}^n \log \left( \frac{\lambda _{1,t}^{k_{1,t}} \lambda _{2,t}^{k_{2,t}} }{ k_{1,t}! k_{2,t}! } \int _{0}^{\infty } \int _{0}^{\infty } \theta _{1}^{k_{1,t}} \theta _{2}^{k_{2,t}} e^{-\lambda _{1,t}\theta _{1} - \lambda _{2,t} \theta _2 } f_{\varvec{\phi }}(\varvec{\theta }) d\theta _1 d\theta _2 \right) \end{aligned} \end{aligned}$$

(7)

is not computational tractable and its maximum likelihood estimators are not straightforward to achieve. Alternatively, we can apply the EM algorithm to estimate the parameters $\Theta = \{\varvec{\beta }_1, \varvec{\beta }_2, \varvec{\phi } \}$. For given random samples ($\textbf{k}_1,... \textbf{k}_n$), suppose now we observe the random effect $(\varvec{\theta }_1,\dots ,\varvec{\theta }_n)$, then the complete likelihood function $\ell _c(\Theta )$ is given by

$$\begin{aligned} \ell _c(\Theta ) = \sum _{t=1}^n \left[ \left( \sum _{i=1}^2 k_{i,t} log(\lambda _{i,t} \theta _{i,t}) - \lambda _{i,t} \theta _{i,t} - \log (k_{i,t}!)\right) + \log f_{\varvec{\phi }}(\varvec{\theta }_t) \right] . \end{aligned}$$

(8)

Compared to $\ell (\Theta )$, the complete log likelihood function $\ell _c(\Theta )$ are simplified in the sense that there is no integration and mixture likelihood are decomposed into Poisson likelihood and the likelihood for mixing density.

However, to evaluate $\ell _c(\Theta )$ we need to find out the conditional (posterior) distribution of $\varvec{\theta }$ given the random samples. Then we define $\eta (\varvec{\theta } \vert \varvec{\lambda }_t,\varvec{\textbf{k}}_t) = e^{-\lambda _{1,t} \theta _{1}- \lambda _{2,t} \theta _{2}} \theta _1^{k_{1,t}} \theta _2^{k_{2,t}}$ and posterior density

$$\begin{aligned} \begin{aligned} \pi (\varvec{\theta } \vert \Theta ^{(j)}, \textbf{k}_t)&= \frac{f_{\varvec{\phi }}(\varvec{\theta }) \prod _{i=1}^2 f_{Po}(k_{i,t} \vert \lambda _{i,t} \theta _i) }{\int _{0}^{\infty } \int _{0}^{\infty } f_{\varvec{\phi }}(\varvec{\theta }) \prod _{i=1}^2 f^{(j)}_{Po}(k_{i,t} \vert \lambda _{i,t} \theta _i) d\theta _1 d\theta _2 } \\&= \frac{ \eta (\varvec{\theta } \vert \varvec{\lambda }_t,\varvec{\textbf{k}}_t) f_{\varvec{\phi }}(\varvec{\theta }) }{\int _{0}^{\infty } \int _{0}^{\infty } \eta (\varvec{\theta } \vert \varvec{\lambda }_t,\varvec{\textbf{k}}_t) f_{\varvec{\phi }}(\varvec{\theta }) d\theta _1 d\theta _2 }. \end{aligned} \end{aligned}$$

(9)

Then posterior expectation for any real value function $h(\varvec{\theta })$ is given by

$$\begin{aligned} \begin{aligned} \mathbb {E}[ h(\varvec{\theta }) \vert \Theta ^{(j)}, \textbf{k}_t ]&= \int _{0}^{\infty } \int _{0}^{\infty } h(\varvec{\theta }) \pi (\varvec{\theta } \vert \Theta ^{(j)}, \textbf{k}_t) d\theta _1 d\theta _2 \\&=: \mathbb {E}_{\varvec{\theta },t}^{(j)}[h(\varvec{\theta })], \end{aligned} \end{aligned}$$

(10)

where $f_{Po}(k \vert \lambda ) = \frac{e^{-\lambda }\lambda ^k}{k!}$ is the probability mass function of a Poisson random variable with rate $\lambda$ and the condition $\Theta ^{(j)}$ means that the posterior density function is evaluated with the parameters estimated at j-th iteration. The subscript $\varvec{\theta }$ of $\mathbb {E}_{\varvec{\theta },t}^{(j)}$ means that the expectation is taken with respect to the $\varvec{\theta }$ for t-th observation.

• E-step: Evaluating the Q function $Q(\Theta ;\Theta ^{(j)})$ given the the parameters estimated at j-th iteration

  $$\begin{aligned} \begin{aligned} Q(\Theta ;\Theta ^{(j)})&\propto \sum _{t=1}^n \sum _{i=1}^2 k_{i,t} \log (\lambda _{i,t}) - \lambda _{i,t} \mathbb {E}[\theta _{i} \vert \Theta ^{(j)},\textbf{k}_t] + \sum _{t=1}^n \mathbb {E}[\log f_{\varvec{\phi }}(\varvec{\theta }) \vert \Theta ^{(j)}, \textbf{k}_t ] \\&= \sum _{t=1}^n \sum _{i=1}^2 k_{i,t} \log (\lambda _{i,t}) - \lambda _{i,t} \mathbb {E}^{(j)}_{\varvec{\theta },t}[\theta _{i}] + \sum _{t=1}^n \mathbb {E}^{(j)}_{\varvec{\theta },t}[\log f_{\varvec{\phi }}(\varvec{\theta }) ]. \end{aligned} \end{aligned}$$

  (11)

• M-step: After finding out the Q function, we update the parameters for the next iteration, $\Theta ^{(j+1)}$, which can be achieved by finding the gradient functions g(.) and the Hessian matrix H(.) of Q functions and then apply the Newton-Raphson algorithm to maximize the Q function for the next iteration. The parameters can be updated separately as Poisson part $\varvec{\beta }_1, \varvec{\beta }_2$ and random effect part $\varvec{\phi }$.

  • For the Poisson part

    $$\begin{aligned} \begin{aligned} \varvec{\beta }^{(j+1)}_i&= \varvec{\beta }_i^{(j)} - H^{-1}( \varvec{\beta }^{(j)}_i) g( \varvec{\beta }^{(j)}_i), \quad i = 1,2\\ g(\varvec{\beta }^{(j)}_i)&= \textbf{Z}^T_i \textbf{V}^{(g)}_{i} \quad H( \varvec{\beta }^{(j)}_i) = \textbf{Z}^T_i \textbf{D}^{(H)}_i \textbf{Z}_i \\ \textbf{V}^{(g)}_i&= \left( \left\{ k_{i,t}- \lambda ^{(j)}_{i,t} \mathbb {E}^{(j)}_{\varvec{\theta },t}[\theta _i] \right\} _{t=1,\dots ,n}\right) \\ \textbf{D}^{(H)}_i&= {\textrm{diag}}\left( \left\{ - \lambda ^{(j)}_{i,t} \mathbb {E}^{(j)}_{\varvec{\theta },t}[\theta _i] \right\} _{t = 1,\dots ,n}\right) \end{aligned} \end{aligned}$$

    (12)

  • For the random effect part, we need to derive the first and second order derivatives of $\log f_{\varvec{\phi }}(\varvec{\theta })$ and then the take posterior expectation to construct its gradient functions and Hessian matrix. In the following, we derive the derivatives for those three mixing densities defined in the last session. Different mixing densities will affect the way we calculate the posterior expectation, and in many cases, we have to rely on numerical evaluation. However, some posterior expectations can be simplified to reduce computational cost when implementing the EM algorithm in practice.

• (a) Univariate Gamma density

  This can be regarded as a special case because the posterior density is known in closed form as another univariate Gamma density with different parameters.

  $$\begin{aligned} \theta \vert \Theta ^{(j)}, \textbf{k}_t \sim \text {Gamma}\left( \phi ^{(j)} + k_{1,t} + k_{2,t}, \ \phi ^{(j)} + \lambda ^{(j)}_{1,t} + \lambda ^{(j)}_{2,t} \right) \end{aligned}$$

  (13)

  Then, the posterior expectation when updating $\varvec{\beta }_i$ can be simplified as

  $$\begin{aligned} \mathbb {E}^{(j)}_{\theta ,t}[\theta _1] = \mathbb {E}^{(j)}_{\theta ,t}[\theta _2] = \frac{\phi ^{(j)} + k_{1,t} + k_{2,t}}{\phi ^{(j)} +\lambda ^{(j)}_{1,t} + \lambda ^{(j)}_{2,t} }. \end{aligned}$$

  (14)

  Finally, to update $\phi$

  $$\begin{aligned} \begin{aligned} \phi ^{(j+1)}&= \phi ^{(j)} - \frac{g(\phi ^{(j)})}{h(\phi ^{(j)})},\\ g(\phi ^{(j)})&= n( \log \phi ^{(j)} - \Psi (\phi ^{(j)}) + 1) + \sum _{t=1}^n \left( \mathbb {E}^{(j)}_{\theta ,t}[ \log \theta ] - \mathbb {E}^{(j)}_{\theta ,t}[\theta ] \right) \\ h(\phi ^{(j)})&= n ( (\phi ^{(j)})^{-1} - \Psi ^{'} (\phi ^{(j)} ) ), \end{aligned} \end{aligned}$$

  (15)

  where $\Psi (x) = \frac{\Gamma '(x)}{\Gamma (x)}$ and $\Psi '(x)$ are digamma and trigamma functions respectively. The posterior expectation $\mathbb {E}^{(j)}_{\theta ,t}[ \log \theta ]$ is given by

  $$\begin{aligned} \mathbb {E}^{(j)}_{\theta ,t}[\log \theta ] = \Psi \left( \phi ^{(j)} + k_{1,t} + k_{2,t}\right) - \log \left( \phi ^{(j)} + \lambda ^{(j)}_{1,t} + \lambda ^{(j)}_{2,t} \right) \end{aligned}$$

  (16)

• (b) Bivariate Lognormal density

  In this case, there is no analytic expression for the posterior density. However, it can be transformed in the following way

  $$\begin{aligned} \begin{aligned} \pi (\varvec{\theta } \vert \Theta ^{(j)}, \textbf{k}_t)&= \frac{ \eta (\varvec{\theta } \vert \varvec{\lambda }_t,\varvec{\textbf{k}}_t) f^{LN}_{\Sigma }(\varvec{\theta }) }{\int _{0}^{\infty } \int _{0}^{\infty } \eta (\varvec{\theta } \vert \varvec{\lambda }_t,\varvec{\textbf{k}}_t) f^{LN}_{\Sigma }(\varvec{\theta }) d\theta _1 d\theta _2 } \\&= \frac{ \eta ( e^{\varvec{\epsilon }} \vert \varvec{\lambda }_t,\varvec{\textbf{k}}_t) f^{N}_{\Sigma }(\varvec{\epsilon }) }{\int _{0}^{\infty } \int _{0}^{\infty } \eta (e^{\varvec{\epsilon }} \vert \varvec{\lambda }_t,\varvec{\textbf{k}}_t) f^{N}_{\Sigma }(\varvec{\epsilon }) d \epsilon _1 d \epsilon _2 }\\&=: \pi (\varvec{\epsilon } \vert \Theta ^{(j)}, \textbf{k}_t). \end{aligned} \end{aligned}$$

  (17)

  Then, all posterior expectations with respect to $\varvec{\theta }$ can be transformed into expectations with respect to $\varvec{\epsilon }$ such that $\mathbb {E}^{(j)}_{\varvec{\theta },t}[h(\varvec{\theta })] = \mathbb {E}^{(j)}_{\varvec{\epsilon },t} [h(e^{\varvec{\epsilon }})]$. Under this transformation, all the posterior expectations can be evaluated by Gauss-Hermite quadrature. Furthermore,

  $$\begin{aligned} \mathbb {E}^{(j)}_{\varvec{\theta },t}[\log f^{LN}_{\Sigma }(\varvec{\theta })] = \mathbb {E}^{(j)}_{\varvec{\epsilon },t} [\log f^{N}_{\Sigma }(\varvec{\epsilon }) - \epsilon _1 - \epsilon _2] \propto \mathbb {E}^{(j)}_{\varvec{\epsilon },t} [\log f^{N}_{\Sigma }(\varvec{\epsilon })]. \end{aligned}$$

  To update $\varvec{\phi } = \{\phi _1, \phi _2, \rho \}$,

  $$\begin{aligned} \begin{aligned} \varvec{\phi }^{(j+1)}&= \varvec{\phi }^{(j)} - H^{-1}(\varvec{\phi }^{(j)} ) g(\varvec{\phi }^{(j)})\\ g(\varvec{\phi }^{(j)})_r&= \sum _{t=1}^n \mathbb {E}^{(j)}_{\varvec{\epsilon },t} \left[ \frac{\partial \log f^N_{\Sigma } (\varvec{\epsilon })}{\partial \varvec{\phi }_r}\right] \\ H(\varvec{\phi }^{(j)})_{r,s}&= \sum _{t=1}^n \mathbb {E}^{(j)}_{\varvec{\epsilon },t} \left[ \frac{\partial ^2 \log f^N_{\Sigma } (\varvec{\epsilon })}{\partial \varvec{\phi }_r \partial \varvec{\phi }_s}\right] , \\ \end{aligned} \end{aligned}$$

  (18)

  where the subscript r denotes the r-th element of a vector and r, s denotes r-th row s-th column entry of a matrix. The first and second order derivatives are given by

  $$\begin{aligned}\small \frac{\partial \log f^N_{\Sigma }(\varvec{\epsilon })}{\partial \phi _i}{} & {} = -\frac{1}{1-\rho ^2} \left( -\frac{1}{\phi _i^3} \epsilon _i^2+ \frac{\rho \phi _{3-i}}{2\phi _i^2} \epsilon _i - \frac{\rho }{2\phi _{3-i}} \epsilon _{3-i} + \frac{\rho }{\phi _i^2 \phi _{3-i}} \epsilon _1\epsilon _2\right. \\{} & {} \quad \left. + \frac{\phi _i - \rho \phi _{3-i}}{4}\right) - \frac{1}{\phi _i}\\ \frac{\partial \log f^N_{\Sigma }(\varvec{\epsilon })}{\partial \rho }{} & {} = -\frac{\rho }{(1-\rho ^2)^2} \left( \frac{1}{\phi _1^2} \epsilon _1^2 + \frac{1}{\phi _2^2} \epsilon _2^2 + (1-\frac{\rho \phi _2}{\phi _1}) \epsilon _1 + (1 -\frac{\rho \phi _1}{\phi _2}) \epsilon _2\right. \\{} & {} \quad \left. + \frac{\phi _1^2 + \phi _2^2 }{4} -\frac{\rho \phi _1\phi _2}{2} \right) \\{} & {} \quad + \frac{1}{1-\rho ^2} \left( \frac{\phi _2}{2\phi _1} \epsilon _1 + \frac{\phi _1}{2\phi _2} \epsilon _2 + \frac{1}{\phi _1 \phi _2} \epsilon _1 \epsilon _2 + \frac{\phi _1\phi _2}{4}\right) + \frac{\rho }{1-\rho ^2}\\ \frac{\partial ^2 \log f^N_{\Sigma }(\varvec{\epsilon })}{\partial \phi _i^2}{} & {} = -\frac{1}{1-\rho ^2} \left( \frac{3}{\phi _i^4} \epsilon _i^2 - \frac{\rho \phi _{3-i}}{\phi _i^3} \epsilon _i - \frac{2\rho }{\phi _i^3\phi _{3-i}} \epsilon _1\epsilon _2 + \frac{1}{4} \right) + \frac{1}{\phi _i^2} \\ \frac{\partial ^2 \log f^N_{\Sigma }(\varvec{\epsilon })}{\partial \rho ^2}{} & {} = \frac{1+3\rho ^2}{(1-\rho ^2)^3} \left( \frac{1}{\phi _1^2} \epsilon _1^2 + \frac{1}{\phi _2^2} \epsilon _2^2 + (1- \frac{\rho \phi _2}{\phi _1}) \epsilon _1 + (1-\frac{\rho \phi _1}{\phi _2}) \epsilon _2 \right) \\{} & {} \quad + \frac{1+3\rho ^2}{(1-\rho ^2)^3}\left( - \frac{2\rho }{\phi _1\phi _2} \epsilon _1\epsilon _2 + \frac{\phi _1^2 + \phi _2^2}{4} - \frac{\rho \phi _1\phi _2}{4} \right) \\{} & {} \quad + \frac{4\rho }{(1-\rho ^2)^2} \left( \frac{\phi _2}{2\phi _1} \epsilon _1 + \frac{\phi _1}{\phi _2} \epsilon _2 + \frac{1}{\phi _1\phi _2} \epsilon _1 \epsilon _2 + \frac{\phi _1\phi _2}{4} \right) \\{} & {} \quad + \frac{1+\rho ^2}{(1-\rho ^2)^2} \\ \frac{\partial ^2 \log f^N_{\Sigma }(\varvec{\epsilon })}{\partial \phi _1 \partial \phi _2}{} & {} = \frac{\rho }{1-\rho ^2} \left( -\frac{1}{2\phi _1^2} \epsilon _1 - \frac{1}{2\phi _2^2} \epsilon _2 + \frac{1}{\phi _1^2\phi _2^2} \epsilon _1 \epsilon _2 + \frac{1}{4} \right) \\ \frac{\partial ^2 \log f^N_{\Sigma }(\varvec{\epsilon })}{\partial \rho \partial \phi _i}{} & {} = -\frac{2\rho }{(1-\rho ^2)^2} \left( -\frac{1}{\phi _i^3} \epsilon _i^2 + \frac{\rho \phi _{3-i}}{2\sigma _i^2} \epsilon _i - \frac{\rho }{2\phi _{3-i}} \epsilon _{3-i}\right. \\{} & {} \quad \left. + \frac{\rho }{\phi _i^2 \phi _{3-i}} \epsilon _1 \epsilon _2 + \frac{1}{4}(\phi _i - \rho \phi _{3-i}) \right) \\{} & {} \quad + \frac{1}{1-\rho ^2} \left( -\frac{\phi _{3-i}}{2\phi _i^2} \epsilon _i + \frac{1}{2\phi _{3-i}} \epsilon _{3-i} - \frac{1}{\phi _i^2 \phi _{3-i}} \epsilon _1\epsilon _2 + \frac{\phi _{3-i}}{4} \right) . \end{aligned}$$

  Notice that all the derivatives are in the linear form of $\epsilon _1^2, \epsilon _2^2, \epsilon _1,\epsilon _2, \epsilon _1\epsilon _2$. Hence, we can evaluate these posterior expectations in each iteration once to avoid repeating calculations.

• (c) Gaussian copula paired with Gamma marginals

  In this case, there is no simplification either for the posterior density or for the posterior expectation. To update $\varvec{\phi } = \{\phi _1,\phi _2,\rho \}$, we have almost the same procedure as for the bivariate Lognormal case.

  $$\begin{aligned} \varvec{\phi }^{(j+1)}{} & {} = \varvec{\phi }^{(j)} - H^{-1}(\varvec{\phi }^{(j)} ) g(\varvec{\phi }^{(j)})\nonumber \\ g(\varvec{\phi }^{(j)})_r{} & {} = \sum _{t=1}^n \mathbb {E}^{(j)}_{\varvec{\theta },t} \left[ \frac{\partial \log f_{GC} (\varvec{\theta })}{\partial \varvec{\phi }_r}\right] \nonumber \\ H(\varvec{\phi }^{(j)})_{r,s}{} & {} = \sum _{t=1}^n \mathbb {E}^{(j)}_{\varvec{\theta },t} \left[ \frac{\partial ^2 \log f_{GC} (\varvec{\theta })}{\partial \varvec{\phi }_r \partial \varvec{\phi }_s}\right] , \end{aligned}$$

  (19)

  where the first and second order partial derivatives are given by

  $$\begin{aligned}\small u_i{} & {} = \int _{0}^{\theta _i} \frac{\phi _i^{\phi _i}}{\Gamma (\phi _i)} y^{\phi _i - 1} e^{-\phi _i y} dy\\ \frac{\partial \log f_{GC}(\varvec{\theta } )}{\partial \phi _i }{} & {} = \left( -\frac{\rho ^2}{1-\rho ^2} \frac{\Phi ^{-1}(u_i)}{f_{sn}(\Phi ^{-1}(u_i))} + \frac{\rho }{1-\rho ^2} \frac{\Phi ^{-1}(u_{3-i})}{f_{sn}(\Phi ^{-1}(u_i))} \right) \frac{\partial u_i}{\partial \phi _i} \\ {}{} & {} \quad + 1 + \log (\phi ) - \Psi (\phi ) + \log (\theta ) - \theta \\ \frac{\partial \log f_{GC}(\varvec{\theta } )}{\partial \rho }{} & {} = \frac{\rho }{1-\rho ^2} - \frac{\rho }{(1-\rho ^2)^2} \left( \Phi ^{-1}(u_1) + \Phi ^{-1}(u_2) \right) \\{} & {} \quad + \frac{1 + \rho ^2}{(1-\rho ^2)^2} \Phi ^{-1}(u_1) \Phi ^{-1}(u_2) \end{aligned}$$
  $$\begin{aligned} \frac{\partial ^2 \log f_{GC}(\varvec{\theta } )}{\partial \phi _i^2}{} & {} = \left( -\frac{\rho ^2}{1-\rho ^2} \frac{1 + \Phi ^{-1}(u_i) ^2}{f_{sn}(\Phi ^{-1}(u_i))^2} + \frac{\rho }{1-\rho ^2} \frac{\Phi ^{-1}(u_1) \Phi ^{-1}(u_2)}{f_{sn}(\Phi ^{-1}(u_i))} \right) \\ {}{} & {} \quad \times \left( \frac{\partial u_i}{\partial \phi _i}\right) ^2 + \frac{\partial \log f_{GC}(\varvec{\theta } )}{\partial \phi _i} \frac{\partial ^2 u_i}{\partial \phi _i^2} + \frac{1}{\phi } - \Psi '(\phi _i)\\ \frac{\partial ^2 \log f_{GC}(\varvec{\theta } )}{\partial \rho ^2}{} & {} = \frac{1 + \rho ^2}{(1-\rho ^2)^2} - \frac{1+3\rho ^2}{(1-\rho ^2)^3} \left( \Phi ^{-1}(u_1) + \Phi ^{-1}(u_2) \right) \\{} & {} \quad + \frac{2\rho ^3 + 6\rho }{(1-\rho ^2)^3} \Phi ^{-1}(u_1) \Phi ^{-1}(u_2)\\ \frac{\partial ^2 \log f_{GC}(\varvec{\theta } )}{\partial \phi _1 \partial \phi _2}{} & {} = \frac{\rho }{1-\rho ^2} \frac{\frac{\partial u_1}{\partial \phi _1} \frac{\partial u_2}{\partial \phi _2} }{f_{sn}(\Phi ^{-1}(u_1)) f_{sn}(\Phi ^{-1}(u_2))} \\ \frac{\partial ^2 \log f_{GC}(\varvec{\theta } )}{\partial \rho \partial \phi _i}{} & {} = \left( -\frac{2\rho }{(1-\rho ^2)^2} \frac{\Phi ^{-1}(u_i)}{f_{sn}(\Phi ^{-1}(u_i))} + \frac{1+\rho ^2}{(1-\rho ^2)^2} \frac{\Phi ^{-1}(u_{3-i})}{f_{sn}(\Phi ^{-1}(u_i))} \right) \frac{\partial u_i}{\partial \phi _i}. \end{aligned}$$

3 The bivariate mixed Poisson INAR(1) regression model

3.1 Model specifications

Let $\textbf{X}$ and $\textbf{R}$ be non-negative integer-valued random vectors in $\mathbb {R}^2$. Let $\textbf{P}$ be a diagonal matrix in $\mathbb {R}^{2 \times 2}$ with elements $p_i \in (0,1)$. The bivariate first-order integer-valued autoregressive model (Bivariate INAR(1)) is defined as

$$\begin{aligned} \textbf{X}_t = \textbf{P} \circ \textbf{X}_{t-1} + \textbf{R}_t = \begin{bmatrix} p_1 &{} 0 \\ 0 &{} p_2 \\ \end{bmatrix} \circ \begin{bmatrix} X_{1,t-1}\\ X_{2,t-1} \\ \end{bmatrix} + \begin{bmatrix} R_{1,t}\\ R_{2,t} \\ \end{bmatrix}, \end{aligned}$$

(20)

where the thinning operator $\circ$ is the widely used binomial thinning operator such that $p_i \circ X_{i,t} = \sum _{k=1}^{X_{i,t}} U_k$ and $U_k$ are independent identically distributed Bernoulli random variables with success probability $p_i$, i.e. $\mathcal {P}(U_k = 1) = p_i$. Hence $p_i \circ X_{i,t}$ is binomially distributed with size $X_{i,t}$ and success probability $p_i$. Then the distribution function $f_{p_i}(x, X_{i,t})$ can be easily written down as

$$\begin{aligned} f_{p_i}(k, X_{i,t}) = \left( {\begin{array}{c}X_{i,t}\\ k\end{array}}\right) p_i^k (1 - p_i)^{X_{i,t} - k}. \end{aligned}$$

(21)

Note that $p_i \circ X_{i,t}$ and $p_j \circ X_{j,t}, i \ne j$ are independent of each other. To adapt the heteroscedasticity arising from the data, $\textbf{R}_t$ is bivariate mixed Poisson regression model such that $R_{i,t} \sim Po( \lambda _{i,t}\theta _i)$ defined in the last session. The joint distribution of the bivariate sequence $\textbf{X}_{t+1}$ conditional on the last state $\textbf{X}_t$ is given by

$$\begin{aligned} \begin{aligned} \mathcal {P}( \textbf{X}_{t+1} \vert \textbf{X}_{t})&= \sum _{k_1=0}^{s_{1,t}} \sum _{k_2=0}^{s_{2,t}} f_{p_1}(k_1, X_{1,t}) f_{p_2}(k_2, X_{2,t})f_{\textbf{R}}(X_{1,t+1}-k_1, X_{2,t+1} - k_2) \\ f_{\textbf{R}}(\textbf{k},t)&= \frac{\lambda _{1,t}^{k_1}}{k_1 !} \frac{\lambda _{2,t}^{k_2}}{k_2 !} \int _{0}^{\infty } \int _{0}^{\infty } \eta (\varvec{\theta } \vert \varvec{\lambda }_t, \textbf{k}_t) f_{\varvec{\phi }}(\varvec{\theta }) d\theta _1 d\theta _2 \\ s_{i,t}&= \min \{X_{i,t+1},X_{i,t}\}, \end{aligned} \end{aligned}$$

(22)

where $f_{\textbf{R}}(\textbf{k},t)$ is a probability mass function of a bivariate mixed Poisson regression model with mixing density $f_{\varvec{\phi }}(\varvec{\theta })$. Under this construction, the bivariate sequence $\textbf{X}_t$ is correlated with each other and its correlation structure mainly depends on the correlation structure of innovation $\textbf{R}_t$.

3.2 The EM algorithm

Similarly, the maximum likelihood estimation is not straightforward to apply as the log likelihood function

$$\begin{aligned} \begin{aligned} \ell (\Theta ) {=} \sum _{t{=}1}^n \log \left( \sum _{k_1{=}0}^{s_{1,t}} \sum _{k_2{=}0}^{s_{2,t}} f_{p_1}(k_1, X_{1,t}) f_{p_2}(k_2, X_{2,t})f_{\textbf{R}}(X_{1,t{+}1}{-}k_1, X_{2,t+1} {-} k_2) \right) \end{aligned} \end{aligned}$$

has discrete convolution and double integrals. Then we can use similar techniques to decompose the log likelihood function as we did in Sect. 2.

Given the observed bivariate sequence $\{\textbf{X}_t\}_{t=1,\dots ,n}$. Let $Y_{i,t} = p_i \circ X_{i,t-1}$ and $\Theta = \{p_1,p_2,\varvec{\beta }_1,\varvec{\beta }_2,\varvec{\phi }\}$ be the parameter space for this model. Suppose now we observe the latent variable $\{Y_t\}_{t=1,...n}$, then the log likelihood function becomes

$$\begin{aligned} \begin{aligned} \ell (\Theta \vert \textbf{Y})&\propto \sum _{t=1}^n \sum _{i=1}^2 (Y_{i,t} \log p_i + (X_{i,t} - Y_{i,t}) \log (1-p_i) ) + \sum _{t=1}^n \log f_{\textbf{R}} (\textbf{R}_t,t) \\ R_{i,t}&= X_{i,t} - Y_{i,t}. \end{aligned} \end{aligned}$$

(23)

Notice that there are still unobserved random variables $\varvec{\theta }$ in $R_{t}$. In some of the examples we discuss in the last section, $f_{\textbf{R}}(\textbf{k},t)$ may not have analytic expression and hence we would like to further break down the likelihood function. Suppose further that we observe the random effect $\{ \varvec{\theta }_t \}_{t = 1\dots n}$, then the complete log likelihood becomes

$$\begin{aligned} \begin{aligned} \ell (\Theta \vert \textbf{Y}, \varvec{\theta })&\propto \sum _{t=1}^n \sum _{i=1}^2 (Y_{i,t} \log p_i + (X_{i,t} - Y_{i,t}) \log (1-p_i) ) \\&+ \sum _{t=1}^n \sum _{i=1}^2 ( R_{i,t} \log (\lambda _{i,t}) - \lambda _{i,t}\theta _{i,t} ) + \sum _{t=1}^n \log f_{\varvec{\phi }}(\varvec{\theta }). \end{aligned} \end{aligned}$$

(24)

Define the following posterior density functions

$$\begin{aligned} \begin{aligned} \pi _1 (\varvec{y} \vert \Theta ^{(j)}, \textbf{X}_{t}, \textbf{X}_{t-1})&= \frac{f_{\textbf{R}}(\textbf{X}_{t-1}- \textbf{y}) \prod _{i=1}^2 f_{p_i}(y_i, X_{i,t-1})}{ \mathcal {P}( \textbf{X}_{t} \vert \textbf{X}_{t-1}) } \\ \pi _{2}(\varvec{\theta } \vert \Theta ^{(j)}, \textbf{R}_t )&= \frac{ \eta (\varvec{\theta } \vert \varvec{\lambda }_t, \textbf{R}_t) f_{\varvec{\theta }}(\varvec{\phi }) }{\int _{0}^{\infty } \int _{0}^{\infty } \eta (\varvec{\theta } \vert \varvec{\lambda }_t, \textbf{R}_t) f_{\varvec{\phi }}(\varvec{\theta }) d\theta _1d\theta _2 }, \end{aligned} \end{aligned}$$

(25)

Define the posterior expectations with respect to real-value functions h(., . )

$$\begin{aligned} \begin{aligned} \mathbb {E}^{(j)}_{\varvec{y},t} [h(\varvec{y})]&=\sum _{y_1=0}^{s_{1,t-1}} \sum _{y_2=0}^{s_{2,t-1}} h(\varvec{y}) \pi _1 (\varvec{y} \vert \Theta ^{(j)}, \textbf{X}_{t}, \textbf{X}_{t-1}) \\ \mathbb {E}^{(j)}_{\varvec{\theta },t}[h(\varvec{\theta }) \vert \textbf{R}_t]&= \int _0^{\infty } \int _{0}^{\infty } h(\varvec{\theta }) \pi _{2}(\varvec{\theta } \vert \Theta ^{(j)}, \textbf{R}_t ) d\theta _1 d\theta _2. \end{aligned} \end{aligned}$$

(26)

• E-step: Evaluating the Q function $Q(\Theta ;\Theta ^{(j)})$ given the the parameters estimated in the j-th iteration,

  $$\begin{aligned} \begin{aligned} Q(\Theta ; \Theta ^{(j)})&= \sum _{t=1}^n \sum _{i=1}^2 ( y^{(j)}_{i,t} \log p_i + (X_{i,t-1} - y^{(j)}_{i,t}) \log (1-p_i) ) \\&\quad + \sum _{t=1}^n \sum _{i=1}^2 ( r^{(j)}_{i,t} \log (\lambda _{i,t}) - \lambda _{i,t} \hat{\theta }^{(j)}_{i,t} ) + \sum _{t=1}^n \mathbb {E}^{(j)}_{\varvec{y},t}[ \mathbb {E}^{(j)}_{\varvec{\theta },t}[ \log f_{\varvec{\phi }}(\varvec{\theta }) \vert \textbf{R}_t] ] \\ y^{(j)}_{i,t}&= \mathbb {E}^{(j)}_{\varvec{y},t} [Y_{i}], \quad r^{(j)}_{i,t} = X_{i,t} - y^{(j)}_{i,t}, \quad \hat{\theta }^{(j)}_{i,t} = \mathbb {E}^{(j)}_{\varvec{y},t}[\mathbb {E}^{(j)}_{\varvec{\theta },t} [\theta _{i} \vert \textbf{R}_t ] ]. \\ \end{aligned} \end{aligned}$$

  (27)

  After breaking down the log likelihood function, it is obvious that except for the log likelihood contributed by binomial distribution, the rest of the terms are almost the same as that of the Q-function of bivariate mixed Poisson regression model discussed in the last session, which means the updating procedure for $\varvec{\beta }_i, \varvec{\phi }$ will be exactly the same, but we need to evaluate different posterior expectations in this case.

• M-step: Similarly, we apply the Newton–Raphson algorithm to update the parameters. Based on the structure of $Q(\Theta ; \Theta ^{(j)})$, the parameters can be updated separately for binomial part $\varvec{p}$, Poisson part $\varvec{\beta }_i$ and random effect part $\varvec{\phi }$

  • The binomial part can be updated simply as the following gradient function has a unique solution

    $$\begin{aligned} \begin{aligned} g(p_i)&= \frac{\sum _{t=1}^n y^{(j)}_{i,t}}{p_i} - \frac{\sum _{t=1}^n (X_{i,t-1} - y^{(j)}_{i,t})}{1-p_i} = 0\\ p_i^{(j+1)}&= \frac{\sum _{t=1}^n y^{(j)}_{i,t}}{\sum _{t=1}^n X_{i,t-1}}, \quad i = 1, 2 \\ y^{(j)}_{i,t}&= {\left\{ \begin{array}{ll} \frac{p_i^{(j)} X_{i,t-1} \mathcal {P}(\textbf{X}_{t} - \textbf{1}_i \vert \textbf{X}_{t-1} - \textbf{1}_i ) }{\mathcal {P}(\textbf{X}_t \vert \textbf{X}_{t-1})}, &{}\quad X_{i,t} \ne 0 \ and \ X_{i,t-1} \ne 0 \\ 0 , &{}\quad otherwise \end{array}\right. } \\ \textbf{1}_1&= (1 , 0)^T \quad \textbf{1}_2 = (0, 1)^T. \end{aligned} \end{aligned}$$

    (28)

    See Appendix A.4 for the derivation of $y^{(j)}_{i,t}$.

  • For the Poisson part, the updating equations are the same with different posterior expectation

    $$\begin{aligned} \begin{aligned} \varvec{\beta }^{(j+1)}_i&= \varvec{\beta }_i^{(j)} - H^{-1}( \varvec{\beta }^{(j)}_i) g( \varvec{\beta }^{(j)}_i), \quad i = 1,2\\ g(\varvec{\beta }^{(j)}_i)&= \textbf{Z}^T_i \textbf{V}^{(g)}_{i} \quad H( \varvec{\beta }^{(j)}_i) = \textbf{Z}^T_i \textbf{D}^{(H)}_i \textbf{Z}_i \\ \textbf{V}^{(g)}_i&= \left( \left\{ k_{i,t}- \lambda ^{(j)}_{i,t} \hat{\theta }^{(j)}_{i,t} \right\} _{t=1,\dots ,n}\right) \\ \textbf{D}^{(H)}_i&= {\textrm{diag}}\left( \left\{ - \lambda ^{(j)}_{i,t} \hat{\theta }^{(j)}_{i,t} \right\} _{t = 1,\dots ,n}\right) . \end{aligned} \end{aligned}$$

    (29)

    Note that when the mixing density $f_{\varvec{\phi }}(\varvec{\theta })$ is univariate Gamma, the posterior expectation for $\varvec{\theta }$ has a simple expression

    $$\begin{aligned} \hat{\theta }^{(j)}_t = \hat{\theta }^{(j)}_{1,t} = \hat{\theta }^{(j)}_{2,t} = \frac{\phi ^{(j)} + r^{(j)}_{1,t} + r^{(j)}_{2,t}}{\phi ^{(j)} + \lambda ^{(j)}_{1,t} + \lambda ^{(j)}_{2,t}}. \end{aligned}$$

  • Similarly, for the random effect part $\varvec{\phi }$,

• (a) Univariate Gamma density

  $$\begin{aligned} \begin{aligned} \phi ^{(j+1)}&= \phi ^{(j)} - \frac{g(\phi ^{(j)})}{h(\phi ^{(j)})},\\ g(\phi ^{(j)})&= n( \log \phi ^{(j)} - \Psi (\phi ^{(j)}) + 1) + \sum _{t=1}^n \left( \mathbb {E}^{(j)}_{\varvec{y},t}[ \mathbb {E}^{(j)}_{\theta ,t}[ \log \theta \vert \textbf{R}_t] ] - \hat{\theta }^{(j)}_t \right) \\ h(\phi ^{(j)})&= n ( (\phi ^{(j)})^{-1} - \Psi ^{'} (\phi ^{(j)} ) ), \end{aligned} \end{aligned}$$

  (30)

• (b) Bivariate Lognormal

  $$\begin{aligned} \begin{aligned} \varvec{\phi }^{(j+1)}&= \varvec{\phi }^{(j)} - H^{-1}(\varvec{\phi }^{(j)} ) g(\varvec{\phi }^{(j)})\\ g(\varvec{\phi }^{(j)})_r&= \sum _{t=1}^n \mathbb {E}^{(j)}_{\varvec{y},t}\left[ \mathbb {E}^{(j)}_{\varvec{\epsilon },t} \left[ \frac{\partial \log f^N_{\Sigma } (\varvec{\epsilon })}{\partial \varvec{\phi }_r} \vert \textbf{R}_t \right] \right] \\ H(\varvec{\phi }^{(j)})_{r,s}&= \sum _{t=1}^n \mathbb {E}^{(j)}_{\varvec{y},t}\left[ \mathbb {E}^{(j)}_{\varvec{\epsilon },t} \left[ \frac{\partial ^2 \log f^N_{\Sigma } (\varvec{\epsilon })}{\partial \varvec{\phi }_r \partial \varvec{\phi }_s} \vert \textbf{R}_t \right] \right] , \\ \end{aligned} \end{aligned}$$

  (31)

• (c) Gaussian copula paired with Gamma marginals

  $$\begin{aligned} \begin{aligned} \varvec{\phi }^{(j+1)}&= \varvec{\phi }^{(j)} - H^{-1}(\varvec{\phi }^{(j)} ) g(\varvec{\phi }^{(j)})\\ g(\varvec{\phi }^{(j)})_r&= \sum _{t=1}^n \mathbb {E}^{(j)}_{\varvec{y},t} \left[ \mathbb {E}^{(j)}_{\varvec{\theta },t} \left[ \frac{\partial \log f_{GC} (\varvec{\theta })}{\partial \varvec{\phi }_r} \vert \textbf{R}_t \right] \right] \\ H(\varvec{\phi }^{(j)})_{r,s}&= \sum _{t=1}^n\mathbb {E}^{(j)}_{\varvec{y},t} \left[ \mathbb {E}^{(j)}_{\varvec{\theta },t} \left[ \frac{\partial ^2 \log f_{GC} (\varvec{\theta })}{\partial \varvec{\phi }_r \partial \varvec{\phi }_s} \vert \textbf{R}_t \right] \right] . \end{aligned} \end{aligned}$$

  (32)

  The partial derivatives inside expectations are derived in the last section.

Remark

This model as well as the EM algorithm can be extent to multivariate case straightforwardly. All the steps and the general form of the formula of the EM algorithm in the multivariate case are exactly the same. The only problem is that it would become cumbersome to evaluate the transition probability $\mathcal {P}(\textbf{X}_t \vert \textbf{X}_{t-1})$ as dimension of $\textbf{X}_t$ increases.

4 Empirical analysis

4.1 Data description and model fitting

The data used in this section come from the Local Government Property Insurance Fund (LGPIF) from the state of Wisconsin. On previous application on this dataset, interested reader can refer to Refs. [28,29,30]. This fund provides property insurance to different types of government units, which includes villages, cities, counties, towns and schools. The LGPIF contains three major groups of property insurance coverage, namely building and contents (BC), contractors’ equipment (IM) and motor vehicles (PN, PO, CN, CO). For exploratory purposes, we focus on modelling jointly the claim frequency of IM, denoted as $X_{1}$, and comprehensive new vehicles collision (CN), denoted as $X_{2}$ as they are both related to land transport. The insurance data cover the period over 2006–2010 with 1234 policyholders in total. Only $n_1= 1048$ of them have complete data over the period 2006–2010, which will be the training dataset. The last year 2011 with $n_2 = 1025$ policyholders, which is the same set of policyholders as in the training dataset, out of 1098 policyholders will be the test dataset. Denote the IM type and CN type claim frequency for a particular policyholder as $X^{(h)}_{1,t}, X^{(h)}_{2,t}$ respectively, where h is the identifier for each policyholder and t is the year. Then the relationship between $X_{i,t}$ and $X^{(h)}_{i,t}$ is simply $X_{i,t} = \sum _{h} X^{(h)}_{i,t}$ with $i = 1,2$.

Some basic statistical analysis is shown in the following Table 1 and Fig. 1. The proportion of zeros for two types of claims are all over 90% during 2006–2010. Both types of claim shows overdispersion as the variance are all higher than their mean over years and the overdispersion for $X_{2,t}$ is even stronger than that of $X_{1,t}$, which indicate the need to apply overdispersed distribution model for the data. The correlation tests over years imply that it is reasonable to introduce correlation structure between $X_{1,t}$ and $X_{2,t}$. The proportion of zeros and kurtosis show that the marginal distributions of $X_{1,t}, X_{2,t}$ are all positively skewed and exhibit a fat-tailed structure which indicates the appropriateness of adopting a positive skewed and fat-tailed distribution (Log Normal distribution). Last but not least, the correlation tests illustrated in Table 2 do support the appropriateness of introduction of time series term in modelling the claim sequence.

Table 1 Summary statistics of two types of claims over years

Table 2 Correlation test for $X_{i,t}$ and $X_{i,t-1}$

Fig. 1

Summary statistics (mean, variance and correlation) for each type of claims across all the policyholders over the years

The description and some summary statistics for all the explanatory variables (covariates $z_{1,t}, z_{2,t}$) that are relevant to $X_{1,t}, X_{2,t}$ are shown in Table 3. Variables 1–5 including ‘TypeVillage’ are categorical variables to indicate the entity types of a policyholder. Due to the strongly heavy-tailed structure appearing in variables 6 and 9, which can drastically distort the model fitting, those variables are transformed by means of the ‘rank’ function in R software and then standardized, which can mitigate the effect of outliers. Variables 6–8 are relevant to IM claim $X_{1,t}$, while variables 9,10 provide information for CN claims $X_{2,t}$. The covariate $z_{1,t}$ includes variables 1-8, and $z_{2,t}$ contains variables 1-5 and variables 9,10. These covariates act as the regression part for $\lambda _{i,t}$ mentioned in Sect. 2, which may help to explain part of the heterogeneity within $X_{1,t}$ and $X_{2,t}$.

Table 3 Summary statistics for the explanatory variables

Due to the large computational cost for evaluating the partial derivatives of copula case (large sample size), all the models except the copula case discussed in Sects. 2 and 3 are applied to model the joint behaviour of $X^{(h)}_{1,t}, X^{(h)}_{2,t}$ across all the policyholders. Instead, a simulation study in the Appendix A.5 shows that the EM algorithm does work for copula case.

Since we would like to model the whole behaviour rather than the individual one, the the likelihood function would simply become

$$\begin{aligned} \ell (\Theta ) = \sum _{h=1}^{n_1} \ell _h(\Theta ) = \sum _{h=1}^{n_1} \sum _{t=1}^4 \log \Pr ( X^{(h)}_{1,t+1}, X^{(h)}_{2,t+1} \vert X^{(h)}_{1,t}, X^{(h)}_{2,t}), \end{aligned}$$

(33)

where $\ell _h(\Theta )$ is the log likelihood function for policyholder h. Note that all the policyholders with the same type of claim $X_{i, }$ will share the same set of parameters $\{p_1,p_2,\varvec{\beta }_1,\varvec{\beta }_2, \varvec{\phi }\}$. In addition, it is necessary to show the appropriateness of introducing crosscorrelation and autocorrelation in BINAR(1) model. Then we also fit the data to following models.

• 1. The joint distribution of $X^{(h)}_{1,t}$ and $X^{(h)}_{2,t}$ are characterized by two independent mixed Poisson (TMP)

  $$\begin{aligned} X^{(h)}_1 \sim Pois(\lambda _1\theta _1), \quad X^{(h)}_2 \sim Pois(\lambda _2\theta _2), \end{aligned}$$

  (34)

  where $\theta _1$ and $\theta _2$ are independent random variables, either Gamma or Log Normal.

• 2. The joint distribution of $X^{(h)}_{1,t}$ and $X^{(h)}_{2,t}$ are assumed to be bivariate mixed Poisson distribution (BMP) with different probability mass function according to the choice of mixing densities, see equations (2) and (4).

• 3. The joint distribution of $X^{(h)}_{1,t}$ and $X^{(h)}_{2,t}$ are characterized by two independent INAR(1) models (TINAR)

  $$\begin{aligned} \begin{aligned} X^{(h)}_{1,t}&= p_1 \circ X^{(h)}_{1,t-1} + R_{1,t} \\ X^{(h)}_{2,t}&= p_2 \circ X^{(h)}_{2,t-1} + R_{2,t}, \end{aligned} \end{aligned}$$

  where $R_{i,t} \sim Pois(\lambda _{i,t} \theta _{i,t}), i=1,2$ and random effect $\theta _{i,t}$ is independent of i and t.

For comparison purpose, we fit these univariate and bivariate Poisson mixture models with training dataset starting from 2007 because they do not need to consider the lag responses. When it comes to the initial values, we use the following. Lag one correlation of each sequence serves as the initial value of $p_i$. We fit a Poisson generalized linear model for each sequence to obtain the initial values of $\varvec{\beta }_i$. Finally, we used the moment estimates of the bivariate Poisson mixture model (without regression) for initial values of $\varvec{\phi } = \{\phi _1, \phi _2, \rho \}$. All the estimation is performed in R software where we implement the EM algorithms derived in previous sections. The standard deviations of the estimators are calculated by inverting the observed information of matrix from the incomplete log-likelihood function (the log likelihood function without unobserved latent variables).

Model fitting results are shown in Table 4. Within the same class of models, compared to univariate Gamma as mixing density, the Log Normal case allows more flexible structures to capture different distributional behaviour within two types of claims. Hence we can observe the improvement of AIC from univariate Gamma case to Log Normal case and hence it is no surprise that the Log Normal is always the best choice within the same class of model. Among different classes of models, it is clear that the adoption of autocorrelation component significantly improves the model fitting. Finally, the significant improvement in terms of AIC from TINAR to BINAR, as well as from TMP to BMP, indicates that it is appropriate to introduce cross correlation between two sequences $X_1, X_2$. The estimated parameters via EM algorithm are shown in Table 5.

Table 4 Goodness of fit for different models with different choices of mixing densities

Table 5 Parameter estimation for the Bivariate mixed Poisson regression model and the bivariate INAR model of insurance claim frequency data with EM algorithm

4.2 Predictive performance

In insurance claims modelling, it is more useful to check the overall distribution for all policyholders rather than prediction of the claim frequency for each policyholder, which can be used for premium calculation, risk management, and so forth. To evaluate the predictive performance, we then calculate the predicted claim frequencies $\text {Freq}(\textbf{X}_t \vert \textbf{X}_{t-1},\hat{\Theta })$, which are the sum of individual probabilities $\mathcal {P}(\textbf{X}^{(h)}_t \vert \textbf{X}^{(h)}_{t-1},\hat{\Theta })$ of joint events $(X^{(h)}_1, X^{(h)}_2) \in \{(i,j), 0 \le i, j \le 10 \}$ based on the estimated parameters, and compare these to the observed frequencies from the test sample $(X_{1,2011}, X_{2,2011})$ (year 2011). In addition to our proposed BINAR model with Log Normal mixing density, we also compute predictive performance of the best TMP, TINAR, BMP models from Table 4 as the benchmark for comparison purposes. Based on the predictive claim frequencies, one can also compute expected number of claims marginally $(\mathbb {E}[X_1], \mathbb {E}[X_2])$,

$$\begin{aligned} \begin{aligned}&\mathbb {E}[X_1] = \sum _{k_1 = 0}^{10} \sum _{k_2 = 0}^{10} k_1 \text {Freq}(k_1,k_2 \vert \textbf{X}_{2010},\hat{\Theta }) \\&\mathbb {E}[X_2] = \sum _{k_1 = 0}^{10} \sum _{k_2 = 0}^{10} k_3 \text {Freq}(k_1,k_2 \vert \textbf{X}_{2010},\hat{\Theta }) \end{aligned} \end{aligned}$$

(35)

and measure the Predictive Sum of Square error:

$$\begin{aligned} \text {PSSE} = (\mathbb {E}[X_1] - X_{1,2011})^2 + (\mathbb {E}[X_2] - X_{2,2011})^2. \end{aligned}$$

(36)

On the other hand, the log likelihood on test samples (TLL) can also be a measure of predictive performance for each model.

$$\begin{aligned} TLL = \sum _{h}^{n_2} \log \mathcal {P}(\textbf{X}^{(h)}_t \vert \textbf{X}^{(h)}_{t-1}, \hat{\Theta }). \end{aligned}$$

(37)

All the results are summarised in Tables 6 and 7 and it is clear that our proposed model, bivariate INAR(1), has the best predictive performance with the smallest PSSE among all other models. Furthermore, TLL result shows that the bivariate INAR outperforms all other models, which is consistent with the model fitting result in Table 4.

Table 6 Predictive and observed joint frequencies for each models

Table 7 Predictive marginal claim frequency

4.3 Application to ratemaking

In this subsection, the analysis of best fitted models from Table 4 for ratemaking is conducted. We select three representative risk profiles under different models, named Good, Average and Bad, illustrated in Table 8. These three risk profiles are selected according to the sign and size of the coefficients in Table 5 and those variables are not mentioned in the following table are taken to be 0. Note that CoverageIM and CoverageCN are selected according to their empirical distribution on test data.

Table 8 The risk profiles for two claim sequences

We then evaluate the mean and variance of $X^{(h)}_{1,t} + X^{(h)}_{2,t}$ under each best TMP, TINAR, BMP and BINAR according to Table 4. The mean and variance for one policyholder is given by two quantity, i.e. $\mathbb {E}[X^{(h)}_1 + X^{(h)} _2 \vert \hat{\Theta }, \textbf{X}_{t-1}, \textbf{Z}_1,\textbf{Z}_2 ]$ and $\text {Var}(X^{(h)}_1 + X^{(h)} _2 \vert \hat{\Theta }, \textbf{X}_{t-1}, \textbf{Z}_1,\textbf{Z}_2 )$. They have following explicit formulae

$$\begin{aligned} \begin{aligned} \mathbb {E}[R_{1,t} + R_{2,t} \vert \hat{\Theta }, \textbf{Z}_1,\textbf{Z}_2]&= \hat{\lambda }_1 + \hat{\lambda }_2 = e^{\textbf{Z}_1 \hat{\beta }_1} + e^{ \textbf{Z}_2 \hat{\beta }_2} \\ \text {Var}(R_{1,t} + R_{2,t} \vert \hat{\Theta }, \textbf{Z}_1,\textbf{Z}_2 )&= \hat{\lambda }_1^2 (e^{\hat{\sigma _1}} -1) + \hat{\lambda }_2^2 (e^{\hat{\sigma _2}} -1) + \hat{\lambda }_1 + \hat{\lambda }_2\\&\quad + 2 \hat{\lambda }_1\hat{\lambda }_2( e^{\hat{\rho }\hat{\sigma }_1\hat{\sigma }_2} - 1) \\ \mathbb {E}[X^{(h)}_1 + X^{(h)} _2 \vert \hat{\Theta }, \textbf{X}_{t-1}, \textbf{Z}_1,\textbf{Z}_2 ]&= \hat{p_1} X^{(h)}_{1,t-1} + \hat{p_2} X^{(h)}_{2,t-1} \\&\quad + \mathbb {E}[R_{1,t} + R_{2,t} \vert \hat{\Theta }, \textbf{Z}_1,\textbf{Z}_2] \\ \text {Var}(X^{(h)}_1 + X^{(h)} _2 \vert \hat{\Theta }, \textbf{X}_{t-1}, \textbf{Z}_1,\textbf{Z}_2 )&= \hat{p_1} (1-\hat{p_1} )X^{(h)}_{1,t-1} + \hat{p_2} (1-\hat{p_2})X^{(h)}_{2,t-1} \\&\quad + \text {Var}(R_{1,t} + R_{2,t} \vert \hat{\Theta }, \textbf{Z}_1,\textbf{Z}_2 ) \end{aligned} \end{aligned}$$

(38)

Tables 9 and 10 summarise the mean and variance under different risk profiles and different claim history structure $(X^{(h)}_{1,t-1},X^{(h)}_{2,t-1})$. As TMP and BMP do not depend on claim history, their mean and variance are all the same within the same risk profiles. It is interesting to see that the variance of INAR models are smaller than that of mixed Poisson models in many cases.

Table 9 Premium calculations from different models: Means

Table 10 Premium calculations from different models: Variances

5 Concluding remarks

In this paper, we consider a new family of bivariate mixed Poisson INAR(1) regression models for modelling multiple time series of different types of claim counts. The proposed family of models accounts for bivariate overdispersion and, similarly to copula-based models, allows for interactions of different signs and magnitude among the two count response variables without using the finite differences of the copula representation which may result in numerical instability in the ML estimation procedure. For illustrative purposes, we derived the BINAR(1)-LN and BINAR(1)-GGA regression models which can be regarded as competitive alternatives to the BINAR(1)-GA regression model for modelling time series of count data. Furthermore, from a computational statistics standpoint, the EM type algorithms we developed for ML estimation of the parameters of all the models were easily implementable and were shown to perform well when we exemplified our approach on LGPIF data from the state of Wisconsin. At this point, it should be noted that we considered the bivariate case and the Gamma and Lognormal correlated random effects for expository purposes. Moreover, the EM estimation framework we proposed is sufficiently flexible and can be used for other continuous mixing densities with a unit mean and, unlike copula-based models, which also allow for both positive and negative correlations, generalizations to any vector size response variables are straightforward. However, in the latter case, EM estimation may be chronologically demanding due to algebraic intractability. Nevertheless, in such cases, due to the structure of the EM algorithm for multivariate INAR(1) models with correlated random effects, the E- and M-steps can be executed in parallel across multiple threads to exploit the processing power available in multicore machines.

Finally, an interesting topic for further research would be to also take into account cross autocorrelation, proceeding along similar lines as in Ref. [4].

Appendix A

1.1 A.1 Abbreviations

Here is a table for all the abbreviations used in this paper (Table 11).

Table 11 The explanation of the Abbreviations used in

1.2 A.2 The Gauss-Hermite quadrature in the high dimensional setting

In this session, we introduce how to transform an integral with respect to multivariate normal density function into a multi-dimension Gauss-Hermite quadrature rule. Starting from one dimensional case, the way we calculate the following integral

$$\begin{aligned} \mathbb {E}[h(X)] =\int _{-\infty }^{\infty } h(x) \frac{1}{\sqrt{2\pi } \sigma } \exp \left\{ -\frac{(x-\mu )^2}{2\sigma ^2} \right\} dx, \end{aligned}$$

where $X \sim N(\mu , \sigma ^2)$, is first to make a linear transformation of integrand and then apply the quadrature rule directly:

$$\begin{aligned} \begin{aligned} \mathbb {E}[h(x)]&= \int _{-\infty }^{\infty } h(\sqrt{2} \sigma y + \mu ) \frac{1}{\sqrt{\pi } } \exp \left\{ -y^2\right\} dy \\&\approx \frac{1}{\sqrt{\pi } } \sum _{i=1}^n h(\sqrt{\sigma } \xi _i + \mu ) w_i \end{aligned} \end{aligned}$$

where $\xi _i$ are the roots of Hermite polynomial of degree n, with a certain weight $w_i$. The quadrature rule approximation of integral will be accurate only when the function h can be well-approximated by a polynomial of degree $2n-1$ or less. Those values can be found from the R function gauss.quad in the package statmod. The idea to extend the result to high dimensional setting is straightforward. Specifically, we need to first transform the density function into the form $\exp \{ \textbf{y}^T \textbf{y}\}$, where $\textbf{y} \in \mathbb {R}^{k \times 1}$, then the k-dimensional integral reduces to a k-fold Gauss-Hermit integral. Suppose the k -dimensional random vector $\textbf{X} \sim N(\varvec{\mu }, \varvec{\Sigma })$, where $\varvec{\mu } \in \mathbb {R}^{k \times 1}$ and $\varvec{\Sigma } \in \mathbb {R}^{k \times k}$. Then a linear transform for this random vector is through eigen decomposition of $\varvec{\Sigma }$ such that

$$\begin{aligned} \textbf{x} = \sqrt{2} \textbf{Q} \varvec{\Lambda }^{\frac{1}{2}} \textbf{y} + \varvec{\mu }, \end{aligned}$$

where $\textbf{Q} = \left( \varvec{\nu }_1,...,\varvec{\nu }_k \right)$ is the matrix formed by eigen vectors and $\varvec{\Lambda }$ is the diagonal matrix with eigen values $(\lambda _1, \dots , \lambda _k)$ such that $\varvec{\Sigma }\varvec{\nu }_i = \lambda _i \varvec{\nu }_i, \quad i = 1,.\dots , k$. Then the exponent of multivariate normal density becomes

$$\begin{aligned} \begin{aligned}&\frac{1}{2} \left( \textbf{x} - \varvec{\mu } \right) ^T \varvec{\Sigma }^{-1} \left( \textbf{x} - \varvec{\mu }\right) \\&\quad = \frac{1}{2} \left( \sqrt{2} \textbf{Q} \varvec{\Lambda }^{\frac{1}{2}} \textbf{y} + \varvec{\mu } - \varvec{\mu } \right) ^T \varvec{\Sigma }^{-1} \left( \sqrt{2} \textbf{Q} \varvec{\Lambda }^{\frac{1}{2}} \textbf{y} + \varvec{\mu } - \varvec{\mu }\right) \\&\quad = \left( \textbf{Q} \varvec{\Lambda }^{\frac{1}{2}} \textbf{y} \right) ^T \left( \textbf{Q}\varvec{\Lambda }^{-1} \textbf{Q}^{-1} \right) \left( \textbf{Q} \varvec{\Lambda }^{\frac{1}{2}} \textbf{y} \right) \\&\quad = \textbf{y}^{T} \varvec{\Lambda }^{\frac{1}{2}} \left( \textbf{Q}^T \textbf{Q} \right) \varvec{\Lambda }^{-1} \left( \textbf{Q}^{-1} \textbf{Q}\right) \varvec{\Lambda }^{\frac{1}{2}} \textbf{y} \\&\quad = \textbf{y}^{T} \varvec{\Lambda }^{\frac{1}{2}} \varvec{\Lambda }^{-1} \varvec{\Lambda }^{\frac{1}{2}} \textbf{y} \\&\quad = \textbf{y}^T \textbf{y}. \end{aligned} \end{aligned}$$

Since $\varvec{\Sigma }$ is symmetric, then $\textbf{Q}^{T} = \textbf{Q}^{-1}$. Finally, the k-dimensional integral becomes

$$\begin{aligned} \begin{aligned} \mathbb {E}[h(\textbf{X})]&{=} \int _{{-}\infty }^{\infty } \dots \int _{{-}\infty }^{\infty } h(\textbf{x})\frac{1}{ (2\pi )^{\frac{k}{2}} \vert \varvec{\Sigma }\vert } \exp \left\{ {-} \frac{1}{2} \left( \textbf{x} {-} \varvec{\mu } \right) ^T \varvec{\Sigma }^{{-}1} \left( \textbf{x} {-} \varvec{\mu }\right) \right\} dx_1 \dots dx_k \\&{=} \int _{{-}\infty }^{\infty } \dots \int _{-\infty }^{\infty } h\left( \sqrt{2} \textbf{Q} \varvec{\Lambda }^{\frac{1}{2}} \textbf{y} + \varvec{\mu }\right) \pi ^{-\frac{k}{2}} \exp \left\{ -\textbf{y}^T \textbf{y} \right\} dy_1 \dots dy_k \\&\approx \pi ^{-\frac{k}{2}} \sum _{i_1 = 1}^n \dots \sum _{i_k = 1}^n h\left( \sqrt{2} \textbf{Q} \varvec{\Lambda }^{\frac{1}{2}} \varvec{\xi } + \varvec{\mu }\right) w_{i_1}\dots w_{i_k}. \end{aligned} \end{aligned}$$

1.3 A.3The Gauss-Legendre Quadrature in the high dimensional setting

The extension of the Gauss-Legendre quadrature rule into high dimensional situation is much more straightforward. The following m-dimensional integral can be approximated by

$$\begin{aligned} \begin{aligned}&\int _{a_1}^{b_1} \dots \int _{a_m}^{b_m} h(y_1,\dots ,y_n) dy_1\dots dy_n \\&\quad \approx \left( \prod _{i=1}^m \frac{b_i -a_i}{2}\right) \sum _{i_1= 1}^n \dots \\&\qquad \qquad \sum _{i_m = 1}^n h\left( \frac{b_1-a_1}{2}\xi _{i_1} + \frac{b_1 + a_1}{2},\dots , \frac{b_n-a_n}{2}\xi _{i_m} + \frac{b_n + a_n}{2} \right) w_{i_1}\dots w_{i_m} \end{aligned} \end{aligned}$$

where $\xi _.$ are roots of Legendre polynomials of degree n and $w_{.}$ are the corresponding weights. These can also be found easily in R by the ‘gauss.quad’ function in the package ‘statmod’. Similarly, the h function should be well-approximated by a polynomial of degree $2n-1$ or less to ensure accuracy of the approximation.

1.4 A.4 Derivation of conditional expectation

The conditional expectation $\mathbb {E}^{(j)}_{y,t}[Y_{i}]$ can be derived explicitly as follows. For simplicity, we just write $p_1,p_2$ instead of $p_1^{(j)}, p_2^{(j)}$

$$\begin{aligned} \begin{aligned} \mathbb {E}^{(j)}_{y,t}[Y_{1}]&= \frac{1}{\mathcal {P}(\varvec{X}_t \vert \varvec{X}_{t-1})} \sum _{k_1 = 0}^{s_{1,t}} \sum _{k_2=0}^{s_{2,t}} k_1 \left( {\begin{array}{c}X_{1,t-1}\\ k_1\end{array}}\right) p_1^{k_1} (1-p_1)^{X_{1,t-1} - k_1} \\&\quad \times f_{p_2}(y_2,X_{2,t-1}) f_{\varvec{R}}(X_{1,t} - k_1, X_{2,t}-k_2) \\&= \frac{p_1 X_{1,t-1} }{\mathcal {P}(\varvec{X}_t \vert \varvec{X}_{t-1})} \sum _{k_1 = 1}^{s_{1,t}} \sum _{k_2=0}^{s_{2,t}} \left( {\begin{array}{c}X_{1,t-1}-1\\ k_1-1\end{array}}\right) p_1^{k_1-1} (1-p_1)^{X_{1,t-1} - k_1} \\&\quad \times f_{p_2}(y_2,X_{2,t-1}) f_{\varvec{R}}(X_{1,t} - k_1, X_{2,t}-k_2) \\&= \frac{p_1 X_{1,t-1} }{\mathcal {P}(\varvec{X}_t \vert \varvec{X}_{t-1})} \sum _{k'_1 = 0}^{s'_{1,t}} \sum _{k_2=0}^{s_{2,t}} \left( {\begin{array}{c}X_{1,t-1}-1\\ k'_1\end{array}}\right) p_1^{k_1'} (1-p_1)^{X_{1,t-1} -1 - k'_1} \\&\quad \times f_{p_2}(y_2,X_{2,t-1}) f_{\varvec{R}}(X_{1,t} -1 - k_1', X_{2,t}-k_2) \\&= p_1 X_{1,t-1} \frac{\mathcal {P}(\varvec{X}_t - \varvec{1}_1 \vert \varvec{X}_{t-1} - \varvec{1}_1)}{\mathcal {P}(\varvec{X}_t \vert \varvec{X}_{t-1})}. \end{aligned} \end{aligned}$$

1.5 A.5 Simulation study for Gaussian copula paired with Gamma marginals

This is to verify that the EM algorithms work for both the bivariate Poisson mixture model and the bivariate INAR model when the random effect is characterized by copula. Two random samples of size 500 are generated from these two models separately with pre-specified parameters, which are listed in the Table 12

Table 12 Parameter setting for simulation

where $\varvec{\mu }_1 = (1,0.3,0.5)^T$, $\varvec{\mu }_2 = (1,0.2,0.4)^T$, $\textbf{D} = {\textrm{diag}}\{0,1,1\}$ and $\text {MVN}$ stands for multivariate normal distribution. Then each model is fitted by two methods: maximising the incomplete likelihood and EM algorithms. These two methods should give almost the same results for $\varvec{p},\varvec{\beta }_1, \varvec{\beta }_2$ which determine the mean of the model and hence have a relatively large contribution to likelihood. On the other hand, this may not be the case for other parameters $\phi _1, \phi _2, \rho$ which determine the variation and correlation of the model, and only contribute relative small part of the likelihood. The final log likelihood values would normally be larger than the log likelihood value evaluated at pre-specific parameters. The estimated results are given in Table 13

Table 13 Simulation study for two estimation methods, where OPTIM is the optimization function implemented in R with conjugate gradient (CG) as method

The difference between estimated parameters $\phi _1, \phi _2, \rho$ and their true values seems larger than others. This is reasonable because these parameters control the variation of distribution and the log likelihood would be less sensitive to them.