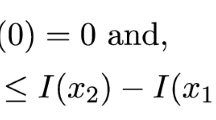Optimal risk transfers in insurance groups

Abstract

Optimal risk transfers are derived within an insurance group consisting of two separate legal entities, operating under potentially different regulatory capital requirements and capital costs. Consistent with regulatory practice, capital requirements for each entity are computed by either a value-at-risk or an expected shortfall risk measure. The optimality criterion consists of minimising the risk-adjusted value of the total group liabilities, with valuation carried out using a cost-of-capital approach. The optimisation problems are analytically solved and it is seen that optimal risk transfers often involve the transfer of tail risk (unlimited reinsurance layers) to the more weakly regulated entity. We show that, in the absence of a capital requirement for the credit risk that specifically arises from the risk transfer, optimal risk transfers achieve capital efficiency at the cost of increasing policyholder deficit. However, when credit risk is properly reflected in the capital requirement, incentives for tail-risk transfers vanish and policyholder welfare is restored.

Appendices

Appendix

Proofs

It is useful to note here that I ₁ and I ₂ are Lipschitz continuous functions with unit constants, i.e. |I _k [y] − I _k [x]| ≤ |y − x| holds for all x,y ≥ 0 and k ∈ {1,2}, due to the fact that I ₁ and I ₂ are non-decreasing functions (see also [8]). In addition, VaR _{α_k} (I _k [X]) = I _k (VaR _{α_k} (X)) is true for all k ∈ {1,2} (see for example [12], p. 19, and [14]).

The following notations,

$$ \begin{aligned} {\mathcal{A}}_1=\left\{(\xi_1,\xi_2):0\leq \xi_1\leq VaR_{\alpha_1}(X),0\leq \xi_2-\xi_1\leq VaR_{\alpha_2}(X)- VaR_{\alpha_1}(X)\right\}& \\ {\mathcal{A}}_2=\left\{(\xi_1,\xi_2):0\leq \xi_2\leq VaR_{\alpha_2}(X),0\leq \xi_1-\xi_2\leq VaR_{\alpha_1}(X)- VaR_{\alpha_2}(X)\right\} & \\ \end{aligned} $$

are useful for explaining all the proofs. In addition, $\Pr(Z\leq z)<\alpha$ is equivalent to z < VaR _α (X).

2.1 Proof of Theorem 2.1

The first part is now investigated assuming that λ₁ > λ₂. The mirror case, λ₁ < λ₂, results by the symmetry property of the objective function from Eq. (2.5). Now, for any arbitrary risk transfer I ₂, we have

$$ \begin{aligned} &(\lambda_1-\lambda_2)E(I_2[X])+\lambda_2 I_2(VaR_{\alpha_2}(X))-\lambda_1 I_2(VaR_{\alpha_1}(X)) \\ &\quad= (\lambda_1-\lambda_2)E(I_2[X]-I_2(VaR_{\alpha_1}(X))) + \lambda_2 (I_2(VaR_{\alpha_2}(X))-I_2(VaR_{\alpha_1}(X))) \\ &\quad\geq (\lambda_1-\lambda_2)E(I_2[\min\{X,VaR_{\alpha_1}(X)\}]-I_2(VaR_{\alpha_1}(X))) \cr& \qquad+\lambda_2 (I_2(VaR_{\min\{\alpha_1,\alpha_2\}}(X))-I_2(VaR_{\alpha_1}(X))) \\ &\quad\geq (\lambda_1-\lambda_2)E(\min\{X,VaR_{\alpha_1}(X)\}-VaR_{\alpha_1}(X))+\lambda_2 (VaR_{\min\{\alpha_1,\alpha_2\}}(X)-VaR_{\alpha_1}(X)) \\ &\quad=(\lambda_1-\lambda_2)E(I^*_2[X])+\lambda_2 I^*_2(VaR_{\alpha_2}(X))-\lambda_1 I^*_2(VaR_{\alpha_1}(X)), \\ \end{aligned} $$

(5.1)

where the second last step is due to the Lipschitz property of function $I_2(\cdot)$. Note that the optimal solution stated in Theorem 2.1i) was $I^*_2[X]=\min\{X,VaR_{\alpha_1}(X)\}$, which concludes this case.

Finally, the λ₁ = λ₂ case is discussed, which is reduced to minimising

$$ I_2(VaR_{\alpha_2}(X))-I_2(VaR_{\alpha_1}(X)). $$

(5.2)

Recall that the Lipschitz property implies

$$ |I_2(VaR_{\alpha_2}(X))-I_2(VaR_{\alpha_1}(X))|\leq |VaR_{\alpha_2}(X)-VaR_{\alpha_1}(X)|. $$

Thus, the solutions of (5.2) only require $I_2(\cdot)$ to be flat on $[VaR_{\alpha_1}(X),VaR_{\alpha_2}(X)]$ whenever VaR _{α_1}(X) < VaR _{α_2}(X), and have a slope of 1 on $[VaR_{\alpha_2}(X),VaR_{\alpha_1}(X)]$ otherwise. The latter and Lipschitz property help in recovering the λ₁ = λ₂ case. The proof is now complete.

2.2 Proof of Theorem 2.2

The proofs are developed in a similar manner as in Theorem 2.1, and therefore we only outline the main steps. The case in which λ₁ > λ₂ can be proved in the same manner as shown in Eq. (5.1). Specifically,

$$ \begin{aligned} &{(\lambda_1-\lambda_2)E(I_2[X])+\lambda_2 ES_{\alpha_2} (I_2[X])-\lambda_1 I_2(VaR_{\alpha_1}(X))} \\ &\quad\geq (\lambda_1-\lambda_2)E(I_2[\min\{X,VaR_{\alpha_1}(X)\}])+\lambda_2 ES_{\alpha_2} (I_2[\min\{X,VaR_{\alpha_1}(X)\}]) \cr&\qquad-\lambda_1 I_2(VaR_{\alpha_1}(X)) \\ &\quad=(\lambda_1-\lambda_2)E(I_2[\min\{X,VaR_{\alpha_1}(X)\}]-I_2(VaR_{\alpha_1} (X))) \\ &\qquad+\lambda_2 ES_{\alpha_2} (I_2[\min\{X,VaR_{\alpha_1}(X)\}]-I_2(VaR_{\alpha_1} (X))) \cr&\quad\geq (\lambda_1\!-\!\lambda_2)E(\!\min\!\{X,VaR_{\alpha_1}(X)\}\!-\!VaR_{\alpha_1}(X))\!+\!\lambda_2 ES_{\alpha_2}(\!\min\!\{X,VaR_{\alpha_1}(X)\}\!-\!VaR_{\alpha_1}(X)) \\ &\quad=(\lambda_1\!-\!\lambda_2)E(I^*_2[X])+\lambda_2 ES_{\alpha_2} (I^*_2[X])-\lambda_1 I^*_2(VaR_{\alpha_1}(X)), \\ \end{aligned} $$

which implies that the optimisation problem from (2.6) is attained at I ^*₂ [X] = min{X,$VaR_{\alpha_{1}}(X)$}.

Similarly, the $[VaR_{\alpha_{1}}(X) \leq VaR_{\alpha_2}(X)]$ case such that λ₁ < λ₂ is examined. Clearly,

$$ (\lambda_1-\lambda_2)E(I_2[X])+\lambda_2 ES_{\alpha_2} (I_2[X])-\lambda_1 I_2(VaR_{\alpha_1}(X)) \geq (\lambda_2-\lambda_1) (ES_{\alpha_2} (I_2[X])-E (I_2[X]))\geq 0. $$

The lower bound is attained whenever I ^*₂ [X] = 0, which fully concludes part 1).

The remaining of part 2), $VaR_{\alpha_{1}}(X)$ > $VaR_{\alpha_{2}}(X)$ with λ₁ < λ₂, needs to be elaborated in greater detail than the previous one. The optimisation problem (2.6) is solved via a two stage optimisation procedure. The mathematical formulation of the first stage optimisation problem becomes

$$ \left\{\begin{array}{l} \displaystyle\min_{I_2\in {\cal F}} (\lambda_1-\lambda_2)E(I_2[X])+\lambda_2 ES_{\alpha_2} (I_2[X])\; {\rm subject\; to}\\ I_2(VaR_{\alpha_1}(X))=\xi_1,\;I_2(VaR_{\alpha_2}(X))=\xi_2, \end{array}\right. $$

where $(\xi_1,\xi_2)\in\mathcal{A}_2$ are some constants. Keeping in mind that λ₁ − λ₂ < 0 and relation (2.1), the function $I_2(\cdot)$ should increase as fast as possible on [0,$VaR_{\alpha_{1}}(X)$], and remain flat on [$VaR_{\alpha_{1}}(X)$,x _F ]. The optimal solution is then pictured in Fig. 5

Fig. 5

The construction of I ^*_2a [X;ξ₁,ξ₂] in Theorem 2.2

One may mathematically formulate the latter risk transfer as

$$ I_{2a}^*[X;\xi_1,\xi_2]=\left\{\begin{array}{ll} \min\{X-VaR_{\alpha_1}(X)+\xi_1,\xi_1\},\; & X>VaR_{\alpha_1}(X)+\xi_2-\xi_1,\\ \min\{X,\xi_2\},\; & {otherwise}. \end{array}\right. $$

Thus, the solution of our second stage optimisation problem

$$ \begin{aligned} \min_{(\xi_1,\xi_2)\in {\mathcal{A}}_2} H(\xi_1,\xi_2)&=(\lambda_1-\lambda_2)\left(\int\limits_0^{\xi_2}\bar{F}(x)\;dx+\int\limits_{VaR_{\alpha_1}(X)+\xi_2-\xi_1}^{VaR_{\alpha_1}(X)}\bar{F}(x)\;dx\right) \\ &\quad+\lambda_2\left(\xi_2+{{1}\over {1-\alpha_2}} \int\limits_{VaR_{\alpha_1}(X)+\xi_2-\xi_1}^{VaR_{\alpha_1}(X)}\bar{F}(x)\;dx\right)-\lambda_1 \xi_1 \end{aligned} $$

replicates the global minimiser of (2.6). The derivative of the above-mentioned function with respect to ξ₁ becomes

$$ {{dH}\over {d\xi_1}}=\left(\lambda_1+\lambda_2 {{\alpha_2}\over {1-\alpha_2}}\right)\bar{F}\left(VaR_{\alpha_1}(X)+\xi_2-\xi_1\right)-\lambda_1, $$

(5.3)

which is non-positive if and only if $VaR_{\alpha_1}(X)+\xi_2-\xi_1\geq VaR_{\alpha_2^*}(X)$. Due to the fact that λ₁ < λ₂, it is not difficult to find that α ^*₂  > α₂. Note that VaR _{α_2}(X) ≤ VaR _{α_1}(X) + ξ₂ − ξ₁ ≤ VaR _{α_1}(X) holds. Having all of these in mind, we may conclude

$$ H(\xi_1,\xi_2)\geq H(\xi_2,\xi_2),\;{\rm if}\;\alpha_2^*\geq \alpha_1 $$

and

$$ H(\xi_1,\xi_2)\geq H(\xi_2+VaR_{\alpha_1}(X)-VaR_{\alpha_2^*}(X),\xi_2),\;{\rm if}\;\alpha_2^*<\alpha_1. $$

Finding the minimum values of the above-right hand side functions over the domain of ξ₂, namely $[0,VaR_{\alpha_2}(X)]$, the global solution of (2.6) is attained at (0,0) and $(VaR_{\alpha_1}(X)-VaR_{\alpha_2^*}(X),0)$, if α ^*₂  ≥ α₁ and α ^*₂  < α₁, respectively. Thus, part 2) is concluded.

Finally, the λ₁ = λ₂ case is under investigation. Our optimisation problem becomes

$$ \min_{I_2 \in\cal{F}} ES_{\alpha_2} (I_2[X]) - VaR_{\alpha_1}I_2[X]. $$

Thus, the first stage optimisation problem is equivalent to minimising $ES_{\alpha_2} (I_2[X])$.

The VaR _{α_1}(X) ≤ VaR _{α_2}(X) subcase makes $I_2(\cdot)$ to be flat for losses higher than VaR _{α_2}(X). Thus, the second stage problem is to minimise ξ₂ − ξ₁ on $\mathcal{A}_1$, and keeping in mind the Lipschitz property, one may recover our claim.

The last subcase, VaR _{α_1}(X) > VaR _{α_2}(X), is developed in greater detail. The first part of A.2 only requires for the function $I_2(\cdot)$ to not increase on $[VaR_{\alpha_2}(X),VaR_{\alpha_1}(X)-(\xi_1-\xi_2)]$, then to increase with a slope of 1 until it reaches the ξ₁ level at VaR _{α_1}(X), and remain flat on $[VaR_{\alpha_1}(X),x_F]$. Thus, the second stage problem of 5.2 becomes

$$ \min_{{\mathcal{A}}_2} \; \xi_2 +{{1}\over {1-\alpha_2}} \int\limits_{VaR_{\alpha_1}(X)-(\xi_1-\xi_2)}^{VaR_{\alpha_1}(X)} \bar{F}(x)\;dx-\xi_1. $$

Therefore, the objective function of the above is non-increasing in ξ₁ for any fixed ξ₂, and straightforward calculations show that the set of optimal solutions is given by

$$ \{(x+VaR_{\alpha_1}(X)-VaR_{\alpha_2}(X),x):x\in [0,VaR_{\alpha_2}(X)]\}, $$

which justifies in full the VaR _α1(X) > VaR _α2(X) subcase. This ends the proof.

2.3 Proof of Theorem 2.3

• 1. If $VaR_{\alpha_1}(X) = VaR_{\alpha_2}(X),$ the first stage optimisation problem is given by

  $$ \min_{I_2\in {\mathcal{F}}} (\lambda_1-\lambda_2)E(I_2[X])+\lambda_2 ES_{\alpha_2} (I_2[X])-\lambda_1 ES_{\alpha_1} (I_2[X])\;{subject\ to}\;I_2(VaR_{\alpha_1}(X))=\xi, $$

  (5.4)

  where $\xi\in[0,VaR_{\alpha_1}(X)]$ represents an arbitrarily chosen constant.

  Let λ₁ > λ₂. It is not difficult to justify via some geometric argumentation that (5.4) has solutions given by $(X-VaR_{\alpha_1}(X)+\xi)_+$ and $\min \{(X-VaR_{\alpha_1}(X)+\xi)_+,\xi\}$ whenever C < 0 and C > 0, respectively.

  Next, it is assumed that C < 0, and plugging the solution of (5.4) in its objective function, the second stage optimisation problem is reduced to minimising

  $$ (\lambda_1-\lambda_2)\int\limits_{VaR_{\alpha_1}(X)-\xi}^{x_F}\bar{F}(x)\;dx+\lambda_2 (\xi+ES_{\alpha_2} (X) -VaR_{\alpha_1}(X))-\lambda_1 (\xi+ES_{\alpha_1} (X)-VaR_{\alpha_1}(X)), $$

  over all possible values of ξ. The latter function is decreasing on $[0,VaR_{\alpha_1}(X)]$, which leads to full transfer of the risk to the second insurance company.

  For positive values of C > 0, the second stage optimisation problem is retrieved by minimising

  $$ (\lambda_1-\lambda_2)\left(\int\limits_{VaR_{\alpha_1}(X)-\xi}^{VaR_{\alpha_1}(X)}\bar{F}(x)\;dx-\xi\right), $$

  over $\xi\in[0,VaR_{\alpha_1}(X)]$ due to the fact that

  $$ ES_{\alpha_1} (\min \{(X-VaR_{\alpha_1}(X)+\xi)_+,\xi\}) =ES_{\alpha_2} (\min \{(X-VaR_{\alpha_1}(X)+\xi)_+,\xi\})=\xi. $$

  The decreasing property of the above-mentioned function implies that $I_2^*[X]=\min\{X,VaR_{\alpha_1}(X)\}$, which concludes the λ₁ > λ₂ case.

  We now consider the situation in which λ₁ < λ₂. One may get that (5.4) is minimised by $\min\{X,\xi\}+(X-VaR_{\alpha_1}(X))_+$ and $\min\{X,\xi\}$ whenever C < 0 and C > 0, respectively. Thus, the second stage problems are the minimisation in ξ of

  $$ (\lambda_1-\lambda_2)\left(\int\limits_0^{\xi}+\int\limits_{VaR_{\alpha_1}(X)}^{x_F}\right)\bar{F}(x)\;dx+(\lambda_2-\lambda_1)(\xi-VaR_{\alpha_1}(X))+\lambda_2 ES_{\alpha_2} (X)-\lambda_1 ES_{\alpha_1} (X) $$

  and

  $$ (\lambda_1-\lambda_2)\left(\int\limits_{VaR_{\alpha_1}(X)-\xi}^{VaR_{\alpha_1}(X)}\bar{F}(x)\;dx-\xi\right), $$

  provided that C < 0 and C > 0, respectively, over the set $[0,VaR_{\alpha_1}(X)]$. Clearly, both functions are increasing on the whole domain, and therefore one may easily recover optimal contracts in our setting, i.e. if λ₁ < λ₂.

  The λ₁ = λ₂ setting is investigated at the moment, for which

  $$ \min_{\cal{F}}\;ES_{\alpha_2} I_2[X]-ES_{\alpha_2} I_2[X] $$

  (5.5)

  needs to be solved. The first stage problem becomes

  $$ \min_{0\leq \xi\leq VaR_{\alpha_1}(X)}\;{{\alpha_2-\alpha_1}\over {(1-\alpha_1)(1-\alpha_2)}}E (I_2[X]-\xi)_+, \;{subject\ to} \; I_2(VaR_{\alpha_1}(X))=\xi $$

  as a result of relation (2.1). Note that C < 0 is the same as α₁ > α₂, which makes $I_2(\cdot)$ to increase with slope 1 from VaR _{α_1}(X) onwards in order to solve . In turn, the C > 0 case requires a leveled $I_2(\cdot)$ function on $[VaR_{\alpha_1}(X),x_F]$, since α₁ < α₂. Thus, the justification of VaR _{α_1}(X) = VaR _{α_2}(X) is now completed.

• 2. The VaR _{α_1}(X) > VaR _{α_2}(X) case is further examined. If λ₁ > λ₂, then

  $$ (\lambda_1-\lambda_2)E(I_2[X])+\lambda_2 ES_{\alpha_2} (I_2[X])-\lambda_1 ES_{\alpha_1} (I_2[X]) \geq (\lambda_2-\lambda_1)(ES_{\alpha_1} (I_2[X])-E (I_2[X])), $$

  and therefore (2.8) is the same as to maximse $ES_{\alpha_1} (I_2[X])-E (I_2[X])$, which in turn is equivalent to minimising $ES_{\alpha_1} (I_1[X])-E (I_1[X])$. Thus, I ^*₁ [X] = 0, which concludes the λ₁ > λ₂ subcase.

  Our main objective from (2.8) can be solved via a two stage optimisation, whenever λ₁ ≤ λ₂. Particularly, the first step can be written in the following fashion

  $$ \left\{ \begin{array}{l}\min_{I_2\in {\mathcal F}} (\lambda_1-\lambda_2)E(I_2[X])+\lambda_2 ES_{\alpha_2} (I_2[X])-\lambda_1 ES_{\alpha_1} (I_2[X])\; {\rm subject\; to}\cr I_2(VaR_{\alpha_1}(X))=\xi_1,\;I_2(VaR_{\alpha_2}(X))=\xi_2, \end{array}\right. $$

  where $(\xi_1,\xi_2)\in\mathcal{A}_2$ is a fixed vector of constants. It can be shown that the solutions are

  $$ I_2^*[X;\xi_1,\xi_2]=\left\{\begin{array}{lll}I_{2a}^*[X;\xi_1,\xi_2],& \lambda_1< \lambda_2,& C>0,\\ I_{2b}^*[X;\xi_1,\xi_2],& \lambda_1< \lambda_2,&C<0,\end{array}\right. $$

  where

  $$ I^*_{2b}[X;\xi_1,\xi_2]=\left\{\begin{array}{ll}X-VaR_{\alpha_1}(X)+\xi_1,& X>VaR_{\alpha_1}(X)+\xi_2-\xi_1, \\ \min\{X,\xi_2\},& {otherwise}.\end{array}\right. $$

  In the case that λ₁ < λ₂ and C < 0, we only need to solve

  $$ \begin{aligned} &{\min_{(\xi_1,\xi_2)\in{\mathcal{A}}_2} H(\xi_1,\xi_2):=(\lambda_1-\lambda_2)\left(\int\limits_0^{\xi_2}+\int\limits_{VaR_{\alpha_1}(X)+\xi_2-\xi_1}^{x_F}\right)\bar{F}(x)\;dx} \\ &\quad+\lambda_2 \left(\xi_2+{{1}\over {1-\alpha_2}} \int\limits_{VaR_{\alpha_1}(X)+\xi_2-\xi_1}^{x_F}\bar{F}(x)\;dx\right)- \lambda_1 \left (\xi_1+{{1}\over {1-\alpha_1}} \int\limits_{VaR_{\alpha_1}(X)}^{x_F}\bar{F}(x)\;dx\right). \end{aligned} $$

  (5.6)

Note that α₂ < α ^*₂  < α₁ is true under this setting. The derivative of the above with respect to ξ₁ is given by (A.3), and it is non-positive if and only if $\xi_2\leq \xi_1\leq \xi_2 + VaR_{\alpha_1}(X)-VaR_{\alpha_2^*}(X).$ Thus,

$$ H(\xi_1,\xi_2)\geq H(\xi_2 + VaR_{\alpha_1}(X)-VaR_{\alpha_2^*}(X),\xi_2)=(\lambda_1-\lambda_2)\left(\int\limits_0^{\xi_2} \bar{F}(x)\;dx-\xi_2\right)+K, $$

where K is a constant with respect to ξ₂. The latter function is increasing in ξ₂ on $[0,VaR_{\alpha_2}(X)]$, and therefore (5.6) is solved by $(\xi_1^*,\xi_2^*)=(VaR_{\alpha_1}(X)-VaR_{\alpha_2^*}(X),0)$, which replicates the optimal risk transfer in this subcase.

The situation in which λ₁ < λ₂ and C > 0 requires minimising over $\mathcal{A}_2$

$$ (\lambda_1-\lambda_2)\left(\int\limits_0^{\xi_2}+\int\limits_{VaR_{\alpha_1}(X)+\xi_2-\xi_1}^{VaR_{\alpha_1}(X)}\right)\bar{F}(x)\;dx +\lambda_2 \left(\xi_2+{{1}\over {1-\alpha_2}} \int\limits_{VaR_{\alpha_1}(X)+\xi_2-\xi_1}^{VaR_{\alpha_1}(X)}\bar{F}(x)\;dx\right)- \lambda_1 \xi_1. $$

Clearly, α₂ < α₁ < α ^*₂ , and therefore the function from above is non-decreasing in ξ₁ for any fixed ξ₂, since again its derivative with respect with ξ₁ is given by Eq. (5.3). Similar derivations to the previous subcases lead to the global minimum to be attained at $(\xi_1^*,\xi_2^*)=(0,0)$.

The final setting, under which λ₁ = λ₂, needs to be justified. The first stage optimisation problem of (5.5) forces the risk transfer to remain flat on $[VaR_{\alpha_2}(X),VaR_{\alpha_1}(X)-(\xi_1-\xi_2)]$, and increase as fast as possible onwards, since α₁ > α₂. The second stage problem becomes

$$ \min_{\cal{A}_2}\;\xi_2-\xi_1+{{1}\over {1-\alpha_2}}\int\limits_{VaR_{\alpha_1}(X)-(\xi_1-\xi_2)}^{x_F} \bar{F}(x)\;dx-{{1}\over {1-\alpha_1}}\int\limits_{VaR_{\alpha_1}(X)}^{x_F} \bar{F}(x)\;dx. $$

(5.7)

Note that the above objective function is non-increasing in ξ₁ for any fixed ξ₂, and therefore the set of solutions for (5.7) is given by

$$ \{(VaR_{\alpha_1}(X)-VaR_{\alpha_2}(X)+x,x):0\leq x\leq VaR_{\alpha_2}(X)\}. $$

Thus, we only need to impose a linear increasing with slope 1 for $I_2(\cdot)$ on [VaR _{α_2}(X),x _F ] in order to solve the initial optimisation problem. This completes the proof.

2.4 Proof of Lemma 3.1

Note that VaR _{α_1}(X ₁) = 0 and $VaR_{\alpha_2}(X_2)=VaR_{\alpha_1^*}(X)$, which together with (2.1) imply that

$$ ES_{\alpha_1}(X_1) ={{1}\over {1-\alpha_1}}\int\limits_{VaR_{\alpha_1^*}(X)}^{VaR_{\alpha_2}(X)} \bar F(x)\;dx. $$

Now,

$$ \begin{aligned} EPD(X_1;ES_{\alpha_1}(X_1))=&\int\limits_{ES_{\alpha_1}(X_1)}^{x_F} P(X_1>z)\;dz \\ =&\int\limits_{\min\{VaR_{\alpha_2}(X),VaR_{\alpha_1^*}(X)+ES_{\alpha_1}(X_1)\}}^{VaR_{\alpha_2}(X)}\bar F(x)\;dx \\ EPD(X_2;VaR_{\alpha_2}(X_2))=&\int\limits_{VaR_{\alpha_2}(X_2)}^{x_F}P(X_2>z)dz=\int\limits_{VaR_{\alpha_2}(X)}^{{x_F}} \bar F(x)\;dx \\ \end{aligned} $$

from which part i) follows. Clearly, $\tilde X_1=(X-VaR_{\alpha_1^*}(X))_+$ and we further have that

$$ ES_{\alpha_1}(\tilde X_1)={{1}\over {1-\alpha_1}}\int\limits_{VaR_{\alpha_1^*}(X)}^{{x_F}} \bar F(x)\;dx, $$

which concludes parts ii) and iii).

The first inequality in the lemma holds as long as

$$ VaR_{\alpha_1^*}(X)+{{1}\over {1-\alpha_1}}\int\limits_{VaR_{\alpha_1^*}(X)}^{VaR_{\alpha_2}(X)} \bar F(x)\;dx \leq VaR_{\alpha_2}(X). $$

The latter holds as a result of

$$ \begin{aligned} {{1}\over {1-\alpha_1}}\int\limits_{VaR_{\alpha_1^*}(X)}^{VaR_{\alpha_2}(X)} \bar F(x)\;dx \leq& {{\bar F ( VaR_{\alpha_1^*}(X))}\over {1-\alpha_1}}(VaR_{\alpha_2}(X)-VaR_{\alpha_1^*}(X)) \cr \leq& {{1-\alpha_1^*}\over {1-\alpha_1}}(VaR_{\alpha_2}(X)-VaR_{\alpha_1^*}(X)) \\ \leq & VaR_{\alpha_2}(X)-VaR_{\alpha_1^*}(X). \end{aligned} $$

It only remains to show the very last inequality from Lemma 3.1, for which it is sufficient to show that

$$ VaR_{\alpha_1^*}(X)+{{1}\over {1-\alpha_1}}\int\limits_{VaR_{\alpha_1^*}(X)}^{{x_F}} \bar F(x)\;dx \geq VaR_{\alpha_1}(X)+{{1}\over {1-\alpha_1}}\int\limits_{VaR_{\alpha_1}(X)}^{{x_F}} \bar F(x)\;dx. $$

The latter is true since $\bar F(VaR_{\alpha_1}(X))\leq 1-\alpha_1$ and the fact that

$$ \begin{aligned} \int\limits_{VaR_{\alpha_1}(X)}^{{x_F}} \bar F(x)\;dx&=\int\limits_{VaR_{\alpha_1}(X)}^{VaR_{\alpha_1^*}(X)} \bar F(x)\;dx+\int\limits_{VaR_{\alpha_1^*}(X)}^{{x_F}} \bar F(x)\;dx \\ &\leq (VaR_{\alpha_1^*}(X)-VaR_{\alpha_1}(X))\bar F(VaR_{\alpha_1}(X))+\int\limits_{VaR_{\alpha_1^*}(X)}^{{x_F}} \bar F(x)\;dx. \end{aligned} $$

2.5 Proof of Lemma 3.2

Note first that VaR _{α_1}(X ₁) = VaR _{α_1}(X) and VaR _{α_2}(X ₂) = 0, which together with (2.1) give that

$$ ES_{\alpha_1}(X_1) =VaR_{\alpha_1}(X)+ {{1}\over {1-\alpha_1}}\int\limits_{VaR_{\alpha_1}(X)}^{VaR_{\alpha_2}(X)} \bar F(x)\;dx. $$

Clearly, $\tilde X_1=X_1+(X_2-VaR_{\alpha_2}(X_2))_+=X$. Now, part 1) simply follows from

$$ \begin{aligned} EPD(X_1;ES_{\alpha_1}(X_1))=&\int\limits_{ES_{\alpha_1}(X_1)}^{x_F} P(X_1>z)dz =\int\limits_{\min\{VaR_{\alpha_2}(X),ES_{\alpha_1}(X_1)\}}^{VaR_{\alpha_2}(X)} \bar F(x)\;dx \\ EPD(X_2;VaR_{\alpha_2}(X_2))=&\int\limits_{VaR_{\alpha_2}(X_2)}^{x_F} P(X_2>z)dz = \int\limits_{VaR_{\alpha_2}(X)}^{{x_F}} \bar F(x)\;dx. \end{aligned} $$

Parts ii) and iii), as well as the equality $EPD(\tilde X_1;ES_{\alpha_1}(\tilde X_1))=EPD(X;ES_{\alpha_1}( X))$ are true since $\tilde X_1=X$. Finally, the inequality at the end of the lemma follows from ES _{α_1}(X ₁) ≤ ES _{α_1}(X).

2.6 Proof of Theorem 3.1

It is easy to obtain

$$ \begin{aligned} E(g[X;\gamma])=&E(I_1[X])+\gamma E(I_2[X]-I_2(VaR_{\alpha_2} (X)))_+ \\ =&E(I_1[X])+\gamma (1-\alpha_2) (ES_{\alpha_2} (I_2[X])-I_2(VaR_{\alpha_2} (X))), \end{aligned} $$

as a result of Eq. (2.1). Moreover,

$$ \begin{aligned} ES_{\alpha_1} (g[X;\gamma])=& ES_{\alpha_1} (I_1[X])+\gamma ES_{\alpha_1} (I_2[X]-I_2(VaR_{\alpha_2} (X)))_+ \\ =& ES_{\alpha_1} (X)-ES_{\alpha_1} (I_2[X]) +\gamma {{1-\alpha_2}\over {1-\alpha_1}} (ES_{\alpha_2} (I_2[X])-I_2(VaR_{\alpha_2} (X))) \end{aligned} $$

due to the co-monotonicity property and relation (2.1). Combining the last two equations, one may reduce our main problem to minimising

$$ h_1(\gamma) I_2(VaR_{\alpha_2} (X)) +(\lambda_1-\lambda_2) E(I_2[X])+ h_2(\gamma)ES_{\alpha_2} (I_2[X])-\lambda_1 ES_{\alpha_1} (I_2[X]), $$

where h ₁(λ) = λ₂ − h ₂(λ) and $h_2(\lambda)=\gamma (1-\alpha_2) (1+\lambda_1 \alpha_1/ (1-\alpha_1))$. Note that

$$ \gamma(1+{{\lambda_1 \alpha_1}\over {1-\alpha_1}})-\lambda_2-{{\lambda_1 \alpha_1}\over {1-\alpha_1}} $$

is negative if $\gamma\in[0,\gamma_1)$ and positive if $\gamma\in(\gamma_1,1]$.

Now, the solution for the first stage problem from part i) needs to increase as slowly as possible on $[0,VaR_{\alpha_1}(X)]$ and increase rapidly on $[VaR_{\alpha_1}(X),VaR_{\alpha_2}(X)]$. In addition, the optimal solution remains flat on $[VaR_{\alpha_2}(X),x_F]$ if γ₁ < γ ≤ 1 and increases with slope 1 whenever 0 ≤ γ < γ₁. All of these facts generate the optimal solution

$$ \left\{ \begin{array}{ll} \min\{(X-VaR_{\alpha_1}(X)+\xi_1)_+,\xi_2\} +(X-VaR_{\alpha_2}(X))_+,& 0\leq\gamma<\gamma_1,\\ \min\{(X-VaR_{\alpha_1}(X)+\xi_1)_+,\xi_2\},& \gamma_1<\gamma\leq1, \end{array}\right. $$

where $(\xi_1,\xi_2)\in\mathcal{A}_1$. Straightforward computations yield that the difference between the objective functions for the second stage problem corresponding to the two scenarios, is a constant with respect to ξ₁ and ξ₂. Therefore, both cases lead to the same solution, which is $(VaR_{\alpha_1}(X),VaR_{\alpha_1^*}(X))$. We only discuss the second case, γ₁ < γ ≤ 1, for which the second stage optimisation problem is equivalent to minimising over $\mathcal{A}_1$

$$ H(\xi_1,\xi_2):=\lambda_2 \xi_2+(\lambda_1\!-\!\lambda_2)\!\int\limits_{VaR_{\alpha_1}(X)-\xi_1}^{VaR_{\alpha_1}(X)+\xi_2-\xi_1} \bar{F}(x)\;dx \!-\!\lambda_1\left(\xi_1\!+\!{{1}\over {1-\alpha_1}}\!\int\limits_{VaR_{\alpha_1}(X)}^{VaR_{\alpha_1}(X)+\xi_2-\xi_1} \bar{F}(x)\;dx\right). $$

Taking the derivative with respect to ξ₂, we get that

$$ H(\xi_1,\xi_2)\geq H(\xi_1,\xi_1+VaR_{\alpha_1^*}(X)-VaR_{\alpha_1}(X)), \;{for\ all}\; (\xi_1,\xi_2)\in\cal{A}_1. $$

The right hand side function is increasing in ξ₁, which justifies the first part of Theorem 3.1.

Part ii) is developed in the same manner as the previous case. The solution for the first stage problem requires a rapid variation on $[0,VaR_{\alpha_2}(X)]$ since λ₁ − λ₂ < 0 and

$$ \lambda_1-\lambda_2 -\lambda_1/(1-\alpha_1)=-\lambda_1 \alpha_1/(1-\alpha_1)-\lambda_2<0. $$

In addition, the optimal solution remains flat on $[VaR_{\alpha_2}(X),x_F]$, if γ₁ < γ ≤ 1 and increases with slope 1 whenever 0 ≤ γ < γ₁. Thus, our solutions are

$$ \left\{ \begin{array}{ll}\min\{X,\xi_1\}+\min\{(X-VaR_{\alpha_1}(X))_+,\xi_2-\xi_1\} +(X-VaR_{\alpha_2}(X))_+,& 0\leq\gamma<\gamma_1,\\ \min\{X,\xi_1\}+\min\{(X-VaR_{\alpha_1}(X))_+,\xi_2-\xi_1\},& \gamma_1<\gamma\leq1, \end{array}\right. $$

where $(\xi_1,\xi_2)\in\mathcal{A}_1$. Similarly, both cases lead to the same solution, which is (0,0). Let us justify this for the case in which γ₁ < γ ≤ 1, where the second stage optimisation problem is equivalent to

$$ \begin{aligned} \min_{{\mathcal{A}}_1}\;H(\xi_1,\xi_2):=&\lambda_2 \xi_2+(\lambda_1-\lambda_2)\left(\int\limits_{0}^{\xi_1}+\int\limits_{VaR_{\alpha_1}(X)}^{VaR_{\alpha_1}(X)+\xi_2-\xi_1} \right) \bar{F}(x)\;dx \cr &-\lambda_1\left(\xi_1+{{1}\over {1-\alpha_1}}\int\limits_{VaR_{\alpha_1}(X)}^{VaR_{\alpha_1}(X)+\xi_2-\xi_1} \bar{F}(x)\;dx\right). \end{aligned} $$

Taking the derivative with respect to ξ₂, we get that $H(\xi_1,\xi_2)\geq H(\xi_1,\xi_1)$ for all $(\xi_1,\xi_2)\in\mathcal{A}_1,$ due to the fact that

$$ \bar{F}(VaR_{\alpha_1}(X)+\xi_2-\xi_1)\leq\bar{F}(VaR_{\alpha_1}(X))\leq 1-\alpha_1\leq {{\lambda_2}\over {\lambda_2+\lambda_1 \alpha_1/(1-\alpha_1)}}. $$

Finally, $H(\xi_1,\xi_1)$ is increasing in ξ₁, which completes the proof of Theorem 3.1.