1 Introduction

Over the last decades, monitoring systems have gained importance in our society [1, 2]. Their main objective is to provide quantitative information on the performance of structures under service conditions to optimize the maintenance programs and avoid severe failures [3].

In the management of civil engineering structures, there are some elements whose correct behavior is critical in the planning of repair and substitution actions due to the high technical and economic costs. Some of these crucial components are bearings, particularly when they employ newly developed technologies or are installed in bridges with unconventional designs. The correct performance of these elements becomes even more important as the management of infrastructures evolves towards predictive maintenance strategies at the network level [4]. In this context, owners have the responsibility to adequately prioritize actions on multiple different bridges based on their real condition [5,6,7,8,9].

There is a great interest on developing improved structural health monitoring (SHM) alternatives to support traditional visual inspections [10, 11]. We can broadly classify these improved SHM methods into model based and data based [11].

Model-based techniques have been traditionally applied in the field of civil engineering [12,13,14,15,16,17,18]. They employ computational models that incorporate the physics of the system, including geometry, material properties, and boundary conditions. They solve an inverse problem by building a physics-based model and then updating its parameters until the response of the model matches that which is measured in the real structure. Although this approach is currently under exhaustive research [19,20,21,22,23,24,25], it still presents some drawbacks in the assessment of real systems. Such drawbacks include the need for high-quality data and the impossibility to provide real-time insight due to the computational effort required to solve the updating problem [26].

Data-based techniques rely exclusively on experimental data acquired during monitoring campaigns and do not require a physics-based model [11]. Instead, they build statistical models and extract higher value information from instrumentation systems with multiple sensing devices [27, 28]. Once trained, they can work autonomously and provide real-time assessment [29,30,31]. We classify data-based algorithms as supervised learning (where training data contain information about the damage of the structure), and unsupervised learning (for which the status of the structure and possible damage scenarios are unknown) [32,33,34].

Machine learning techniques can identify damage due to their ability to learn complex input–output relations present in the systems under study [28, 35]. Some recently applied algorithms include artificial neural networks (ANNs) [36, 37], support vector machines [38, 39], or k-nearest neighbor [40]. There are also several works that employ unsupervised machine learning approaches to civil engineering applications [41,42,43,44,45], but these are more powerful in supervised learning contexts, where there is full knowledge about the outcome of each training sample [11].

When working with civil engineering structures under service, we often employ unsupervised learning techniques due to the lack of damaged data [11, 43]. This situation leads to the implementation of novelty detection algorithms, which detect deviations from what it is considered the reference behavior but are unable to characterize the type and extent of the damage [46].

The simplest unsupervised learning approach for novelty detection is control charts, which monitor some features extracted from measurements and find departures from their expected values [30, 47, 48]. SHM has adopted this technique from the industrial machinery field, where a much more controlled environment holds [11, 30]. Unfortunately, in the case of bridge structures, greater manufacturing inaccuracies occur, and also environmental and operational effects strongly affect measurements [29]. Statistical pattern recognition (SPR) methods represent a more robust novelty detection technique that deals with this variability [11, 28, 41, 49,50,51]. SPR algorithms employ monitoring data to create statistical models that represent the undamaged or reference condition of a system [27]. When the probability of a new measurement is below a predefined threshold value, it corresponds to an outlier [29, 30, 52].

Statistical methods become more feasible when there exists long-term monitoring data to obtain reference patterns of a system. Yet, we find very few works in the literature that employ long-term monitoring data from real civil engineering structures. In [53], authors investigate the applicability of an autoregression SPR algorithm to dynamic field data using information from the Z24 bridge in Switzerland. This bridge contains measurements under progressive damage scenarios acquired during its controlled demolition. In [54], authors use a strain regression model to calculate a health indicator based on the statistical process control theory to detect behavior changes during the 14-year monitoring period in the presence of opening cracks.

In [55] and [56], authors focus on temperature–displacement correlation analysis and regression models to remove environmental effects and normalize displacements. The recent work [57] investigates the longitudinal behavior of a jointless railway bridge and defines regression models to remove the temperature-induced displacements and implement a robust early warning system.

In this work, we propose a data-based SHM approach to assess the global behavior of Beltran bridge, a singular asymmetric prestressed concrete viaduct in Mexico. The objective is to provide reliable information on the longitudinal response of the bridge against horizontal loads. We assess the global behavior of the sliding bearings that limit the lateral loads transmitted to the substructure. To do so, we employ long-term monitoring data from four fiber optic sensors that measure the relative displacement at each bearing location. Changes in temperature during the monitoring period induce a significant variability in the measurements [33]. However, since this phenomenon affects the structure globally, there exists a high correlation between displacements from the different sensors [58], as demonstrated later in the present work.

The presence of damage at the sliding surface of the bearing increases its friction coefficient and reduces the allowable displacement for a particular load [59,60,61]. Thus, a malfunction at any of the support devices will restrict the sliding of the deck over the corresponding pier. This situation will substantially affect the correlation condition that holds during normal operation (without damage) [58]. As a consequence of the malfunction, the affected pier cap will suffer larger displacements, leading to the appearance of cracks that may compromise the structural integrity of the bridge [59].

In this work, we first apply principal component analysis (PCA) based on the presence of sensor correlation to deal with environmental variability instead of using complex thermal sensor arrays and regression models [31]. Hence, the temperature is not required as an additional variable. We calculate a single-value performance indicator from the results of PCA that has low environmental sensitivity [62]. Next, we generate a statistical model for this indicator to represent the undamaged condition of the structure [63]. To do so, we employ a kernel density function [11, 57]. We then calculate a threshold value over the model that sets the limit for outlier detection based on a confidence level. A malfunction of a bearing will result in a reduction of the existing correlation between measurements at the four locations, and, therefore, in an outlier.

Finally, to prove the efficiency of the algorithm, we submit it to a validation phase using the test dataset. To account for the presence of damage at one of the bearings, we apply a reduction of the corresponding relative displacement (50% loss of its sliding capability).

The proposed method offers a SHM tool for early warning on the real condition of bridges, which can assist managers in the scheduling of maintenance actions at the network level. The methodology also helps to complement visual inspections for individual elements with more quantitative insight regarding the global behavior of the structure. We envision the present work as a complementary tool that should work together with other SHM assessment practices, including deterministic approaches to locate and quantify the damage.

2 Methodology

2.1 Data acquisition and pre-processing

Monitoring large civil engineering structures mainly consists of acquiring long-term measurements of the structural response under ambient excitation that results mainly from environmental and operational loads (e.g. temperature, wind, traffic).

When implementing data-driven algorithms, we split the available information into a training and a testing subset. We use the training subset for optimization and the testing one is kept for validation. We denote the training dataset by \(\hat{\user2{X}} \in R^{m \times d}\). It is a multivariate dataset that contains \(m\) measurement samples from \(d\) sensors in the undamaged state of the structure. Thus, each sensor has an associated measurement vector \(\hat{\user2{x}} \in R^{m}\).

2.2 Principal component analysis

Principal component analysis is a data analysis technique that re-expresses the original data in a new basis where the information is arranged in terms of maximal variance and minimal redundancy [64, 65]. In the field of SHM and novelty detection, it is important to characterize those changes occurring under normal operation, as they may compromise the efficiency of the assessment method [43, 51]. Further details of this procedure are available in [66,67,68], where authors present various applications for SHM. In here, we briefly describe the main steps involved in the procedure, namely (i) to rescale data, (ii) to calculate the covariance matrix, (iii) to extract principal components and (iv) to compute a single-value performance indicator.

2.3 Data rescaling

Rescaling variables is a key step [66]. This step becomes critical when sensors of different types are involved [66]. Herein, we define a rescaling function \(R_{i}\) for each sensor with \(i = 1,2, \ldots , d\)

$$R_{i} \left( {\hat{\user2{x}}_{i} } \right) = \frac{{\hat{\user2{x}}_{i} - \mu_{i} }}{{\sigma_{i} }},$$
(1)

where \(\mu_{i}\) and \(\sigma_{i}\) are the mean and standard deviation of measurement vector of the \(i\)th sensor, respectively. For each sensor dataset \(\hat{\user2{x}}_{i}\), we obtain the rescaled measurement vector \({\varvec{x}}_{i} = R_{i} \left( {\hat{\user2{x}}_{i} } \right)\). We denote to the rescaled training dataset by \({\varvec{X}} \in R^{m \times d}\).

2.4 Covariance matrix calculation

The covariance matrix measures the presence of relationships in the data and demonstrates the existence of correlations [64]. For any pair of measurement vectors corresponding to two different sensors \(\left( {{\varvec{x}}_{i} , {\varvec{x}}_{j} } \right) \in R^{m}\), the covariance is:

$$C\left( {{\varvec{x}}_{i} ,{\varvec{x}}_{j} } \right) = \frac{{\mathop \sum \nolimits_{k = 1}^{m} \left( {{\varvec{x}}_{i,k} - \mu_{i} } \right)\cdot\left( {{\varvec{x}}_{j,k} - \mu_{j} } \right)}}{m - 1} ,$$
(2)

where \(\mu_{i}\) and \(\mu_{j}\) are the mean values of the \(i\)th and \(j\)th variables, respectively. The covariance matrix \(C\) is symmetric and contains the covariance values of the \(d\) variables.

2.5 Extraction of principal components

Principal components represent the directions of the data space that contain most of the original information in terms of variability [68]. We calculate them as the eigenvectors of the covariance matrix, and its weight in the analysis depends on the amount of the original variability they contain, which is directly related to the magnitude of the corresponding eigenvalue [65, 66, 68]. Since principal components indicate the directions of maximum variability in the measurements, we can isolate environmental effects by creating two different subspaces [69].

The first subspace contains most of the variability, and it is represented by the most important eigenvectors (i.e., those with larger eigenvalues) [70]. The second subspace is formed by the remaining principal components, which are associated to the lowest eigenvalues [70]. Since the second subspace has very little variability, this allows for the calculation of a robust performance indicator.

Hence, we must decide the number of components that are sufficient to account for the environmental variability and form the first subspace. We can justify this decision on the cumulative percentage of variance \({\text{CPV}}\) [68], which measures the amount of variance captured by the first \(k\) components, such that

$$CPV\left( k \right) = \frac{{\mathop \sum \nolimits_{j = 1}^{k} \lambda_{j} }}{{\mathop \sum \nolimits_{j = 1}^{p} \lambda_{j} }}\cdot100 ,$$
(3)

where \(\lambda_{j}\) represents the \(j\)th eigenvalue. An acceptable level of variance for the first subspace is typically around 90–95% [64, 71].

Let \({\varvec{P}} \in R^{d \times d}\) be a square matrix containing the principal components of the training dataset \({\varvec{X}}\). We divide \({\varvec{P}}\) into two submatrices, \({\varvec{P}}_{s1} \in R^{d \times k}\) and \({\varvec{P}}_{s2} \in R^{{d \times \left( {d - k} \right)}}\), associated with the first and second subspaces, respectively.

2.6 Single-value performance indicator

In this step, we calculate the distance of the original data in the training set to the two previously defined subspaces, \({\varvec{P}}_{s1}\) and \({\varvec{P}}_{s2}\). The Hotelling’s or \(T^{2}\)statistic measures the distance from the first subspace \({\varvec{P}}_{s1}\) [65, 72]. For each measurement example \({\varvec{x}}\left( j \right) = \left( {x_{1} ,x_{2} , \ldots , x_{d} } \right)\) in the training set with \(j = 1,2, \ldots ,m\), we compute the performance indicator as

$$T^{2} \left( j \right) = {\varvec{x}}\left( j \right)\cdot\left( {{\varvec{P}}_{s1} \cdot\Lambda^{ - 1} \cdot{\varvec{P}}_{s1}^{T} } \right)\cdot{\varvec{x}}\left( j \right)^{T} \user2{ },$$
(4)

where matrix \(\Lambda \in R^{k \times k}\) is a diagonal matrix containing the first \(k\) eigenvalues. Complementarily, \(Q\) statistic, also referred to as squared prediction error, quantifies the distance from the second subspace [42]:

$$Q\left( j \right) = {\varvec{x}}\left( j \right)\cdot\left( {{\varvec{P}}_{s2} \cdot\Lambda_{2}^{ - 1} \cdot{\varvec{P}}_{s2}^{T} } \right)\cdot{\varvec{x}}\left( j \right)^{T}$$
(5)

Here \(\Lambda_{2} \in R^{{\left( {d - k} \right) \times \left( {d - k} \right)}}\) is the diagonal matrix that contains the less meaningful eigenvalues. During normal operation, the \(Q\) statistic takes small values due to its low variability content. This enables to find a statistical representative model for the outlier detection algorithm.

2.7 Baseline model generation

The baseline model stems from the statistical characterization of the \(Q\) statistic sample in the undamaged state. For that purpose, we employ Kernel density estimation [73, 74]. This technique provides a continuous function that accurately fits the distribution of the reference performance indicator sample and constitutes the baseline pattern for damage detection [57, 75].

2.8 Threshold value calculation

The assessment methodology for outlier detection developed in this work belongs to the unsupervised learning domain. This is the most common situation in SHM strategies to in-service structures since data from possible damage states are rarely available [11, 56, 76]. The main goal of this approach is to detect deviations from what is considered to be the reference state, which is statistically defined as the baseline model.

In the baseline model, we select an uncertainty level over which we assume the structure may have some unknown damage. In our case, we select a 5% uncertainty level (95% confidence level) to achieve a strong enough SHM assessment tool [11]. The limit value is directly obtained by calculating the 95 percentile of the corresponding kernel density function [73, 77, 78].

2.9 Validation

Once we have constructed the baseline model and set the threshold value to detect outliers, we validate the algorithm using the test dataset. Let \({\varvec{X}}_{test} \in R^{n \times d}\) be the test matrix that contains \(n\) new examples unseen by the algorithm. We evaluate the performance of the algorithm based on the main machine learning metrics, i.e. accuracy, precision, recall, and F1 score [79].

3 Case study

In this work, we employ a data-driven SHM approach for bearing behavior assessment. This technique provides a “single-value” tool for decision-making and bearing damage assessment in structural management.

3.1 Bridge description

This study considers the Beltran bridge, located in kilometer point (KP) 119.5 of the Guadalajara–Colima highway in Mexico. Its design incorporates one pier of considerable height and only two expansion joints in the deck, located over the abutments. This structural profile is typically employed to cross abrupt areas, such as valleys [80]. A representative view is shown in Fig. 1.

Fig. 1
figure 1

Structural profile of the singular Beltran bridge. Detail of the fixed point

Full size image

Its continuous superstructure is 297.49 m long and it is distributed in four spans (73.60 + 12.40 + 134.90 + 76.59 m). The prestressed concrete deck is a single box girder with variable depth from 4.40 m in the mid-section of the main span to 7.50 m in support sections. The top and bottom slabs are 0.50 m and 0.75 m thick, respectively. Figure 2 shows the section specifications.

Fig. 2
figure 2

Bridge section details

Full size image

Pier 4 is rigidly connected to the deck and it represents the theoretical fixed point in the structure for longitudinal loads. This pier is 120.45 m height. Its width varies linearly (1:60) from 6.00 m at the foundation to 4.00 m at the cap. The thickness of the walls is 0.80 m.

Piers 2 and 3 are made of concrete and they have box sections of 0.40 m thickness. They have a height of 24.25 m. The deck-pier contact is established with pot bearings allowing for sliding in the longitudinal direction. This kind of sliding bearing carries vertical loads by compression on an elastomeric element confined within the machined pot plate that works under a triaxial pressure. It offers low resistance to deformation but high vertical stiffness [61, 81]. These elements limit the horizontal force transmitted to the piers by allowing certain translation to accommodate longitudinal displacements [61].

The structural scheme of the bridge must withstand horizontal loads that are likely to occur during the bridge lifetime as a result of temperature variations, wind, small seismic-induced motions, or strong braking forces from vehicles, among others [82]. Sliding bearings limit the horizontal force that reaches the pier and causes displacements at the pier cap [82]. We can model these devices as a friction element whose behavior is governed by a parameter \(\mu\) that represents its sliding capabilities. A degradation on the sliding surface of the bearing will reduce the required relative displacement between the deck and the piers [57, 60, 82].

Figure 3 illustrates the pier-deck structural system, where \(u_{a} ,u_{p}\) and \(u_{b}\) stand for the longitudinal displacement of the deck, the pier, and the bearing, respectively. \(M_{d}\) and \(M_{p}\) represent the mass of the deck and the pier, \(\mu\) is the friction coefficient of the bearing and \(K_{p}\) is the longitudinal stiffness of the pier. We express the displacement at the pier cap as

$$u_{p} = u_{a} - u_{b} .$$
(6)
Fig. 3
figure 3

Simplified approximation of the structural system deck-bearing pier

Full size image

Based on this model, pot bearings can operate in two different regions, as shown in Fig. 4 [59, 61, 83]. When the external loads are below the friction force, there is no displacement of the bearing (static friction) [84]. On the other hand, when exceeding the limit friction force, the energy transmitted to the pier is limited due to a displacement of the bearing [61].

Fig. 4
figure 4

Operating schemes for an undamaged and a damaged pot bearing

Full size image

For an undamaged bearing, the friction coefficient is very low (\(\mu \varepsilon \left[ {0.02 - 0.05} \right]\)), and except for very small loads, it will work in the sliding region [59]. In this situation, the transmitted load is the critical friction force that will be small enough to ensure the correct longitudinal behavior [61, 84]. The presence of damage at the sliding surfaces of the bearing causes a reduction of its allowable displacement for a certain load [59,60,61]. We can mathematically model this situation as an increase in the friction coefficient [59].

Figure 4 compares the behavior diagram of an undamaged and a damaged bearing, where \(\mu^{u}\) and \(\mu^{d}\) represent the friction coefficient in the undamaged and the damaged state, respectively [59, 85].

For the same external load, a damaged bearing will transmit higher loads to the pier cap and cause cracks that may compromise the structural integrity. Hence, assessing the performance of these devices in the long term is key to ensure a correct structural response against horizontal loads.

3.2 The monitoring system

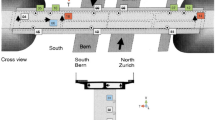
Given the structural particularities of Beltran bridge, a long-term monitoring system was installed in 2012. The bridge was equipped exclusively with fiber optic sensors [86,87,88]. In this work, we had access to the four fiber optic displacement sensors that record the longitudinal displacements of the deck over the substructure of the bridge. Figure 5 describes their location. These measurements correspond to the relative displacement of the sliding bearings, \(u_{b}\).

Fig. 5
figure 5

Locations of the displacement sensors

Full size image

Pier 4 represents the fixed point of the structure for longitudinal forces. Although no relative displacement exists there, it is subjected to absolute displacements. Displacement sensors are located at the top of piers 1, 2, 3 and 5, where pot bearings connect the piers with the deck to allow for sliding in the longitudinal direction. Bearings are critical elements to ensure the structural integrity of this bridge.

3.3 Data acquisition

The monitoring system was activated in August 2012 and worked continuously until July 2013. Due to some temporary outages, the total recording period lasted approximately 9 months.

The data acquisition process was carried out at a sampling frequency of 200 Hz. The transmission of the data was done monthly and contained the mean values of the displacements measured every ten minutes for each sensor. This subsampling suffices to analyze the long-term variations of longitudinal displacements at the bearing locations (\(u_{b}\)) and reduces the storage space to 40.5 MB for the whole dataset. After training statistical the model, it is possible to transmit the data daily for real-time damage assessment. With the previous specifications, we obtained a total of 38,592 measurements for each displacement sensor during the monitoring period. After removing zero values, the final number of measurements per sensor is 37,692. Finally, we split the data into training and test subspaces. We select the first 80% of samples to train the algorithm, resulting in a training dataset \({\varvec{X}} \in R^{30154 \times 4}\). We employ the final 20% to evaluate the performance of the algorithm against unseen data during the validation phase.

3.4 Data pre-processing

Temperature changes affect the structure globally. Accordingly, there must exist a correlation between measurements at different locationsFootnote 1 [55, 58, 62]. Following [62], the use of linear PCA is justified since there exists a linear correlation between variables, i.e. relative displacements at the four bearing locations. In [62], where the analysis variables are dynamic features of the structure, it was also proven that linear PCA works even in slightly nonlinear cases. Figure 6 shows the presence of these correlations through the scatterplot of each pair of variables together with the value of the Pearson’s coefficient of correlation, verifying that the monitoring period corresponds to the undamaged or reference condition of the support devices. Figure 6 also includes the histogram for the training dataset of each sensor (\(THL1\) to \(THL4\)).

Fig. 6
figure 6

Correlation summary of the four displacement sensors

Full size image

3.5 Data processing

In long-term monitoring, environmental changes (i.e. temperature) strongly affect longitudinal displacements during normal operation. For this reason, these measurements are inadequate for outlier detection since they exhibit a large variability even under normal operation. Given the existing correlation between sensor measurements at the different locations (as shown in Fig. 6), we look for a damage indicator that is robust to these phenomena. We use principal component analysis (PCA) to find and isolate any variance induced by temperature in the training dataset. We emphasize that temperature is unmeasured, and the force–displacement response of isolate bearings is untreated. Instead, we focus on the existing correlations in the displacement measurements of the bearings at different locations.

We firstly rescale the training dataset by applying the corresponding function \(R^{i}\) to each sensor dataset with \(i = \left( {1,2,3,4} \right)\).

The covariance matrix \(C\) for the four standardized displacement sensors is

$$C = \left( {\begin{array}{*{20}c} {\begin{array}{*{20}c} {1.00} \\ {\begin{array}{*{20}c} {0.77} \\ {\begin{array}{*{20}c} { - 0.78} \\ {0.77} \\ \end{array} } \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} {0.77} \\ {\begin{array}{*{20}c} {1.00} \\ {\begin{array}{*{20}c} { - 0.8} \\ {0.51} \\ \end{array} } \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} { - 0.78} \\ {\begin{array}{*{20}c} { - 0.80} \\ {\begin{array}{*{20}c} {1.000} \\ { - 0.61} \\ \end{array} } \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} {0.77} \\ {\begin{array}{*{20}c} {0.51} \\ {\begin{array}{*{20}c} { - 0.61} \\ {1.000} \\ \end{array} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \right).$$
(7)

According to the theory of PCA, we obtain the principal components as the eigenvectors of matrix \(C\). Table 1 shows the four principal components.

Table 1 Eigenvector decomposition
Full size table

The analysis requires an exhaustive evaluation of the principal components to understand how powerful PCA is to manage multivariate data [67, 68]. Table 2 summarizes the most relevant information.

Table 2 Statistical evaluation of components
Full size table

An acceptable level of variance for the first subspace is typically around 90–95% of the total variance [64, 71]. In this case, we only need two components to reach almost 91% of the total variance, so we define the first subspace with half of the total components and leave the other two components for the second subspace. Since principal components indicate the directions of maximum variability in the measurements, the first subspace contains most of the variation present in the data, and the second subspace contains the remaining noise. Here, the main source of variability comes from environmental effects, i.e., temperature variations. Thus, the first subspace contains environmental variability. The matrices representing both subspaces are, respectively.

$$P_{s1} = \left( {\begin{array}{*{20}c} {\begin{array}{*{20}c} { - 0.5329} \\ { - 0.4976} \\ \end{array} } & {\begin{array}{*{20}c} { - 0.1336} \\ {0.5181} \\ \end{array} } \\ {\begin{array}{*{20}c} {0.5108} \\ { - 0.4555} \\ \end{array} } & {\begin{array}{*{20}c} { - 0.3286} \\ { - 0.7783} \\ \end{array} } \\ \end{array} } \right),$$
(8)
$$P_{s2} = \left( {\begin{array}{*{20}c} {\begin{array}{*{20}c} {0.3541} \\ {0.4938} \\ \end{array} } & {\begin{array}{*{20}c} {0.7569} \\ { - 0.4900} \\ \end{array} } \\ {\begin{array}{*{20}c} {0.7915} \\ { - 0.0662} \\ \end{array} } & {\begin{array}{*{20}c} { - 0.0686} \\ { - 0.4271} \\ \end{array} } \\ \end{array} } \right).$$
(9)

Next, we calculate both statistics for the training set and obtain the corresponding samples \({\varvec{T}}^{2} \in R^{m}\) and \({\varvec{Q}} \in R^{m}\) that are representative of the undamaged condition of the structure. The temporary representation (see Fig. 7) of both statistics for the training set provides an insightful interpretation on the distribution of the existing variability. On the one hand, \({\varvec{T}}^{2}\) statistic contains most of the variability, in this case induced by seasonal temperature changes. On the other hand, \({\varvec{Q}}\) statistic shows a much lower fluctuation, indicating that its value is poorly affected by the inherent environmental trends.

Fig. 7
figure 7

Representation of \(T^{2}\) and \(Q\) statistics for the training set

Full size image

Table 3 gathers the statistical properties of both indicators, including the mean value and the standard deviation. This information supports the decision of employing \(Q\) statistic as the damage sensitive feature for outlier detection.

Table 3 Statistical properties of the training dataset for both statistics
Full size table

We first generate the statistical baseline model for the \(Q\) statistic vector calculated for the training dataset using the kernel density estimation approach. Onto this baseline model, we select an uncertainty level over which we will assume the bridge may have some unknown damage. We consider that those indicators exceeding the threshold value are more likely to belong to the unknown damage state. In our case, we select a 5% uncertainty level (95% confidence level) to achieve a strong enough SHM assessment tool towards false negatives (undetected damage), as they are of great importance in the civil engineering field [74].

The limit value is directly obtained by calculating the 95 percentile over the corresponding kernel model [73, 77, 78], being \(Q_{{{\text{limit}}}} = 0.9845\).

Figure 8 shows graphically the limit between the two possible states. The green-shadowed region, which includes 95% of the sample data, represents the undamaged state, while the red-shadowed region stands for the unknown state of the structure. Hence, we identify the abnormal behavior or damaged state as any departure from the previously calculated threshold value in the \(Q\) statistic indicator with 95% certainty.

Fig. 8
figure 8

Classification threshold over the reference model with a 5% uncertainty

Full size image

4 Validation results

In this section, we use the test dataset, which contains the final 20% of the available measurements, i.e. \(X_{{{\text{test}}}} \in R^{7538 \times 4}\). Since the whole monitoring period belongs to the undamaged condition of the structure, this dataset only tests the algorithm against false positives. We additionally account for the presence of damage at one of the bearings, assuming that it results in a reduction of the measured displacement, indicating a loss of its sliding properties. We apply this reduction to the measurements of the sensor associated to the bearing at pier 2. We assume the following relations between displacements in the undamaged state:

$$u_{b,u} = \alpha \cdot u_{a,u} ,$$
(11)
$$u_{p,u} = \left( {1 - \alpha } \right)\cdot u_{a,u} ,$$
(12)

where \(\alpha\) expresses the distribution of the absolute displacement (\(u_{a,u}\)) between the pier and the bearing. In the undamaged state, we set a value of \(\alpha = 0.9\) since the bearing absorbs most of the absolute displacement. Then, we represent the damaged scenario through a reduction in \(\alpha\), as:

$$\alpha^{\prime} = \alpha - x,$$
(13)

where \(\alpha ^{\prime}\) measures the new fraction of absolute displacement that goes to the bearing in the damaged condition and \(x\) indicates the corresponding reduction with respect to the undamaged state. These bearings must always allow sliding at operational loads. Despite bridges are generally calculated assuming a total blockage of the supports, this is a critical situation. In here, we apply a reduction factor of \(x = 0.45\), meaning a 50% loss of the sliding capabilities of a bearing. This scenario is sufficiently far from the limit situation but reasonably indicates the need of an intervention. We reach the following relation between damaged and undamaged bearing displacements:

$$u_{b,d} = \frac{{\left( {\alpha - x} \right)}}{\alpha } \cdot u_{b,u} = 0.50 \cdot u_{b,u} ,$$
(14)

Hence, the final test dataset contains two parts: the original test dataset and the damaged test dataset, resulting in a total of \(2 \cdot n = 15076\) testing examples. Figure 9 shows the results delivered by the algorithm after calculating the \(Q\) indicators, where the first half of the test corresponds to undamaged bearings and the last half represents the damaged bearing situation. In addition, Table 4 gathers the main metrics that evaluate the algorithm performance.

Fig. 9
figure 9

Performance indicator in the test dataset

Full size image
Table 4 Validation results
Full size table

These results prove the ability of the algorithm to detect novel measurements and also its low sensitivity to environmental variability. When new long-term monitoring measurements are registered, we can recalibrate the algorithm. However, to prove the ability of the algorithm to detect damage would require the occurrence of the damage while the monitoring system is activated.

5 Conclusions

This work addresses the problem of structural performance assessment with a data-based approach as opposed to more traditional model-based methods. The main advantage of this data-driven scope lies in its expected flexibility to fit any type of system or structure where correlations are detected in the response measurements from various sensors.

Due to the characteristics of this bridge, any repair or substitution work is complicated and requires expensive interventions according to its complexity. Therefore, any action should be justified towards an efficient budget allocation.

With the use of the proposed method, we evaluate quantitatively the behavior of the structure, where we can detect anomalies by comparing a single damage indicator with a threshold value, isolating the effects from changing environmental conditions and providing a robust performance statistic.

The damage indicator \(Q\) shows to be a powerful measure of the correlation found between displacements at different locations. It gathers the information from all of the considered displacement sensors and provides a global vision for decision-making in the management of the bridge. In addition, this statistic is isolated from the variability induced by environmental and operational phenomena during normal service, giving robustness to the methodology.

With the temporary representation of the new damage indicators registered during a monitoring period in an unknown state, we detect departures from the normal condition and identify trends in the evolution of the statistic. In addition, once an alert is raised, the location of the damaged bearing can be identified just by looking at the current displacement data and finding the abnormal sensor measurement that is causing the loss of correlation at that moment.

The tool configuration is useful for the scheduling of periodic inspections as a supplement to traditional bridge inspections, providing a more objective approach to complete the information and help managers in decision-making.

In conclusion, this study demonstrates the utility of exploiting and managing the available historical data stemming from periodical monitoring processes to control and predict the evolution of the behavior of certain critical elements in structures, helping managers to prioritize maintenance actions and take decisions at the network level.

Future work includes the application of this method to different bridges to further prove the validity of the approach. We also envision to replace the PCA method by a residual deep neural network that exploits also nonlinear correlations between the different sensors.