Production forecast of fractured shale gas reservoir considering multi-scale gas flow

Abstract

The shale gas experiences many different spatial scales during its flow in the reservoir, which will engender different flow mechanisms. In order to accurately simulate the production performance of shale gas well, it is essential to establish a multi-continuum model for shale gas reservoir. Based on the geometrical scenario of multistage horizontal well fracturing, this paper builds up a triple-continuum model incorporating three systems: matrix with extremely low permeability, less permeable natural fractures and highly permeable hydraulic fractures. This numerical model employs Langmuir adsorption equation to present the influence of desorption gas in matrix and considers the Klinkenberg effect in matrix and natural fractures by adjusting the apparent permeability. The solution of this model is achieved using implicit scheme. Eventually, this model is applied on the single well production situation in a synthetic reservoir, production decline curves and cumulative production curves are obtained, then the sensitivity analysis is made on various kinds of parameters; thus, the influences of these parameters on production rate are obtained: The gas rate will rise with the increase in hydraulic fracture half-length, meshing size, Langmuir volume and Langmuir pressure, but with the decrease in hydraulic fracture spacing.

Introduction

Nowadays, shale gas production has been making a significant contribution to the world’s gross energy supply (Li 2009) and accounts for over 50 % of American natural gas production (Montgomery et al. 2005). The exploration shows that China is also abundant in terms of the total recoverable shale gas reserves (Hu et al. 2010). Shale gas reservoir distinguishes itself by its extremely low permeability and low porosity, which engenders great difficulty on the exploitation and production of shale gas (Curtis 2002; Li et al. 2015). In addition, the pore size in shale matrix is only about 2–50 nm and 0.1–5 μm for the natural fractures (Sondergeld et al. 2010). Instead of the conventional method, the effective and economic development of shale gas reservoir requires the formation to be hydraulically fractured, and the multistage hydraulic fracturing method has been prevalently employed in shale gas reservoir (Ozcan et al. 2014).

Naturally fractured reservoir (NFR) can be defined as a reservoir contains a connected network of fractures created by natural processes and proved to have an effect on fluid flow (Javadpour 2009; Sun et al. 2016). NFR contains more than 20 % of the world’s hydrocarbon reserves (Sarma and Aziz 2006). Shale gas reservoir generally contains natural fractures; thus, shale gas reservoir can be classified into NFR. In shales, natural fractures provide permeability and the matrix provides storage for most of the gas (Bello and Wattenbarger 2010). The gas molecules are stored by a combination of compression in the pores and adsorption on the surface of the solid shale matter (Bello and Wattenbarger 2008). It is believed that compared to the induced fractures, the permeability of natural fractures is too small to be considered. Yet this is proved to be wrong because the natural fracture network can actually enhance the productivity of the reservoir greatly (Cipolla et al. 2010); thus, the local natural fractures shall not be ignored.

From the nanoscale matrix to the hydraulic fractures whose width is several millimeters, shale gas experiences many different spatial scales during its flow in the reservoir (Sheng et al. 2012; Guo et al. 2015). According to different spatial scales, the flow of gas in the shale formation will result in many different mechanisms (Jiang and Wang 2014; Xu et al. 2015). As the natural fractures and the hydraulic fractures present a big difference in terms of fracture conductivity and connectivity, it is more realistic to assume fractures having different properties (Hassan and Wattenbarger 2011).

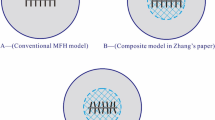
Commonly, the dual-porosity model is often used for the simulation of oil and gas reservoir, but only two continuums are unable to fully describe the multi-mechanism and multi-scale gas flow in shale formation (Cheng and Dong 2012). In order to accurately simulate the complicated shale gas flow and production, multi-continuum models shall be built up (Zhu and Zhang 2013). Furthermore, some microscopic mechanisms, such as desorption and diffusion effect, should be considered in the model as well (Ozkan et al. 2010); thus, triple-continuum model begins to emerge (Fig. 1).

Fig. 1

Illustration of gas flow from nanoscale to macroscale

The first triple porosity was introduced by Abdassah and Ershaghi (1986), and they divided the matrix to have different properties with single fracture. Then Al-Ahmadi and Ershaghi (1996) first assume the fractures to have different properties, their model was presented using a radial system, and the natural fractures and the hydraulic fractures can both feed the well. Drier (2004) improved the triple-continuum model originally proposed by Al-Ahmadi and Ershaghi (1996) by considering transient flow condition between natural fractures and hydraulic fractures. Bello and Wattenberger (2008, 2009, 2010) applied the triple-continuum model to analyze the production rate in horizontal well in tight fractured reservoirs. Ozkan et al. (2009) proposed a trilinear model comprising three continuous media: finite conductivity hydraulic fractures, dual-porosity inner reservoir between the hydraulic fractures and outer reservoir beyond the tip of the hydraulic fractures. Apaydin et al. (2012) examine the effects of matrix micro-fractures on effective matrix permeability of a dual-porosity medium. They stated that matrix micro-fractures accelerate production by providing earlier and more effective contribution of the matrix into flow rates. Therefore, the multi-continuum model for shale gas reservoir commonly comprises three media: matrix, natural fractures and hydraulic fractures, which is also called dual-fracture model (Al-Ahmadi and Ershaghi 1996).

The triple-continuum model has undergone great development recently, and models for reservoirs with sophisticated geometries and conditions have been built up in previous work. The findings show that the triple-continuum model can capture the reservoir heterogeneity very well (Al-Ahmadi 2010). Nonetheless, most previous triple-continuum models were solved using analytical method instead of numerical approach to predict the transient pressure in the reservoir. In addition, diffusion mechanism, which is proved to have significant impact on gas flow, was rarely considered in previous models. In this work, a new numerical triple-continuum model incorporating desorption and diffusion is proposed and applied for the production simulation in fractured shale gas reservoir.

Incorporated mechanisms

Adsorption and desorption of shale gas

Shale gas can exist as free gas phase or as adsorbed gas on solids in pores, and the methane molecules are mainly adsorbed to the carbon-rich components, i.e., kerogen (Lu et al. 1995). As observed, the adsorbed gas accounts for a significant fraction of gas reserves in place. With the drawdown of the formation pressure, the adsorbed gas is released from the surface of solids and becomes free gas, contributing to the total production. In this work, the mass flux of the adsorbed gas in a micro-unit within a short time is described as:

$$q_{\text{ad}} = - \frac{{\partial (\rho_{\text{g}} V_{\text{E}} )}}{\partial t}{\text{d}}x{\text{d}}y{\text{d}}z{\text{d}}t$$

(1)

Here the Langmuir adsorption model is employed to represent the adsorbed gas content V _E:

$$V_{\text{E}} = \frac{{V_{\text{L}} p}}{{p_{\text{L}} + p}}$$

(2)

Where V _L stands for the Langmuir volume, p _L is the Langmuir pressure, and p is the reservoir pressure.

Klinkenberg effect

In low-permeability shale gas reservoirs with small pore space, the Klinkenberg effect may alter the permeability significantly, especially in low reservoir pressure conditions (Wu et al. 1998). In this work, Klinkenberg effect is incorporated into the gas flow equations by modifying the apparent permeability of gas as a function of pressure (Wu et al. 2009):

$$k_{\text{a}} = k_{\text{i}} \left[ {1 + \frac{b}{p}} \right]$$

(3)

where k _a is the apparent permeability of the gas phase; k _i is the constant, equals to the gas permeability in large pores without Klinkenberg effect; b is the Klinkenberg factor.

Although the Klinkenberg factor may change with gas nature and pore size, we adopt b as a constant in our simulation, and its value can be calculated as (Yao et al. 2013):

$$b_{{}} = \frac{{4k_{\text{i}} }}{{2.81708k_{i} \sqrt {\frac{{k_{\text{i}} }}{\phi }} }}\sqrt {\frac{\pi RT}{{2M_{\text{g}} }}}$$

(4)

Model construction

Model assumptions

Before building the triple-continuum model, some assumptions are made based on the characteristics of each medium:

• 1. Three media are incorporated in the model: matrix, less permeable natural fractures and more permeable hydraulic fractures.

• 2. As shown in Fig. 2, the hydraulic fractures perpendicular to the horizontal well are discretely distributed, and the gas flow in hydraulic fractures is considered as one-dimensional flow, whereas the matrix system and the natural fracture system are continuously distributed over the whole rectangular reservoir, and the flow in these two media is considered as two-dimensional flow.

  Fig. 2

  

  Geometric model of the fractured shale gas reservoir

• 3. Flow is sequential from one medium to another: from matrix to natural fractures to hydraulic fractures.

• 4. The desorption of adsorbed gas is only considered in matrix, and the Klinkenberg effect exerts influences on both matrix and natural fractures.

• 5. The rock is incompressible, and the porosity is seen as a constant.

• 6. The gas is regarded as compressible real gas, and the gas viscosity and gas compressibility factors are both the function of pressure.

The flow equation of matrix

The continuity equation of matrix is given by:

$$- \left[ {\frac{{\partial (\rho_{\text{g}} v_{x} )}}{\partial x} + \frac{{\partial (\rho_{\text{g}} v_{y} )}}{\partial y}} \right] - q_{\text{m}} = \frac{{\partial (\rho_{\text{g}} \phi_{m} + \rho_{\text{g}} V_{\text{E}} )}}{\partial t}$$

(5)

q _m is the inter-porosity flow term from matrix to natural fractures, which is expressed as:

$$q_{\text{m}} = \frac{{\rho_{\text{g}} k_{\text{ma}} \alpha_{\text{mf}} (p_{\text{m}} - p_{\text{f}} )}}{{\mu_{\text{g}} }}$$

(6)

$$\alpha_{\text{mf}} = \frac{{A_{\text{mf}} }}{{L_{\text{f}} }}$$

(7)

where α _mf is the shape factor from matrix to natural fractures, A _mf represents the interface area between matrix and natural fractures per unit volume, and L_f represent the characteristic length of natural fracture, which can be seen as its average spacing. The natural fracture spacing in the shale formation is generally 0.05–10 m (Bustin et al. 2008).

In the continuity equation of matrix, when considering Klinkenberg effect, the apparent permeability in the kinetic equation shall be adjusted:

$$v_{\text{m}} = - \frac{{k_{\text{ma}} }}{{\mu_{\text{g}} }}\frac{{\partial p_{\text{m}} }}{\partial L}$$

(8)

$$k_{ma} = k_{mi} \left[ {1 + \frac{{b_{m} }}{{p_{m} }}} \right]$$

(9)

And the gas density can be expressed as:

$$\rho_{\text{g}} = \frac{Mp}{RTZ}$$

(10)

Substituting Eqs. (6)–(10) into Eq. (5), then we obtain:

$$\frac{\partial }{\partial x}\left( {\frac{{p_{\text{m}} }}{\mu Z}\frac{{\partial p_{\text{m}} }}{\partial x}} \right) + \frac{\partial }{\partial y}\left( {\frac{{p_{\text{m}} }}{\mu Z}\frac{{\partial p_{\text{m}} }}{\partial y}} \right) - \frac{{\alpha_{\text{mf}} p_{\text{m}} (p_{\text{m}} - p_{\text{f}} )}}{\mu Z} = \left[ {\frac{{\phi_{\text{m}} }}{{k_{ma} }} + \frac{{V_{\text{L}} p_{\text{m}} (2p_{\text{L}} + p_{\text{m}} )}}{{k_{\text{ma}} (p_{\text{L}} + p_{\text{m}} )^{2} }}} \right] \cdot \frac{\partial }{\partial t}\left( {\frac{{p_{\text{m}} }}{Z}} \right)$$

(11)

Taking the transformation we can obtain:

$$\frac{\partial }{\partial t}\left( {\frac{p}{Z}} \right) = \frac{1}{Z}\frac{\partial p}{\partial t} + p\frac{\text{d}}{{{\text{d}}p}}\left( {\frac{1}{Z}} \right)\frac{\partial p}{\partial t} = \left( {\frac{1}{p} - \frac{1}{Z}\frac{{{\text{d}}Z}}{{{\text{d}}p}}} \right)\frac{\partial p}{\partial t} = C_{\text{g}} \frac{\partial p}{\partial t}$$

(12)

Substituting Eq. (12) into Eq. (11), we obtain:

$$\frac{\partial }{\partial x}\left( {\frac{{p_{\text{m}} }}{\mu Z}\frac{{\partial p_{m} }}{\partial x}} \right) + \frac{\partial }{\partial y}\left( {\frac{{p_{\text{m}} }}{\mu Z}\frac{{\partial p_{\text{m}} }}{\partial y}} \right) - \frac{{\alpha_{\text{mf}} p_{\text{m}} (p_{\text{m}} - p_{\text{f}} )}}{\mu Z} = \left[ {\frac{{\phi_{\text{m}} p_{\text{m}} C_{\text{g}} }}{{k_{ma} Z}} + \frac{{V_{\text{L}} p_{\text{m}}^{2} (2p_{\text{L}} + p_{\text{m}} )C_{\text{g}} }}{{k_{\text{ma}} (p_{\text{L}} + p_{\text{m}} )^{2} Z}}} \right] \cdot \frac{{\partial p_{\text{m}} }}{\partial t}$$

(13)

Equation (13) is final form of the flow equation of matrix system, and its initial and boundary conditions are:

$${\text{Initial}}\,{\text{condition:}}\;p_{\text{m}} = p_{\text{i}} ,\quad t = 0$$

(14)

$${\text{Boundary condition:}}\;\left. {\frac{{\partial p_{\text{m}} }}{\partial n}} \right|_{\varGamma } = 0,\quad t > 0$$

(15)

The flow equation of natural fractures

The continuity equation in natural fracture is:

$$- \frac{{\partial (\rho_{\text{g}} v_{x} )}}{\partial x} - \frac{{\partial (\rho_{\text{g}} v_{y} )}}{\partial y} + q_{\text{m}} - q_{\text{f}} = \frac{{\partial (\rho_{\text{g}} \phi_{\text{f}} )}}{\partial t}$$

(16)

where q _f is the flow term from the natural fractures to the hydraulic fractures:

$$q_{\text{f}} = \frac{{\rho_{\text{g}} k_{\text{fa}} \alpha_{\text{fF}} (p_{\text{f}} - p_{\text{F}} )}}{{\mu_{\text{g}} }}$$

(17)

α _fF is the shape factor from natural fractures to hydraulic fractures, and it is defined as the interface area of natural fractures and hydraulic fractures per unit volume divided by the characteristic length of hydraulic fracture.

$$\alpha_{\text{fF}} = \frac{{A_{\text{fF}} }}{{L_{\text{F}}^{{}} }}$$

(18)

When considering Klinkenberg effect in the natural fractures:

$$k_{\text{fa}} = k_{\text{fi}} \left[ {1 + \frac{{b_{\text{f}} }}{{p_{\text{f}} }}} \right]$$

(19)

$$b_{\text{f}} = \frac{{4k_{\text{fi}} }}{{2.81708k_{\text{fi}} \sqrt {\frac{{k_{\text{fi}} }}{{\varphi_{\text{f}} }}} }}\sqrt {\frac{\pi RT}{{2M_{\text{g}} }}}$$

(20)

Substituting Eqs. (19) and (20) into Eq. (16), we obtain:

$$\frac{\partial }{\partial x}\left( {\frac{{p_{\text{f}} }}{\mu Z}\frac{{\partial p_{\text{f}} }}{\partial x}} \right) + \frac{\partial }{\partial y}\left( {\frac{{p_{\text{f}} }}{\mu Z}\frac{{\partial p_{\text{f}} }}{\partial y}} \right) + \frac{{k_{\text{ma}} \alpha_{\text{mf}} p_{\text{f}} (p_{\text{f}} - p_{\text{F}} )}}{{k_{\text{fa}} \mu Z}} - \frac{{\alpha_{\text{fF}} p_{\text{f}} (p_{\text{f}} - p_{F} )}}{\mu Z} = \frac{{\phi_{\text{f}} p_{\text{f}} C_{\text{g}} }}{{k_{\text{fa}} Z}}\frac{{\partial p_{\text{f}} }}{\partial t}$$

(21)

Equation (21) is final form of the flow equation of natural fractures, and its initial and boundary conditions are:

$${\text{Initial}}\,{\text{condition:}}\;p_{\text{f}} = p_{\text{i}} ,\quad t = 0$$

(22)

$${\text{Boundary condition:}}\;\left. {\frac{{\partial p_{\text{f}} }}{\partial n}} \right|_{\varGamma } = 0,\quad t > 0$$

(23)

The flow equation of hydraulic fractures

Unlike the matrix and the natural fractures, hydraulic fractures are discretely distributed with a certain spacing over the reservoir; consequently, the flow in the hydraulic fractures is viewed as one-dimensional flow. Moreover, neither the desorption nor the Klinkenberg effect is considered in the hydraulic fractures; thus, its flow equation is:

$$- \frac{{\partial (\rho_{\text{g}} v_{y} )}}{\partial y} + q_{\text{f}} - (q_{\text{w}} ) = \frac{{\partial (\rho_{\text{g}} \phi_{\text{F}} )}}{\partial t}$$

(24)

where q _w is the flow term from hydraulic fractures to the horizontal well, V _i,j is the volume of the grid at which the hydraulic fractures intersect with the wellbore, and q is the gas production rate. Figure 3 is an illustration of flow in hydraulic fracture grids.

Fig. 3

Illustration of flow in hydraulic fractures

$$q_{\text{w}} = \frac{q}{{V_{i,j} }} = \frac{{2\pi \rho_{\text{g}} k_{\text{F}} (p_{\text{Fi,j}} - p_{\text{w}} )}}{{\Delta x\Delta y\mu_{\text{g}} \ln (r_{\text{e}} /r_{\text{w}} )}}\quad \left( {{\text{At}}\,{\text{the}}\,{\text{grids}}\,{\text{intersect}}\,{\text{with}}\,{\text{wellbore}}} \right)$$

(25)

$$q_{\text{w}} = 0\quad \left( {\text{Other HF grids}} \right)$$

(26)

$$q = \frac{{2\pi \rho_{\text{g}} hk_{\text{F}} (p_{{{\text{F}}_{i,j} }} - p_{\text{w}} )}}{{\mu_{\text{g}} (\ln (r_{\text{e}} /r_{\text{w}} ) + S - 0.75)}}$$

(27)

$$r_{\text{e}} = 0.14\sqrt {\Delta x^{2} +\Delta y^{2} }$$

(28)

Note that q _f is the inter-porosity flow from NF to HF and this is applied to all hydraulic fracture grids, because each HF grid receives flow from NF system. q _w is the flow term from HF to the horizontal well, it is only applied to the grid where the HF intersects with the horizontal well, and the production rate is assumed to be constant.

Substituting all the related equations into Eq. (24), we obtain the flow equation of hydraulic fractures, followed by its initial and boundary conditions:

$$\frac{\partial }{\partial y}\left( {\frac{{p_{\text{F}} }}{\mu Z}\frac{{\partial p_{\text{F}} }}{\partial y}} \right) + \frac{{k_{\text{fa}} \alpha p_{\text{f}} (p_{\text{f}} - p_{\text{F}} )}}{{k_{\text{Fa}} \mu Z}} - \left( {\frac{{2\pi p_{{{\text{F}}_{i,j} }} (p_{{{\text{F}}_{i,j} }} - p_{\text{w}} )}}{{\mu Z\Delta x\Delta y\ln (r_{\text{e}} /r_{\text{w}} )}}} \right) = \frac{{\phi_{\text{F}} p_{\text{F}} C_{\text{g}} }}{{k_{\text{Fa}} Z}}\frac{{\partial p_{\text{F}} }}{\partial t}$$

(29)

$${\text{Initial}}\,{\text{condition:}}\;p_{\text{F}} = p_{\text{i}} ,\quad t = 0$$

(30)

$${\text{Outer boundary condition:}}\;\left. {\frac{{\partial p_{\text{m}} }}{\partial n}} \right|_{\varGamma } = 0,\quad t > 0$$

(31)

$${\text{Inner boundary condition:}}\;q_{\text{w}} = \frac{q}{{V_{i,j} }} = \frac{{2\pi \rho_{\text{g}} k_{\text{F}} (p_{\text{F}} - p_{\text{w}} )}}{{\Delta x\Delta y\mu_{\text{g}} [\ln (r_{\text{e}} /r_{\text{w}} ) + S - 0.75]}},\quad t > 0$$

(32)

So far we have derived the differential equations for the three media [Eqs. (13), (21) and (29)] together with their initial and boundary conditions; therefore, the entire triple-continuum model is established.

Solution of the mathematical model

This triple-continuum model is solved using finite difference approach, and we discretized the differential equations in each medium via implicit scheme. Within the same time step, we first solve the hydraulic fracture equation to obtain the hydraulic fracture pressure p _F and then put it into the natural fracture equation to derive p _f, and eventually p _m is obtained by solving the matrix equation. By substituting p _F into Eq. (28), the production rate of each time cycle is calculated.

Based on this solving algorithm, a program is developed for our simulator. In the program, the gas compressibility factor is calculated by iterative calculation and an empirical equation is employed to calculate the gas viscosity. The detailed calculation procedures for gas properties are shown in Appendix A and B.

Model application and discussion

Model validation

To verify the correctness of this model, we compare the gas rate curve obtained from our model with the prediction from an existing model proposed by Wang (2015). Here we neglect the desorption and Klinkenberg effect and set the parameters of the reservoir according to their paper (reservoir length = 100 m, reservoir width = 100 m, HF height = 100 m, HF half length = 40 m, reservoir permeability = 10⁻³mD, reservoir porosity = 0.1, reservoir initial pressure = 15 MPa, bottom-hole pressure = 5 MPa). Figure 4 presents the result of the comparison.

Fig. 4

Contrast between this study and the result proposed by Wang (2015)

From the results, we can notice that the gas rate curve predicted using our model declines slower than the reference curve in the early stage of the production, it may due to the different calculation of the gas compressibility factor and gas viscosity in the program, and after 400 days of production time, the two gas rate curves can match with each other with negligible disparity. Therefore, despite minor difference from the existing model in the early stage, our model is quite reliable in general.

Reservoir description and model setup

A synthetic shale gas reservoir is employed to demonstrate the application of our proposed model. The reservoir is drilled by a horizontal well and followed by multistage fracturing, and the basic parameters of the shale gas reservoir and the horizontal well are listed in Table 1.

Table 1 Basic parameters for the reservoir and horizontal well

This hypothetical shale reservoir is nominally assumed to be 1500 m deep, and a horizontal well with six hydraulic fractures is incorporated in the model. The size of the reservoir is set to be 1300 m × 600 m × 20 m, the grid size is 75 × 33 × 1 in X, Y and Z direction, and the flow on the vertical direction is neglected. The width of the grids containing hydraulic fractures is set to be 2 m, and the mesh size near the fractures and horizontal well is smaller and finer in order to increase the accuracy. The actual width of hydraulic fracture is assumed to be 5 mm; thus, in our numerical model, the effective permeability for HF grids is calculated using the equation: k _eff = k _F W _F/W _grid = 20md (Rubin 2010). This synthetic reservoir is set for the following sensitivity analysis, and the model setup maybe moderately adjusted for the convenience of sensitivity analysis.

The influence of meshing size on gas rate

In order to verify the stableness of this mathematical model, the near wellbore meshing size is altered for different simulation processes, and its influence on gas rate is examined and illustrated in Fig. 5.

Fig. 5

Production performances for different values of meshing size

As we can see from Fig. 5, although it shows difference between the three curves at the beginning of the simulation, this difference disappears gradually with time elapsing and only small difference can be seen in the later stage of the simulation. Consequently, the gas rate is insensitive to the change of meshing size, which indicates good stableness of the proposed model as well (Wang 2015).

The influence of fracture half-length on gas rate

Using our triple-continuum model, the production of the reservoir is predicted based on four different values of hydraulic fracture half-length (66, 106, 146 and 186 m), and other parameters are set according to Table 1. The results are shown in Fig. 6.

Fig. 6

Production performances for different values of hydraulic fracture half-length

The four curves manifest that the gas rate will rise with the increase in the fracture half-length, and this is especially obvious in the beginning of the production. This is due to the fact that the creation of the hydraulic fractures will substantially promote reservoir’s productivity, and longer fracture half-length can better communicate with the natural fractures, providing a larger pressure drop area which can attract more fluid influx from unstimulated area (Raghavan et al. 1997; Jiang et al. 2014).

However, if we quantitatively analyze the difference between these curves in the later stage of production, we can see: When the fracture half-length increases from 66 to 106 m, then to 146 m and finally to 186 m, the increments of gas rate are about 3500, 3200 and 2400 m³, respectively; thus, the positive effect of hydraulic fracturing stimulation is becoming less apparent. This is because longer HF half length can only provide faster drop of average reservoir pressure, after the pressure drop spreads to the boundary for a long time, the produced gas mainly comes from the desorption gas in matrix, and gas rate mainly depends on matrix permeability. Consequently, the effect of longer HF half length would not be obvious anymore.

The influence of fracture spacing on gas rate

Three different values of hydraulic fracture spacing (100, 140 and 180 m) are selected for the comparison in this case, but the length of the horizontal well is kept constant as 800 m, and the other parameters are set according to Table 1. The production decline curves and cumulative production curves are both shown in Fig. 7.

Fig. 7

Production performances for different values of hydraulic fracture spacing

It can be noticed that smaller hydraulic fracture spacing leads to higher gas rate, and the differences are almost 4000 m³. Smaller hydraulic fracture spacing can increase the volume of the stimulated zone near the horizontal well and better communicate with the local natural fractures (Sun and David 2015), thus more effectively enhance the recovery. But we should not neglect that when the length of the horizontal section is fixed, smaller hydraulic fracture spacing indicates the larger amount of hydraulic fractures, in other words, higher cost for the fracturing process. Therefore, there exists an optimal hydraulic fracture spacing economically.

The influence of desorption on gas rate

Langmuir volume V _L is an important parameter in the simulation of shale gas reservoir, and it is defined as maximum amount of adsorbed gas per unit volume of rock at a given temperature. To investigate how the desorption effect will affect the gas rate, the Langmuir volume is changed from 0 to 2 cm³/cm³ (V _L = 0 indicates neglecting desorption), and different extents of influence are presented schematically in Fig. 8.

Fig. 8

Production performances for different values of Langmuir volume

It is evident that the black curve (V _L = 0) is much lower than the other three curves, which suggests that the desorption effect will greatly increase the productivity of the reservoir. The adsorbed gas provides about 25 % of the total recovery in the later stage of production. In addition, when V _L increases from 0.2 to 2 cm³/cm³, both the production decline curves and the cumulative production curves will rise with small extents. Its reason is that when the reservoir pressure decreases with production, the shale gas in the matrix will continuously desorb from the surface of the matrix pore, and the desorbed gas will feed the natural fractures and the hydraulic fractures, thus enhancing the productivity. Consequently, the gas rate will decline more slowly with larger Langmuir volume.

Apart from Langmuir volume, another important parameter in Langmuir equation is the Langmuir pressure p _L, and it represents the pressure at which the adsorbed gas content equals to V _L/2. Here Langmuir pressure is changed from 5 to 15 MPa, and the contrast of the simulation results is shown in Fig. 9.

Fig. 9

Production performances for different values of Langmuir pressure

It can be observed that the production rate is enhanced when Langmuir pressure grows higher, because the Langmuir pressure indicates the difficulty of the gas desorption, higher Langmuir pressure indicates easier gas desorption in matrix (Liu et al. 2015); thus, the gas rate would decline more slowly. However, the three curves are very close to each other showing very small differences (only 700 m³/day compared to about 18,000 m³/day), which means the production is insensitive to the change of Langmuir pressure.

The influence of Klinkenberg effect on gas rate

Figure 10 demonstrates the influence of Knudsen effect on the gas rate, and we can notice that the gas rate will increase when considering Klinkenberg effect. When the radius of the gas flow path is very small, the gas apparent permeability is greatly increased by Klinkenberg effect, thus enhancing the productivity. In addition, when the pressure drops down, the Klinkenberg effect would become more obvious.

Fig. 10

Production performances for different values of Langmuir pressure

In order to gain an insight into the Klinkenberg effect, the apparent permeability is predicted using our simulator and permeability prediction is made on one grid which experiences significant pressure change during the simulation. The alteration of matrix apparent permeability and natural fracture apparent permeability is presented in Fig. 10.

From Fig. 11 we can see that the matrix apparent permeability becomes 4–8 times of its initial permeability, whereas the natural fracture apparent permeability becomes only 1.1 times of its initial permeability. In conclusion, the Klinkenberg effect exerts great influence on matrix but very small influence on natural fracture. The reason is that the pore radius and the intrinsic permeability in matrix are smaller than that in natural fracture system; thus, from the formula introduced in 2.2 we know that the Klinkenberg factor b in matrix is larger, resulting in more significant influence of Klinkenberg effect.

Fig. 11

Permeability predictions for the two media

Conclusions

The shale gas experiences many different spatial scales during its flow from the reservoir to the wellbore, resulting in different flow mechanisms. The proposed triple-continuum model can better represent this feature and can simulate the production performance of shale gas well more accurately.

The adsorbed gas in place accounts for considerable fraction of gas reserves and recovery, and the desorption effect will greatly enhance the productivity, especially in the later stage of production; thus, desorption should not be neglected.

The Klinkenberg effect will increase the gas rate by increasing the apparent permeability in matrix and natural fracture, and it exerts greater influence on matrix system than natural fracture.

According to our simulator, the gas rate will rise with the increase in meshing size, hydraulic fracture half-length, Langmuir volume and Langmuir pressure, but with the decrease in hydraulic fracture spacing. Nonetheless, the production is insensitive to the change of meshing size and the Langmuir pressure.

Appendices

Appendix 1: Calculation for gas compressibility factor Z

For the convenience of programming, here we chose RKS method (Liu et al. 1993), and for the calculation of gas compressibility factor Z, the procedure is shown as follows:

$$Z_{k + 1} = Z_{k} - f(Z_{k} )/f^{\prime } (Z_{k} )$$

(33)

where

$$f(Z) = Z^{3} - Z^{2} + Z(A - B - B^{2} ) - AB$$

(34)

$$f^{\prime } (Z) = 3Z^{2} - 2Z + A - B - B^{2}$$

(35)

$$A = 0.42748 \times q \times p_{r} /t_{r} /t_{r}$$

(36)

$$B = 0.08664 \times p_{r} /t_{r}$$

(37)

$$q = (1 + m(1 - \sqrt {t_{r} } ))^{2}$$

(38)

$$m = 0.48 + 1.574 \times w - 0.176 \times w \times w$$

(39)

w is the acentric factor and 0.3 is always adopted (Liu et al. 1993). Based on the equations mentioned above, we can obtain the Z factor using iterative calculation.

Appendix 2: Calculation for gas viscosity

As for the calculation of gas viscosity, we adopt the empirical equation proposed by Huanlin (1988); following equations are the procedure.

$$\mu_{\text{g}} = \mu_{{{\text{g}},0.1}} \sum\limits_{i = 1}^{4} {\sum\limits_{j = 1}^{7} {a(i,j)X^{i - 1} Y^{j - 1} } }$$

(40)

where

$$X = \frac{1}{{T_{r}^{3.5} }} - 0.020749164082295$$

(41)

$$Y = 2^{{\ln p_{r} }} - 2.8563672849294$$

(42)

$$a(j,i) = \left( {\begin{array}{*{20}l} {1.7910} \hfill & {4.7507} \hfill & {5.1681} \hfill & { - 4.9379} \hfill \\ {0.5584} \hfill & {3.3023} \hfill & {1.4228} \hfill & { - 11.1170} \hfill \\ {0.0599} \hfill & { - 0.3729} \hfill & { - 3.4106} \hfill & {2.1534} \hfill \\ { - 0.0221} \hfill & { - 0.3088} \hfill & { - 0.1468} \hfill & {3.8417} \hfill \\ {0.1727} \hfill & {0.0167} \hfill & {0.3309} \hfill & {2.3739} \hfill \\ {0.0994} \hfill & {0.1044} \hfill & { - 0.0806} \hfill & { - 0.1322} \hfill \\ { - 0.0632} \hfill & {0.0179} \hfill & {0.0476} \hfill & { - 0.6844} \hfill \\ \end{array} } \right)$$

(43)

μ _g,0.1 means the gas viscosity under standard conditions, here we adopt 0.013 mPa s. So for the given temperature and pressure, we can calculate the gas viscosity based on above equations.