Introduction

Water has a vital role in life on earth. High level of nitrate anion in aquatic environments is a serious environmental worldwide problem, because this anion is implicated in the eutrophication of receiving surface waters and also the presence of nitrate anions in drinking water causes many public health problems (Kapoor and Viraraghavan 1997). Agricultural and urban wastewater, improper disposal of municipal and industrial wastes, leakage in septic systems, landfill leachate, animal manure are sources of nitrate anion contamination (Bhatnagar et al. 2010). While nitrate is relatively nontoxic to adults, because of nitrate excretion from the kidneys, concentrations >10 mg/l N–NO3 − are fatal for children under 6 months. A sort of “blue baby syndrome” is caused by the reduction of nitrate to nitrite, resulting in the decrement of O2 carrying capacity of hemoglobin in the blood and finally death. US EPA has set a most extreme contaminant level of 10 mg/l of N–NO3 − in drinking water (EPA 2010). Eutrophication is the abundance of aquatic plants, the growth of algae, and depletion of dissolved oxygen (Levine and Schindler 1989).

Several processes were investigated for the removal of nitrate in water and wastewaters which include chemical denitrification using zero-valent iron (Fe0) (Cheng et al. 1997; Huang and Zhang 2004), ionic exchange (Broséus et al. 2009), reverse osmosis (Schoeman and Steyn 2003), electrodialysis (Hell et al. 1998), catalytic denitrification (Pintar et al. 2001) and biological denitrification (Soares 2000). Though, current available technologies for water treatment of nitrate are found to be expensive, inefficient and generate additional by-products. Among them, adsorption systems are favorable, because they permit straightforward and economical operation, bringing about less sludge generation and disposal issues. So that adsorbents have been developed to remove various pollutants of aquatic environments.

Mesoporous silica materials have gotten extensive consideration due to their high specific surface area, well-defined pore size and pore shape (Beck et al. 1992). Mostly, the functionalizations of mesoporous silica have been investigated. For example, Yoshitake et al. (2002) investigated the amino-functionalized mesoporous silicas for removal of arsenate from an aqueous solution. Heidari et al. (2009) prepared an adsorbent from mesoporous silica Mobil Composite Material No. 41 (MCM-41) by grafting organic amine groups for removal of heavy metal pollution. Hamoudi et al. (2007b) evaluated the potential of removing nitrate and phosphate from aqueous solutions using ammonium-functionalized mesoporous silica MCM-48. However, that is necessary to provide treatment method for removing nitrate anion by other mesoporous silica materials. In this study, mesoporous MCM-41 silica functionalized with amine organic groups was used for nitrate anion adsorption. Amino-functionalized mesoporous MCM-41 silica was synthesized with post-synthesis Grafting method. The grafting method consists in reacting a suitable organosilane with surface silanol groups belonging to a previously synthesized mesoporous material using an appropriate solvent under reflux conditions (Lim and Stein 1999).

In the present study, the adsorption properties of adsorbents for nitrate anion adsorption were investigated using batch and fixed-bed column systems. The Freundlich and Langmuir isotherms were utilized to demonstrate the equilibrium adsorption data. The kinetic data of adsorption and the evaluation of equilibrium parameters were described by the pseudo-second-order equations. Also, the investigation was performed to remove nitrate anion from aqueous solution by amine functionalized mesoporous silica MCM-41 in a fixed-bed column and also to investigate the impacts of operating conditions, for example, bed height, flow rate and initial concentration on the column dynamics. A breakthrough analysis for the adsorption of nitrate on NNN-MCM-41 sieve was performed. The adsorption capacity was calculated based on the breakthrough analysis and Thomas and Yan models.

Experimental section

Chemicals

3-Aminopropyltriethoxysilane (99 %), cetyltrimethylammonium bromide (CTAB, 99 %), hydrochloric acid (HCl, 37 %), dry toluene (99.9 %) and sodium nitrate (NaNO3) were purchased from Merck (Germany). Tetraethylorthosilicate (TEOS, 98 %) and sodium hydroxide (NaOH) were obtained from Sigma-Aldrich (USA). [3-(2-Aminoethylamino)propyl]trimethoxysilane (99 %) and 3-[2-(2-Aminoethylamino)ethylamino] propyltrimethoxysilane (99 %) were purchased from Alfa Aesar.

Adsorbents synthesis

Synthesis of MCM-41

The source of silicon was TEOS and the structure directing factor was CTAB. MCM-41 was prepared by slowly adding 20.41 g of TEOS into a solution containing 3.64 g of CTAB and 1.2 g of NaOH in 108 ml of deionized water (Chen and Wang 2002). After mixing for 1 h at room temperature, the subsequent homogeneous blend was solidified under static hydrothermal conditions at 110 °C in a Teflon bottle for 96 h. The molar composition of the starting gel mixture was 1.0:0.1:0.3:60 TEOS/CTAB/NaOH/H2O. The final product was acquired by filtration, washed with deionized water, ethanol reflux for 48 h, and then dried at 100 °C overnight, and calcined 6 h at 540 °C (heated from room temperature to 540 °C with a heating rate of 3 °C/min).

Synthesis of amine functionalized silica MCM-41 by grafting

The mesoporous materials MCM-41 with amino (i.e., monoamine, diamine and triamine) were prepared according to the method described in the literature (McKittrick and Jones 2003). Prior to the functionalization with organic grapes, calcined MCM-41 was dried in a vacuum oven for 4 h at approximately 150 °C. To graft the silica surface, 1 g of so-obtained MCM-41 materials was suspended in dried toluene (25 ml) and then 6 mmol (1.381 ml) of 3-aminopropyltriethoxysilane precursor was slowly added to the mixture. This mixture was refluxed for 24 h. The functionalization of MCM-41 with diamine and triamine groups was conducted by the same aforementioned procedure, but 1.268 ml (6 mmol) of [3-(2-aminoethylamino)propyl]trimethoxysilane and 1.592 ml (6 mmol) of 3-[2-(2-aminoethylamino)ethylamino]propyltrimethoxysilane was added in each run instead. Solid materials were collected by filtration, washed with dried toluene, ethanol reflux for 24 h and then dried at 70 °C overnight. Amine-grafted silica materials were labeled N-MCM-41, NN-MCM-41 and NNN-MCM-41 compared to organic chains containing one, two and three amino-functional groups, as shown in Fig. 1.

Fig. 1
figure 1

Synthesis of amino-functionalized mesoporous silica materials via post-synthesis grafting method

Full size image

Characterizations

X-ray powder diffraction (XRD) experiments were carried out with Cu radiation (MMA007, manufactured by GBC Australia). The scans were made in the 2θ range 0.5°–10° (low angle diffraction). The morphology of the mesoporous adsorbents was acquired by electron scanning microscopy (SEM, LEO 1455VP, Cambridge, UK). Nitrogen adsorption–desorption isotherms were evaluated at −196 °C using a volumetric adsorption analyzer (BEL sorp-mini II, Japan) to ascertain the textural properties. Before the analysis, approximately 0.1 g of all MCM-41 samples was degassed at 100 °C for 3 h under argon gas flow. The specific surface area was assessed utilizing the Brunauer–Emmett–Teller (BET) technique, and the pore size distribution was estimated from desorption branches of nitrogen isotherms using the Barrett–Joyner–Halenda (BJH) system. FT-IR measurements were accomplished on a TENSOR27 (manufactured by Bruker, Germany) in the range of 400–4000 cm−1. A thermogravimetric analysis (TGA) of sample was also carried out on a Pyris Diamond Thermogravimetric analyzer (PerkinElmer, UK). The sample was heated under nitrogen atmosphere from an ambient temperature to 840 °C at 10 °C/min.

Adsorption experiments in batch system

The adsorption capability was investigated of the synthesized adsorbent materials toward nitrate anions, using aqueous solutions of NaNO3. Adsorption was performed batchwise in Erlenmeyer flasks on a stirrer at 150 rpm under the following conditions: adsorbent loading, 0.5–15 g/l; anion initial concentration, 30–250 mg/l; and pH 4–8. Preliminary adsorption tests with sampling intervals of 5 min showed that equilibrium was attained within 10–15 min. Thus, for all the adsorption tests presented thereafter, the stirring was continued for 120 min before aliquots of the solutions were withdrawn, centrifuged (236 HK, Hermle, German) for 10 min at 12,000 rpm and 25 °C and subsequently filtered with filter paper (0.45 μm) to remove the adsorbent. The concentration of nitrate anion was measured using a UV visible spectrophotometer set at 210 nm (Lambda 25, Perkin-Elmer, USA).

The percent of removed nitrate anions by the adsorbents was calculated by the following equation:

$$ R = \frac{C_0 - C_t }{C_0 } \times 100 $$
(1)

where R is the removal efficiency of the nitrate anions, C 0 is the initial concentration and C t is the concentration of the nitrate anions at t time in mg/l. The amount of nitrate adsorbed (q e in mg/g) was calculated as follows:

$$ q_{\text{e}} = \frac{{({C_o - C_{\text{e}} })V}}{m} $$
(2)

where C e is the equilibrium concentration of nitrate anion in the aqueous solution (mg/l), V is the volume of solution (l) and m is the quantity of the adsorbent (g).

The equilibrium adsorption data of nitrate anions were fitted into both the Freundlich and Langmuir isotherm equations. In the Langmuir model, it is presumed that the adsorption surface places have the same energy and each adsorbate molecule has been situated on a solitary site and thus this model anticipates the formation of monolayer of an adsorbate on the adsorbent surface (Heidari et al. 2009; Vasconcelos et al. 2008). The Langmuir isotherm is given by the following equation:

$$ q_{\text{e}} = \frac{{q_{\text{m}} bC_{\text{e}} }}{{1 + bC_{\text{e}} }} $$
(3)

where q e is the equilibrium sorption capacity of sorbent in mg anion/g sorbent, C e is the equilibrium concentration of nitrate anion in mg/l, q m is the maximum amount of anion sorbed in mg nitrate/g sorbent, and b is the factor that alludes to the bonding energy of adsorption in l/mg. Nonlinear regression analysis was performed in SigmaPlot software (SigmaPlot 12.0, SPSS Inc., USA) to estimate the values of q m and b parameters.

The Freundlich model depicts a reversible heterogeneous adsorption, since it does not limit itself to a monolayer of adsorbent covering (Ghorbani et al. 2008). Actually, the Freundlich isotherm predicts that the concentration of nitrate anion on the adsorbent will rise until there is an increment of the anion concentration in the liquid solution (Vaghetti et al. 2009). The Freundlich isotherm is given by the following equation:

$$ q_{\text{e}} = K_f C_{\text{e}}^{\frac{1}{n}} $$
(4)

where q e is the adsorption capacity at equilibrium time in mg anion/g adsorbent, C e is the equilibrium concentration of nitrate anion in mg/l, K f and n are the parameters identified with the adsorption capacity in mg nitrate/g adsorbent, and the adsorption intensity of the sorbent, respectively. Nonlinear regression analysis was done by SigmaPlot software (SigmaPlot 12.0, SPSS Inc., USA) to predict the K f and n parameters.

Two kinetic models (pseudo-first-order and pseudo-second-order) are used to test the experimental data for showing the controlling mechanisms of adsorption processes. The rate constant of adsorption is assigned from the subsequent pseudo-first-order rate expression given by Lagergreen (Soner Altundoğan et al. 2000; Wu et al. 2001).

$$ \log ({q_{\text{e}} - q_t }) = \log q_{\text{e}} - \frac{k_1 t}{2.303} $$
(5)

where q e and q t are the quantity of nitrate adsorbed (mg/g) at the equilibrium and t times (min), respectively, and k 1 (l/min) is the rate constant of first-order adsorption (Sivaraj et al. 2001). A pseudo-second-order equation based on equilibrium adsorption capacity may be represented as:

$$ \frac{t}{q_t } = \frac{1}{{k_2 q_{\text{e}}^2 }} + \frac{t}{{q_{\text{e}} }} $$
(6)

where k 2 g/(min mg) is the rate constant of second-order adsorption.

Adsorption experiments in a fixed-bed column

The adsorption efficiency of NNN-MCM-41 for removal of nitrate anion was investigated using fixed-bed glass column. A glass column of 24 cm length and 1 cm internal diameter was used to fixed bed column adsorption. The column was shut by glass wool, which guarantees good liquid distribution. A solution containing the nitrate anion was pumped upward to the column. A peristaltic pump was used to control the flow rate at the inlet and outlet (pump drive 5101, Heidolph, Germany). Samples of the effluent were collected periodically and analyzed for the remaining nitrate anion concentration using a spectrophotometer. For improving the column dynamics, adsorption analyses were done at various bed heights (2, 4 and 6 cm but the same inner diameter 6 mm) of NNN-MCM-41, various influent flow rates (0.8, 1.6 and 2.4 ml/min) and various initial concentrations (70, 110 and 150 mg/l) at pH 7 and ambient temperature.

The breakthrough curves show the loading behavior of NNNMCM-41 for the removal of nitrate from aqueous solution in a fixed-bed column. The area under the breakthrough curve obtained by integrating the adsorbed concentration of nitrate anion (mg/l) versus time (min) plot can be used to find the total adsorbed quantity of nitrate anion (q total, mg) and for a certain inlet concentration and fluid flow rate (ml/min) and it can be calculated from Eq. (7) (Aksu et al. 2002; Aksu and Gönen 2004):

$$ q_{\text{total}} = \frac{QC_0 }{1000}\int_0^t {\left({1 - \frac{{C_{\text{e}} }}{C_0 }}\right)} {\text{d}}t $$
(7)

where C 0 is the initial concentration of nitrate anion, t e is the exhaustion time, (1 − C e/C 0) is the concentration of anion adsorbed (mg/l), Q is the flow rate (ml/min) that can be computed by dividing the effluent volume (V e, ml) to the total time (t total, min). The total mass of nitrate anion adsorbed to column (m total) can be found from Eq. (8) (Vijayaraghavan et al. 2005a):

$$ m_{\text{total}} = \frac{{QC_0 t_{\text{e}} }}{1000} $$
(8)

Total removal percent of nitrate anion (column performance) with respect to flow time can also be found from the ratio of the total adsorbed amount of nitrate (q total) to the total of a quantity of nitrate anion sent to column (m total) Eq. (9):

$$ R = \frac{{q_{\text{total}} }}{{m_{\text{total}} }} \times 100 $$
(9)

The equilibrium adsorption capacity, q e (mg/g), can be calculated using the following equation:

$$ q_{\text{e}} = \frac{{q_{\text{total}} }}{m} $$
(10)

where m is the mass of the adsorbent (g).

Equilibrium studies on adsorption provide information about the adsorbent capacity or the quantity required to eliminate a unit mass of pollutants under the system. The column flow data were evaluated using various models. Two mathematical models including the Thomas model and Yan model were used. The Thomas model is expressed in the following form:

$$ \frac{{C_{\text{e}} }}{C_0 } = \frac{1}{{1 + \exp [{\frac{{k_{\text{Th}} }}{Q}({q_0 m - C_0 V})}]}} $$
(11)

where C e is the effluent concentration (mg/l), C 0 is the influent concentration (mg/l), Q is the flow rate (ml/min), V is the effluent volume (ml), m is the mass of the adsorbent (g), t is the time (min) k Th is the Thomas rate constant (ml/min mg) and q 0 is the maximum adsorption capacity (mg/g). The Thomas model parameters (k Th, q Th) can be assigned from the plot of C e/C 0 against t using nonlinear regression analysis (Thomas 1944). Yan model proposed an empirical equation which could overcome the drawback in the Thomas model, especially its serious deficiency in predicting the effluent concentration at time zero (Yan and Viraraghavan 2001):

$$ \frac{C}{C_0 } = 1 - \frac{1}{{1 + ({\frac{QC_o }{{q_{\text{Y}} m}}t})^a }} $$
(12)

where C 0 is the initial solution concentration (mg/l), Q is the flow rate (ml/min), q Y is the maximum adsorption capacity (mg/g) of anion nitrate estimated by Yan model, and m is the amount of adsorbent (g).

Results and discussion

Characterization of adsorbents

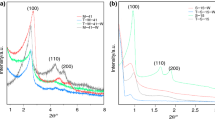
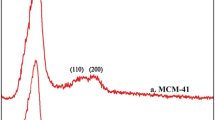
Figure 2 gives the X-ray diffraction patterns of mesoporous MCM-41 silica before and after functionalization with amino groups. In the pattern of mesoporous MCM-41 silica as shown in Fig. 2a, a dominant (100) peak with a small (110), (200) and (210) reflections is attributed to the hexagonal structure (Yoshitake et al. 2002). The prominent peak at 2θ ranging between 2° and 2.5° corresponds to (100) plane, which is indicative of standard MCM-41 (Parida and Rath 2009). The XRD peak intensities of the MCM-41 mesoporous silica grafted by amino functionalized groups are lower than that of MCM-41 (Fig. 2b–d). The decrease in peak intensity provides evidence that amino-functionalized groups occurred mainly inside the mesopore channels.

Fig. 2
figure 2

XRD patterns of (a) MCM-41, (b) N-MCM-41, (c) NN-MCM-41and (d) NNN-MCM-41

Full size image

The estimated hexagonal pore diameters from d 100 values are listed in Table 1. The results of N2 sorption experiments are listed in Table 1. The specific surface area, pore size distribution and total pore volume of the mesoporous adsorbents were determined by the BET equation. MCM-41 was a porous material with a surface area of 1001 m2/g and mean pore diameter of 2.8 nm. The BET surface area, total pore volume, and pore diameter decreased with increasing number of nitrogen atoms in amino-functionalized MCM-41.

Table 1 Physical properties of products mesoporous materials obtained by BET and XRD
Full size table

The morphology of the MCM-41 was analyzed by a scanning electron microscope. A typical image is presented in Fig. 3, which shows that many amorphous and spherical shapes with the sizes of the particles range from 400 to 900 nm, which is in good agreement with the MCM-41 morphology presented in previous reports (Chen and Wang 2002; Luan et al. 1995).

Fig. 3
figure 3

SEM figures of mesoporous MCM-41 silica

Full size image

Figure 4 shows the infrared spectra of MCM-41 prior to and following functionalized with amino groups. In all the materials, the bands around 473, 795, 1080 and 1220 cm−1 are assigned to links of (Si–O–Si), which is associated with the formation of a condensed silica network (Wang et al. 2005). A very wide absorption band focused at 3431 cm−1 determined to hydrogen-bonded Si–OH groups was intruded by physically adsorbed water, while a sharp absorption is perceived at 3740 cm−1 ascribed to free Si–OH groups. After amino-functionalization, the band at 3740 cm−1 for free Si–OH groups was evacuated (Peng et al. 2004). The presence of bands in 690, 1460 and 2937 cm−1 is assigned to N–H bending vibration, N–H asymmetric bending vibration and C–H link, respectively (Li et al. 2008).

Fig. 4
figure 4

FT-IR spectra of (a) MCM-41, (b) N-MCM-41, (c) NN-MCM-41 and (d) NNN-MCM-41

Full size image

The organic content of the surface modified mesoporous silica MCM-41, assessed by TGA is shown in Fig. 5. The weight loss of MCM-41 is relatively low due to the removal of absorbed water. The amino-functionalized MCM-41 showed a higher weight loss. In all materials, the weight loss below 150 °C corresponds to the desorption of water molecules. The curve corresponding to the MCM-41 (Fig. 5a) shows that the weight loss at higher temperatures (above 150 °C) is assigned to dehydroxylation of silanol groups. This is because the surfactant well was removed in the final stages of synthesis (Budi Hartono et al. 2009; Maria Chong and Zhao 2003). In curves corresponding to amino-functionalized MCM-41, the weight loss at above 150 °C is due to the decomposition of amine anchored to the pore walls (Parida and Rath 2009).

Fig. 5
figure 5

TGA of (a) MCM-41, (b) N-MCM-41, (c) NN-MCM-41 and (d) NNN-MCM-41

Full size image

Adsorption of nitrate anion in batch system

Effect of pH

The pH of the solution is a significant factor in the investigated adsorption process. So that the chemical characteristics of adsorbent and anion changed by changing the pH. The effect of the solution pH on the sorption of nitrate anions by amino-functionalized MCM-41 is shown in Fig. 6. For all adsorbents, the results of the adsorption tests showed that removal of nitrate anion increased with increase in pH up to 6, thereafter no significant change was observed (pH 6-7), but further increasing the pH from 7 to 8 resulted to a decrease in the removal percentage of nitrate anion. This may be due to the competition for the active sites by OH− ions and the electrostatic repulsion of anionic nitrate by the negatively charged mesoporous surface by adsorption of nitrate anion at higher pH (Bhatnagar et al. 2010). Although the highest nitrate removal was achieved at pH 6, the adsorption experiments were performed at the pH 7 (neutral conditions), since only about 2 % of adsorbed nitrate was increased at pH 6. Hamoudi et al. (2007b) investigated the adsorptive removal of phosphate and nitrate anions using ammonium-functionalized mesoporous silica. Their results showed that the nitrate adsorption performance depends on pH and the obtained optimum pH was 6 that is in agreement with this study.

Fig. 6
figure 6

Effect of pH on nitrate anion removal by N-MCM-41, NN-MCM-41and NNN-MCM-41: operated at anion concentration of 110 mg/l, adsorption dose of 5 g/l

Full size image

Effect of adsorbent dose

The amount of adsorbent determines the adsorption capacity in a given initial concentration of nitrate concentration. The adsorbent concentration was varied between 0.5 and 15 g/l in this set of experiments. The effect of the adsorbent doses on the removal efficiency of nitrate anions is shown in Fig. 7. It was found that the adsorption of nitrate anion in aqueous solution enhanced with an increment of adsorbent dose. It is due to the rising of interference between activating sites of adsorbent at higher sorbent dosages and also increase in the number of adsorptive site and surface area (Phuengprasop et al. 2011; Rome and Gadd 1987). The highest amount of nitrate anion removal in different adsorbents was observed in the amount of 15 g/l adsorbent dose. As percents of nitrate anion removal for N-MCM-41, NN-MCM-41 and NNN-MCM-41 obtained were 77.7, 80.5 and 82.9 %, respectively. On the other hand, the adsorption capacity reduced by increasing the adsorbent dose. At low dose of amine-modified MCM-41, the available binding sites on the adsorbent surface were occupied by nitrate ion, since the nitrate ion concentration raised the binding site yielding high equilibrium adsorbent nitrate concentration. However, at high dose of amine-modified MCM-41, a large number of binding sites were available on the adsorbent surface and only a fraction of those binding sites was occupied by nitrate ions yielding low solid-phase concentration

Fig. 7
figure 7

Effect of adsorbent dose on the nitrate anion removal efficiency by N-MCM-41, NN-MCM-41 and NNN-MCM-41: operated at anion concentration of 110 mg/l, pH 7

Full size image

Adsorption isotherms

There are numerous mathematical equations for examining experimental adsorption equilibrium data. The parameters of these equilibrium models regularly give some information about the adsorption mechanism, the surface features and affinity of the adsorbent. The nonlinear Langmuir and Freundlich adsorption isotherms of nitrate anions obtained at the adsorbent dose of 5 g/l and temperature of 25 °C are shown in Fig. 8. The b, q m, n, K f values and the nonlinear regression coefficient of determination (R 2) for Langmuir and Freundlich isotherms are given in Table 2. The coefficient of determination indicates that adsorption was fitted better by the Langmuir (R 2 = 0.98–0.99) than the Freundlich model (R 2 = 0.94–0.97). Therefore, the adsorption process can be described by the formation of a monolayer coverage of the adsorbate on the adsorbent surface (Myers 2002). The amount of b in NNN-MCM-41 adsorbent was more than the other two adsorbents, indicating that bonding energy of sorption in this adsorbent was more from other two adsorbents. The maximum adsorption capacity (q m) by Langmuir model was determined as 31.68, 38.58 and 38.81 mg/g for N-MCM-41, NN-MCM-41 and NNN-MCM-41, respectively. The sample NNN-MCM-41 exhibited a higher adsorption capacity than N- and NN-MCM-41. It is apparent that the adsorption capacities of nitrate improved by changing the amine type. By altering amine type from diamine to triamine, the number of adsorption places on the surface of amine functionalized MCM-41 increases, leading to a rise in the quantity of adsorbed nitrate anion. This trend was observed in the study conducted by Bui (2013). They functionalized SBA-16 with amine groups (mono-, di- and tri-ammonium silane) via post-synthesis grafting and utilized as potential adsorbent for nitrate adsorption from water. Their results show that the adsorption capacity values increase from 52.75 to 58.5, then 83.25 for g N-, NN-, NNN-SBA-16, respectively.

Fig. 8
figure 8

Adsorption isotherm of nitrate anion on N-MCM-41, NN-MCM-41 and NNN-MCM-41: Langmuir and Freundlich at the adsorbent dose of 5 g/l, pH 7.0 and temperature of 25 °C

Full size image
Table 2 Langmuir and Freundlich parameters for adsorption of nitrate anion onto N-MCM-41, NN-MCM-41 and NNN-MCM-41
Full size table

Compassion with other adsorbent

Table 3 compares the maximum adsorption capacity for nitrate anion removal with various silica material adsorbents reported in the literature. As can be seen, different adsorbents exhibit different adsorption capacities for nitrate anion adsorption, which indicates the role of a kind and property of a grafted functional group on the surface of sorbents. For instance, Saad et al. (2008) synthesized three different ammonium-functionalized mesoporous materials (MCM-41, MCM-48 and SBA-15) through post-synthesis grafting procedures and investigated their efficiency to remove nitrate anions in aqueous solutions. The adsorbents presented great adsorption capacities reaching 46.5 mg/g for N-MCM-48 and 36 mg/g for the MCM-41 and SBA-15, under the operating conditions explored. Also, Hamoudi et al. (2007a) modified MCM-48 with ammonium groups and used as an adsorbent for removing nitrate ion from aqueous solution. The adsorbent was effective for the removal of nitrate and the maximum adsorption capacity of 51.8 mg/g was obtained at 5 °C. Besides, Dioum and Hamoudi (2014) compared the adsorptive performances of mono and quaternary ammonium-functionalized SBA-15 through post-synthesis grafting method for the removal of nitrate ion from aqueous solution. The results showed that adsorption capacity was affected by the organic functional group nature, thus the quaternary ammonium-functionalized SBA-15 has remarkably high adsorption capacity (63 mg/g) compared to mono one (55 mg/g). A similar tendency was observed in this study between N-MCM-41 (31.7 mg/g) and NNN-MCM-41 (38.8 mg/g). Moreover, the adsorption of nitrate ion from water onto functionalized amine SBA-16 mesoporous silica was investigated by Bui (2013). The adsorbents were synthesized by post-synthesis grafting method using mono-, di-, tri-ammonium functional groups. Based on the results, the maximum adsorption capacity was found to be 70.46 mg/g at a temperature of 5 °C. The quantity of adsorbed nitrate increased by changing the amine type from mono-, di-amine to tri-amine, which was in agreement with the results of this study. Comparison was made between the results of this study and the others from the above-mentioned studies of the nitrate adsorption on the amine-modified mesoporous silica according to the adsorption capacity and removal efficiency. The result showed that the adsorption capacity and removal efficiency NNN-MCM-41 synthesized in this study were higher than those mono-amine functionalized MCM-41 in the literature, while presented smaller adsorption capacity compared to MCM-48 and SBA-15 materials mentioned above (Table 3).

Table 3 Comparative evaluation adsorption capacities of mesoporous silica material with other adsorbents for nitrate removal
Full size table

Adsorption kinetics

The adsorption kinetic study has an important role in the treatment of wastewater as it gives significant information on the pathways and mechanism of adsorption reactions. The kinetic rates of the nitrate anion adsorption process were investigated by the pseudo first-order and the pseudo second-order models, but the pseudo-second-order model were found to explain the experimental adsorption kinetic data, as shown in Fig. 9. The kinetic parameters (R 2, q e2 and K 2) of the pseudo-second-order sorption kinetics model were determined from the plots at different concentrations (Fig. 9). The values of R 2 and K 2 are presented in Table 4. As can be seen from Table 4, the coefficient of determination values of the pseudo-second-order model was >0.99 and the estimated adsorption capacity values acquired from pseudo-second-order model were more compatible with the experimental amounts of adsorption capacity. This suggested that the pseudo-second-order model represented better the sorption kinetics of nitrate anion. As seen in Fig. 9, the rate of nitrate adsorption increased rapidly for all the adsorbents, during the first 30 min of the experiment, then reduced gradually and reached steady state, 2 h after the beginning of the experiment. Since pseudo-second-order kinetic model assumes that the adsorption occurred via chemisorption (Bouhamed et al. 2012; Ho et al. 2003), so here, it implied that nitrate anion adsorption onto amino-functionalized MCM-41 may occur through a chemical procedure including valence forces through the sharing or trade of electrons. A good correlation coefficient of the kinetics data can show the mechanism of the nitrate adsorption to the solid phase (Ho and McKay 2000), whereas the pseudo-second-order kinetic model presumes that chemisorption may be the rate-limiting step (Low et al. 2000).

Fig. 9
figure 9

Pseudo-second-order kinetic for adsorption of nitrate anion onto N-MCM-41 (a), NN-MCM-41 (b) and NNN-MCM-41 (c)

Full size image
Table 4 Kinetic adsorption parameters obtained using pseudo-second-order models
Full size table

Desorption studies

Recovery and regeneration of the adsorbent and adsorbate have obtained economic, scientific and environmental motivations in recent years (Hamoudi et al. 2007a). For example, desorption study is helpful for elucidating the mechanism of adsorption, to regenerate the adsorbent, to recover nitrate from the adsorbent and to protect the environment from the solid waste disposal problem. For these purposes and for examining desorption process, adsorbent was entered into the NaOH solution with concentration of 0.01 M. Afterward for the sake of activation, the adsorbent surface was entered into HCl solution with a concentration of 0.01 M. The desorption kinetics of nitrate anion in amino-functionalized MCM-41 in NaOH solutions is depicted (figure not shown). As observed, the desorption was rapid and complete for nitrate anions within 10 min. A maximum desorption of above 95 % N-MCM-41, NN-MCM-41 and NNN-MCM-41 was achieved by contact with NaOH (0.01 M), pH 7 and an adsorbent dose of 5 g/l for 10 min. Due to this, the adsorption of this anion with amino-functionalized adsorbents is completely reversible. The adsorbent was reused in four successive adsorption–desorption cycles. The adsorption capacity of the nitrate anion after three cycles indicated a loss in the adsorption capacity of only 5.5 % by N-MCM-41, 5.1 % by NN-MCM-41 and 5.7 % by NNN-MCM-41 compared to the initial cycle, indicating a good regeneration capacity of the adsorbent. Therefore, amino-functionalized MCM-41 can be used for the removal of nitrate anion from polluted waters.

Adsorption of nitrate anion in fixed-bed column

For continuous adsorption experiments, NNN-MCM-41 adsorbent was used for the removal of nitrate anion from aqueous solutions due to high adsorption performance which obtained from batch experiments.

Effect of bed height

Accumulation of nitrate in the packed bed column is mostly determined by the amount of adsorbent inside the column. The effect of NNN-MCM-41 bed height on nitrate anion adsorption in fixed-bed column was investigated using three different bed heights of 2, 4, and 6 cm at a constant flow rate of 1.6 ml/min and influent concentration of 110 mg/l. The adsorption breakthrough curves at different bed heights for studied anion are shown in Fig. 10a and the breakthrough analysis is summarized in Table 5. From this figure, it can be observed that the slope of breakthrough curves decreased by increasing the bed height. Both breakthrough and exhaust times were found to be increased with increasing the bed height from 2 to 6 cm, which resulted in a higher removal percentage of nitrate anion in the column because of the more prominent number of binding sites for adsorption process and also because the transfer zone requires more time to reach the column end for the nitrate anion to have more time to be in contact with NNN-MCM-41. Besides, it is well noted that the exhaustion time was 100, 220 and 320 min at the bed depth of 2, 4 and 6, respectively (Table 5). Further, the breakthrough analysis showed the increased maximum adsorption capacity and the equilibrium adsorption capacity of nitrate anion in the solution with increasing bed height. In this study, the equilibrium adsorption capacity of the nitrate anion increased from 20.13 to 23.01 mg/g with increasing bed height from 2 to 6 cm. It means that high uptake was observed at the highest bed height (6 cm). The reason for this is that the adsorption efficiency is dependent on the number of available adsorption sites for nitrate adsorption resulting in a higher surface area and hence higher capacity for adsorption (Baral et al. 2009; Vijayaraghavan et al. 2005a).

Fig. 10
figure 10

Experimental breakthrough curve a at 1.6 ml/min flow rate, 110 mg/l concentration and different bed heights and b at 110 mg/l concentration, 4 cm bed height and different flow rate and c at 1.6 ml/min flow rate, 4 cm bed height and different concentration for nitrate anion removal by the NNN-MCM-41

Full size image
Table 5 The breakthrough analysis and parameters of Thomas and Yan models of NNN-MCM-41 for nitrate anion removal of various column conditions
Full size table

Effect of flow rate

The flow rate is one of the significant properties in assessing adsorbents for continuous treatment of nitrate effluents on an industrial scale. So, in the second stage of removal studies in the fixed-bed column with NNN-MCM-41, the impact of flow rate was examined by changing the flow rate from 0.8 to 2.4 ml/min while the inlet nitrate anion concentration in the feed was held constant at 110 mg/l and 4 cm bed height. The breakthrough curves of nitrate anion concentration versus time at different flow rates are given in Fig. 10b and the breakthrough analysis is summarized in Table 5. The results indicated that the adsorption of nitrate on the NNN-MCM-41 was strongly influenced by the flow rate. All the breakthrough curves had a comparable shape. In general, with the increasing flow rate, the percentage removal and slope of breakthrough curves increased. As indicated in Fig. 10b, at the lowest flow rate of 0.8 ml/min, relatively higher nitrate removal values were observed for nitrate adsorption to NNN-MCM-41. In contrast to bed height results, both exhaustion time and adsorption capacity of nitrate anion decreased with the increasing flow rate. Earlier breakthrough time and saturation time were appeared for higher flow rate, resulting in low uptake and minimum percent removal. This behavior can be explained that nitrate anion adsorption by NNN-MCM-41 is affected by insufficient residence time of the solute in the column, due to the reduced contact time between adsorbent and the nitrate anion in the column (Akar et al. 2009; Qaiser et al. 2009; Vijayaraghavan et al. 2005b). It is also observed that maximum nitrate uptake and nitrate removal obtained were 21.87 mg/g and 85.29 % at 2.4 and 1.6 ml/min, respectively (Table 5). Therefore, this should be emphasized that the fixed-bed column system has a good performance at the lower flow rate.

Effect of influent nitrate anion concentration

The adsorption performance of NNN-MCM-41 was tested at various nitrate anion inlet concentrations. The sorption breakthrough curves obtained by changing the inlet nitrate anion concentration from 70 to 150 mg/l at 1.6 ml/min flow rate and 4 cm bed height are given in Fig. 10c. As seen from Fig. 10c, a decreased inlet nitrate concentration gave an extended breakthrough curve and the time needed for the saturation of NNN-MCM-41 was longer at lower concentrations of nitrate in the influent. At the most nitrate concentration (150 mg/l), the NNN-MCM-41 was saturated rapidly, leading to earlier column stoppage and steeper breakthrough and exhaustion time. The breakthrough parameters of different nitrate anion concentrations are listed in Table 5. A maximum adsorption capacity (21.87 mg/g) was obtained with initial nitrate concentration 110 mg/l and at 1.6 ml/min flow rate and 4 cm bed height. The difference between the concentration of nitrate anions on the adsorbent and that in the aqueous solution is considered as the driving force (Aksu and Gönen 2004). Thus, the high driving force due to the high nitrate concentration resulted in better nitrate uptake. However, with increasing initial nitrate concentration, the removal efficiency decreased. This is because the functional groups in the adsorbent are not probably enough for adsorbed all the adsorbate molecules. Hence, with the increment of nitrate concentration, the number of available places becomes less for the adsorption of nitrate anion moles in solution.

Mathematical modeling of breakthrough curves

All the breakthrough curves acquired with various bed heights, flow rates and initial nitrate concentrations were fitted well to sigmoidal-type mathematical models, namely, Thomas and Yan and models (Fig. 10) and the adsorption capacity was calculated based on the fitting results (Table 5). The Thomas model is one of the most general and broadly utilized models for depicting column breakthrough data. The Thomas model, which accepts Langmuir adsorption and desorption kinetics and no axial dispersion, is determined with the adsorption that the rate driving force complies second-order kinetics (Aksu and Gönen 2004; Vijayaraghavan et al. 2005a). The fixed-bed column data were fitted to the Thomas model to determine maximum solid-phase concentration (q Th). Fig. 10 shows the comparison of experimentally determined and the Thomas model predicted breakthrough curves of nitrate adsorption by NNN-MCM-41 at a flow rate of 1.6 ml/min, influent concentration of 110 mg/l and different bed height. The Thomas rate constant (k Th) and the maximum adsorption capacity (q Th) along with the coefficient of determination, under different conditions, are given in Table 5. It is clear from Fig. 10 that the model gave a good fit of the experimental data obtained from all flow rates, bed heights and initial nitrate anion concentration with a correlation coefficient, r 2, ranging from 0.978 to 0.995 for NNN-MCM-41, which agrees well with the breakthrough experiments. As can be seen from Table 5, the estimations of k Th and q Th were impacted by different conditions. As the bed height increased, the values of q Th increased and the values of k Th decreased. The maximum amount of q Th was 23.43 mg/g at bed height 6 cm. The capacity q Th diminished and Thomas constant k Th expanded with expanding flow rate. In contrast, q Th improved and k Th reduced with increasing initial nitrate concentration.

Although the high coefficient of determination was acquired utilizing the Thomas model, Yan model allows us to predict with great precision, the breakthrough curve, in the whole range of effluent concentration and at time zero and also this model resolves the error resulting from the use of the Thomas model, (Yan and Chen 2001; Pokhrel and Viraraghavan 2008). The breakthrough curves predicted by the Yan model under different conditions are shown in Fig. 10. The model constants (R 2, k y , q Y) obtained by the nonlinear fit of the data are presented in Table 5. At all conditions examined, the breakthrough behavior of the nitrate fed column packed with NNN-MCM-41 was fitted well with the Yan model (based on the R 2 value). Also the maximum adsorption capacity (q Y) predicted by the Yan model showed the same trend predicted by the Thomas model. Due to the high regression coefficient of determination and close to q e of experimental value and q y in each of the three column heights, it can be concluded that Yan model can be a well-described nitrate anion adsorption with mesoporous NNN-MCM-41 in the continuous system. The quantity of nitrate uptake predicted by this model corresponding to 2, 4 and 6 cm bed height of the column was 20.27, 21.13 and 23.41 mg/g, respectively.

Conclusions

The adsorption of nitrate anion with amino-functionalized mesoporous silica was investigated in batch and fixed-bed column systems. Due to their high surface areas, their open pore structure and their appropriate surface functionalization, these adsorbents proved to be high capacity for nitrate anions in water. Batch experiments were conducted at different pH, initial concentration of anions, and adsorbent dose. The results show that the highest removal of nitrate was achieved at pH 7 and adsorption capacity increased with the adsorbent loading. The experimental equilibrium data of nitrate anion fitted with the Langmuir isotherm better than the Freundlich isotherm, with a higher coefficient of determination. The maximum uptake capacity for nitrate anion was 31.68, 38.58 and 38.81 mg/g for N-MCM-41, NN-MCM-41 and NNN-MCM-41, respectively. The kinetics of nitrate anion adsorption onto amino-functionalized MCM-41 revealed that adsorption satisfactorily follows the pseudo-second-order equation. Desorption was rapid and it was completely achieved within 10 min for nitrate anion using NaOH at 0.01 M. Continuous experiments in the fixed-bed column were performed to investigate the impact of bed height, flow rate and initial nitrate concentration. On the basis of the experimental results, the increase of influent concentration and flow rate decreased the breakthrough and exhausted times. In contrast, both breakthrough and exhaust times were found to be increased with increasing the bed height. The Thomas and Yan models are used to describe column data obtained at different conditions. Both models were able to predict breakthrough curves with a coefficient of determination ranging from 0.97 to 0.995.