Introduction

Maize (Zea mays L.) is one of the most important grains in the tropics and temperate regions of the world and is the third most important grain in the world in production after wheat and rice (Mousavi et al. 2021). Due to the increase in the area under maize cultivation in recent years in Iran and achieving high yields per unit area, it is necessary to study the reaction of new hybrids in different regions and years to identify the best genotypes after removing the interaction between genotype and environment and be introduced as high-yielding cultivars (Choukan et al. 2005; Illés et al. 2020; Bojtor et al. 2021).

Inbreeding programs, genotypes should be evaluated in a wide range of environmental variation in different places and years to provide information from estimating compatibility and yield stability of genotypes as a more reliable criterion in recommending cultivars and developing their cultivation, and increasing the efficiency of selection and introduction (Khajeh Ahmad Attari. 1989). The concept of stability was first used in regional performance tests in 1917 (Scapim et al. 2000; Berzsenyi et al. 2007). Parametric methods of genotype response to the environment were considered a one-variable relationship. All univariate methods tried to justify the genotype response to the environment by calculating a stable index. Therefore, a particular genotype may be identified as stable in one assessment and unstable and may not produce the same result. The main reason for this is that the response of genotypes to the environment is a multivariate relationship and cannot be justified by a single stability index (Jadhav et al. 2019; Lin et al., 1986; Lidansky et al. 1998).

Lin et al. (1986) divided parametric conservation methods into three types: Type I: A stable genotype with slight variance between environments. Type II: A stable genotype whose response to environments is parallel to the total responses of genotypes to the environment. Type III is a stable genotype in which the remaining of the regression model is small on its environmental index. In the study of 20 barley genotypes by Bahrami et al. 2008, some of these methods, such as calculating environmental variance, were used to calculate the coefficient of variation by Eberhart and Russell's method identified stable genotypes. In another study investigating durum wheat genotypes, various univariate parametric methods such as regression coefficient, the sum of squares, deviation from Eberhart and Russell regression line, detection coefficient, Shukla stability variance, Wrick’s equivalence, and environmental variance. Finally, two genotypes were introduced as the most stable genotypes (Becker et al.1988; Akcura et al. 2006). Shukla stability variance (i2δ) and Wrick’s equivalence (Wi2) statistics indicate the type II stability of Lin et al. (1986). Hayward et al. (1993) have three factors: genotype, environmental effect, and interaction together. Genotype and environment were implicated in the occurrence of a phenotype. Also, they believed that the genotype in environment interaction reduces phenotypic and genotypic value and may lead to the selection of individuals from one environment that perform poorly in other environments.

Pinthus 1973 suggested that instead of the mean squared deviation from the regression line (S2di), it is better to use the detection coefficient because R2 is strongly dependent on S2di. Also, they believed that the genotype in environment interaction reduces phenotypic and genotypic value and may lead to the selection of individuals from one environment that perform poorly in other environments. Also, suggested that instead of the mean squared deviation from the regression line (S2di), it is better to use the detection coefficient because R2 is strongly dependent on S2di. Using different stability analysis methods such as Roemer environmental variance, coefficient of variation, Wrick’s equivalence, and Eberhart and Russell regression, Soughi et al. Identified stable genotypes in wheat (Soughi et al. 2009).

In another study, regression Eberhart and Russell method was used to evaluate the compatibility and stability of mutant lines in peas. This method was reported as an effective and helpful method in identifying suitable lines for breeding programs (Vassilevska and Naidenova 2006). Finally, some researchers examined the correlation between parametric statistics and grain yield in rain-fed barley. They reported that the equilibrium statistics of Wrick’s equivalence and the Shukla stability variance had a positive and significant correlation (Abdipour et al. 2019; Karimizadeh et al., 2009). This study aimed to investigate genotype by environment interaction and determine the stability of the studied genotypes in different regions in Iran.

Materials and methods

In this study, 12 maize hybrids were cultivated and tested in four regions in Iran during two cropping years (2018–2019) to evaluate the stability using univariate statistical methods. The characteristics are presented in Table 1, and the geographical characteristics are described of the studied areas in Table 2. This experiment was held uniformly in all areas and a randomized complete block design with three replications and each plot consisting of four rows. Experiments were planted with 0.75 m inter-row spacing and 0.20 m in-row spacing. Hand sowing did do in 2 rows of 4 m length. Plots were over-sown and followed by thinning to achieve a plant population of 66,667 plants ha − 1. Sampling was performed from the two middle rows in order to eliminate the marginal effects. In order to analyze the obtained data, simple variance analysis was used and investigate the presence or absence of significant or no significant differences in genotypes and the interaction of genotype and environment, and combined analysis. The mean comparison was performed based on the Duncan test. To evaluate the genotype stability and environmental variance stability parameters were used the coefficient of variation (Francis and Kannenberg 1978), Wrick’s equivalence (Wricke 1962), Shukla stability variance (Shukla 1972), Eberhart and Russel regression coefficient (Eberhart and Russel 1966), and detection coefficients.

Table 1 Geographical characteristics and average rainfall in study stations
Full size table
Table 2 Name of hybrids and comparison of mean grain yield using Duncan test
Full size table

Shukla stability variance (1972):

In order to evaluate the stability of the Shukla genotype (1972) based on the residue obtained from the two-way classification of the interaction of genotype x environment, he proposed an odd estimate of the variance of genotypes in all environments and named this stability parameter as the variance of stability, and is obtained from the following relation:

$$\begin{aligned}\delta_{i}^{2} &= \left[ {\frac{P}{(p - 2)(q - 1)}} \right] \times (x_{ij} - \overline{x}_{10} - \overline{x}.j + \overline{x}_{00} )^{2} \\&\quad - \frac{SSGE}{{(p - 1)(p - 2)(q - 1)}} \end{aligned}$$

In the above formula, the sum of the squares of the interaction of genotype × environment obtained as follows:

$$SSGE = \sum\limits_{i} {W_{i} = \sum\limits_{i}^{p} {\sum\limits_{i}^{q} {(xij - \overline{x}_{i} - \overline{x}.j + \overline{x}..)}^{2} } }$$

According to stability variance (1972), Shukla is a stable genotype in which the amount of stability variance minimal.

Results

In order to investigate significant differences between genotypes in each year and each station studied, a simple analysis of variance was performed in the tested data. The results showed that the studied genotypes had significant differences in each year and each station. Also, based on this analysis, the block effect became meaningless in most areas, indicating the test sites' uniformity. The results of this analysis are presented in Table 3.

Table 3 Simple analysis of variance yield of 12 maize hybrids at four stations in two years
Full size table

Also, in order to investigate the presence or absence of significant or insignificant was used differences in genotypes and the interaction of genotype and environment, a combined analysis. This analysis showed that it had a significant effect on the environment, the interaction of genotype × environment, and the effect (Table. 4) of genotype. The differences in study stations showed that the environments differed in terms of grain yield in genotypes. The significant interaction between genotype and environment indicated that genotype yield (Table. 5) differed from one environment to another.

Table 4 Combined analysis of variance of grain yield of maize hybrids in eight environments (four stations and two years)
Full size table
Table 5 Mean grain yield and 6 parametric methods of stability in 12 maize hybrids in 5 experimental areas
Full size table

Based on environmental variance, the genotypes with the lowest amount of this statistic are selected as the most desirable hybrids. Accordingly, KSC707, KSC260, and SC302 genotypes had a minor environmental variance than the rest of the genotypes, but considering that KSC260 genotypes, KSC707 had a higher average yield and were introduced as the most desirable genotypes in this method. KSC706, KSC704, SC647, and KSC400 genotypes were introduced as the most unstable hybrids due to their highest environmental variance. the coefficient of variation (CVi) is a stable genotype with the lowest amount of this parameter. Accordingly, SC302, KSC705, KSC260, KSC707, and SC604 genotypes had the lowest parameter, considering KSC705, KSC707 genotypes KSC260 had the highest average yield introduced as the most stable hybrids in this method. Also, according to Eberhart and Russell regression coefficient method, each genotype that has the lowest value of this statistic has more stability. As a result, KSC400, SC647, SC302 and KSC260 genotypes had the lowest value of this parameter. However, considering that KSC400 and SC647 genotypes had the highest mean yield compared to the average total yield, they were introduced as the most stable hybrids. Also, KSC704 and SC301 genotypes were introduced as the most unstable genotypes because they had the highest parameter. Based on the method, the genetic coefficient of diagnosis is stable, which has the highest statistic rate. Accordingly, KSC703, KSC707, and KSC260 hybrids had the highest rate, but KSC707 and KSC703 genotypes had the highest average yield compared to the average total yield. Therefore, the genotypes were identified as the most stable. Also, KSC400, KSC704, and SC647 genotypes were introduced as the most unstable hybrids due to the high rate of this statistic.

Data analysis of stability parameters showed a positive and significant correlation between the S2di parameter in the first and second years and the mean of two crop years with the CVi parameter. This parameter was positively correlated with the bi parameter (Stability variance of Finlay and Wilkinson) the first year and the mean of two crop years. S2di had a positive and significant correlation with Wi2 and SH parameters in the second crop year and had a negative and significant correlation with Ri2 (detection coefficient). The CVi parameter in the first crop year and the mean of the two years studied positively correlated with the bi parameter (Stability variance of Finlay and Wilkinson). A positive correlation was found between Wi2 and SH parameters in the second crop year, and a negative and significant correlation between Wi2 and Ri2. This parameter revealed only a positive and significant correlation with S2di and Ri2 parameters in the first crop year. The Wi2 parameter had a positive and significant correlation with the SH parameter in all the three first, second, and average two-year cultivars. The Ri2 parameter (detection coefficient) had a negative and significant correlation. Also, this parameter showed a significant negative correlation between the bi parameter (Stability variance of Finlay and Wilkinson) in the first year and the mean of two crop years. The SH parameter had a significant negative correlation between the bi(Stability variance of Finlay and Wilkinson) and Ri2 parameters (detection coefficient) in the first, second, and two-year averages in all three conditions. bi parameter (Stability variance of Finlay and Wilkinson) had a positive and significant correlation with Ri2 parameter (detection coefficient) in all the three conditions of the first, second, and the mean of two years. In the second year, this parameter had a positive and significant correlation with S2di. S2di had a significant positive correlation with Ri2 (detection coefficient) only in the second crop year. Based on the above studies and considering that some parameters showed the same results in all the three conditions (the first year, the second year, and mean of two crop years), it can be concluded that the Si2 parameter is positively and significantly correlated with CVi and Wi2 parameter with SH parameter, and bi parameter (Stability variance of Finlay and Wilkinson) with Ri2 parameter (detection coefficient). Moreover, the Wi2 parameter is negatively and significantly correlated with Ri2 (detection coefficient), SH parameter with bi (Stability variance of Finlay and Wilkinson), and Ri2 (detection coefficient).

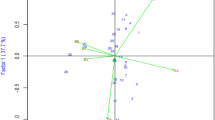
Graphical correlation analysis was used to examine the correlation of stability statistics (Fig. 1). In this cosine biplot diagram, the angle between the attribute vectors indicates the intensity of the correlation between the traits. If the angle between the vectors is less than 90 degrees, the correlation between the vectors is equal to + 1, if the angle between the vectors of the traits is 90 degrees, the correlation between the vectors of the attributes is zero, and correlation is -1 if the angle between the vectors 180 degrees. According to Fig. 1, the statistics of Wrick’s equivalence, Shukla stability variance, Eberhart and Russell coefficient of variation, environmental variance, and coefficient of variation had a positive and significant correlation with the mean grain yield. Also, the coefficient of detection coefficient had a negative and significant correlation with the average grain yield. Based on this figure, Wrick’s equivalence and Shukla variance statistics positively correlated with each other. Eberhart and Russell regression coefficients, Shukla variance, and environmental variance showed a positive and significant correlation. The two statistics of coefficient of variation and Wrick’s equivalence did not correlate concerning the 90° angle of the vector, and the correlation was zero between these two statistics. Diagnostic coefficient statistics had a significant negative correlation with Shukla stability variance and Wrick’s equivalence statistics (Table 6, Fig. 1).

Fig. 1
figure 1

Biplot of correlation between univariate stability statistics in 12 maize hybrids in 5 regions. CVi: the coefficient of variation, Si2: environmental variance, Wi2: Wrick’s equivalence, SH: Shokla variance, S2di: Eberhart and Russell regression coefficient, Ri2: detection coefficient

Full size image
Table 6 Correlation between stability parametric measures for 12 hybrids across four environments
Full size table

Discussion

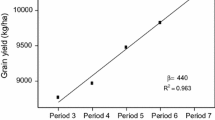
The result is that the performance stability of these hybrids can be examined and identified, and hybrids with private adaptation to each environment and hybrids with general adaptation to all environments. Mean yield in genotypes was done using Duncan's multiple range test at 0.05 level of probability. This analysis showed that the KSC705 genotype with an average yield of 7.21 (t\h) and KSC704 genotype with an average yield of 7.04 (t\h) had the highest average yield. SC301, SC302, and KSC260 genotypes with average yields of 4.8(t\h), 4.9(t\h), and 4.54 (t\h) had the lowest mean yields among hybrids. Although the above methods have some similarities in introducing stable genotypes, differences in introducing genotypes indicate that the results of the above parameters are not entirely consistent. A nonparametric method presented the criterion of total rank for the simultaneous selection of stable and maximum yielding genotypes in yield rank and Shukla stability variance rank. In this method, a genotype with the highest yield is ranked first, and a genotype with the lowest variance value is ranked first. Then, yield rank and variance rank for each genotype are added together, and this sum is used as a statistic to determine the stable genotype. In this method, a genotype is stable that has the least amount of sum (Pinto et al. 2019). As can be seen, in the environmental variance method of KSC707, KSC260, and SC302 hybrids, in the environmental variation coefficient method of KSC707, KSC705, and KSC260 hybrids, in the method based on the genotypic variance of KSC400, SC647 hybrids, in the regression coefficient method of Eberhart and Russell SC647, KSC707 and KSC703 hybrids were selected as the most stable genotypes in the method of detection coefficient. These results indicate differences in the selection of hybrids. In introducing the most unstable hybrids based on the coefficient of variation of KSC400, KSC704, KSC706, and SC647 genotypes, based on the coefficient of variation methods of SC647, KSC706, KSC400, KSC704, and SC301 genotypes and based on KSC variance4 genotype methods and KSC707, based on Eberhart and Russell regression coefficient, KSC704, KSC703, and SC301 genotypes were introduced and based on the detection coefficient of KSC704, KSC400, and SC647 genotypes, among which genotype six was identified as unstable genotype in all the above methods. Although yield combines genotype effect, environment effect, and genotype × environment interaction effect, only genotype and genotype × environment interaction effect are related to genotypes evaluation. Therefore, it is not easy to identify and control the environment (Olivoto et al. 2021). Grain yield and stability have always been used in many years and regions and are important in selecting genotypes (Yamamoto et al. 2021). Esmaeilzadeh Moghaddam et al. 2010 used regression methods of Eberhart and Russell, Wrick’s equivalence and Shukla stability variance, grain yield stability, and genotype and environment interaction in 21 bread wheat cultivars. Tarinejad et al. 2015 studied grain yield stability in bread wheat using various parameters such as Roemer’s environmental variance and phenotypic variation coefficient. The stability of a product is its ability to survive in a particular environment. The plant should withstand cold, heat, water shortages, changes in day length, light intensity, and a wide range of chemical and physical conditions of the soil. Complex major and minor genes control this adaptation (Rezende et al. 2020). A large proportion of yield variability is usually justified by the environment (80% or higher), while the genotype effect and the between genotype × environment interaction are usually small (De Oliveira et al. 2013). Vaezi et al. 2019 concluded that the combination of different stability criteria could be useful in identifying stable genotypes with high yield. Kaplan et al., 2017 used different stability and cluster analysis methods to identify stable cultivars in corn and concluded that the average yield and stability parameters could effectively identify stable corn genotypes.

Conclusion

The results showed that the studied genotypes had significant differences in each year and each station. These results indicate differences in the selection of hybrids. For example, KSC400, KSC704, KSC706, and genotypes had the most unstable hybrids based on stability coefficient. On the other hand, KSC707, SC647, and KSC703 genotypes had the most stable genotypes in the method of stability coefficient.