Skip to main content
SpringerLink
Log in

A Novel Decision-Making Method Based on Probabilistic Linguistic Information

  • Published:
Cognitive Computation Aims and scope Submit manuscript

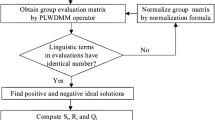
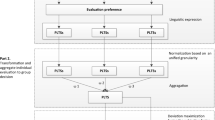
Abstract

The Maclaurin symmetric mean (MSM) operator has the characteristic of capturing the interrelationship among multi-input arguments, the probabilistic linguistic terms set (PLTS) can reflect the different degrees of importance or weights of all possible evaluation values, and the improved operational laws of probabilistic linguistic information (PLI) can not only avoid the operational values out of bounds for the linguistic terms set (LTS) but also keep the probability information complete after operations; hence, it is very meaningful to extend the MSM operator to PLTS based on the operational laws. To fully take advantage of the MSM operator and the improved operational laws of PLI, the MSM operator is extended to PLI. At the same time, two new aggregated operators are proposed, including the probabilistic linguistic MSM (PLMSM) operator and the weighted probabilistic linguistic MSM (WPLMSM) operator. Simultaneously, the properties and the special cases of these operators are discussed. Further, based on the proposed WPLMSM operator, a novel approach for multiple attribute decision-making (MADM) problems with PLI is proposed. With a given numerical example, the feasibility of the proposed method is proven, and a comparison with the existing methods can show the advantages of the new method in this paper. The developed method adopts the new operational rules with the accurate operations, and it can overcome some existing weaknesses and capture the interrelationship among the multi-input PLTSs, which easily express the qualitative information given by the decision-makers’ cognition.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Abu-Saris R, Hajja M. On gauss compounding of symmetric weighted arithmetic means. J Math Anal Appl. 2006;322:729–34.

    Google Scholar 

  2. Baležentis T, Baležentis A. Group decision making procedure based on trapezoidal intuitionistic fuzzy numbers: multimoora methodology. Econom Comput Econom Cybernet. Stud Res. 2016;50(1):103–22.

    Google Scholar 

  3. Bapat RB. Symmetrical function means and permanents. Linear Algebra Appl. 1993;182:101–8.

    Google Scholar 

  4. Bai CZ, Zhang R, Qian LX, Wu YN. Comparisons of probabilistic linguistic term sets for multi-criteria decision making. Knowl-Based Syst. 2016.

  5. Cuttler A, Greene C, Skandera M. Inequalities for symmetric means. Eur J Comb. 2011;32:745–61.

    Google Scholar 

  6. Detemple D, Robertson J. On generalized symmetric means of two variables. Univ Beograd Publ Elektrotehn Fak Ser Mat Fiz. 1979;677(634):236–8.

    Google Scholar 

  7. Dong YC, Li CC, Herrera F. An optimization-based approach to adjusting unbalanced linguistic preference relations to obtain a required consistency level. Inf Sci. 2015;292:27–38.

    Google Scholar 

  8. Gao P. On a conjecture on the symmetric means. J Math Anal Appl. 2008;337:416–24.

    Google Scholar 

  9. Gou X, Xu Z. Novel basic operational laws for linguistic terms, hesitant fuzzy linguistic term sets and probabilistic linguistic term sets. Inf Sci. 2016;372:407–27.

    Google Scholar 

  10. Gou X, Xu Z, Liao H, Multiple criteria decision making based on Bonferroni means with hesitant fuzzy linguistic information, Soft Comput (2016) 1–15.

  11. He YD, He Z, Chen HY. Intuitionistic fuzzy interaction Bonferroni means and its application to multiple attribute decision making. IEEE Trans Cybernet. 2015;45:116–28.

    Google Scholar 

  12. He YD, He Z. Extensions of Atanassov’s intuitionistic fuzzy interaction Bonferroni means and their application to multiple attribute decision making. IEEE Trans Fuzzy Syst. 2016;24(3):558–73.

    Google Scholar 

  13. He YD, He Z, Lee D-H, Kim K-J, Zhang L, Yang X. Robust fuzzy programming method for MRO problems considering location effect, dispersion effect and model uncertainty. Comput Ind Eng. 2017;105:76–83.

    Google Scholar 

  14. Liu PD. Some geometric aggregation operators based intervalvalued intuitionistic uncertain linguistic variables and their application to group decision making. Appl Math Model. 2013;37:2430–44.

    Google Scholar 

  15. Liu P. Special issue: intuitionistic fuzzy theory and its application in economy, technology and management. Technol Econ Dev Econ. 2016;22(3):327–35.

    CAS  Google Scholar 

  16. Liu PD. Multiple attribute group decision making method based on interval-valued intuitionistic fuzzy power Heronian aggregation operators. Comput Ind Eng. 2017;108:199–212.

    Google Scholar 

  17. Liu P, Li Y, Antuchevičienė J. Multi-criteria decision-making method based on intuitionistic trapezoidal fuzzy prioritised OWA operator. Technol Econ Dev Econ. 2016;22(3):453–69.

    Google Scholar 

  18. Liu PD, Chen SM, Liu JL. Some intuitionistic fuzzy interaction partitioned Bonferroni mean operators and their application to multi-attribute group decision making. Inf Sci. 2017;411:98–121.

    Google Scholar 

  19. Liu PD, Jin F. Methods for aggregating intuitionistic uncertain linguistic variables and their application to group decision making. Inf Sci. 2012;205:58–71.

    Google Scholar 

  20. Liu PD, Li HG. Interval-valued intuitionistic fuzzy power Bonferroni aggregation operators and their application to group decision making. Cogn Comput. 2017;9(4):494–512.

    Google Scholar 

  21. Liu PD, Liu ZM, Zhang X. Some intuitionistic uncertain linguistic Heronian mean operators and their application to group decision making. Appl Math Comput. 2014;230:570–86.

    Google Scholar 

  22. Liu PD, Shi LL. Some neutrosophic uncertain linguistic number Heronian mean operators and their application to multi-attribute group decision making. Neural Comput & Applic. 2017;28(5):1079–93.

    Google Scholar 

  23. Liu PD, Tang GL. Multi-criteria group decision-making based on interval neutrosophic uncertain linguistic variables and Choquet integral. Cogn Comput. 2016;8(6):1036–56.

    Google Scholar 

  24. Maclaurin C. A second letter to Martin Folkes, Esq.; concerning the roots of equations, with demonstration of other rules of algebra. Philos Trans R Soc Lond. 1729;36:59–96.

    Google Scholar 

  25. Merigó JM. Decision-making under risk and uncertainty and its application in strategic management. J Bus Econ Manag. 2015;16(1):93–116.

    Google Scholar 

  26. Pang Q, Xu ZS, Wang H. Probabilistic linguistic term sets in multi-attribute group decision making. Inf Sci. 2016;369:128–43.

    Google Scholar 

  27. Peng JJ, Wang JQ, Wu XH. Novel multi-criteria decision-making approaches based on hesitant fuzzy sets and prospect theory. Int J Inf Technol Decis Mak. 2016;15(3):621–43.

    Google Scholar 

  28. Qin JD, Liu XW. An approach to intuitionistic fuzzy multiple attribute decision making based on Maclaurin symmetric mean operators. J Intell Fuzzy Syst. 2014;27(5):2177–90.

    Google Scholar 

  29. Rodriguez RM, Martinez L, Herrera F. Hesitant fuzzy linguistic term sets for decision making. IEEE Trans Fuzzy Syst. 2012;20:109–19.

    Google Scholar 

  30. Rong LL, Liu PD, Chu Y. Multiple attribute group decision making methods based on intuitionistic fuzzy generalized hamacher aggregation operator. Econom Comput Econom Cybernet Stud Res. 2016;50(2):211–30.

    Google Scholar 

  31. Stanujkic D, Zavadskas EK, Brauers WKM. An extension of the MULTIMOORA method for solving complex decision-making problems based on the use of interval-valued triangular fuzzy numbers. Transform Bus Econ. 2015;14(2B):355–77.

    Google Scholar 

  32. Wang JQ, Li JJ. The multi-criteria group decision making method based on multi-granularity intuitionistic two semantics. Sci Technol Inform. 2009;33:8–9.

    CAS  Google Scholar 

  33. Wang JQ, Yang Y, Li L. Multi-criteria decision-making method based on single-valued neutrosophic linguistic Maclaurin symmetric mean operators. Neural Comput & Applic. 2018;30(5):1529–47 (4)2016 1–19.

    Google Scholar 

  34. Wu J, Chiclana F, Herrera-Viedma E. Trust based consensus model for social network in an incomplete linguistic information context. Appl Soft Comput. 2015;35:827–39.

    Google Scholar 

  35. Xu ZS. Deviation measures of linguistic preference relations in group decision making. Omega. 2005;33:249–54.

    Google Scholar 

  36. Xu ZS. Linguistic decision making: theory and methods. Berlin, Heidelberg: Springer-Verlag; 2012.

    Google Scholar 

  37. Xu ZS, Yager RR. Intuitionistic fuzzy Bonferroni means. IEEE Trans Syst Man and Cybernet Part B: Cybernet. 2011;41(2):568–78.

    Google Scholar 

  38. Yu DJ, Wu YY. Interval-valued intuitionistic fuzzy Heronian mean operators and their application in multi-criteria decision making. Afr J Bus Manag. 2012;6(11):4158–68.

    Google Scholar 

  39. Zadeh LA. The concept of a linguistic variable and its application to approximate reasoning—I. Inf Sci. 1975;8:199–249.

    Google Scholar 

  40. Zadeh LA. The concept of a linguistic variable and its application to approximate reasoning—II. Inf Sci. 1975;8:301–57.

    Google Scholar 

  41. Zadeh LA. The concept of a linguistic variable and its application to approximate reasoning—III. Inf Sci. 1975;9:43–80.

    Google Scholar 

  42. Zavadskas EK, Antucheviciene J, Hajiagha SHR. Extension of weighted aggregated sum product assessment with interval-valued intuitionistic fuzzy numbers (WASPAS-IVIF). Appl Soft Comput. 2014;24:1013–21.

    Google Scholar 

  43. Zeng S, Su W, Zhang C. Intuitionistic fuzzy generalized probabilistic ordered weighted averaging operator and its application to group decision making. Technol Econ Dev Econ. 2016;22(2):177–93.

    Google Scholar 

  44. Zhang XL, Xing XM. Probabilistic linguistic VIKOR method to evaluate green supply chain initiatives. Sustainability. 2017;9(7):1231.

    Google Scholar 

  45. Zhang XM, Haining Z. S-geometric convexity of a function involving Maclaurin’s elementary symmetric mean. J Inequal Pure Appl Math. 2007;8:156–65.

    CAS  Google Scholar 

  46. Zhang YX, Xu ZS, Wang H, Liao HC. Consistency-based risk assessment with probabilistic linguistic preference relation. Appl Soft Comput J. 2016;49:817–33.

    Google Scholar 

  47. Zhang ZH, Xiao ZG, Srivastava HM. A general family of weighted elementary symmetric means. Appl Math Lett. 2009;22:24–30.

    CAS  Google Scholar 

  48. Zhu B, Xu ZS. Extended hesitant fuzzy sets. Technol Econ Dev Econ. 2016;22(1):1–22.

    Google Scholar 

Download references

Acknowledgments

This paper is supported by the National Natural Science Foundation of China (Nos. 71771140 and 71471172), the Special Funds of Taishan Scholars Project of Shandong Province (No. ts201511045), the Humanities and Social Sciences Research Project of Ministry of Education of China (No. 19YJC630023).

Author information

Authors and Affiliations

  1. School of Management Science and Engineering, Shandong University of Finance and Economics, Jinan, 250014, Shandong, China

    Peide Liu & Ying Li

Authors
  1. Peide Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ying Li
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Peide Liu.

Ethics declarations

Conflict of Interest

The authors declare that they have no conflict of interest.

Research Involving Human Participants and/or Animals

This article does not contain any studies with human participants or animals performed by any of the authors.

Additional information

Publisher’s Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Liu, P., Li, Y. A Novel Decision-Making Method Based on Probabilistic Linguistic Information. Cogn Comput 11, 735–747 (2019). https://doi.org/10.1007/s12559-019-09648-w

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12559-019-09648-w

Keywords

Search

Navigation