Optimal Design of Sensors via Geometric Criteria

Abstract

We consider a convex set $\Omega$ and look for the optimal convex sensor $\omega \subset \Omega$ of a given measure that minimizes the maximal distance to the points of $\Omega .$ This problem can be written as follows

$$\begin{aligned} \inf \{d^H(\omega ,\Omega ) \ |\ |\omega |=c\ \text {and}\ \omega \subset \Omega \}, \end{aligned}$$

where $c\in (0,|\Omega |),$ $d^H$ being the Hausdorff distance. We show that the parametrization via the support functions allows us to formulate the geometric optimal shape design problem as an analytic one. By proving a judicious equivalence result, the shape optimization problem is approximated by a simpler minimization problem of a quadratic function under linear constraints. We then present some numerical results and qualitative properties of the optimal sensors and exhibit an unexpected symmetry breaking phenomenon.

1 Introduction

The optimal shape and placement of sensors frequently arises in industrial applications such as urban planning and temperature and pressure control in gas networks. Roughly, a sensor is optimally designed and placed if it assures the maximum observation of the phenomenon under consideration. Naturally, it is often designed in a goal oriented manner, constrained by a suitable PDE, accounting for the physics of the process. For more examples and details, we refer to the following non exhaustive list of works [12, 19,20,21]. Recently, with the emergence of data driven methods, several authors considered approaches based on Machine Learning in order to accelerate the computations, we refer for example to [22, 24, 26, 28].

Here, we address the problem in a purely geometric setting, without involving the specific PDE model. We consider a simple and natural geometric criterion of performance, based on distance functions. But, as we shall see, tackling it will require to employ geometric analysis methods.

More precisely, we address the issue of designing an optimal sensor inside a given set in such a way to minimize the maximal distance from the sensor to all the points of the largest domain. This type of questions naturally arises in optimal resources distribution problems as one wants to minimize the maximal distance between the resources and the species present in the considered environment. Also in urban planning, it makes sense to look for the optimal design and placement of some facility (for example a park or an artificial lake) inside a city while taking into account a certain equity and accessibility criterion that consists in minimizing the maximal distance from any point in the city to the facility.

These problems can then be formulated in a shape optimization framework. Indeed, given a set $\Omega \subset \mathbb {R}^2,$ and a mass fraction $c\in (0,|\Omega |),$ the problem can be mathematically formulated as follows:

$$\begin{aligned} \inf \left\{ \sup _{x\in \Omega } d(x,\omega )\ |\ |\omega |=c\ \text {and}\ \omega \subset \Omega \right\} , \end{aligned}$$

where $d(x,\omega ):= \inf _{y\in \omega }\Vert x-y\Vert$ is the minimal distance from x to $\omega .$ In fact, the problem can be written in terms of the classical Hausdorff distance $d^H$ (see Sect. 2.2) as when $\omega \subset \Omega ,$ one has

$$\begin{aligned} \sup _{x\in \Omega } d(x,\omega ) = d^H(\omega ,\Omega ). \end{aligned}$$

We are then interested in considering the following problem

$$\begin{aligned} \inf \{d^H(\omega ,\Omega ) \ |\ |\omega |=c\ \text {and}\ \omega \subset \Omega \}, \end{aligned}$$

(1)

where $c\in (0,|\Omega |).$

By using a homogenization strategy, which consists in uniformly distributing the mass of the sensor over $\Omega$ (see Fig. 1), we see that problem (1) does not admit a solution as the infimum vanishes and is asymptotically attained by a sequence of disconnected sets with an increasing number of connected components. It is then necessary to impose additional constraints on $\omega$ in order to obtain the existence of optimal solutions. In the present paper, we focus on the convexity constraint and assume that both the set $\Omega$ and the sensor $\omega$ are planar convex bodies. Then, given a convex bounded domain $\Omega \in \mathbb {R}^2,$ we are interested in the numerical and theoretical study of the following problem:

$$\begin{aligned} \inf \{d^H(\omega ,\Omega ) \ |\ \omega \ \text {is convex},\ |\omega |=c\ \text {and}\ \omega \subset \Omega \}, \end{aligned}$$

(2)

where $c\in (0,|\Omega |).$

Fig. 1

The homogenization strategy

We note that the convexity constraint is classically considered in shape optimization and sometimes appears as a natural simplifying hypothesis in physical problems. For example, one of the first problems in the calculus of variations is a least resistance problem posed by Newton in his Principia.

The problem is to consider a convex body that moves forward in a homogeneous medium composed of point particles. The medium is extremely rare, so as to assume that there is no mutual interaction. The particles are assumed to be initially at rest. When colliding with the body, each particle is reflected elastically. As a result of collisions, there appears a drag force that acts on the body and slows down its motion.

Take a coordinate system in $\mathbb {R}^3$ and assume that the body is travelling in positive z-direction. Let the upper part of the convex body’s surface be the graph of a concave function $u:\Omega \longrightarrow \mathbb {R},$ where $\Omega$ is the projection of the body on the (x, y)-plane. By elementary physics arguments, Newton obtained the following resistance functional

$$\begin{aligned} J(u) = \int _\Omega \frac{1}{1+|\nabla u|^2} dx \end{aligned}$$

and introduced the following natural problem

$$\begin{aligned} \inf \{J(u)\ |\ u:\Omega \longrightarrow \mathbb {R}\ \text {is concave}\}, \end{aligned}$$

which consists in looking for the shape of the convex body that minimizes the resistance. We refer to [5] for a detailed discussion of the model and the history of this problem.

Let us now state the main results of the present paper. A first important theorem is the following:

Theorem 1

The function $f:c\in [0,|\Omega |]\longmapsto \inf \{d^H(\omega ,\Omega )\ |\ \omega \ \text {is convex,}\ |\omega |=c\ \text {and}\ \omega \subset \Omega \}$ is continuous and strictly decreasing. Moreover,  for every $c\in [0,|\Omega |],$ problem (2) admits solutions and is equivalent to the following shape optimization problems : 

• (I) $\min \{d^H(\omega ,\Omega )\ |\ \omega \ \text {is convex,}\ |\omega |\le c\ \text {and}\ \omega \subset \Omega \},$

• (II) $\min \{|\omega |\ |\ \omega \text {is convex},\ d^H(\omega ,\Omega )=f(c)\ \text {and}\ \omega \subset \Omega \},$

• (III) $\min \{|\omega |\ |\ \omega \text { is convex},\ d^H(\omega ,\Omega )\le f(c)\ \text {and}\ \omega \subset \Omega \},$

in the sense that any solution of one of the problems also solves the other ones.

Let us give a few comments on this theorem:

• The results hold in higher dimensions. Nevertheless, we have made the choice to state them in the planar framework for readability sake and coherence with the qualitative and numerical results obtained in the planar case, see Sects. 4 and 5.

• On the other hand, in addition to its importance from a theoretical point of view (as we shall see in Sect. 4), the equivalence result above allows to drastically simplify the numerical resolution of problem (2): indeed, as it is explained in Sect. 5.1, the equivalent problem (III) can be reformulated via the support functions h and $h_\Omega$ of the sets $\omega$ and $\Omega$ in the following analytical form:

  $$\begin{aligned} \left\{ \begin{array}{l} \inf _{h\in {H^1}_{\text {per}}(0,2\pi )} \frac{1}{2}\int _0^{2\pi }({h'}^2-h^2)d\theta ,\\ h''+h\ge 0\ \quad (\text {in the sense of distributions}),\\ h_\Omega -f(c)\le h\le h_\Omega , \end{array}\right. \end{aligned}$$

  where $H^1_{\text {per}}(0,2\pi )$ is the set of $H^1$ functions that are $2\pi$-periodic and $c\in [0,|\Omega |].$ This analytical problem is then approximated by a finite dimensional one, involving the truncated Fourier series of the support functions h as in [2, 3], which yields to a simple minimization problem of a quadratic function under linear constraints. For more details on the support function parametrization, we refer to Sect. 2.1 and for the complete description of the numerical scheme used in the paper, we refer to Sect. 5.

One could expect that solutions of (2) will inherit the symmetries of the set $\Omega .$ We show that this is not always the case and highlight a symmetry breaking phenomenon appearing when $\Omega$ is a square, see Fig. 2. Our result can be stated as follows:

Theorem 2

Let $\Omega =[0,1]\times [0,1]$ be the unit square. There exists a threshold $c_0\in (0,1)$ such that : 

• If $c\in [c_0,1],$ then the solution of (2) is given by the square of area c and same axes of symmetry as $\Omega .$

• If $c\in [0,c_0),$ then the solution of (2) is given by a suitable rectangle.

Fig. 2

Optimal shapes when $\Omega$ is a square, for $c\in \{0.7,0.5,0.2,0.1,0\}$

The paper is organized as follows: in Sect. 2, we present the notations used and recall some classical results on the support function which is a classical parametrization of convex sets that allows to formulate the considered geometric problems as purely analytic ones. In Sect. 3, we present the proof of Theorem 1. Section 4 is devoted to the proof of Theorem 2 and some qualitative properties of intrinsic interest: namely, we prove that when the set $\Omega$ is a polygon, the optimal sensor is also a polygon. At last, in Sect. 5, we present a numerical framework for solving the problem and show that thanks to the equivalence result of Theorem 1, problem (2) can be numerically addressed by a simple minimization of a quadratic function under some linear constrains.

2 Notations and Useful Results

2.1 Definition of the Support Function and Classical Results

If $\Omega$ is convex (not necessarily containing the origin), its support function is defined as follows:

$$\begin{aligned} h_\Omega :x\in \mathbb {R}^2\longmapsto \sup \{\langle x,y \rangle \ |\ y\in \Omega \}. \end{aligned}$$

Since the functions $h_\Omega$ satisfy the scaling property $h_\Omega (t x) = t h_\Omega (x)$ for $t>0,$ it can be characterized by its values on the unit sphere ${\mathbb {S}}^{1}$ or, equivalently, on the interval $[0,2\pi ].$ We then adopt the following definition:

Definition 3

The support function of a planar bounded convex set $\Omega$ is defined on $[0,2\pi ]$ as follows (Fig. 3):

$$\begin{aligned} h_\Omega :[0,2\pi )\longmapsto \sup \left\{ \left\langle \left( {\begin{array}{c}\cos {\theta }\\ \sin {\theta }\end{array}}\right) , y \right\rangle \ |\ y\in \Omega \right\} . \end{aligned}$$

Fig. 3

The support function of the convex $\Omega$

The support function has some interesting properties:

• It allows to provide a simple criterion of the convexity of $\Omega .$ Indeed, $\Omega$ is convex if and only if $h_\Omega ''+h_\Omega \ge 0$ in the sense of distributions, see for example [23, (2.60)].

• It is linear for the Minkowski sum and dilatation. Indeed, if $\Omega _1$ and $\Omega _2$ are two convex bodies and $\alpha , \beta >0,$ we have

  $$\begin{aligned} h_{\alpha \Omega _1 + \beta \Omega _2}= \alpha h_{\Omega _1}+ \beta h_{\Omega _2}, \end{aligned}$$

  see [23, Section 1.7.1].

• It allows to parametrize the inclusion in a simple way. Indeed, if $\Omega _1$ and $\Omega _2$ are two convex sets, we have

  $$\begin{aligned} \Omega _1\subset \Omega _2\Longleftrightarrow h_{\Omega _1}\le h_{\Omega _2}. \end{aligned}$$

• It also provides elegant formulas for some geometric quantities. For example, the perimeter and the area of a convex body $\Omega$ are respectively given by

  $$\begin{aligned} P(\Omega )= & {} \int _0^{2\pi }h_\Omega (\theta )d\theta \quad \text {and}\quad |\Omega |= \frac{1}{2}\int _0^{2\pi } h_\Omega (\theta )(h_\Omega ''(\theta )+h_\Omega (\theta ))d\theta \\= & {} \frac{1}{2} \int _0^{2\pi } ({h_\Omega '}^2-h_\Omega ^2)d\theta \end{aligned}$$

  and the Hausdorff distance between two convex bodies $\Omega _1$ and $\Omega _2$ is given by

  $$\begin{aligned} d^H(\Omega _1,\Omega _2)=\max _{\theta \in [0,2\pi ]} |h_{\Omega _1}(\theta )-h_{\Omega _2}(\theta )|, \end{aligned}$$

  see [23, Lemma 1.8.14].

2.2 Notations

• $\mathcal {K}_c$ corresponds to the class of planar, closed, bounded and convex subsets of $\Omega ,$ of area c,  where $c\in [0,|\Omega |].$

• If X and Y are two subsets of $\mathbb {R}^n,$ the Hausdorff distance between the sets X and Y is defined as follows

  $$\begin{aligned} d^H(X,Y) = \max \left( \sup _{x\in X}d(x,Y),\sup _{y\in Y}d(y,X)\right) , \end{aligned}$$

  where $d(a,B):= \inf _{b\in B}\Vert a-b\Vert$ quantifies the distance from the point a to the set B. Note that when $\omega \subset \Omega ,$ as it is the case in the problems considered in the present paper, the Hausdorff distance is given by

  $$\begin{aligned} d^H(\omega ,\Omega ):= \sup _{x\in \Omega } d(x,\omega ). \end{aligned}$$

• If $\Omega$ is a convex set, then $h_\Omega$ corresponds to its support function as defined in Sect. 2.1.

• Given a convex set $\Omega ,$ we denote by $\Omega _{-t}$ its inner parallel set at distance $t\ge 0,$ which is defined by

  $$\begin{aligned} \Omega _{-t}:=\{x\ |\ d(x,\partial \Omega )\ge t\}. \end{aligned}$$

• $H^1_{\text {per}}(0,2\pi )$ is the set of $H^1$ functions that are $2\pi$-periodic.

3 Proof of Theorem 1

For the convenience of the reader, we decomposed the proof in 3 parts: first, we prove the existence of solutions of problem (2). Then, we prove the monotonicity and continuity of the function $f:c\in [0,|\Omega |]\longmapsto \min \{d^H(\omega ,\Omega )\ |\ \omega \in \mathcal {K}_c \}.$ At last, we present the proof of the equivalence between the four shape optimization problems stated in Theorem 1.

3.1 Existence of Minimizers

Proposition 4

Problem (2) admits at least one solution.

Proof

First, we note that the functional $\omega \longmapsto d^H(\omega ,\Omega )$ is 1-Lipschitz (thus continuous) with respect to the Hausdorff distance. Indeed, for every convex sets $\omega _1$ and $\omega _2,$ we have

$$\begin{aligned}{} & {} |d^H(\omega _1,\Omega )-d^H(\omega _2,\Omega )| = \big |\Vert h_\Omega -h_{\omega _1}\Vert _{\infty }- \Vert h_\Omega -h_{\omega _2}\Vert _{\infty } \big |\\{} & {} \le \Vert h_{\omega _1}-h_{\omega _2}\Vert _{\infty }= d^H(\omega _1,\omega _2). \end{aligned}$$

Let $(\omega _n)$ be a minimizing sequence for problem (2), i.e., such that $\omega _n\in \mathcal {K}_c$ and

$$\begin{aligned} \lim _{n\rightarrow +\infty } d^H(\omega _n,\Omega ) =\inf \{d^H(\omega ,\Omega )\ |\ \omega \in \mathcal {K}_c \}. \end{aligned}$$

Since all the convex sets $\omega _n$ are included in the bounded set $\Omega ,$ we have, by Blaschke’s selection Theorem (see [23, Th 1.8.7]), that there exists a convex set $\omega ^*\subset \Omega$ such that $(\omega _n)$ converges up to a subsequence (that we also denote by $(\omega _n)$) to $\omega ^*$ with respect to the Hausdorff distance. By the continuity of the volume functional with respect to the Hausdorff distance, we have

$$\begin{aligned} |\omega ^*| = \lim _{n\rightarrow +\infty } |\omega _n| = c, \end{aligned}$$

which means that $\omega ^*\in \mathcal {K}_c.$ Moreover, by the continuity of $\omega \longmapsto d^H(\omega ,\Omega )$ with respect to the Hausdorff distance, we have that

$$\begin{aligned} \lim _{n\rightarrow +\infty } d^H(\omega _n,\Omega ) = d^H(\omega ^*,\Omega ). \end{aligned}$$

This shows that $\omega ^*$ is a solution of problem (2). $\square$

3.2 Monotonicity and Continuity

Proposition 5

The function $f:c\in [0,|\Omega |]\longmapsto \min \{d^H(\omega ,\Omega )\ |\ \omega \in \mathcal {K}_c \}$ is continuous and strictly decreasing.

Proof

Continuity: Let $c_0\in (0,|\Omega |).$ By Proposition 4, for every $c\in [0,|\Omega |],$ there exists $\omega _c$ solution of the problem

$$\begin{aligned} \min \{d^H(\omega ,\Omega )\ |\ \omega \in \mathcal {K}_c\}. \end{aligned}$$

• We first show an inferior limit inequality. Let $(c_n)_{n\ge 1}$ be a sequence converging to $c_0$ such that

  $$\begin{aligned} \liminf _{c\rightarrow c_0} d^H(\omega _c,\Omega )=\lim _{n\rightarrow +\infty } d^H(\omega _{c_n},\Omega ). \end{aligned}$$

  Since all the convex sets $\omega _{c_n}$ are included in the bounded set $\Omega ,$ we have, by Blaschke selection theorem and the continuity of the functional $\omega \longmapsto d(\omega ,\Omega )$ and the volume, the existence of a set $\omega ^*\in \mathcal {K}_{c_0}$ as a limit of a subsequence still denoted by $(\omega _{c_n})$ with respect to the Hausdorff distance. We then have

  $$\begin{aligned} f(c_0)\le d^H(\omega ^*,\Omega ) = \lim _{n\rightarrow +\infty } d^H(\omega _{c_n},\Omega ) = \liminf _{c\rightarrow c_0} d^H(\omega _c,\Omega )=\liminf _{c\rightarrow c_0} f(c). \end{aligned}$$

• It remains to prove a superior limit inequality. Let $(c_n)_{n\ge 1}$ be a sequence converging to $c_0$ such that

  $$\begin{aligned} \limsup _{c\rightarrow c_0} f(c)=\lim _{n\rightarrow +\infty } f(c_n). \end{aligned}$$

  Let us now consider the following family of convex sets

  $$\begin{aligned} Q_c:= \left\{ \begin{array}{ll} (\omega _{c_0})_{- \tau _c} &{}\quad \hbox {if}\ c\le c_0,\\ (1-t_c)\omega _{c_0}+t_c\Omega &{}\quad \hbox {if}\ c> c_0, \end{array}\right. \end{aligned}$$

  where $\tau _c$ is chosen in $\mathbb {R}^+$ in such a way that

  $$\begin{aligned} |(\omega _{c_0})_{- \tau _c}| = c \end{aligned}$$

  and $t_c$ is chosen in [0, 1] in such a way that

  $$\begin{aligned} |(1-t_c)\omega _{c_0}+t_c\Omega |=c. \end{aligned}$$

  The map $c\in [0,|\Omega |]\longmapsto Q_c$ is continuous with respect to the Hausdorff distance and $Q_{c_0}=\omega _{c_0}.$ Using the definition of f,  we have

  $$\begin{aligned} \forall n\in \mathbb {N}^*,\quad f(c_n)\le d^H(Q_{c_n},\Omega ). \end{aligned}$$

  Passing to the limit, we get

  $$\begin{aligned} \limsup _{c\rightarrow c_0} f(c) = \lim _{n\rightarrow +\infty } f(c_n) \le \lim _{n\rightarrow +\infty } d^H(Q_{c_n},\Omega )= d^H(\omega _{c_0},\Omega ) = f(c_0). \end{aligned}$$

As a consequence, we finally get $\lim _{c\rightarrow c_0} f(c) = f(c_0),$ which proves the continuity of f.

Monotonicity: Let $0\le c<c' \le |\Omega |.$ We consider $\omega \in \mathcal {K}_{c}$ such that $f(c)=d^H(\omega ,\Omega ).$ We have

$$\begin{aligned} f(c')\le & {} d^H((1-t_{c'})\omega +t_{c'}\Omega ,\Omega ) = \Vert h_{(1-t_{c'})\omega +t_{c'}\Omega }-h_\Omega \Vert _{\infty } \\= & {} (1-t_{c'})\Vert h_\omega -h_\Omega \Vert _{\infty }=(1-t_{c'})f(c)< f(c), \end{aligned}$$

where $t_{c'}\in (0,1]$ is chosen such that $|(1-t_{c'})\omega +t_{c'}\Omega | = c'.$ $\square$

3.3 The Equivalence Between the Problems

We then obtain the following important proposition that provides the equivalence between four different shape optimization problems.

Proposition 6

Let $c\in [0,|\Omega |].$ The following shape optimization problems are equivalent

• (I) $\min \{d^H(\omega ,\Omega )\ |\ \omega \ \text {is convex,}\ |\omega |= c\ \text {and}\ \omega \subset \Omega \},$

• (II) $\min \{d^H(\omega ,\Omega )\ |\ \omega \ \text {is convex,}\ |\omega |\le c\ \text {and}\ \omega \subset \Omega \},$

• (III) $\min \{|\omega |\ |\ \omega \text { is convex},\ d^H(\omega ,\Omega )=f(c)\ \text {and}\ \omega \subset \Omega \},$

• (IV) $\min \{|\omega |\ |\ \omega \text { is convex},\ d^H(\omega ,\Omega )\le f(c)\ \text {and}\ \omega \subset \Omega \},$

in the sense that any solution to one of the problems also solves the other ones.

Proof

Let us prove the equivalence between the four problems.

• We first show that any solution of (I) solves (II): let $\omega _{c}$ be a solution to (I). Then for every convex $\omega \subset \Omega$ such that $|\omega |\le c,$ one has

  $$\begin{aligned} d^H(\omega ,\Omega ) \ge f\big (|\omega |\big ) \ge f(c) = d^H(\omega _c,\Omega ), \end{aligned}$$

  where we used the monotonicity of f given by Theorem 5: therefore $\omega _{c}$ solves (II).

• Reciprocally, let now $\omega ^c$ be a solution of (II): we want to show that $\omega ^c$ must be of volume c. We notice that

  $$\begin{aligned} f(c) \ge d^H(\omega ^c,\Omega )\ge f\big (|\omega ^c|\big ) \ge f(c), \end{aligned}$$

  where the first inequality follows as the problem (II) allows more candidates than in the definition of f,  and the last inequality uses again the monotonicity of f. Therefore $f(c) = f\big (|\omega ^c|\big ),$ and since f is continuous and strictly decreasing, we obtain $|\omega ^c| = c,$ which implies that $\omega ^c$ solves (I).

We proved the equivalence between problems (I) and (II); the equivalence between problems (III) and (IV) is shown by similar arguments. It remains to prove the equivalence between (I) and (III).

• Let $\omega _{c}$ be a solution of (I), which means that $\omega _c\in \mathcal {K}_c$ and $d^H(\omega _c,\Omega ) = f(c).$ Then for every convex $\omega \subset \Omega$ such that $d^H(\omega ,\Omega ) = f(c),$ we have

  $$\begin{aligned} f(c) = d^H(\omega ,\Omega )\ge f\big (|\omega |\big ). \end{aligned}$$

  Thus, since f is decreasing, we get $c = |\omega _c| \le |\omega |,$ which means that $\omega _c$ solves (III).

• Let now $\omega _{c}'$ be a solution of (III). We have

  $$\begin{aligned} f(c)=d^H(\omega '_c,\Omega )\ge f\big (|\omega '_c|\big ). \end{aligned}$$

  Thus, by the monotonicity of f we get $c\ge |\omega '_c|.$ On the other hand, since $\omega '_c$ solves (III) and there exists a solution $\omega _{c}$ of (I), we have $|\omega '_c| \ge c,$ which finally gives $|\omega '_c|=c$ and shows that $\omega '_c$ solves (I).

$\square$

Remark 7

For clarity purposes, the results of Sect. 3 have been stated and proved in the planar case. Nevertheless, it is not difficult to see that all the results hold in higher dimensions $n\ge 2.$ Indeed, one just has to consider support functions defined on the unit sphere ${\mathbb {S}}^{n-1}$ (see for example [23, Section 1.7.1]) and reproduce the exact same steps.

4 Proof of Theorem 2 and Some Qualitative Results

4.1 Saturation of the Hausdorff Distance

Proposition 8

Let $\omega$ be a solution of problem (2). Then,  there exist (at least) two different couples of points $(x_1,y_1),(x_2,y_2)\in \partial \omega \times \partial \Omega$ such that

$$\begin{aligned} \Vert x_1-y_1\Vert = \Vert x_2-y_2\Vert = d^H(\omega ,\Omega ). \end{aligned}$$

Proof

Let us argue by contradiction. We assume that there exists only one couple $(x_1,y_1)\in \partial \omega \times \partial \Omega$ such that

$$\begin{aligned} \Vert x_1-y_1\Vert = d^H(\omega ,\Omega ). \end{aligned}$$

Let $x\in \partial \omega$ be a point different from $x_1.$ By cutting an infinitesimal portion of the convex $\omega$ (see Fig. 4), we obtain a set $\omega _\varepsilon$ such that $d^H(\omega ,\Omega )=d^H(\omega _\varepsilon ,\Omega )$ (because we assumed that the Hausdorff distance is attained at only one couple of points) and $|\omega |>|\omega _\varepsilon |,$ for sufficiently small values of $\varepsilon .$ Thus, $\omega$ is not a solution of the third problem of Proposition 6, which is absurd since $\omega$ is assumed to be a solution of problem (2) (which is proven to be equivalent to the later one in Proposition 6). $\square$

Fig. 4

The sets $\omega$ (in red) and $\omega _\varepsilon$ (in blue)

4.2 Polygonal Domains

Proposition 9

If the set $\Omega$ is a polygon of N sides,  then any solution of problem (2) is also a polygon of at most N sides.

Proof

Let us denote by $v_1,\ldots ,v_N,$ with $N\ge 3,$ the vertices of the polygon $\Omega$ and consider a solution $\omega$ of problem (3).

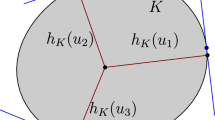
The distance function $x\longmapsto \min _{y\in \omega } \Vert x-y\Vert$ is convex, thus, it is well known that its maximal value on the convex polygon $\Omega$ is attained at some vertices that we denote by $(v'_k)_{k\in \llbracket 1,K\rrbracket },$ where $K\le N.$ Note that since $\omega$ a solution of problem (3), we have $K\ge 2$ by Proposition 8. Moreover, for every $k\in \llbracket 1,K\rrbracket$ there exists a unique $u_k\in \partial \omega$ such that $\Vert v'_k-u_k\Vert =d^H(\omega ,\Omega ),$ which is the projection of the vertex $v'_k$ onto the convex sensor $\omega .$ Let us consider two successive projection points $u_1$ and $u_2$ and assume without loss of generality that their coordinates are given by (0, 0) and $(x_0,0),$ with $x_0>0,$ see Fig. 5.

We consider the altitude $h\ge 0$ defined as follows

$$\begin{aligned} h:=\sup \{s\ |\ \exists x\in [0,x_0],\ \text {such that }\ (x,s)\in \omega \}. \end{aligned}$$

Let us argue by contradiction and assume that $h>0.$ For $\varepsilon >0,$ we consider $\omega _\varepsilon :=\omega \cap \{y\le h- \varepsilon \},$ see Fig. 5. For sufficiently small values of $\varepsilon >0,$ we have

$$\begin{aligned} d^H(\omega _\varepsilon ,\Omega ) = d^H(\omega ,\Omega )\quad \text {and}\quad |\omega _\varepsilon |<|\omega |, \end{aligned}$$

which means that $\omega$ is not a solution of the problem

$$\begin{aligned} \min \{|\omega |\ |\ d^H(\omega ,\Omega )=f(c)\ \text {and}\ \omega \subset \Omega \}, \end{aligned}$$

that is equivalent to problem (2) by Proposition 6. This provides a contradiction since $\omega$ is assumed to be a solution of problem (2). We then have that $h=0,$ which means that the segment of extremities $u_1$ and $u_2$ is included in the boundary of the optimal set $\omega .$ By repeating the same argument with the successive couple of points $u_k$ and $u_{k+1}$ (with the convention $u_{k+1}=u_1$), we prove that the boundary of the optimal set $\omega$ is exactly given by the union of the segments of extremities $u_k$ and $u_{k+1}$ which means that $\omega$ is a polygon (of K sides). $\square$

Fig. 5

The polygon $\Omega$ and the sensor $\omega$ (Color figure online)

4.3 Application to the Square: Symmetry Breaking

In this section, we combine the results of Propositions 6 and 9 to solve problem (3) when $\Omega$ is a square. This leads to observe the non uniqueness of the optimal shape and a symmetry breaking phenomenon. The phenomenon might seem surprising as one could expect that the optimal sensor will inherit all the symmetries of $\Omega .$

Let $\Omega =[0,1]\times [0,1].$ We are interested in solving problem (2) stated as follows

$$\begin{aligned} \min \{d^H(\omega ,\Omega )\ |\ \omega \subset \Omega \ \text {is convex and}\ |\omega |=c \}, \end{aligned}$$

(3)

with $c\in [0,|\Omega |].$

Before presenting the proof, we exhibit the solutions for different values of c,  when $\Omega$ is a square.

Fig. 6

Optimal shapes when $\Omega$ is a square, for $c\in \{0.7,0.5,0.2,0.1,0\}$

Remark 10

As one observes in Fig. 6, for values of c close to $|\Omega |=1,$ the optimal sensor is a square with the same symmetries of $\Omega ,$ but for small values of c,  the optimal sensor is no longer the square but a certain rectangle. One should then note that the optimal sensor is not necessarily unique (as one can consider rotating the rectangle with an angle $\pi /2$) and it does not necessarily inherit all the symmetries of the shape $\Omega$ (as it is not symmetric with respect to the diagonals of $\Omega$).

Let us now present the details of the proof. By Propositions 6 and 9, problem (3) is equivalent to the following one:

$$\begin{aligned} \min \{|\omega |\ |\ \omega \subset \Omega \ \text {is a convex quadrilateral and}\ d^H(\omega ,\Omega )=\delta \}, \end{aligned}$$

(4)

with $\delta \in [0,\frac{1}{2}].$ In the following proposition, we completely solve problem (4).

Proposition 11

Let $\Omega =[0,1]\times [0,1]$ be the unit square and $\delta \in [0,\frac{1}{2}).$ The solution of problem (4) is given by

• the square of vertices

  $$\begin{aligned} \left\{ \begin{array}{l} M_1(\delta \frac{\sqrt{2}}{2},\delta \frac{\sqrt{2}}{2}),\\ M_2(1- \delta \frac{\sqrt{2}}{2},\delta \frac{\sqrt{2}}{2}),\\ M_3(1- \delta \frac{\sqrt{2}}{2},1- \delta \frac{\sqrt{2}}{2}),\\ M_4(\delta \frac{\sqrt{2}}{2},1- \delta \frac{\sqrt{2}}{2}), \end{array}\right. \end{aligned}$$

  if $\delta \le \frac{1}{2\sqrt{2}},$

• and by one of the two rectangles of vertices

  $$\begin{aligned} \left\{ \begin{array}{l} M_1(\delta \cos {\theta _{\delta }},\delta \sin {\theta _{\delta }}),\\ M_2(1- \delta \cos {\theta _{\delta }},\delta \sin {\theta _{\delta }}),\\ M_3(1- \delta \cos {\theta _{\delta }},1- \delta \sin {\theta _{\delta }}),\\ M_4(\delta \cos {\theta _{\delta }},1- \delta \sin {\theta _{\delta }}), \end{array}\right. \end{aligned}$$

  with $\theta _{\delta }\in \{\arcsin {\left( \frac{1}{2\sqrt{2}\delta }\right) }- \frac{\pi }{4},\frac{3\pi }{4}- \arcsin {\left( \frac{1}{2\sqrt{2}\delta }\right) }\},$ if $\delta \in [\frac{1}{2\sqrt{2}},\frac{1}{2}].$

Proof

We denote by $A_1(0,0),$ $A_2(1,0),$ $A_3(1,1)$ and $A_4(0,1)$ the vertices of the square $\Omega$ and by $B_1,$ $B_2,$ $B_3$ and $B_4$ the balls of radius $\delta$ and centers respectively $A_1,$ $A_2,$ $A_3$ and $A_4,$ see Fig. 7.

Let $\omega$ be a solution of problem (4) (it is then also a solution of problem (3) by Proposition 6). By the result of Proposition 9, since $\Omega$ is a square (in particular a polygon), the optimal shape $\omega$ is also a polygon with at most four vertices. Since $d^H(\omega ,\Omega )=\delta ,$ the polygon $\omega$ has four different vertices. Each one of them is contained in a set $B_k\cap \Omega ,$ with $k\in \llbracket 1, 4\rrbracket .$

In fact, since the optimal set $\omega$ minimises the area for a given Hausdorff distance, we deduce that all its vertices are located on the arcs of circles $\partial B_k\cap \Omega$ given by the intersection of the boundaries of the balls $B_k$ and the square $\Omega .$ Indeed, if it were not the case, one could easily construct a convex polygon strictly included in $\omega$ (thus, with strictly less volume) such that its Hausdorff distance to the square $\Omega$ is equal to $\delta ,$ see Fig. 7

Fig. 7

The polygon in red has a smallest area than the one in green and its Hausdorff distance to the square $\Omega$ is equal to $\delta$ (Color figure online)

Now that we know that each vertex of the optimal sensor $\omega$ is located on a (different) arc of circle $\partial B_k\cap \Omega ,$ with $k\in \llbracket 1, 4 \rrbracket ,$ let us denote them by

$$\begin{aligned} \left\{ \begin{array}{l} M_1(\delta \cos {\theta _1},\delta \sin {\theta _1}),\\ M_2(1- \delta \cos {\theta _2},\delta \sin {\theta _2}),\\ M_3(1- \delta \cos {\theta _3},1- \delta \sin {\theta _3}),\\ M_4(\delta \cos {\theta _4},1- \delta \sin {\theta _4}), \end{array}\right. \end{aligned}$$

where $\theta _1,\theta _2,\theta _3,\theta _4\in [0,\frac{\pi }{2}],$ see Fig. 8.

Fig. 8

Parametrization via the angles $\theta _1,$ $\theta _2,$ $\theta _3$ and $\theta _4$

The area of the polygon $\omega$ can be expressed via the coordinates of its vertices as follows:

$$\begin{aligned} |\omega | = \frac{1}{2}\sum _{k=1}^4 (x_k y_{k+1}-x_{k+1}y_k), \end{aligned}$$

where $(x_k,y_k)$ correspond to the coordinates of the points $M_k,$ with the convention $(x_5,y_5):=(x_1,y_1).$

By straightforward computations, we obtain

$$\begin{aligned} |\omega | = 1 - \frac{1}{2}\delta \sum _{k=1}^4 \cos {\theta _k} - \frac{1}{2}\delta \sum _{k=1}^4 \sin {\theta _k}+\frac{1}{2}\delta ^2 \sum _{k=1}^4 (\cos {\theta _k}\sin {\theta _{k+1}}+\cos {\theta _{k+1}}\sin {\theta _{k}}), \end{aligned}$$

with the convention $\theta _5=\theta _1.$

We then perform a judicious factorization to obtain the following formula

$$\begin{aligned} |\omega |= & {} \frac{1}{2}\big ( (1- \delta \cos {\theta _1}- \delta \cos {\theta _3})(1- \delta \sin {\theta _2}- \delta \sin {\theta _4}) \\{} & {} +(1- \delta \cos {\theta _2}- \delta \cos {\theta _4})(1- \delta \sin {\theta _1}- \delta \sin {\theta _3}) \big ). \end{aligned}$$

We then use the inequality $a+b\ge 2\sqrt{ab},$ where the equality holds if and only if $a=b,$ and obtain

$$\begin{aligned} \left\{ \begin{matrix} 1- \delta \cos {\theta _1}- \delta \cos {\theta _3} = (\frac{1}{2}- \delta \cos {\theta _1})+(\frac{1}{2}- \delta \cos {\theta _3})\ge 2\sqrt{(\frac{1}{2}- \delta \cos {\theta _1})(\frac{1}{2}- \delta \cos {\theta _3})},\\ 1- \delta \sin {\theta _2}- \delta \sin {\theta _4} = (\frac{1}{2}- \delta \sin {\theta _2})+(\frac{1}{2}- \delta \sin {\theta _4})\ge 2\sqrt{(\frac{1}{2}- \delta \sin {\theta _2})(\frac{1}{2}- \delta \sin {\theta _4})},\\ 1- \delta \cos {\theta _2}- \delta \cos {\theta _4} = (\frac{1}{2}- \delta \cos {\theta _2})+(\frac{1}{2}- \delta \cos {\theta _4})\ge 2\sqrt{(\frac{1}{2}- \delta \cos {\theta _2})(\frac{1}{2}- \delta \cos {\theta _4})},\\ 1- \delta \sin {\theta _1}- \delta \sin {\theta _3} = (\frac{1}{2}- \delta \sin {\theta _1})+(\frac{1}{2}- \delta \sin {\theta _3})\ge 2\sqrt{(\frac{1}{2}- \delta \sin {\theta _1})(\frac{1}{2}- \delta \sin {\theta _3})},\\ \end{matrix}\right. \end{aligned}$$

with equality if and only if

$$\begin{aligned} \theta _1=\theta _3\quad \text {and}\quad \theta _2=\theta _4. \end{aligned}$$

(5)

We then write

$$\begin{aligned} |\omega |&\ge \sqrt{\left( \frac{1}{2}- \delta \cos {\theta _1}\right) \left( \frac{1}{2}- \delta \cos {\theta _3}\right) } \sqrt{\left( \frac{1}{2}- \delta \sin {\theta _2}\right) \left( \frac{1}{2}- \delta \sin {\theta _4}\right) } \\&\quad + \sqrt{\left( \frac{1}{2}- \delta \cos {\theta _2}\right) \left( \frac{1}{2}- \delta \cos {\theta _4}\right) } \sqrt{\left( \frac{1}{2}- \delta \sin {\theta _1}\right) \left( \frac{1}{2}- \delta \sin {\theta _3}\right) } \end{aligned}$$

and use again the inequality $a+b\ge 2\sqrt{ab}$ to obtain

$$\begin{aligned} |\omega | \ge 2\left( \left( \frac{1}{2}- \delta \cos {\theta _1}\right) \left( \frac{1}{2}- \delta \cos {\theta _3}\right) \left( \frac{1}{2}- \delta \sin {\theta _2}\right) \left( \frac{1}{2}- \delta \sin {\theta _4}\right) \right) ^{\frac{1}{4}}\nonumber \\ \quad \cdot \left( \left( \frac{1}{2}- \delta \cos {\theta _2}\right) \left( \frac{1}{2}- \delta \cos {\theta _4}\right) \left( \frac{1}{2}- \delta \sin {\theta _1}\right) \left( \frac{1}{2}- \delta \sin {\theta _3}\right) \right) ^{\frac{1}{4}}, \end{aligned}$$

(6)

where the equality holds if and only if one has

$$\begin{aligned}{} & {} \left( \frac{1}{2}- \delta \cos {\theta _1}\right) \left( \frac{1}{2}- \delta \cos {\theta _3}\right) \left( \frac{1}{2}- \delta \sin {\theta _2}\right) \left( \frac{1}{2}- \delta \sin {\theta _4}\right) \nonumber \\{} & {} \quad =\left( \frac{1}{2}- \delta \cos {\theta _2}\right) \left( \frac{1}{2}- \delta \cos {\theta _4}\right) \left( \frac{1}{2}- \delta \sin {\theta _1}\right) \left( \frac{1}{2}- \delta \sin {\theta _3}\right) . \end{aligned}$$

(7)

By combining the equality conditions (5) and (7), we show that the inequality (6) is an equality if and only if $\theta _1=\theta _3,$ $\theta _2=\theta _4$ and

$$\begin{aligned} \left( \frac{1}{2}- \delta \cos {\theta _1}\right) \left( \frac{1}{2}- \delta \sin {\theta _2}\right) = \left( \frac{1}{2}- \delta \sin {\theta _1}\right) \left( \frac{1}{2}- \delta \cos {\theta _2}\right) , \end{aligned}$$

which is equivalent to

$$\begin{aligned} \frac{\frac{1}{2}- \delta \cos {\theta _1}}{\frac{1}{2}- \delta \sin {\theta _1}} = \frac{\frac{1}{2}- \delta \cos {\theta _2}}{\frac{1}{2}- \delta \sin {\theta _2}}, \end{aligned}$$

which holds if and only if $\theta _1=\theta _2,$ because the function $\theta \longmapsto \frac{\frac{1}{2}- \delta \cos {\theta }}{\frac{1}{2}- \delta \sin {\theta }}$ is a bijection from $[0,\frac{\pi }{2}]$ to $[1-2\delta ,\frac{1}{1-2\delta }].$

We then conclude that the equality in (6) holds if and only if $\theta _1 = \theta _2 = \theta _3 = \theta _4,$ which means that the optimal sensor is a rectangle that corresponds to the value of $\theta _{\delta }$ that minimizes the function

$$\begin{aligned} f_{\delta }:\theta \in \left[ 0,\frac{\pi }{2}\right] \longmapsto \left( \frac{1}{2}- \delta \cos {\theta }\right) \left( \frac{1}{2}- \delta \sin {\theta }\right) . \end{aligned}$$

Since we have $f_{\delta }(\frac{\pi }{2}- \theta )= f_{\delta }(\theta )$ for every $\theta \in [0,\frac{\pi }{4}],$ we deduce by symmetry that it suffices to study the function $f_{\delta }$ on the interval $[0,\frac{\pi }{4}];$ we have

$$\begin{aligned} \forall \theta \in \left[ 0,\frac{\pi }{4}\right] ,\ \quad f'_{\delta }(\theta ) = \delta (\cos {\theta }- \sin {\theta })\left( - \frac{1}{2}+\delta \cos {\theta }+\delta \sin {\theta }\right) . \end{aligned}$$

The function $g_{\delta }:\theta \longmapsto - \frac{1}{2}+\delta \cos {\theta }+\delta \sin {\theta }$ is continuous and strictly increasing on $[0,\frac{\pi }{4}].$ Thus,

$$\begin{aligned} g_{\delta }\left( \left[ 0,\frac{\pi }{4}\right] \right) = \left[ g_{\delta }(0),g_{\delta }\left( \frac{\pi }{4}\right) \right] =\left[ -\frac{1}{2}+\delta ,-\frac{1}{2}+\delta \sqrt{2}\right] . \end{aligned}$$

Then, the sign of $g_{\delta }$ on $[0,\frac{\pi }{4}]$ (and thus the variation of $f_{\delta },$ see Fig. 9) depends on the value of $\delta \in [0,\frac{1}{2}).$ Indeed:

• If $\delta \le \frac{1}{2\sqrt{2}}$ (i.e., $g_{\delta }(\frac{\pi }{4})\le 0$), then $g'<0$ on $(0,\frac{\pi }{4}),$ which means that $f_{\delta }$ is strictly decreasing on $[0,\frac{\pi }{4}]$ and thus attains its minimal value at $\theta _{\delta } = \frac{\pi }{4}.$

• If $\delta > \frac{1}{2\sqrt{2}}$ (i.e., $g_{\delta }(\frac{\pi }{4})> 0$), straightforward computations show that the function $f_{\delta }$ is strictly decreasing on $[0,\theta _{\delta }]$ and increasing on $[\theta _{\delta },\frac{\pi }{4}],$ with $\theta _{\delta } = \arcsin {\left( \frac{1}{2\sqrt{2}\delta }\right) }-\frac{\pi }{4}.$ Thus, $f_{\delta }$ attains its minimal value at $\theta _{\delta }.$

$\square$

Fig. 9

The graphs of the function $f_{\delta }$ for the cases: $\delta = 0.25$ in the left and $\delta = 0.4$ in the right

5 Numerical Simulations

In this section, we present the numerical scheme adopted to solve the problems under consideration in the present paper. In particular, we focus on the following (equivalent) problems:

$$\begin{aligned} \min \{d^H(\omega ,\Omega ) \ |\ \omega \ \text {is convex},\ |\omega |=c\ \text {and}\ \omega \subset \Omega \}, \end{aligned}$$

(8)

and

$$\begin{aligned} \min \{|\omega |\ |\ \omega \text { is convex},\ d^H(\omega ,\Omega )\le d\ \text {and}\ \omega \subset \Omega \}, \end{aligned}$$

(9)

where $c,d\ge 0.$

As we shall see, even-though the problems are equivalent (see Theorem 6), problem (9) is much easier to solve numerically as it is approximated by a simple problem of minimizing a quadratic function under linear constraints.

5.1 Parametrization of the Functionals

In Sect. 2.1 we recalled that if both $\Omega$ and $\omega$ are convex, we have the following formulae for the Hausdorff distance between $\omega$ and $\Omega$

$$\begin{aligned} d^H(\omega ,\Omega )=\Vert h_\Omega -h_\omega \Vert _{\infty }:=\max _{\theta \in [0,2\pi ]} |h_{\Omega }(\theta )-h_{\omega }(\theta )| \end{aligned}$$

and the area of $\omega$

$$\begin{aligned} |\omega | = \frac{1}{2}\int _0^{2\pi } h_\omega (h_\omega ''+h_\omega )d\theta =\frac{1}{2} \int _0^{2\pi } (h_\omega ^2-{h_\omega '}^2)d\theta , \end{aligned}$$

where $h_\Omega$ and $h_\omega$ respectively correspond to the support functions of the convex sets $\Omega$ and $\omega .$

On the other hand, the inclusion constraint $\omega \subset \Omega$ can be expressed by $h_\omega \le h_\Omega$ on $[0,2\pi ]$ and the convexity of the sensor $\omega$ can also be analytically expressed as follows

$$\begin{aligned} h_\omega ''+h_\omega \ge 0, \end{aligned}$$

in the sense of distributions. We refer to [23] for more details and results on convexity.

Therefore, the use of the support functions allows to respectively transform the purely geometric problems (8) and (9) into the following analytical ones

$$\begin{aligned} \left\{ \begin{array}{l} \inf _{h\in H^1_{\text {per}}(0,2\pi )} \Vert h_\Omega -h\Vert _{\infty },\\ h\le h_\Omega ,\\ h''+h\ge 0,\\ \frac{1}{2}\int _0^{2\pi } h(h''+h)d\theta = c \end{array}\right. \end{aligned}$$

(10)

and

$$\begin{aligned} \left\{ \begin{array}{l} \inf _{h\in H^1_{\text {per}}(0,2\pi )} \frac{1}{2}\int _0^{2\pi } h(h''+h)d\theta ,\\ h\le h_\Omega ,\\ h''+h\ge 0,\\ \Vert h_\Omega -h\Vert _{\infty } \le d, \end{array}\right. \end{aligned}$$

(11)

where $H^1_{\text {per}}(0,2\pi )$ is the set of $H^1$ functions that are $2\pi$-periodic.

Since

$$\begin{aligned} \left\{ \begin{array}{l} h\le h_\Omega ,\\ \Vert h_\Omega -h\Vert _{\infty } \le d \end{array}\right. \Longleftrightarrow h_\Omega -d\le h\le h_\Omega , \end{aligned}$$

problem (11) can be reformulated as follows

$$\begin{aligned} \left\{ \begin{array}{l} \inf _{h\in H^1_{\text {per}}(0,2\pi )} \frac{1}{2}\int _0^{2\pi } h(h''+h)d\theta ,\\ h''+h\ge 0,\\ h_\Omega -d\le h\le h_\Omega . \end{array}\right. \end{aligned}$$

(12)

To perform the numerical approximation of optimal shape, we have to retrieve a finite dimensional setting. We then follow the same ideas in [2, 3] and parametrize the sets via Fourier coefficients of their support functions truncated at a certain order $N\ge 1.$ Thus, we look for solutions in the set

$$\begin{aligned} {\mathcal {H}}_N:= \left\{ \theta \longmapsto a_0 + \sum _{k=1}^N \big (a_k \cos {(k\theta )}+ b_k\sin {(k\theta )}\big ) \ \big |\ a_0,\ldots ,a_N,b_1,\ldots ,b_N\in \mathbb {R}\right\} . \end{aligned}$$

This approach is justified by the following approximation proposition:

Proposition 12

[23, Section 3.4] Let $\Omega \in \mathcal {K}^2$ and $\varepsilon >0.$ Then there exists $N_\varepsilon$ and $\Omega _\varepsilon$ with support function $h_{\Omega _\varepsilon }\in {\mathcal {H}}_{N_\varepsilon }$ such that $d^H(\Omega ,\Omega _\varepsilon )<\varepsilon .$

We refer to [2, 4] for other and applications to different problems and some theoretical convergence results.

Let us now consider the regular subdivision $(\theta _k)_{k\in \llbracket 1,M \rrbracket }$ of $[0,2\pi ],$ where $\theta _k= {2k\pi }/{M}$ and $M\in \mathbb {N}^*.$ The inclusion constraints $h_\Omega (\theta )-d\le h(\theta )\le h_\Omega (\theta )$ and the convexity constraint $h''(\theta )+h(\theta )\ge 0$ are approximated by the following 3M linear constraints on the Fourier coefficients:

$$\begin{aligned} \forall k\in \llbracket 1,M\rrbracket ,\ \quad \ \left\{ \begin{array}{l} h_\Omega (\theta _k)-d\le a_0+\sum _{j=1}^N \big (a_j \cos {(j\theta _k)}+ b_j\sin {(j\theta _k)}\big )\le h_\Omega (\theta _k),\\ a_0+\sum _{j=1}^N \big ((1-j^2)\cos {(j\theta _k)}a_j + (1-j^2)\sin {(j\theta _k)}b_j \big )\ge 0. \end{array}\right. \end{aligned}$$

At last, the area of the convex set corresponding to the truncated support function of $\omega$ at the order N is given by the following quadratic formula:

$$\begin{aligned} |\omega |=\pi a_0^2 + \frac{\pi }{2} \sum _{j=1}^N(1-j^2)(a_j^2+b_j^2). \end{aligned}$$

Thus, the infinitely dimensional problems (10) and (12) are approximated by the following finitely dimensional ones:

$$\begin{aligned} \left\{ \begin{array}{l} \inf _{(a_0,a_1,\ldots ,a_N,b_1,\ldots ,b_N)\in \mathbb {R}^{2N+1}} \max _{\theta \in [0,2\pi ]} h_\Omega (\theta ) - a_0 - \sum _{j=1}^N \big (a_j \cos {(j\theta )}+b_j\sin {(j\theta )}\big ),\\ \forall k\in \llbracket 1,M\rrbracket ,\quad a_0+\sum _{j=1}^N \big (a_j \cos {(j\theta _k)}+ b_j\sin {(j\theta _k)}\big )\le h_\Omega (\theta _k),\\ \forall k\in \llbracket 1,M\rrbracket ,\quad a_0+\sum _{j=1}^N \big ((1-j^2)\cos {(j\theta _k)}a_j + (1-j^2)\sin {(j\theta _k)}b_j \big )\ge 0,\\ \pi a_0^2 + \frac{\pi }{2} \sum _{j=1}^N(1-j^2)(a_j^2+b_j^2) = c \end{array}\right. \end{aligned}$$

(13)

and

$$\begin{aligned} \left\{ \begin{matrix} \inf _{(a_0,a_1,\ldots ,a_N,b_1,\ldots ,b_N)\in \mathbb {R}^{2N+1}}\pi a_0^2 + \frac{\pi }{2} \sum _{j=1}^N(1-j^2)(a_j^2+b_j^2),\\ \forall k\in \llbracket 1,M\rrbracket ,\quad h_\Omega (\theta _k) - d \le a_0+\sum _{j=1}^N \big (a_j \cos {(j\theta _k)}+ b_j\sin {(j\theta _k)}\big )\le h_\Omega (\theta _k),\\ \forall k\in \llbracket 1,M\rrbracket ,\quad a_0+\sum _{j=1}^N \big ((1-j^2)\cos {(j\theta _k)}a_j + (1-j^2)\sin {(j\theta _k)}b_j \big )\ge 0. \end{matrix}\right. \nonumber \\ \end{aligned}$$

(14)

Remark 13

We conclude that the shape optimization problems considered in the present paper are approximated by problem (14), which simply consists in minimizing a quadratic function under linear constraints.

5.2 Computation of the Gradients

A very important step in shape optimization is the computation of the gradients. In our case, the convexity and inclusion constraints are linear and the area constraint is quadratic. Thus, its gradients are obtained by direct computations. Nevertheless, the computation of the gradient of the objective function in Problem (13) is not straightforward as it is defined as a supremum. This is why we use a Danskin’s differentiation scheme [9] to compute the derivative.

Proposition 14

Let us consider

$$\begin{aligned} g:(\theta ,a_0,\ldots ,b_N)\longmapsto h_\Omega (\theta ) - a_0 - \sum _{k=1}^N \big (a_k \cos {(k\theta )}+b_k\sin {(k\theta )}\big ) \end{aligned}$$

and

$$\begin{aligned} j:(a_0,\ldots ,b_N)\longmapsto \max _{\theta \in [0,2\pi ]} g(\theta ,a_0,\ldots ,b_N). \end{aligned}$$

The function j admits directional derivatives in every direction and we have

$$\begin{aligned} \frac{\partial j}{\partial a_0} = -1, \end{aligned}$$

and for every $k\in \llbracket 1,N \rrbracket ,$

$$\begin{aligned} \left\{ \begin{array}{cc} \frac{\partial j}{\partial a_k} = \max _{\theta ^*\in \Theta } -\cos {(k \theta ^*)},\\ \frac{\partial j}{\partial b_k} = \max _{\theta ^*\in \Theta } -\sin {(k\theta ^*)}, \end{array}\right. \end{aligned}$$

where

$$\begin{aligned} \Theta :=\{\theta ^*\in [0,2\pi ]\ \ |\ \ G(\theta ^*,a_0,\ldots ,b_N) = \max _{\theta \in [0,2\pi ]} G(\theta ,a_0,\ldots ,b_N)\}. \end{aligned}$$

Proof

Since the same scheme is followed for every coordinate, we limit ourselves to present the proof for the first coordinate $a_0.$ In order to simplify the notations, we will write for every $x\in \mathbb {R},$

$$\begin{aligned}{} & {} j(x):= j(a_0,\ldots ,a_{k-1},x,a_{k+1}\ldots ,b_N)\quad \text {and}\quad \\{} & {} G(\theta ,x):= G(\theta ,a_0,\ldots ,a_{k-1},x,a_{k+1}\ldots ,b_N). \end{aligned}$$

For every $t\ge 0,$ we denote by $\theta _t\in [0,2\pi ]$ a point such that

$$\begin{aligned} G(\theta _t,a_k+t) = j(a_k+t) = \max _{\theta \in [0,2\pi ]} G(\theta ,a_k+t). \end{aligned}$$

We have

$$\begin{aligned}{} & {} j(a_k+t)-j(a_k)= G(\theta _t,a_k+t)-G(\theta _0,a_k)\\{} & {} \ge G(\theta _0,a_k+t)-G(\theta _0,a_k)= -t \cos {(k \theta _0)}. \end{aligned}$$

Thus,

$$\begin{aligned} \forall \theta _0\in \Theta ,\quad \liminf _{t\rightarrow 0^+} \frac{j(a_k+t)-j(a_k)}{t} \ge -\cos {(k \theta _0)}, \end{aligned}$$

which means that

$$\begin{aligned} \liminf _{t\rightarrow 0^+} \frac{j(a_k+t)-j(a_k)}{t} \ge \max _{\theta _0\in \Theta }-\cos {(k \theta _0)}. \end{aligned}$$

(15)

Let us now consider a sequence $(t_n)$ of positive numbers decreasing to 0,  such that

$$\begin{aligned} \lim _{n\rightarrow +\infty } \frac{j(a_k+t_n)-j(a_k)}{t_n} = \limsup _{t\rightarrow 0^+} \frac{j(a_k+t)-j(a_k)}{t}. \end{aligned}$$

We have, for every $n\ge 0,$

$$\begin{aligned}{} & {} j(a_k+t_n)-j(a_k)= G(\theta _{t_n},a_k+t_n)-G(\theta _0,a_k)\le G(\theta _{t_n},a_k+t_n)-G(\theta _{t_n},a_k)\\{} & {} \quad =-t_n\cos {(k \theta _{t_n})}. \end{aligned}$$

Thus,

$$\begin{aligned}{} & {} \limsup _{t\rightarrow 0^+} \frac{j(a_k+t)-j(a_k)}{t} = \lim _{n\rightarrow +\infty } \frac{j(a_k+t_n)-j(a_k)}{t_n}\\{} & {} \le \limsup _{n\rightarrow +\infty }-\cos {(k\theta _{n})}=-\cos {(k\theta _{\infty })}, \end{aligned}$$

where $\theta _{\infty }$ is an accumulation point of the sequence $(\theta _n).$ It is not difficult to check that $\theta _{\infty } \in \Theta .$ Thus, we have

$$\begin{aligned} \limsup _{t\rightarrow 0^+} \frac{j(a_k+t)-j(a_k)}{t} \le \max _{\theta _0\in \Theta }-\cos {(k \theta _0)}. \end{aligned}$$

(16)

By the inequalities (15) and (16) we deduce the announced formula for the derivative. $\square$

5.3 Numerical Results

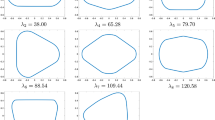
Now that we have parameterized the problem and computed the gradients, we are in position to perform numerical shape optimization. We use the ‘fmincon’ Matlab routine. In the following figures we present the results obtained for different shapes and different mass fractions $c_0:=\alpha _0|\Omega |,$ where $\alpha _0\in \{0.01,0.1,0.4,0.7\}.$

Fig. 10

Obtained optimal shapes for $\alpha _0\in \{0.01,0.1,0.4,0.7\}$ and different choices of $\Omega$

Remark 15

The numerical simulations presented in Fig. 10 suggest that for large mass fractions ($\alpha _0\approx 1$), the optimal sensor is exactly given by an inner parallel set of the domain $\Omega$ (see Sect. 2.2 for the definition of inner parallel sets). In the work in preparation [10], we prove that this statement holds under some regularity assumptions on the set $\Omega$ and investigate its relation with the apparition of caustics when computing the distance function to the boundary $\partial \Omega$ by solving following the eikonal equation

$$\begin{aligned} \left\{ \begin{array}{ll} |\nabla u| = 1&{}\quad \hbox {in}\ \Omega ,\\ u = 0&{} \quad \hbox {on}\ \partial \Omega . \end{array}\right. \end{aligned}$$

5.4 Optimal Spherical Sensors and Relation with Chebyshev Centers

In this section, we show that the ideas developed in the last sections can be efficiently used to numerically solve the problem of optimal placement of a spherical sensor inside the convex set $\Omega .$ We show also that this problem is related to the task of finding the Chebyshev center of the set, i.e., the center of the minimal-radius ball enclosing the entire set $\Omega .$

We are then considering the following optimal placement problem

$$\begin{aligned} \min \{d^H(B,\Omega )\ |\ B\ \hbox { is a ball included in}\ \Omega \hbox { and of radius} R\}, \end{aligned}$$

(17)

with $R\in [0,r(\Omega )],$ where $r(\Omega )$ is the inradius of $\Omega ,$ that is the radius of the biggest ball contained in $\Omega .$

Since the support function of a ball B of center (x, y) and radius R is simply given by $h_B:\theta \longmapsto R+ x\cos {\theta }+y\sin {\theta },$ problem (17) can be formulated in terms of support functions as follows:

$$\begin{aligned}{} & {} \min _{(x,y)}\{\Vert h_\Omega -R+ x\cos {\theta }+y\sin {\theta }\Vert _{\infty }\ |\ \forall \theta \in [0,2\pi ],\nonumber \\{} & {} \quad R+ x\cos {\theta }+y\sin {\theta }\le h_\Omega (\theta )\}. \end{aligned}$$

(18)

Here also, as in Sect. 5.1, the inclusion constraint $B\subset \Omega$ (i.e., $h_B\le h_\Omega$) can be approximated by a finite number of linear inequalities

$$\begin{aligned} R+x\cos {\theta _k}+y\sin {\theta _k}\le h_\Omega (\theta _k), \end{aligned}$$

where $\theta _k:={2k\pi }/{M},$ with $k\in \llbracket 1,M \rrbracket$ and M chosen equal to 500.

Thus, we retrieve a problem of minimizing the non linear function $(x,y)\longmapsto \Vert h_\Omega -R+ x\cos {\theta }+y\sin {\theta }\Vert _{\infty }$ (whose gradient is computed by using the result of Proposition 14) with a finite number of linear constraints.

In Fig. 11, we present some numerical results.

Fig. 11

Optimal placement of spherical sensors with different radii $R\in \{0.25,1,2,3\}$

At last, we note that solving problem (17) with $R=0$ is equivalent to finding the Chebyshev center of $\Omega$ that is the center of the minimal-radius ball enclosing the entire set $\Omega ,$ see Fig. 12. This center has been considered by several authors in different settings, especially in functional analysis, we refer for example to [1, 14, 17, 18].

Fig. 12

Chebyshev centers and circumcircles of different convex sets

Fig. 13

The Hausdorff distance between the disconnected sensor $\omega _1\cup \omega _2$ and the set $\Omega$

6 Conclusion and Perspectives

The present paper is devoted to the design of one convex sensor inside a given convex domain minimizing the farthest distance between the two sets. Many natural extensions could be considered. In this section we discuss some possible development and present some ideas that we are planning to develop for future works.

• Multiple sensors on domains and networks. A natural extension would be the optimal placement and design of multiple sensors inside a given region or a network. These cases are out of the scope of the present work and we believe that different techniques should be considered for their treatment. Indeed, our approach is mainly based on parametrizing the boundaries of the set $\Omega$ and the sensor $\omega$ via their support functions $h_\Omega$ and $h_\omega$ and use them to compute the Hausdorff distance between $\Omega$ and $\omega$ via the formula

  $$\begin{aligned} d^H(\omega ,\Omega ) = \Vert h_\Omega -h_\omega \Vert _{\infty }. \end{aligned}$$

  We believe that no similar formula for the Hausdorff distance between the union of two or more sensors and the set $\Omega$ could be found. Indeed, in contrary to the case of one sensor where the Hausdorff distance is always attained at points on the boundaries of the sets $\omega$ and $\Omega$ (see Fig. 4), in the case of multiple sensors the Hausdorff distance may be attained at a point inside the domain $\Omega$ (see Fig. 13), which makes the parametrization via support functions irrelevant. It is then natural to investigate the optimal design and placement of N sensors $(S_k)$ inside a domain or a network $\Omega$ in such a way that any point in $\Omega$ is “easily" reachable from one of the sensors. This problem can be mathematically formulated as follows

  $$\begin{aligned} \min \left\{ d^H(\Omega ,\cup _{k=1}^N S_k) = \max _{y\in \Omega } d(y,\cup _{k=1}^N S_k) \ \ |\ \forall k\in \llbracket 1,N \rrbracket ,\ S_k\subset \Omega \right\} , \end{aligned}$$

  (19)

  where $d(y,\cup _{k=1}^N S_k)$ is the minimal (geodesic if $\Omega$ is a network) distance from the point y to the union of the sensors. If we consider $(v_\varepsilon )$ a family of functions approximating the distance function $y\longmapsto d(y,\cup _{k=1}^N S_k)$ when $\varepsilon$ goes to 0 (such as the ones defined below in Theorems 16 and 17), we may consider approximating problem (19) by the following one

  $$\begin{aligned} \min \left\{ \max _{y\in \Omega } v_\varepsilon \ \ |\ \forall k\in \llbracket 1,N \rrbracket ,\ S_k\subset \Omega \right\} . \end{aligned}$$

  (20)

  The advantage of such approximated problems is that they involve elliptic equations that are much easier to deal with from the theoretical and numerical points of views. Once problem (20) is solved, the next natural step would be to justify that the obtained solutions converge to those of the initial problem (19). This is classically done by proving $\Gamma$-convergence results, see for example [16, Section 6].

• Approximation of the distance function. The problems studied in the present paper involve the distance function, that satisfies the classical eikonal equation

  $$\begin{aligned} |\nabla u| = 1. \end{aligned}$$

  Such equation is nonlinear and hyperbolic, which makes it quite difficult to deal with from a numerical perspective, especially in the context numerical shape optimization.

It may then be interesting to use a suitable approximation of the distance function based on some PDE results in the spirit of Crane et al. in [8], where the authors introduce a new approach to compute distances based on a heat flow result of Varadhan [27], which says that the geodesic distance $\phi (x,y)$ between any pair of points x and y on a Riemannian manifold can be recovered via a simple pointwise transformation of the heat kernel

$$\begin{aligned} \phi (x,y) = \lim _{t\longrightarrow 0 } \sqrt{-4t \log k_{t,x}(y)}, \end{aligned}$$

where $k_{t,x}(y)$ is the heat kernel, which measures the heat transferred from a source x to a destination y after time t. We refer to [8, 27] for more details and to [25] for an extension to graphs.

In the same spirit, one could use a suitable approximation of the distance function in terms of the solution of an elliptic PDE, inspired by the following classical result:

Theorem 16

[27, Th. 2.3] Let $\Omega$ be an open subset of $\mathbb {R}^{n}$ and $\varepsilon >0,$ we consider the problem

$$\begin{aligned} \left\{ \begin{array}{ll} {w_{\varepsilon }}- \varepsilon \Delta {w_{\varepsilon }}=0 &{}\quad \text {in}\ \Omega ,\\ {w_{\varepsilon }} = 1 &{}\quad \text {on}\ \partial \Omega . \end{array}\right. \end{aligned}$$

(21)

We have

$$\begin{aligned} \lim _{\varepsilon \rightarrow 0} - \sqrt{\varepsilon }\ln {w_\varepsilon (x)} = d(x,\partial \Omega ):= \inf _{y\in \partial \Omega } \Vert x-y\Vert , \end{aligned}$$

uniformly over compact subsets of $\Omega .$

In Fig. 14, we plot the approximation of the distance function to the boundary obtained via the result of Theorem 16.

We note that there are other results of approximation of the distance function via PDEs, see [11] and references therein. We recall for example the following result of Bernd Kawohl:

Theorem 17

[13, Th. 1] We consider the problem

$$\begin{aligned} \left\{ \begin{array}{ll} -\Delta _p u_p=1 &{}\quad \hbox {in}\ \Omega ,\\ u_p = 0&{}\quad \hbox {on}\ \partial \Omega , \end{array}\right. \end{aligned}$$

where $\Delta _p$ corresponds to the p-Laplace operator,  defined as follows

$$\begin{aligned} \Delta _p v = \text {div}(|\nabla v|^{p-2}\nabla v). \end{aligned}$$

We have

$$\begin{aligned} \lim _{p\rightarrow +\infty } u_p(x) = d(x,\partial \Omega )\quad \hbox {uniformly in}\ \Omega . \end{aligned}$$

Fig. 14

Approximation of the distance function to the boundary via Varadhan’s result of Theorem 16, where we have used Matlab’s toolbox ‘PDEtool’ to solve problem (21), with $\varepsilon =10^{-4}$

One advantage of such approximation methods is that they allow to introduce relevant PDE based problems that may be easier to consider from a numerical point of view than the initial ones involving the distance function and that are of intrinsic interest. Let us conclude by presenting some examples of such problems:

• The average distance problem. Given a set $\Omega \subset \mathbb {R}^n$ and a subset $\Sigma \subset \Omega ,$ the average distance to $\Sigma$ is defined as follows:

  $$\begin{aligned} {\mathcal {J}}_p(\Sigma ):= \int _\Omega d(x,\Sigma )^p dx, \end{aligned}$$

  where p is a positive parameter.

The main focus here is to study the shapes $\Sigma$ that minimize the average distance and investigate their properties such as symmetries and regularity. This problem has been introduced in [6, 7] and studied by many authors in the last years. For a presentation of the problem, we refer to [15] and to the references therein for related results.

Even if these problems are easy to formulate, they are quite difficult to tackle both theoretically and numerically. It is then interesting to use the approximation results of the distance function to approximate the functional ${\mathcal {J}}_p$ by some functional ${\mathcal {J}}_{p,\varepsilon }(\Sigma ):= \int _\Omega v_\varepsilon ^p dx,$ where $(v_\varepsilon )$ is a family of functions uniformly converging to $d(\cdot ,\Sigma )$ on $\Omega$ when $\varepsilon$ goes to 0.

We are then led to consider shape optimization problems of functionals involving solutions of simple elliptic PDEs. Several results for such functionals are easier to obtain such as Hadamard formulas for the shape derivatives, which are of crucial importance for numerical simulations.