Visualization of drained rock volume (DRV) in hydraulically fractured reservoirs with and without natural fractures using complex analysis methods (CAMs)

Abstract

The drainage areas (and volumes) near hydraulically fractured wells, computed and visualized in our study at high resolution, may be critically affected by the presence of natural fractures. Using a recently developed algorithm based on complex analysis methods (CAMs), the drained rock volume (DRV) is visualized for a range of synthetic constellations of natural fractures near hydraulic fractures. First, flow interference effects near a single hydraulic fracture are systematically investigated for a variety of natural fracture sets. The permeability contrast between the matrix and the natural fractures is increased stepwise in order to better understand the effect on the DRV. Next, a larger-scale model investigates flow interference for a full hydraulically fractured well with a variety of natural fracture sets. The time of flight contours (TOFCs) outlining the DRV are for all cases with natural fractures compared to a base case without any natural fractures. Discrete natural fractures, with different orientations, hydraulic conductivity, and fracture density, may shift the TOFC patterns in the reservoir region drained by the hydraulically fractured well, essentially shifting the location of the well’s drainage area. The CAM-based models provide a computationally efficient method to quantify and visualize the drainage in both naturally and hydraulically fractured reservoirs.

1 Introduction

Modeling of an unconventional petroleum reservoir is quite complicated, partly due to uncertainties in characterization of the sub-surface properties (e.g., heterogeneity and anisotropy in permeability) and also due to the complex physics of the process of oil recovery (e.g., capillarity, gravity and phase behavior) (Kresse et al. 2013). Natural fractures introduce additional complexity, which may affect hydrocarbon flow in the reservoir, and thus may impact well performance (Aguilera 2008). Modeling the flow near natural fractures and their interaction with hydraulic fractures, therefore, is relevant for comprehending any changes in well productivity due to variations in the fracture treatment design (Tutuncu et al. 2018). Natural fractures, even if non-conductive, may profoundly affect the sweep pattern due to waterflood between injection and production wells (Weijermars and van Harmelen 2017). Likewise, conventional reservoirs produced via hydraulically fractured wells in the presence of highly conductive fractures and non-conductive natural fractures will affect the flow region near the hydraulic fractures (Doe et al. 2013). Consequently, the most accurate flow simulation and production forecasting models must strive to account for the impact of natural fractures, based on their orientations, distributions, connectivity, strengths and interactions with the hydraulic fractures (Olson 2008; Cipolla et al. 2011; Kang et al. 2011).

Naturally fractured reservoirs with a randomly distributed network of natural fractures are commonly represented using variations of the dual-porosity model, first introduced by Warren and Root (1963). Although naturally fractured reservoirs consist of irregular fractures, in a dual-porosity model, they are represented by equivalent homogeneous matrix blocks separated by orthogonal uniform natural fractures. The matrix blocks are assumed to be isotropic and homogenous with no direct communication between them (Warren and Root 1963). The natural fractures and matrix are assumed to have different fluid storage and conductivity characteristics. The fractures are more conductive than the matrix (higher permeability); however, the volume of the hydrocarbons stored in the natural fractures is much smaller than in the matrix. In a dual-porosity model, any fluid stored in the natural fractures travels to the wellbore early in the well-life and is rapidly produced. While the natural fractures are drained, fluid from the matrix exclusively moves into the fracture space, and then to the wellbore. Thus, the matrix contains most of the oil, but the production of oil to the wells occurs via the natural fractures resulting in a complex interaction between the matrix and the natural fractures, influenced by the inter-porosity flow coefficient (λ) and fracture storativity ratio (ω). The inter-porosity flow coefficient is a measure of flow capacity between the matrix and the fractures, whereas the storativity ratio is a measure of the quantity of fluid that the natural fractures can store to which both the matrix and the fractures can contribute.

Kazemi et al. (1976) proposed modifications to the Warren and Root (1963) model to include multiphase flow and a new matrix shape factor. The matrix shape factor, introduced to account for variations in the geometry of the individual matrix blocks, was further modified in later studies with transfer functions to better model the flow of fluid in naturally fractured reservoirs (Thomas et al. 1983; Ueda et al. 1989; Coats 1989; Lim and Aziz 1995; Sarma and Aziz 2006). However, the applicability of the classic double-porosity model with constant shape factors in flow simulations of low-permeability reservoirs has been questioned (Cai et al. 2015). Modern dual-porosity models (Nie et al. 2012) and, more recently, triple-porosity models (Huang et al. 2014; Sang et al. 2016; Khoshghadam et al. 2016) have been introduced to simulate naturally fractured reservoirs. In spite of all modification efforts, the double- and triple-porosity models have limited accuracy, especially when the natural fractures do not intersect (Karimi-Fard and Firoozabadi 2003). Such models do not describe discrete fractures, which pose the primary challenge in reservoir models of naturally fractured reservoirs (Chen et al. 2008; Presho et al. 2011; Soleimani 2017). Another significant shortcoming of the dual-porosity model is that it does not explicitly account for fracture density. Shape factor and transfer functions used in dual-porosity models account for the exchange of fluid between the matrix and the fractures, which may not capture the complex flow behavior, resulting in incorrect pressure gradients (Weijermars and van Harmelen 2018).

History matching of naturally fractured reservoirs remains challenging even with discrete fracture network (DFN) models, as the finite element model needs to be re-gridded when more fractures are added or deleted (Salimi and Bruining 2010). DFN models consider fluid flow and transport processes in fractured rock masses through a system of connected natural fractures. The technique was created in the 1980s for both 2D and 3D problems (Long et al. 1982; Elsworth 1986; Andersson and Dverstorp 1987; Dershowitz and Einstein 1987), and continuously evolved with many applications in civil, environmental, geothermal and reservoir engineering and other geoscience and geoengineering fields (Jing and Stephansson 2007). Thus, the DFN method is the most useful for the study of fluid flow and mass transport in fractured rocks for which an equivalent continuum model is difficult to establish or not necessary, or for the derivation of equivalent continuum flow and transport properties in the fractured rocks for subsequent use in faster, upscaled (but implicit) reservoir models (Zimmerman and Bodvarsson 1996; Yu et al. 2018). DFN models are currently used for a wide range of flow problems of fractured rocks. Principal applications include (1) small-scale simulations where the dominance of fracture geometry makes any continuum approximation invalid, and (2) large-scale simulations where the properties of the fractured reservoir need to be approximated through upscaling and homogenization into equivalent permeability tensors using a DFN model (Jing and Stephansson 2007).

DFN models may suffer from limitations due to the detailed inputs required for such models to work, which requires a detailed specification of fracture system geometry, aperture, and transmissivity of the individual fractures. Fracture geometry in discrete fracture models is often generated stochastically, based on probability functions of the variables according to field studies. Although field mapping can be conducted at surface exposures, such outcrops provide only partial analogs for the sub-surface. Additionally, the transmissibility needs to be estimated, which is difficult because in situ and laboratory tests can only be performed with a limited number of fracture samples from restricted locations, while it is difficult to determine the effect of sample size (Jing and Stephansson 2007). Modeling a typical naturally fractured reservoir through DFN is conducted with a conventional fine grid and is computationally intensive, especially for multi-stage wells, which may have several hundred perforation zones in a single well (Weijermars and van Harmelen 2018).

The broad application of DFN models in reservoir simulators is currently limited due to the complexity of fracture patterns, complicated gridding issues and high computational cost. The embedded discrete fracture model (EDFM) was recently developed to overcome these issues related to traditional DFN. EDFM allows for complex fractures to be implemented in conventionally structured matrix grids without the need of local grid refinement (LGR) in the vicinity of the fractures (Yu and Sepehrnoori 2018). EDFM uses a hybrid approach, where the dual-porosity model is used for the small/medium fractures, and DFN is used to model the large fractures (Li and Lee 2008). One of the advantages of EDFM is the use of a structured grid to represent the matrix and the fractures. Initially developed for planer 2D cases, EDFM has been recently expanded for 3D models with obliquely dipping fractures (Moinfar et al. 2014), for simulating the stimulated reservoir volume (SRV) to reduce the computational cost associated with LGR (Jiang and Younis 2015; Wang et al. 2017), and for assisted history matching in unconventional reservoirs (Yu et al. 2018). Despite these benefits, EDFM might still be computationally intensive and expensive when used for highly complex reservoirs with multiple hydraulic and natural fractures. The CAM model presented in this study presents a gridless approach which can efficiently model the flow of fluid in naturally fractured reservoirs.

The present study is an extension of recent studies where closed-form analytical solutions based on complex analysis methods (CAM) are applied to single-phase flow reservoirs, assuming either hydraulic fractures only (Weijermars et al. 2017a, b; Weijermars and Alves 2018; Khanal and Weijermars 2019) or natural fractures only (van Harmelen and Weijermars 2018; Weijermars and van Harmelen 2018). In these prior studies, the drainage patterns and drained rock volume (DRV) due to hydraulic fracture and natural fractures were separately evaluated using a Eulerian particle tracking method. The fluid particles are tracked at each time-step during the simulation to determine their spatial position, which can be used to determine the drained rock volume. In the current work, we present an integrated model where the interaction of the natural fractures of different strengths, orientations and densities with hydraulic fractures and horizontal wells is studied. The primary purpose of the present study is to apply an efficient 2D analytical formulation in order to model the flow near natural fractures (1) in close proximity to a single hydraulic fracture, and (2) between hydraulically fractured wells, and visualize how the DRV and related flow patterns change due to the presence of the natural fractures.

2 CAM methodology and algorithms

2.1 Novelty in our approach

Any 2D velocity vector field described by an appropriate complex analytical function that fulfills the Laplace equation allows the determination of fluid particle paths in two possible ways. The first method integrates the system of ordinary differential equations (Strack 1989; Sato 2015):

$$ \frac{{\text{d} x}}{{\text{d} t}} = u(x,y)\;{\text{and}}\;\frac{{\text{d} y}}{{\text{d} t}} = v(x,y)\quad ({\text{ft/day}}) $$

(1)

For any valid complex potential, there exists an analytical function $f(z) = u(x,y) - iv(x,y)$, the conjugate of which solves the velocity field $\overline{f(z)} = \text{d} z/\text{d} t$ in every location of the complex plane, $z = x + iy$. The parameterized solution of z(t) gives the streamlines (Olver 2018). The limitation of the integral method to map particle paths is that only solutions for steady-state flows can be obtained. The second method tracks the particle paths by a Eulerian time-stepping schedule as that was first applied to reservoir models with complex analysis in Weijermars et al. (2016). The latter work was an extension of earlier applications of the Eulerian time-stepping in models of lava flows and other gravity flows (Weijermars 2014; Weijermars et al. 2014). The Eulerian method allows the integration for time-dependent flows by superimposing closed-form solutions for each state separated by a small time increment. Discretization of the nonlinear flow problem is achieved by stringing together linear solutions, individually valid for small time increments only, such that nonlinear, transient flows can be described by a series of superimposed solutions with a negligible error when the time-step is sufficiently small (Weijermars and Alves 2018). Previous studies include validation of the analytical flow field and pressure field solutions against those obtained with independent commercial, finite difference-based reservoir model platforms, which showed no discernable difference in accuracy (Weijermars et al. 2016, 2017a, b), with the added advantage of infinite spatial resolution for the CAM-based solutions.

2.2 Analytical elements

The flow near hydraulic fractures can be modeled using analytical solutions based on the complex potential for an interval sink or interval source (determined by the sign of the time-dependent strength) along the interval [a, b] (Potter 2008):

$$ \varOmega (z,t) = \frac{m(t)}{2\uppi (b - a)}[(z - a)\log (z - a) - (z - b)\log (z - b)]\quad ({\text{ft}}^{2} / {\text{day}}) $$

(2)

where m(t) (ft²/day) is the strength of the producers/source ($m(t) > 0$) or injectors ($m(t) < 0$) and z is an arbitrary location on the complex plane. Natural fractures are modeled using a new complex potential proposed by van Harmelen and Weijermars (2018), created by superposing an infinite number of line dipoles (Weijermars and van Harmelen 2016) (Fig. 1):

$$ \varOmega (z,t) = \frac{{ - i \cdot \upsilon (t) \cdot {\text{e}}^{ - i\gamma } }}{2\uppi \cdot h \cdot n \cdot L \cdot W}[(z - z_{a2} ) \cdot \log ( - {\text{e}}^{ - i\gamma } (z - z_{a2} )) - (z - z_{a1} ) \cdot \log ( - {\text{e}}^{ - i\gamma } (z - z_{a1} )) + (z - z_{b1} )\log ( - {\text{e}}^{ - i\gamma } (z - z_{b1} )) - (z - z_{b2} )\log ( - {\text{e}}^{ - i\gamma } (z - z_{b2} ))]\quad ({\text{ft}}^{2} / {\text{day}}) $$

(3)

where υ(t) (ft⁴/day) is the strength of the natural fracture; L, W, and h (ft) are the length, width, and height of the natural fracture, respectively; n is porosity; γ is the tilt angle of the natural fracture as shown in Fig. 1. The corner points of the natural fracture domain are given by z_a1, z_a2, z_b1 and z_b2.

Fig. 1

Natural fracture model. L and W are the length and width; z_c is the center; z_a1, z_a2, z_b1 and z_b2 are the corners; β is the wall angles, while γ is the rotation angle of the natural fracture. Intended flow direction indicated with blue arrows (van Harmelen and Weijermars 2018)

Equations (2) and (3) are both based on the superposition of point sources and point sinks. The complex potential for a point source/sink centered at z_c with time-dependent strength m(t) is:

$$ \varOmega (z,t) = \frac{m(t)}{2\uppi }\log (z - z_{\text{c}} )\quad ({\text{ft}}^{2} / {\text{day}}) $$

(4)

The velocity field for each of the analytical elements represented by complex potentials in Eqs. (2), (3) and (4) can be obtained by differentiating with respect to z. The corresponding generalized velocity potential (V(z, t)) for a line source/sink (hydraulic fracture), superposed dipoles (natural fractures), and point source/sink (well entry) are given in Eqs. (5), (6) and (7):

$$ V(z,t) = \frac{m(t)}{2\uppi (b - a)}[\log (z - a) - \log (z - b)]\quad ({\text{ft/day}}) $$

(5)

$$ V(z,t) = \frac{{ - i \cdot \upsilon (t) \cdot {\text{e}}^{ - i\gamma } }}{2\uppi \cdot h \cdot n \cdot L \cdot W}\left[ {\log \left( { - {\text{e}}^{ - i\gamma } (z - z_{\text{a2}} )} \right) - \log \left( { - {\text{e}}^{ - i\gamma } (z - z_{\text{a1}} )} \right) + \log \left( { - {\text{e}}^{ - i\gamma } (z - z_{{{\text{b}}1}} )} \right) - \log \left( { - {\text{e}}^{ - i\gamma } (z - z_{{{\text{b}}2}} )} \right)} \right]\quad ({\text{ft/day}}) $$

(6)

$$ V(z,t) = \frac{m(t)}{{2\uppi (z - z_{\text{c}} )}}\quad ({\text{ft}}^{2} / {\text{day}}) $$

(7)

Equations (5)–(7) can be superimposed if multiple analytical elements are present in a model as shown later for interval sources [in Eqs. (11) and (12)], as all the complex potentials used in the present study are based on superposed collections of point sources and sinks.

For an element with center (x_c) and total length (L), the interval source in Eq. (5) can be rewritten as:

$$ V(z,t) = \frac{m(t)}{2\uppi (b - a)}[\log (z - x_{\text{c}} + 0.5L) - \log (z - x_{\text{c}} - 0.5L)]\quad ({\text{ft/day}}) $$

(8)

For an interval source, with endpoints between $z_{\text{a}} = z_{\text{c}} - 0.5L{\text{e}}^{i\beta }$ and $z_{\text{b}} = z_{\text{c}} + 0.5L{\text{e}}^{i\beta }$, where z_a, z_b, z_c, L and β are the endpoints, center, length and tilt angle, respectively, the complex potential Ω(z) is:

$$ \varOmega (z,t) = \frac{m(t)}{2\uppi L}\left[ {(z - z_{\text{a}} )\log \left[ {{\text{e}}^{ - i\beta } (z - z_{\text{a}} )} \right] - (z - z_{\text{b}} )\log \left[ {{\text{e}}^{ - i\beta } (z - z_{\text{b}} )} \right]} \right]\quad ({\text{ft}}^{2} / {\text{day}}) $$

(9)

The velocity potential is again obtained by differentiating the above expression with respect to z:

$$ V(z,t) = \frac{m(t)}{2\uppi L}\left[ {\log \left[ {{\text{e}}^{ - i\beta } (z - z_{\text{a}} )} \right] - \log \left[ {{\text{e}}^{ - i\beta } (z - z_{\text{b}} )} \right]} \right]\quad ({\text{ft/day}}) $$

(10)

The generalized expression for N interval sources can be derived from Eqs. (3) and (4):

$$ \varOmega (z,t) = \sum\limits_{k = 1}^{N} {\frac{{m_{k} (t)}}{{2\uppi L_{k} }}\left( {({\text{e}}^{{ - i\beta_{k} }} (z - z_{{{\text{c}}k}} ) + 0.5L_{k} )\log \left[ {{\text{e}}^{ - i\beta } (z - z_{{{\text{c}}k}} ) + 0.5L_{k} } \right]} \right.} \left. { - ({\text{e}}^{{ - i\beta_{k} }} (z - z_{{{\text{c}}k}} ) - 0.5L_{k} )\log \left[ {{\text{e}}^{ - i\beta } (z - z_{{{\text{c}}k}} ) - 0.5L_{k} } \right]} \right)\quad ({\text{ft}}^{2} / {\text{day}}) $$

(11)

$$ V(z,t) = \sum\limits_{k = 1}^{N} {\frac{{m_{k} (t)}}{{2\uppi L_{k} }}{\text{e}}^{{ - i\beta_{k} }} \left( {\log \left[ {{\text{e}}^{ - i\beta } (z - z_{{{\text{c}}k}} ) + 0.5L_{k} } \right]} \right.} \left. { - (\log \left[ {{\text{e}}^{ - i\beta } (z - z_{{{\text{c}}k}} ) - 0.5L_{k} } \right]} \right)\quad ({\text{ft/day}}) $$

(12)

Strength m(t), for a well with productivity of q(t) (ft³/day) with a reservoir height of h (ft) and reservoir porosity n, is:

$$ m(t) = \frac{Bq(t)}{{hn(1 - R_{\text{s}} )}}\quad ({\text{ft}}^{2} / {\text{day}}) $$

(13)

where m, h, R_s and n are the time-dependent strength, thickness of the reservoir, residual oil saturation and porosity, respectively. Equation (13) can be modified for a horizontal well with multiple fractures by allocating the production based on the number of fractures (or effective surface area).

Superimposed forms of Eqs. (5) and (6) are the expressions used in the present study to model natural fractures and hydraulic fractures with multiple orientations and lengths to construct a discrete fracture model. The advantage of CAM-based models is the ability to superpose various analytical elements to construct complex flow solutions. For example, a vertical well represented by an analytical point source/sink element in Eq. (7) can be combined with the interval source/sink in Eq. (5) to simulate a well with multiple hydraulic fractures. Superposition of Eq. (6) accounts for natural fractures.

2.3 Time of flight contours

The CAM model developed uses streamlines and time of flight contours (TOFC) generated by an Eulerian particle tracking method ($z_{n + 1} \approx z_{n} + v(z_{n} )$). The velocities (v_x and v_y) of the particles are mapped using the real and imaginary parts of the complex potential:

$$ V(z,t) = v_{x} - iv_{y} \quad ({\text{ft/day}}) $$

(14)

Further details and derivation for Eq. (14) are given by Weijermars et al. (2017a, b). Equation (14) is used to calculate the velocity field solutions from specific velocity field expressions defined for hydraulic and natural fractures [Eqs. (5) and (6)]. Tracing each streamline is accomplished by first choosing an initial position z₀ at time t₀ = 0 and calculating the initial velocity. By choosing an appropriate time-step, Δt, the position $z_{1} (t_{1} )$ of the tracer at a time $t_{1} = t_{0} + \Delta t$ is:

$$ z_{1} (t_{1} ) \approx z_{0} (t_{0} ) + v(z_{0} (t_{0} ))\Delta t\quad ({\text{ft}}) $$

(15)

The position $z_{j} (t_{j} )$ of the tracer at any other time t_j is:

$$ z_{j} (t_{j} ) \approx z_{j - 1} (t_{j - 1} ) + v(z_{j - 1} (t_{j - 1} ))\Delta t\quad ({\text{ft}}) $$

(16)

The time of flight contour (TOFC) is determined by plotting the location of all the tracers for a particular time-step. The selection of an appropriate time-step is a crucial decision in the Eulerian particle tracking method. An overly coarse time-step in combination with sharply curving streamline results in overshooting of the particles, which then jump from one streamline to the other, which is inaccurate. For cases where the decline of the well is rapid, such as during the early production phase, a very small time-step is required to avoid inaccuracies in the displacement of the particles due to the high instantaneous velocity. However, a coarser time-step can be used in cases where the change decline is not drastic in order to reduce the computational time.

2.4 Basic flow simulation

In this section, basic flow simulations for a vertical well are conducted to illustrate the applicability of the model based on the expressions in Sect. 2.2 and 2.3. These simulations are implemented using the concept of flow reversal, where the produced fluid from a well is allocated based on surface area of the hydraulic fractures and injected back into the reservoir (Weijermars et al. 2017a, b). An alternate method of production allocation to hydraulic fractures includes the proppant concentration as a factor in production allocation (Parsegov et al. 2018). The drainage contours and streamlines are evaluated using synthetic production data generated by a traditional Arps hyperbolic decline model. Exponential decline and hyperbolic decline models were used to generate the production decline curve for a vertical well for 30 years to illustrate the variation in flow patterns.

Figure 2a (left) shows the streamline pattern (blue) for a vertical well producing at an exponential decline with an initial production rate of 86 STB/d and nominal decline of 0.7/year for 30 years modeled with a point sink analytical element in Eq. (7). The EUR at the end of 30-year production is 45 MSTB. The height of the reservoir is assumed to be 300 ft, which needs to be accounted for when calculating the drainage using streamlines and time of flight contours (TOFC). The TOFC (red) represent the drainage area gain for 1.5 years increments of production in Fig. 2a (right). The bulk portion of the drainage occurs in the first 3 years. The area covered by the successive TOFC shrinks rapidly, which is a direct result of reduced production from the successive time periods. The Arps decline curve for the production in Fig. 2a is shown in Fig. 2c (left).

Fig. 2

a A generic vertical well with EUR of 45 MSTB, showing an exponential decline, modeled with a point source by flow reversal technique for 30 years of production. The streamlines (ft) (left) are represented by blue segments and each of the TOFC (ft) (right), representing 1.5 years, was modeled by red segments each. b A generic vertical well with EUR of 120 MSTB, showing a hyperbolic decline, modeled with a point source by flow reversal technique. The streamlines (ft) (left) are represented by blue segments and each of the TOFC (ft) (right), representing 1.5 years, was modeled by red segments. c Exponential decline curve used for (a). d Hyperbolic decline curve used for (b)

Figure 2b (left) shows the streamline pattern (blue) for a well producing with a hyperbolic decline with an initial production rate of 86 STB/d and nominal decline of 0.7/year and Arps decline parameter b of 0.7 for 30 years modeled using a point sink analytical element in Eq. (7). The EUR for the hyperbolic model at the end of the 30-year production is 120 MSTB. The TOFC (red) is visualized on the right, and each of the TOFC represents the drainage after 1.5 years of production in Fig. 2a (right). Even though the decline is rapid in the first 1.5 years, an appreciable amount of production persists after the first 3 years of production depicted by the reduction in the area covered by each successive TOFC [Fig. 2b (left)]. The Arps decline curve for the production in Fig. 2b is shown in Fig. 2d.

Comparison of Fig. 2a, b shows that the drainage in the exponential model occurs only for the first few years shown by the TOFC which become crowded after that duration. However, with a hyperbolic decline model, the production decline is less steep as shown by the time of flight contours becoming less crowded as compared to the exponential decline case. For the same initial production rate, hyperbolic decline (Fig. 2b) shows more substantial drainage, which can be calculated by measuring the area covered by each TOFC. Although for a simple case with just one injector/producer, the same information can be gleaned from rate-versus-time curves, pictured in Fig. 1c, d, the flow visualization technique using TOFC is particularly valuable for cases with multiple hydraulic and natural fractures, as will be shown later in the study.

3 Impact of natural fractures on flow near hydraulic fractures

Natural fractures are ubiquitous in shale plays. Shale Formations are very tight, and hydrocarbon production is considered only possible when extensive networks of natural fractures exist (Carlson and Mercer 1991). However, some studies have also shown that calcite-filled closed or open natural fractures can be detrimental to shale gas production (Bowker 2007). In this section, we implement the analytical expressions described in Sect. 2.2 to model the interaction of discrete natural fractures with hydraulic fractures to study the effect on drainage area. As shown by earlier studies, the drainage area around a hydraulic fracture in unconventional shale oil reservoirs is limited to only a few hundred feet (Weijermars et al. 2017a, b; Weijermars and Alves 2018; Khanal and Weijermars 2019), which is due to the extremely rapid decline rates in unconventional reservoirs. For this reason, only one hydraulic fracture is simulated first in this section to visualize the drained rock volume (DRV). A multi-well case with a constant rate production is used to visualize the effect of natural fractures on DRV in a later section (Sect. 4).

For the base case, production data from a well in the Eagle Ford play described in earlier companion studies were used (Hu et al. 2018; Khanal and Weijermars 2019). Hu et al. (2018) matched around 26 months of production data to generate a 30-year production forecast for various wells in the lease using different decline curve methods. Figure 3 includes the Arps DCA history match parameters for the particular well used in the present study (Well H1). Well H1 has 131 individual fractures and 22 fracture stages. Equation (13) is used to allocate flow to the well, which is further divided into 22 fracture stages by assuming equal fracture half-length and fracture-height.

Fig. 3

The base case with a single hydraulic fracture (without natural fractures). a Streamlines represented by blue curves. b TOFC for 30 years of production. The length of the hydraulic fracture is 150 ft. c Associated decline curve used to model (a) and (b), based on Well H1 from an earlier study located in the Eagle Ford Shale. Well H1 consists of 22 fracture stages, which is used to allocate flow to each of the line sources (~ 12 MSTB). The initial strength (m₀) of the hydraulic fracture is 56.8 ft²/day, which declines based on the decline curve shown in c. d DCA parameters for Well H1. e 3D reservoir model showing the drainage area for the base case. Each layer is identical to the top layer as the reservoir is homogenous. Only the top 50 ft (of 60 ft) height is shown in the figure

Several authors have previously used techniques such as fault likelihood attribute (Hale 2013; Lomask et al. 2017; Wu and Hale 2015; Ramsay et al. 2017) to interpret 3D seismic images and generate a spatial constraint of the natural fractures. Others have recommended a stochastic approach based on geostatistical analysis of the 3D seismic images (Admasu et al. 2006). Despite these techniques used for natural fracture characterization, significant sub-surface uncertainty exists about natural fracture orientation, conductivity, and density. The natural fracture network characterization is outside the scope of the current study. We only present a novel technique based on CAM to conduct flow simulation in natural fractures. In this method, the conductivity is defined by varying the strength parameter [υ(t) (ft⁴/day)] shown in Eq. (6), which defines the permeability contrast of natural fractures and matrix. Although natural fractures within a formation can have varying degrees of cementation, in the present work, all the natural fractures are assumed to be conductive and open. They are, however, unconnected to the hydraulic fractures or the wellbore. The present study does not consider the propagation or post-faulting re-orientation of the natural fractures which depends on lithology, energy release rate, fracture energy, grain size distribution, temperature and cementation (Ramsay et al. 2018). The goal of the present study is not to investigate the orientation of natural fractures due to the rotation of the principal horizontal stress field during seismic faulting. The focus is an investigation of the flow patterns and drained rock volumes (DRV) in the presence of natural fractures, with pre-defined density and orientation in the proximity of hydraulic fractures of horizontal wells.

Figure 3a shows the DRV around a single hydraulic fracture (red line) simulated for 30 years by implementing the flow reversal principal. Fluid flux is allocated according to a decline curve-based production profile, assuming each fracture represents a fracture stage with flux proportional to the number of hydraulic fractures in the well. Streamlines are represented by blue lines, and TOFC are represented by rainbow colors, each representing a 3-year drainage period. Figure 3a shows that for a single hydraulic fracture representing a stage (with six fractures and stage spacing of 300 ft), even after 30 years of production, the particle paths remain confined within an elliptical region with axes of ± 129 ft parallel and ± 62 ft perpendicular to the hydraulic fracture. In our earlier studies (Weijermars and Alves 2018; Khanal and Weijermars 2019), a different drainage area was reported from the flow simulation with the same production data. A key distinction between the results calculated in the present study and the earlier study (Weijermars and Alves 2018; Khanal and Weijermars 2019) is the assumed dimensions and the number of the hydraulic fractures per drainage area. In the current study, we model a fracture stage comprised of six hydraulic fractures, which results in a larger drainage area (confined between ± 129 ft parallel and ± 62 ft perpendicular to the hydraulic fracture) compared to the area confined between ± 229 ft parallel and 17 ft perpendicular to the hydraulic fracture in Khanal and Weijermars (2019). Additionally, the drainage area in the present study is different from Weijermars and Alves (2018) which assumed different fracture dimensions (500 ft fracture half-length), different effective height and only one effective fracture per stage. Although each study results in a different drainage area, the results obtained in the present study can be upscaled or downscaled depending on the fracture dimensions and the number of discrete fractures used in the simulation.

Figure 3b shows that most of the drainage occurs from the reservoir in the first 3 years. The area covered by each TOFC (represented by distinct colors) shrinks at each subsequent time of flight contours. The corresponding decline curve and the corresponding Arps hyperbolic parameters are given in Fig. 3c, d respectively. The history-matched decline curves used in Fig. 3 have no natural fractures. Figure 3e shows the 3D representation of the reservoir where the top layer shows the drainage area for corresponding TOFC.

Next, natural fractures are introduced to the base case to understand their effect on the DRV. Several possible variations are investigated, which are the density determined by the number of discrete natural fracture elements, orientations determined by the angle of natural fractures with respect to the hydraulic fracture, distance from the hydraulic fractures and the relative conductivity or strength of the natural fractures. The permeability ratio (R_k) of the natural fractures to the matrix has been studied in our companion study (Weijermars and Khanal 2019a), where Eq. (17) was derived as follows:

$$ R_{k} (t) = \frac{{\upsilon_{\text{f}} (t)}}{{\nu_{\text{m}} (t)w_{\text{f}} H_{\text{f}} L_{\text{f}} }} $$

(17)

where R_k is the permeability ratio, $\upsilon_{\text{f}} (t)$ (ft⁴/s) is the time-dependent strength of the natural fracture, $\nu_{\text{m}} (t)$ is the time-dependent matrix strength (determined by far field velocity, ft/s), w_f (ft) is the width, H_f is the height and L_f is the length of the natural fracture. In the present study, the permeability ratio is calculated with respect to the hydraulic fracture element. So, Eq. (17) is modified as follows:

$$ R_{k} (t) = \frac{{\upsilon_{\text{f}} (t)L}}{{m(t)w_{\text{f}} H_{\text{f}} L_{\text{f}} }} $$

(18)

where m(t) (ft²/s) and L (ft) are the strength and length of the hydraulic fractures defined in Eq. (8), respectively. Equations (17) and (18) work the best when the natural fractures are aligned in the direction of the flow of fluid defined by the streamlines. Although the DRV shown in the present study follows a complex pattern, Eq. (18) still provides a good estimate for the permeability ratio. Other techniques that can be used to calculate the permeability ratio are discussed in greater detail in Weijermars and Khanal (2019a). As the strength of both natural and hydraulic fractures is time-dependent, the permeability ratio also varies with time. However, in this study as the strength of the natural fractures is indexed to the strength of the hydraulic fractures, the ratio $\upsilon_{\text{f}} (t)/m(t)$ remains constant, which corresponds to a constant permeability ratio. The permeability ratio, which gives an idea of the strength of the natural fractures relative to the hydraulic fractures, is calculated and presented in Table 1 along with other input values used for the study.

Table 1 Input summary for reservoir and natural fractures simulated in Sect. 3

3.1 Case A: oblique natural fractures close to the hydraulic fracture

Case A has 12 natural fractures on each side of the hydraulic fracture (Fig. 4), and the center of the natural fractures is at a distance of 10 ft from the hydraulic fracture. Each natural fracture is 20 ft long and is assumed to be distributed uniformly between − 25 ft and 25 ft in the horizontal direction. The natural fractures on the upper side of the hydraulic fractures are assumed to be oriented at 45°, whereas those below the hydraulic fracture are assumed to be oriented at 225° with respect to the hydraulic fracture. Although the actual orientation of the natural fractures in the upper and lower side of the hydraulic fracture in the map view of Fig. 4 appear the same, the 45° vs 225° refers to opposite flow polarities. The natural fractures accelerate the fluid particles in the far-field travel direction which is imposed by the hydraulic fracture. The strength of the natural fractures is indexed to the strength of the hydraulic fractures, such that the natural fractures influence the production at a rate proportional to production from the hydraulic fractures. The natural fractures are not connected to the hydraulic fractures, thus only accelerate the fluid flow toward the hydraulic fracture by facilitating pressure communication.

Figure 4a–d shows the effect of uniformly distributed natural fractures with different strengths on the drained rock volume. The strength of natural fractures is varied from 204 to 4088 ft⁴/day. The corresponding permeability ratios of the natural fractures to the matrix are included in Table 1. Figure 4a shows that for the minimum strength, the effect of the natural fractures on both streamlines and drainage area is negligible. A slight change in drainage area results when the strength of the natural fracture is increased by a factor of 5 as shown in Fig. 4b. For the natural fractures with a significantly higher strength, the DRV is drastically changed compared to the case with no natural fractures as shown in Fig. 4c, d. Particle tracking becomes locally inaccurate in Fig. 4d due to the high fracture density and fast flow rates in the natural fractures, which causes some TOFC to cross. This can be remedied by significantly reducing the time-step, at the cost of computational efficiency. The visualization of Fig. 4d provides a compromise between computational speed and accuracy.

Fig. 4

Case A. a–d (Top images): streamlines represented by blue lines show the movement of particles after 30 years. a–d (Bottom images): drainage area at 3-year interval shown by different colors. The strength of the natural fractures is: a 204 ft⁴/day, b 1022 ft⁴/day, c 2044 ft⁴/day and d 4088 ft⁴/day. Flux into the hydraulic fracture is allocated according to the decline curve shown in Fig. 2c. The strength of the natural fractures is indexed to hydraulic fracture’s flux rate at a particular time. Fracture dimensions: The hydraulic and natural fractures are represented by red segments. The total length of the hydraulic fractures is 150 ft. There are 24 natural fractures, each close to the hydraulic fracture. The length and width of the natural fractures are 20 ft and 0.5 ft, respectively

Figure 4a–d shows that the DRV is changed due to the influence of the natural fractures; however, their effect is localized. Since the total flux is conserved, we can see that the outer portion of the DRV shrinks, whereas the middle portion where the natural fractures are located expands covering a larger surface area. Although the natural fractures locally enhance the movement of fluid from a region, the fluid comes from an adjoining region which would have been drained in the absence of the natural fractures. Thus, the presence of the natural fractures does not increase the overall production potential from a well.

3.2 Case B: localized natural fractures perpendicular to the hydraulic fracture

Case B has 12 mutually parallel natural fractures on each side of the hydraulic fracture (Fig. 5), and the center of the fractures is at a distance of 50 ft from the hydraulic fracture. Each natural fracture is 20 ft long and occurs uniformly spaced between − 25 ft and 25 ft in the horizontal direction. The natural fractures on the top side of the hydraulic fracture are assumed to be oriented at 90°, whereas those below the hydraulic fracture are assumed to be oriented at 270° with respect to the hydraulic fracture. The strength of the natural fractures is indexed to the strength of the hydraulic fracture so that the natural fractures influence the production at a rate proportional to production from the hydraulic fracture.

Figure 5a–d show the effect on the shape of the drained rock volume of uniformly distributed natural fractures with different strengths when oriented perpendicular to the hydraulic fracture. The strength of the natural fractures is stepwise increased from 204 to 4088 ft⁴/day. Figure 5a shows that for the minimum strength, the effect of the natural fracture on both streamlines and drainage area is negligible (only limited to the regions with natural fractures). There is a significant change in the DRV shape when the strength of the natural fractures is further increased. For the natural fractures with a significantly higher strength, the DRV shape changes and the location shifts (Figs. 5b-d) compared to the case with natural fractures oriented at 45° (Fig. 4a–d). The streamlines and the DRV travel to almost 100 ft in the vertical direction, which reduces the flux on other regions as shown in Fig. 5c, d. Since the total flux is conserved, the outer portion of the DRV shrinks, whereas the middle portion (where the natural fractures are located) expands, locally draining a larger surface area. The communication between the adjoining fractures is increased by the natural fractures (not shown), which can in some cases negatively affect the overall production of the well (Walton and McLennan 2013).

Fig. 5

Case B. a–d (Top images): streamlines represented by blue lines show the movement of particles after 30 years. a–d (Bottom images): drainage area at 3-year interval shown by different colors. The strength of the natural fractures is: a 204 ft⁴/day, b 1022 ft⁴/day, c 2044 ft⁴/day and d 4088 ft⁴/day. Flux into the hydraulic fracture is allocated according to the decline curve shown in Fig. 2c. The strength of the natural fractures is indexed to the hydraulic fracture’s flux rate at a particular time. Fracture dimensions: The hydraulic and natural fractures are represented by red segments. The total length of the hydraulic fracture is 150 ft. There are 24 natural fractures, each close to the hydraulic fracture. The length and width of the natural fractures are 20 ft and 0.5 ft, respectively

3.3 Case C: oblique natural fractures encompassing the hydraulic fractures evenly

Case C is a modification of Case A, where the natural fractures are evenly distributed around the hydraulic fracture (Fig. 6). There are seven natural fractures on each side of the hydraulic fracture, and the center of the fractures is at a distance of 10 ft from the hydraulic fracture. Each natural fracture is 20 ft long and is assumed to be distributed uniformly between − 75 ft and 75 ft in the horizontal direction. The natural fractures on the top side of the hydraulic fractures are assumed to be oriented at 45°, whereas those below the hydraulic fracture are assumed to be oriented at 225° with respect to the hydraulic fracture. In contrast to Case A, fewer natural fractures are introduced into Case C. Figure 6c, d shows that the changes in the DRV shape and location are comparable to those for Case A (Fig. 4a–d). Even though the shape and location of the DRV are changed due to the evenly distributed natural fractures, the maximum displacement of particles in the vertical direction is similar to that in Case A (Fig. 4d). Figure 6d shows several regions where the fluid bypasses the matrix when the strength of the natural fractures is 4088 ft⁴/day. The rapid flow of fluids by the natural fractures results in several regions left undrained during the economic life of the well (shown by the white space between the natural fractures).

Fig. 6

Case C. a–d (Top images): streamlines represented by blue lines show the movement of particles after 30 years. a–d (Bottom images): drainage area at 3-year intervals shown by different colors. The strength of the natural fractures is: a 204 ft⁴/day, b 1022 ft⁴/day, c 2044 ft⁴/day and d 4088 ft⁴/day. Flux into the hydraulic fracture is allocated according to the decline curve shown in Fig. 2c. The strength of the natural fractures is indexed to the hydraulic fracture’s flux rate at a particular time. Fracture dimensions: The hydraulic and natural fractures are represented by red segments. The total length of the hydraulic fracture is 150 ft. There are 14 natural fractures each close to the hydraulic fracture. The length and width of the natural fractures are 20 ft and 0.5 ft, respectively

3.4 Case D: complex crossing natural fractures

Case D investigates the effect of two conjugate sets of mutually perpendicular and crossing natural fractures occurring at either side of the hydraulic fracture (Fig. 7). There are 12 natural fractures which are 20 ft long on each side of the hydraulic fracture, and the center of the fractures occurs at a distance of 15 ft from the hydraulic fracture. The two natural fracture sets cross each other at right angles. The effect of these natural fractures on the DRV is negligible when the strength of the natural fractures is 204 ft⁴/day (Fig. 7a). Even for the natural fractures with relatively strong influence, the overall change in DRV is not as significant (Fig. 7b–d) as for Case C (Fig. 6b–d), where a single set of natural fractures affects the flow pattern near the the hydraulic fracture.

Fig. 7

Case D. a–d (Top images): streamlines represented by blue lines show the movement of particles after 30 years. a–d (Bottom images): drainage area at 3-year interval shown by different colors. The strength of the natural fractures is: a 204 ft⁴/day, b 1022 ft⁴/day, c 2044 ft⁴/day and d 4088 ft⁴/day. Flux into the hydraulic fracture is allocated according to the decline curve shown in Fig. 2c. The strength of the natural fractures is indexed to the hydraulic fracture’s flux rate at a particular time. Fracture dimensions: The hydraulic and natural fractures are represented by red segments. The total length of the hydraulic fracture is 150 ft. There are 24 natural fractures each close to the hydraulic fracture. The length and width of the natural fractures are 20 ft and 0.5 ft, respectively

3.5 Case E: evenly distributed natural fractures with higher density

Case E includes several short, non-crossing micro-fractures with different orientations (Fig. 8). There are 28 natural fractures, 14 on each side of the hydraulic fracture. Each natural fracture is assumed to be 10 ft long and oriented at an angle of 45° and 90° as shown in Fig. 8. The strength is indexed to the hydraulic fracture and is varied from 204 to 4088 ft⁴/day. Figure 8c, d shows that the DRV is slightly reduced in the horizontal direction (with respect to hydraulic fracture), whereas a slight increase is observed in the vertical direction. Unlike Case C (Fig. 6a–d), no significant flow stagnation regions are seen in Case E. However, the amount of drainage in the vertical direction is not as extensive as for Case B, where only vertical natural fractures are present. Figure 8a–d also shows that although DRV shape changes due to evenly distributed natural fractures, their effect is limited. The drainage in the vertical direction is larger when the strength is higher than 4088 ft⁴/day and the flow stagnation remains absent as compared to Case C.

Fig. 8

Case E. a–d (Top images): streamlines represented by blue lines showing the movement of particles after 30 years. a–d (Bottom images): drainage area at 3-year interval shown by different colors. The strength of the natural fractures is: a 204 ft⁴/day, b 1022 ft⁴/day, c 2044 ft⁴/day and d 4088 ft⁴/day. Flux into the hydraulic fracture is allocated according to the decline curve shown in Fig. 2c. The strength of the natural fractures is indexed to hydraulic fracture’s flux rate at a particular time. Fracture dimensions: The hydraulic and natural fractures are represented by red segments. The total length of the hydraulic fracture is 150 ft. There are 28 natural fractures each close to the hydraulic fracture. The length and width of the natural fractures are 10 ft and 0.5 ft, respectively

3.6 Accuracy of results

The models used in this study apply a Eulerian particle tracking scheme, which uses the velocity of a particle at a particular time and specific location to calculate the future position of the particle using finite time increments (Δt). The value of Δt used in the particle tracking algorithm is an important parameter, constrained by the computational resources. The process of increased accuracy, of course, is a continual trade-off between acceptable computation durations and required accuracy. Some models may need smaller time-steps, depending on the orientation, strength and density of the natural fractures. In particular, a small Δt is required for production episodes and locations where the particles have a high velocity; otherwise, the particle paths become less accurate, and overlapping TOFC may occur. Most simulations in our present study used a time-step Δt = 1 day for particle tracking, which may introduce some inaccuracy for the cases with high permeability contrast (maximum natural fracture strength). For example, Fig. 9a–e shows the more accurate solutions for the high permeability contrast runs of Cases A–E with Δt reduced to 0.05 days. The smaller time-step results in smoother particle paths and more accurate TOFCs, as is most apparent by comparing Case C in Fig. 9c and Fig. 6d. For the other cases, minor differences are observed between the slower simulation Δt = 0.05 days (more accurate; Fig. 9a, b, d, e) as compared to the faster simulation with Δt = 1 day (less accurate; Figs. 4d, 5d, 7d, and 8d, respectively).

Fig. 9

Calculation of DRV with Δt = 0.05 day (compared to Δt = 1 day for Figs. 4–8) for fracture orientations in a to e which correspond to Cases A through E (cases d in Figs. 4–8). Left column: the top view of the DRV. Right column: 3D reservoir model showing the drainage area. Each layer is identical to the top layer as the reservoir is homogenous and all fractures are assumed to extend vertically downward in the reservoir, confined between the lower and upper boundaries of the producing layer. Only the top 50 ft (of 60 ft) height is shown in the figure, which is limited to flow around a single hydraulic fracture (the focus of Sect. 3)

The algorithms used for modeling hydraulic fractures in this study have previously been validated against a commercial numerical simulator with good accuracy. Weijermars et al. (2017a) compared the results of the CAM for flow in a reservoir with planar hydraulic fractures against the streamlines and time of flight contours obtained from Eclipse as shown in Fig. 10. The algorithm for natural fractures used in the present study is also based on CAM (van Harmelen and Weijermars 2018), and will be further validated in future studies.

Fig. 10

Streamlines with drainage contours: a streamlines (blue), time of flight contours (red), stagnation points (green) generated with CAM. Fractures represented as black lines. b Streamlines, time of flight contours (rainbow colors) and stagnation point generated with Eclipse streamline simulator (Weijermars et al. 2017a)

4 Natural fractures between two adjoining wells

4.1 Base case: multiple wells with no natural fractures

In Sect. 3, we investigated the impact of natural fractures around a single hydraulic fracture on the DRV. Several non-exhaustive scenarios were evaluated using field production data from an Eagle Ford Well. Next, we investigated a scenario where multiple wells with multiple hydraulic fractures produce at the same time. Well-spacing in unconventional reservoirs is very important and thus needs to be optimized to improve the production performance of the individual wells (Khanal et al. 2015a, b, 2017). As shown by earlier companion studies, the drainage area for an unconventional well with declining production is on the orders of tens of feet around the fractures (Hu et al. 2018; Weijermars and Alves 2018; Khanal and Weijermars 2019). The visualization for wells with declining data remains limited to a very narrow strip; hence, for the multi-well case model, a synthetic well with a constant production rate is used for generating conceptual and systematic insight.

Figure 11 shows the full-scale map view of the three parallel base case wells. Each well is assumed to have 119 hydraulic fractures with a half-length of 150 ft. The fracture spacing is 50 ft. The wells are spaced at 1250 ft and are assumed to be producing as parent wells at a constant rate of 13.6 ft³/day per fracture (~ 3.23 bbls/day per fracture) with a water-to-oil ratio (WOR) of 0.17. The height of the reservoir is 60 ft. During simulation, fluid particles from the middle five fractures are tracked with streamlines (blue), simulated for 30 years. However, all 119 fractures are active in our simulation and contribute to the overall DRV.

Fig. 11

The base case with multiple wells. Top view of three full-scale wells (horizontal in map view) parallel to the x-direction located at y = 0, 1250 and − 1250 ft. Each of the wells has 119 transverse hydraulic fractures with a fracture half-length of 150 ft. Each hydraulic fracture is assumed to be identical and producing at a constant rate of 13.6 ft³/day (2.4 bbl/day) for 30 years. The initial strength (m₀) of each hydraulic fracture is 8.48 ft²/day. Although all 119 fractures influence the fluid flow and are included in the flow simulation, streamline tracking is limited to the central five hydraulic fractures of the middle well. Streamlines (blue) show the position of fluid after 30 years of constant rate production starting from the fractures. Although 30 years of constant rate production is not feasible in practice, the steady rate case is chosen to illustrate the effect of natural fractures among three active wells

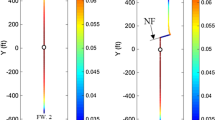
Detailed map views of the central well with streamlines (blue) and time of flight contours (red) are shown in Fig. 12a, b, respectively. The horizontal axis is extended (left image) to show the details, and true to scale streamlines and time of flight contours are shown in the right image. Figure 12a, b shows the stagnation surfaces occur between two adjacent hydraulic fractures, across which no fluid exchange occurs. A more detailed discussion of flow stagnation surfaces between hydraulic fractures is given in Weijermars et al. (2017a, 2018). The DRV is calculated by evaluating the area covered by each TOFC, which grows at a steady rate for each time interval due to the constant production rate. The DRV visualized in Fig. 12b is for the base case with no natural fractures between the hydraulic fractures and the wells.

Fig. 12

Top view of five hydraulic fractures (black line segments) for the central horizontal well in Fig. 11 (without any natural fractures). a Streamlines (blue) show the movement of the fluid particles after 30 years of a constant flow rate. The horizontal axis is enhanced in the left image to highlight the details. Streamlines true to scale in the right image (showing only the upper portion of flow field in left image). b Time of flight contours (red, left image) showing the drainage at each 3-year interval. The horizontal axis is enhanced in the left image to highlight the details. Right image true to scale: TOFC for each 3-year period represented by the rainbow colors

4.2 Cases F and G: natural fractures between two wells (moderate angle with hydraulic fractures)

In the remainder of Sect. 4, the effect of natural fractures between the wells is further investigated. Table 2 summarizes the input summary for reservoir properties for natural fractures from Cases F through M.

Table 2 Input summary for reservoir and natural fractures simulated in Sect. 4

This section introduces natural fractures between the top two wells shown in Fig. 11. This study does not use the fault likelihood (Hale 2013) to identify natural fracture networks from, for example, micro-seismic data. Our goal is instead to use possible sets of natural fractures with different lengths, orientations, and strengths to identify their effects on DRV. In future studies, we plan to use improved fracture diagnostics to define realistic natural fracture networks, but constraining the fracture permeability and aperture may remain beyond the practical limits of contemporary fracture characterization tools.

Case F (Fig. 13) assumes that there are six equally spaced natural fractures between 2850 ft and 3150 ft horizontally and 400 ft vertically. A second set occurs at the same distance horizontally and at 700 ft vertically. Each of the natural fractures is 150 ft long and oriented at 45° with respect to the wellbore. Since the hydraulic fractures are producing at a constant rate, the effect of natural fractures remains constant throughout the simulation period. The natural fractures have a steady strength of 6 × 10³ ft⁴/day; the corresponding permeability ratio of the natural fractures to the matrix is included in Table 2 calculated by Eq. 18. Each natural fracture has a height (or depth) of 60 ft (h in Eq. 6) such that it spans the entire reservoir depth.

Fig. 13

Case F. Top view of central five fractures for the second well with six natural fractures embedded at an angle of 45°. The strength of the natural fractures is 6 × 10³ ft⁴/day. Left image: streamlines (blue) show the movement of the fluid particles after 30 years of constant flow rate production. Right image: time of flight contours (multi-colored) showing the drainage at each 3-year interval. Both figures are true to scale

Figure 13 shows the streamlines (left, blue) and time of flight contours (multi-colored) after 30 years of simulation for Case F. In comparison with the base case (Fig. 12), the DRV in Fig. 13 is slightly shifted because of flow deflection via the natural fractures. Figure 13 also shows that the maximum distance traveled by the fluid slightly increases in the vertical direction and shrinks horizontally as compared to the base case of Fig. 12 (as the total flux to the hydraulic fractures remains constant).

In Case G (Fig. 14), the strength of the natural fractures is increased to 60 × 10³ ft⁴/day. Figure 14 shows the effect of natural fractures with increased strength on the DRV, using color-coded streamlines (blue, left) to establish TOFC (multi-colored, right). The symmetric drainage area in the base case (Fig. 12b, right image) becomes now seriously distorted (Fig. 14, right), and the fluid particles are drained from around 1000 ft away from the well (Fig. 14) as compared to only 800 ft when the natural fractures are absent (Fig. 12). Previously, it has been argued that the natural fractures are detrimental to productivity as a result of extensive communication between wells (Walton and McLennan 2013). Figure 14 shows that the communication between two neighboring wells may increase due to the presence of highly conductive natural fractures extending the drainage reach of a well.

Fig. 14

Case G. Top view of central five hydraulic fractures for the middle well (along the x-axis) with six natural fractures embedded in the adjacent matrix at an angle of 45°. The strength of the natural fractures is 60 × 10³ ft⁴/day. Left image: streamlines (blue) show the movement of the fluid particles after 30 years of constant flow rate production. Right image: time of flight contours (multi-colored) showing the drainage at each 3-year interval. Both figures are true to scale

Fig. 15

a, b Case H. Top view of central five hydraulic fractures for the central well (along the x-axis) with 14 natural fractures embedded in the reservoir matrix at an angle of 45°. The strength of the natural fractures is 6 × 10³ ft⁴/day. a Streamlines (blue) show the movement of the fluid particles after 30 years of constant flow rate production. b Time of flight contours (multi-colored) showing the drainage at each 3-year interval. c, d Case K. Top view of central five hydraulic fractures with 14 natural fractures embedded in the adjacent matrix at an angle of 45°. The strength of the natural fractures is 60 × 10³ ft⁴/day. c Streamlines (blue) show the movement of the fluid particles after 30 years of constant flow rate production. d Time of flight contours (multi-colored) showing the drainage at each 3-year interval. All figures are true to scale

4.3 Cases H and K: slanted natural fractures (higher density) between two wells (moderate angle with hydraulic fractures)

Next, the density of the natural fractures was intensified by increasing the number of discrete natural fractures from 6 to 14 for Cases H and K as shown in Fig. 15a–d. The strength of natural fractures was kept constant at 6 × 10³ ft⁴/day and 60 × 10³ ft⁴/day for Cases H and K, respectively. Figure 15a, b shows the streamlines (blue) and TOFC (multi-colored) for the Case H, respectively. Even for a dense natural fracture distribution, the DRV is minimally distorted due to the effect of the natural fractures. In contrast, Fig. 15c, d shows that for Case K with stronger natural fractures (60 × 10³ ft⁴/day), the DRV is distinctly distorted due to a higher density of natural fractures. Figure 15c, d also shows that when the natural fracture density is high, and the strength (or permeability contrast with the matrix) of the natural fracture is high, there is limited drainage from the matrix blocks between the natural fractures. Fluid channels into the natural fractures (and then to hydraulic fractures), which may lead to large undrained regions in between the natural fractures.

4.4 Cases L and M: slanted natural fractures between two wells (high angle with hydraulic fractures)

A final experiment changes the orientation of the natural fractures to almost horizontal (10°) with respect to the x-axis (Fig. 16a–d), with the fracture center at the same distance as in Figs. 13, 14, and 15 to investigate the effect of natural fracture orientation on DRV. A natural fracture strength of 6 × 10³ ft⁴/day had little effect on the DRV, but a higher strength of 60 × 10³ ft⁴/day is used in Fig. 16a–d. Comparing Figs. 14 and 16a, b, we can conclude that the orientation of the natural fractures has a prominent impact on the DRV shape. The drainage around the natural fractures leaves fewer undrained regions (Fig. 16a–d) as compared to the previous cases with natural fractures at a smaller inclination angle (Figs. 14, 15c, d). Such natural fractures that are more aligned with the flow direction imposed by the hydraulic fractures caused matrix blocks between the natural fractures to remain undrained. The flow channeling into the natural fractures is the cause of the matrix blocks between the natural fractures being bypassed. Higher communication between the adjoining wells may result from the flow channeling in the natural fractures. However, limited effect on production occurs when the wells are sufficiently spaced, which is a function primarily of matrix permeability, as presented in the Eagle Ford case study by Khanal and Weijermars (2019). Case M (Fig. 16c, d) further demonstrates that the flow channeling and bypassing of the matrix blocks seen in Case K (Fig. 15c, d) are alleviated when the natural fractures are oriented at a higher angle to the dominant flow path in the matrix.

Fig. 16

a, b Case L. Top view of central five hydraulic fractures for the central well (along the x-axis) with six natural fractures embedded in the matrix at an angle of 10°. The strength of the natural fractures is 60 × 10³ ft⁴/day. a Streamlines (blue) show the movement of the fluid particles after 30 years of constant flow × 10³ ft⁴/day. a Streamlines (blue) show the movement of the fluid particles after 30 years of constant flow rate production. b Time of flight contours (multi-colored) showing the drainage at each 3-year interval. Both figures are true to scale. c, d. Case M. Top view of central five hydraulic fractures with 14 natural fractures embedded in the adjacent matrix at an angle of 10°. The strength of the natural fractures is 60 × 10³ ft⁴/day. c Streamlines (blue) show the movement of the fluid particles after 30 years of constant flow rate production. d Time of flight contours (multi-colored) showing the drainage at each 3-year interval. All figures are true to scale

5 Discussion

The present study explores the use of a 2D analytical model for visualizing the flow near discrete natural fractures occurring in the immediate vicinity of individual hydraulic fractures and between adjacent wells. The model applies analytical solutions for natural fractures that were recently developed by superposing an infinite number of line dipoles (van Harmelen and Weijermars 2018). Natural fractures may accelerate the flow locally due to the enhanced permeability contrast with the matrix. The analytical elements can be used to model an unlimited, but finite, number of natural fractures and are combined in the present study with hydraulic fractures to visualize the impact on the DRV. The upscaling of equivalent permeability based on discrete fracture models using the same method as applied in the current study is explored in a companion study (Weijermars and Khanal 2019a), where it is concluded that natural fractures do not directly increase the production from a reservoir. The primary reason is that natural fractures do not act as pressure sinks, unlike hydraulic fractures connected to the wellbore. However, natural fractures may affect and shift the DRV location depending on the permeability contrast with the matrix. In the present study, the effect of interaction between natural fractures and hydraulic fractures on the DRV was further investigated in some detail. All the natural fractures simulated in the present study were assumed to be uncemented and to have a permeability higher than the ambient matrix rock. The conductivity is assigned by a strength variable which together with fracture density, location, length and orientation of the natural fractures, controls the distortion of the flow path. For cases with natural fracture conductivity close to that of the matrix permeability, the fluid particles move without any distortion. In contrast, the cases with high natural fracture conductivity show that the DRV may become highly distorted. Some of the key results in the present study are discussed below.

5.1 Effect of natural fractures between two hydraulic fractures

Section 3 investigated the effect of natural fractures on the DRV when such fractures occur close to the hydraulic fractures. Since realistic declining production data were used in our analysis, the base case shows an extremely limited DRV. Results from the study in Sect. 3 show that the natural fractures have only a localized effect on the fluid path near individual hydraulic fractures. The natural fractures result in an instantaneous acceleration of fluid particles; however, such acceleration is short lived. The orientation of the natural fractures may have a significant impact on the change in the DRV pattern. Case B (Fig. 5) shows that the natural fractures perpendicular to a hydraulic fracture (in the direction of fluid flow between adjacent hydraulic fractures) result in the most significant change in the shape of the DRV. The corresponding increase in fluid flow in the y-direction results in an equivalent decrease in fluid flux in the x-direction. If additional hydraulic fractures are assumed to be located parallel to the original hydraulic fracture in Case B (Fig. 5), the natural fractures will enhance flow interference. However, flow stagnation points developing between the two hydraulic fractures will separate the respective drainage regions and form flow separation surfaces (Fig. 12), which will suppress flow across any nearby natural fracture, annulling much of the fracture interference effect (not shown here). The optimal number of hydraulic fractures depends on the strength, orientation, and density of the natural fractures. Results from Case C (Fig. 6d and 9c) show that the highly conductive natural fractures which are sparsely distributed around a hydraulic fracture result in several zones in the matrix between the fractures where drainage is slowed down in favor of increased drainage via the tips of the natural fractures. In contrast, compact or dense natural fractures, as in Case A (Fig. 4) and Case E (Fig. 8), result in fewer zones where the matrix is not penetrated by the fluid particles in the time frame of the production period.

5.2 Effect of natural fractures on the inter-well space DRV

An unconventional well produced entirely until primary depletion occurred shows an extremely small DRV after a 30-year production period (Weijermars and Alves 2018; Weijermars et al. 2018). In the present study, a synthetic well with a constant production rate is used for generating conceptual and systematic insight. The critical observation from Figs. 13 and 14 is when the natural fractures are sufficiently strong (high permeability as compared to the matrix), the DRV is shifted toward the adjoining well, which can result in increased well interference. This concept differs from direct well communication via hydraulic fracture hits, which are commonly held responsible for well interference (Kim et al. 2015). However, our study shows that the natural fractures, not directly connected to either of the wells can also cause well interference by connecting the DRV in the zone with the largest density of natural fractures. Additionally, Fig. 15c, d shows that when the inter-well space has a large density of highly conductive natural fractures, a substantial portion of the matrix between the natural fractures remains undrained. The orientation and density of the natural fractures play a crucial role in determining the extent of the DRV. Figure 16a, b shows that when the natural fractures are oriented at a high angle to the flow direction close to the hydraulic fractures, the matrix area between the natural fractures is effectively drained. The movement of fluid for Cases L and M (Fig. 16a, b) leaves fewer undrained matrix blocks as compared to Cases G (Fig. 14) and K (Fig. 15b) with natural fractures oriented at 45° (with respect to the well), which may also result in reduced well interference. For the case with a large number of natural fractures which are oriented at 45° (Fig. 15c, d), we observe flow channeling, where fluid travels from the natural fractures and bulk of the matrix is not utilized by the fluid migration path. Such fracture channeling does still occur when the natural fractures are oriented at a higher angle to the hydraulic fracture tips (Cases L and M, Fig. 16), but then no undrained matrix blocks occur between the natural fractures (Fig. 16c, d). Fracture channeling results in large undrained rock volume between the natural fractures only when the natural fractures are parallel to the flow direction imposed by the hydraulic fractures (see Figs. 14 and 15).

5.3 Effect of natural fractures on well productivity

Prior studies have offered mixed conclusions regarding the effect of natural fractures on well productivity. Some have argued that the natural fractures can lead to improved productivity (Aguilera 2008; Bahrami et al. 2012; Moradian et al. 2016), while others have argued that productivity can be negatively affected due to cementation and extensive communication between the adjoining wells (Walton and McLennan 2013). Hydraulic fractures in reservoirs are directly connected to a producer wellbore and therefore aid in draining reservoir fluids. In contrast, the natural fractures are flow channels that locally increase the fluid velocity due to their enhanced permeability or fluid carrying capacity. However, such natural fractures do not act as pressure sinks, unlike hydraulic fractures. Thus, the natural fractures can change the location of the DRV but do not increase production from a reservoir, unless directly connected to the hydraulic fracture, resulting in an enlarged pressure sink contact with the matrix of the reservoir. The topic of the difficulty to properly interpret the impact of upscaled, equivalent permeability tensor on flow in naturally fractured porous media is discussed extensively in our companion paper (Weijermars and Khanal 2019a).

5.4 Effect of time-steps on accuracy of the results

This study uses the Eulerian particle tracking method described in Sect. 2.3 to calculate the streamlines, time of flight contours and DRV. The velocity of fluid particles at all points in a complex plane is calculated using Eq. (14). After calculating the velocity, a set of fluid particles is displaced from their initial positions to a new location based on Eq. (15). The position of a particle at a certain arbitrary time is determined by (a) the position of the particle at an earlier time-step, (b) the velocity at that position and (c) the time-step used and for which the velocity is assumed to be constant. Each of these parameters is inter-related, and ideally, the time-step needs to be continually updated based on the velocities and positions of the particles at a particular time. For example, if the particles have a large velocity in a certain section of the flow domain, the time-step should be as small as computationally possible. This technique minimizes the error in the future positions of the particles in the subsequent time-step. If a small enough time-step is not chosen, the particle will overshoot its true path and land on an adjacent particle path, resulting in a significant error. However, when both the local velocity and the curvature of the particle paths are small, then a large time-step facilitates a rapid simulation with minimal error. The trial-and-error method implemented in this study can be improved by implementing an adaptive time-step selection process, which however is outside the scope of this study.

6 Conclusions

Development of unconventional reservoirs requires an extensive application of hydraulic fracture stimulation, inducing multiple transverse hydraulic fractures to enhance access to the reservoir. The flow to the hydraulic fractures may interact with natural fracture systems that are either originally present or newly opened in the matrix rock by the fracture treatment. When such natural fractures are present, complex drainage patterns may result. In preliminary fracture treatment studies, the presence of natural fractures is often ignored, due to the limited understanding and modeling limitations. When the natural fractures occur and are ignored or not included in the fracture treatment plan, the estimated drainage pattern and optimum well-spacing and fracture spacing become increasingly inaccurate. If possible, the characterization of natural fractures is necessary during the well-planning stage, because the spacing and length of hydraulic fractures need to interact optimally with the locations of natural fractures.

The interaction between the natural fractures of varying orientation and conductivity with induced fractures was analyzed on a small-scale (single hydraulic fracture, Sect. 3) and large-scale (multiple wells, Sect. 4) to determine their effects on the DRV. High-resolution study of the DRV using time of flight contours for fluid that moved into the hydraulic fractures of the producing well has become possible due to advances in complex analysis methods (CAM, see Weijermars and Khanal 2019b; van Harmelen and Weijermars 2018). Based on the results from the present study, the following conclusions can be drawn:

• 1. Natural fracture networks play a significant role in determining the reservoir region drained by hydraulically fractured wells. As such, the natural fractures should be included in hydraulic fracture simulation models (numerical or analytical) before fracture treatment as well as during history matching of production data to yield better agreement of simulation model with field data and generate more accurate predictions of future well performance.

• 2. The orientation of natural fractures plays a vital role when determining the DRV due to hydraulic fractures. The natural fractures oriented at 90° between individual hydraulic fractures (Fig. 5) results in a maximum shift of DRV toward the adjoining hydraulic fracture. The shift in DRV can lead to an increased interference between the hydraulic fractures of a single well.

• 3. The natural fractures (Fig. 15c, d) between two parent wells may leave certain areas between the natural fractures undrained due to flow channeling into the natural fractures, which bypasses the matrix blocks between such natural fractures. In contrast, when the natural fractures are oriented in the direction of the well (Fig. 16a–d), fewer undrained regions occur.

• 4. Although the secondary “natural” fractures may be formed due to hydraulic fracturing (and possibly mitigated), the location and position of primary natural fractures cannot be controlled. In any case, characterization of primary natural fractures, and induced secondary fractures isolated in the matrix may play a vital role during well planning and hydraulic fracture design. For example, a reservoir with highly conductive, but widely spaced, natural fractures needs closely spaced hydraulic fractures to avoid undrained matrix zones. Conversely, a reservoir with numerous natural fractures may suffice with fewer hydraulic fractures because the natural fractures will predominantly direct the matrix regions that will be drained.

The method presented in this study provides an efficient technique to simulate the flow in porous media. The method provides an accurate alternative to delineate the DRV compared to pressure depletion plots. The current technique is applicable only to single-phase two-dimensional oil reservoirs, which can be a major limitation for reservoirs with multiple heterogeneous layers. However, future work may include adoptions of our code to account for multiphase flow effects (Weijermars and Khanal 2019a). We also intend to apply the CAM fracture flow model to field cases and integrate the model in commercial reservoir software such that the DRV can be easily visualized and compared to pressure depletion plots. However, constraining the permeability and aperture of natural fractures may remain beyond the practical limits of contemporary fracture characterization tools for some time.