1 Introduction

Wellbore stability problems are major causes of non-productive drilling time and have been investigated by researchers for decades. Understanding wellbore behaviour plays an important role in many well operations during drilling and production. In general, wellbore instability occurs through changes in the original stress state due to rock removal, temperature change, changes of differential pressures as drawdown occurs, and many other factors. A significant number of available publications discuss wellbore stability (Frydman and da Fontoura 2000; Kårstad and Aadnøy 2005; Hawkes 2007; Pasic et al. 2007; Ahmed et al. 2009). However, these studies generally involve a single wellbore. Wells with multilateral junctions involve greater risk and require a detailed stability analysis. In fact, both junction instability and debris are the most common causes of failure in multilateral implementations (Brister 2000). Failures in multilaterals were reported in different fields across the globe, for example in the Statfjord field in the North Sea, East Wilmington field in California, Gulf of Mexico, and the UK sector of the North Sea (Hovda et al. 1998; Brister 1997; Brister 1997). There are various multilateral categories as defined by the Technology Advancement of MultiLaterals TAML (Chamber 1998; Westgard 2002). Most multilateral wells drilled since 1953 are Level 1 and Level 2 (Bosworth et al. 1998). The focus of this paper is to examine the stability of Level 1. In such type, both main and lateral wells are open holes. The junction is thus left uncased and unsupported. Level 1 is widely applied in Europe, Canada, USA, and the Middle East, with up to six laterals drilled from the mother bore. A multilateral well, if successful, can reduce the overall drilling cost by replacing several vertical wellbores. In addition, multilateral wells help increasing the recoverable reserves.

Previous work examining the stability of multilaterals was mostly focused on the drilling stage and from a mechanical point of view. Both elastic (Aadnøy and Edland 1999; Bargui and Abousleiman 2000) and plastic (Manríquez et al. 2004; Plischke et al. 2004) models have been used. However, stress state and stability risk will change at later production stages as the result of fluid flow and depletion. It is therefore necessary to consider the combined effect of fluid flow and mechanics. This paper is devoted to simulating the nonlinear rock behaviour due to the excavation process while drilling the main and lateral wells and due to fluid flow at the vicinity of the junction during the production phase.

Wellbore failure can occur at different stages of operations. For example, wellbore collapse might happen during drilling and/or during production. The drilling process in subsurface rock formations results in the removal of already stressed in situ rock material. As a result, the stress originally carried by the removed rock mass is redistributed to the surrounding rock around the wellbore. This stress redistribution causes stress concentrations higher than the original in situ earth stresses. If the induced stresses near the wellbore exceed the strength of the surrounding rock, wellbore failure occurs. The production process also changes the effective stresses around the wellbore. Such changes in effective stress can be significant for high drawdown pressures and trigger wellbore failure. Apart from the stress concentrations at the wellbore wall due to geometrical effects, formation anisotropy, the presence of bedding planes, fractures, discontinuities, preferred grain alignment and orientation can also result in localized failure, which needs to be differentiated from the stress-induced wellbore failure.

Because of their structural geometry, multilateral junctions are more susceptible to failure than single wellbores and are likely to develop higher differential stresses. It is therefore important to take into account all the factors contributing to wellbore instability, such as well geometry, magnitude of in situ stresses, direction of the in situ horizontal stresses, pore pressure, mechanical properties and fluid flow properties.

In this context, the Mohr–Coulomb failure criterion with a hyperbolic hardening is used to describe the mechanical behaviour of sandstone. The model parameters are identified from conventional triaxial compression tests. Comparisons between numerical predictions and triaxial compression test data are presented to demonstrate the capabilities of the constitutive model to describe the main mechanical features of sandstone. Numerical simulations of multilateral junction stability experiments are conducted to examine the capabilities of the model to predict the failure zone around the junction area. An open-hole multilateral well was simulated to investigate wellbore and junction stability during drilling and production.

2 Mohr–Coulomb with hyperbolic hardening constitutive model

In this section, the Mohr–Coulomb elastoplastic model with a hyperbolic hardening is used. The incremental total strain tensor, \({\text{d}}\underline{\underline{\varepsilon }}\), is decomposed into an elastic part (reversible), \({\text{d}}\underline{\underline{\varepsilon }}^{\text{e}}\), and a plastic part (irreversible), \(\text{d} \underline{\underline{\varepsilon }}^{\text{p}}\):

$${\text{d}}\underline{\underline{\varepsilon }} = {\text{d}}\underline{\underline{\varepsilon }}^{\text{e}} + {\text{d}}\underline{\underline{\varepsilon }}^{\text{p}}$$
(1)

where \({\text{d}}\underline{\underline{\varepsilon }}\) is the incremental total strain tensor, \({\text{d}}\underline{\underline{\varepsilon }}^{\text{e}}\) is the incremental elastic strain tensor, and \(\text{d} \underline{\underline{\varepsilon }}^{\text{p}}\) is the incremental plastic strain tensor.

Sandstone is considered as a porous medium saturated with one fluid phase. The general framework of a saturated medium defined initially by Biot (1941; 1955; 1973) and then by Coussy (1991; 1995; 2004) was adopted. Considering that stresses are negative and pressure is positive for compression, the effective stress tensor of a saturated porous medium, under isothermal conditions, is written as:

$$\underline{\underline{\sigma }}^{\prime } = \underline{\underline{\sigma }} + \alpha p\underline{\underline{\delta }}$$
(2)

The poro-elastic behaviour is written as:

$${\text{d}}\underline{\underline{\sigma }} = \left( {K_{\text{b}} - \frac{2}{3}G} \right){\text{d}}\underline{\underline{{\varepsilon^{\text{e}} }}} + 2G{\text{d}}\underline{\underline{{\varepsilon^{\text{e}} }}} - \alpha \text{d}p\underline{\underline{\delta }}$$
(3)

where \(\underline{\underline{\sigma }} ,\underline{\underline{\sigma }}^{{\prime }} ,\alpha ,p,{\text{d}}\underline{\underline{\sigma }} ,{\text{d}}\underline{\underline{{\varepsilon^{\text{e}} }}} \;{\text{and}}\;\delta\) denote, respectively, the total stress tensor, effective stress tensor, Biot’s coefficient, pore pressure, incremental stress tensor, incremental elastic strain tensor, and the Kronecker delta tensor. \(K_{\text{b}}\) and G are bulk modulus and shear modulus, respectively. Assuming that Terzaghi’s effective stress (Terzaghi 1943) is valid for elastic and plastic behaviour, Biot’s coefficient was considered equal to 1.

The plastic deformation of the sandstone is described by a plastic yield surface, plastic potential, hardening law, and a failure surface.

The Mohr–Coulomb failure surface adopted in this paper reads as (Chen and Saleeb 1982; Clausen et al. 2010)

$$F = \frac{{I_{1} '}}{3}\sin \phi_{\text{f}} + \sqrt J_{2} \left( {\cos \theta - \frac{{\sin \theta \sin \phi_{\text{f}} }}{\sqrt 3 }} \right) - C_{\text{f}} \cos \phi_{\text{f}} = 0$$
(4)

where \(C_{\text{f}}\) and \(\phi_{\text{f}}\) are the cohesion and friction angle at failure; I1′ represents the first invariant of the effective stress tensor σ ′ ij ; J2 is the second invariant of the deviatoric stress tensor Sij, and θ is the Lode angle which describes the variation of yield stress with loading direction in the deviatoric plane. The three invariants are defined by

$$I_{1} ' =\text{ tr}(\underline{\underline{\sigma '}} ),\,J_{2} = \frac{1}{2}S_{ij} S_{ij} ,S_{ij} = \sigma_{ij} - \frac{{I_{1} }}{3}\delta_{ij} ,\theta = \frac{1}{3}\arcsin \left( {\frac{{ - 3\sqrt 3 J_{3} }}{{2\sqrt {J_{2}^{3} } }}} \right)\;{\text{and}}\;J_{3} = \frac{1}{3}S_{ij} S_{jk} S_{ki}$$
(5)

By introducing plastic hardening laws in Eq. (2), the plastic yield surface can be expressed in the following functional form (Wang et al. 2012)

$$f_{\text{p}} = \frac{{I_{1} '}}{3}\sin \phi_{\text{p}} + \sqrt J_{2} \left( {\cos \theta - \frac{{\sin \theta \sin \phi_{\text{p}} }}{\sqrt 3 }} \right) - C_{\text{p}} \cos \phi_{\text{p}} = 0$$
(6)

where \(f_{\text{p}}\) is the plastic yield surface, \(\phi_{\text{p}}\) is the friction in the plastic hardening phase, \(C_{\text{p}}\) is the cohesion in the plastic hardening phase.

The classical Mohr–Coulomb model assumes a linear hardening law, by which cohesion changes from an initial value at the yield point into a final value at failure. In addition, the friction angle is taken as constant. However, laboratory evidence showed that cohesion and friction angle evolve nonlinearly in the hardening phase, wherein the values of both cohesion and friction angle (C, ϕ), vary from (C0, ϕ0) at the initial yield state to (Cf, ϕf) when the failure surface is reached: \(\left( {f_{\text{p}} \to F} \right)\). Therefore, hyperbolic hardening laws are applied that capture this behaviour of the cohesion and friction coefficient more accurately (Mohamad-Hussein and Shao 2007a; b):

$$C_{\text{p}} = C_{0} + \left( {C_{\text{f}} - C_{0} } \right)\frac{{\xi^{\text{p}} }}{{H_{1} E + \xi^{\text{p}} }}$$
(7)
$$\tan \left( {\phi_{\text{p}} } \right) = \tan (\phi_{0} ) + \left[ {\tan (\phi_{\text{f}} ) - \tan (\phi_{0} )} \right]\frac{{\xi^{\text{p}} }}{{H_{2} E + \xi^{\text{p}} }}$$
(8)

where \(\xi^{\text{p}}\) is the generalized equivalent plastic strain, E is Young’s modulus, H1 and H2 are two parameters that control the kinetics of cohesion and friction coefficient in the hardening phase, respectively.

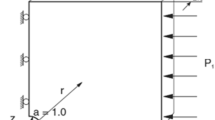
Figure 1 shows the yield and failure surfaces in the stress plane.

Fig. 1
figure 1

Illustration of the yield and failure surface in the stress plane

Full size image

Triaxial tests carried out on sandstone show plastic volume dilation caused by the imposed deviatoric stress. The transition from plastic compressibility to plastic dilation is described by a non-associated flow rule. The plastic flow rule is controlled by the plastic potential which is given by the same equation as the failure surface but with the friction angle replaced by the dilation angle (Smith and Griffiths 2005; Fjær et al. 2008). It is expressed as

$$Q = \frac{{I_{1} '}}{3}\sin \psi_{\text{p}} + \sqrt J_{2} \left( {\cos \theta - \frac{{\sin \theta \sin \psi_{\text{p}} }}{\sqrt 3 }} \right) - C_{\text{p}} \cos \psi_{\text{p}} = 0$$
(9)

where Q is the plastic potential, \(\psi_{\text{p}}\) is the dilation angle, which describes the transition between plastic compressibility and the plastic dilatancy.

The plastic strain increment is calculated from the following expression (Owen and Hinton 1980; Smith and Griffiths 2005)

$$\text{d}\underline{\underline{\varepsilon }}^{\text{p}} = \text{d}\lambda \frac{\partial Q}{{\partial \underline{\underline{\sigma '}} }}$$
(10)

\(\text{d} \lambda\) is the plastic multiplier that can be determined from the consistency condition:

$${\text{d}}f_{\text{p}} = \frac{{\partial f_{\text{p}} }}{{\partial \underline{\underline{\sigma }}^{\prime } }}:{\text{d}}\underline{\underline{\sigma }}^{\prime } + \frac{{\partial f_{\text{p}} }}{{\partial \xi^{\text{p}} }}{\text{d}}\xi^{\text{p}} = 0$$
(11)

The generalized plastic distortion \({\text{d}}\xi^{\text{p}}\) can be deduced as follows:

$${\text{d}}\xi^{\text{p}} = h\text{d}\lambda;\;h = \sqrt {\frac{2}{3}{\text{dev}}\left( {\frac{\partial Q}{{\partial \underline{\underline{\sigma }}^{\prime } }}} \right):{\text{dev}}\left( {\frac{\partial Q}{{\partial \underline{\underline{\sigma }}^{\prime } }}} \right)}$$
(12)

where \({\text{dev}}\left( {\underline{\underline{x}} } \right)\) is the deviatoric part of the tensor x.

The rate form of the constitutive equations reads:

$${\text{d}}\underline{\underline{\sigma }} = C:\left( {\underline{\underline{\varepsilon }} - \underline{\underline{\varepsilon }}^{\text{e}} } \right) - \alpha {\text{d}}p\underline{\underline{\delta }}$$
(13)

Using Eqs. (12) and (13) in Eq. (11), the plastic multiplier is calculated as:

$$\text{d}\lambda = \frac{{\frac{{\partial f_{\text{p}} }}{{\partial \underline{\underline{\sigma }}^{\prime } }}:C:\text{d}\underline{\underline{\varepsilon }} }}{{\frac{{\partial f_{\text{p}} }}{{\partial \underline{\underline{\sigma }}^{\prime } }}:C:\frac{\partial Q}{{\partial \underline{\underline{\sigma }}^{\prime } }} - \frac{{\partial f_{\text{p}} }}{{\partial \xi^{\text{p}} }}\sqrt {\frac{2}{3}{\text{dev}}\left( {\frac{\partial Q}{{\partial \underline{\underline{\sigma }}^{\prime } }}} \right):{\text{dev}}\left( {\frac{\partial Q}{{\partial \underline{\underline{\sigma }}^{\prime } }}} \right)} }}$$
(14)

where \(C\) is the fourth order stiffness tensor, ɛ is the total strain.

3 Computation procedure of the constitutive model

In the context of the finite element method, nodal displacements and pore pressure are the main unknowns. The loading path is divided into several load steps. In each load step, the governing equations are verified in the global system in weak form. The local integration of the constitutive model is composed of the elastic prediction and the plastic correction. For each loading increment, an increment of strain is prescribed at each gauss point; the local integration of the constitutive equation consists of updating the stress, plastic strain, and internal variables according to loading history and current increments of strains.

  1. 1.

    At the n-th load step, input the converged values of \({\underline{\underline{\sigma }}_{n - 1} , \underline{\underline{\varepsilon }}_{n - 1}^{\text{p}} , \underline{\underline{\varepsilon }}_{n - 1}^{\text{e}} \;{\text{and}}\;\underline{\underline{\xi }}_{n - 1}^{\text{p}}}\) at (n − 1)-th step

  2. 2.

    Given that \({\text{d}}\underline{\underline{\varepsilon }}_{n}\) is the prescribed strain at the n-th load step

  3. 3.

    Make elastic prediction: \(\underline{\underline{{\tilde{\sigma }}}}_{n} = \underline{\underline{\sigma }}_{n - 1} + {\text{d}} \underline{\underline{{\tilde{\sigma }}}}_{n} = \underline{\underline{\sigma }}_{n - 1} + C:{\text{d}}\underline{\underline{\varepsilon }}_{n}\)

    From the elastic prediction, it is worth checking the corresponding behaviour. In practice, two cases can be distinguished with respect to the plastic criterion:

    • If \(f_{\text{p}} \left( {\underline{\underline{{\tilde{\sigma }}}}_{n} ,\xi_{n - 1}^{\text{p}} } \right) < 0\), then the stress state is within the elastic range and in this case, the elastic prediction is then taken as the real solution;

    • If \(f_{\text{p}} \left( {\underline{\underline{{\tilde{\sigma }}}}_{n} ,\xi_{n - 1}^{\text{p}} } \right) \ge 0\), then the stress state is outside or on the yield surface. In this case, the plastic mechanism is violated, and therefore, plastic correction is needed to make the plastic stress state admissible.

  4. 4.

    Plastic correction:

When the plastic mechanism is violated, it is necessary to correct the stress state. The plastic multiplier is determined from Eq. (13). Then, the increment of plastic strain is computed from Eq. (9). After updating the variable of hardening law, one can determine the increment of updated stresses: \(\underline{\underline{\sigma }}_{n} = \underline{\underline{{\tilde{\sigma }}}}_{n} - C:\text{d}\underline{\underline{\varepsilon }}_{n}^{\text{p}}\)

The algorithm of integration of the constitutive model is presented in Fig. 2.

Fig. 2
figure 2

Algorithm of local integration of the constitutive model

Full size image

4 Hydromechanical coupling in saturated porous media

For an isotropic material, under isothermal conditions, the poro-elastic behaviour follows Eq. (3). The incremental pore pressure is written as:

$${\text{d}}p = M\left[ { - \alpha {\text{d}}\varepsilon_{\text{v}}^{\text{e}} + \frac{{{\text{d}}m}}{{\rho_{\text{f}} }}} \right]$$
(15)

where M is Biot’s modulus, \(\varepsilon_{\text{v}}^{\text{e}}\) is the elastic volumetric strain, \({\text{d}}m\) represents the change in fluid mass per unit initial volume, and \(\rho_{\text{f}}\) is the volumetric mass of fluid. Biot’s coefficient α (considered equal to 1 in this study) and Biot’s modulus \(M\) are two parameters that characterize the poro-elastic coupling. Those two poro-elastic coupling parameters are related to the properties of the constituents of the porous medium and expressed by:

$$\alpha = 1 - \frac{{K_{\text{b}} }}{{K_{\text{m}} }}$$
(16)
$$\frac{1}{M} = \frac{\alpha - \varphi }{{K_{\text{m}} }} + \frac{\varphi }{{K_{\text{f}} }}$$
(17)

where \(K_{\text{m}}\) and \(K_{\text{f}}\) are the compressibility modulus of the solid matrix and the fluid, respectively. The variable φ represents the total porosity of the porous medium.

The governing equations for the hydromechanical coupling system in saturated porous media include Darcy’s law, mass conservation of fluid, and the mechanical equilibrium:

  • Darcy’s law:

    $$\frac{{\vec{w}_{\text{f}} }}{{\rho_{\text{f}} }} = \frac{k}{{\mu_{\text{f}} }}\left( { - \vec{\nabla }p + \rho_{\text{f}} \vec{g}} \right)$$
    (18)

  • Mass conservation equation for fluid:

    $$\frac{\partial m}{\partial t} = - {\text{div}}\left( {\vec{w}_{\text{f}} } \right)$$
    (19)

  • Momentum balance equation:

    $${\text{div}}\left( {\underline{\underline{\sigma }} } \right) + \rho_{\text{m}} \vec{g} = 0$$
    (20)

  • where \(\vec{w}_{\text{f}}\) is the vector of fluid flow rate, k is the intrinsic permeability, \(\mu_{\text{f}}\) is the fluid dynamic viscosity, \(\vec{g}\) is the gravitational acceleration, and \(\rho_{\text{m}}\) is the volumetric mass of sandstone.

    By applying Darcy’s law [Eq. (18)] to the mass conservation [Eq. (19)] and combining the constitutive [Eq. (3)] in saturated porous media, the following generalized liquid diffusion equation can be obtained:

    $$\frac{k}{{\mu_{\text{f}} }}{\text{div}}\left( {\vec{\nabla }p} \right) = \frac{1}{M}\frac{\partial p}{\partial t} + \alpha \frac{{\partial \varepsilon_{v}^{\text{e}} }}{\partial t}$$
    (21)

Using a suitable finite element method such as the Galerkin method to the diffusion equation, the numerical resolution of the hydromechanical boundary value problem is obtained.

5 Determination of model parameters

The mechanical behaviour of the rock formation is mainly characterized by nine elastic and strength parameters. These parameters were determined from conventional triaxial compression tests performed on Vosges sandstone and reported by Khazraei (1995).

The initial elastic properties (Young’s modulus and Poisson’s ratio) were identified from the linear part of the behaviour curve in a triaxial compression test.

Figure 3 illustrates the linear section and the initial Young’s modulus on the stress–strain curve and determined as

Fig. 3
figure 3

Illustration of the linear elastic region and initial Young’s modulus

Full size image
$$E = \frac{\Delta q}{{\Delta \varepsilon_{\text{axial}} }}$$
(22)
$$\nu = - \frac{{\Delta \varepsilon_{\text{radial}} }}{{\Delta \varepsilon_{\text{axial}} }}$$
(23)

where q is the deviatoric stress, \(\varepsilon_{\text{axial}}\) is the axial strain, and \(\varepsilon_{\text{radial}}\) is the radial strain.

For the determination yield and strength properties, Mohr circles were plotted at yield and peak points for the individual triaxial tests. Then, linear lines tangent to the circles were traced representing the yield and failure surfaces, as illustrated in Fig. 4. The initial cohesion and failure cohesion are then computed from the intersection of the yield and failure surfaces with the deviatoric stress axis, respectively. The initial and failure friction angles are determined from the slope of the yield and failure surface, respectively.

Fig. 4
figure 4

Illustration of the yield and failure surfaces

Full size image

The hardening parameters H1 and H2 are determined by computing the cohesion and the coefficient of friction angle for selected points on stress–strain curves in the triaxial compression tests. Then, hyperbolic lines are plotted to fit the experimental points to obtain representative values for H1 and H2. The evolution of both cohesion and coefficient of friction with plastic shear strain, within the hardening phase, is shown in Fig. 5.

Fig. 5
figure 5

Evolution of cohesion (left) and coefficient of friction (right) with plastic shear strain within the hardening phase

Full size image

The values of the model parameters are listed in Table 1.

Table 1 Model parameters for Vosges sandstone
Full size table

6 Simulations of triaxial compression tests

In this section, the simulations of triaxial compression tests are presented for Vosges sandstone.

Figure 6 shows the comparisons of experimental data and numerical simulations for triaxial compression tests with confining pressures of 5, 10, 20, and 40 MPa. There is a reasonable agreement between experimental data and numerical simulations for tests with confining pressure of 5, 10, and 20 MPa. The model is able to predict the main features of sandstone behaviour such as elasticity, yield, hardening, and failure. However, for the test with high confining pressure (40 MPa for instance), the error between the numerical response and the data becomes significant. This is mainly related to the fact that failure of Vosges sandstone depends on confining pressure (or equivalently on the mean stress). Therefore, linear failure surfaces such as the classic Mohr–Coulomb criterion overestimate rock failure at high confining pressure. As depicted in Fig. 4, the difference between the linear failure surface and Mohr circle becomes significant with the increase in confining pressure. Mohamad-Hussein and Shao (2007b) proposed a quadratic function to describe the failure of sandstone. With such a numerical model, the mechanical behaviour for Vosges sandstone could be predicted for all range of confining pressures.

Fig. 6
figure 6

Comparison of numerical simulations and experimental data in triaxial compression tests with confining pressure of 5, 10, 20, and 40 MPa

Full size image

7 Modelling of multilateral junction stability experiments

True triaxial tests were carried out for parent and lateral holes. The tested rock is Vosges sandstone. The tests were performed at University of Lille and reported by Papanastasiou et al. (2002). Cubic blocks of dimensions 40 cm × 40 cm × 40 cm were used. Each block consisted of a parent hole of 37 mm diameter and a lateral hole of 31 mm diameter. The inclination of the lateral hole from the parent hole was assumed to be 22.5°. The block samples were subjected to hydrostatic stresses applied at the external boundaries. Deformation and failure of the holes was monitored at different stress levels of 27, 36, and 45 MPa.

Figure 7 shows the geometric configuration of the test and illustrates the loading steps.

Fig. 7
figure 7

Geometric configuration of the test (left) and loading steps (right)

Full size image

A three-dimensional (3D) finite element model has been built to simulate the experiments.

Figure 8 shows the 3D near-wellbore model and the finite element grid. The total number of elements is 650,000 first-order tetrahedra.

Fig. 8
figure 8

3D near-wellbore model (left) and the 3D grid (right)

Full size image

Figures 9 and 10 present the comparison between experimental results and numerical simulations. The results show the yield/failure zone occurring around the multilateral junction for 27, 36, and 45 MPa external stresses. The results of the numerical simulations match with respect to the level of applied stress and the junction yield/failure occurrence. Due to the increase in the external stress, a yield zone develops around the junction area at approximately 27 MPa external stress. This is followed by a failure zone around the junction with a further increase in external stress due to the development and coalescence of cracks (36 MPa external stress). The failure zone intensifies and grows at a higher stress level of 45 MPa. It is important to note that for low external stress, the failure pattern is in reasonable agreement between the numerical and experimental results. For example, when the external stress is 36 MPa, the failure pattern is generally localized at the intersection of the two holes and yielding occurs at some locations around the holes. However, there exist discrepancies of failure pattern for high external stress (45 MPa). The experimental result shows a wider failure pattern that occurs around the two holes. This could be due to:

Fig. 9
figure 9

Experimental results (Papanastasiou et al. 2002): failed area around the multilateral junction for 27 MPa stress (left), 36 MPa stress (middle) and 45 MPa stress (right)

Full size image
Fig. 10
figure 10

Numerical simulation results. Distribution of maximum plastic strain showing failed area around the multilateral junction for 27 MPa stress (left), 36 MPa stress (middle) and 45 MPa stress (right)

Full size image

  • Usage of linear failure surface: As has been stipulated in the previous section, the range of error between the simulation results and experimental data increases with the increase in confining pressure due to the usage of a linear failure surface;

  • Heterogeneity of material: There might be variability of properties in the sample due to microstructures/inclusions, whereas homogenous mechanical properties were used in the numerical modelling.

In general, this example demonstrates the predictive power of the numerical method to simulate multilateral junction stability analysis problems for different stress levels.

8 Numerical example of multilateral junction stability

The numerical simulations of the triaxial compression tests and the multilateral junction stability tests show the capability of the model to predict sandstone mechanical behaviour. Therefore, this section is devoted to numerical modelling of multilateral junction stability. The key objective is to examine the junction stability during drilling and production from open-hole wells.

A three-dimensional (3D) near-wellbore model encompassing the main well of 15 cm diameter and the lateral well of 10 cm diameter was constructed. The junction is located in a normal stress regime zone at a depth of 1000 m below ground level. Therefore, assuming hydrostatic pore pressure gradient and formation unit weight of 22.6 kPa/m, the preproduction initial stresses and initial pore pressure were taken as

$$\left\{ \begin{array}{l} \sigma_{\text{v}}^{00} = 22.6\;{\text{MPa}} \hfill \\ \sigma_{{ \hbox{Hmax} }}^{00} = 0.9\sigma_{\text{v}}^{00} \hfill \\ \sigma_{{ \hbox{hmin} }}^{00} = 0.8\sigma_{\text{v}}^{00} \hfill \\ P^{00} = 10\;\text{MPa} \hfill \\ \end{array} \right.$$
(24)

where \(\sigma_{\text{v}}^{00}\) is the pre-drill initial vertical stress, \(\sigma_{{ \hbox{Hmax} }}^{00}\) is the pre-drill initial maximum horizontal stress, \(\sigma_{{{ \hbox{hmin} }}}^{00}\) is the pre-drill minimum horizontal stress, and P00 is the initial pore pressure.

The maximum horizontal stress was aligned along north–south (y-axis).

The modelling was performed in three main phases:

  1. 1.

    In the initial stress step, the pre-drilling stresses and pore pressure are imposed to the grid.

  2. 2.

    In the wellbore excavation step, the material inside the wellbore is removed. The mud weight applied inside the wellbore is taken equal to the pore pressure.

  3. 3.

    In the production step, production is simulated by applying a drawdown pressure of 3 MPa at the wellbore wall for a period of 2 days. The pore pressure change is assumed to be zero at the far boundary of the model. Transient flow is considered in the production step.

The 3D wellbore grid, the distribution of cells around the wellbore, and the main and lateral well grid are shown in Fig. 11.

Fig. 11
figure 11

3D wellbore grid (left), top view (middle) and main and lateral well grid (right)

Full size image

Figure 12 shows the distribution of pore pressure change away from the wellbore wall obtained from transient flow simulation after 1 day and 2 days of production. Due to the applied drawdown pressure at the wellbore wall, pore pressure tends to change around the main and lateral wells. The amount of change and distance it propagates depend on the reservoir permeability.

Fig. 12
figure 12

Pore pressure change profile in MPa along a horizontal line away from the wellbore wall for various times

Full size image

Figure 13 illustrates the distribution of pore pressure change around the wellbores along a vertical cross section after 2 days of production.

Fig. 13
figure 13

Distribution of pore pressure change in MPa along a vertical cross section after 2 days of production (left) and selected horizontal cross sections (right)

Full size image

Figure 14 illustrates the distribution of pore pressure changes around the wellbores at different horizontal cross sections. In addition, the profiles depicting the pore pressure change are summarized in Fig. 15. The decrease in pore pressure around the wellbores gives rise to changes in effective stresses. If the changes in effective stresses are significant, formation damage might occur, and this will cause instability around the wellbores. To illustrate the influence of fluid flow due to hydrocarbon production, the profiles of shear stress have been plotted (Fig. 16) along the main well after drilling (no fluid flow) and after 2 days of production (with fluid flow). The profiles of shear stress show shear stress concentration at the location of the multilateral junction. The average increase in shear stress due to production with respect to drilling state along the entire well is approximately 11.5% (Fig. 17).

Fig. 14
figure 14

Distribution of pore pressure change in MPa at different horizontal cross sections after 2 days of production

Full size image
Fig. 15
figure 15

Pore pressure change profiles in MPa along a horizontal line for different horizontal cross sections after 2 days of production

Full size image
Fig. 16
figure 16

Profile of shear stress in MPa along the main well after drilling and after production

Full size image
Fig. 17
figure 17

Percentage of shear stress increase due to production

Full size image

This comparison shows clearly the influence of fluid flow on the shear stress distribution. Overall, shear stress increases around the wellbore where the pore pressure change is the highest.

Plastic strain representing irreversible deformation is a good indicator for permanent rock damage.

Figure 18 presents the plastic strain distribution along horizontal cross sections.

Fig. 18
figure 18

Distribution of maximum plastic principal strain in percent at different cross sections

Full size image

The numerical results are illustrated in terms of a failure value which is calculated from the function F in Eq. (2). The failure value shown in Fig. 19 is an indicator of the state of stress within the formation. A zero-failure value indicates rock failure, so the state of stress lies on the Mohr–Coulomb failure envelope. On the other hand, a negative failure value indicates that the state of stress is below the failure envelope, i.e. the material has not failed. The highest formation damage occurs at the locations near the junction where the two wells intersect. The computed plastic strain profile shown in Fig. 20 demonstrates that the extent of the damage zone is approximately 30 cm, which is in the order of twice the diameter of the main well.

Fig. 19
figure 19

Distribution of failure value in MPa showing failure zone at the junction (left) and the failure value profile along the main well

Full size image
Fig. 20
figure 20

Maximum plastic principal strain profile along a horizontal line AB

Full size image

High shear stress concentration around the multilateral junction and drilling-induced damage represent increased risk towards rock failure around the wellbore. Fluid flow due to hydrocarbon production and resulted pore pressure depletion further increase the stress concentration and therefore may lead to failure at the junction. It is important to note that the production time is assumed to be short in this example. For longer periods, fluid flow will contribute to further increase formation damage around the junction. In summary, the results show the development of a localized failure zone proximate to the area where the two wellbore tracks join together, particularly on the side with a sharp approaching angle, which would significantly increase the risk of wellbore collapse at the junction.

9 Conclusions

A Mohr–Coulomb criterion with a hyperbolic hardening model is used to model the behaviour of sandstone. The numerical model has been tested and validated with laboratory test data. The rock mechanical test data include triaxial compression tests and multilateral junction stability. The comparison of the numerical simulations and the experimental data confirms that the model can reproduce correctly the main mechanical features of sandstone such as elasticity, yield, hardening, and failure. In addition, the model is able to reproduce the failure pattern at the multilateral junction for different levels of applied stresses.

A numerical example to examine multilateral junction stability in open holes during drilling and production is presented. The oil production process is simulated by applying a drawdown pressure at the walls of the main and lateral wells. The results show the development of localized failure zone proximate to the area where the two wellbore tracks join, particularly on the side with sharp approaching angle, which would significantly increase the risk of wellbore collapse at the junction. High shear stress concentration around the multilateral junction and drilling-induced damage represent increased risk towards rock failure around the wellbore. Fluid flow due to hydrocarbon production and resulting pore pressure depletion further increase the stress concentration and therefore may lead to failure at the junction.

This study demonstrates that numerical modelling of the near-wellbore region can be used to predict borehole stability before and during production for complex drilling scenarios including sidetracks from a main well.