The Umwelt of an embodied agent—a measure-theoretic definition

Abstract

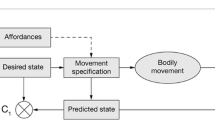
We consider a general model of the sensorimotor loop of an agent interacting with the world. This formalises Uexküll’s notion of a function-circle. Here, we assume a particular causal structure, mechanistically described in terms of Markov kernels. In this generality, we define two $\sigma$-algebras of events in the world that describe two respective perspectives: (1) the perspective of an external observer, (2) the intrinsic perspective of the agent. Not all aspects of the world, seen from the external perspective, are accessible to the agent. This is expressed by the fact that the second $\sigma$-algebra is a subalgebra of the first one. We propose the smaller one as formalisation of Uexküll’s Umwelt concept. We show that, under continuity and compactness assumptions, the global dynamics of the world can be simplified without changing the internal process. This simplification can serve as a minimal world model that the system must have in order to be consistent with the internal process.

Appendix: state reduction and quotient construction

Let $(X, \mathcal {F})$ be a measurable space. The atom of $\mathcal {F}$ containing $x\in X$ and the set of atoms of $\mathcal {F}$ are defined as

$$\begin{aligned}{}[x]_{\mathcal {F}} := \bigcap _{x\in F\in \mathcal {F}} F \quad \mathrm{and} \quad {{\mathrm{At}}}(\mathcal {F}) := \bigl \{\, [x]_{\mathcal {F}} | x\in X \,\bigr \}. \end{aligned}$$

Note that if $\mathcal {F}$ is countably generated, $[x]_{\mathcal {F}}$ is a measurable set, $[x]_{\mathcal {F}}\in \mathcal {F}$. In general, however, $[x]_{\mathcal {F}}$ need not be measurable. We recall Blackwell’s theorem.

Blackwell’s theorem Let X be a Souslin space and $\mathcal {F}\subseteq \mathfrak {B}(X)$ a countably generated sub- $\sigma$ -algebra of the Borel $\sigma$ -algebra. Then

$$\begin{aligned} \mathcal {F}= \Bigl \{\, F\in {\mathfrak {B}}(X) | F=\bigcup _{x\in F} [x]_{\mathcal {F}} \,\Bigr \}. \end{aligned}$$

Corollary 11

Let X be a Souslin space, $\mathcal {F}\subseteq {\mathfrak {B}}(X)$ a countably generated $\sigma$-algebra, and $f: X\rightarrow \mathbb {R}$ measurable. Then f is $\mathcal {F}$-measurable if and only if it is constant on the atoms of $\mathcal {F}$.

According to Blackwell’s theorem, a countably generated sub-$\sigma$-algebra of a Souslin space X is uniquely determined by the set of it atoms. ${{\mathrm{At}}}(\mathcal {F})$ is a partition of X into ${\mathfrak {B}}(X)$-measurable sets. Note, however, that not every partition of X into measurable sets is the set of atoms of a countably generated sub-$\sigma$-algebra of ${\mathfrak {B}}(X)$.

Given any measurable space $(X, \mathcal {F})$, we can define the quotient space $X_\mathcal {F}$ as the set ${{\mathrm{At}}}(\mathcal {F})$ of atoms of $\mathcal {F}$ equipped with the final $\sigma$-algebra $\mathcal {X}_{\mathcal {F}}$ of the canonical projection $[\,\cdot \,]_{\mathcal {F}}: X\rightarrow {{\mathrm{At}}}(\mathcal {F})$. Then a set $B\subseteq X_\mathcal {F}$ of atoms is by definition measurable iff $\bigcup B=\bigcup _{[x]_{\mathcal {F}}\in B} [x]_{\mathcal {F}} \in \mathcal {F}$. Note that, obviously, $B\mapsto \bigcup B$ is a complete isomorphism of boolean algebras from $\mathcal {X}_{\mathcal {F}}$ onto $\mathcal {F}$. The following lemma follows easily from the standard theory of analytic measurable spaces and is one of the reasons why Souslin spaces, rather than Polish spaces, are the “right” class of spaces to work with in our setting.

Lemma 12

Let X be a Souslin space and $\mathcal {F}\subseteq {\mathfrak {B}}(X)$ a sub-$\sigma$ -algebra. Then $\mathcal {X}_{\mathcal {F}}$ is the Borel $\sigma$-algebra of some Souslin topology on $X_\mathcal {F}$ if and only if $\mathcal {F}$ is countably generated.